Generalized Ordinary Differential Equation Models

Abstract

Existing estimation methods for ordinary differential equation (ODE) models are not applicable to discrete data. The generalized ODE (GODE) model is therefore proposed and investigated for the first time. We develop the likelihood-based parameter estimation and inference methods for GODE models. We propose robust computing algorithms and rigorously investigate the asymptotic properties of the proposed estimator by considering both measurement errors and numerical errors in solving ODEs. The simulation study and application of our methods to an influenza viral dynamics study suggest that the proposed methods have a superior performance in terms of accuracy over the existing ODE model estimation approach and the extended smoothing-based (ESB) method.

1 Introduction and Motivating Example

The use of mathematical modeling in various disciplines (e.g., biomedical research) has led to significant scientific findings (e.g. Ho et al., 1995; Perelson et al., 1997) and its importance is thus being gradually recognized in statistical research communities. In particular, ordinary differential equation (ODE) models have been playing a prominent role in physics, engineering, econometrics, biomedical sciences among other scientific fields. Time-course data for fitting ODE models are increasingly available and attracting greater attention especially from biomedical research communities (Perelson and Nelson, 1999; Nowak and May, 2000; Baccam et al., 2006; Lee et al., 2009; Miao et al., 2010). However, in contrast to the maturity of various mathematical techniques for studying numerical or theoretical properties of ODE models (e.g., sensitivity analysis and bifurcation analysis), the statistical inference methodologies and corresponding theoretical development for ODE models are still on the way. Further investigation of parameter estimation and statistical inference for ODE models is desirable.

Most of the early work on estimation methods for ODE models were developed in the nonlinear least squares (NLS) realm that requires repeatedly solving ODEs (Hemker, 1972; Li et al., 2005; Xue et al., 2010). To reduce the high computing costs associated with the standard NLS method, the smoothing-based approach was proposed (Varah, 1982; Brunel, 2008; Liang and Wu, 2008; Chen and Wu, 2008a,b; Wu et al., 2012), which avoids solving ODEs numerically. Such methods can be much more efficient than the standard LS method in terms of computing costs, however, at a price of losing estimation accuracy (Liang et al., 2010). An alternative method was proposed by Ramsay (1996), called the principal differential analysis (PDA). Ramsay et al. (2007) extended the PDA approach. A few studies also investigated the estimation methods for specific types of ODE models, for example, ODE models with time-varying parameters (Li et al., 2002; Chen and Wu, 2008b; Liang et al., 2010; Xue et al., 2010) or mixed-effect ODE models for longitudinal data (Li et al., 2002; Huang et al., 2006).

Usually, the observations for fitting ODE models are deemed to be continuous since ODEs can only model dynamics of continuous variables. However, in many practical applications, the data generated by a particular technology or a biomedical assay may not be continuous although such data can be linked to a set of continuous variables whose dynamic interactions can be modeled by ODEs. A motivating example is the recent study on within-host immune responses against influenza A virus (IAV) infection reported in Miao et al. (2010). In this study, mouse lung was harvested post-influenza infection at multiple time points, and its homogenates were sequentially diluted and inoculated into embryonated hen eggs in order to determine the 50% egg infectious dose (called EID₅₀). For each dilution factor, the binary responses of multiple eggs (infected or not infected) by the lung homogenates were recorded. That is, the raw data were either one (the egg was infected) or zero (the egg was not infected). However, due to lack of estimation methods for ODE models with binary data, the viral dynamic model was not fitted to the original binary data in Miao et al. (2010); instead, an ad hoc method was used to pre-determine the EID₅₀ based on 18 to 36 binary responses (6 responses per dilution factor with a total of 3 to 6 dilution levels for each mouse lung), and then the following continuous ODE model was fitted to the pre-determined EID₅₀ data:

$$\frac{d}{dt}{E}_p\left(t\right)={\rho }_E{E}_p-{\beta }_E{E}_{p}V,$$ (1.1)

$$\frac{d}{dt}{E}_p^{\ast }\left(t\right)={\beta }_E{E}_{p}V-{\delta }_{E^{\ast }}{E}_p^{\ast },$$ (1.2)

$$\frac{d}{dt}V\left(t\right)={\gamma }_{E^{\ast }}{E}_p^{\ast }-c_{V}V,$$ (1.3)

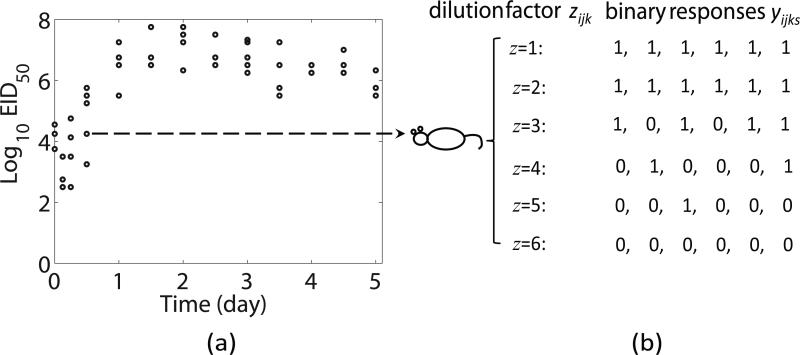
where E_p denotes the number of healthy epithelial cells, $E_p^{\ast }$ the number of infected epithelial cells, V the viral titer, and (ρ_E; β_E; δ_E*, γ_E*, c_V ) the unknown model parameters. More details of this continuous ODE model fitting can be found in Miao et al. (2010). One obvious problem of the approach in Miao et al. (2010) is the loss of efficiency and accuracy due to reducing each set of 18 to 36 binary responses into one single continuous EID₅₀ value in an ad hoc manner. Moreover, the statistical inference based on the summarized EID₅₀ data may not be valid since the distributional feature of the raw discrete (binary) data is not considered. For illustration purpose, the data structure and experimental design of the study in Miao et al. (2010) are depicted in Fig. 1.

Figure 1.

Illustrative example of data structure for GODE model with each log₁₀ EID₅₀ in the left figure corresponds to a number of binary outcome measured at different dilution factors in the right figure. (a) Summarized continuous data (log₁₀ EID₅₀); (b) A raw binary data example.

Motivated by the real problem above, in this article, we propose a framework of generalized ordinary differential equation (GODE) models and develop corresponding statistical inference methods. Briefly, we investigate the case that observed data (either continuous or discrete) follow a distribution from the exponential family; meanwhile, the link function is dynamic (function of time) and related to latent continuous state variables (and maybe additional covariates) that are governed by ODEs. Categorical time series have been proposed for modeling time-course discrete values with random time-dependent covariates; for example, the generalized linear models (Kaufmann, 1987; Fokianos and Kedem, 1998), state-spaces models (Fahrmeir and Tutz, 2001), integer autoregressive processes (Mckenzie, 1986; Al-Osh and Alzaid, 1987), discrete autoregressive moving average models (Jacobs and Lewis, 1978; Song et al., 2013), mixture transition distribution models (Raftery, 1985). See Fokianos and Kedem (2003) for a comprehensive review. The proposed GODE models provide an alternative approach to time-course discrete data modeling, and to the best knowledge of authors, this is the first time that an attempt has been ever made to fit ODE models to discrete data.

The remainder of this article is organized as follows. In Section 2, we formulate the GODE model into a form similar to that of generalized linear/nonlinear models. We develop the likelihood-based estimation and statistical inference methods in Section 3. The identifiability analysis, computing algorithm and implementation are also developed and discussed in this section. In Section 4, the theoretical properties of the proposed estimator are established. In Section 5, we apply the proposed methodology to the data from the motivating example and compare the estimation results to those obtained using the conventional estimation method in Miao et al. (2010) and the extended smoothing-based approach originated from Ramsay et al. (2007). In Section 6, we perform a number of simulation studies to evaluate the performance of the proposed estimator for observations that follow either a discrete (Binomial and Poisson) or continuous (Gamma and Normal) distribution. Finally, in Section 7, we summarize our results and discuss potential extensions of the proposed method. The detailed technical proofs are given in the Supplementary Materials.

2 Generalized Ordinary Differential Equation Models

Similar to the well-known generalized linear models (GLM) (McCullagh and Nelder, 1989) and generalized nonlinear models (GNM) (Wei, 1998; Kosmidis and Firth, 2009; Biedermann and Woods, 2011), a generalized ordinary differential equation (GODE) model can be formulated as follows. For simplicity, we consider the univariate case only and let y denote the measured variable. However, the following derivation can be easily generalized to multivariate cases with more tedious notations. Now let y_iks denote the sth observation (s = 1; 2,. . . , S_ik) under an experimental condition k (k = 1; 2, . . . , K_i) at time t_i (i = 1, 2, . . . , n). Assume that the observation y_iks follows a distribution from the exponential family with the probability mass (or density) function of

$$f(y_{iks};{\xi }_{ik},{\varphi }_{ik})=\exp \left(\frac{y_{iks}{\xi }_{ik}-b\left({\xi }_{ik}\right)}{a\left({\varphi }_{ik}\right)}+c(y_{iks},{\varphi }_{ik})\right)$$ (2.4)

with respect to a σ-finite measure π, where a(·), b(·) and c(·) are some pre-specified functions, ξ_ik is the natural parameter and ϕ_ik is the dispersion parameter under the kth experimental condition at time t_i. Then we have

$$E\left(y_{iks}\right)={\mu }_{ik}=b^{\prime }\left({\xi }_{ik}\right)\text{and}Var\left(y_{iks}\right)=b^{\prime }\left({\xi }_{ik}\right)a\left({\varphi }_{ik}\right),$$

where b^′(ξ) and b^′′(ξ) are the first and second order derivatives of b(ξ) with respect to ξ, respectively.

Define a dynamic link function as a function of two components: one component is a vector of unobservable (latent) dynamic state variables x(t) and another is a vector of additional covariates z which may also depend on time t, we can write this link function as

$${\eta }_k\left(t_i\right)=g\left({\mu }_{ik}\right)=g^{\ast }\{{\mathit{z}}_k\left(t_i\right),\mathit{x}\left(t_i\right),\beta \}.$$ (2.5)

Here g(·) is a known monotonic link function and usually the canonical link function can be used (Wei, 1998; McCullagh and Nelder, 1989); g* (·) is a known function of a vector of observed covariates z_ik = z_k(t_i), a vector of unknown parameters β associated with z, and a vector of unobservable (latent) dynamic state variables x(t_i). In particular, x follows an ordinary differential equation (ODE) model with a vector of unknown parameters θ, that is,

$${\mathit{x}}^{\prime }\left(t\right)=\mathit{h}(t,\mathit{x}\left(t\right),\theta )\text{with}\mathit{x}\left(t_0\right)={\mathit{x}}_0,$$ (2.6)

where t ∈ [t₀; T ] (–∞ < t₀ < T < ∞) is the time (independent) variable, x(t) = {x₁(t), . . . , x_κ (t)}^T is a κ-dimensional state variable vector (or dependent variables), x^′(t) = dx(t)=dt is the first order derivative of x(t) with respect to time t, θ ∈ R^q is the kinetic parameter vector, and h(·) is an explicitly given function. Also, x₀ is the initial conditions of the dynamic system, which could be unknown and can be estimated from the data. Finally, z can be random or fixed; if z is random, it is reasonable to assume that its distribution function does not involve the parameter vector (β, ϕ, θ ).

Note that, even if the function g* (·) is linearly related to z_ik and x_i = x(t_i) = x(t_i, θ), it may still be nonlinearly related to unknown parameters θ in the ODE model (2.6). Essentially the dynamic link function (2.5) is a nonlinear function of unknown parameters. Thus, the GODE model can be considered as a dynamic generalized nonlinear model (DGNM). If there is no connection between the link function (2.5) and the ODE model (2.6), the GODE or DGNM model reduces to a standard GNM model (Wei, 1998). All the state variables x(t, θ) in Eq. (2.6) are continuous with respect to t by definition. Our objective is to obtain the estimate and inference for the unknown parameters (β, θ) in the dynamic link function (2.5) and the dynamic ODE model (2.6) simultaneously based on observed data, which could be continuous or discrete.

3 Estimation and Inference

3.1 Likelihood Function and Inference

The likelihood-based estimation and inference methods are usually used for generalized linear models (McCullagh and Nelder, 1989) and generalized nonlinear models (Wei, 1998). For notation simplicity, we assume that all ϕ_ik are the same for any i and k so that we can drop the subscription of ϕ_ik. Let α = (θ^T,β^T , ϕ)^T denote the full parameter vector and assume that all y_iks are independent, then the log-likelihood function is given by

$$L(\alpha ;\mathit{y},\mathit{x},\mathit{z})=\sum _{i=1}^n\sum _{k=1}^{K_i}\sum _{s=1}^{S_{ik}}\ell (\alpha ;y_{iks},{\mathit{x}}_i,{\mathit{z}}_{ik}),$$ (3.7)

with y = {y_iks : 1 ≤ i ≤ n, 1 ≤ k ≤ K_i, 1 ≤ s ≤ S_ik}, x = {x_i : 1 ≤ i ≤ n}, z = {z_ik : 1 ≤ i ≤ n, 1 ≤ k ≤ K_i} and

$$\ell (\alpha ;y_{iks},{\mathit{x}}_i,{\mathit{z}}_{ik})=\log f(y_{iks};{\xi }_{ik},\varphi )=\frac{y_{iks}{\xi }_{ik}-b\left({\xi }_{ik}\right)}{a\left(\varphi \right)}+c(y_{iks},\varphi ),$$ (3.8)

where ξ_ik = b^′−1 ○ g⁻¹ ○ g* (z, _ik x_i, β ) with b^′−1 and g⁻¹ denoting the inverse functions of b^′ and g, respectively, and the symbol ○ denoting the product of two functions (as mappings). For completeness, the deviance of GODE models associated with the exponential family is given by

$$D(\mathit{y},\mu )=\sum _{i=1}^n\sum _{k=1}^{K_i}\sum _{s=1}^{S_{ik}}2[\{y_{iks}q\left(y_{iks}\right)-b\left(q\left(y_{iks}\right)\right)\}-\{y_{iks}q\left({\mu }_{ik}\right)-b\left(q\left({\mu }_{ik}\right)\right)\}]$$ (3.9)

where q(μ_ik) = b^′−1(μ_ik) = ξ_ik. For more details about the deviance or deviance-related inferences (e.g., the likelihood-ratio test), the interested reader is referred to McCullagh and Nelder (1989) and Wei (1998).

In practice, usually there exists no closed-form solution of x(t) for a general ODE model (2.6), especially if h(·) is nonlinear. Then numerical methods such as the Runge-Kutta method are needed to approximate x(t). Here we consider the 4th-order Runge-Kutta algorithm (Hairer et al., 2000), which has been well developed and widely used in practice. However, all of the methodologies and computing algorithms developed here can be easily extended to any one-step numerical algorithm for solving ODEs. First, we resort to numerical techniques to obtain numerical solutions at discrete time points. Let t₀ = s₀ < s₁ < < s_{m 1} = T be grid points on the interval [t₀, T], δ_j = s_j − s_j−1 be the step size and $\delta =\underset{1\le j\le m-1}{\max }{\delta }_j$ be the maximum step size, and $x_j^{\delta }$ and $x_{j+1}^{\delta }$ be the numerical approximations to the true solutions x(s_j) and x(s_j+1), respectively, which can be written as

$${\mathit{x}}_{j+1}^{\delta }={\mathit{x}}_j^{\delta }+\delta \Phi (s_j,{\mathit{x}}_j^{\delta },{\mathit{x}}_{j+1}^{\delta },\delta ),$$ (3.10)

where $\Phi (s_j,x_j^{\delta },x_{j+1}^{\delta },\delta )=\frac{k_1}{6}+\frac{k_2}{3}+\frac{k_3}{3}+\frac{k_4}{6}$, with k₁ = h(s_j, x(s_j), θ), k₂ = h(s_j + δ_j=2, x(s_j) + δ_jk₁=2, θ ), k₃ = h(s_j + δ_j=2, x(s_j) + δ_jk₂=2, θ ), k₄ = h(s_j + δ_j, x(s_j) + δ_jk₃, θ ).

Second, the interpolation technique such as the cubic Hermite spline interpolation is commonly used if the measurement points {t_i, i = 1, 2,..., n} are not coincident with the grid points {s_j, j = 0, 2,..., m 1} of the numerical method. Let x̃(t, θ) denote the interpolated value of x(t) based on the numerical solution of x(t) obtained from the Runge-Kutta method for given θ and x̃_i = x̃(t_i,) , then from Eq. (2.5), we have the following approximation

$${\mu }_{ik}=g^{-1}\circ g^{\ast }(z_{ik},{\mathit{x}}_i,\beta )\sim g^{-1}\circ g^{\ast }({\mathit{z}}_{ik},{\tilde{\mathit{x}}}_i,\beta ).$$

Now the log-likelihood function in Eq. (3.7) becomes

$$L(\alpha ;\mathit{y},\tilde{\mathit{x}},\mathit{z})=\sum _{i=1}^n\sum _{k=1}^{K_i}\sum _{s=1}^{S_{ik}}\ell (\alpha ;y_{iks},{\tilde{\mathit{x}}}_i,{\mathit{z}}_{ik})=\sum _{i=1}^n\sum _{k=1}^{K_i}\sum _{s=1}^{S_{ki}}\left[\frac{y_{iks}\cdot b^{\prime -1}\circ g^{-1}\circ g^{\ast }({\mathit{z}}_{ik},{\tilde{\mathit{x}}}_i,\beta )-b\{b^{\prime -1}\circ g^{-1}\circ g^{\ast }({\mathit{z}}_{ik},{\tilde{\mathit{x}}}_i,\beta )\}}{a\left(\varphi \right)}=c(y_{iks},\varphi )\right].$$ (3.11)

The maximum likelihood estimator (MLE) of α can be defined as

$$\widehat{\alpha }=\arg \underset{\alpha }{\max }L(\alpha ;\mathit{y},\tilde{\mathit{x}},\mathit{z}),$$ (3.12)

and the confidence interval can be calculated from the inverse of the observed Fisher information matrix

$$\mathbf{F}={\phantom{\mid }-L^{″}(\alpha ;\mathit{y},\tilde{\mathit{x}},\mathit{z})\mid }_{\alpha =\widehat{\alpha }}$$ (3.13)

with $L^{″}(\alpha ;y,\tilde{x},z)=\frac{{\partial }^{2}L(\alpha ;y,\tilde{x},z)}{\partial \alpha \partial {\alpha }^T}$. However, due to numerical instability of the derivative calculation in (3.13), the weighted bootstrap method is recommended in practice (Barbe and Bertail, 1995, Ma and Kosorok, 2005). Let w_iks (i = 1, . . . , n, k = 1, . . . , K_i and s = 1, . . . , S_ki) denote the positive random weights, which are i.i.d. samples of a continuous random variable w that satisfies E(w) = 1 and 0 ≤ V ar(w) = v₀ < ∞ and is independent of (t, y, z; α ), then the weighted maximum likelihood estimator ${\widehat{\alpha }}^{\ast }$ maximizes the following objective function

$$\sum _{i=1}^n\sum _{k=1}^{K_i}\sum _{s=1}^{S_{ik}}(w_{iks}\ell (\alpha ;y_{iks},{\tilde{\mathit{x}}}_i,{\mathit{z}}_{ik}).$$ (3.14)

The implementation of the weighted bootstrap method includes three steps: i) generate multiple sets (e.g., 500) of random weights; ii) obtain the weighted maximum likelihood estimate ${\widehat{\alpha }}^{\ast }$ for each set of weights; iii) determine the 95% confidence intervals by locating the 2.5% and 97.5% percentiles of these estimates. Remark 1. The primary reason of using the weighted bootstrap in this study is for the convenience of theoretical derivations. The empirical bootstrap has been used in statistical inference for ODE models (Joshi et al., 2006), but the associated asymptotic properties are difficult to derive. We thus considered the weighted bootstrap here, and found that, once the asymptotic properties for the ordinary parametric M-estimators are established, those for the weighted bootstrap estimators can be verified almost automatically (see the proof of Theorem 3 in Supplementary Materials), which was also pointed out by Ma and Kosorok (2005) for semiparametric weighted bootstrap M-estimators. Barbe and Bertail (1995) (Sections II.3 and II.4) provides certain guidelines on how to choose “optimal” weights for comparatively simple problems (e.g., arithmetic mean of a sample) using Edgeworth expansion; unfortunately, for our case, such “optimal” weights cannot be theoretically derived as in Barbe and Bertail (1995) because the nonlinear ODE model under consideration does not have a closed-form solution. Alternatively, we made an assumption on the weights (see Assumption 11, which is the same as Assumption E1.6 in Ma and Kosorok (2005)) and explicitly considered the variance of the weights (that is, V ar(w) = v₀) when deriving Theorem 3, from which we can tell that the distribution type of weights has no impact on the asymptotic variance of the weighted MLE. This is reasonable because the weights are independent of (t; y; z; α ). We also used both the exponential (highly skewed) and the truncated normal (approximately symmetric) distributions to generate weights and then compute the bootstrap confidence intervals. We found that the results from exponentially- or truncated normally-distributed weights are close to each other (results not shown). In real data analysis (see Section 5), we used weights generated from an exponential distribution with mean one and variance one.

3.2 Identifiability Analysis of GODE Model

The identifiability of parameters α needs to be verified before parameter estimation. For ODE models, a variety of analysis techniques such as differential algebra (e.g. Ljung and Glad, 1994) and implicit function theorem-based approaches (e.g. Xia and Moog, 2003) have been proposed. The basic idea of these approaches is to eliminate all the unobserved variables from the original ODEs such that the unknown model parameters can be solved and expressed in terms of only given inputs and measured outputs. For details, the interested reader is referred to Miao et al. (2011). In this section, we focus on the identifiability of GODE models and illustrate the analysis technique using our example application. Consider a general ODE model in (2.6), the way we connect the latent variables $x\left(t\right)\in {\mathcal{R}}^{\kappa }$ to the likelihood function is through the link function (2.5) and a pre-specified relationship between x(t) and z(t) such as

$$\mathbf{C}\cdot \mathit{x}\left(t\right)=\psi \left(\mathit{z}\left(t\right)\right),$$

where C is a constant matrix of a rank less than κ for a partially observed ODE model. Let C⁻ denote the generalized inverse of C, we have x(t) = C⁻ · ψ (z(t)) and thus

$${\mathbf{C}}^{-}\cdot {\psi }^{\prime }\left(\mathit{z}\left(t\right)\right)=\mathit{h}(t,{\mathbf{C}}^{-}\cdot \psi \left(\mathit{z}\left(t\right)\right),\theta ).$$

Therefore, the identifiability of θ can be verified only based on the ODE model structure above. This observation significantly simplifies the identifiability analysis for α since the identifiability of θ and β can now be separately verified. The verification of β 's identifiability is straightforward, so we only illustrate how to verify θ 's identifiability. For the model in (1.1)~(1.3), we can take higher order derivatives of V to incorporate the first two model equations into (1.3) to obtain

$$\mathbb{I}=V^{\prime ″}-(V^{″}+\mathbb{B})({\rho }_E-{\beta }_{E}V+V^{\prime }{V}^{-1})+{\mathbb{B}}^{\prime }=0,$$

where $\mathbb{B}={\delta }_{E^{\ast }}(V^{\prime }+c_{V}V)+c_V{V}^{\prime }$ According to the implicit function theorem (Xia and Moog, 2003; Wu et al., 2008), θ is identifiable if and only if $\frac{\partial \mathbb{I}\left(t_i\right)}{\partial \theta }(i=1,2,\dots ,q)$ is of full rank. For our example, one can tell that γ_E* vanishes from $\mathbb{I}$ and thus is unidentifiable; therefore, γ_E* is fixed as 100 EID₅₀·cell^{− 1} · day^{− 1} in later sections. The remaining parameters (ρ_E, β_E, δ_E* ; c_V ) are verified to be locally identifiable for the given relationship log₁₀ V = z.

3.3 Optimization Scheme

To obtain an accurate estimate of α , the development of robust and reliable computing algorithms is necessary due to the nonlinearity of the GODE. In addition, the majority of ODE models in practice are not only nonlinear but also have no close-form solutions, which makes the parameter estimation problem of GODE models even more challenging. The iteratively reweighted least squares (IRWLS) method has long been used to fit generalized linear/nonlinear models (McCullagh and Nelder, 1989; Wei, 1998). The basic idea of the IRWLS algorithm is to derive an iterative formula of parameter estimates based on the score function (Green, 1984)

$$\frac{\partial L}{\partial \alpha }=\frac{\partial L}{\partial \eta }\cdot \frac{\partial \eta }{\partial \alpha }=0.$$ (3.15)

Using the classical Newton-Raphson method, we can obtain the following equation by a Taylor series expansion for $\frac{\partial L}{\partial \alpha }$ in (3.15)

$$\left(\frac{-{\partial }^{2}L}{\approx \partial {\alpha }^{\left(m\right)}{\alpha }^{\left(m\right)T}}\right)({\alpha }^{(m+1)}-{\alpha }^{\left(m\right)})=\frac{\partial L}{\partial \eta }\cdot \frac{\partial \eta }{\partial {\alpha }^{\left(m\right)}}.$$ (3.16)

The second order derivative in (3.16) can be approximated as follows

$$\frac{-{\partial }^{2}L}{\partial {\alpha }^{\left(m\right)}{\alpha }^{\left(m\right)T}}\approx -\sum \frac{\partial L}{\partial {\eta }_i}\cdot \frac{{\partial }^2{\eta }_i}{\partial {\alpha }^{\left(m\right)}{\alpha }^{\left(m\right)T}}-{\left(\frac{\partial \eta }{\partial {\alpha }^{\left(m\right)}}\right)}^T\cdot \frac{{\partial }^{2}L}{\partial \eta {\eta }^T}\cdot \left(\frac{\partial \eta }{\partial {\alpha }^{\left(m\right)}}\right).$$

Now replace $\frac{\partial L}{\partial {\eta }_i}$ and $\frac{-{\partial }^{2}L}{\partial \eta {\eta }^T}$ at the right-hand side of the equation above with their expectations $E\left[\frac{\partial L}{\partial {\eta }_i}\right]=0$ and $\mathbf{W}=E\left[\frac{-{\partial }^2}{\partial \eta {\eta }^T}\right]$, we obtain the IRWLS formulas as follows

$$\left[{\left(\frac{\partial \eta }{\partial {\alpha }^{\left(m\right)}}\right)}^T\cdot {\mathbf{W}}^{\left(m\right)}\cdot \left(\frac{\approx \partial \eta }{\partial {\alpha }^{\left(m\right)}}\right)\right]\cdot ({\alpha }^{(m+1)}-{\alpha }^{\left(m\right)})=\frac{\partial L}{\partial \eta }\cdot \frac{\partial \eta }{\partial {\alpha }^{\left(m\right)}}.$$ (3.17)

However, the IRWLS algorithm is a local optimization method, and such local algorithms have been shown to frequently fail to converge, especially for nonlinear ODE problems and noisy data even if the starting parameter values are close to the true values (Miao et al., 2008). In this study, we propose to use the evolutionary hybrid (EH) algorithm to address the computational issues. The key idea of the EH algorithm is to combine the evolutionary algorithms with local optimization algorithms. Genetic algorithms (GA) are typical evolutionary algorithms, which mimic the gene evolution to mutate candidate solutions and adaptively select the better solutions subject to the selection force (e.g., the likelihood function value). Local optimization algorithms are mainly gradient-based methods such as (quasi-) Newton methods (Nocedal and Wright, 1999), which start from an initial position and search a better solution within a neighborhood along a direction guided by the gradient. Liang et al. (2010) proposed an algorithm called DESQP, which consists of the Differential Evolution (DE) algorithm (Storn and Price, 1997) and the Sequential Quadratic Programming (SQP) combined with the Interior Point (IP) method (Ye, 1987). Both the DE and the SQP-IP methods are the representative approaches in a category of their own, and their performances have been extensively evaluated in many previous studies (Moles et al., 2004; Paterlini and Krink, 2006; Gill et al., 2005). In addition, the DESQP algorithm itself has been shown to be capable of obtaining accurate parameter estimates for different types of dynamic models (Miao et al., 2012).

Different from Liang et al. (2010), we design and implement a more efficient strategy to incorporate the DE and the SQP-IP algorithm in this study. The DE algorithm will automatically generate an initial population of parameter vectors that are uniformly distributed within a given search range, and the subsequent population inherits and mutates by randomly mixing the previous generation with certain weights. For each population, Liang et al. (2010) applied the SQP-IP algorithm to the top 20 best parameter vectors (defined in terms of the objective function value) to make sure that the algorithm converges to nearby local optima. Therefore, the performance of DESQP is at least as good as the local gradient-based methods. However, the call to SQP-IP algorithm is expensive; also, we find that the top 20 parameter vectors usually become close to each other after a number of iterations such that it is likely to converge to the same local optimum after applying SQPIP. Therefore, we consider the pool of parameter vectors that have an objective function value being at most 50% smaller than the best one's (for maximization problem), from which we select at most 5 vectors that are farthest away from the best parameter vector. This new strategy can often reduce the computing cost by 30% and locate the global optimum more efficiently by considering the diversity in starting points when applying SQP-IP.

4 Asymptotic Properties

The asymptotic properties of the proposed estimator are studied in this section. In particular, note that there are usually no closed-form solutions for a general ODE model (2.6), numerical solvers such as the Runge-Kunta method are often used to numerically solve for x(t, θ ) when θ is given. Thus, we need to take the numerical error into consideration when we derive the asymptotic properties of the proposed estimator. Define $e^{\delta }=\underset{0\le j\le m-1}{\max }\Vert \mathit{x}\left(s_j\right)-{\mathit{x}}_j^{\delta }\Vert$, which is called the numerical error or the global discretization error (Hairer et al., 2000; Mattheij and Molenaar, 2002). If e^δ = O(δ^p), p is called the order of the numerical method. For the 4th-order Runge-Kutta method, p = 4.

For simplicity, we focus on the case that the regressors t_i and z_ik are random and assume that the observed data {(t_i, z_ik, y_iks) : 1 ≤ i ≤ n, 1 ≤ k ≤ K_i, 1 ≤ s ≤ S_ik} are i.i.d. copies of (t, z, y). Let E₀ denote the expectation with respect to P_α0 α₀, the joint probability distribution of (t, z, y). Let $N={\sum }_{i=1}^n{\sum }_{i=1}^{K_i}{S}_{ik}$ denote the total number of observations, and denote $\tilde{\alpha }=\arg {\max }_{\alpha }{E}_0\left[\ell (\alpha ;y,\tilde{\mathit{x}},\mathit{z})\right]$ Define

$$\mathbf{H}\left(\alpha \right)=\left(\begin{array}{cc}\hfill -E_0\left[\frac{{\partial }^2\ell (\alpha ;\mathit{y},\mathit{x},\mathit{z})}{\partial ({\theta }^T,{\beta }^T)\partial ({\theta }^T,{\beta }^T)}\right]\hfill & \hfill 0\hfill \\ \hfill 0^T\hfill & \hfill -E_0[\frac{{\partial }^2\ell (\alpha ;\mathit{y},\mathit{x},\mathit{z})}{\partial {\varphi }^2}\hfill \end{array}\right)$$ (4.8)

and Ĥ(α) = H(α )|_x=x̃, where 0 is a (q + d)-dimensional vector with each component zero. Denote H = H(α ₀) and $\tilde{\mathbf{H}}=\tilde{\mathbf{H}}\left(\tilde{\alpha }\right)$. The following assumptions are needed to establish our theoretical results:

• A1. θ ∈ Θ, $\beta \in \mathcal{B}$ and ϕ ∈ Φ, where Θ, $\mathcal{B}$ and Φ are compact subsets of ${\mathcal{R}}^q$, ${\mathcal{R}}^d$ and $\mathcal{R}$, respectively.

• A2. The numerical method for solving ODEs is of order p.

• A3. All partial derivatives of h(t, x, θ) up to order p with respect to t and x exist and are continuous.

• A4. For random design points, t₁, . . . , t_n are i.i.d. Moreover, there exist two constants 0 < c₁ < c₂ < ∞ such that the density function ψ(t) of t satisfies c₁ ≤ ψ(t) ≤ c₂ for all t ∈ [t₀, T ].

• A5. In the exponential distribution (2.4), the functions a(·) and b(·) have third order derivatives, c(·) has third order partial derivative respective to ϕ, and g has third order derivative, and g* has third order partial derivatives respective to x and β . All the above derivatives are continuous. Moreover, inf b^′′(ξ) > 0 and sup |b⁽³⁾(ξ)| < ∞.

• A6. For any $\alpha \in ϴ\times \mathcal{B}\times \Phi$ and α ≠= α ₀, f(y, ξ, ϕ) ≠= f(y, ξ₀, ϕ₀) with ξ = b^′−1 ○ g* ¹ ○ g* {z(t), x(t, θ ), β}.

• A7. The first and second partial derivatives, $\frac{\partial x(t,\theta )}{\partial \theta }$ and $\frac{{\partial }^{2}x(t,\theta )}{\partial \theta \partial {\theta }^T}$, exist and are continuous and uniformly bounded for all t ∈ [t₀, T] and θ ∈ Θ.

• A8. For the ODE numerical solution x̃(t,θ ), the first and second partial derivatives, $\frac{\partial \tilde{x}(t,\theta )}{\partial \theta }$ and $\frac{{\partial }^2\tilde{x}(t,\theta )}{\partial \theta \partial {\theta }^T}$, exist and are continuous and uniformly bounded for all t ∈ [t₀, T] and θ ∈ Θ.

• A9. The true parameter vector α ₀ is an interior point of $ϴ\times \mathcal{B}\times \Phi$.

• A10. H is nonsingular.

• A11. The positive weight w satisfies E(w) = 1 and 0 ≤ V ar(w) = v₀ < ∞ and is independent of (t, y, z, α ). Also, there exists a constant Q such that w < Q < ∞.

Assumption A1 is a general requirement for ODE models. Assumptions A2-A3 define the precision of the numerical algorithm (Hairer et al., 2000; Mattheij and Molenaar, 2002). For the 4th-order Runge-Kutta algorithm given in Section 3, it is of order 4. Hairer et al. (2000) provide sufficient and necessary conditions for the numerical method to be of order p. Assumptions A4-A8 are needed for consistency, where Assumption A6 is required for identifiability and can be verified by combining the common identifiability of GNM models (Wei, 1998) and the at-a-point identifiability of ODE models (see Definition 2 in Xue et al. (2010)). Assumptions A9-A10 are needed for the proof of asymptotic normality. Assumption A11 is required for the weight w defined in Section 3.1 and the same assumption has been made in Ma and Kosorok (2005). Assumptions A1, A5, A6 and A9 are similar to Assumptions A and B in Wei (1998). Assumption A10 is different from Assumption C in Wei (1998), since we are considering a random design while Wei (1998) considered the fixed design. So our observations are i.i.d., but Wei (1998)'s are independent but not necessarily identically distributed. Fahrmeir and Kaufmann (1985) considered both cases of random and fixed designs. Assumptions A2-A4 and A7-A8 are similar to those in Xue et al. (2010).

Theorem 1

Assume that there exists a λ > 0 such that δ = O(N^−λ), then under Assumptions A1-A8, we have $\widehat{\alpha }\stackrel{p}{\to }{\alpha }_0$.

Theorem 2

1. For δ = O(N^−λ) with λ > 1=(p^ 4) where p is the order of the numerical method, under Assumptions A1-A10, we have that $\sqrt{N}(\widehat{\alpha }-{\alpha }_0)\stackrel{d}{\to }\mathcal{N}(0,{\mathbf{H}}^{-1})$;

2. For δ = O(N^−λ) with 0 < ≤ 1=(p^ 4), under Assumptions A1-A10, we have that $\sqrt{N}(\widehat{\alpha }-\tilde{\alpha })\stackrel{d}{\to }\mathcal{N}(0,{\tilde{\mathbf{H}}}^{-1})$ with $\Vert \tilde{\alpha }-{\alpha }_0\Vert =O_p\left({\delta }^{(p\wedge 4)∕2}\right)=O_p\left(N^{-\lambda (p\wedge 4)∕2}\right)$ and $\Vert \tilde{\mathbf{H}}-\mathbf{H}\Vert =O_p\left({\delta }^{(p\wedge 4)∕2}\right)=O_p\left(N^{-\lambda (p\wedge 4)∕2}\right)$.

Theorem 3

For the weighted MLE ${\widehat{\alpha }}^{\ast }$ in (3.14), under the same assumptions as those in Theorem 2 as well as Assumption A11, we have that,

1. for λ > 1/(p^ 4), $\sqrt{N∕v_0}({\widehat{\alpha }}^{\ast }-\widehat{\alpha })$ has the same conditional limiting distribution as $\sqrt{N}(\widehat{\alpha }-{\alpha }_0)$ has unconditionally, i.e., $(\sqrt{N∕v_0}({\widehat{\alpha }}^{\ast }-\widehat{\alpha })\mid \{t_i,z_{ik},y_{iks}\})\stackrel{d}{\to }\sqrt{N}(\widehat{\alpha }-{\alpha }_0)$. Thus $\sqrt{N}({\widehat{\alpha }}^{ast}-{\alpha }_0)\stackrel{d}{\to }N(0,(1+v_0){\mathbf{H}}^{-1})$.

2. for $0<\lambda \le 1∕(p\wedge 4)$, $(\sqrt{N∕v_0}({\widehat{\alpha }}^{\ast }-\widehat{\alpha })\mid \{t_i,z_{ik},y_{iks}\})\stackrel{d}{\to }\sqrt{N}(\widehat{\alpha }-\tilde{\alpha })$. Thus $\sqrt{N}({\widehat{\alpha }}^{\ast }-\tilde{\alpha })\stackrel{d}{\to }N(0,(1+v_0){\widehat{\mathbf{H}}}^{-1})$.

It is not trivial to establish the theoretical properties for the proposed estimation. The objective function (3.7) has no closed-form, and can only be approximated by (3.11) through the numerical solutions of the state variables, which results in numerical errors (the differences between the numerical solutions and the true solutions of the state variables). If we directly apply the standard asymptotic theories for the maximum likelihood estimation of GLM (Jorgensen, 1983; Fahrmeir and Kaufmann, 1985) or GNM (Wei, 1998) to (3.11), then we can only obtain the asymptotic properties of $\widehat{\alpha }-\tilde{\alpha }$, not $\widehat{\alpha }-{\alpha }_0$ which does not consider the numerical errors. In order to account for both numerical errors and measurement errors, we establish a relationship between the number of grid points m (or the maximum step size δ) and the sample size of measurements N by the assumption δ = O(N^−λ), and thus the asymptotic properties of $\widehat{\alpha }-{\alpha }_0$ can be derived.

Remark 2

We consider the influence of numeric errors of ODE solutions on parameter estimates when deriving asymptotic properties. It is natural to expect that the smaller the step size is, the more accurate the numeric solution of an ODE is when a rational ODE solver is employed. However, a smaller step size could dramatically increase the computing cost, especially when the ODE system is large. In such circumstances, it is important to investigate the trade-off between the numerical error and measurement error so we can obtain accurate estimates efficiently. Our asymptotic properties for MLE of GODE models provide a theoretical basis to understand the relationship between the step size and sample size, which control the numerical error and the measurement error, respectively. Specifically, our theoretical results show that, only when the step size goes to zero at a rate faster than n^{−1/p^4)}, the MLE converges to the true parameter value at the rate of $\sqrt{n}$ In addition, the asymptotic variance of MLE is the one as if the true solution x(t) is exactly known.

5 Application to Influenza Viral Dynamics

As described in Miao et al. (2010), the only measurable output variable in Eqns (1.1)~(1.3) is the viral titer V . C57BL/6 mice (Jackson Labs, Maine) of an age between 6 and 16 weeks were infected with H3N2 A/Hong Kong/X31 influenza A virus. On days 0.125 (3 hr), 0.25 (6 hr), 0.5 (12 hr), 1, 1.5, 2, 2.5, 3, 3.5, 4, 4.5, 5, 5.5, 6, 6.5, 7, 8, 9, 10, 12, and 14, lung tissues from 3 ~ 6 mice were harvested. The lung homogenate from each mouse were then diluted at different factors (0, 10, 10², . . . , 10⁶) to determine the EID₅₀ (that is, the viral titer V ) by the hemagglutination (HA) assay (Miao et al., 2010).

Let t_i (i = 1, 2, . . . , n) denote distinct time points on which data are collected, a state variable, V (t_i), in the ODEs (1.1)ξ(1.3) is the predicted viral titer at time t_i, denote z_ijk (k = 1, 2, . . . , K_ij) as the kth dilution factor in log₁₀ scale used for the lung homogenate from mouse j (j = 1, 2, . . . , n_i) sacrificed at time t_i (note that 10^{− 2} was used to replace dilution factors of 0s in the original scale for a meaningful log-transformation), and let y_ijks (s = 1, 2, . . . , S_ijk) denote the binary response of the sth egg at the dilution factor z_ijk. Assume that y_ijks follows a Bernoulli distribution with a mean π_ijk = π_ij(z_ijk), which denotes the probability of a positive egg response at z_ijk. Under the independent Bernoulli trial assumption, the total number m_ijk of positive responses at one dilution factor z_ijk follows a Binomial distribution $m_{ijk}={\sum }_{s=1}^{S_{ijk}}{y}_{ijks}\sim Binomial(S_{ijk},{\pi }_{ijk})$. Based on the independency assumption, the log-likelihood function is therefore

$$L_B=\sum _{i=1}^n\sum _{j=1}^{n_i}\sum _{k=1}^{K_{ij}}\left[\log \left(\begin{array}{c}\hfill S_{ijk}\hfill \\ \hfill m_{ijk}\hfill \end{array}\right)+m_{ijk}\log {\pi }_{ijk}+(S_{ijk}-m_{ijk})\log (1-{\pi }_{ijk})\right].$$ (5.19)

We consider the logistic link function

$${\eta }_{ijk}=g\left({\pi }_{ijk}\right)=\log \left[{\pi }_{ijk}∕(1-{\pi }_{ijk})\right]=r_{ij}-\beta z_{ijk},$$ (5.20)

where r_ij is an intercept parameter which is related to the true virus concentration (for the jth sample at time t_i) that can be quantified by EID₅₀ or viral titer, and β > 0 is the slope parameter for the dilution factor of z_ijk which reflects the feature of the assay. Our preliminary studies (data not shown) suggest that the virus concentration in the sample is not sensitive to β so that we can assume β to be the same for all samples. By the definition of EID₅₀ or viral titer V (t_i) at time t_i, the dilution factor (in log₁₀ scale) corresponds to 50% eggs infected; that is, π_ij(z) = 0.5 or equivalently, r_ij = βlog₁₀ V (t_i). Now substitute this equation into Eq. (5.20), we have

$${\pi }_{ijk}=\frac{e^{\beta \cdot ({\log }_{10}V\left(t_i\right)-z_{ijk})}}{1+e^{\beta \cdot ({\log }_{10}V\left(t_i\right)-z_{ijk})}},$$ (5.21)

where for a set of given parameter values θ = (ρ_E, β_E, δ_E* , γ_E* , c_V ) in (1.1)ξ(1.3), a unique trajectory of V (t) can be numerically calculated and it can be treated as a function of θ . Thus, the link function or the function (5.21) connects the observational data with the ODEs (1.1)~(1.3) via V (t). That is, π_ijk is a function of unknown parameters θ and β, which can be denoted by π_ijk(θ, β ) for simplicity.

The maximum likelihood estimator (MLE) is thus given by

$$(\widehat{\theta },\widehat{\beta })=\arg \underset{\theta ,\beta }{\max }{L}_B(\theta ,\beta ;\mathit{y},V\left(t\right),\mathit{z}),$$ (5.22)

where L_B(θ, β; y, V (t); z) is the log-likelihood function given in Eq. (5.19) and Eq. (5.21). The proposed inference method and computational algorithm (the EH algorithm) in Section 3 are used to obtain the estimates of the unknown parameters and the confidence intervals are calculated using the weighted bootstrap method as discussed in Section 3. Here we fix the unidentifiable parameter γ_E* as 100 EID₅₀·cell^{− 1} · day^{− 1} as suggested in Miao et al. (2010). The initial conditions as suggested in Miao et al. (2010) are fixed as E_p(0) = 5.8 × 10⁵ cells per lung, $E_p^{\ast }\left(0\right)=0$ cells per lung, and V (0) = 1473 EID₅₀/ml. All parameter estimates and their 95% confidence intervals are summarized in Table 1. For convenience, the original estimates of these parameters based on the pre-calculated EID₅₀ in Miao et al. (2010) are also included in the table.

Table 1.

Parameter estimates and 95% bootstrap confidence intervals based on 400 runs for the given initial conditions E_p(0) = 5.8 × 10⁵ cells per lung, $E_p^{\ast }\left(0\right)=0$ cells per lung, V(0) = 1473 EID₅₀/ml and with γ_E* fixed as 100 EID₅₀·cell^–1·day^–1.

Parameter	Estimate via GODE	95% C.I. via GODE	Estimates in Miao et al. (2010)	95 % C.I. in Miao et al. (2010)	Estimate via ESB	95% C.I. via ESB
ρ E	9.24 × 10–7	[9.24 × 10–8, 1.00]	6.2 × 10–8	[3.9 × 10–9, 9.6 × 10–8]	3.48 × 10–1	[2.81 × 10–3, 7.39 × 10–1]
β E	2.31 × 10–6	[1.62 × 10–6, 8.93 × 10–6]	2.4 × 10–6	[3.8 × 10–7, 1.1 × 10–5]	5.51 × 10–7	[3.88 × 10–7, 8.44 × 10–6]
δ E*	7.43 × 10–1	[4.42 × 10–4, 1.61]	6.0 × 10–1	[4.5 × 10–2, 27.0]	1.40	[0.36, 2.95]
cV	2.84	[1.28, 24.1]	4.2	[0.43, 120]	2.70	[1.11, 5.69]
β	1.93	[1.55, 2.27]	–	–	1.90	[1.61, 2.26]
ρ E	0 (fixed)	–	–	–	0 (fixed)	–
β E	2.31 × 10–6	[1.68 × 10–6, 3.37 × 10–6]	–	–	6.46 × 10–7	[4.72 × 10–7, 6.78 × 10–6]
δ E*	7.43 × 10–1	[3.65 × 10–1, 1.63]	–	–	1.08	[0.29, 2.43]
cV	2.84	[1.23, 6.26]	–	–	2.66	[1.06, 5.44]
β	1.93	[1.62, 2.29]	–	–	1.90	[1.61, 2.26]

For comparison, we also consider the alternative approaches. Specifically, Ramsay et al. (2007) proposed a smoothing-based method for ODE model fitting, which approximates the state variables using certain basis functions and treats the ODE model as a penalized constraint. The smoothing-based approach has the advantage of not using any ODE solver and could therefore significantly reduce the computing cost. However, the original approach in Ramsay et al. (2007) was developed for continuous data, we need to extend the Ramsay's method to accommodate time-course discrete data, which is referred as the extended smoothing- based (ESB) method from now on. Without loss of generality, the state variable vector can be approximated as follows

$$\mathit{x}\left(t\right)\approx \mathbf{C}\cdot \mathit{b}\left(t\right),$$ (5.23)

where C _κ×m is a constant coefficient matrix, b_{m× 1} is the basis function vector, and m is the number of basis functions. Substitute Eq. (5.23) into (2.6), we obtain

$$\mathbf{C}\cdot {\mathit{b}}^{\prime }\left(t\right)-\mathit{h}(t,\mathbf{C}\cdot \mathit{b}\left(t\right),\theta )=0.$$ (5.24)

The smoothing-based parameter estimator is now given by

$$\widehat{\alpha }=\arg \underset{\alpha ,\mathbf{C}}{\min }\left\{-L(\alpha ,\mathit{y},\mathbf{C}\cdot \mathit{b}\left(t\right),\mathit{z})+\sum _{i=1}^{\kappa }{\lambda }_i\int {[{\mathit{c}}_i\cdot {\mathit{b}}^{\prime }\left(t\right)-h_i(t,\mathbf{C}\cdot \mathit{b}\left(t\right),\theta )]}^{2}dt\right\},$$ (5.25)

where c_i is the i-th row of the matrix C, and λ_i are the Lagrange multipliers. The objective function at the right-hand side can be directly minimized using the powerful DESQP algorithm, which simplifies the implementation with respect to the profiling procedure in Ramsay et al. (2007). We apply the extended smoothing-based method in (5.25) to our real example and simulated data; however, the investigation of the theoretic properties of the ESB method is out of the scope of this article and we will address it carefully in the future.

From the upper part of Table 1, we see that the relative differences in parameter estimates are 93.3% for ρ_E, 3.89% for β_E, 19.2% for δ_E* , and 47.9% for c_V respectively between the GODE method and the method by fitting the ODE model to the pre-calculated continuous EID₅₀ data in Miao et al. (2010), although the estimates from the two methods are in similar magnitudes. This observation suggests that the GODE estimates could be significantly different (potentially due to the use of more accurate statistical models for raw data) from the estimates based on the pre-calculated continuous EID₅₀ data in Miao et al. (2010). Furthermore, except for parameter ρ_E which was claimed to be practically insignificant in Miao et al. (2010), we obtain much shorter confidence intervals for all parameter estimates via the GODE method in comparison with the results in Miao et al. (2010), given that the weighted bootstrap method is used in both studies. For example, the confidence interval length of c_V obtained via the GODE method is only 19% of that in Miao et al. (2010). The possible reason for this improvement is that the GODE method fully utilizes all information in the raw data while the pre-calculated EID₅₀ in Miao et al. (2010) lost some information in summarizing the raw data as a continuous value by an ad hoc method.

Before the discussion of the parameter estimates obtained by the ESB method, the key computing configurations should be described. First, the widely-used cubic basis spline is employed to approximate E_p, $E_p^{\ast }$ and V . Second, spline knots are equally-spaced within the time window of interest for generality. Third, five different values of the number of the basis functions are tried (m = 4; 5; 6; 7; 8), and no further improvement in model fitting can be observed if m > 6. Therefore, the results in Table 1 are those obtained when m = 6. Fourth, as recommended by a few previous studies (e.g. Qi and Zhao, 2010), we used a sufficiently large value for λ such that the performance of the ESB method is not impaired. Fifth, the DESQP algorithm and the same computing parameters as in the GODE method are employed to optimize the objective function (5.25) so we can rule out the difference in estimation results caused by differences in optimization algorithms and settings. The estimates of c_V and β by the ESB method are very close to those by GODE (relative difference less than 5%); however, the relative differences in the estimates of δ_E* and β_E by ESB and GODE are 76% and 88%, respectively. To explain such a difference in estimates obtained by different methods, further simulation studies are conducted in the next section to compare the performances of ESB and GODE. Also, we defer the discussion on ρ_E (the lower half of Table 1) to the next section as more evidence in simulation studies are needed to verify whether this parameter can be reliably determined.

6 Simulation Study

In this section, we evaluate and compare the performance of the GODE estimation method with the ESB method by considering different distributions of y from the exponential family, including the Binomial, Poisson, Gamma and Normal distributions. Specifically, we use the same mathematical model as in the application section (Section 5). Also, the number and locations of time points, the number of replicates at each time point, and the number and locations of dilution factors for each replicate all match the real data setting described in Section 5. However, we change the number of observations for each dilution factor so the performance of the GODE method can be evaluated for different sample sizes. Furthermore, the Binomial and Poisson distributions are of single parameter and thus their variance cannot be changed separately. Therefore, we only investigate the effects of variance changes on parameter estimates for the Gamma and Normal distributions.

In particular, the parameter estimates in Table 1 from the real data example are used to generate 500 simulated data sets for each situation. At each dilution factor for each subject at one time point, the number of observations n =5, 10, and 20 are considered. Since the maximum variance at each dilution factor is max_p np(1 p) = 1.5 in the real data, a variance of σ²=0.75, 1.5, or 3.0 is considered for the Gamma and Normal distributions, respectively. See Table 2 for details. In addition, the maximum likelihood estimation method and the proposed computational algorithm (the EH algorithm) in Section 3 are used for the simulated data. The likelihood functions for the Poisson, Gamma and Normal distributions can be derived similarly as in Eq. (5.19). The logistic link function, Eq. (5.20), is used for all different distributions in this study for consistency; however, different link functions can be used in practice for other problems.

Table 2.

Evaluation of the GODE method by calculating average relative errors (ARE) in parameter estimates based on 500 simulation runs.

distribution	# of obs. per dilu. factor	variance	ARE(%) of GODE					ARE(%) of ESB
			ρ E	β E	δ E*	cV	β	ρ E	β E	δ E*	cV	β
binomial	5	-	47.8%	8.72%	27.9%	26.6%	3.98%	3.29 × 107%	89.1%	69.1%	36.3%	4.03%
	10	-	49.6%	5.90%	19.2%	19.2%	2.68%	3.66 × 107%	94.9%	72.4%	28.9%	2.78%
	20	-	49.7%	4.55%	13.7%	13.4%	1.85%	3.93 × 107%	91.2%	41.1%	20.4%	2.19%
Poisson	5	-	46.1%	14.0%	41.5%	43.4%	6.52%	1.21 × 107%	72.6%	95.9%	39.4%	6.66%
	10	-	49.5%	9.14%	37.4%	32.7%	4.32%	1.61 × 107%	72.4%	77.3%	28.1%	4.49%
	20	-	48.4%	5.86%	23.2%	19.8%	3.24%	2.40 × 107%	70.8%	71.3%	20.9%	3.37%
Gamma	5	3.0	12.3%	10.1%	50.6%	58.0%	84.3%	3.50 × 107%	92.7%	93.8%	55.7%	84.6%
	10	1.5	11.6%	6.40%	50.7%	45.1%	76.9%	4.53 × 107%	105%	84.3%	30.0%	77.1%
	20	0.75	13.1%	11.7%	36.0%	24.8%	69.5%	4.95 × 107%	115%	95.4%	19.9%	69.7%
normal	5	3.0	36.8%	44.0%	77.2%	104%	58.0%	1.93 × 107%	65.4%	84.5%	50.4%	76.4%
	10	1.5	39.3%	21.4%	52.8%	59.2%	13.5%	1.95 × 107%	64.7%	73.6%	32.8%	13.9%
	20	0.75	46.8%	9.02%	27.8%	26.7%	6.21%	2.12 × 107%	67.5%	68.1%	22.7%	6.20%

The average relative error (ARE), calculated as follows, is used to evaluate the performance of the proposed estimation method and the alternative ESB method,

$$ARE=\frac{1}{N_{sim}}\sum _{j=1}^{N_{sim}}\mid \frac{{\theta }_j-{\widehat{\theta }}_j}{{\theta }_j}\mid \times 100\%,$$ (6.26)

where ${\widehat{\theta }}_j$ denotes the estimate of true parameter θ_j based on the j-th simulated data set, and N_sim the total number of simulation runs. In this study, AREs are calculated based on N_sim = 500 simulation runs as summarized in Table 2.

For the one-parameter distributions (Binomial and Poisson), as the number of observations at each dilution factor increases from 5 to 20, Table 2 shows that for the GODE method, the AREs of all parameters decrease except ρ_E, suggesting that the GODE estimator is asymptotically consistent and unbiased. For example, the ARE of β_E decreases from 14.0% to 5.86% for the Poisson distribution. For the two-parameter distributions, Gamma and Normal, we consider three combinations of sample sizes and variances; the worst scenario is 5 observations at each dilution factor with a variance of 3.0, and the best scenario is 20 observations at each dilution factor with a variance of 0.75. As suggested in Table 2, the AREs of parameter estimates for both the Gamma and Normal distributions clearly decrease as the sample size increases and the variance decreases in most cases. We also observe that, for both Binomial and Poisson distributions, parameters β_E and β are very well estimated for all the cases, parameters δ_E and c_V can be reasonably estimated if the sample is large, but the parameter ρ_E cannot be well estimated even for the large sample size. For Gamma distribution, parameters ρ_E and β_E can be well estimated, but the AREs of all other parameters are large for all the cases while the AREs of β are the largest ranging from 69.5% to 84.3%. For the Normal distribution case, parameters β_E and β can be well estimated when the sample size is large (10 or 20) and the variance is small (0.75 and 1.5), but for all other scenarios, the AREs of all the parameter estimates are large. Note that, in our simulations, we used the same link function and assumed that the observations follow different distributions but with the same mean. Thus, the performance differences in different parameter estimates are clearly caused by different distributional assumptions of the observational data. So reducing the raw data into a single value by ignoring the distribution of the raw data in the analysis in Miao et al. (2010) may potentially produce the biased estimates.

The ESB method is also applied to the same simulated data sets for the comparison purpose. For parameters β and c_V , the ESB method has a performance close to the GODE method. For example, in Table 2, the AREs of β are 3.98% and 4.03% for the GODE and the ESB methods, respectively, when the number of observations from a binomial distribution is 5 per dilution factor. If look at c_V alone, the ESB method can even produce a slightly smaller ARE than that of the GODE method in a few cases. However, the estimates of ρ_E obtained by the ESB method are significantly biased (AREs on the order of 10⁷%), and we think that this parameter cannot be reliably determined without any time-course data for E when the ESB method is used (see the next paragraph for detail). Overall, we conclude that the GODE method has a superior performance over the ESB method in terms of parameter estimation accuracy, which could be due to the approximation error in Ĉ · b^′(t) used in smoothing-based approaches (Liang et al., 2010; Wu et al., 2014); however, we also find that the computing cost of the ESB method is 80% less than that of the GODE method because the ESB method does not use the initial value ODE solver.

Finally, it should be mentioned that ρ_E is practically insignificant and cannot be reliably estimated, no matter whether the GODE or the ESB method is used. We verify this by two approaches. First, for real data, we drop the five parameters one by one from the model and calculate the corresponding likelihood, AIC, BIC and AICc scores. It turns out that dropping ρ_E has no effect on the likelihood value and the corresponding AIC, BIC and AICc scores do decrease by at least 2. However, dropping any other parameter significantly affects the likelihood value and the model selection scores become much larger. Second, the experimental results in Rawlins and Hogan (2008) suggests that the epithelial cells can have a lifespan as long as 17 months, indicating an almost undetectable proliferation rate at the steady state. Therefore, both model selection and experimental results suggest that ρ_E is practically insignificant and cannot be reliably estimated. Such a fact is well reflected in Tables 1 and 2 by our GODE approach and the ESB method while the method in Miao et al. (2010) failed to give any clue. For completeness, we fixed ρ_E at zero and re-calculated the parameter estimates and confidence intervals for real data (see the lower half of Table 1); we also performed all the simulation studies for ρ_E = 0 and the results were presented in the Supplementary Materials (Table B.1). Since ρ_E is practically insignificant, it is not surprising that the results in these tables with ρ_E being fixed or estimated are close to each other.

7 Concluding Remarks

In this article, we have proposed the generalized ODE (GODE) models and associated inference methods for both continuous and discrete data from the exponential family. We have systematically formulated the GODE models and the inference problems. We proposed a generally applicable computing algorithm for parameter estimation, which has a number of advantages over existing algorithms and we investigated the asymptotic properties of the proposed estimator by explicitly taking the numerical errors for solving ODEs into consideration. The application example for modeling influenza viral dynamics clearly suggested an improvement in the interval estimation and our simulation studies confirmed the performance and generality of the proposed methods in different scenarios. However, we also admit some limitations of the proposed method. For example, the proposed DESQP algorithm requires more computing time than the gradient-based local optimization methods or the smoothing approach in Ramsay et al. (2007). However, such a problem can be solved by taking the advantage of powerful parallelized computing techniques in the future.

This is the first time that the GODE models and associated inference methods have been ever proposed and investigated. Given the fact that ODE models have long been used in various disciplines, the proposed methods are of great interests and importance especially when measurable outcomes are discrete in nature. Some extensions of the proposed methodologies are warranted. For examples, we extended the popular smoothing method (Ramsay et al., 2007) for ODE models to generalized ODE models and compared its performance with our approach for the example in consideration. The proposed GODE models can also be extended to mixed-effects models for longitudinal data analysis (Verbeke and Molenberghs, 2000), and this work provides a basis for such future investigations.