Abstract
Longitudinal data enables detecting the effect of aging/time, and as a repeated measures design is statistically more efficient compared to cross-sectional data if the correlations between repeated measurements are not large. In particular, when genotyping cost is more expensive than phenotyping cost, the collection of longitudinal data can be an efficient strategy for genetic association analysis. However, in spite of these advantages, genome-wide association studies (GWAS) with longitudinal data have rarely been analyzed taking this into account. In this report, we calculate the required sample size to achieve 80% power at the genome-wide significance level for both longitudinal and cross-sectional data, and compare their statistical efficiency. Furthermore, we analyzed the GWAS of eight phenotypes with three observations on each individual in the Korean Association Resource (KARE). A linear mixed model allowing for the correlations between observations for each individual was applied to analyze the longitudinal data, and linear regression was used to analyze the first observation on each individual as cross-sectional data. We found 12 novel genome-wide significant disease susceptibility loci that were then confirmed in the Health Examination cohort, as well as some significant interactions between age/sex and SNPs.
Keywords: longitudinal data, cross-sectional data, Korean Association Resource (KARE) cohort, Health Examinee (HEXA) cohort
1. Introduction
Disease prognosis and personalized medicine require the identification of genetic and non-genetic risk factors and, with the rapid improvement of genotyping technology, more than ten thousand genome-wide association studies (GWAS) have been conducted to discover disease susceptibility loci. Since the first such successful study in 2005 [1], more than ten thousand disease susceptibility loci have been successfully identified and these findings have improved our understanding of the genetic background of human diseases. However, in spite of these successes in GWAS, causal genetic variants identified by GWAS explain only a small proportion of the heritability [2,3]. Various reasons, including the common disease/rare variant hypothesis, have been put forward to explain this so-called missing heritability [4]. However, the missing heritability is partially attributable to a large number of false negative findings induced by insufficient sample sizes when controlling for multiple testing [5], and various strategies, such as GWAS using multiple phenotypes or longitudinal data [6,7], have been considered to overcome these problems. The analysis of multiple phenotypes can suffer from their inherent heterogeneity, but the analysis of the multiple measures of the same phenotype provided by longitudinal data may avoid this issue and, if measurement errors are substantial, GWAS with longitudinal data can be expected to mitigate the sample size problem.
Even though there are few GWAS using longitudinal data [8,9,10], compared to cross-sectional data longitudinal data have various useful features. First, although phenotyping is sometimes more expensive than the cost of genotyping, in those situations where the cost of genotyping is more expensive than that of phenotyping, repeated measurements at different time points have the virtual effect of enlarging the sample size. Second, with longitudinal data, the total phenotypic variance can be decomposed into among-subject and within-subject components. Third, phenotypes at different time points can be compared with baseline phenotypes and any confounding effect due to age can be prevented. Fourth, the onset of some diseases is sometimes affected by genetic variants, and gene × age interaction can be estimated with better accuracy. In this report, we conducted GWAS with longitudinal data in the Korean Association Resource (KARE) cohort. Phenotypes in the KARE cohort were measured every two years from 2001 to 2005, and we performed GWAS for eight phenotypes with three repeated measurements: systolic blood pressure (SBP), diastolic blood pressure (DBP), fasting plasma glucose (GLU0), 2-h OGTT glucose (GLU120), height, body mass index (BMI), high-density lipoprotein (HDL) and aspartate aminotransferase (AST). Results from the longitudinal GWAS were compared with those from GWAS using cross-sectional data, and our results showed that GWAS using longitudinal data provided more significant results. We identified 12 novel variants associated with phenotypes: rs11067763 (near MED13L) for DBP; rs12991703 (near MARCO) and rs7197218 (in XYLT1) for GLU0; rs17178527 (in AK097143) for BMI; rs12292858 (in SIK3), rs11066280 (in HECTD4) and rs183786 (near ALDH1A2) for HDL; and rs10849915 (in CCDC63), rs3782889 (in MYL2), rs12229654 (near MYL2-CUX2), rs11066280 (in HECTD4) and rs2072134 (in OAS3) for log-transformed AST. These variant associations were found to replicate in the Health Examinee (HEXA) cohort and thus illustrate the practical value of a longitudinal data analysis.
2. Materials and Methods
2.1. The Korean Association Resource (KARE) Cohort
The KARE cohort consists of a total of 10,038 individuals (5018 and 5020 individuals from Ansung and Ansan, respectively). Participants ranged from 40 to 69 years old, and their phenotypes were consecutively measured with two-year intervals from 2001 to 2005. Among the 10,038 participants, 10,004 individuals were genotyped for 500,568 SNPs with the Affymetrix Genome-Wide Human SNP array 5.0. Individuals and SNPs with call rates less than 95% were excluded from the analysis. SNPs with p-values for Hardy-Weinberg equilibrium (HWE) less than 10−6, or with minor allele frequencies (MAF) less than 0.01, were eliminated. Furthermore, individuals with tumors, gender inconsistencies, or whose heterozygosity rates were more than 30%, or identity in state (IBS) more than 0.8, were excluded from the analysis [11]. In total, 8842 individuals with 352,228 SNPs were available at the baseline time-point. At the second and third time-points, there were some missing phenotypes, and phenotypes for 7568 and 6675 individuals, respectively, were available.
2.2. The Health Examinee (HEXA) Cohort
Independent individuals in the HEXA cohort were from a second population based cohort sample provided by the Health study. This study combines subjects from the Wonju, Pyeong Chang, Gangneung, Geumsan, and Naju regional cohorts in Korea. There are 120,000 participants in the HEXA cohort, 4302 of whom, between 40 and 69 years old, were randomly selected for genotyping with the Affymetrix Genome-Wide Human SNP array 6.0. Individuals in the HEXA cohort were used to replicate the significant findings found in the KARE cohort, and individuals with tumors, large heterozygosity rates, gender inconsistencies, evidence of non-Asian ancestry, or whose IBS was more than 0.8 or call rates were less than 95%, were excluded from analysis [12]. SNPs with p-values for HWE less than 10−6, genotype call rates less than 95%, or MAF less than 0.01, were excluded, and the remaining SNPs for 3703 individuals were used for the analysis. In particular, the HEXA cohort is a cross-sectional study, and if there are some SNPs which have a progressing effect on phenotypes, results from HEXA and KARE cohort could be heterogeneous.
2.3. Sample Size Calculation for a Longitudinal Study
Sample sizes required to achieve 0.8 power at the 10−8 significance level were calculated in both the presence and absence of population substructure. We denote the number of individuals and measurements for each individual by n and t, respectively. We assume that t is same for all individuals. The additively coded value of the genotype for individual i is denoted by Xi. We assume Hardy-Weinberg equilibrium and each individual’s genotype is assumed to follow a trinomial distribution. The effect of the disease allele is assumed to be β. We assume a matrix of environmental effects that does not contain time-varying covariates for individual i, denoted by Zi, and its coefficient is assumed to be the column vector α. The columns of Zi denote each covariate. The phenotype for individual i at time-point j is denoted by Yij, and the corresponding t-dimensional vector by Yi. Letting 1t be the t-dimensional column vector with elements 1, Yi was assumed to be:
| (1) |
where ci indicates the random effect which explains the similarity of repeated measurements for each individual attributable to a non-polygenic effect. We denote σp2 = σg2 + σc2 + σε2 and ρ = σc2/σp2. Thus ρ measures the proportion of the variance of ci relative to the phenotypic variance. In particular, we included in the model to provide a polygenic effect for individual i, and assumed as an approximation follows the multivariate normal distribution with mean vector 0 and variance-covariance matrix where Φ corresponds to the genetic relationship matrix. If is 0, the correlation matrix R of Yi becomes compound symmetric. The null hypothesis H0 is β = 0, and β is assumed to be βa under the alternative hypothesis.
For sample size calculation, we assumed that there is no covariate effect other than the genotypes, and then we could assume that the environmental variable Zi is 1t. Then if we let πl = P(Xi = δl, Zi = 1) = P(Xi = δl) for the coded genotype δl where δ1 = 0, δ2 = 1 and δ3 = 2, and K = π1(π2 + 2π3)2 + π2(π3 − π1)2 + π3(1 + π1 − π3)2, the required sample size for 1 − ϕ power at the significance level α can be derived to be:
| (2) |
(see the Appendix for the detailed derivation). Liu and Liang [13] derived the required sample sizes when Xi is binary and our results are based on their derivations. We extend their result to Xi with arbitrary many levels. For nα, we assume that σc2 + σ ε2 = 1 and:
| (3) |
In the presence of population substructure, σg2 is assumed to be larger than 0. The required sample size cannot be directly calculated, and we calculated na by simulation studies based on a Monte Carlo method. In our simulations, we assumed that σg2 + σc2 + σ ε2 = 1 and the effect of disease the allele, β, was calculated with the following assumptions:
| (4) |
where these equations indicate that the proportion of genetic variance explained by the causal genotype is 0.005 and heritability is 0.3. For convenience, Φ was assumed to be a compound symmetric matrix with off-diagonal elements 0.1. The off-diagonal elements are asymptotically equivalent to twice the kinship coefficient between two individuals, and 0.1 means that the individuals are genetically remote relatives.
2.4. Genome-Wide Association Studies (GWAS) Using Longitudinal and Cross-Sectional Data
In the Korean Association Resource (KARE) data, eight phenotypes (SBP, DBP, GLU0, GLU120, height, BMI, HDL, and AST) were observed every two years from 2001 to 2005, so that three observations were available for each phenotype. Genotypes and phenotypes for 8842 individuals were initially available. However, there were some missing phenotypes for follow-up observations, and only 7568 and 6675 individuals were observed for the second and third time-points, respectively. Reasons for dropout were not known, but may include death, immigration, and non-response.
GWAS using longitudinal data were performed by generalized least squares using the nlme package in the R software. The phenotype for individual i is denoted by Yi which is a three dimensional vector. The matrix Zi indicates a covariate vector for environmental effects, including the intercept as the first column, and sex, age and age2 at the first time-point were included as covariates for all eight phenotypes. In particular, weight is known to be related to glucose levels, and thus it was included as an additional covariate for the GWAS of GLU0 and GLU120 [14,15]. The coefficient vector of Zi is denoted by a vector α. The effect of the time interval can be understood as the effect of aging, and it was denoted by the vector w. Here, w is a three-dimensional row vector and its coefficient is η. The population substructure between individuals was adjusted for with the EIGENSTRAT approach [16] and the remaining potential bias unadjusted by EIGENSTRAT was further adjusted for by the genomic control method [17]. In particular, the IBS matrix is often better than the identity-by-descent matrix for capturing the long-distance relationships that result from variations at the population level [18] and we used the IBS matrix for EIGENSTRAT. The first five principal component (PC) scores accounted for 75% of the variation in the IBS matrix, and they were used as covariates to adjust for any population substructure. The PC score vectors for individual i and its coefficient vector are PCi and γ, respectively. The additively coded value of the genotype for individual i is denoted by Xi. The effect of the disease allele is assumed to be β. The variance-covariance matrix for εi is denoted Σ and assumed to be an unstructured symmetric matrix. For longitudinal analysis, our final model is:
| (5) |
where , is distributed as for i = 1,2, …, 8842.
Furthermore, we conducted GWAS using cross-sectional data for comparison with the GWAS using longitudinal data. For this we took the phenotypes at the first-time point in the KARE cohort, and the GWAS were conducted with linear regression. For the cross-sectional analysis, we used the same covariates except for time interval, with the linear model:
| (6) |
where is distributed as for i = 1,2, …, 8842. The results from longitudinal and cross-sectional data were compared.
We tested whether there exist any interaction effects between our significant findings and environmental variables by adding interaction terms as covariates. We considered age, sex and time interval as environmental variables, and their statistical interaction with the SNPs were tested. Significant results were further tested for replication in the HEXA cohort (other than time interval, because the HEXA cohort only has cross-sectional data). Finally, we tested all the significant findings from the KARE cohort, as a discovery dataset, in the HEXA cohort, as a replication dataset.
3. Results
3.1. Sample Size for a Longitudinal Cohort Design
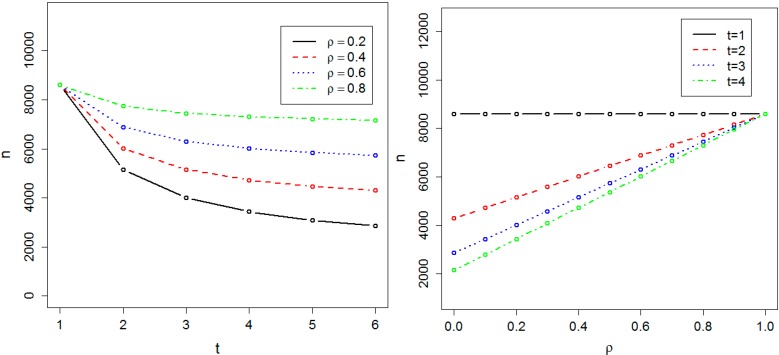
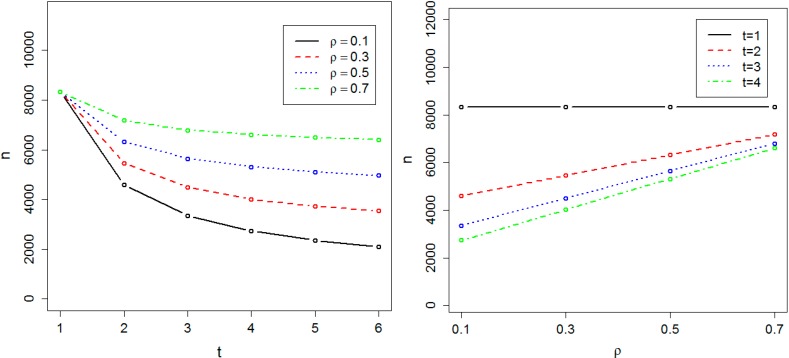
We calculated the sample size required to achieve 0.8 power at the genome-wide significance level α = 10−8 in both the absence and presence of population substructure. Figure 1 and Figure 2 respectively show the required sample size nα, in the absence and presence of population substructure, as a function of the number of time points t and the common correlation ρ between phenotype measures on the same person. We found the required sample size nα is proportionally related to t and inversely related to ρ. Sample size is minimized for small ρ and large t, and the effect of t on sample size is maximal when ρ = 0. These results illustrate the practical efficiency of GWAS with longitudinal data. For instance, if ρ = 0.4 and t = 3, then 5158 individuals are sufficient to achieve 0.8 power at the genome-wide significance level and, compared to cross-sectional data, genotyping costs for 3438 individuals can be saved vs. the cost of obtaining 6878 phenotypes.
Figure 1.
Required sample size in the absence of population substructure. The sample size is indicated by n. The required sample size to achieve 0.8 power at the significance level α = 10−8 has been calculated as a function of t, the number of time points, and ρ, the correlation between measurements at two different time-points.
Figure 2.
Required sample size in the presence of population substructure. The sample size is indicated by n. The required sample size to achieve 0.8 power at the significance level α = 10−8 has been calculated as a function of t, the number of time points, and ρ, the correlation between measurements at two different time-points.
3.2. Genome-Wide Association Studies (GWAS) with Longitudinal Data for Eight Phenotypes
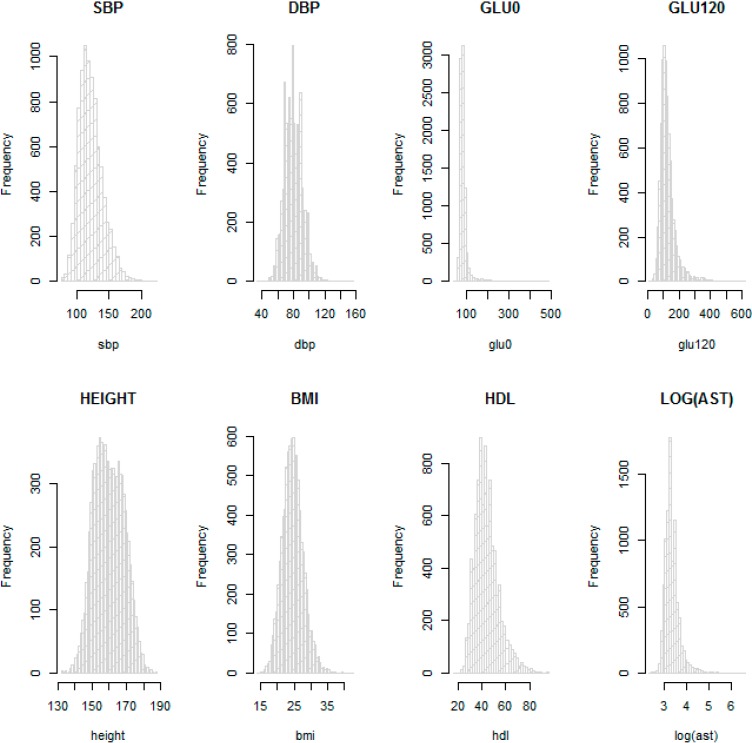
Table 1 and Table 2 provide descriptive statistics for sex, age and other available phenotypes from the KARE and HEXA cohorts. These show that the distributions of phenotypes are similar in the HEXA cohort the KARE cohort at each time point. We checked the normality of the eight phenotypes with histograms. In particular, AST was not normally distributed and so was log-transformed. Figure 3 shows that log-transformed AST and the other seven phenotypes on the original scale are about normally distributed, so these were used for the GWAS.
Table 1.
Sample sizes for Korean Association Resource (KARE) cohort.
| Time Point | KARE | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| N(Ansan/Ansung) | Age(s.d) | N(Ansan/Ansung) | Age(s.d) | N(Ansan/Ansung) | Age(s.d) | |
| Male | 2374/1809 | 51.78(8.79) | 1967/1642 | 53.71(8.82) | 1758/1424 | 55.58(8.71) |
| Female | 2263/2396 | 52.61(9.02) | 1764/2213 | 54.60(8.99) | 1543/1950 | 56.48(8.90) |
| Total | 4637/4205 | 52.22(8.92) | 3731/3855 | 54.18(8.92) | 3301/3374 | 56.05(8.82) |
Table 2.
Descriptive statistics for eight quantitative phenotypes examined in the Korean Association Resource (KARE) and Health Examinee (HEXA) cohorts.
| Time Point | KARE Cohort | HEXA Cohort | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||||
| Phenotype | Mean(s.d) | N | Mean(s.d) | N | Mean(s.d) | N | Mean(s.d) | N |
| SBP | 121.65(18.61) | 8842 | 118.6(17.3) | 7504 | 116.6(16.62) | 6646 | 121.69(14.36) | 3703 |
| DBP | 80.26(11.46) | 8842 | 78.49(10.96) | 7504 | 77.69(10.25) | 6646 | 77.05(9.84) | 3703 |
| GLU0 | 87.66(21.88) | 8581 | 92.74(15.14) | 6688 | 92.31(15.15) | 5985 | 94.10(24.56) | 3703 |
| GLU120 | 126.76(51.03) | 8387 | 125.77(41.59) | 4865 | 134.07(50.56) | 5985 | Not available | |
| height | 160(8.67) | 8842 | 159.93(8.74) | 7461 | 159.95(8.76) | 6596 | 161.49(8.10) | 3703 |
| BMI | 24.6(3.12) | 8838 | 24.59(3.09) | 7456 | 24.52(3.05) | 6596 | 23.96(2.88) | 3703 |
| HDL | 44.65(10.09) | 8841 | 46.27(9.90) | 7495 | 44.04(10.25) | 6640 | 54.60(13.27) | 3703 |
| AST | 29.81(18.41) | 8841 | 24.67(14.95) | 7495 | 25.87(19.02) | 6640 | 24.51(12.94) | 3703 |
Figure 3.
Histograms for SBP, DBP, GLU0, GLU120, HEIGHT, BMI, HDL and log AST in the KARE cohort.
The results of the GWAS with longitudinal data in the KARE cohort were compared with the results from GWAS using cross-sectional data. For the cross-sectional data we used the phenotypes at the first time-point, applying linear regression. Population substructure was adjusted for with the EIGENSTRAT method, and five principal component (PC) scores were included as covariates in both the longitudinal and cross-sectional data analyses. We found that five PC scores explain roughly 75% of the kinship matrix, and Table 3 shows the estimated variance inflation factors, λ, obtained by genomic control [17]. The estimated variance inflation factors from the longitudinal data analyses were always slightly larger than those from the cross-sectional data analyses, which suggests that longitudinal data analysis tends to be more sensitive to population substructure. Even though more detailed sensitivity analyses are necessary to confirm whether the model assumption for longitudinal data analyses are satisfied, our findings are probably not affected by population substructure because the quantile-quantile (QQ) and Manhattan plots for the eight phenotypes in Supplementary Figures 1–4 consistently show the validity of our analysis.
Table 3.
Inflation factors by genomic control.
| Phenotype | Cross-Sectional Data | Longitudinal Data |
|---|---|---|
| SBP | 1.040 | 1.051 |
| DBP | 1.028 | 1.053 |
| GLU0 | 1.022 | 1.026 |
| GLU120 | 1.026 | 1.037 |
| height | 1.069 | 1.071 |
| BMI | 1.046 | 1.052 |
| HDL | 1.034 | 1.039 |
| log AST | 1.023 | 1.030 |
We calculated the correlations between the different time-points for each phenotype and they are presented in Table 4. The correlations for height and BMI are usually very large and those for log AST are the smallest. Therefore, the improvement in power on using longitudinal data is expected to be the most substantial for log AST, and it seems to be almost negligible for height and BMI. Table 5 and Table 6 show the results from GWAS using longitudinal data and cross-sectional data in the KARE cohort, and the significant results were further tested in the HEXA cohort. The cross-sectional data for the KARE cohort are the first measurements for each individual in the longitudinal data. Cross-sectional and longitudinal data in the KARE cohort were analyzed with linear regression and a linear mixed model, respectively, and SNPs with p-values from either the cross-sectional or longitudinal data analysis less than 10−6 were selected for the replication studies. For the discovery analyses, the genome-wide significance level by Bonferroni correction is 1.4E − 07. For replication, we calculated the one-sided p-value for the direction from the longitudinal analysis using the KARE data, and used 0.05 as the significance level. Whenever the results from the two cohorts were in different directions, the p-values from the HEXA cohort were larger than 0.5. In Table 5 and Table 6, we added results from previous studies. If a SNP has not been significantly reported but SNPs in genes in linkage disequilibrium with it have been significantly reported, those SNPs are denoted by “*”. Table 5 and Table 6 show that GWAS using the longitudinal data in the KARE cohort identified 29 significant SNPs, 20 of which have been reported in previous GWAS, while the cross-sectional data identified only 19 genome-wide significant SNPs. Therefore we can conclude that the longitudinal data lead to substantial power improvement. In our GWAS using the longitudinal data, nine SNPs were newly detected, six of which were significantly replicated in the HEXA cohort.
Table 4.
Correlations between different time-points for each phenotype.
| Time point Phenotype | Correlation between time-points | ||
|---|---|---|---|
| 1–2 | 2–3 | 1–3 | |
| SBP | 0.608 | 0.604 | 0.552 |
| DBP | 0.550 | 0.596 | 0.517 |
| GLU0 | 0.700 | 0.795 | 0.822 |
| GLU120 | 0.675 | 0.748 | 0.715 |
| height | 0.984 | 0.985 | 0.984 |
| BMI | 0.942 | 0.941 | 0.916 |
| HDL | 0.690 | 0.684 | 0.667 |
| log AST | 0.444 | 0.432 | 0.468 |
Table 5.
Results for SBP, DBP, GLU0 and GLU120. SNPs with p-values less than 10−6 from cross-sectional or longitudinal data are listed.
| SNP | Chr | Position | Nearby Gene | Minor Allele | MAF | Discovery | Replication | Previously Published | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cross-Sectional | Longitudinal | Cross-Sectional | ||||||||||
| beta ± s.e | P | beta ± s.e | P | beta ± s.e | one-side P | |||||||
| SBP | ||||||||||||
| rs17249754 | 12 | 88584717 | ATP2B1 | A | 0.3732 | −1.63 ± 0.27 | 9.73E − 10 | −1.27 ± 0.22 | 1.11E − 08 | −0.86 ± 0.49 | 5.30E − 03 | Cho et al. NG 2009 [11] |
| rs11066280 | 12 | 111302166 | in HECTD4 | T | 0.1717 | −1.45 ± 0.34 | 2.52E − 05 | −1.59 ± 0.29 | 2.95E − 08 | −1.65 ± 0.43 | 6.35E − 05 | Kato et al. NG 2011 [27] |
| rs2401887 | 14 | 89952963 | CALM1 | C | 0.02125 | −3.19 ± 0.93 | 5.89E − 04 | −3.84 ± 0.78 | 8.58E − 07 | |||
| DBP | ||||||||||||
| rs10030362 | 4 | 102841866 | in BANK1 | C | 0.2081 | −0.72 ± 0.21 | 4.34E − 04 | −0.87 ± 0.17 | 3.21E − 07 | −0.22 ± 0.27 | 2.11E-01 | * Zhang et al. Hypertension Res 2012 [43] |
| rs3025047 | 6 | 43854388 | in VEGFA | A | 0.01024 | −2.65 ± 0.2 | 1.75E − 03 | −3.64 ± 0.71 | 3.07E − 07 | |||
| rs7100467 | 10 | 108153198 | SORCS1 | T | 0.02356 | −2.43 ± 0.53 | 1.81E − 04 | −2.82 ± 0.55 | 3.43E − 07 | |||
| rs17249754 | 12 | 88584717 | ATP2B1 | A | 0.3732 | −0.94 ± 0.17 | 4.33E − 08 | −0.8 ± 0.14 | 2.01E − 08 | −0.56 ± 0.23 | 8.50E − 03 | Cho et al. NG 2009 [11] |
| rs11066280 | 12 | 111302166 | in HECTD4 | T | 0.1717 | −0.94 ± 0.22 | 1.97E − 05 | −0.98 ± 0.18 | 9.25E − 08 | −0.76 ± 0.38 | 5.35E − 03 | Kato et al. NG 2011 [27] |
| rs11067763 | 12 | 114682724 | MED13L | G | 0.3297 | −0.78 ± 0.18 | 1.04E − 05 | −0.79 ± 0.15 | 8.75E − 08 | 0 ± 0.35 | 5.04E − 01 | |
| GLU0 | ||||||||||||
| rs12991703 | 2 | 119536716 | MARCO | A | 0.05655 | 3.62 ± 0.68 | 1.18E − 07 | 2.51 ± 0.58 | 1.55E − 05 | −1.14 ± 0.7 | 9.11E − 01 | |
| rs7754840 | 6 | 20769229 | in CDKAL1 | C | 0.4761 | 1.8 ± 0.32 | 1.72E − 08 | 1.78 ± 0.27 | 5.16E − 11 | 0.98 ± 0.74 | 3.99E − 02 | Kwak et al. Diabetes 2012 [44] |
| rs9460546 | 6 | 20771611 | in CDKAL1 | G | 0.4808 | 1.75 ± 0.32 | 3.38E − 08 | 1.76 ± 0.27 | 3.76E − 11 | |||
| rs2191346 | 7 | 15020403 | DGKB | C | 0.2891 | −1.72 ± 0.36 | 1.33E − 06 | −1.53 ± 0.3 | 3.64E − 07 | −0.62 ± 0.62 | 1.55E − 01 | |
| rs6494306 | 15 | VPS13C | A | 0.3435 | −1.43 ± 0.33 | 1.71E − 05 | −1.46 ± 0.28 | 1.92E − 07 | −1.21 ± 0.59 | 2.08E − 02 | * Manning et al. NG 2012 [45] | |
| rs7197218 | 16 | 17319136 | in XYLT1 | G | 0.01456 | 7.23 ± 0.68 | 1.23E − 07 | 4.29 ± 1.17 | 2.48E − 04 | |||
| GLU120 | ||||||||||||
| rs7754840 | 6 | 20769229 | in CDKAL1 | C | 0.4761 | 4.73 ± 0.78 | 1.51E − 09 | 4.73 ± 0.73 | 1.10E − 10 | Kwak et al. Diabetes 2012 [44] | ||
| rs12229654 | 12 | 109898844 | MYL2-CUX2 | G | 0.1426 | −4.84 ± 1.11 | 1.21E − 05 | −5.16 ± 1.03 | 5.84E − 07 | Go et al. J Hum Genet 2013 [46] | ||
| rs2074356 | 12 | 111129784 | in HECTD4 | T | 0.1467 | −5.19 ± 1.09 | 2.02E − 06 | −5.2 ± 1.02 | 3.44E − 07 | Go et al. J Hum Genet 2013 [46] | ||
| rs6031492 | 20 | 42330963 | in GDAPL1L | G | 0.4949 | 3.84 ± 0.77 | 6.91E − 07 | 3.03 ± 0.72 | 2.81E − 05 | |||
| rs2868088 | 20 | 42347066 | GDAPL1L | A | 0.4377 | −3.99 ± 0.78 | 2.68E − 07 | −3.54 ± 0.72 | 1.04E − 06 | |||
Table 6.
Results for Height, BMI, HDL and log AST. SNPs with p-values less than 10−6 from cross-sectional or longitudinal data are listed.
| SNP | Chr | Position | Nearby gene | Minor Allele | MAF | Discovery | Replication | Previously Published | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cross-sectional | Longitudinal | Cross-Sectional | ||||||||||
| beta ± s.e | P | beta ± s.e | P | beta ± s.e | one-side P | |||||||
| Height | ||||||||||||
| rs17038182 | 1 | 118669928 | SPAG17 | G | 0.4188 | −0.45 ± 0.08 | 4.08E − 08 | −0.45 ± 0.08 | 5.58E − 08 | −0.13 ± 0.13 | 1.53E − 01 | Cho et al. Nat Genet 2009 [11] |
| rs10513137 | 3 | 142626120 | in ZBTB38 | A | 0.2605 | 0.49 ± 0.09 | 8.14E − 08 | 0.49 ± 0.09 | 5.85E − 08 | 0.43 ± 0.14 | 7.40E − 04 | Kim et al. J Hum Genet 2009 [47] |
| rs6918981 | 6 | 34346492 | RPL35P2-NUDT3 | G | 0.2092 | 0.55 ± 0.1 | 2.98E − 08 | 0.55 ± 0.1 | 1.72E − 08 | 0.1 ± 0.15 | 2.51E − 01 | Kim et al. J Hum Genet 2009 [47] |
| BMI | ||||||||||||
| rs17178527 | 6 | 141947773 | in AK097143 | A | 0.2486 | −0.32 ± 0.05 | 2.96E − 09 | −0.31 ± 0.05 | 6.35E-09 | 0.05 ± 0.08 | 7.47E − 01 | |
| rs11000212 | 10 | 73625658 | in ANAPC16 in ASCC1 | G | 0.2057 | 0.27 ± 0.06 | 1.85E − 06 | 0.28 ± 0.06 | 5.14E − 07 | 0.05 ± 0.08 | 2.90E − 01 | |
| rs9939609 | 16 | 52378028 | in FTO | T | 0.1262 | 0.34 ± 0.07 | 1.29E − 06 | 0.34 ± 0.07 | 7.36E − 07 | 0.23 ± 0.1 | 1.29E − 02 | Cho et al. Nat Genet 2009 [11] |
| HDL | ||||||||||||
| rs271 | 8 | 19857982 | in LPL | T | 0.2064 | 1.15 ± 0.19 | 4.84E − 10 | 1.12 ± 0.17 | 2.15E − 11 | 1.81 ± 0.38 | 7.70E − 07 | |
| rs17482753 | 8 | 19876926 | LPL | T | 0.1243 | 1.95 ± 0.23 | 8.83E − 18 | 1.91 ± 0.21 | 1.42E − 20 | 3.48 ± 0.46 | 2.71E − 14 | Heid et al. Circ Cardiovasc Genet 2008 [48] |
| rs17410962 | 8 | 19892360 | LPL | A | 0.1244 | 1.95 ± 0.23 | 8.25E − 18 | 1.91 ± 0.21 | 1.76E − 20 | 3.48 ± 0.46 | 2.35E − 14 | |
| rs12686004 | 9 | 106693247 | in ABCA1 | T | 0.2136 | −1.26 ± 0.2 | 7.01E − 12 | −1.37 ± 0.17 | 1.62E − 16 | −1.19 ± 0.32 | 6.10E − 04 | Kim et al. Nat Genet 2011 [12] |
| rs11216126 | 11 | 116122450 | BUD13 | C | 0.2027 | 1.43 ± 0.19 | 2.69E − 14 | 1.36 ± 0.17 | 1.54E − 15 | 1.44 ± 0.5 | 7.45E − 05 | Kim et al. Nat Genet 2011 [12] |
| rs6589566 | 11 | 116157633 | in ZNF259 | C | 0.2176 | −1.25 ± 0.18 | 1.10E − 11 | −1.15 ± 0.17 | 4.47E − 12 | −1.89 ± 0.32 | 8.15E − 08 | * Waterworth et al. Arteriosclear Thromb Vasc Biol 2010 [49] |
| rs12292858 | 11 | 116319189 | in SIK3 | C | 0.1759 | 1.05 ± 0.2 | 7.73E − 08 | 0.88 ± 0.18 | 7.68E − 07 | 0.9 ± 0.35 | 1.11E − 02 | |
| rs12229654 | 12 | 109898844 | MYL2-CUX2 | G | 0.1426 | −1.25 ± 0.24 | 6.42E − 09 | −1.21 ± 0.2 | 7.35E − 10 | −1.66 ± 0.46 | 1.25E − 04 | Kim et al. Nat Genet 2011 [12] |
| rs2238153 | 12 | 110423930 | in ATXN2 | A | 0.4579 | −0.68 ± 0.16 | 8.76E − 06 | −0.71±0.14 | 3.29E − 07 | |||
| rs11066280 | 12 | 111302166 | in HECTD4 | T | 0.1717 | −1.4 ± 0.15 | 3.10E − 12 | −1.35±0.18 | 1.17E − 13 | −1.92 ± 0.4 | 8.95E − 07 | |
| rs2072134 | 12 | 111893559 | in OAS3 | A | 0.1143 | −1.39 ± 0.19 | 4.53E − 09 | −1.31 ± 0.22 | 1.25E − 09 | −1.36 ± 0.4 | 2.33E − 03 | Kim et al. Nat Genet 2011 [12] |
| rs183786 | 15 | 56455402 | ALDH1A2 | T | 0.305 | −0.8 ± 0.16 | 8.53E − 07 | −0.83 ± 0.15 | 2.33E − 08 | −0.61 ± 0.33 | 3.13E-02 | |
| rs16940212 | 15 | 56481312 | LIPC | T | 0.3405 | 1.27 ± 0.16 | 1.05E − 15 | 1.3 ± 0.14 | 1.95E − 19 | 1.11 ± 0.47 | 2.04E − 04 | Kim et al. Nat Genet 2011 [12] |
| rs6494005 | 15 | 56511816 | in LIPC | G | 0.2678 | −0.89 ± 0.2 | 1.34E − 07 | −0.89 ± 0.15 | 5.82E − 09 | −0.79 ± 0.39 | 1.05E − 02 | |
| rs12708980 | 16 | 55569880 | in CETP | C | 0.0984 | −1.67 ± 0.25 | 3.63E − 11 | −1.65 ± 0.23 | 5.61E − 13 | −1.88 ± 0.5 | 7.40E − 05 | Kim et al. Nat Genet 2011 [12] |
| rs2156552 | 18 | 45435666 | LIPG | A | 0.164 | −0.89 ± 0.21 | 1.53E − 05 | −0.93 ± 0.19 | 5.90E − 07 | −1.15 ± 0.4 | 2.29E − 03 | Waterworth et al. Arteriosclear Thromb Vasc Biol 2010 [49] |
| rs4420638 | 19 | 50114786 | APOC1 | C | 0.1121 | −1.3 ± 0.16 | 4.21E − 08 | −1.14 ± 0.21 | 1.23E − 07 | −2.01 ± 0.47 | 1.88E − 05 | Willer et al. Nat Genet 2013 [50] |
| AST | ||||||||||||
| rs9837421 | 3 | 15322297 | in SH3BP5 | G | 0.193 | −0.02 ± 0.01 | 2.14E − 04 | −0.03 ± 0.01 | 5.79E − 07 | 0 ± 0 | 5.32E − 01 | |
| rs10849915 | 12 | 109818005 | in CCDC63 | G | 0.1758 | −0.03 ± 0.01 | 2.00E − 06 | −0.03 ± 0.01 | 1.81E − 08 | −0.02 ± 0 | 3.68E − 02 | |
| rs3782889 | 12 | 109835038 | in MYL2 | C | 0.1726 | −0.03 ± 0.01 | 3.79E − 06 | −0.03 ± 0.01 | 7.26E − 09 | −0.02 ± 0 | 2.02E − 02 | |
| rs12229654 | 12 | 109898844 | MYL2-CUX2 | G | 0.1426 | −0.04 ± 0.01 | 7.34E − 08 | −0.04 ± 0.01 | 4.74E − 11 | −0.02 ± 0 | 2.80E − 02 | |
| rs11066280 | 12 | 111302166 | in HECTD4 | T | 0.1717 | −0.05 ± 0.01 | 8.17E − 13 | −0.05 ± 0.01 | 1.70E − 18 | −0.03 ± 0 | 1.94E − 04 | |
| rs11066453 | 12 | 111850004 | in OAS1 | G | 0.1265 | −0.03 ± 0.01 | 5.26E − 06 | −0.03±0.01 | 8.72E − 07 | −0.02 ± 0 | 7.75E − 02 | |
| rs2072134 | 12 | 111893559 | in OAS3 | A | 0.1143 | −0.04 ± 0.01 | 7.31E − 08 | −0.04 ± 0.01 | 8.42E − 09 | −0.02 ± 0 | 6.75E − 02 | |
| rs12483959 | 22 | 42657329 | in PNPLA3 | A | 0.4157 | 0.03 ± 0 | 1.79E − 09 | 0.03 ± 0 | 1.02E − 12 | 0.03 ± 0 | 2.14E − 06 | * Kamatani et al. Nat Genet 2010 [38] |
| rs2143571 | 22 | 42723019 | in SAMM50 | T | 0.4136 | 0.02 ± 0.01 | 6.45E − 07 | 0.03 ± 0 | 7.73E − 10 | 0.03 ± 0 | 4.22E − 05 | * Kawaguchi et al. PLoS One 2012 [39] |
Table 5 shows that rs2401887 located in CALM1 is more significantly associated with SBP in the longitudinal data analysis. GWAS of DBP identified three significant SNPs; rs3025047 in the VEGFA gene, rs7100467 near SORCS1 and rs11067763 near MED13L. It has been reported that VEGFA is related to type-2 diabetes, coronary artery disease, age-related macular degeneration and body fat [19,20,21]. For GLU0, rs12991703 located near the MARCO gene was genome-wide significant using the cross-sectional data, and rs2191346 and rs6494306, which are respectively in linkage disequilibrium with DGKB and VPS13C, were more significant using the longitudinal data.
rs7197218 in the XYLT1 gene, which is related to corneal astigmatism [22], was genome-wide significant using the cross-sectional data. rs6031492, located in GDAPL1L, is more significantly associated with GLU120 in the cross-sectional data analysis. Table 6 shows that we detected rs17178527 in AK097143 and rs11000212 in ANAPC16 as associated with BMI. rs12292858 in SIK3 was more significant using the cross-sectional data, and rs2238153 in ATXN2, rs11066280 in HECTD4 and rs183786 near ALDH1A2 were more significantly associated with HDL by longitudinal data analysis. ATXN2, HECTD4 and ALDH1A2 have been reported to have significant associations for phenotypes related to HDL [12,23,24,25,26,27,28,29,30,31,32,33,34], and the significant associations for HECTD4 and ALDH1A2 were successfully replicated in the HEXA cohort. We also performed GWAS of log-transformed AST, and Table 6 shows nine significant SNPs, rs9837421 in SH3BP5, rs10849915 in CCDC63, rs3782889 in MYL2, rs12229654 near MYL2-CUX2, rs11066280 in HECTD4, rs11066453 in OAS1, rs2072134 in OAS3, rs12483959 in PNPLA3 and rs2143571 in SAMM50. Previous studies have reported that SH3BP5, CCDC63, MYL2 and OAS3 are related to alcohol dependence phenotypes [35,36,37], and PNPLA3 and SAMM50 are related to nonalcoholic fatty liver disease [38,39], and so our results strengthen their importance in liver disease.
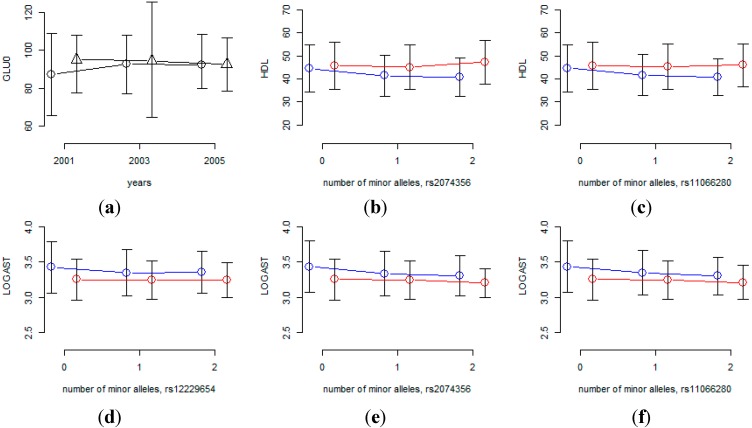
We also performed association analysis to detect gene×environment interaction, and SNPs that interact with aging, sex and time interval were identified by using the longitudinal data in the KARE cohort. Table 7 and Table 8 list SNPs with p-values for gene×environment interaction less than 10−6. Table 7 shows that rs7197218 seems to be a promising candidate SNP for interaction with aging for GLU0, and Figure 4 shows that the age effects are substantially different for this SNP. However, the MAF of rs7197218 is 0.01456, and neither it nor any other SNPs that are in linkage disequilibrium with it, were found in the HEXA cohort. Thus the significant association of this SNP could not be confirmed and it will need to be further investigated in follow-up studies. Table 8 shows that rs2074356 and rs11066280 interact significantly with sex for HDL, and rs2074356, rs11066280 and rs12229654 do so for log-transformed AST. Interestingly, rs2074356 and rs11066280 have significant interaction effects with sex for both HDL and AST. We further confirmed these significant gene×environment interactions in the HEXA cohort. Based on the direction of the coefficients for these interactions, we calculated one-sided p-values, and the combined p-values by Fisher’s and Liptak’s methods [40,41]. It has been shown that the most efficient method is achieved by Liptak’s methods if the effect sizes are expected to be the same [42]. Table 9 shows that these significant interactions were further replicated in the HEXA cohort, and the combined p-values become smaller. Figure 4 shows that the effects of these SNPs are substantially different for males and females and, therefore, we can conclude that the effects of these SNPs are significantly different for males and females.
Table 7.
Gene × environment interaction effect in the KARE cohort. Interactions of time interval with SNP were tested, and p-values for SNPs with genome-wide significant interaction are listed.
| Effect | rs7197218 for GLU0 | ||
|---|---|---|---|
| beta | Std.Error | p-value | |
| SNP | 5.92 | 1.21 | 1.08E − 06 |
| time×SNP | −1.27 | 0.25 | 2.65E − 07 |
Table 8.
Gene × environment interaction effect in the KARE cohort. Interactions of sex with SNPs were tested, and p-values for SNPs with genome-wide significant interaction are listed.
| Effect | rs2074356 for HDL | rs11066280 for HDL | rs2074356 for Log(AST) | rs11066280 for Log(AST) | rs12229654 for Log(AST) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| beta | Std.Error | p-value | beta | Std.Error | p-value | beta | Std.Error | p-value | beta | Std.Error | p-value | Beta | Std.Error | p-value | |
| SNP | −4.80 | 0.62 | 7.28E − 15 | −4.69 | 0.58 | 4.60E − 16 | −0.13 | 0.02 | 5.52E − 13 | −0.17 | 0.02 | 2.81E − 20 | −0.15 | 0.02 | 1.32E − 19 |
| sex×SNP | 2.26 | 0.39 | 4.46E − 09 | 2.21 | 0.36 | 1.06E − 09 | 0.06 | 0.01 | 5.82E − 08 | 0.08 | 0.01 | 8.25E − 12 | 0.07 | 0.01 | 3.24E − 11 |
Figure 4.
Interaction effects of SNPs with sex or time interval. (a) Mean of GLU0 at each time-point for each of two rs7197218 genotypes (circles indicate homozygous genotypes with no minor alleles, triangles indicate heterozygous genotypes); (b-f) phenotypic mean of each genotype for males and females (blue and red lines indicate male and female, respectively).
Table 9.
Combined p-values for gene × environment interaction. For replication, interactions of sex with SNPs were tested in the HEXA cohort and a combined p-value was calculated using both Fisher’s and Liptak’s methods.
| Sex × SNP | HEXA Cohort p-value | Combined p-value Using Fisher’s Method | Combined p-value Using Liptak’s Method |
|---|---|---|---|
| rs2074356 for HDL | 3.58E − 01 | 3.39E − 08 | 2.52E − 07 |
| rs11066280 for HDL | 2.184E − 01 | 5.37E − 09 | 2.52E − 08 |
| rs2074356 for Log(AST) | 4.86E − 02 | 5.86E − 08 | 4.41E − 08 |
| rs11066280 for Log(AST) | 1.23E − 02 | 3.13E − 12 | 3.10E − 12 |
| rs12229654 for Log(AST) | 7.42E − 03 | 7.22E − 12 | 4.96E − 12 |
In summary, we can conclude that GWAS with longitudinal data provide an efficient strategy, and our overall results show that the improvement in power is substantial, its effect being inversely proportional to ρ.
4. Discussion
It is well known that longitudinal analysis is useful to detect aging effects, and statistically efficient for detecting significant associations. In this report, we numerically calculated the sample sizes required to achieve statistical power at the genome-wide significance level, and our results showed that the power is proportionally related to the number of observations on each individual and inversely related to the correlation between the pairs of observations on an individual. In a large-scale genetic analysis, genotyping cost may be larger than the phenotyping cost, and then we can conclude that analyzing longitudinal data is an efficient strategy to improve the rate of false negative findings. However if the proportion of missing data is large, statistical power loss can be substantial; and if the missingness is not at random, even a small proportion of missing phenotypes can generate a serious bias [51]. In spite of the statistical efficiency of longitudinal data analysis, any possibility of potential bias from the missingness pattern should be carefully investigated; and it should be noted that a little carelessness can lead to a substantial bias.
Furthermore, we performed GWAS with both longitudinal and cross-sectional data, and significant results from a longitudinal data analysis in the KARE cohort were further tested in the HEXA cohort. 12 SNPs that have not been reported elsewhere were identified, and the significant p-values from replication studies strengthened the possibility that they are causal. In particular, GWAS with longitudinal data showed that rs3025047 is significantly associated with DBP even though it is not significantly associated in GWAS with cross-sectional data. The MAF of rs3025047 is 0.01, so it is a variant with relatively low frequency. In the HEXA cohort, rs3025047 was not available, nor were any SNPs in linkage disequilibrium with it. Even though further studies are necessary to confirm whether rs3025047 is a true causal variant, our analysis results illustrate that GWAS using longitudinal data can be an efficient strategy for rare variant association analysis.
During the last decade, more than ten thousand GWAS successfully identified disease susceptibility loci, and these findings increase our understanding of diseases. However, the so-called missing heritability [4] reveals that efficient analysis algorithms should be investigated, and GWAS of longitudinal data seem to provide a useful strategy that may bridge the gap.
5. Conclusions
Analyzed as a repeated measure design, the power of longitudinal data is proportionally related to the number of observations on each individual and inversely related to the correlation between the multiple observations on an individual. This facilitates finding causal SNPs and their interactions with environmental variables, as well as with age and sex. In two Korean cohorts it enabled us to find 12 novel genome-wide significant SNPs associated with eight phenotypes, and significant gene × environment interaction. Therefore, we can conclude that longitudinal data seem to provide efficient strategies for GWAS.
Acknowledgments
Data was provided by a grant from Korea Centers for Disease Control and Prevention (4845-301, 4851-302, 4851-307). This research was provided by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education 45 (2013R1A1A2010437), and an intramural grant from the Korean National Institute of Health (2013-NG73002-00). This research was supported by Basic Science Research Program through the NRF funded by the Ministry of Science, ICT & Future Planning(NRF-2013R1A1A2010437), and by Basic Science Research Program through the NRF funded by the Ministry of Science, ICT & Future Planning (NRF-2014S1A2A2028559). Woojoo Lee was supported by Basic Science Research Program through the NRF funded by the Ministry of Education, Science and Technology (NRF-2013R1A1A1061332).
Supplementary Files
Appendix
We assume that the null hypothesis is β = 0, and β = βa under the alternative hypothesis. According to Liu and Liang [13], the score for our hypothesis can be defined by:
| (7) |
and we denote by the expected variance-covariance matrix of the score function Sβ under the alternative hypothesis in the absence of population substructure. Letting be the chi-square noncentrality parameter to achieve 1 – ϕ power at the α significance level, Liu and Liang [13] showed that the required sample size for the score test becomes:
| (8) |
We let 1w be a w-dimensional column vector with elements 1. We assume that (Xi, Zi) can be (δl, ψl), where l = 1, … , L, and define πl = P(Xi = δl, Zi = ψl). If we assume , is diagonal matrix, , , and d denotes the number of rows of , the elements of the Fisher information matrices for β and α are found to be:
| (9) |
In the absence of population substructure, can be shown to be:
| (10) |
Furthermore:
| (11) |
leads to:
| (12) |
We let , and, because , we have:
| (13) |
Thus, we have:
| (14) |
Consequently, if we let , some tedious algebraic manipulations lead to:
| (15) |
If we denote by K, the required sample size becomes:
| (16) |
because . This completes the derivation for nα.
Author Contributions
The study was designed by Woojoo Lee and Sungho Won. Statistical analysis was performed by Young Lee, Suyeon Park, Sanghoon Moon and Juyoung Lee. The manuscript was written by Young Lee, Robert C. Elston and Sungho Won. All authors reviewed the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- 1.Klein R.J., Zeiss C., Chew E.Y., Tsai J.Y., Sackler R.S., Haynes C., Henning A.K., SanGiovanni J.P., Mane S.M., Mayne S.T., et al. Complement factor h polymorphism in age-related macular degeneration. Science. 2005;308:385–389. doi: 10.1126/science.1109557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Maher B. Personal genomes: The case of the missing heritability. Nature. 2008;456:18–21. doi: 10.1038/456018a. [DOI] [PubMed] [Google Scholar]
- 3.Manolio T.A., Collins F.S., Cox N.J., Goldstein D.B., Hindorff L.A., Hunter D.J., McCarthy M.I., Ramos E.M., Cardon L.R., Chakravarti A., et al. Finding the missing heritability of complex diseases. Nature. 2009;461:747–753. doi: 10.1038/nature08494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Visscher P.M., Brown M.A., McCarthy M.I., Yang J. Five years of gwas discovery. Am. J. Hum. Genet. 2012;90:7–24. doi: 10.1016/j.ajhg.2011.11.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Pearson T.A., Manolio T.A. How to interpret a genome-wide association study. J. Am. Med. Assoc. 2008;299:1335–1344. doi: 10.1001/jama.299.11.1335. [DOI] [PubMed] [Google Scholar]
- 6.Diggle P., Diggle P. Analysis of Longitudinal Data. 2nd ed. Oxford University Press; Oxford, UK/New York, NY, USA: 2002. [Google Scholar]
- 7.OʼReilly P.F., Hoggart C.J., Pomyen Y., Calboli F.C., Elliott P., Jarvelin M.R., Coin L.J. Multiphen: Joint model of multiple phenotypes can increase discovery in gwas. PLoS One. 2012;7 doi: 10.1371/journal.pone.0034861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Gray D.J., Thrift A.P., Williams G.M., Zheng F., Li Y.S., Guo J., Chen H., Wang T., Xu X.J., Zhu R., et al. Five-year longitudinal assessment of the downstream impact on schistosomiasis transmission following closure of the three gorges dam. PLoS Negl. Trop. Dis. 2012;6 doi: 10.1371/journal.pntd.0001588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Smith E.N., Chen W., Kahonen M., Kettunen J., Lehtimaki T., Peltonen L., Raitakari O.T., Salem R.M., Schork N.J., Shaw M., et al. Longitudinal genome-wide association of cardiovascular disease risk factors in the bogalusa heart study. PLoS Genet. 2010;6 doi: 10.1371/journal.pgen.1001094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zhu W., Cho K., Chen X., Zhang M., Wang M., Zhang H. A genome-wide association analysis of framingham heart study longitudinal data using multivariate adaptive splines. BMC Proc. 2009;3 doi: 10.1186/1753-6561-3-s7-s119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cho Y.S., Go M.J., Kim Y.J., Heo J.Y., Oh J.H., Ban H.J., Yoon D., Lee M.H., Kim D.J., Park M., et al. A large-scale genome-wide association study of asian populations uncovers genetic factors influencing eight quantitative traits. Nat. Genet. 2009;41:527–534. doi: 10.1038/ng.357. [DOI] [PubMed] [Google Scholar]
- 12.Kim Y.J., Go M.J., Hu C., Hong C.B., Kim Y.K., Lee J.Y., Hwang J.Y., Oh J.H., Kim D.J., Kim N.H., et al. Large-scale genome-wide association studies in east asians identify new genetic loci influencing metabolic traits. Nat. Genet. 2011;43:990–995. doi: 10.1038/ng.939. [DOI] [PubMed] [Google Scholar]
- 13.Liu G., Liang K.Y. Sample size calculations for studies with correlated observations. Biometrics. 1997;53:937–947. doi: 10.2307/2533554. [DOI] [PubMed] [Google Scholar]
- 14.Camastra S., Bonora E., Del Prato S., Rett K., Weck M., Ferrannini E. Effect of obesity and insulin resistance on resting and glucose-induced thermogenesis in man. Egir (European group for the study of insulin resistance) Int. J. Obesity Relat. Metab. Disord. 1999;23:1307–1313. doi: 10.1038/sj.ijo.0801072. [DOI] [PubMed] [Google Scholar]
- 15.McCarthy M.I. Genomics, type 2 diabetes, and obesity. N Engl. J. Med. 2010;363:2339–2350. doi: 10.1056/NEJMra0906948. [DOI] [PubMed] [Google Scholar]
- 16.Price A.L., Patterson N.J., Plenge R.M., Weinblatt M.E., Shadick N.A., Reich D. Principal components analysis corrects for stratification in genome-wide association studies. Nat. Genet. 2006;38:904–909. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
- 17.Devlin B., Roeder K., Wasserman L. Genomic control, a new approach to genetic-based association studies. Theor. Popul. Biol. 2001;60:155–166. doi: 10.1006/tpbi.2001.1542. [DOI] [PubMed] [Google Scholar]
- 18.Kang H.M., Sul J.H., Service S.K., Zaitlen N.A., Kong S.Y., Freimer N.B., Sabatti C., Eskin E. Variance component model to account for sample structure in genome-wide association studies. Nat. Genet. 2010;42:348–354. doi: 10.1038/ng.548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Davies R.W., Wells G.A., Stewart A.F., Erdmann J., Shah S.H., Ferguson J.F., Hall A.S., Anand S.S., Burnett M.S., Epstein S.E., et al. A genome-wide association study for coronary artery disease identifies a novel susceptibility locus in the major histocompatibility complex. Circulation. Cardiovasc. Genet. 2012;5:217–225. doi: 10.1161/CIRCGENETICS.111.961243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Yu Y., Bhangale T.R., Fagerness J., Ripke S., Thorleifsson G., Tan P.L., Souied E.H., Richardson A.J., Merriam J.E., Buitendijk G.H., et al. Common variants near frk/col10a1 and vegfa are associated with advanced age-related macular degeneration. Hum. Mol. Genet. 2011;20:3699–3709. doi: 10.1093/hmg/ddr270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zeggini E., Scott L.J., Saxena R., Voight B.F., Marchini J.L., Hu T., de Bakker P.I., Abecasis G.R., Almgren P., Andersen G., et al. Meta-analysis of genome-wide association data and large-scale replication identifies additional susceptibility loci for type 2 diabetes. Nat. Genet. 2008;40:638–645. doi: 10.1038/ng.120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lopes M.C., Hysi P.G., Verhoeven V.J., Macgregor S., Hewitt A.W., Montgomery G.W., Cumberland P., Vingerling J.R., Young T.L., van Duijn C.M., et al. Identification of a candidate gene for astigmatism. Investig. Ophthalmol. Vis. Sci. 2013;54:1260–1267. doi: 10.1167/iovs.12-10463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Adeyemo A., Gerry N., Chen G., Herbert A., Doumatey A., Huang H., Zhou J., Lashley K., Chen Y., Christman M., et al. A genome-wide association study of hypertension and blood pressure in african americans. PLoS Genet. 2009;5 doi: 10.1371/journal.pgen.1000564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ganesh S.K., Zakai N.A., van Rooij F.J., Soranzo N., Smith A.V., Nalls M.A., Chen M.H., Kottgen A., Glazer N.L., Dehghan A., et al. Multiple loci influence erythrocyte phenotypes in the charge consortium. Nat. Genet. 2009;41:1191–1198. doi: 10.1038/ng.466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hunt K.A., Zhernakova A., Turner G., Heap G.A., Franke L., Bruinenberg M., Romanos J., Dinesen L.C., Ryan A.W., Panesar D., et al. Newly identified genetic risk variants for celiac disease related to the immune response. Nat. Genet. 2008;40:395–402. doi: 10.1038/ng.102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ikram M.K., Sim X., Jensen R.A., Cotch M.F., Hewitt A.W., Ikram M.A., Wang J.J., Klein R., Klein B.E., Breteler M.M., et al. Four novel loci (19q13, 6q24, 12q24, and 5q14) influence the microcirculation in vivo. PLoS Genet. 2010;6 doi: 10.1371/journal.pgen.1001184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kato N., Takeuchi F., Tabara Y., Kelly T.N., Go M.J., Sim X., Tay W.T., Chen C.H., Zhang Y., Yamamoto K., et al. Meta-analysis of genome-wide association studies identifies common variants associated with blood pressure variation in east asians. Nat. Genet. 2011;43:531–538. doi: 10.1038/ng.834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kottgen A., Albrecht E., Teumer A., Vitart V., Krumsiek J., Hundertmark C., Pistis G., Ruggiero D., OʼSeaghdha C.M., Haller T., et al. Genome-wide association analyses identify 18 new loci associated with serum urate concentrations. Nat. Genet. 2013;45:145–154. doi: 10.1038/ng.2500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kottgen A., Pattaro C., Boger C.A., Fuchsberger C., Olden M., Glazer N.L., Parsa A., Gao X., Yang Q., Smith A.V., et al. New loci associated with kidney function and chronic kidney disease. Nat. Genet. 2010;42:376–384. doi: 10.1038/ng.568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lu X., Wang L., Chen S., He L., Yang X., Shi Y., Cheng J., Zhang L., Gu C.C., Huang J., et al. Genome-wide association study in han chinese identifies four new susceptibility loci for coronary artery disease. Nat. Genet. 2012;44:890–894. doi: 10.1038/ng.2337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Newton-Cheh C., Johnson T., Gateva V., Tobin M.D., Bochud M., Coin L., Najjar S.S., Zhao J.H., Heath S.C., Eyheramendy S., et al. Genome-wide association study identifies eight loci associated with blood pressure. Nat. Genet. 2009;41:666–676. doi: 10.1038/ng.361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wain L.V., Verwoert G.C., OʼReilly P.F., Shi G., Johnson T., Johnson A.D., Bochud M., Rice K.M., Henneman P., Smith A.V., et al. Genome-wide association study identifies six new loci influencing pulse pressure and mean arterial pressure. Nat. Genet. 2011;43:1005–1011. doi: 10.1038/ng.922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Wu C., Hu Z., He Z., Jia W., Wang F., Zhou Y., Liu Z., Zhan Q., Liu Y., Yu D., et al. Genome-wide association study identifies three new susceptibility loci for esophageal squamous-cell carcinoma in chinese populations. Nat. Genet. 2011;43:679–684. doi: 10.1038/ng.849. [DOI] [PubMed] [Google Scholar]
- 34.Yang X., Lu X., Wang L., Chen S., Li J., Cao J., Chen J., Hao Y., Li Y., Zhao L., et al. Common variants at 12q24 are associated with drinking behavior in han chinese. Am. J. Clin. Nutr. 2013;97:545–551. doi: 10.3945/ajcn.112.046482. [DOI] [PubMed] [Google Scholar]
- 35.Baik I., Cho N.H., Kim S.H., Han B.G., Shin C. Genome-wide association studies identify genetic loci related to alcohol consumption in korean men. Am. J. Clin. Nutr. 2011;93:809–816. doi: 10.3945/ajcn.110.001776. [DOI] [PubMed] [Google Scholar]
- 36.Zuo L., Gelernter J., Zhang C.K., Zhao H., Lu L., Kranzler H.R., Malison R.T., Li C.S., Wang F., Zhang X.Y., et al. Genome-wide association study of alcohol dependence implicates kiaa0040 on chromosome 1q. Neuropsychopharmacology. 2012;37:557–566. doi: 10.1038/npp.2011.229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Zuo L., Zhang F., Zhang H., Zhang X.Y., Wang F., Li C.S., Lu L., Hong J., Lu L., Krystal J., et al. Genome-wide search for replicable risk gene regions in alcohol and nicotine co-dependence. Am. J. Med. Genet. Part B Neuropsychiatr. Genet. 2012;159B:437–444. doi: 10.1002/ajmg.b.32047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kamatani Y., Matsuda K., Okada Y., Kubo M., Hosono N., Daigo Y., Nakamura Y., Kamatani N. Genome-wide association study of hematological and biochemical traits in a japanese population. Nat. Genet. 2010;42:210–215. doi: 10.1038/ng.531. [DOI] [PubMed] [Google Scholar]
- 39.Kawaguchi T., Sumida Y., Umemura A., Matsuo K., Takahashi M., Takamura T., Yasui K., Saibara T., Hashimoto E., Kawanaka M., et al. Genetic polymorphisms of the human pnpla3 gene are strongly associated with severity of non-alcoholic fatty liver disease in japanese. PLoS One. 2012;7 doi: 10.1371/journal.pone.0038322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Fisher R.A. Statistical Methods for Research Workers. 11th ed. Oliver and Boyd; Edinburgh, UK: 1950. [Google Scholar]
- 41.Liptak T. On the combination of independent tests. Magyar Tudom Aanyos Akad Aemia Matematikai Kutat Ao Intezetenek Kozlemenyei. 1958;3:171–197. [Google Scholar]
- 42.Won S., Morris N., Lu Q., Elston R.C. Choosing an optimal method to combine p-values. Stat. Med. 2009;28:1537–1553. doi: 10.1002/sim.3569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Zhang D., Pang Z., Li S., Jiang W., Wang S., Thomassen M., Hjelmborg J.V., Kruse T.A., Ohm Kyvik K., Christensen K., et al. Genome-wide linkage and association scans for pulse pressure in chinese twins. Hypertens. Res. 2012;35:1051–1057. doi: 10.1038/hr.2012.90. [DOI] [PubMed] [Google Scholar]
- 44.Kwak S.H., Kim S.H., Cho Y.M., Go M.J., Cho Y.S., Choi S.H., Moon M.K., Jung H.S., Shin H.D., Kang H.M., et al. A genome-wide association study of gestational diabetes mellitus in korean women. Diabetes. 2012;61:531–541. doi: 10.2337/db11-1034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Manning A.K., Hivert M.F., Scott R.A., Grimsby J.L., Bouatia-Naji N., Chen H., Rybin D., Liu C.T., Bielak L.F., Prokopenko I., et al. A genome-wide approach accounting for body mass index identifies genetic variants influencing fasting glycemic traits and insulin resistance. Nat. Genet. 2012;44:659–669. doi: 10.1038/ng.2274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Go M.J., Hwang J.Y., Kim Y.J., Hee Oh J., Kim Y.J., Heon Kwak S., Soo Park K., Lee J., Kim B.J., Han B.G., et al. New susceptibility loci in myl2, c12orf51 and oas1 associated with 1-h plasma glucose as predisposing risk factors for type 2 diabetes in the korean population. J. Hum. Genet. 2013;58:362–365. doi: 10.1038/jhg.2013.14. [DOI] [PubMed] [Google Scholar]
- 47.Kim J.J., Lee H.I., Park T., Kim K., Lee J.E., Cho N.H., Shin C., Cho Y.S., Lee J.Y., Han B.G., et al. Identification of 15 loci influencing height in a korean population. J. Hum. Genet. 2010;55:27–31. doi: 10.1038/jhg.2009.116. [DOI] [PubMed] [Google Scholar]
- 48.Heid I.M., Boes E., Muller M., Kollerits B., Lamina C., Coassin S., Gieger C., Doring A., Klopp N., Frikke-Schmidt R., et al. Genome-wide association analysis of high-density lipoprotein cholesterol in the population-based kora study sheds new light on intergenic regions. Circ. Cardiovasc. Genet. 2008;1:10–20. doi: 10.1161/CIRCGENETICS.108.776708. [DOI] [PubMed] [Google Scholar]
- 49.Waterworth D.M., Ricketts S.L., Song K., Chen L., Zhao J.H., Ripatti S., Aulchenko Y.S., Zhang W., Yuan X., Lim N., et al. Genetic variants influencing circulating lipid levels and risk of coronary artery disease. Arterioscler. Thromb. Vasc. Biol. 2010;30:2264–2276. doi: 10.1161/ATVBAHA.109.201020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Global Lipids Genetics C., Willer C.J., Schmidt E.M., Sengupta S., Peloso G.M., Gustafsson S., Kanoni S., Ganna A., Chen J., Buchkovich M.L., et al. Discovery and refinement of loci associated with lipid levels. Nat. Genet. 2013;45:1274–1283. doi: 10.1038/ng.2797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Graham J.W. Missing data analysis: Making it work in the real world. Annu. Rev. Psychol. 2009;60:549–576. doi: 10.1146/annurev.psych.58.110405.085530. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.