Abstract
We investigate numerically and analytically the coupled dynamics of transmembrane voltage and intracellular calcium cycling in paced cardiac cells using a detailed physiological model, and its reduction to a three-dimensional discrete map. The results provide a theoretical framework to interpret various experimentally observed modes of instability ranging from electromechanically concordant and discordant alternans to quasi-periodic oscillations of voltage and calcium.
I. INTRODUCTION
Over the last decade, there has been a growing recognition that dynamic instability of the cardiac action potential can play a crucial role in the initiation of life-threatening arrhythmias [1–6]. Most studies to date have focused on the dynamics of the transmembrane voltage governed by the standard equation
| (1) |
where Cm is the membrane capacitance, Iion is the total membrane current, which is the sum of the individual currents for Na+, K+, and Ca+ ions depicted schematically in Fig. 1, and Iext is a current stimulus applied at equally spaced time intervals T. A widely used approach to model the nonlinear dynamics of voltage is the one-dimensional discrete map An+1 = f(T−An) which relates the action potential duration (APD) at two subsequent beats via the restitution curve, An+1 = f(Dn), where Dn is the interval between the end of the previous action potential and the next [1–6]. The periodic fixed point of this map corresponding to the stable 1:1 rhythm undergoes a period-doubling instability to alternans, a sequence of long (L) and short (S) (LSLS…) APD, when the slope of the restitution curve is >1.
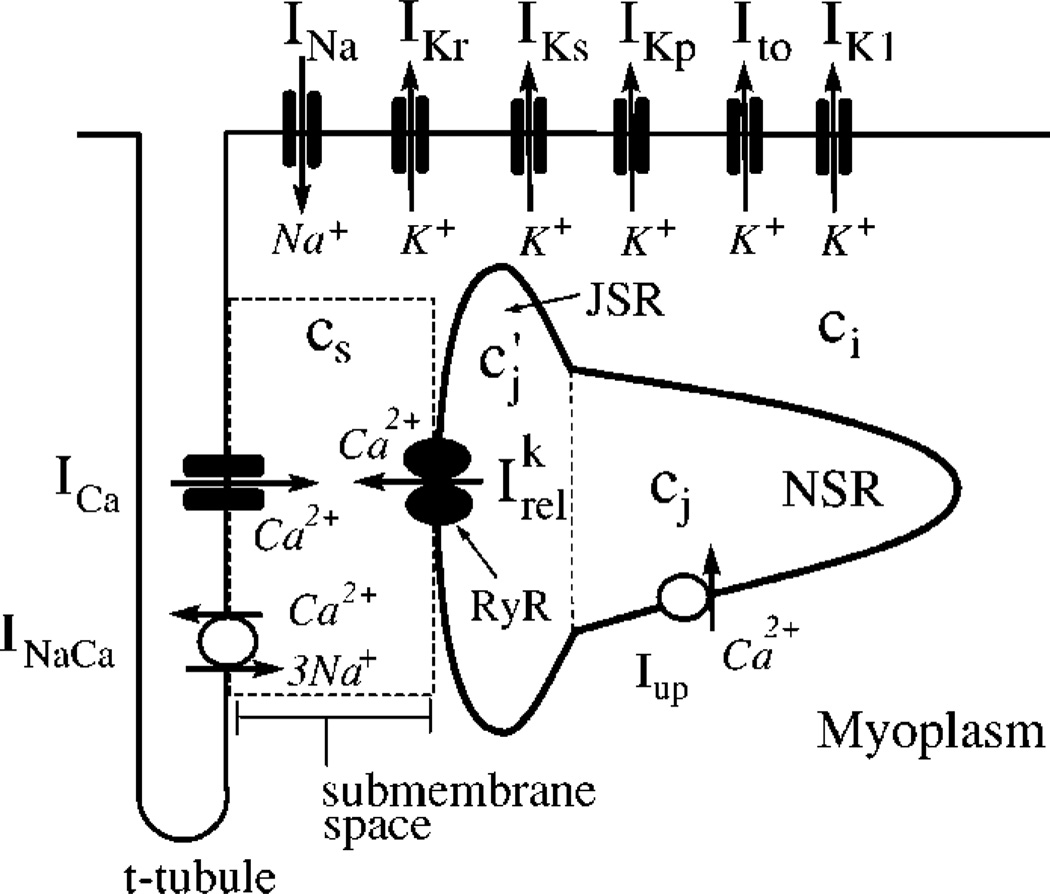
FIG. 1.
Illustration of currents that control the dynamics of voltage and intracellular calcium cycling.
Even though this map has been successful to model the unstable dynamics of voltage in some ionic models [3] and experiments [4], its predictions are inconsistent with a wide range of observations [5–8]. For example, Hall et al. [5] found that alternans can be absent even when the slope of the experimentally measured restitution curve is significantly larger than one, and conversely alternans are observed under ischemic conditions in which the restitution curve is flat [8]. Furthermore, recent experimental [7,9,10] and theoretical studies [11] suggest that alternans may result from an instability of intracellular calcium cycling. This result clearly indicates that the dynamical behavior of a cardiac cell is governed by nonlinear processes that are not taken into account by the restitution relationship.
In this article we explore the coupled nonlinear dynamics of voltage and calcium cycling in paced cardiac cells using a physiologically based ionic model. We demonstrate that a paced cell can be unstable to three distinct dynamical modes: concordant alternans with a long/short APD corresponding to a large/small calcium transient on alternate beats, discordant alternans with a long/short APD corresponding to a small/large calcium transient, and modulated voltage/calcium alternans with amplitudes that vary sinusoidally in time. The physiological conditions which favor a given dynamical behavior are explained. Finally, we interpret the model results in terms of a three variable iterated map which describes the beat-to-beat dynamics of calcium and voltage.
II. IONIC MODEL
A. Calcium cycling
To describe the electrophysiology of a cardiac myocyte we integrate a recently developed model of calcium (Ca2+) cycling [11], with an established ionic model due to Fox et al. [12] that is based on the Luo-Rudy currents [13]. The ionic currents, along with elements of the calcium cycling system, are illustrated in Fig. 1. The movement of calcium inside the cell is described by
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
where cs, ci, and cj are the concentrations of free calcium in a thin layer just below the cell membrane (submembrane space), in the bulk myoplasm, and the sarcoplasmic recticulum (SR), with volumes υs, υi, and υsr, respectively, where the SR volume includes both the junctional SR (JSR) and the network SR (NSR); is the average JSR concentration in the whole cell as defined in Ref. [11]. The concentrations cs and ci are in units of µM, whereas cj and are in units of µMυsr/υi. All calcium fluxes are divided by υi and have units of µM/s. Instantaneous buffering of calcium to SR and calmodulin sites in υi and υs is accounted for by the functions βs ≡ β(cs) and βi ≡ β(ci), and the currents describe time-dependent buffering to troponin C [11].
Calcium release from the SR is triggered by calcium entry into the cell via calcium-induced calcium release (CICR) [14]. Release occurs at a very large number of junctions where several L-type calcium channels (ICa) and a few release channels (ryanodine receptors; RyRs) face each other in close proximity. Only one of these junctions is shown in Fig. 1 for clarity. The total release current for the whole cell is the sum , of local currents at each junction where release channels are activated. The number of sparks N(t) varies in time since sparks are recruited stochastically and extinguish. The spatially localized nature of release is described by the dynamical equation for the release current [Eq. (6)], which captures phenomenologically three key experimental observations: (i) sparks are recruited at a rate proportional to the whole cell ICa, or N~ ICa [16], which insures that calcium release is graded with respect to calcium entry [15,17], (ii) the spark lifetime τr is approximately constant, and (iii) the amount of calcium released increases with SR concentration (SR load) [18].
B. Instability mechanisms
Calcium alternans, a period-doubling sequence of large (l) and small (s) calcium transient (lsls…peak ci), can occur independently of voltage alternans in experiments with a single cell paced with a periodic voltage wave form [9]. Both theoretical analyses [11,19] and recent experiments [10] support that a steep dependence of release on SR load is the underlying mechanism of these alternans. The sensitivity of release to SR load is controlled in the model by the slope of the function at high load
| (7) |
For a large enough slope, the model produces calcium alternans when paced with a periodic voltage wave form [11] as in the experiments of Ref. [9].
Steep APD restitution in the absence of calcium alternans can also induce APD alternans. This steepness is especially sensitive to the recovery from inactivation of the calcium current [12,13]
| (8) |
where iCa is the single channel current and d(f) is a fast (slow) voltage-dependent activation (inactivation) gate. For the intermediate range of pacing rates studied in the present work, increasing the time constant τf of the f gate in the equation f = [f∞(V) − f]/τf steepens APD restitution and promotes voltage alternans.
C. Voltage-calcium coupling
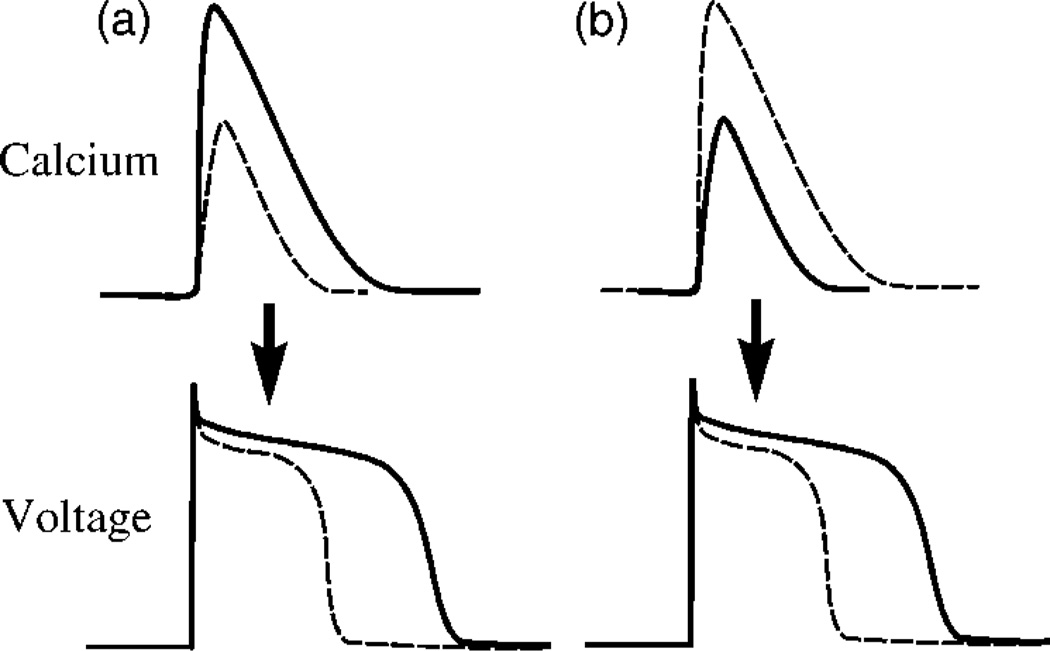
The mutual influence of voltage and calcium during the action potential is controlled by the membrane currents that depend on intracellular calcium concentration. These include ICa and the sodium-calcium exchanger INaCa. A larger calcium transient following a larger release enhances inactivation of ICa via the calcium-dependent gate fCa, and hence shortens the APD, but increases the chemical driving force for calcium extrusion from the cell via the exchanger. Since three Na+ ions enter the cell for every Ca2+ ion extruded, this increase in driving force increases the inward membrane current which prolongs the APD. Therefore, depending on the relative contributions of ICa and INaCa, increasing the magnitude of the calcium transient can either prolong (positive coupling) or shorten (negative coupling) the APD, as illustrated in Fig. 2. The sign of this coupling can be changed in the model by varying the exponent γ in the phenomenological expression
| (9) |
for the steady-state value of fCa, where the constant c̃s sets the concentration range for inactivation. Increasing γ enhances calcium-dependent inactivation of ICa and tends to make the coupling negative.
FIG. 2.
Illustration of the effect of an increase in the magnitude of the calcium transient, which can prolong or shorten the APD for (a) positive and (b) negative coupling, respectively. The sign of the coupling depends on the relative contributions of ICa and INaCa to the APD. The solid or dashed lines correspond to the same beat.
III. NUMERICAL RESULTS
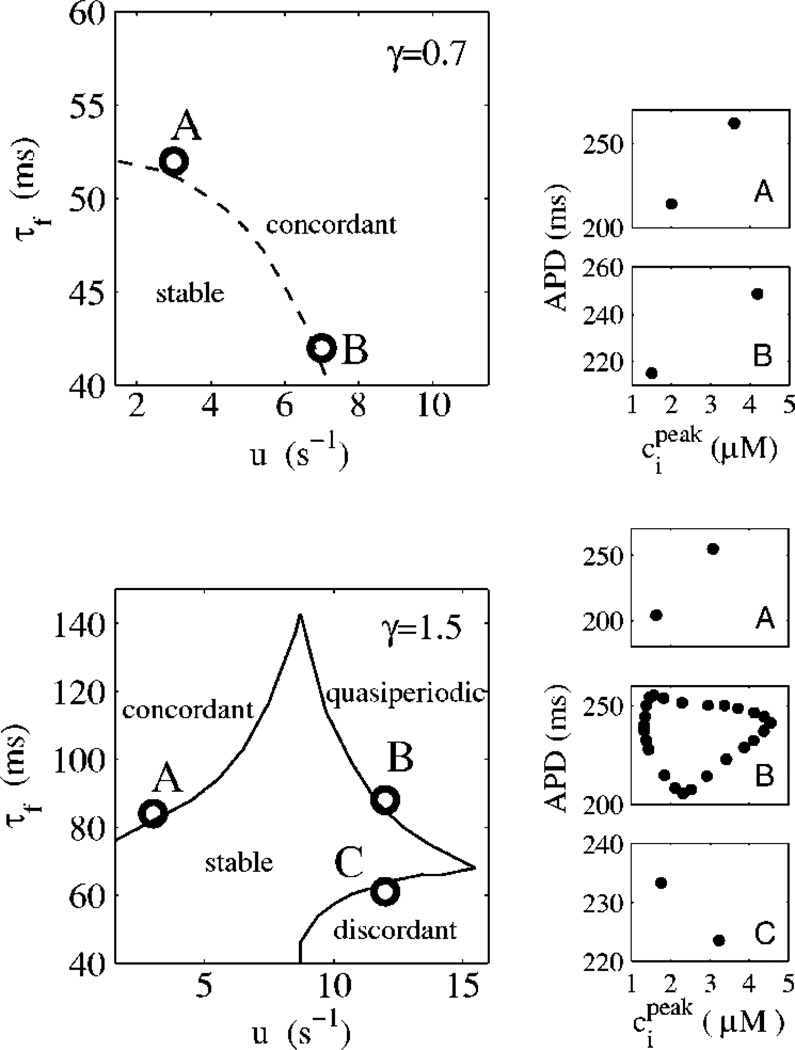
The dynamics of the system was studied numerically as a function of the two instability parameters u and τf which promote calcium and voltage alternans, respectively, and for two values of γ that were found to yield a positive (γ = 0.7) and a negative (γ = 1.5) coupling between voltage and calcium. All the other parameters are the same as in Refs. [11,12]. We study the stability of the periodic fixed by computing the steady-state APD, and the corresponding peak calcium transient . The APD is computed by measuring the time interval to 80% repolarization. In Fig. 3 we plot the stability boundaries as a function of the model parameters at a fixed pacing rate of T = 300 ms.
FIG. 3.
Stability boundaries in the ionic model for positive (dashed line; γ = 0.7) and negative (solid line; γ = 1.5) coupling. T = 300 ms. Examples of steady-state dynamics close to the stability boundaries are illustrated by plots of peak calcium concentration vs APD for a few labeled points. Higher order periodicities and irregular dynamics are observed further away from these boundaries.
The results plotted in Fig. 3 highlight the crucial role of the coupling between voltage and calcium in the dynamics. For positive coupling, the instability of the 1:1 periodic state always occurs through a period-doubling bifurcation to electromechanically concordant alternans with the long (short) APD corresponding to a large (small) calcium transient, independently of whether voltage or calcium is the dominant instability mechanism. In contrast, for negative coupling, three distinct modes of instability are found that correspond to: (i) concordant alternans, as for positive coupling, but only when the instability is dominated by voltage (large τf and small u), (ii) electromechanically discordant alternans with the long (short) APD corresponding to a small (large) calcium transient when the instability is dominated by calcium (small τf and large u), and (iii) quasiperiodic oscillations of APD and calcium transient amplitude with a phase and a Hopf frequency that vary with τf and u for the in between case where the instability is driven by both voltage and calcium. Both electromechanically concordant and discordant alternans have been widely observed experimentally under various conditions [20]. In addition, there is experimental evidence for quasiperiodicity in recordings of voltage [21] and, more recently, calcium [22].
IV. ITERATED MAP ANALYSIS
A. Iterated map of voltage-calcium dynamics
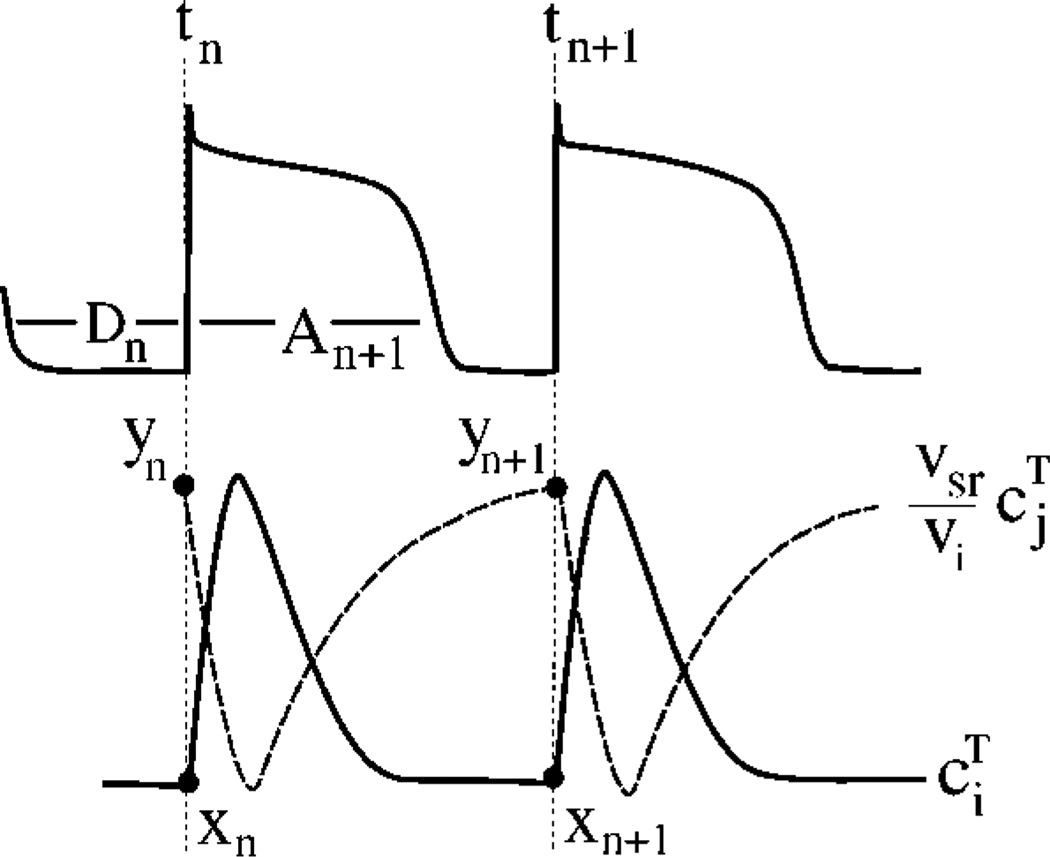
The numerical findings in the previous section were found to apply at a wide range of pacing intervals T. To interpret our results, and investigate the generality of the findings, we extend the two-dimensional (2D) iterated map developed in Ref. [11] for calcium cycling when the cell is paced with a fixed periodic voltage wave form, to the present case where the voltage is unclamped. To a good approximation, cs ≈ ci and preceding a stimulus [11], such that we only need to track beat-to-beat changes of ci and cj. Furthermore, we assume for simplicity that buffering of calcium is instantaneous such that there exists a unique nonlinear relationship between the concentration of free calcium ci(cj) and total calcium (free plus bound) . The basic variables of the map (Fig. 4) are then and at time tn = nT of the nth+1 stimulus, defined by and where both xn and yn are in units of µM, and the APD corresponding to this stimulus, An+1.
FIG. 4.
Definition of map variables.
The map is obtained by extending the restitution map to include the effect of calcium on the APD and by integrating the calcium flux equations
| (10) |
| (11) |
from time tn to time tn+1. This yields
| (12) |
| (13) |
| (14) |
respectively, where Rn, Un, and Δn are the integrals of Irel, Iup, and −ICa+INaCa over the time interval [tn, tn+1], respectively, and are functions of (Dn, xn, yn) for a fixed pacing period; υiRn and υiUn are the total amount of calcium released from and pumped into the SR over one beat, respectively, and υiΔn is the net total calcium entry into the cell over one beat which can be positive (negative) if the exchanger extrudes more (less) calcium from the cell than ICa brings into the cell.
B. Stability analysis
To make contact with the numerical stability boundaries in Fig. 3, we study the stability of the fixed point of the iterated map. The fixed point will be denoted by (A*,x*, y*). To begin, we exploit the fact that the total amount of calcium inside the cell is approximately constant during steady-state pacing. Hence, we can approximate the three-dimensional (3D) map [Eqs. (12)–(14)] by a 2D map by assuming that zn ≈ z*, where υizn ≡ υi(xn+yn) is the total calcium in the cell at time tn. This 2D map is given by Eqs. (12) and (13) with Dn = T−An, Δn = 0, and yn = z*−xn. A linear stability analysis of this 2D map yields the eigenvalues
| (15) |
where we have defined the quantities
| (16) |
| (17) |
| (18) |
which are evaluated at the fixed point of the map. Here, λυ and λc govern the degree of instability of the voltage and calcium systems, respectively, while C determines the sign of the coupling between the two systems. Making APD restitution (∂F/∂Dn) or the relationship between release and SR load (∂Rn/∂yn) steeper by increasing τf and u in the ionic model is equivalent to increasing λυ and λc, respectively. Graded release implies that ∂(Rn−Un)/∂Dn is positive for high pacing rates where ICa depends on Dn, such that the sign of C is governed by ∂F/∂yn−∂F/∂xn where the latter reflects the effect of the magnitude of the calcium transient on APD via ICa and INaCa (Fig. 2). The periodic fixed point undergoes a period-doubling bifurcation when |λ−| = 1 and a Hopf bifurcation for (λυ−λc)2+4C<0 when the pair of complex eigenvalues λ± = rei(π±ω), with and , crosses the unit circle (r = 1). For the latter case, the beat-to-beat oscillations of voltage and calcium are modulated with a period 2π/ω. Examination of the eigenvectors for C<0 reveals that alternans are discordant when λ− is real and λc>λυ.
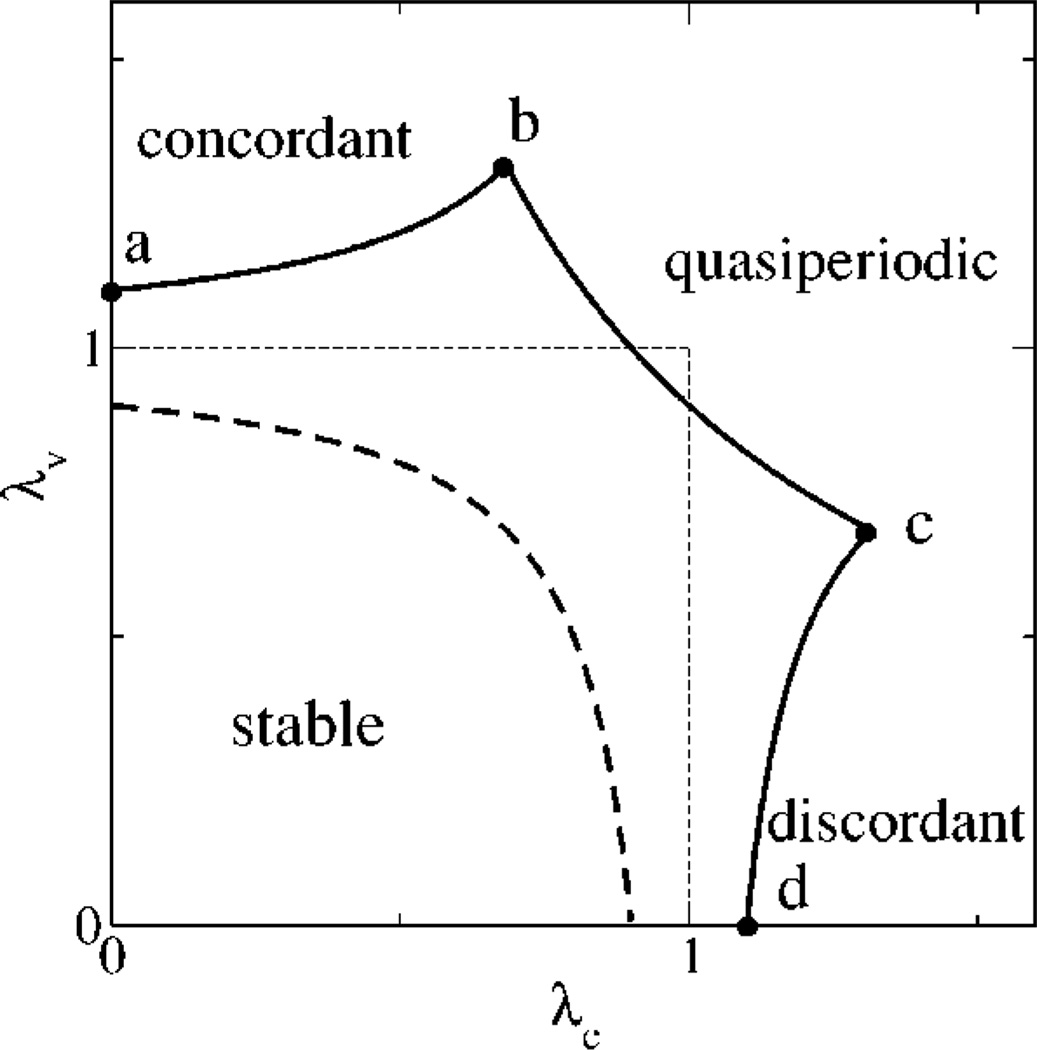
In Fig. 5 we plot the corresponding stability boundaries for positive and negative coupling in the (λc,λυ) plane. We find that the boundaries of stability are remarkably isomorphic to that obtained by simulations of the ionic model in the (u,τf) plane of Fig. 3. Note that we have not used explicit functional forms for the map terms, but only exploited the basic structure of the map given by Eqs. (12)–(14), along with the important assumption that total calcium is constant from beat to beat. This agreement shows that the coupled dynamics of voltage and calcium can be understood qualitatively in terms of the basic features of the system.
FIG. 5.
Stability boundaries from the map analysis for positive coupling C = 0.1 with concordant alternans along the dashed line, and negative coupling C = −0.1 (solid line), with concordant alternans, discordant alternans, and quasiperiodicity along the segments a–b, c–d, and b–c, respectively.
V. CONCLUSION
The numerical study of both the ionic model and the map in the nonlinear regime reveals the existence of a rich dynamical behavior including higher order periodicities (3:3, 4:4, etc.) as well as transitions to chaos mediated by a period-doubling cascade or intermittency depending on the parameters. Moreover, this model naturally contains memory [21,23] due to the slow change of total calcium concentration over several beats. Both of these aspects will be discussed in more detail elsewhere.
In conclusion, we have outlined the essential three-dimensional parameter space that controls dynamic instability of membrane voltage coupled to calcium cycling, and we have presented a theoretical framework in which to interpret experiments beyond the limitations of the one-dimensional restitution relationship. The main axes of this parameter space are the degree of instability of the voltage and calcium systems, and the sign of the coupling between the two systems, which is an important parameter to emerge from this work. These results provide a starting point to explore the role of calcium cycling in the spatiotemporal dynamics of tissue scale phenomenon. For instance, it will be interesting to see how the more complex single cell dynamics presented here, influences the dynamics of spiral waves in tissue. Studies in this direction may shed light on the role of calcium cycling on cardiac rhythm disorders.
ACNOWLEDGMENT
This research was supported by NIH SCOR P50-HL52319.
References
- 1.Karma A. Chaos. 1994;4:461. doi: 10.1063/1.166024. [DOI] [PubMed] [Google Scholar]
- 2.Garfinkel A, et al. Proc. Natl. Acad. Sci. U.S.A. 2000;97:6061. doi: 10.1073/pnas.090492697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Courtemanche M, Glass L, Keener JP. Phys. Rev. Lett. 1993;70:2182. doi: 10.1103/PhysRevLett.70.2182. [DOI] [PubMed] [Google Scholar]; Echebarria B, Karma A. ibid. 2002;88:208101. doi: 10.1103/PhysRevLett.88.208101. [DOI] [PubMed] [Google Scholar]
- 4.Nolasco JB, Dahlen RW. J. Appl. Physiol. 1968;25:191. doi: 10.1152/jappl.1968.25.2.191. [DOI] [PubMed] [Google Scholar]; Guevara MR, et al. Proceedings of the 11th Computers in Cardiology Conference; IEEE Computer Society; Los Angeles. 1984. p. 167. [Google Scholar]
- 5.Hall GM, Bahar S, Gauthier DJ. Phys. Rev. Lett. 1999;82:2995. [Google Scholar]; Hall GM, Gauthier DJ. ibid. 2002;88:198102. doi: 10.1103/PhysRevLett.88.198102. [DOI] [PubMed] [Google Scholar]
- 6.Fox JJ, Bodenschatz E, Gilmour RF., Jr Phys. Rev. Lett. 2002;89:138101. doi: 10.1103/PhysRevLett.89.138101. [DOI] [PubMed] [Google Scholar]
- 7.Pruvot EJ, et al. Circ. Res. 2004;94:1083. doi: 10.1161/01.RES.0000125629.72053.95. [DOI] [PubMed] [Google Scholar]
- 8.Dilly SG, Lab MJ. J. Physiol. (London) 1988;402:315. doi: 10.1113/jphysiol.1988.sp017206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chudin EJ, et al. Biophys. J. 1999;77:2930. doi: 10.1016/S0006-3495(99)77126-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Díaz ME, ONeill SC, Eisner DA. Circ. Res. 2004;94:650. doi: 10.1161/01.RES.0000119923.64774.72. [DOI] [PubMed] [Google Scholar]
- 11.Shiferaw Y, et al. Biophys. J. 2003;85:3666. doi: 10.1016/S0006-3495(03)74784-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Fox JJ, McHarg JL, Gilmour RF. Am. J. Physiol. 2002;282:H1534. doi: 10.1152/ajpheart.00612.2001. [DOI] [PubMed] [Google Scholar]
- 13.Luo CH, Rudy Y. Circ. Res. 1994;74:1071. doi: 10.1161/01.res.74.6.1071. [DOI] [PubMed] [Google Scholar]
- 14.Fabiato A. J. Gen. Physiol. 1985;85:189. doi: 10.1085/jgp.85.2.189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bers DM. Excitation-contraction Coupling and Cardiac Contractile Force. Boston: Kluwer; 2001. [Google Scholar]
- 16.Collier ML, Thomas AP, Berlin JR. J. Physiol. (London) 1999;516:117. doi: 10.1111/j.1469-7793.1999.117aa.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wier WG, et al. J. Physiol. (London) 1994;474:463. doi: 10.1113/jphysiol.1994.sp020037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Shannon TR, Ginsburg KS, Bers DM. Biophys. J. 2000;78:334. doi: 10.1016/S0006-3495(00)76596-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Eisner DA, et al. Circ. Res. 2000;87:1087. doi: 10.1161/01.res.87.12.1087. [DOI] [PubMed] [Google Scholar]
- 20. Rubenstein DS, Lipsius SL. Circulation. 1995;91:201. doi: 10.1161/01.cir.91.1.201. Walker ML, Rosenbaum DS. Cardiovasc. Res. 2003;57:599. doi: 10.1016/s0008-6363(02)00737-x. and earlier references therein.
- 21.Gilmour RF, Otani NF, Watanabe MA. Am. J. Physiol. 1997;272:H1826. doi: 10.1152/ajpheart.1997.272.4.H1826. [DOI] [PubMed] [Google Scholar]; Otani NF, Gilmour RF. J. Theor. Biol. 1997;187:409. doi: 10.1006/jtbi.1997.0447. [DOI] [PubMed] [Google Scholar]
- 22.Yin L, Bien H, Entcheva E. (unpublished). [Google Scholar]
- 23.Watanabe MA, Koller ML. Am. J. Physiol. 2002;282:H1534. doi: 10.1152/ajpheart.00351.2001. [DOI] [PubMed] [Google Scholar]