rMATS: Robust and flexible detection of differential alternative splicing from replicate RNA-Seq data

Significance

Alternative splicing (AS) is an important mechanism of eukaryotic gene regulation. Deep RNA sequencing (RNA-Seq) has become a powerful approach for quantitative profiling of AS. With the increasing capacity of high-throughput sequencers, it has become common for RNA-Seq studies of AS to examine multiple biological replicates. We developed rMATS, a new statistical method for robust and flexible detection of differential AS from replicate RNA-Seq data. Besides the analysis of unpaired replicates, rMATS includes a model specifically designed for paired replicates, such as case–control matched pairs in clinical RNA-Seq datasets. We expect rMATS will be useful for genome-wide studies of AS in diverse research projects. Our data also provide new insights about the experimental design for RNA-Seq studies of AS.

Abstract

Ultra-deep RNA sequencing (RNA-Seq) has become a powerful approach for genome-wide analysis of pre-mRNA alternative splicing. We previously developed multivariate analysis of transcript splicing (MATS), a statistical method for detecting differential alternative splicing between two RNA-Seq samples. Here we describe a new statistical model and computer program, replicate MATS (rMATS), designed for detection of differential alternative splicing from replicate RNA-Seq data. rMATS uses a hierarchical model to simultaneously account for sampling uncertainty in individual replicates and variability among replicates. In addition to the analysis of unpaired replicates, rMATS also includes a model specifically designed for paired replicates between sample groups. The hypothesis-testing framework of rMATS is flexible and can assess the statistical significance over any user-defined magnitude of splicing change. The performance of rMATS is evaluated by the analysis of simulated and real RNA-Seq data. rMATS outperformed two existing methods for replicate RNA-Seq data in all simulation settings, and RT-PCR yielded a high validation rate (94%) in an RNA-Seq dataset of prostate cancer cell lines. Our data also provide guiding principles for designing RNA-Seq studies of alternative splicing. We demonstrate that it is essential to incorporate biological replicates in the study design. Of note, pooling RNAs or merging RNA-Seq data from multiple replicates is not an effective approach to account for variability, and the result is particularly sensitive to outliers. The rMATS source code is freely available at rnaseq-mats.sourceforge.net/. As the popularity of RNA-Seq continues to grow, we expect rMATS will be useful for studies of alternative splicing in diverse RNA-Seq projects.

Alternative splicing generates tremendous transcriptomic and proteomic complexity in higher eukaryotes (1–4). Changes in alternative splicing underlie gene regulation in diverse biological and disease processes (5–7). However, it has been challenging to globally determine and compare gene splicing profiles among biological states. The RNA sequencing (RNA-Seq) technology has become a powerful tool for quantitative profiling of alternative splicing (3, 4, 8). Due to the high cost, earlier RNA-Seq studies of alternative splicing typically did not incorporate replicates in the study design (9–12). Nonetheless, it is important to note that biological variability remains a critical issue in high-throughput sequencing studies (13). Furthermore, as the cost of sequencing continues to decline, it has become feasible and increasingly common to carry out RNA-Seq on a large number of samples, with sufficient coverage to quantify alternative splicing in each individual sample. This creates an urgent need for new and robust analytic tools to detect alternative splicing changes from replicate RNA-Seq data.

Although a variety of computational methods have been developed for RNA-Seq analysis of alternative splicing (14), the existing methods have serious limitations and drawbacks for replicate RNA-Seq data. MISO (9), SpliceTrap (15), ALEXA-seq (16), and rSeqDiff (17) are designed for two-sample comparison and do not handle replicates. Cufflinks (18), FDM (19), and DiffSplice (20) use the Jensen–Shannon divergence metric to detect differential isoform proportion while accounting for variability among replicates. However, FDM and DiffSplice do not model the estimation uncertainty of isoform proportion in individual replicates (19, 20), a critical issue in alternative splicing quantitation as shown in the MISO paper (9). Cufflinks considers the estimation uncertainty but the test statistic does not distinguish the contributions from replicates with high or low degrees of estimation uncertainty (18). DEXSeq adopts a different approach of testing for the deviation of read counts on individual exons from the counts of the whole gene (21), but the statistical model does not estimate isoform proportion or use the information about alternative splicing patterns in splice junction reads. Importantly, no existing method handles paired replicate data, a popular study design in many basic and translational research settings (e.g., studies involving case–control matched pairs). Therefore, there is a need for new and robust analytic tools to detect alternative splicing changes from replicate RNA-Seq data, with the flexibility to handle different types of replicate study design (unpaired or paired).

We previously developed multivariate analysis of transcript splicing (MATS), a method for detecting differential alternative splicing between two RNA-Seq samples (22). Here we report a new statistical model and computer program, replicate MATS (rMATS), designed for analysis of replicate RNA-Seq data. Compared with existing methods for alternative splicing analysis of RNA-Seq data, rMATS has several key features. First, rMATS uses a hierarchical framework to model exon inclusion levels [denoted as $\psi$, or percent spliced in (9)], which simultaneously accounts for estimation uncertainty in individual replicates and variability among replicates. Second, in addition to the analysis of unpaired replicate data, rMATS includes a model specifically designed for paired replicates. This is achieved by introducing a bivariate normal distribution with a correlation parameter to model the correlation among matched pairs. The use of pairing information in paired replicate data improves the statistical power. Third, rMATS incorporates a flexible hypothesis-testing framework in which the null and alternative hypotheses for differential alternative splicing are defined by users. Specifically, rMATS uses a likelihood-ratio test to calculate the P value that the difference in the mean $\psi$ values between two sample groups exceeds a given threshold (e.g., $\left|\mathrm{\Delta }\psi \right|\hspace{0.17em}=\hspace{0.17em}|{\psi }_{i1}-{\psi }_{i2}|\hspace{0.17em}>5\%$). Under this framework, rMATS can assess the statistical significance over any user-defined magnitude of splicing change, as opposed to only testing the equality of $\psi$ between sample groups. Additionally, the use of the likelihood-ratio test in rMATS, as opposed to the sampling-based P value calculation in MATS (22), substantially improves the speed of the computation. Finally, it should be noted that the statistical model of rMATS normalizes the lengths of individual splice variants. This allows rMATS to analyze all major types of alternative splicing patterns and use RNA-Seq reads mapped to both exons and splice junctions. The rMATS software and user manual are freely available for download at rnaseq-mats.sourceforge.net/.

Results

rMATS Statistical Model for Unpaired Replicates.

The basic principle in RNA-Seq analysis of alternative splicing is to use RNA-Seq reads mapped to different isoforms to estimate the isoform proportion (3, 4). For example, for an alternatively spliced cassette exon, we can use the counts of reads mapped to the exon inclusion or skipping isoform to estimate the exon inclusion level $\psi$, defined as the percentage of the exon inclusion transcripts that splice from the upstream exon into the alternative exon and then into the downstream exon, among all such exon inclusion transcripts plus exon skipping transcripts that splice from the upstream exon directly into the downstream exon (Fig. 1). In a two-group RNA-Seq dataset with replicates, the estimate of $\psi$ is influenced by multiple factors. In each individual sample, the estimation uncertainty of $\psi$ is influenced by the sequencing coverage for the event of interest, with a higher RNA-Seq read count leading to a more reliable estimate (9). Within each sample group, there is variability among replicates due to biological or technical reasons. A robust method for differential alternative splicing analysis of replicate RNA-Seq data needs to consider these factors.

Fig. 1.

The schematic diagram of an exon skipping event. The exon inclusion reads $\left(I\right)$ are the reads from the upstream splice junction, the alternative exon itself, and the downstream splice junction. The exon skipping reads $\left(S\right)$ are the reads from the skipping splice junction that directly connects the upstream exon to the downstream exon.

In rMATS, we use a hierarchical framework to simultaneously account for estimation uncertainty in individual replicates and variability among replicates. Below we briefly introduce the notation and statistical model of rMATS, using the exon skipping type of alternative splicing events as the example. For a skipped exon, the exon inclusion level $\psi$ can be estimated by the count of reads specific to the exon inclusion isoform $\left(I\right)$ and the count of reads specific to the exon skipping isoform $\left(S\right)$ (illustration in Fig. 1). The exon inclusion reads are the reads from the upstream splice junction, the alternative exon itself, and the downstream splice junction. The exon skipping reads are the reads from the skipping splice junction that directly connects the upstream exon to the downstream exon. Other types of alternative splicing events can also be modeled by this framework with details illustrated in Fig. S1. Given the effective lengths (i.e., the number of unique isoform-specific read positions) of the inclusion isoform $\left(l_I\right)$ and the skipping isoform $\left(l_S\right)$, the exon inclusion level $\psi$ can be estimated as $\widehat{\psi }=\left(I/l_I\right)/\left(I/l_I+S/l_S\right)$. Assuming that the inclusion read count $I$ follows a binomial distribution with the total read count $n=I+S$, we have

$$I|\psi \sim \text{Binomial}\left(n=I+S,p=f\left(\psi \right)=\frac{l_I\psi }{l_I\psi +l_S(1-\psi )}\right),$$ [1]

where the binomial distribution models the estimation uncertainty of $\psi$ as influenced by the total read count $n$, and the proportion of reads from the exon inclusion isoform is represented by the length normalization function $f\left(\psi \right)$ that normalizes the exon inclusion level $\psi$ by the effective lengths of the isoforms.

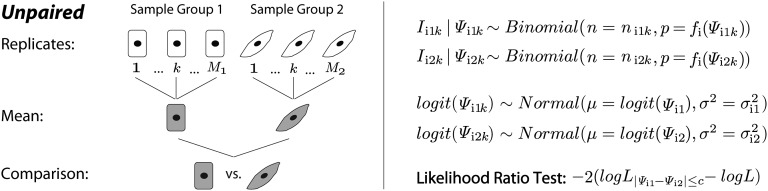
The variability within a sample group reflects the difference of exon inclusion levels among replicates. The variability can be modeled by random effects in a mixed model. Considering two sample groups $j=1,\hspace{0.5em}2$, the first group has $M_1$ replicates $\left(k=1,\hspace{0.5em}...\hspace{0.5em},M_1\right)$ and the second group has $M_2$ replicates $\left(k=1,\hspace{0.5em}...\hspace{0.5em},M_2\right)$. For each exon $i$, we estimate the group mean of exon inclusion levels of groups 1 and 2 (${\psi }_{i1}$ and ${\psi }_{i2}$) as fixed effects. Then we assume that the logit transformation of exon inclusion levels in individual replicate $k\hspace{0.17em}\left({\psi }_{ijk}\right)$ follows a normal distribution with the logit of the group mean $\left({\psi }_{ij}\right)$ and the group variance $\left({\sigma }_{ij}\right)$ for modeling the variability among replicates:

$$\text{logit}\left({\psi }_{ijk}\right)\sim \text{Normal}\left(\mu =\text{logit}\left({\psi }_{ij}\right),{\sigma }^2={\sigma }_{ij}^2\right).$$ [2]

In sum, rMATS accounts for the estimation uncertainty of individual replicates (Eq. 1) and the variability among replicates (Eq. 2) in a hierarchical model (Fig. 2), which simultaneously estimates both effects. Using a likelihood-ratio test, we test whether the difference of the group mean between the two sample groups exceeds a user-defined threshold $c$, against the null hypothesis $\left|\mathrm{\Delta }{\psi }_i\right|\hspace{0.17em}=\hspace{0.17em}|{\psi }_{i1}-{\psi }_{i2}|\hspace{0.17em}\le c$. Compared with the commonly used equality test of whether the difference is greater than 0 (i.e., null hypothesis $|{\psi }_{i1}-{\psi }_{i2}|\hspace{0.17em}=0$), our approach is more generic and provides the flexibility to assess the statistical significance over any user-defined magnitude of effect. Details of the rMATS parameter estimation algorithm and likelihood-ratio test are described in SI Materials and Methods.

Fig. 2.

The statistical framework of the unpaired rMATS model. For exon $i$ and the $k\text{th}$ replicate, the total RNA-Seq read counts for the exon inclusion and skipping isoforms are denoted as $n_{i1k},n_{i2k}$ for sample groups 1 and 2, respectively. The read counts for the exon inclusion isoform are denoted as $I_{i1k},I_{i2k}$. The exon inclusion levels are denoted as ${\psi }_{i1k},{\psi }_{i2k}$. The proportion of the read count from the exon inclusion isoform is adjusted by a normalization function $f_i$ that considers the lengths of the exon inclusion and skipping isoforms. rMATS uses a binomial distribution to model the read count from the exon inclusion isoform given the exon inclusion level in each individual replicate and a logit-normal distribution to model the variation among replicates within sample group. The mean and variance of exon inclusion levels in the two sample groups are denoted as ${\psi }_{i1},{\psi }_{i2}$ and ${\sigma }_{i1}^2,{\sigma }_{i2}^2$. A likelihood-ratio test is used to calculate the P value that the difference between ${\psi }_{i1}$ and ${\psi }_{i2}$ exceeds a given user-defined threshold $c$.

Simulation Studies of rMATS.

We first evaluated the performance of rMATS using a simulation study. In total 5,000 exons were simulated for two sample groups, with 5% of the exons from the alternative hypothesis that the exons were differentially spliced ($\left|\mathrm{\Delta }\psi \right|>5\%$ between sample groups) and 95% of the exons from the null hypothesis that the exons were not differentially spliced ($\left|\mathrm{\Delta }\psi \right|\le 5\%$ between sample groups). Three levels of standard deviations (SDs) of 0.01, 0.02, or 0.05 were used in the simulation to represent the variability of $\psi$ among replicates. The read counts of exons were sampled empirically from an RNA-Seq dataset of prostate cancer cell lines (Materials and Methods).

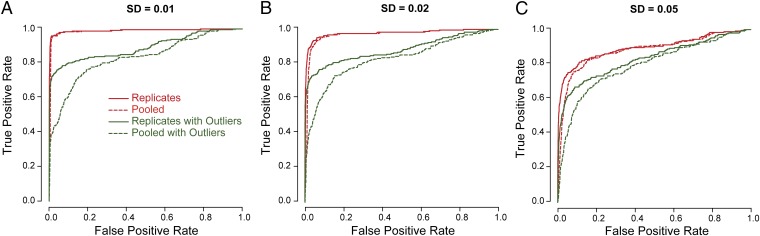
We analyzed these simulated data using rMATS. As a comparison, we pooled data from individual replicates and analyzed the pooled data, using a reduced version of rMATS that adopted the same likelihood-ratio test for two-sample comparison. This is equivalent to performing RNA-Seq on RNA pooled from multiple biological replicates. In all three sets of simulations, the analysis by rMATS on the replicate data outperformed the analysis of the pooled data, especially when the sample variability increased (Fig. 3).

Fig. 3.

Simulation studies to assess the performance of rMATS and the importance of replicates. We simulated 5,000 exons, where 5% of the exons were differentially spliced and the rest were not differentially spliced. We simulated five replicates in each sample group. The exon inclusion levels in individual replicates were simulated from a normal distribution with different SDs in three different studies: (A) SD = 0.01, (B) SD = 0.02, and (C) SD = 0.05. To assess the effect of outliers, we also simulated an additional dataset where 1 of the 10 replicates (of the two sample groups) had a large SD of 0.2. In all scenarios, the analysis by rMATS on replicate data always outperformed the analysis of pooled data (without the information of replicates), as indicated by the receiver operating characteristic (ROC) curves. In addition, the analyses on replicate data were more robust against outliers because rMATS modeled the variation within sample groups, whereas the ROC curves of the pooled data (without the information of replicates) were heavily influenced by outliers.

To investigate the effect of outliers, we performed a new round of simulation. Specifically, we simulated 1 outlier replicate of 10 replicates from the two sample groups with a large SD of 0.2 in the normal distribution. The introduction of outliers caused a modest drop in the performance of rMATS on the replicate data, but a much more significant drop on the pooled data (Fig. 3), indicating that the study design incorporating replicates is much more robust against outliers. For example, in the presence of outliers, at the 5% false positive rate the true positive rates on the replicate data were 76%, 72%, and 61%, respectively, for the three levels of within-group variation (Fig. 3 A–C), compared with 46%, 47%, and 40% on the pooled data. Together, these results suggest that with a fixed RNA-Seq budget, we will obtain more reliable results by indexing and sequencing multiple replicates from individual sample groups, as opposed to pooling biological replicates before sequencing. The use of replicates is especially critical in studies with a large sample-to-sample variation or a high probability of outlier samples.

In addition to the setting of 5% alternative exons being differentially spliced, we also performed simulation tests in which 10% (Fig. S2) or 20% (Fig. S3) of the exons were simulated from the alternative hypothesis (i.e., differentially spliced) and the rest were from the null hypothesis. We obtained similar results in these settings (Figs. S2 and S3).

rMATS Analysis of Prostate Cancer Cell Lines.

To demonstrate the utility of rMATS, we analyzed an RNA-Seq dataset generated on three independent cell cultures of two prostate cancer cell lines, PC3E and GS689 (23, 24). The PC3E cell line has epithelial cell characteristics whereas the GS689 cell line is recovered from a secondary metastatic liver tumor and exhibits mesenchymal and invasive properties (24). The RNA-Seq data consisted of 746 million 2 × 101-bp paired reads for six unpaired replicates (three replicates per cell line, Table S1).

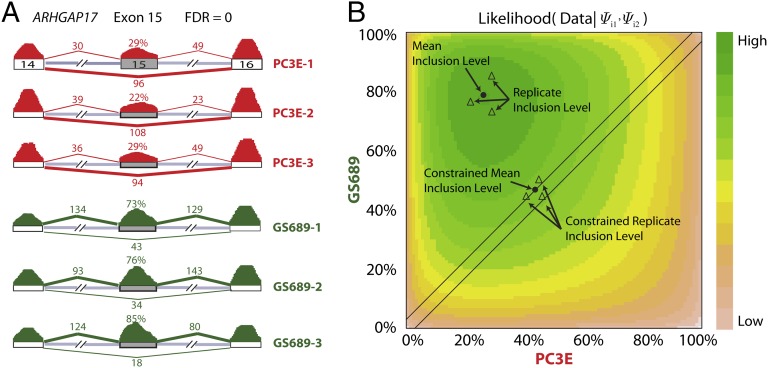
At the threshold of $\left|\mathrm{\Delta }\psi \right|>5\%$ and false discovery rate (FDR) of ≤1%, rMATS identified 721 differential alternative splicing events (Table S2) between the two cell lines, using both the splice junction counts and the exon body counts as the input for rMATS. An example of a differentially spliced exon in ARHGAP17 is shown in Fig. 4. We randomly selected 34 exon skipping events for validation by quantitative fluorescent RT-PCR (Fig. S4). These 34 exons covered a broad range of $\psi$ values with the between-group difference $\left|\mathrm{\Delta }\psi \right|$ ranging from 0.10 to 0.90. The $\mathrm{\Delta }\psi$ values estimated by RNA-Seq and RT-PCR were highly correlated (Pearson’s correlation coefficient r = 0.96, Fig. S5). Thirty-two of the 34 candidate exons were validated by RT-PCR (Fig. S4 and Datasets S1 and S2), yielding a high validation rate of 94%.

Fig. 4.

An example of rMATS unpaired analysis of prostate cancer cell lines. (A) The RNA-Seq read counts and estimated exon inclusion levels of ARHGAP17 exon 15 in a pair of epithelial (PC3E) and mesenchymal (GS689) cell lines, each with three biological replicates. (B) The log likelihood of observing the data given all possible combinations of ${\psi }_{i1},{\psi }_{i2}$. In this likelihood-ratio test, the null hypothesis is $\left|{\psi }_{i1}-{\psi }_{i2}\right|\le 5\%$ and the alternative hypothesis is $\left|{\psi }_{i1}-{\psi }_{i2}\right|>5\%$. The combination of ${\psi }_{i1},{\psi }_{i2}$ that maximizes the likelihood of observing the data under the constraint of the null hypothesis or without such a constraint is indicated.

The Influence of Sample Size and Sequencing Depth on Detection Accuracy.

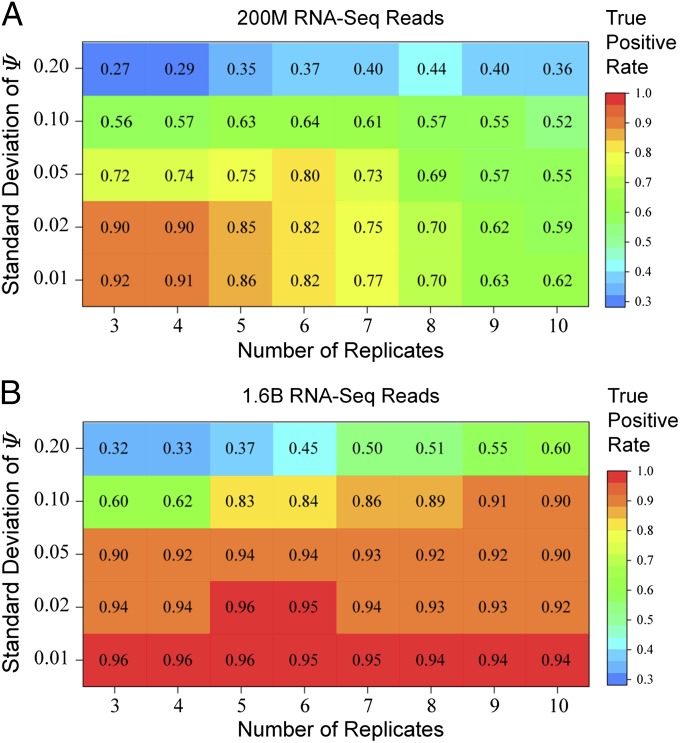
A common question in designing RNA-Seq studies is the optimal RNA-Seq depth for analysis of alternative splicing. With a fixed budget, an investigator has to consider the trade-off between the number of replicates to profile and the sequencing depth in each replicate. A better estimation of the variability among replicates can be achieved by increasing the number of replicates, but doing so will reduce the sequencing depth and increase the estimation uncertainty in individual replicates. On the other hand, a smaller number of replicates will distribute more reads to each replicate and reduce the estimation uncertainty in individual replicates, but at the risk of having insufficient replicates to estimate the variability among replicates. To address this issue, we designed a simulation study to evaluate the effect of sample size and sequencing depth on detection accuracy. In the first set of simulations, we set a budget of generating 200 million paired-end RNA-Seq reads in each sample group. This is comparable to one lane of RNA-Seq per sample group on the Illumina sequencer. Under each sample size (from 3 to 10 replicates per sample group), five different levels of SDs (SD = 0.01, 0.02, 0.05, 0.10, and 0.20) were used to model different levels of variability among replicates. The RNA-Seq read counts were simulated mimicking the read count distribution in the prostate cancer cell line data, using the procedure described in Materials and Methods.

Our analysis shows that the choice of optimal sample size and sequencing depth is heavily influenced by the level of within-group variability. We compared the true positive rate at the 5% false positive rate under different scenarios. With a small SD, the variability among replicates was low. Therefore, only a small number of replicates were needed to reach the highest true positive rate. For example, at SD = 0.01 and 0.02, only three replicates were needed to reach the highest true positive rates of 92% and 90%, respectively (Fig. 5A). Perhaps not surprisingly, further increasing the number of replicates led to a reduction in the true positive rate, likely due to the reduced sequencing depth and increased estimation uncertainty in each individual replicate. By contrast, when the level of variability among replicates was high, more replicates were needed to achieve the best possible true positive rate. At SD = 0.05 and 0.10, under 5% false positive rate six replicates were needed to reach the highest true positive rates of 80% and 64%, respectively. At SD = 0.20, eight replicates were needed for the highest true positive rate of 44% (Fig. 5A).

Fig. 5.

Simulation studies to assess the influence of sample size and sequencing depth on detection accuracy. We simulated five different SDs (SD = 0.01, 0.02, 0.05, 0.10, and 0.20) within the sample group. The true positive rate at 5% false positive rate was calculated and plotted for each set of simulated data. (A) A total of 200 million paired-end reads were simulated for each sample group and distributed among 3–10 replicates. (B) A total of 1.6 billion paired-end reads were simulated for each sample group and distributed among 3–10 replicates.

We also investigated the situation where a larger budget allowed 1.6 billion reads in each sample group, comparable to one flow cell of Illumina RNA-Seq per sample group (Fig. 5B). The increased sequencing depth reduced estimation uncertainty in individual replicates. As expected, this always improved the detection accuracy compared with the low coverage data of 200 million reads per sample group (Fig. 5B vs. Fig. 5A). At this high sequencing depth, with low levels of within-group variability (SD = 0.01–0.05) we always obtained a true positive rate of ≥90% at 5% false positive rate, regardless of the number of replicates (3–10). As the within-group variability increased (SD = 0.10 and 0.20), more replicates were needed to achieve the best possible true positive rate. For example, at SD = 0.10, 9 replicates were needed to achieve the highest true positive rate of 91%. At SD = 0.20, 10 replicates were needed to achieve the highest true positive rate of 60%. These data suggest when the total sequencing coverage is high, the estimation uncertainty in individual replicates is not a major concern, and it is generally preferable to increase the sample size to better capture the extent of within-group variability.

rMATS Statistical Model for Paired Replicates.

Transcriptome studies often adopt paired study design, for example disease-control matched pairs in the analysis of patient tissue specimens. In principle, the use of pairing information can reduce individual-specific variation and improve the statistical power. However, currently no method is available for alternative splicing analysis of paired RNA-Seq data. To fill this gap, we developed a model of rMATS for RNA-Seq data with paired replicates. This model uses a covariance structure to model the paired replicates between two sample groups. For each exon $i$, the correlation between paired replicates is modeled by the parameter ${\rho }_i$ in the covariance structure (Fig. 6; details in Materials and Methods and SI Materials and Methods). We observed that some exons had more variation among different individuals and less variation in the difference between the two paired samples from the same individual. These exons had strong correlations between paired samples. By contrast, some other exons had less variation among different individuals and more variation in the difference between the two paired samples, leading to weak correlations between paired samples. Therefore, we consider that each exon $i$ has an exon-specific correlation parameter ${\rho }_i$ between paired replicates, which can be estimated from data. Details of the parameter estimation procedure are described in SI Materials and Methods.

Fig. 6.

The statistical framework of the paired rMATS model. Each replicate in sample group 1 is paired with another replicate in sample group 2. For exon $i$ and the $k\text{th}$ replicate, the total RNA-Seq read counts for the exon inclusion and skipping isoforms are denoted as $n_{i1k},n_{i2k}$ for sample groups 1 and 2, respectively. The read counts for the exon inclusion isoform are denoted as $I_{i1k},I_{i2k}$. The exon inclusion levels are denoted as ${\psi }_{i1k},{\psi }_{i2k}$. The proportion of the read count from the exon inclusion isoform is adjusted by a normalization function $f_i$ that considers the lengths of the exon inclusion and skipping isoforms. rMATS uses a bivariate normal distribution to model the variation among replicates within sample group and the correlation between paired replicates. The mean and variance of exon inclusion levels in the two sample groups are denoted as ${\psi }_{i1},{\psi }_{i2}$ and ${\sigma }_{i1}^2,{\sigma }_{i2}^2$. The correlation parameter is denoted as ${\rho }_i$.

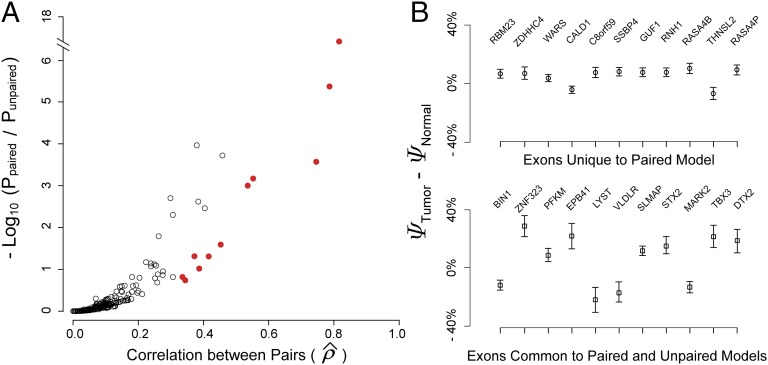
To illustrate the utility of the rMATS paired model, we used it to identify differential alternative splicing events from 65 tumor-normal matched pairs in the clear cell renal cell carcinoma (ccRCC) RNA-Seq data from The Cancer Genome Atlas (TCGA) (25), at a threshold of $\left|\mathrm{\Delta }\psi \right|>5\%$ (i.e., the null hypothesis $\left|\mathrm{\Delta }\psi \right|\hspace{0.17em}\le 5\%$) and FDR ≤ 1%. For comparison, we also applied the unpaired rMATS model to the same RNA-Seq data, using the same statistical criteria. The unpaired rMATS model identified 304 differential exon skipping events. The paired rMATS model identified 315 differential exon skipping events (Dataset S3), including all 304 events identified by the unpaired rMATS. The 11 additional events identified only by the paired rMATS are listed in Dataset S4. Of these 315 exons, 80 were also differentially spliced between the PC3E and GS689 cell lines (Fisher’s exact test P = 5.0 × 10⁻⁴⁹ for the significance of overlap over random expectation), with the splicing profile of tumor samples resembling that of the mesenchymal GS689 cell line. This is consistent with the mesenchymal phenotype of ccRCC (26). As expected, the use of pairing information generally led to increased statistical significance (smaller P value), particularly for exons with a high degree of correlation among matched pairs across patients (Fig. 7A). Compared with exons common to both models, the 11 exons unique to paired rMATS had smaller $\left|\mathrm{\Delta }\psi \right|$ between tumor and normal samples (Wilcoxon’s two-sided test P = 1.4 × 10⁻¹¹), but the SD of $\mathrm{\Delta }\psi$ between matched pairs was also smaller (Wilcoxon’s two-sided test P = 0.02) (Fig. 7B). This suggests the paired rMATS model can reveal more subtle but consistent changes in splicing in paired replicates.

Fig. 7.

A comparison between paired and unpaired rMATS models. (A) We applied paired and unpaired rMATS to 65 tumor-normal matched pairs in TCGA RNA-Seq data of clear cell renal cell carcinoma (ccRCC). For 315 exons with FDR ≤ 1% by either model, we compared the P values from the paired and unpaired models, relative to the estimated correlation parameter $\rho$ between pairs. Paired rMATS produced smaller (more significant) P values, especially for exons with a high degree of correlation among matched pairs. The 11 exons unique to paired rMATS are marked with red circles. (B) The mean and the SEM of Δψ (between tumor-normal matched pairs) for the 11 exons unique to paired rMATS and 11 randomly selected exons common to both paired and unpaired rMATS.

To confirm that the normal distribution appropriately models the distribution of logit exon inclusion levels, we used the TCGA ccRCC RNA-Seq data to inspect the distribution of logit exon inclusion levels. Figs. S6 and S7 show the histograms of logit exon inclusion levels of 25 randomly selected alternative exons in normal controls or tumor samples. As demonstrated by these histograms, the logit exon inclusion levels can be approximated by a normal distribution. We also analyzed the SDs of exon inclusion levels in the ccRCC dataset (Fig. S8). In normal samples, the vast majority (90%) of exons had SD ≤ 0.2, including 57% with SD ≤ 0.1 and 15% with SD ≤ 0.05. Interestingly, the ccRCC tumor samples had larger SDs of exon inclusion levels compared with the normal samples (one-sided Kolmogorov–Smirnov test P = 3.4 × 10⁻⁸), likely reflecting the increased heterogeneity among tumor samples.

Comparison of rMATS to Other Methods.

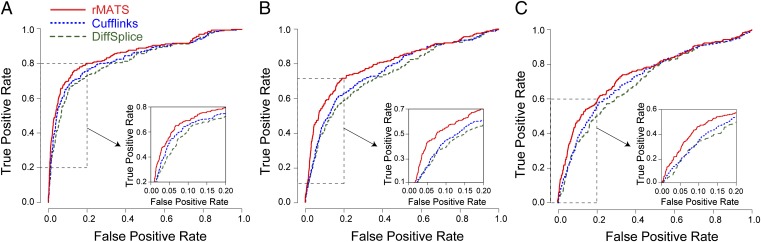
We performed simulation studies to compare the performance of rMATS (the unpaired model) to Cufflinks (2.2.1) (18) and DiffSplice (0.1.1) (20), which use the Jensen–Shannon divergence (JSD) metric to test the difference in splicing levels/isoform proportions between two sample groups. Our model and the JSD-based methods have conceptual differences in how they treat data points with different read counts and varying degrees of estimation uncertainty. Intuitively, in rMATS individual replicates with small read counts have smaller effects on the overall test statistic than replicates with large read counts. By contrast, all of the replicates have the same level of contribution to the JSD-based test statistic, regardless of the read counts and degrees of estimation uncertainty. To perform a direct comparison between these methods, we conducted a simulation study following the read count distribution from TCGA ccRCC RNA-Seq data (details of the simulation study are in Materials and Methods). Although rMATS has the flexibility to test splicing difference above any user-defined threshold $\left(\left|\mathrm{\Delta }\psi \right|\hspace{0.17em}>c\right)$, because both Cufflinks and DiffSplice only test the equality of $\psi$ between sample groups, to perform a fair comparison we ran rMATS to test nonzero group difference $\left(\left|\mathrm{\Delta }\psi \right|>0\%\right)$. As shown by the receiver operating characteristic (ROC) curves (Fig. 8A), rMATS outperformed Cufflinks and DiffSplice with area under the curve (AUC) of 86% vs. 83% and 81%, respectively. The difference was more prominent in the most critical area of the ROC curve where the false positive rate was low (<0.2), with an improvement in the true positive rate of up to 8% and 15% over Cufflinks and DiffSplice, respectively (Fig. 8A, Inset). To assess the effects of small read counts or outliers, we performed additional tests in which one of the replicates was randomly set to have only 10% of the typical read coverage (Fig. 8B) or with a large SD of exon inclusion levels (Fig. 8C) (Materials and Methods). In these simulations, the improvement of rMATS over Cufflinks and DiffSplice became more significant. Specifically, when the false positive rate was low (<0.2), we observed an improvement in the true positive rate of up to 19% over both Cufflinks and DiffSplice in Fig. 8B (Inset) and up to 16% over both in Fig. 8C (Inset). In summary, rMATS consistently outperformed the two JSD-based methods in all three settings, illustrating the benefit of appropriately accounting for the estimation uncertainty of isoform proportions.

Fig. 8.

(A–C) Simulation studies to compare the performance of rMATS, Cufflinks, and DiffSplice. The performances of these methods on a simulated dataset are indicated by their respective receiver operating characteristic (ROC) curves. Insets (Bottom Right) highlight the most critical area of the ROC curve where the false positive rate is low (<0.2). (A) Five replicates were simulated for each sample group. The exon inclusion levels in individual replicates were simulated from a normal distribution with SD = 0.05. The read counts were sampled from TCGA ccRCC RNA-Seq data. (B) One of the replicates was randomly set to have only 10% of the typical read coverage. (C) One of the replicates was randomly set as an outlier with large SD of exon inclusion levels (SD = 0.2).

Discussion

RNA-Seq has become a widely used technology for transcriptome studies, especially the analysis of alternative splicing. Due to the cost, earlier RNA-Seq studies typically represented each sample condition by a single or pooled RNA sample without replicates (9–12). Consequently, many first-generation tools for alternative splicing analysis of RNA-Seq data were developed for two-sample comparison without replicates (9, 15–17, 22). As the cost of RNA-Seq has declined rapidly in the past few years, it has become common for RNA-Seq studies to analyze multiple replicates. Moreover, in studies of clinical RNA samples where the sample-by-sample variability is expected to be significant, biological replicates are essential. We have developed rMATS, a new statistical model to identify differential alternative splicing events from two-group RNA-Seq data with replicates. rMATS uses a hierarchical framework to simultaneously model the variability among replicates and the estimation uncertainty of isoform proportion in individual replicates. It should be noted that the estimation uncertainty of isoform proportion is a well-recognized issue in RNA-Seq analysis of alternative splicing, because the confidence level of such estimates depends on the sequencing coverage for individual splicing events (4, 9). By appropriately modeling the estimation uncertainty, rMATS improves over other existing methods for differential alternative splicing analysis of replicate RNA-Seq data, as evidenced by our simulation studies comparing rMATS, Cufflinks, and DiffSplice in multiple experimental settings (Fig. 8). Another important feature of rMATS is its much greater flexibility in the detection of differential alternative splicing. Different from all other methods that test only the equality of isoform proportion between sample groups, the hypothesis-testing framework of rMATS can assess the statistical significance over any given user-defined magnitude of splicing change. Additionally, rMATS provides a statistical model for detecting differential alternative splicing from paired RNA-Seq replicates. Through simulation studies and the analysis of real RNA-Seq data together with RT-PCR validation, we demonstrate that rMATS is a robust and flexible method for differential splicing analysis of replicate RNA-Seq data.

We carried out a series of simulation studies to evaluate factors that influence RNA-Seq analysis of differential alternative splicing. Previous studies have investigated the experimental design for RNA-Seq with respect to the use of replicates, sample size, and sequencing depth (27–31). These studies have focused on the goal of detecting differential gene expression. For example, Liu et al. suggested that 10 million reads would be the appropriate sequencing depth for differential expression studies (30). There is little information in the literature regarding these issues in the experimental design for alternative splicing studies, which have unique challenges as reliable quantitative estimates of individual alternative splicing events would require a much higher sequencing depth. Here, the statistical framework of rMATS allows us to perform a series of simulation studies to assess how various experimental factors influence the ability to detect differential alternative splicing. Our data suggest that even with the need for much higher sequencing depth, the use of replicates remains essential for differential alternative splicing studies, and it is preferable to incorporate at minimum several replicates even at the expense of reduced sequencing depth on individual replicates. Moreover, certain commonly used experimental design or data analysis strategies in RNA-Seq studies of alternative splicing, such as pooling RNAs or merging RNA-Seq data from multiple replicates, are not recommended because they do not properly account for variability. Specifically, when the total sequencing count is fixed, the analysis of replicates always outperforms the analysis of a single RNA sample pooled from the individual replicates (Fig. 3). The improvement is particularly significant when the within-group variability is large or when there are outlier samples. We further evaluated the influence of sample size and sequencing depth on the detection accuracy of differential alternative splicing events. We observed that when there was large variability among replicates, increasing the number of replicates could increase the statistical power by up to 31% (Fig. 5). However, when the total budget was not enough to generate a large number of reads, overly increasing the number of replicates reduced the statistical power by increasing the estimation uncertainty in individual replicates. Therefore, under a fixed budget researchers need to consider the trade-off between sample size and sequencing depth in designing their RNA-Seq studies. For large projects, it may be worthwhile to perform a pilot round of low-coverage RNA-Seq and estimate the level of within-group variability, before making decisions on the optimal sample size and sequencing depth.

The rMATS statistical framework provides the foundation for future extensions. rMATS uses the raw (unadjusted) RNA-Seq read counts as the input. It should be noted that a series of studies have revealed systematic biases in RNA-Seq data and have proposed methods to correct for the raw RNA-Seq read counts (32–35). However, in previous work we tested several well-known bias correction methods for RNA-Seq data, but did not observe any improvement in the estimates of exon inclusion level (22, 36). Nonetheless, the rMATS statistical framework can readily take the adjusted counts from any bias correction method, if it is demonstrated to improve the accuracy of splicing analysis. Another potential area of improvement is to generalize the two-isoform model of rMATS for any number of isoforms. Currently, rMATS is designed to analyze basic types of alternative splicing events involving two isoforms from an alternatively spliced region. These types include exon skipping, alternative 5′ splice sites, alternative 3′ splice sites, mutually exclusive exons, and retained introns (Fig. S1). This is the common analytic approach in many existing tools for RNA-Seq analysis of alternative splicing (9, 15, 16, 22). However, we note these basic types of alternative splicing events can be coupled to produce more than two isoforms from a single exon or multiple adjacent exons. It is possible to extend the binomial distribution in the current rMATS model to a multinomial distribution, which will enable the analysis of complex alternative splicing events involving more than two isoforms.

The rMATS source code and user manual are freely available for download at rnaseq-mats.sourceforge.net/. The rMATS software takes the raw RNA-Seq reads, a genome sequence file, and a transcript annotation file as the input. It identifies alternative splicing events corresponding to all major types of alternative splicing patterns (Fig. S1) and calculates the P value and FDR for differential splicing. For species with poor transcript annotations, users can apply de novo RNA-Seq transcript assembly tools to generate transcript annotations, before analysis of differential alternative splicing by rMATS. We anticipate that rMATS will be a useful tool for robust and flexible analysis of alternative splicing in diverse RNA-Seq projects. Moreover, as a general method for analyzing mRNA isoform ratios using sequence count data, the statistical model of rMATS is also applicable to sequencing-based analyses of other types of mRNA isoform variation, such as alternative polyadenylation and RNA editing.

Materials and Methods

rMATS Hierarchical Model for Unpaired Replicates.

For replicates that are not paired between sample groups, the hierarchical framework of rMATS combines the binomial distribution for modeling the estimation uncertainty in individual replicates and the normal distribution for modeling the variability among replicates (Fig. 2),

$$\begin{array}{l}{I}_{ijk}|{\psi }_{ijk}\sim \text{Binomial}\left(n=I_{ijk}+S_{ijk},p=f_i\left({\psi }_{ijk}\right)\right),\\ \text{logit}\left({\psi }_{ijk}\right)\sim \text{Normal}\left(\mu =\text{logit}\left({\psi }_{ij}\right),{\sigma }^2={\sigma }_{ij}^2\right),\end{array}$$ [3]

in which $I_{ijk},S_{ijk}$, and ${\psi }_{ijk}$ are the inclusion read counts, the skipping read counts, and exon inclusion levels for exon $i$, sample group $j=1,\hspace{0.5em}2$, and replicate $k$. $f_i\left({\psi }_{ijk}\right)$ is the length normalization function of exon $i$ that transforms the exon inclusion level ${\psi }_{ijk}$ into the proportion of reads from the exon inclusion isoform, using the effective lengths of the isoforms. ${\psi }_{ij}$ is the mean inclusion level of group $j$; ${\sigma }_{ij}$ is the variance of the group. Based on model 3, we use a likelihood-ratio test to calculate the P value that the between-group difference of the mean exon inclusion levels exceeds a given threshold $c$. For each exon $i$, the null hypothesis is that the difference of the mean exon inclusion levels is smaller than or equal to the user-defined threshold $c$ (i.e., $\left|\mathrm{\Delta }\psi \right|\hspace{0.17em}=\hspace{0.17em}|{\psi }_{i1}-{\psi }_{i2}|\hspace{0.17em}\le c$), whereas the alternative hypothesis is $|{\psi }_{i1}-{\psi }_{i2}|\hspace{0.17em}>c$. The likelihood-ratio test compares the maximum value of the likelihood function under the constraint of the null hypothesis to the maximum value of the likelihood function without any constraints (details of the likelihood-ratio test are in SI Materials and Methods).

Without the length normalization function $f_i\left({\psi }_{ijk}\right)$, model 3 is equivalent to a standard generalized linear mixed model with the binomial distribution and the logit link function, whose estimation procedure is implemented in common statistical software. However, the length normalization function creates a unique link function. Because of it, we need to reprogram the model-fitting algorithm of our model. The details of our parameter estimation and model-fitting algorithm are described in SI Materials and Methods.

rMATS Hierarchical Model for Paired Replicates.

For each exon $i$, we model the correlation between paired replicates by the parameter ${\rho }_i$ in the covariance structure. This leads to a bivariate normal distribution in the hierarchical model for paired replicates (Fig. 6),

$$\begin{array}{l}{I}_{ijk}|{\psi }_{ijk}\sim \text{Binomial}\left(n=I_{ijk}+S_{ijk},p=f_i\left({\psi }_{ijk}\right)\right),\\ \left[\begin{array}{c}\text{logit}\left({\psi }_{i1k}\right)\\ \text{logit}\left({\psi }_{i2k}\right)\end{array}\right]\sim N\left(\mu =\left[\begin{array}{c}\text{logit}\left({\psi }_{i1}\right)\\ \text{logit}\left({\psi }_{i2}\right)\end{array}\right],\sum =\left[\begin{array}{cc}{\sigma }_{i1}^2& {\rho }_i{\sigma }_{i1}{\sigma }_{i2}\\ {\rho }_i{\sigma }_{i1}{\sigma }_{i2}& {\sigma }_{i2}^2\end{array}\right]\right),\end{array}$$ [4]

in which $I_{ijk},S_{ijk}$, and ${\psi }_{ijk}$ are the inclusion read counts, the skipping read counts, and exon inclusion levels for exon $i$, sample group $j=1,\hspace{0.5em}2$, and replicate $k$. ${\psi }_{i1}$ and ${\psi }_{i2}$ are the mean inclusion levels of groups 1 and 2; ${\sigma }_{i1}$ and ${\sigma }_{i2}$ are the variances of the two groups. The parameter ${\rho }_i$ models the correlation between paired replicates. The paired rMATS model tests the same hypothesis as in the unpaired model. For each exon $i$, the null hypothesis is that the difference of the mean exon inclusion levels is smaller than or equal to the user-defined threshold $c$ (i.e., $\left|\mathrm{\Delta }\psi \right|\hspace{0.17em}=\hspace{0.17em}|{\psi }_{i1}-{\psi }_{i2}|\hspace{0.17em}\le c$), whereas the alternative hypothesis is $|{\psi }_{i1}-{\psi }_{i2}|\hspace{0.17em}>c$. The paired rMATS model is more generalized than the unpaired model because of its covariance structure. If ${\rho }_i=0$, the paired model is reduced to the unpaired model. The details of the paired rMATS model including the model-fitting algorithm and the test statistics are described in SI Materials and Methods.

Simulation Studies of rMATS on Replicate and Pooled Data.

We evaluated the performance of rMATS with a simulation study. A total of 5,000 exons were simulated for two sample groups, with 5% of the exons from the alternative hypothesis that the exons were differentially spliced ($\left|\mathrm{\Delta }\psi \right|>5\%$ between sample groups) and 95% of the exons from the null hypothesis that the exons were not differentially spliced ($\left|\mathrm{\Delta }\psi \right|\le 5\%$ between sample groups). For each exon, we simulated 5 replicates for each of the two sample groups (totally 10 replicates). The replicate read counts of each exon were simulated with a two-step approach, where we first randomly selected one exon from the significant exon skipping events (FDR ≤ 1%) of the prostate cancer cell line data and then simulated read counts in individual replicates by randomly sampling the read counts of the selected exon in the prostate cancer cell line data. We generated data for the null hypothesis by sampling the mean exon inclusion level of sample group 1 from a uniform (0, 1) distribution and randomly added or subtracted a value sampled from a uniform (0, 0.05) distribution to generate the mean exon inclusion level of sample group 2. If the random value caused the mean exon inclusion level of sample group 2 to be above 1 or below 0, the sampling step would be repeated until the mean exon inclusion level of sample group 2 was within [0, 1]. Data for the alternative hypothesis were simulated with a similar procedure, except that the value randomly added or subtracted to generate the mean exon inclusion level of sample group 2 was sampled from a uniform (0.05, 1) distribution. The exon inclusion levels in individual replicates were sampled from a normal distribution with the mean equal to the simulated mean inclusion level for that sample group and the SD at three different levels at 0.01, 0.02, and 0.05, respectively. In each replicate, the read count of the exon inclusion isoform was sampled from a binomial distribution of total read counts and exon inclusion levels. To investigate the effect of outliers, we also simulated 1 outlier replicate (of 10 replicates from the two sample groups) with a large SD of 0.2 in the normal distribution. The pooled data were generated by pooling the read counts of all 5 replicates in each sample group. After the simulation data were generated, we used rMATS to calculate the P value and FDR of differential splicing, using 5% as the threshold for between-group difference in exon inclusion levels $\left(\left|\mathrm{\Delta }\psi \right|>5\%\right)$.

Simulation Studies to Evaluate the Influence of Sample Size and Sequencing Depth on Detection Accuracy.

We designed a simulation study to evaluate the influence of sample size and sequencing depth on detection accuracy. In the first set of simulations, we set a scenario where the budget was to generate 200 million paired-end RNA-Seq reads in each of the two sample groups. Assuming that these read counts are evenly distributed to all replicates, we simulated 3–10 replicates per sample group, with total read counts per replicate $N_k=$ 67–20 million. We mimicked the read count distribution in the prostate cancer cell line data when distributing the total read counts to each alternative splicing event. Specifically, we randomly selected one exon $i$ from the exon skipping events of the prostate cancer cell line data. For each simulated replicate k of this exon $i$, the simulated replicate read count $n_{ik}$ was generated by randomly sampling replicate read counts of this exon in the real data, scaled by the total read counts per replicate in the simulated data (67–20 million) and in the real data (∼120 million reads). After generating the read count for each replicate, the replicate exon inclusion levels and the inclusion/skipping read counts were simulated using the same procedure as described above. In total we simulated data for 5,000 exons in this manner. For each number of replicates (from 3 to 10 replicates), five different SDs were used (SD = 0.01, 0.02, 0.05, 0.10, and 0.20), representing different levels of variability of exon inclusion levels within the sample group. A second set of simulations was carried out under the budget of 1.6 billion paired-end RNA-Seq reads in each of the two sample groups.

Simulation Studies to Compare rMATS with Other Methods.

We designed a simulation study to evaluate the performance of rMATS to Cufflinks (2.2.1) (18) and DiffSplice (0.1.1) (20). A total of 5,000 exons were simulated for two sample groups, with 5% of the exons from the alternative hypothesis that the exons were differentially spliced ($\left|\mathrm{\Delta }\psi \right|>0\%$ between sample groups) and 95% of the exons from the null hypothesis that the exons were not differentially spliced ($\mathrm{\Delta }\psi =0\%$ between sample groups). For each exon, we simulated 5 replicates for each of the two sample groups (10 replicates in total) with a within-group SD of $\psi$ of 0.05. The individual replicate read counts of each exon were randomly sampled from TCGA ccRCC RNA-Seq data. We used the same procedure as in other simulations to generate the inclusion and skipping isoform read counts. To input the simulated data into Cufflinks and DiffSplice, we made artificial RNA-Seq SAM files with inclusion and skipping reads generated based on the simulated inclusion and skipping read counts. To assess the effects of small read counts or outliers, we performed additional tests in which one of the replicates was randomly set to have only 10% of the typical read coverage or with a large SD (SD = 0.2) of exon inclusion levels.

RNA-Seq Analysis of PC3E and GS689 Cell Lines.

We analyzed our RNA-Seq data on two prostate cancer cell lines, PC3E and GS689 (23, 24). The PC3E cell line was obtained by selecting E-cadherin positive PC-3 cells, using fluorescence-activated cell sorting (FACS). The GS689 cell line was isolated from a secondary metastatic liver tumor after intravenous injection of PC-3 cells into mouse. As a result, the PC3E cell line had epithelial cell characteristics whereas the GS689 cell line exhibited mesenchymal and invasive properties (24). The RNA-Seq data are available at the National Center for Biotechnology Information (NCBI) Sequence Read Archive (SRA) under accession no. SRS354082.

We first mapped RNA-Seq reads to the Ensembl transcripts (release 65), using the software TopHat (37), allowing up to 2-bp mismatches per 25-bp seed. After mapping to the Ensembl transcripts, TopHat mapped the remaining reads to the human genome (hg19) and discovered novel splice junctions not present in the Ensembl transcripts. Each mapped splice junction read required at least 8 bp (anchor length) from each side of the splice junction. Major categories of alternative splicing events (i.e., skipped exons, alternative 5′ splice sites, alternative 3′ splice sites, mutually exclusive exons, and retained introns) were then detected from the RNA-Seq mapping results by our software. For the identified alternative splicing events, we used the splice junction counts plus the exon body counts or the splice junction counts alone as the input for rMATS.

TCGA Data of Tumor-Normal Matched Pairs of ccRCC.

We obtained the RNA-Seq read counts of 65 matched tumor and normal samples in the ccRCC RNA-Seq data from TCGA. The sample IDs of these 65 tumor-normal matched pairs are provided in Dataset S5. The RNA-Seq data were mapped to the splice junctions by TCGA consortium. We downloaded the mapped splice junction read counts from TCGA data portal (tcga-data.nci.nih.gov/tcga/). In total, 956 million splice junction reads were mapped to the 65 tumor samples, with 3–23 million reads per tumor sample. A total of 944 million splice junction reads were mapped to the 65 normal samples, with 4–23 million reads per normal sample.

RT-PCR Validation.

Quantitation of exon inclusion levels was carried out using fluorescently labeled RT-PCR as described previously (36). Because we used rMATS to test whether the difference in mean $\psi$ values between two sample groups exceeded 5% $\left(\left|\mathrm{\Delta }\psi \right|\hspace{0.17em}>5\%\right)$, we defined a candidate differential alternative splicing event as validated if the average RT-PCR–based exon inclusion levels differed by at least 5% between the three replicates of the PC3E and GS689 cell lines, with the direction of the change matching the RNA-Seq prediction.