Detecting range expansions from genetic data

Abstract

We propose a method that uses genetic data to test for the occurrence of a recent range expansion and to infer the location of the origin of the expansion. We introduce a statistic ψ (the directionality index) that detects asymmetries in the two-dimensional allele frequency spectrum of pairs of population. These asymmetries are caused by the series of founder events that happen during an expansion and they arise because low frequency alleles tend to be lost during founder events, thus creating clines in the frequencies of surviving low-frequency alleles. Using simulations, we show that ψ is more powerful for detecting range expansions than both F_ST and clines in heterozygosity. We also show how we can adapt our approach to more complicated scenarios such as expansions with multiple origins or barriers to migration and we illustrate the utility of ψ by applying it to a data set from modern humans.

Introduction

Range expansions are ubiquitous in natural populations, and they are responsible for numerous biological phenomena. Range expansions result in a series of founder events that cause the newly founded populations to differ genetically from the source population. Some well-known examples are biological invasions (Handley et al., 2011), the post-ice age patterns of migration in several European taxa (François et al., 2008; Hewitt, 1999; Schmitt, 2007), and the colonization of Eurasia, North and South America by modern humans (Cavalli-Sforza et al., 1994; Ramachandran et al., 2005; Tishkoff et al., 2009). Some of the descendants of an ancestral source population may remain near the location of that ancestral population. For example, the European population of the brown bear Ursus arctos most likely survived the last ice age in refugia in Spain and Greece. Brown bears followed the receding glaciers to colonize most of Europe, but populations at the locations of the former refugia persisted until the populations were driven to the verge of extinction by humans in the 20th century (Taberlet et al., 1998). Humans provide another example; derived populations are found all over the world, but there are also descendants of the first humans still living in Africa.

Sometimes, the routes of migration are known from direct observations, historical records and archaeological evidence. Frequently, however, the exact history of a species is unknown, and we want to use population genetic methods to gain more information. In this paper, we use genetic data to address two related problems: detecting whether a range expansion has occurred and inferring the geographic origin of a range expansion.

Characterizing the influence of geographic structure on genetic diversity has been one of the major goals of population genetics theory, with important contributions from Wright (1943), Malécot (1950), Kimura (1964) and many others. While there are many statistics designed to infer differentiation between populations (Balakrishnan and Sanghvi, 1968; Goldstein et al., 1995; Nei, 1972; Reynolds et al., 1983), the most widely used statistic to detect differentiation between populations is the fixation index F_ST, which traces to Wright (1949). A variety of estimators of F_ST have been developed (e.g. Reynolds et al., 1983; Weir and Cockerham, 1984). Roughly speaking, F_ST measures how much diversity exists between subpopulations compared to the diversity in the entire population; an F_ST value of 0 indicates that the two subpopulations are indistinguishable, whereas a value of 1 indicates that two populations are maximally differentiated. F_ST has been directly linked to the migration rate in several models, including the finite island (Slatkin and Voelm, 1991) and stepping-stone models (Cox and Durrett, 2002). Although F_ST can be used to estimate the amount of gene flow between equilibrium populations, it cannot be used to infer directionality of gene flow.

Two other methods that are widely used to detect geographic patterns are clustering algorithms and ordination methods. Clustering algorithms (Corander et al., 2004; François et al., 2008, 2010; Pritchard et al., 2000) such as STRUCTURE (Pritchard et al., 2000) classify individuals into discrete groups, which can then be used for further analysis. Ordination techniques (Cavalli-Sforza and Edwards, 1967), such as principal components analysis and multidimensional scaling, summarize data by indicating the overall similarity of populations. For example, principal component analysis has shown that genetic diversity is correlated with the geographic distribution of humans on a continental (Novembre et al., 2008) and global (Cavalli-Sforza et al., 1996; Wang et al., 2012) scale.

It is also possible to use likelihood methods to infer past features of population history. For example, the program IM (Hey, 2010) estimates the time of separation of populations and migration rates between them using data from multiple unlinked loci, and the program dadi (Gutenkunst et al., 2009) estimates past rates of population growth from the joint allele frequency spectrum of two or three populations. Both of these programs are computationally intensive and analysis for more than a few populations is infeasible.

Most statistics applied to subdivided populations do not provide information about asymmetries. F_ST and most genetic distances are defined in such a way that they are commutative (i.e. F_ST between populations A and B is the same as F_ST between B and A), and hence the value depends only on the amount of migration, not whether migrants moved mostly from A to B or from B to A. Clustering algorithms can produce groupings of populations that can be interpreted as describing an expansion, but expansion-specific information is lost in the process and the results of clustering analysis is often sensitive to tuning parameters such as the number of clusters. For principal components analysis, the view that the first principal component axis follows the direction of expansion (Menozzi et al., 1978) has recently been challenged (DeGiorgio and Rosenberg, 2012; François et al., 2010; Novembre et al., 2008), and it has recently been shown that, depending on the parameter values and the locations of the populations sampled, the first principal component axis may be parallel to or orthogonal to the axis of expansion, or at an angle in between.

Population genetics theory has shown that a range expansion can be detected from the characteristic reduction in genetic diversity with increasing distance from the origin of the expansion (Austerlitz et al., 1997; DeGiorgio et al., 2009; Edmonds et al., 2004; Hallatschek et al., 2007; Ramachandran et al., 2005; Slatkin and Excoffier, 2012). The reason is that the succession of founder events during the expansion causes the progressive loss of genetic variants. In extreme cases, this can lead to relatively rapid fixation of neutral or even deleterious alleles, a process called allele surfing (Hallatschek et al., 2007; Klopfstein et al., 2006). The prediction of decreasing diversity has been confirmed by comparing the numbers of mtDNA haplotypes found in Southern European refugia and in central Europe (Taberlet et al., 1998). The same pattern can also been seen in humans where both a reduction in heterozygosity and an increase in linkage disequilibrium with increasing distance from the presumed origin of the expansion in Africa can be seen (Ramachandran et al., 2005).

In addition to creating a gradient in genetic diversity, range expansions tend to create clines in the frequencies of neutral alleles, with the frequency increasing on average in the direction of the expansion (Slatkin and Excoffier, 2012). An intuitive reason for this pattern is that each founder event results in additional genetic drift, and populations further away from the origin of expansion will therefore have experienced more drift. This can be seen from the following argument: The expected frequency of a neutral allele in the newly founded population is the same as in the source population. But some alleles will have zero frequency in the new population. Therefore, the average frequency of alleles in the newly founded population, given that they have non-zero frequency is expected to be higher than in the source population, thus creating the cline. This observation provides the foundation for our method of detecting range expansions.

In this paper, we introduce a statistic, the directionality index ψ, defined for pairs of populations. ψ is sensitive to patterns created by range expansions because it detects the allele frequency clines created by successive founder events. We show, using simulations, that the expectation of ψ is zero in an equilibrium isolation-by-distance model, and that its expectation is positive in the direction of the expansion. We also show that, using multiple samples, ψ can be used to infer the origin of a range expansion and the locations of barriers to expansion. We explore the power and robustness of our methods and finally apply it to human genetic data.

Results

In this section, we define the directionality index, give an intuitive explanation and discuss some of its properties. We will show that the directionality index is sensitive to recent range expansions in a one or two dimensional stepping-stone model, and then explore some more advanced applications.

Definition Of The Directionality Index

Consider two samples of size n, n ≥ 2 taken from two subpopulations S₁, S₂. Each sample consists of L biallelic markers (e.g. SNPs) that are shared between S₁ and S₂. The directionality index is defined as

$$\psi (S_1,S_2)=\frac{1}{n}\left({\overline{f}}^{(S_1)}-{\overline{f}}^{(S_2)}\right)=\frac{1}{nL}\sum _{l=1}^L\left(f_l^{(S_1)}-f_l^{(S_2)}\right),$$ (1a)

where f̄^(S) is the average allele frequency of all derived alleles in population S, and $f_l^{(S)}$ is the number of copies of the derived allele at locus l in the sample from population S. It is important that the average and the sum are over only those alleles that are present in both populations; sites where either population is fixed for the ancestral copy are excluded. Equivalently, ψ can also be defined in terms of the two-dimensional site frequency spectrum (2D-SFS):

$$\psi =\sum _{i=1}^n\sum _{j=1}^n(i-j)f_{ij}.$$ (1b)

where f_ij denotes the proportion of SNP in the sample that are at frequency i in S₁ and at frequency j in S₂, and the SFS is normalized such that

$$\sum _{i=1}^n\sum _{j=1}^n{f}_{ij}=1.$$

This normalization is unusual in that allels private to either of the two populations are excluded. In the special case where we compare two diploid genomes, n = 2 and equation 1b reduces to

$$\psi =f_{21}-f_{12}.$$ (1c)

These three definitions are equivalent and represent different interpretations of the directionality index. To aid intuition, we discuss them briefly. Equation 1a corresponds to the model we introduced in the introduction; we compare the average allele frequencies in the two populations. Because the population further away from the expansion origin is expected to have experienced more genetic drift, its alleles are expected to be at a higher frequency on average. Thus a positive ψ indicates that f̄^(S₁) > f̄^(S₂) and that S₁ is further away from the origin of the expansion than S₂. If both populations have experienced similar amounts of genetic drift, then the average frequencies of shared alleles will be equal, ψ ≈ 0 and we will not detect an expansion. Equation 1b is based on the SFS, and we see that ψ will be positive if f_ij is usually greater than f_ji. Thus, we are comparing the SFS entries that are reflected along the x = y diagonal, and the directionality index measures the “skew” in the 2D-SFS. If there are more SNP that fall in the upper left triangle of the SFS (where j > i), ψ will be negative, and we infer an expansion from S₁ to S₂. The opposite conclusion will be drawn if there is an excess of SNP in the lower right triangle, and if the SNP are distributed symmetrically around the x = y diagonal, ψ will be zero. Much of the paper will be focused on the case where each population is represented by a single genome, a case that will be particularly common in genomic studies. In that case, equation 1b reduces to 1c and we are simply comparing the abundance of SNP fixed for the derived allele in sample S₁ and heterozygous in S₂ to the number heterozygous in S₁ and fixed in S₂. If either number is significantly larger than the other, we infer expansion in the direction of the population with the larger number. It is also worth comparing the computation times. Equation 1a scales proportionally to the number of loci in the sample, whereas equation 1b scales with the square of the sample size if the site frequency spectrum has been previously calculated. As this is often required for calculation of other statistics such as F_ST, equation (1b) should be used for data sets where L ≫ n². It is important to note that we have to assume that the sample sizes are the same in the two populations we are comparing. The reason is that the probability that an allele is absent in a sample is a complicated function of the sample size and the expected site frequency spectrum, and cannot be easily computed. When there are samples of unequal size we downsample the larger sample to the size of the smaller sample.

Determining Whether A Range Expansion Occurred

We first test the power of ψ to distinguish pairs of populations sampled from a recent range expansion to pairs of populations sampled under isolation-by-distance at equilibrium in a 1D-model. Figure 1 shows that F_ST increases at approximately the same rate under an equilibrium stepping-stone model with only isolation-by-distance (Panel A) and a model with a range expansion (Panel B), indicating that the two scenarios are comparable. We see that ψ is nearly zero in the isolation-by-distance model, regardless of the distance between the samples. In contrast, ψ increases with distance under the expansion model. Interestingly, ψ increases almost linearly with the distance between the origin and the population sampled, a fact we exploit later to infer the origin of the expansion. We also plotted the heterozygosity, a statistic that is also expected to be constant under an equilibrium model (Durrett, 2008) and decreasing under an expansion (Austerlitz et al., 1997; Ramachandran et al., 2005). However, our simulations show that heterozygosity is larger in the center of the habitat than near the boundaries because of the boundary effects. This is in contrast to most theoretical results (Durrett, 2008), which either assume either a circular model or an infinitely long stepping stone model, and where the heterozygosity is independent of the deme sampled. This observed gradient in heterozygosity has been observed previously and has been explained by longer coalescence times for a sample taken close to the boundary (Wilkins and Wakeley, 2002). It is also worth noting that this effect is much weaker in a two dimensional population.

Figure 1. Behavior of H (red, full line), ψ (black, dotted) and F_ST (blue, dashed) in one-dimensional (A) isolation-by-distance and (B) population-expansion models.

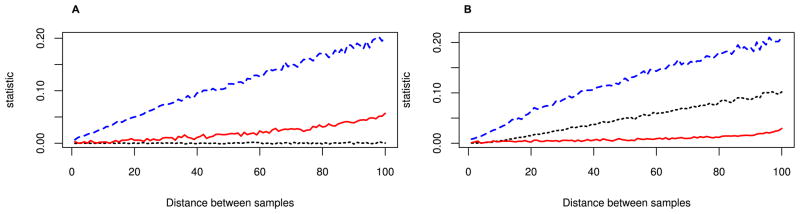
Simulations were performed on a 200 demestepping-stone model with scaled migration rate M=100 between adjacent demes, and expansion events every 0.001 coalescence units. F_ST increases linearly with distance in both models and ψ is zero in the isolation-by-distance model, but increases approximately linearly in the expansion model. Heterozygosity is plotted for demes from the center of the population (left) to the border of the habitat (right), and given as the difference to the central deme.

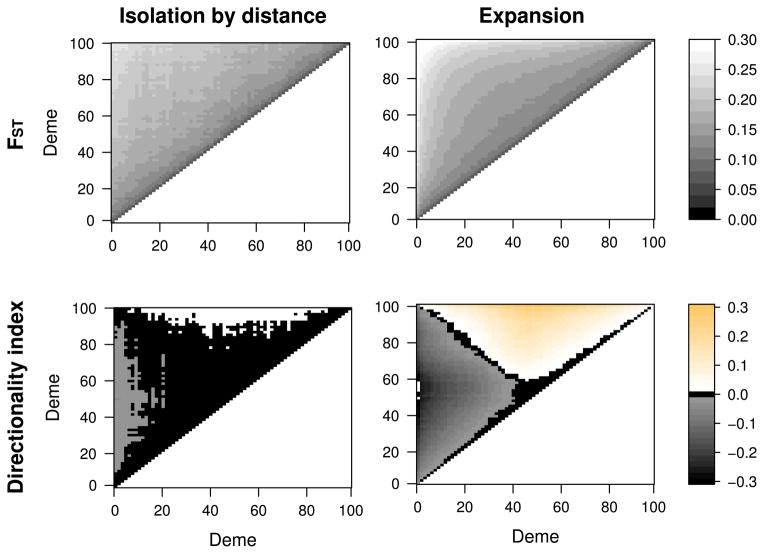
Similar results for F_ST and ψ were obtained in 2D (Figure 2). F_ST is slightly larger in the case of a range expansion than in the isolation-by-distance model (Panels A and C), but qualitatively we see an increase of F_ST with distance under either model. The pattern for ψ, however, is again different (Panels B and D): under the isolation-by-distance model, ψ < 0.01 for almost all comparisons, with the exception of a few demes that are at the boundary of the simulated region. In contrast, the magnitude and sign of ψ nicely illustrate the effect of the range expansion. ψ is zero only for demes that are very close to each other or pairs of demes equally far away from the expansion origin. The latter is due to symmetry: two samples that are an equal distance apart from the origin will have a symmetric SFS, resulting in a ψ close to zero.

Figure 2. Behavior of F_ST and ψ in isolation-by-distance and population expansion model.

Each panel gives the value of the pairwise statistics F_ST and ψ under an isolation-by-distance model and an expansion model with the expansion starting in the central deme (50,50). Simulations were performed on a 101 × 101 deme stepping stone model, and a diagonal transect from demes at coordinates (0,0) to (100,100) was sampled, and all pairwise statistics were calculated. Black regions correspond to regions where F_ST and ψ are very low (below 1%). The orange and grey regions denote areas with positive and negative ψ, respectively. Whereas F_ST behaves qualitatively similar under both models, the behavior of ψ is very different. Under isolation-by-distance, ψ is very close to zero, with some deviations due to boundary effects. Under an expansion, however, we see a clear signal for all demes, except demes that are very close to each other, or demes that have the same distance to the origin, but in different directions.

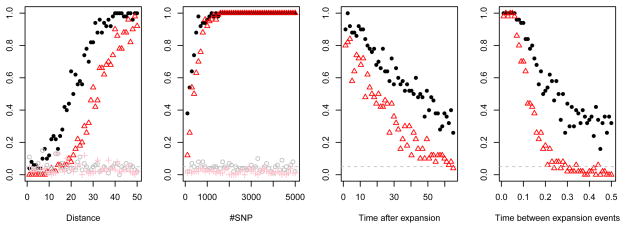
In Figure 3 we show the effect of the most important parameters on our ability to reject the null hypothesis of equilibrium isolation-by-distance for pairs of samples of size two. For all parameters, we find that using the directionality index results in higher power than comparing differences in heterozygosity, while false-positive rates are low and roughly the same for the two methods. We find that we have comparatively little power to reject the null hypothesis if the two sampled individuals are close to each other(Panel 3A). This is expected, since there are fewer founder events separating the two individuals. Therefore we expect ψ to be lower for nearby populations, as shown in Figures 1 and 2. Panel B shows that a moderate number of shared SNP is necessary, i.e. more than one thousand, to get high power to reject equilibrium isolation-by-distance. In addition, we find that slow expansions are harder to detect than rapid expansions, and more recent expansions are easier to detect than expansions that happened a longer time in the past (Panels C and D). Neither of these findings are unexpected; after an expansion, genetic drift will affect the loci in both populations equally. The number of shared SNP that are due to the range expansion will decrease with time and be partially replaced by SNP that only experienced the equilibrium population structure and hence do not carry a signal of the expansion. Similarly, if the time between expansion events is large, the founder effects caused by the expansion will become less important relative to genetic drift that occurs between expansion events, weakening the signal of the expansion. For these slow expansions, the power of heterozygosity to detect an expansion decays much faster than the power of ψ. Finally, we note that the false positive rate, denoted in grey and pink in Figure 3, is independent of both the distance between loci and the number of SNP for both ψ and H.

Figure 3. True/false positive rates of detecting range expansion.

Each panel give the proportion of replicates in which the null model was rejected at the 5% significance level. Black circles correspond to ψ under an expansion model and an isolation-by-distance model, red triangles and plus signs denote simulations correspond to using H to distinguish an expansion model and isolation by distance model, respectively. The grey dashed line at 0.05 gives the expected proportion of false positives under the null hypothesis. Baseline parameters for the simulations were of 2 chromosomes (one diploid individual) at each location sampled, with locations a distance of 50 each other. Fixed parameters used for generating the data sets are 1,000 independent SNP from one diploid individual per sampled deme. Time between expansion events was set to 0.1 (coalescence units) and the data was observed immediately after the expansion ended.

Inferring The Origin Of A Range Expansion

In addition to showing that a range expansion occurred, the results in Figures 1 and 2 suggest that spatial patterns in pairwise values of ψ can indicate the origin of an expansion if more than two populations are sampled. For this purpose, we employ a method commonly used by engineers in problems of localization and navigation (Gustafsson and Gunnarsson, 2003), called Time Difference of Arrival location estimation (TDOA). TDOA methods are used in remote sensing and to locate cell phones (Gustafsson and Gunnarsson, 2003). The key assumption of the TDOA algorithm is that the magnitude of a pairwise statistic between two sample locations i and j is proportional to the difference in distance from i to the origin and the distance from j to the origin. If i is very close to the origin and j far away, the TDOA statistic will be large, but if i and j are at the roughly the same distance from the origin, then the TDOA statistic will be close to zero. In engineering applications the TDOA statistic is the time difference between the arrival of a signal emitted from different sources (hence the name). In our application, ψ takes on the role of the time difference with the implicit assumption that the magnitude is proportional to the difference in distances of the two samples from the origin. To illustrate, we first consider the special case of ψ_ij = 0. Assuming that we have already rejected isolation-by-distance in favor of a range expansion, we know that i and j are equally far from the origin and the origin must therefore lie on the line perpendicular to the line through i and j. If we had three or more samples all at the same distance from the origin so that the pairwise ψ values are all zero, we could infer the origin was at the center of the circle passing through the three points.

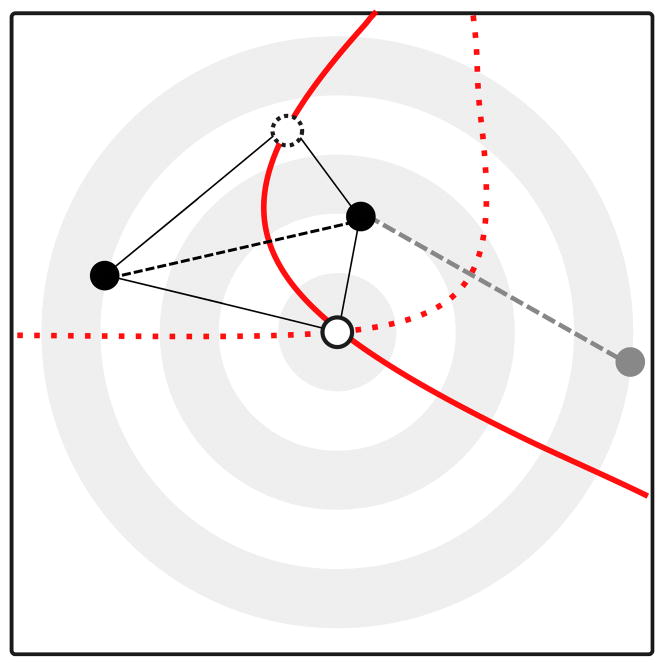
In general, however, ψ_ij will be non-zero. In that case, we know from elementary geometry that the set of candidate points based on a one pair of samples is not a straight line, but a hyperbola with the sample locations as its foci. (see Figure 4). For samples from k locations, we calculate ψ for k(k − 1)/2 pairs and hence obtain k(k − 1)/2 hyperbolas. In a perfect, noiseless world, all hyperbolas would intersect in a single point, the origin of the expansion. In practice, genetic data is stochastic and we have to estimate the location of origin. To do this, we interpret each hyperbola as a non-linear equation with three unknowns, the sample coordinates x, y and the speed of expansion v. v is a nuisance parameter that describes how much the allele frequency increases per unit distance from the origin. For more than three samples the system is over determined and, rather than solving the system of equations explicitly, we use weighted non-linear least squares.

Figure 4. Illustration of the method used to infer the origin of a range expansion.

The black and grey points correspond to genetic samples taken, the white point corresponds to the (unknown) origin of the expansion. Using the directionality index ψ, we can infer the difference in distance from the samples to the origin (dashed lines). The set of all points that has the same difference in distance to the origin corresponds to the arm of a hyperbola (red), which comprises all candidate points according to ψ and the location of two points. Using a second pair of points (the grey and top black point), we can identify a second hyperbola (dotted), and find an unique location of the origin. In practice, we use more than three sampling locations. Sampling noise will cause the hyperbolas to not intersect in a single point and we use a least-squares criterion to estimate the location of the origin.

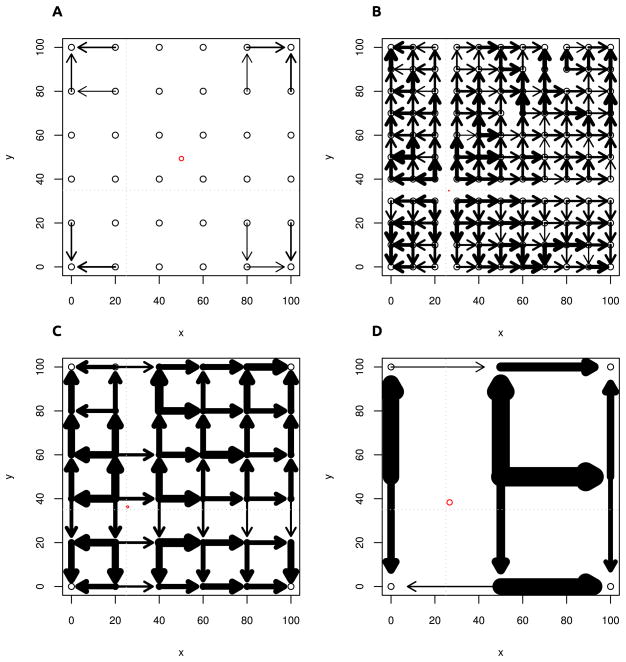
We first illustrate this approach on simulated data, where we sample a regular grid (Figure 5. We simulated a range expansion in a 101 × 101 stepping-stone model. In all simulations, we chose the coordinate system such that each deme corresponds to one unit of distance. The start of the expansion is in deme (25,35), indicated by the grey dotted lines in Figure 5. The direction of the arrows plotted in Figure 5 indicate the sign of the pairwise ψ-value, between adjacent samples on a grid, and the thickness of each arrow corresponds to the magnitude of ψ. A missing arrow denotes a non-significant ψ value. In Panel 5A we performed a simulation under an equilibrium isolation-by-distance model. We see that in this scenario, only 11 out of the 60 pairwise comparisons are significant; all of them point towards the corners and are due to the boundary effects of the simulations. The red ellipse is a 95% confidence ellipse of the inferred origin. Under the isolation-by-distance model, this is located in the center of the population, illustrating that the TDOA approach will yield an answer even if there is no expansion has occurred, so it is important to first test if an expansion has actually occurred. From Panels B–D we see that the expansion signal is clearly portrayed by the directionality indices and we get high confidence in the estimated origin. In fact, the confidence region is so narrow that the ellipse is barely visible in Panel B. The confidence region becomes larger when we reduce the number of samples. Furthermore, we see in Panels C and D that the origin is slightly biased towards the center of the population. This is again due to a boundary effect, and goes away if we take all samples at least 10 demes away from the boundary of the population.

Figure 5. Detecting the origin of a range expansion.

Each panel corresponds to a 101 × 101 grid of populations that were simulated. The expansion began at point (25,35) (indicated by gray dotted lines). Black bordered circles indicate sampling locations, black arrows correspond to ψ > 1% between adjacent samples, with the direction of the arrow indicating the sign of ψ. Thicker arrows correspond to larger ψ. The red ellipse corresponds to the 95% confidence interval of the estimated location of the origin. Panel a: no expansion (isolation-by-distance model). Edge effects cause the estimated origin to be close to the center of the grid of populations. Panels b–d: Expansion with parameters M = 1, t = 0.1 and samples taken every 10th, 20th and 50th deme. While the confidence region is larger for smaller numbers of samples, we get a very accurate result even when we have only 9 samples.

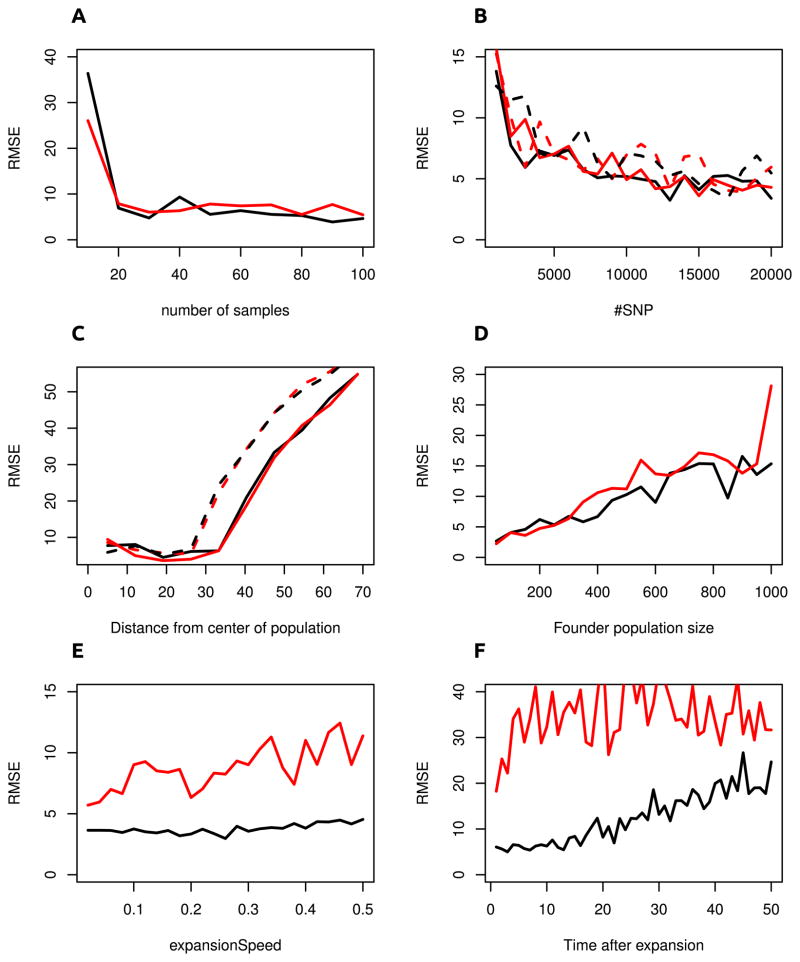
To assess the properties of this method more systematically, we report the root mean squared error (RMSE) under several scenarios (Figure 6). The RMSE is the square of the Euclidean distance between the estimated origin and true origin. We also compare our method to the method of Ramachandran et al. Ramachandran et al. (2005), who used a linear regression of the heterozygosity on the distance to a set of candidate origins. Their inferred origin of the expansion is the point with the highest associated regression coefficient, conditional on the slope of the regression curve being negative. Most data in Figure 6 was simulated with a fairly rapid expansion; the time between subsequent expansion events was set to 0.001 coalescence units, so that the complete expansion was completed in 0.13 coalescence units. This speed is roughly that of the out-of-Africa expansion of humans. For these parameters (Figure 6A–D) the two methods have similar performance, with only marginal improvements in how the methods perform with different amounts of data. We find that with adequate numbers of samples and data, the RMSE for both method is around four, with less than one distance unit of difference between the two methods. Overall, the ideal amount of data for this method lies around 20 diploid samples and 7,000 independent SNP. Having more data will not substantially improve performance. For the set of simulations with increasing numbers of SNP, we also tested the effects of sampling on a grid versus taking samples from random locations. The latter scenario is probably closer to real sampling schemes. Interestingly, we found only negligible differences, indicating that the sampling locations are only a minor issue unless the sampling locations are very skewed (for example if they all lie on a transect).

Figure 6. Performance of TDOA method.

We present the root mean squared errors (RSME) of our TDOA method (black) compare it with the method of Ramachandran et al. 2005 (red). Samples taken on a grid ware represented by full lines, whereas dashed lines denote samples that were taken from random coordinates in the simulated region. Our method is superior when the expansion occurred slowly or when it finished some time in the past; but the method perform very similar for recent, fast expansions.

Changing the position of the origin has little effect on the RMSE for the first 30 distance units, indicating that the method is accurate if the origin is sufficiently far away from the boundary. If the origin is outside the region sampled, the the performance is significantly worse. This has two causes: first, we would expect it to be easier to infer the origin if it lies in the middle of the sample, as compared to an origin that is far from all samples. This part also explains the difference between samples taken on a grid and random samples: In the grid, the corners are systematically sampled (since we force a grid sample to be there), whereas in many random samples there may be fewer samples on one side of the origin than on the other, resulting in a loss of accuracy. A second factor resulting in reduced accuracy are again boundary effects, which skew the effect of the expansion if samples happen to be close to the boundary.

We next focus our attention on the effect of varying the parameters of the expansion (Figure 6C–F): The number of founders (Figure 6D) has an almost linear effect on the estimation accuracy. Fewer founders imply a stronger founder effect and hence a stronger signal of expansion (Slatkin and Excoffier, 2012), which makes the origin easier to detect. We find the biggest difference in how our method performs in comparison to the Ramachandran method is when the expansion is slower, or when we want to detect an expansion that occurred at more times in the past. Interestingly, our method has almost the same accuracy for different expansion speeds, whereas the Ramachandran method is less accurate if the expansion is slower. Also, we find that the heterozygosity gradient disappears soon after the expansion has finished (6F), whereas the ψ retains the signature of the range expansion for much longer.

Adding Environmental Complexity

The previous section assumes an idealized population in a homogeneous habitat. In practice, however, habitats are heterogeneous and barriers to gene flow and range expansion often exist. In the following sections, we show how our method performs in slightly more complex scenarios. First, we allow demes with different population sizes. While we kept the mean size of demes the same, we followed Wegmann et al. (2006) in drawing deme sizes from a gamma distribution. Next, we include barriers to dispersal that affect both the initial expansion and gene flow following the expansion. We illustrate how we can use algorithms from graph theory to locate barriers. Finally, we model an expansion starting from multiple origins.

Heterogeneous Population Sizes

The effect of variance in deme size on demographic expansions was explored by Wegmann et al. (2006). They found that heterogeneous populations have a higher rate of population differentiation between demes, and predicted that detecting range expansion would be more difficult because of the increased noise. Our simulations confirmed this prediction but only if there is substantial variation in deme size (Figure S1). We found that heterogeneity in deme size has little effect if the variance in deme size is low, with RMSE only differing slightly from the case with equal deme sizes. A variance of 0.5 in deme size, for example, corresponds to a size difference of around two orders of magnitude. But the average RMSE for the location estimate only increased to 5.43, compared to 4.57 in a comparable model without variation in deme size. However, this value corresponds to some kind of “tipping point”: when we further increase the variance in deme size, some deme sizes will become effectively zero in size and this greatly reduces the accuracy of the estimated origin.

Barriers

We can use pairwise directionality indices to gain qualitative information about colonization paths, i.e. the corridors through which the population expanded. To do so, we interpret the matrix of pairwise values of ψ as the adjacency matrix of a graph. A positive ψ between populations S₁ and S₂ is interpreted as meaning “Population S₂ was colonized after population S₁” and can be visually represented by an arrow between S₁ and S₂. To improve the visual representation of the graph, we apply standard algorithms to remove some of the edges. In particular, we apply the transitive reduction algorithm (Aho et al., 1972) to find the graph with the fewest edges that retains the connectivity of the original graph. If ψ is positive between populations S₁ and S₂, but there is also an indirect path with ψ > 0 when comparing S₁ and S₃ and S₃ and S₂, we remove the direct connection from S₁ to S₂. This is justified by noting that colonization of S₂ through S₃ is more parsimonious than colonization of S₂ both through S₃ and directly from S₁. We obtained a further reduction by computing a maximum spanning tree (Korte and Vygen, 2008), which reduces the graph to n − 1 edges, where n is the number of sample locations. The maximum spanning tree identifies major migration paths, and does not cross strong barriers to expansion and gene flow (Figure 7). Furthermore, we can obtain an ordering of all samples by simply summing all ψ values that sample is involved in:

$${\psi }_i=\sum _{j\in \text{samples}}{\psi }_{ij}.$$ (2)

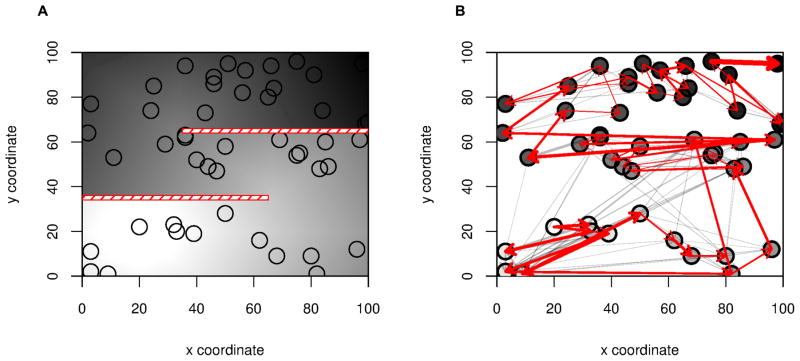
Figure 7. Identifying complex patterns of migration.

We simulated data on a S-shaped habitat with two impermeable barriers (Panel A) The darkness of the shading is proportional to the arrival time of the expansion, which began in deme (20,20). Black circles correspond to locations sampled. In Panel B we show the inferred pairwise directionality, with all edges remaining after thinning the graph shown in grey, and a maximum spanning tree in red. We also show the inferred ordering of the samples as a color gradient of the samples from light (closest to origin) to dark. The barriers can be identified from panel B by the absence of any indication of gene flow across the barriers and by examining the ordering of the samples.

The smallest value of ψ_i indicates the sample taken closest to the origin, and the largest value of ψ_i indicates the sample furthest along the expansion. In Figure 7B we show that both the maximum spanning tree and the ordering are useful qualitative tools to identify barriers.

Multiple Origins

Range expansions may have more than one origin. A classical example is the colonization of Central Europe after the last glacial maximum. Species with Southern European refugia in the Balkan Penisula, Italy and the Iberian peninsula followed the receding glaciers and explain many biogeographical pattern we observe today (Schmitt, 2007). A straightforward way to apply our method to such expansions is to first estimate which populations were colonized predominantly from each potential origin, and then use only those populations to infer the location of each origin. There are several ways to assign sampled individuals to clusters corresponding to a each origin. In classical studies, often mtDNA haplotypes were used for this purpose (e.g. (Hewitt, 1999; Taberlet et al., 1998)), but programs such as STRUCTURE (Pritchard et al., 2000) or simple clustering based on the observed polymorphism frequencies may yield more accurate results. In our simulations, a simple K-means clustering algorithm was able to correctly identify the number of clusters in all cases, even when the two founder populations were drawn from the same original population. The resulting estimates of the locations of the origins are slightly less precise than with a single origin (Figure 8), but that is to be expected because there are fewer samples contributing to the location estimate for each origin. Also, the estimates were worse when the two origins were close together.

Figure 8. Detecting multiple origins.

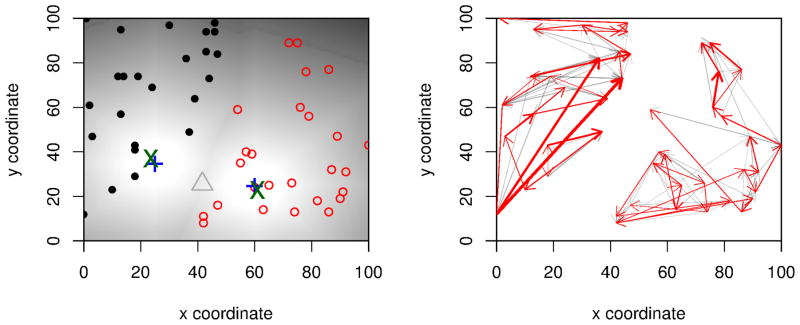
Panel a: We simulated two expansions that originated at the same time from origins indicated by the blue crosses. The color gradient in the background corresponds to the time of colonization time of each deme. We address the problem of inferring the origin of multiple expansions using a two-step procedure. First, we cluster the samples into discrete clusters (red and black circles, respectively) and then estimate the expansion signal and origins independently for the clusters, resulting in high accuracy for both estimated origins (green X) when compared to the actual origins (blue +). The grey triangle denotes the estimated single origin if we did not do the two step procedure; it lies approximately half way between the two actual origins. The right panel shows the inferred migration patterns after a transitive reduction (grey/red arrows) and a maximum spanning tree (red arrows).

Application

Human Diversity

We applied our method to a data set from 55 human populations from the Human Genome Diversity Panel and HapMap III (Altshuler et al., 2010; Cann et al., 2002; Fumagalli et al., 2011). The results are given in Figure 9. We calculated ψ and its standard error for all pairs of populations and transformed this into a Z-score. As expected from a data set with several hundred thousand loci, the vast majority of comparisons were highly significant, with a median absolute Z-score of 28.1, and a mean absolute Z-score of 41.9 across all comparisons. Globally, we could detect four major clusters: i) Africans, ii) Europeans and Pakistani, iii) East Asians and iv) Native Americans. Here, a cluster is loosely defined as a group of sampled populations that all show the same signal when compared to other groups of populations. For example, all 450 comparisons made between African and Non-African populations showed evidence for expansion out of Africa, consistent with the out-of-Africa hypothesis. Similarly, with few exceptions all comparisons between Europeans and Native Americans showed that Europe was colonized before the Americas.

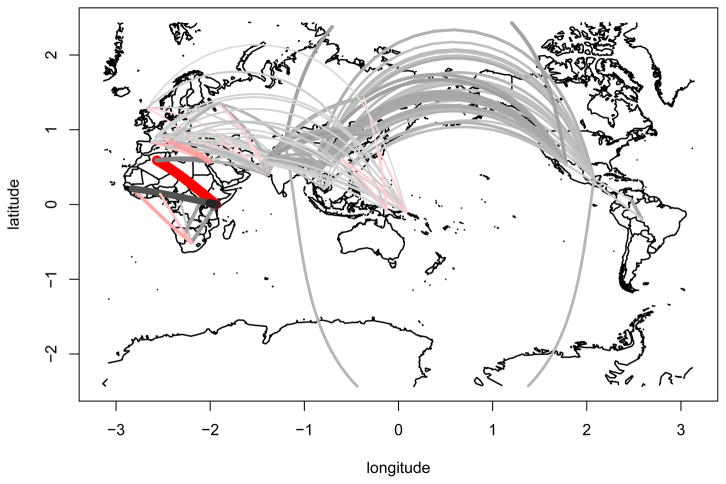
Figure 9. Inference of human migration routes.

The figure shows a visual representation of the pairwise directionality indices between human populations in HGDP and HapMap. Each line corresponds to the pairwise ψ statistic, with thicker and brighter lines corresponding to higher values. Grey and red lines denote eastward and westward migration, respectively. Lines with an absolute Z-score below 5 were omitted.

Within Africa, we found all comparisons to be significant, and all pairwise ψ values agreeing on a single origin of the expansion. The San people were the only population that had positive ψ values when compared to all other populations, indicating that they are closest to the origin. They are followed by the Biaka- and Mbuti-pygmies, which are have negative ψ values with the San. This is followed by the southern Bantu sample, and a cluster consisting of Yerubans, Luhya, Mandenka and Northern Bantu, each having a negative ψ with the others previously mentioned, and positive values for all other populations. The African populations furthest from the origin were the Maasai and Mosabite, the latter being very distinct from the sub-Saharan populations.

The closest outside Africa are the Bedouin and Palestinian populations, both from the Middle East. The third Middle Eastern population present in our data, the Druze, fall in a larger group containing almost all European, Pakistani and Indian populations. Within Europe, the three Italian population all have non-significant ψ scores with one another, but are found to be ancestral to the other European populations. They are followed by the French and French-Basque, which also cannot be distinguished, and the Orcadian, Adygei and Russians. In Pakistan, we find the Makrani to be the most ancestral population, followed by the Brahui and Balochi, Sindhi, Kalash and Burusho. It is noteworthy that this list corresponds to their distances from Africa, with the exceptions that the Brahui and Balochi are switched, and the Hazara are not in the main Pakistani cluster, but rather form a distinct group with the Uygur. Besides the Uygur, all other East Asian populations form a single large cluster with very little resolution. Clearly distinct from this cluster are the Papuans and Melanesians, which are similar with asymmetry between them(ψ = 0.0019, SEψ = 9.2e − 4, Z = −2.05). They are closer to the African populations than to the East Asian populations, but further away than the Pakistani and European populations.

Finally, Native American populations form a distinct cluster, which are strongly separated from all other populations. Within the Native American populations, we find evidence of a North to South colonization pattern with the Pima population being closest to the Eurasian populations, followed by the Maya and Colombians. The most distant populations are the South American Karitiana and Surui, which have a nonsignificant pairwise ψ between them.

We also tested our ability to infer the origin of humans using the TDOA approach. As continents most likely act as strong migration barriers, we did not use the TDOA approach on the entire HGDP data set. Instead, we applied our method to the data set of Henn et al. (2011) which contains 30 African populations. We estimate an origin of the Human expansion at 30° S 13° E, which lies in central South Africa, closest to the location of the San sample (28.5° S 21° E and 22° S 20° E).

Discussion

We introduce a new statistic, the directionality index ψ and showed that ψ can be used to test for a range expansion and to characterize it. Although we have focused on range expansions, ψ is sensitive to other deviations from symmetric migration. While a range expansion might be a plausible explanation in many cases, alternative scenarios such as a source-sink population structure or a large differences in effective population sizes should also be considered. One of the main advantages of the directionality index is that the assumptions and limitations of the approach are easy to discern: the directionality index is zero if the 2D-SFS is roughly symmetric about the diagonal. This is certainly true under most equilibrium models considered in theoretical studies, such as island and stepping stone models, particularly as the boundary conditions in the latter are typically chosen such that the model is symmetric. The directionality index can be used to determine how appropriate these models are for a given data set. If ψ differs from zero then care should be taken in applying methods that are based on these theoretical models. On the other hand, if ψ is close to zero, we can interpret this as justification for using the powerful theoretical results for these models (Durrett, 2008).

In this regard, the directionality index can be seen as a “first step” analysis that can be computed very easily, is able to answer very broad questions about a data set and may act as a guide to what parametric models might be employed, e.g. Approximate Bayesian Computation (Beaumont et al., 2002; Wegmann et al., 2010) or dadi (Gutenkunst et al., 2009). We have also shown how we can introduce the physical location of the samples in our inference framework. In many cases, natural populations are well described by a continuous distribution (Guillot et al., 2009; Rosenberg et al., 2005), and as we show in the TDOA analysis, using a simple statistic together with the physical locations can result in a powerful method. Our approach is also different from most other methods dealing with spatial data in that it explicitly assumes a non-stationary population. In this paper, we link the ancestral demographic process of a range expansion to the observed patterns of genetic diversity. While the effect of the expansion on F_ST appears to be quite small, our ψ statistic can be used to distinguish between equilibrium and non-equilibrium models. Finally, we show how we can extend our method to deal with more realistic landscapes. Whereas the TDOA analysis is not robust to large barriers of gene flow, interpreting the pairwise ψ statistics as a graph can unmask important details of a species’ history.

Simulation Results

We find that ψ is well suited to distinguishing between isolation-by-distance and range expansion when demes are sufficiently far apart and the range expansion is recent and occurs at a fast rate. These restrictions are not surprising. Geographically close demes will be genetically more similar, regardless of their history, and historical processes should therefore be harder to distinguish. That a recent expansion is easier to detect than an older one is also easily explained by the eventual convergence to equilibrium isolation-by-distance pattern, and similarly, a rapid range expansion leaves less time for genetic drift to blur the patterns created by the range expansion. Lastly, increasing the amount of data will increase the power to distinguish asymmetric from symmetric processes as each SNP contributes only a little information about the history of dispersal. In all cases, our ψ statistic outperforms ΔH. From the analyses of the stepping-stone model we see one of the main differences between ψ and F_ST. In an isolation-by-distance model, as the distance between the sampled locations increases, F_ST will increase but ψ will remain small. Again, this makes sense intuitively. The number of shared genetic variants decreases with distance, and hence F_ST increases. However, this reduction in shared polymorphisms is symmetric, and hence will have no effect on ψ. The pattern is different in the model of a population expansion: when comparing with a sample from the origin of expansion, both F_ST and ψ increase with distance. The signal diminishes, when migration rates are high, however. This is apparent from Panel D in Figure 1, where ψ is zero for the first ten demes. Here, migration had enough time to undo the effect of the range expansion in the demes that are furthest away from the origin.

We find that we can get surprising estimates of the location of the origin of an expansion from relatively small datasets. 20 samples with around 10,000 SNP yield accurate estimates. This result indicates that our method is not applicable to mtDNA or microsatellite data, but it should be applicable to transcriptome data, which can be assembled for many non-model organisms. It is also worth noting that the error does not go to zero even with larger amounts of data. There are several reasons for this. The linearity assumption we made for the TDOA approach is not completely accurate. ψ does not increase perfectly linearly with distance especially near boundaries. A more subtle reason is the algorithm we use; although least-squares is easy to implement and yields good results, other optimization algorithms might reduce the RMSE. A third reason is the intrinsic stochasticity of genetic processes. We demonstrated how our method can be adapted to incorporate more complex models. We showed that small differences in deme size have little effect on our ability to estimate the location of origin. If however, the habitat is very heterogeneous our method becomes less accurate. This implies that when analyzing species that live in very patchy habitats,, the TDOA method should not been applied, because the assumption that ψ is proportional to physical distance is violated. In that case, while it is not possible to infer an origin that is distinct from the samples, it is nevertheless possible to find the sample that is closest to the origin, which in many cases might suffice. Also, we have shown that we can apply graphical algorithms to get an accurate representation of the expansion pattern.

Human Genetic Diversity

When analyzing the human data set, we found that i) ψ scores are correlated with distance and ii) if population i is closer to Africa than population j, then ψ(i, j) is in most cases negative, a pattern that is expected under a model of expansion from Africa. As explained previously, the directionality index depends not only on the two population compared but also on the history of the other populations. We find the South African San people to be the population closest to the origin of humans both using the TDOA method and when interpreting all pairwise directionality indices. This supports the interpretation that the origin of modern humans is somewhere in Southern Africa (Henn et al., 2011; Tishkoff et al., 2009). Another interesting result is that the Melanesian and Papuan samples, while very similar, show positive ψ values when compared to other East Asian populations, but the directionality index is negative when compared to the Pakistani, European and African populations. This is consistent with a “two-wave” model of colonization of South-East Asia, with a first wave consisting of present-day Papuans and Melanesians, and a second wave consisting of the present day Chinese populations(Rasmussen et al., 2011). Our results are also in agreement to the results obtained by Hofer et al. (2009), who analyzed the HGDP data set and found that neutral processes might be an explanation for large differences in allele frequency between human population groups. Our results support their findings, and extend them by giving an explanation on how the increase in derived allele frequencies might have arisen.

Methods

Simulations

We implemented a simulator that performs continuous time coalescent simulations on a discrete stepping stone model (Kimura, 1964; Malécot, 1950) of finite size. We assumed that the backward migration rates were equal between all pairs of adjacent demes and that the boundaries were reflecting. We used a modified version of the expansion model of (Slatkin and Excoffier, 2012), where an expansion is modeled with a one-generation bottleneck of reduced size. In our backward-in-time framework, this corresponds to moving all lineages present in a deme being colonized to a randomly chosen neighboring deme. We introduce a founder effect by adding additional coalescence events according to the appropriate backward Wright-Fisher transition probability (Page 62 in (Wakeley, 2009)). Unless noted otherwise, all expansions were done with a founder size of 200. Once the final deme is reached, an regular island model coalescent is run where each island corresponds to a founder population (in most simulation, the number of islands is one).

Throughout this paper, we simulated unlinked SNP using an importance sampling scheme. After generating 1,000 gene trees, we calculate the appropriate multi-dimensional site frequency spectrum, where each sampled population corresponds to a dimension. We can then draw SNP with replacement from this site frequency spectrum.

The parameters used for the majority of the power simulations are as follows: We simulated on a 101 × 101 stepping stone model, with deme coordinates starting at (−50,50) at the lower left corner and (50,50) in the upper right corner. Each deme exchanges migrants to the neighboring demes to the north, south, east and west at scaled migration rate of M = 2Nm = 1. For the power simulation, we sampled a single diploid individual each from two colonies at (−25,−25) and (−25,25). For the TDOA simulations we simulated one individual each from a deme on a quadratic grid between (−30,−30) and (30,30), with 36 samples in total. This corresponds to a distance of 12 demes between any two sampled demes. We usually generated 1,000 independent coalescent trees and then used importance sampling to generate 100,000 SNP from the population, conditioning on them being shared between at least two of the samples. In the case of a range expansion, the standard point of origin was set to (−15,−25) and the expansion occurred at a rate of one expansion event every 0.001 coalescence units, with the expansion being observed 0.13 coalescent units after it started, where coalescent units are measured on the time scale of a local deme. These parameters were chosen to roughly correspond to the human out-of-Africa expansion: if we assume a local human population size of N ≈ 10, 000 and a generation time of 25 years, this corresponds to an expansion that started 65,000 years ago. The directionality index ψ and F_ST were calculated in Python; for ψ we used equation (1b), and F_ST was estimated using Reynold’s estimator (Reynolds et al., 1983). Note that these are only baseline parameters, and exploring the effect of changing these parameters was the purpose of our power simulations.

Various significance tests can be used to determine the significance of ψ between two populations; for the case of n = 2 in both samples we can simply perform a binomial test on the absolute frequencies f₂₁ and f₁₂. If their proportions differ significantly from 0.5, we can reject the null hypothesis of symmetric migration between the two demes. When comparing samples of size n > 2, we can generate a null distribution using a permutation test, i.e randomly assigning the allele frequencies for each SNP to either population. However, both these tests will underestimate the variance in the data if SNP are not in linkage equilibrium. In that case the “effective” number of loci will be lower than the actual number. To take linkage into account we use a computationally more computationally intensive block-jackknife approach (Busing et al., 1999; Reich et al., 2009) to analyze the human data.

To generate data for the 1D stepping stone model analyzed in Figure 1, we simulated a 201 × 1 habitat, with scaled migration rates M = 1, 10 between adjacent demes. Sampling was done in demes −i/2 and i/2, with the center deme having coordinate 0. In case of range expansions, the expansion started in deme −i/2.

SNP ascertainment may influence our results, because most ascertainment schemes favor high frequency alleles in the populations where the ascertainment was performed. To assess the effect of ascertainent bias on the value of ψ, we performed simulations in an isolation-by-distance stepping stone model with samples at coordinates (0,0), (10,0), (20,0), (30,0), (40,0), (50,0) as well as (0,10) and (15,10) and then computed ψ between the (10,0) and (20,0) sample. We then simulated ascertainment by selecting a set of population, and rejection sampled SNP so their 1D-SFS followed a Beta(2,4/3) distribution, which roughly matches the SFS in the HGDP data set and is very different from the expectation without ascertainment bias. We chose this ascertainment scheme as the original ascertainment scheme for HGDP is unknown. If ψ differs significantly from zero, then we know that ascertainment is important. Results are given in Figure S2; ascertainment is important if it is performed in one of the populations that we calculate ψ for. However, the effect of ascertainment is negligible if the population we calculate ψ for are different from the ascertainment population, even if the ascertainment population is much more closely related to some populations than to others.

Estimating the origin of a range expansion

We use a time-difference of arrival (TDOA) approach (Gustafsson and Gunnarsson, 2003) to estimate the origin of a range expansion. TDOA was originally used in naval navigation during the Second World War, and is currently widely used to solve localization and navigation problems. It is based on the assumption that a single source emits a signal that decays with increasing distance from the origin. For range expansions, this signal is the difference in frequency of shared alleles. At the origin, the allele frequency is expected to be lowest (Slatkin and Excoffier, 2012) and to increase approximately linearly with distance. However, since we do not know the allele frequency at the origin, we have to use the indirect approach by comparing pairs of populations. To be precise, if we know that shared alleles have a lower frequency at point S_i compared to point S_j, then we know that S_i is closer to the origin than S_j. If the habitat is two-dimensional, however, this does not tell us the direction of the expansion. Let ||S_i, S_j|| denote the Euclidean distance between two points S_i and S_j. Then,

$$\Vert S_i,O\Vert -\Vert S_j,O\Vert \approx v{\psi }_{i,j},$$ (3)

where O denotes the unknown origin ψ_i,j is the directionality index between samples S_i and S_j and v is a constant that links space to allele frequency (i.e how much does the allele frequency change per unit of space). In words, ψ_i,j is approximately proportional to the difference of the distances ||S_i, O|| and ||S_j, O|| (see also Figure 5). We assume that the sampling locations of S_i and S_j are known without error, and that ψ_i,j can be estimated from genetic data, along with its sample variance Var(ψ_i,j). We estimate the variance by doing 1,000 bootstrap replicates on the SNP. The unknowns that remain are the coordinates of the origin O and the proportionality constant v. To infer these parameters, we solve for ψ, subtract ψ from the equation and sum over all pairs of samples:

$$\left(\widehat{O},\widehat{v}\right)=\underset{O,v}{\text{argmax}}\sum _{i<j}\frac{1}{\text{Var}({\psi }_{i,j})}\left(\frac{\Vert S_i,O\Vert -\Vert S_j,O\Vert }{v}-{\psi }_{i,j}\right).$$ (4)

In most biological application, space will be two-dimensional and therefore we can make this equation more explicit by writing O = (x, y) and S_i = (x_i, y_i). Then,

$$(\widehat{x},\widehat{y},\widehat{v})=\underset{x,y,v}{\text{argmax}}\sum _{i<j}\frac{1}{\text{Var}({\psi }_{i,j})}\left(\frac{1}{v}\left(\sqrt{{(x_i-x)}^2+{(y_i-y)}^2}-\sqrt{{(x_j-x)}^2+{(y_j-y)}^2}\right)-{\psi }_{i,j}\right).$$ (5)

The variance terms correspond to weighting terms; terms where ψ has a high variance are weighted down, whereas terms where we can infer ψ with high accuracy are given a larger weight. We can then find a solution to this equation using nonlinear least squares.

Software

A program to calculate ψ and to estimate the origin of a range expansion is available from www.bpeter.org