Fast and Exact Continuous Collision Detection with Bernstein Sign Classification

Abstract

We present fast algorithms to perform accurate CCD queries between triangulated models. Our formulation uses properties of the Bernstein basis and Bézier curves and reduces the problem to evaluating signs of polynomials. We present a geometrically exact CCD algorithm based on the exact geometric computation paradigm to perform reliable Boolean collision queries. Our algorithm is more than an order of magnitude faster than prior exact algorithms. We evaluate its performance for cloth and FEM simulations on CPUs and GPUs, and highlight the benefits.

1 Introduction

The problem of fast and reliable collision detection arises in physically-based simulation, geometric computing, and robotics. Many applications require accurate algorithms that do not miss a single collision and maintain intersection-free meshes throughout the simulation. Some of the widely-used algorithms for contact computation are based on continuous collision detection (CCD). Given two discrete instances or configurations of rigid or deformable models, CCD algorithms model the motion of each object or a mesh element using a continuous trajectory between the configurations and check for collisions along the trajectory. These algorithms are widely used for cloth simulation [Provot 1997; Bridson et al. 2002; Harmon et al. 2008; Brochu et al. 2012], rigid-body simulation [Redon et al. 2002], hair simulation [Selle et al. 2008], FEM simulation [Tang et al. 2011], robot motion planning [LaValle 2006; Tang et al. 2010a], dynamic solvers [Stam 2009], etc.

The simplest algorithms for triangular meshes linearly interpolate the trajectories of the vertices. In this case, contact computation reduces to performing a series of elementary tests between the vertices, edges, and faces using cubic polynomial root solvers [Provot 1997; Bridson et al. 2002]. Many high-level culling techniques have also been proposed to reduce the number of elementary tests performed between the meshes of complex models.

The elementary tests are typically implemented using finite-precision or floating-point arithmetic and use error tolerances. The numerical errors in arithmetic operations along with the tolerances can impact these elementary tests’ accuracy (Fig. 1). There are two types of problems: false negatives, when the CCD algorithm may miss a collision; and false positives, when the CCD algorithm, acting conservatively, flags a non-colliding configuration as a collision. In order to overcome these problems, Brochu et al. [2012] proposed algorithms for exact CCD computation that can perform reliable collision queries. However, their approach can be relatively expensive due to use of large number of exact arithmetic operations. Moreover, its portability may be limited as efficient implementations of exact computation libraries are not easily available on all processors (e.g. GPUs).

Figure 1. Benefits of Reliable CCD Queries.

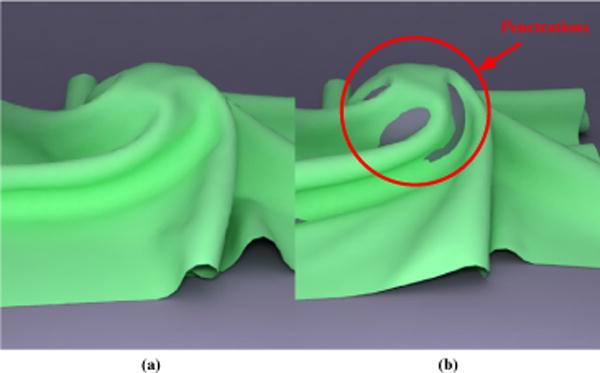
We highlight the benefits of our exact CCD algorithm on cloth simulation. Our algorithm can be used to generate a plausible simulation (a). If parameters are not properly tuned, floating-point-based CCD algorithms (b) can result in penetrations and artifacts.

Main Results

We present fast and accurate algorithms to perform reliable CCD queries. Our approach is based on using coplanarity and inside tests and reduces the computation to finding roots of algebraic equations and inequalities (i.e. a semi-algebraic set). We represent these functions using the Bernstein basis and exploit geometric properties of Bézier curves to design an efficient and reliable Bernstein sign classification (BSC) approach for CCD. The overall collision query is reduced to performing a series of sign evaluations of algebraic expressions and involves simple arithmetic operations. We also present a conservative elementary culling algorithm to improve the algorithm’s performance. We use BSC to design two algorithms:

1. BSC-exact: This is an exact algorithm to perform CCD queries based on the exact geometric computation paradigm [Yap 2004] and is not susceptible to false positives or false negatives. We use extended precision arithmetic operations and accelerate the performance using floating-point filters. As compared to prior exact CCD algorithm [Brochu et al. 2012], we observe 10 – 25X speedup on a single CPU core.

2. BSC-float: This is a finite-precision variant and is implemented using floating-point arithmetic operations. We have evaluated its performance on CPUs and GPUs and observe considerable speedups over prior floating-point CCD algorithms. Furthermore, we observe significant improvement in accuracy, i.e. significant reduction in the number of false positives and false negatives using our algorithm.

The overall algorithms are simple to implement, using only addition, subtraction, and multiplication operations. The use of the Bernstein basis and simple arithmetic operations results in reduced errors and improved efficiency. We highlight the benefits of algorithms using cloth and FEM simulation benchmarks.

2 Related Work

In this section, we give a brief overview of prior work on CCD algorithms, high-level collision culling, and the computation of the roots of polynomials.

Many techniques have been proposed for CCD between rigid models [Redon et al. 2002; Kim and Rossignac 2003], articulated models [Zhang et al. 2007], and deformable models [Volino and Thalmann 1994; Govindaraju et al. 2005; Hutter and Fuhrmann 2007; Tang et al. 2011]. At the lowest level, these algorithms perform elementary tests between triangle pairs. The elementary tests are typically performed by computing roots of cubic polynomials. Other CCD algorithms are based on conservative local advancement [Tang et al. 2009b]. All these methods are prone to floating-point errors and numerical tolerances. Therefore, they can result in false negatives and false positives. Wang [2014] has performed forward error analysis for elementary tests and used that analysis to derive tight error bounds for floating-point computation. This is used to reduce the number of false positive. In contrast, our BSC-exact algorithm and the approach described in [Brochu et al. 2012] are reliable. The tight error bounds in [Wang 2014] can be used to derive tighter error bounds for BSC-float.

High-level Culling

Many high-level techniques have been proposed to accelerate CCD computations by reducing the number of elementary tests between the triangle pairs, such as removing redundant elementary tests [Curtis et al. 2008; Tang et al. 2009a; Wong and Baciu 2006]. The simplest culling algorithms use BVHs (bounding volume hierarchies) based on k-DOPs or AABBs. Other methods use bounds on surface normals and curvature [Volino and Thalmann 1994; Provot 1997; Mezger et al. 2003] or perform self-collision culling [Schvartzman et al. 2010; Pabst et al. 2010; Zheng and James 2012]. Many of these algorithms are implemented using floating-point arithmetic operations and are prone to numerical errors.

Polynomial Root Evaluation

Many numerical iterative methods have been proposed to compute roots of polynomial equations. They tend to use tolerances and can result in false positives or false negatives for CCD computations. In computer graphics and geometric modeling, polynomials are represented using the spline basis, and their roots can be computed using the geometric subdivision methods, such as de Casteljau’s algorithm [Farin 2002] or Bézier clipping [Sederberg and Nishita 1990]. These subdivision methods are implemented using finite-precision arithmetic and are also prone to roundoff errors. There is extensive literature in symbolic computation and computational geometry on reliably computing the roots of polynomials using exact arithmetic [Yap 2004; Mourrain et al. 2005].

3 CCD and Algebraic Formulation

In this section, we formulate CCD queries in terms of algebraic equations and inequalities. We assume that the vertices of the mesh move with a constant velocity during the time interval and that the CCD query reduces to performing two types of Boolean queries or elementary tests [Provot 1997; Bridson et al. 2002; Brochu et al. 2012]. These include the VF query, which checks whether a moving vertex intersects with a moving triangle, and the EE query, which checks whether a moving edge intersects with another moving edge. All these queries assume that the time interval is t ∈ [0, 1] and that the initial configuration at t = 0 is intersection-free. If the Boolean query returns a positive answer, we can use techniques based on interval arithmetic to compute the intersection points or first time of contact to a desired precision. In many applications, only the parity of the number of collisions is needed for robust simulation [Brochu et al. 2012]. As a result, we focus on reliably computing a yes/no answer to the Boolean queries. The exact root and the first time of contact can be computed using root isolation and interval arithmetic techniques.

We first introduce the notations used in the rest of the paper. Next, we present some properties of Bernstein basis functions and Bézier curves that are used by our CCD algorithm.

3.1 Notations

We use following notations in the rest of the paper: Lower case letters in normal fonts (e.g. a, b, a_i,) represent scalar variables. Upper case letters (e.g., L, J(t))) represent scalar functions. Lower case letters in bold face fonts (e.g. a, b_t) represent vector quantities. Upper case letters in bold face fonts (e.g., L, J(t)) represent vector-valued functions. F′(t) and F″(t) are the 1st and 2nd order of derivatives of a scalar function F(t), respectively. The operators ‘*’, ‘·’, and ‘×’ denote the usual scalar multiplication, dot product, and cross product, respectively. Operator Sign() returns the sign of a scalar variable. All the proofs of the lemmas, theorems and corollaries are in the supplementary material.

3.2 Bézier Curves and Bernstein Basis

We use the symbol $B_i^n(t)$ to represent the i^th basis function of the Bernstein polynomials of degree n, i.e. $B_i^n(t)=\frac{n!}{i!(n-i)!}{(1-t)}^{n-i}{t}^i$, where t ∈ [0, 1] and 0 ≤ i ≤ n. The Bernstein polynomial basis is widely used in geometric modeling for curve and surface representation as well as in numerical analysis and computer algebra for root computations [Mourrain et al. 2005]. It is well-known that the polynomials expressed in the Bernstein basis have better numerical stability under perturbation of their coefficients than do those in the power basis [Farouki and Rajan 1987]. As a result, we represent the semi-algebraic set used for CCD queries in Bernstein basis.

Given a cubic polynomial Y(t), it can be expressed using the Bernstein basis, i.e.

$$Y(t)=k_0\ast B_0^3(t)+k_1\ast B_1^3(t)+k_2\ast B_2^3(t)+k_3\ast B_3^3(t).$$ (1)

It corresponds to a cubic Bézier curve F(t) in a plane, where:

$$\begin{array}{l}\mathbf{F}(t)=\left(\begin{array}{c}t\\ Y(t)\end{array}\right)=\left(\begin{array}{c}0\\ k_0\end{array}\right)\ast B_0^3(t)+\left(\begin{array}{c}1/3\\ k_1\end{array}\right)\ast B_1^3(t)\hfill \\ +\left(\begin{array}{c}2/3\\ k_2\end{array}\right)\ast B_2^3(t)+\left(\begin{array}{c}1\\ k_3\end{array}\right)\ast B_3^3(t).\hfill \end{array}$$ (2)

We exploit some geometric properties of cubic Bézier curves in order to characterize inflection points and extreme points. An inflection point occurs where the curvature vanishes or changes its bending direction. The extreme points correspond to local minima or maxima. Every cubic Bézier curve can be classified into three categories (as shown in Fig. 2), depending on whether it has any inflection point or extreme point over its domain (t ∈ [0, 1]) [Farin 2002]:

• Case (a): The curve has an inflection point.

• Case (b): The curve has no inflection point, but an extreme point.

• Case (c): The curve has neither an inflection point nor an extreme point.

Figure 2. Bézier Classifications.

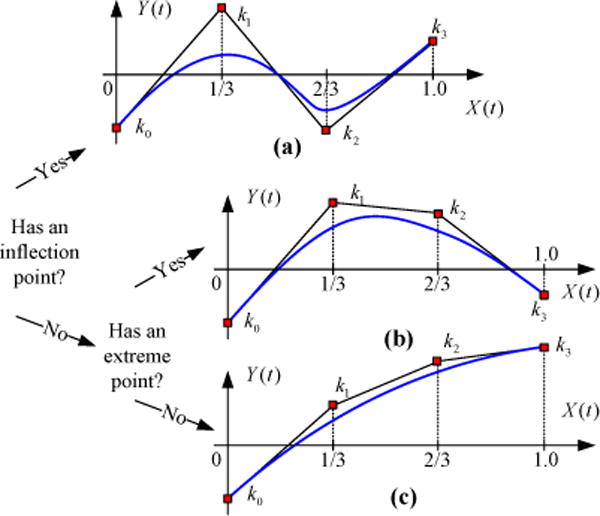
We classify the cubic Bézier curve into three categories (a)–(c), depending on whether it has an inflection point or an extreme point.

The existence of an inflection point or an extreme point can be checked based on the lemmas in the supplementary material.

A cubic Bernstein polynomial can be decomposed into lower-degree polynomials based on the following theorem:

Polynomial Decomposition Theorem

Let G(t) and H(t) be a cubic polynomial and a quadratic polynomial, respectively:

$$\begin{array}{l}G(t)=i_0\ast B_0^3(t)+i_1\ast B_1^3(t)+i_2\ast B_2^3(t)+i_3\ast B_3^3(t),\\ H(t)=j_0\ast B_0^2(t)+j_1\ast B_1^2(t)+j_2\ast B_2^2(t).\end{array}$$ (3)

G(t) can be decomposed as:

$$G(t)=L(t)\ast H(t)+K(t),$$ (4)

where L(t) and K(t) are two linear polynomials:

$$\begin{array}{l}L(t)=u_0\ast B_0^1(t)+u_1\ast B_1^1(t),\\ K(t)={\upsilon }_0\ast B_0^1(t)+{\upsilon }_1\ast B_1^1(t),\end{array}$$ (5)

where u_[0,1] and υ_[0,1] can be calculated from i_[0…3] and j_[0…2].

3.3 CCD Queries

The CCD test between a triangle pair reduces to performing 6 VF queries and 9 EE queries. Each of these queries can be further decomposed into two parts [Provot 1997; Bridson et al. 2002]:

• Coplanarity test: The VF and EE queries involve the use of four deforming vertices. In order for a collision to occur, it is necessary that those four vertices be coplanar.

• Inside test: In addition to satisfy the coplanarity condition, we need to check whether the moving vertex is inside the triangle (VF), or the two edges intersect with each other at an interior point (EE).

The coplanarity test for a VF pair can be expressed as:

$$({\mathbf{p}}_t-{\mathbf{a}}_t)·{\mathbf{n}}_t=0,$$ (6)

where p_t corresponds to the moving vertex, a_t, b_t, c_t are the vertices of the deforming triangle, and n_t is the normal vector of the triangle (i.e. n_t = (b_t − a_t) × (c_t − a_t)).

In order to perform an inside test for a VF pair, we need to perform three one-sided tests, i.e. p_t needs to be inside the triangle. This can be expressed based on the following inequalities:

$$(({\mathbf{b}}_t-{\mathbf{p}}_t)\times ({\mathbf{c}}_t-{\mathbf{p}}_t))·{\mathbf{n}}_t\ge 0,$$ (7)

$$(({\mathbf{c}}_t-{\mathbf{p}}_t)\times ({\mathbf{a}}_t-{\mathbf{p}}_t))·{\mathbf{n}}_t\ge 0,$$ (8)

$$(({\mathbf{a}}_t-{\mathbf{p}}_t)\times ({\mathbf{b}}_t-{\mathbf{p}}_t))·{\mathbf{n}}_t\ge 0.$$ (9)

The coplanarity and inside tests can be combined to find a common root of the following system of algebraic equation and inequalities (i.e. a semi-algebraic set). The VF query reduces to checking whether this semi-algebraic set has a real solution for t ∈ [0, 1].

$$\{\begin{array}{l}({\mathbf{p}}_t-{\mathbf{a}}_t)·{\mathbf{n}}_t=0,\\ (({\mathbf{b}}_t-{\mathbf{p}}_t)\times ({\mathbf{c}}_t-{\mathbf{p}}_t))·{\mathbf{n}}_t\ge 0,\\ (({\mathbf{c}}_t-{\mathbf{p}}_t)\times ({\mathbf{a}}_t-{\mathbf{p}}_t))·{\mathbf{n}}_t\ge 0,\\ (({\mathbf{a}}_t-{\mathbf{p}}_t)\times ({\mathbf{b}}_t-{\mathbf{p}}_t))·{\mathbf{n}}_t\ge 0.\end{array}$$ (10)

3.4 Coplanarity Tests using Bernstein Polynomials

In order to check the coplanarity of a vertex p_t and a triangle (defined by a_t, b_t, and c_t), we need to calculate the projected distance between them along the direction of n_t. If this distance becomes zero at any time in the interval, the four vertices are classified as coplanar based on following theorem.

Coplanarity Test Theorem for a VF Pair

For a deforming triangle, whose initial and final positions are given as (a₀, b₀, c₀) and (a₁, b₁, c₁) and a vertex with initial and final positions as p₀ and p₁, the coplanarity test can be formulated in terms of the following equation:

$$\begin{array}{l}Y(t)=({\mathbf{p}}_t-{\mathbf{a}}_t)·{\mathbf{n}}_t=0\\ =k_0\ast B_0^3(t)+k_1\ast B_1^3(t)+k_2\ast B_2^3(t)+k_3\ast B_3^3(t),\end{array}$$ (11)

where k_[0…3] are scalars can be calculated from (a₀, b₀, c₀, p₀) and (a₁, b₁, c₁, p₁).

The coplanarity test reduces to checking whether the 2D cubic Bézier curve F(t) (Equation (2)) defined in the (X, Y) plane intersects with the X-axis.

3.5 Inside Tests using Bernstein Polynomials

We can also formulate the inside tests using Bernstein polynomials.

Inside Test Theorem for a VF Pair

Given the triangle and the vertex defined by start and end positions over the interval [0, 1], the inside test can be formulated in terms of the following inequality:

$$\begin{array}{r}(({\mathbf{b}}_{\mathbf{t}}-{\mathbf{p}}_{\mathbf{t}})\times ({\mathbf{c}}_{\mathbf{t}}-{\mathbf{p}}_{\mathbf{t}}))·{\mathbf{n}}_{\mathbf{t}}=l_0\ast B_0^4(t)+l_1\ast B_1^4(t)\\ +l_2\ast B_2^4(t)+l_3\ast B_3^4(t)+l_4\ast B_4^4(t)\ge 0,\end{array}$$ (12)

where l_[0…4] are scalars that can be calculated from (a₀, b₀, c₀, p₀) and (a₁, b₁, c₁, p₁).

Simplified Inside Test Theorem for a VF pair

Based on combining Inequality (12) with Equation (11) and algebraic elimination, this inside test can be reduced to the following degree-two formulation:

$$P(t)=p_0\ast B_0^2(t)+p_1\ast B_1^2(t)+p_2\ast B_2^2(t)\ge 0,$$ (13)

where p_[0…2] are scalars, which can be calculated based on k_[0…3] and l_[0…4], as shown in the supplementary material.

3.6 CCD Tests using Bernstein Polynomials

The formulations for coplanarity and inside tests can be combined into the following system of equations and inequalities in terms of Bernstein polynomials:

$$\{\begin{array}{c}{k}_0\ast B_0^3(t)+k_1\ast B_1^3(t)+k_2\ast B_2^3(t)+k_3\ast B_3^3(t)=0,\\ p_0\ast B_0^2(t)+p_1\ast B_1^2(t)+p_2\ast B_2^2(t)\ge 0,\\ q_0\ast B_0^2(t)+q_1\ast B_1^2(t)+q_2\ast B_2^2(t)\ge 0,\\ r_0\ast B_0^2(t)+r_1\ast B_1^2(t)+r_2\ast B_2^2(t)\ge 0.\end{array}$$

where k_[0…3] and p_[0…2] are scalars defined above, q_[0…2] and r_[0…2] are the coefficients corresponding to 2 other inside tests.

4 CCD Query Using Sign Evaluations

In this section, we use the formulation of CCD computation in terms of Bernstein polynomials and present accurate algorithms to perform CCD queries. Our formulation consists of two stages:

• Geometric Coplanarity Test: By deducing the signs of the polynomials at its extreme points and comparing with the signs of its end points in the interval [0, 1], we can check for the existence of roots for coplanarity equations.

• Geometric Inside Tests: During this stage, we evaluate the signs of the inequalities at the roots that have passed coplanarity tests to check whether these roots also satisfy the inside tests.

4.1 Geometric Coplanarity Test

Our goal is to compute the roots of a cubic polynomial Y(t) (defined by Equation (11) in domain [0, 1]). We use the characterization of Bézier curves into three different cases presented in Section 3.2. For the Case (a) in Section 3.2, we subdivide the curve at its inflection point, i.e. $t=\frac{k_2-2\ast k_1+k_0}{k_0-3\ast k_1+3\ast k_2-k_3}$, using de Casteljau’s algorithm. The two subdivided curves either correspond to Case (b) or Case (c) in Section 3.2. We discuss both these cases:

• Case (b): If k₀ and k₃ have different signs, there is only one root in the domain. Otherwise, we use the following Root-Finding Lemma to determine whether there are zero roots or two roots in the domain.

• Case (c): If k₀ and k₃ have the same sign, there is no root; otherwise there is one root in its domain.

Root-Finding Lemma

For a cubic polynomial Y(t) (defined by Equation (11)) with an extreme point in its domain, its 1st derivative Y′(t) is:

$$\begin{array}{l}Y\prime (t)=3\ast (k_1-k_0)\ast B_0^2(t)+3\ast (k_2-k_1)\ast B_1^2(t)\\ +3\ast (k_3-k_2)\ast B_2^2(t).\end{array}$$

We decompose Y(t) = Y′(t) * S(t) + T(t), where S(t) and T(t) are two linear polynomials and can be calculated with the Polynomial Decomposition Theorem in Section 3.2. We use the classification in Fig. 3 to compute the number of roots of Y(t).

Figure 3. Computing the Number of Roots of Y(t).

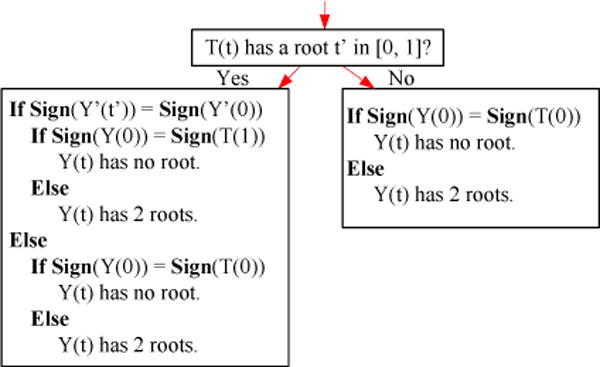
We can compute them based on sign evaluations.

Based on this formulation, we can compute the number of roots for Case (b) and Case (c), and consequently for Case (a).

4.2 Geometric Inside Tests

In order to perform a specific inside test, along with the coplanarity test, we need to test the following system:

$$\{\begin{array}{l}Y(t)=0,\\ P(t)\ge 0.\end{array}$$ (14)

Here Y(t) and P(t) are defined by Equation (11) and Equation (13), respectively. We compute a similar system for the other two inside tests.

Based on the Polynomial Decomposition Theorem in Section 3.2, we can express:

$$Y(t)=L(t)\ast P(t)+K(t),$$ (15)

where L(t) and K(t) are linear polynomials.

Let $\widehat{t}$ be a root of Y(t) in the domain [0, 1], i.e. $Y(\widehat{t})=0$, $\widehat{t}\in [0,1]$. From Equation (15), we obtain $P(\widehat{t})=-K(\widehat{t})/L(\widehat{t})$. Therefore, the problem of computing the sign of $P(\widehat{t})$ reduces to computing the signs of $K(\widehat{t})$ and $L(\widehat{t})$.

We use following theorems to compute the signs of $K(\widehat{t})$ and $L(\widehat{t})$:

Sign Determination Theorem I

Let L(t) be a linear polynomial and Y(t) be a cubic polynomial which corresponds to the Bézier curve of Case (b) in the domain [0, 1] (Fig. 4(a)). Let:

• L(t′) = 0, and t′ ∈ [0, 1],

• $Y(\widehat{t})=0$, and $\widehat{t}\in [0,1]$.

Figure 4. Evaluate the Sign of $L(\widehat{t})$.

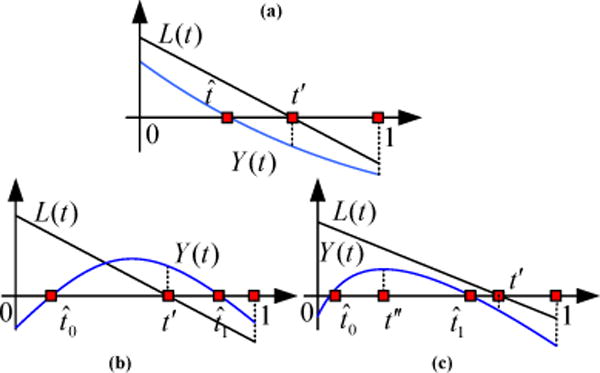
Based on Sign Determination Theorem I and Sign Determination Theorem II, we can evaluate the sign of $L(\widehat{t})$.

We can use the rules in Fig. 5(a) to evaluate the sign of $L(\widehat{t})$).

Figure 5. Rules for Evaluating the Sign of $L(\widehat{t})$, $L({\widehat{t}}_0)$, and $L({\widehat{t}}_1)$.

We use the rules in (a) and (b) for Sign Determination Theorem I and Sign Determination Theorem II, respectively.

Sign Determination Theorem II

Let L(t) be a linear polynomial and Y(t) be a cubic polynomial that corresponds to the Bézier curve of Case (c) in the domain [0, 1] (Fig. 4(b) and Fig. 4(c)). Let:

• L(t′) = 0, and t′ ∈ [0, 1],

• $Y({\widehat{t}}_0)=0$ and $Y({\widehat{t}}_1)=0$, and ${\widehat{t}}_0\in [0,1]$, ${\widehat{t}}_1\in [0,1]$, ${\widehat{t}}_0<{\widehat{t}}_1$,

• Y′(t″) = 0, and t″∈ [0, 1]. Y′(t) is the 1st order of derivative of Y(t).

We can use the rules in Fig. 5(b) to determine the sign of $L({\widehat{t}}_0)$) and $L({\widehat{t}}_1)$).

Based on Sign Determination Theorem I and Sign Determination Theorem II, we can determine the sign of $L(\widehat{t})$.

Sign of $K(\widehat{t})$

The algorithm used to compute the sign of $L(\widehat{t})$ can be directly used to compute the sign of $K(\widehat{t})$.

Based on the signs of $L(\widehat{t})$ and $K(\widehat{t})$, we can compute the sign of $P(\widehat{t})$ and consequently check whether the equality and inequality in Equation (14) are satisfied or not. This is repeated for the other two inequalities as well. If all of them are satisfied, then the answer to the CCD query is positive.

4.3 Conservative Culling Test

Many times there is no collision, and we use a simple culling scheme to accelerate the algorithm. This is similar to using the non-penetration filter [Tang et al. 2010b] or plane-culling [Brochu et al. 2012]. Our goal is to eliminate many VF pairs that do not satisfy the coplanarity condition (see Equation (11)). One sufficient condition is when all the coefficients k_[0…3] are either greater than zero or less than zero. Instead of computing k_[0…3] exactly, we use floating-point filters [Burnikel et al. 2001] to perform conservative culling. In other words, we compute k_[0…3] using floating-point arithmetic. Instead of comparing them with zeros, we check whether they are all greater than $\widehat{\in }$, or all less than $-\widehat{\in }$, where $\widehat{\in }$ is a conservative error bound. The detailed method for computing $\widehat{\in }$ is in the supplementary material.

Algorithm 1 VF-Test: CCD test for a VF pair.
Input: Positions at t = 0 and t = 1 for a deforming triangle (a0, a1, b0, b1, c0, c1) and a moving vertex (p0, p1).
Output: True or False for has a collision or no collision in [0, 1].
1:	GetCoefficients() // Get coefficients of Y(t)).
2:	// Perform conservative culling test.
3:	if ConservativeFilter() then
4:	Return False.
5:	end if
6:	ctype ← BezierType() // Get type of the Bézier curve.
7:	// For case (a), subdivide and check on interval [0, t′] and [t′, 1].
8:	// Here t′ is corresponding to the inflection point.
9:	if ctype = Case A then
10:	Subdivide into two intervals [0, t′] and [t′, 1].
11:	Return VF-Test([0, t′]) OR VF-Test([t′, 1]).
12:	end if
13:	// For case (b) and case (c), continue checking.
14:	// Perform Coplanarity Test (Section 4.1).
15:	if !CoplanarityTest() then
16:	Return False.
17:	end if
18:	// Perform Inside Test (Section 4.2).
19:	if !InsideTest() then
20:	Return False.
21:	end if
22:	Return True. // A valid collision has been detected.

4.4 Overall VF Query Algorithm

Our overall algorithm for VF query is described in Algorithm 1. We first compute the coefficients of Y(t), i.e. k_[0…3] (Line 1), and perform the conservative culling test (Line 3–5). If the culling test fails, we classify the type of Bézier curves (Line 6). For case (a), we subdivide the interval [0, 1] into two sub-intervals [0, t′] and [t′, 1], and recursively perform CCD tests on these sub-intervals (Line 9–12). For case (b) and (c), we perform the coplanarity test (Line 15–17) and inside tests (Line 19–21). If all these tests are positive, the response to VF collision query is positive (Line 22).

We use a similar algorithm for EE tests. The details of its derivation are given in the supplementary material. The main difference with respect to the VF test is in terms of the inequalities used for the inside tests.

BSC-exact: Exact VF Computation

In order to perform reliable collision queries, we use the well-known paradigm of Exact Geometric Computation [Yap 2004], which is widely used for geometric computations and has also been used to perform exact Boolean answers for CCD [Brochu et al. 2012]. The underlying philosophy is that we compute the correct answer to these Boolean queries assuming that we use exact arithmetic and there are no errors due to use of fixed precision or floating-point arithmetic or user specified tolerances. Our exact algorithm, BSC-exact, uses a combination of extended precision arithmetic operations and floating point filters. Our conservative-culling test only uses floating point filters and does not perform exact arithmetic operations. The rest of the computations include many expressions and evaluating signs of polynomials. All these computations can be accelerated using floating point filters.

BSC-float: Floating-point Algorithm

In some cases, optimized libraries for extended precision-arithmetic operations are not available on certain processors (e.g. GPUs). In this case, all the steps of Algorithm 1 are implemented using floating-point arithmetic and are prone to numerical errors. Our resulting algorithm, BSC-float, is based on the IEEE floating-point standard.

5 Implementation and Performance

In this section, we describe our implementation and highlight the performance of our algorithm on several benchmarks.

5.1 Implementation

We have implemented our algorithms on a standard PC (Intel i7-3770K CPU @3.5GHz, 4GB RAM, 64-bits Window 7 OS, NVIDIA Tesla K40c GPU). This includes a CPU-based C++ implementation of BSC-exact that uses a single core and uses an exact computation library based on interval arithmetic [Brochu et al. 2012]. We have also implemented BSC-float on a CPU (with C++) and a GPU (using CUDA 5.5) using hardware-supported floating-point operations.

We compare the performance of our algorithms with the following algorithms:

1. El-Topo-exact: This is the implementation of the exact algorithm of [Brochu et al. 2012], made available by the authors. It also uses plane-based culling to accelerate the computation, along with interval arithmetic-based filters and exact expansions for exact arithmetic operations. In order to compare the performance with BSC-exact, we use the same implementation of exact arithmetic operations.

2. El-Topo-float: This is a floating-point-based cubic root solver CCD implementation, available as part of El-Topo surface-tracking library [Brochu and Bridson 2009]. We measured its performance using a single thread on the CPU.

3. BSC-float-GPU and El-Topo-float-GPU: We also ported BSC-float and El-Topo-float algorithms to GPUs and tested their performance with multiple threads, referred to as BSC-float-GPU and El-Topo-float-GPU, respectively.

5.2 Benchmarks

In order to test the performance of our algorithms, we used five different benchmarks arising from different simulation scenarios that use CCD queries.

• Dancer: A dancer wearing a simple skirt with 5K – 10K triangles, the number of triangles change during the simulation due to adaptive computations. This benchmark has a high number of self-collisions (Figure 6(d)).

• Twisting: A cloth with 2K – 50K triangles twists severely as the underlying ball is rotating. This benchmark has a high number of self-collisions (Figure 6(a)).

• Flamenco: A fiery Flamenco dancer wearing a colorful skirt with ruffles. This benchmark (49K triangles) has many inter-and intra-object collisions (Figure 6(c)).

• Funnel: A cloth with 2K – 42K triangles falls into a funnel and folds to fit into the funnel with many self-collisions (Figure 6(b)).

• Crashing: A Ford Explorer with 1.1M triangles crashes against a rigid wall and the deformation is simulated using finite-element meshing (Figure 6(e)).

Figure 6. Benchmarks.

We use five different benchmarks arising from cloth and FEM simulations.

The first three benchmarks (Dancer, Twisting, and Funnel) are generated by integrating our CCD algorithm into a cloth simulation system, ArcSim [Narain et al. 2012]. The input for the Flamenco and the Crashing benchmarks is given as discrete keyframes. We use linear interpolation between key-frames and check for inter-object and self-collisions. We also use BVH-based hierarchical culling (using AABBs) to reduce the number of elementary tests.

Worst-Case Query Performance

If there is no collision, our culling algorithm is able to discard many of those instances. The query time is higher when there is an actual contact. The worst-case query times for our algorithm vs. prior algorithms are:

• BSC-exact: The worst-case time for EE and VF queries are about 876 ns. In contrast, the worst-case query times for El-Topo-exact are 15 ms and 11μs for EE and VE queries, respectively.

• BSC-float: The worst-case time for EE and VF queries are about 105 ns. In contrast, the worst-case query times for El-Topo-float are about 953 ns for both queries on a CPU core. Moreover, we observe fewer incorrect query results using BSC-float.

5.3 Relative Performance on a CPU

Figure 7 highlights the performance of our algorithms, BSC-exact and BSC-float, and compares them with two prior CCD algorithms, El-Topo-exact and El-Topo-float, on a single CPU core. For all these benchmarks, the performance of BSC-exact is about 10–25X faster than El-Topo-exact, and offers similar reliability. Furthermore, we observe up to an order of magnitude speedup in the floating point implementations. Our approach, BSC-float, involves fewer arithmetic operations, as compared to El-Topo-float. The combination of fewer operations and improved numerical stability properties of Bernstein polynomials also improves the accuracy of BSC-float, i.e. fewer incorrect results to the collision queries in terms of false-negatives or false-positives.

Figure 7. Performance and Comparison.

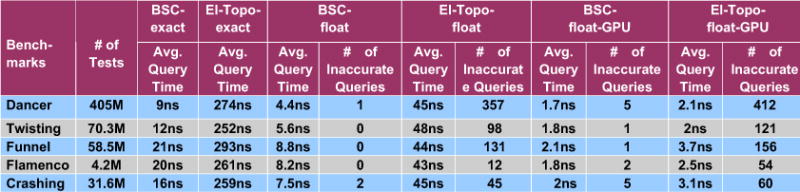
We highlight the performance of various CPU and GPU-based algorithms on different benchmarks. We observe significant speedups using our algorithms based on BSC vs. prior algorithms implemented as part of El Topo [Provot 1997; Bridson et al. 2002; Brochu and Bridson 2009; Brochu et al. 2012]. Even though BSC-float is not guaranteed to be reliable, we observe very high accuracy in our benchmarks, i.e. very few incorrect answers to the queries.

5.4 Relative Performance on a GPU

We have also evaluated the performance on the NVIDIA Tesla K40c GPU. We are not aware of any widely optimized extended precision libraries on GPUs, so we only evaluated the relative performance of BSC-float-GPU and El-Topo-float-GPU on various benchmarks. We compared the accuracy of query results with those computed by exact CPU-based implementations. In this case, BSC-float-GPU results in much fewer inaccurate collision queries as compared to El-Topo-float-GPU. The internal registers used in GPUs may have different precision from CPUs, so we may observe considerable differences in the accuracy results of BSC-float-GPU and El-Topo-float-GPU, as compared to their CPU counterparts. For example, many Intel processors use 80-bit internal registers for floating-point operations, and this may result in higher accuracy for CPU-based implementations. We have also integrated BSC-float and El-Topo-float into a GPU-based cloth simulation system [Tang et al. 2013] and compared the runtime query performance of both CCD algorithms within that system. Figure 7 highlights the performance of BSC-float-GPU and El-Topo-float-GPU. Due to parallelism, the relative performance improvement of BSC-float-GPU over El-Topo-float-GPU is less than those on the CPUs.

5.5 Analysis

The computational costs of our exact CCD algorithm (BSC-exact) varies with respect to different cases described in Section 3.2:

• Case (c): No operation cost for the coplanarity test; involves 3 polynomial decompositions and 3 polynomial evaluations (of degree 3) for inside tests.

• Case (b): Its operation cost includes 1 polynomial decomposition and 1 polynomial evaluation (of degree 2) for the coplanarity test; 3 polynomial decompositions and 6 polynomial evaluations (three of degree 2 and three of degree 3) for the inside test.

• Case (a): Its total operation cost is the sum of (c) and (b).

The overall operation count of our algorithm is much lower than Eltopo-exact and this results in considerable speedups, as shown in Fig. 7. Furthermore, we only perform simple arithmetic operations such as additions, subtractions, and multiplications (see details in the appendix). In terms of extended precision computations, the division operations are more expensive than these three operations and we avoid those expensive operations in our algorithm.

The first time of contact can be easily computed using root isolation We perform mid-point subdivision (using Bernstein formulation) recursively, after Algorithm 1 returns true. The subdivision terminates when the size of the interval containing the root is less than a user-threshold. The mid-point of the interval is used to compute the intersection points. This takes about 30 – 40 ns/query.

We also compared the performance of our solver with the Jenkins-Traub solver¹. It is more accurate than Newton-interval solver (e.g. used in El Topo-float), but about 3X slower. All such numeric solvers are prone to floating-point errors and can result in false-positives and false-negatives. In contrast, our BSC-exact algorithm is reliable and faster than most of these numeric solvers.

6 Limitations, Conclusions and Future Work

We have presented novel algorithms to perform accurate CCD queries between triangular meshes. We exploit properties of Bernstein functions and Bézier curves, reducing the CCD queries to evaluating signs of Bernstein polynomials and algebraic expressions. We present two versions of the algorithm based on exact geometric computation and IEEE floating-point implementations. We have implemented these algorithms on CPUs and GPUs. Our exact algorithm is more than an order of magnitude faster than prior exact algorithms. Furthermore, our floating-point variant is faster and more accurate than prior solvers for elementary tests.

Our approach has some limitations. Our current formulation assumes that the vertices move with a constant velocity. Our reliable algorithm assumes exact representation of vertices, edges, and faces and does not take into account any errors in the input. Our floating-point variant (BSC-float) is faster and more accurate than prior methods, but it does not guarantee a safe and reliable solution. We perform only Boolean collision queries; and additional computations based on root isolation would be needed to compute the first-time-of-contact.

There are many avenues for future work. Besides overcoming these limitations, it may be useful to derive a tight error bound on our floating-point variant and the exact number of bits needed for extended precision. This would help explain its high accuracy in our benchmarks. It would be useful to use our reliable CCD algorithm for other applications including hair simulation and dynamic solvers [Zhao et al. 2012]. Finally, we would like to develop reliable algorithms for high-level CCD culling and collision-response.