Kinetic Mechanisms Governing Stable Ribonucleotide Incorporation in Individual DNA Polymerase Complexes

Abstract

Ribonucleoside triphosphates (rNTPs) are frequently incorporated during DNA synthesis by replicative DNA polymerases (DNAPs), and once incorporated are not efficiently edited by the DNAP exonucleolytic function. We examined the kinetic mechanisms that govern selection of complementary deoxyribonucleoside triphosphates (dNTPs) over complementary rNTPs and that govern the probability of a complementary ribonucleotide at the primer terminus escaping exonucleolytic editing and becoming stably incorporated. We studied the quantitative responses of individual Φ29 DNAP complexes to ribonucleotides using a kinetic framework, based on our prior work, in which transfer of the primer strand from the polymerase to exonuclease site occurs prior to translocation, and translocation precedes dNTP binding. We determined transition rates between the pre-translocation and post-translocation states, between the polymerase and exonuclease sites, and for dNTP or rNTP binding, with single-nucleotide spatial precision and submillisecond temporal resolution, from ionic current time traces recorded when individual DNAP complexes are held atop a nanopore in an electric field. The predominant response to the presence of a ribonucleotide in Φ29 DNAP complexes before and after covalent incorporation is significant destabilization, relative to the presence of a deoxyribonucleotide. This destabilization is manifested in the post-translocation state prior to incorporation as a substantially higher rNTP dissociation rate and manifested in the pre-translocation state after incorporation as rate increases for both primer strand transfer to the exonuclease site and the forward translocation, with the probability of editing not directly increased. In the post-translocation state, the primer terminal 2′-OH group also destabilizes dNTP binding.

While RNA has the same coding potential as DNA, the genomes of contemporary cellular organisms consist of DNA, which is more chemically stable. Nonetheless, a mounting body of evidence has revealed that ribonucleoside triphosphates (rNTPs), which are more abundant in cells than deoxyribonucleoside triphosphates (dNTPs),¹⁻³ are frequently incorporated during DNA synthesis catalyzed by replicative DNA polymerases (DNAPs) both in vitro and in vivo.^2,4−8 For example, yeast Pol ε, the B-family DNAP that catalyzes leading strand nuclear replication in eukaryotes, incorporates one ribonucleoside monophosphate (rNMP) residue per 1250 deoxyribonucleoside monophosphates (dNMPs) in the presence of physiological concentrations of dNTPs and rNTPs in vitro.² Under the same conditions, yeast Pol δ, the B-family DNAP responsible for lagging strand nuclear replication in eukaryotes, incorporates one rNMP per 5000 dNMPs.²

When an rNMP residue is incorporated during replication, the 2′-OH group renders the linkage more labile than DNA linkages and can lead to replicative stress and genome instability.⁹⁻¹² The rNMP-containing product can be repaired after synthesis, primarily via RNase H2-mediated pathways.^11,13−17 If left unrepaired, DNAPs may encounter rNMPs in the template strand during subsequent rounds of replication, and these encounters can lead to termination of DNA synthesis.^2,4 In addition to these potentially deleterious effects, incorporated rNMPs have also been implicated as strand-marking signals in the mismatch repair pathway.^7,15,18,19

DNAPs favor the initial selection of complementary dNTPs over complementary rNTPs, due to polymerase active site structural features that discriminate sterically against rNTPs,²⁰⁻²⁴ and due to conformational checkpoints that selectively promote optimal alignment of complementary dNTP and misalignment of complementary rNTP.²⁵⁻²⁷ Levels of selectivity of dNTP over rNTP range from ∼10³ to >10⁶, depending upon the DNAP and the identity of the base pair examined.²⁶ Nonetheless, rNTPs can escape these initial discrimination mechanisms and become incorporated at significant levels during replication. For example, the incorporation of one rNMP per 5000 dNMPs by yeast Pol δ occurs despite rNTP discrimination levels for this enzyme ranging from 10⁴ to >10⁶ (depending upon the base pair).² It is therefore essential to understand the mechanisms that govern the probability of replicative DNAPs continuing processive synthesis once an rNMP is incorporated.

In addition to an active site for polymerization, many DNAPs have a separate active site for 3′–5′ exonucleolytic editing of newly incorporated replication errors. The exonuclease and polymerase sites of DNAPs are located in separate protein domains (or in some cases, in separate subunits), typically separated by ∼30 Å,²⁸⁻³² and primer strand transfer from the polymerase to exonuclease site requires that ∼3 base pairs of the primer–template duplex be melted.³³ In contrast to noncomplementary dNMPs, when complementary rNMPs are incorporated they are not efficiently edited by replicative DNAPs, including yeast Pol ε, human and yeast Pol δ, and the B-family replicative DNAP from bacteriophage Φ29.^22,34,35

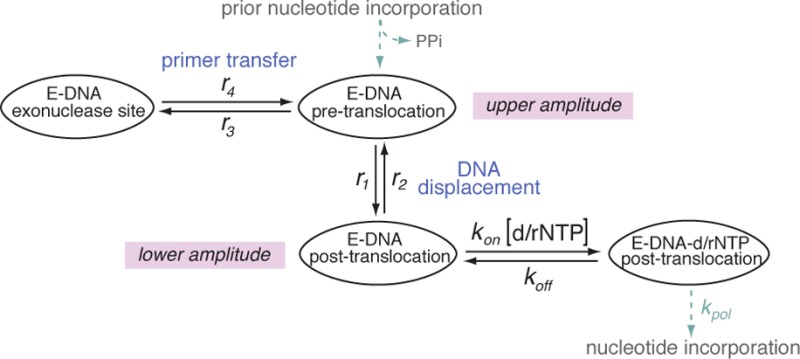
During replication DNAPs translocate along their DNA substrates in single nucleotide increments. We have developed a single-molecule approach using a nanoscale pore to quantify the rates of translocation, primer strand transfer between the polymerase and exonuclease sites, and dNTP binding, with single-nucleotide spatial precision and submillisecond temporal resolution³⁶⁻⁴⁰ (see also Supporting Information). When individual DNAP complexes are captured atop an α-hemolysin (α-HL) nanopore in an electric field, forward and reverse fluctuations across the translocation step are observed as discrete transitions between two amplitudes in time traces of ionic current. Rates of the translocation fluctuations, rates of primer strand transfer in both directions between the polymerase and exonuclease sites, and rates of dNTP binding can be quantified mathematically from dwell time samples extracted from the ionic current time traces.^37,38,40 Using the Φ29 DNAP as a model system, we have shown that transfer of the primer strand from the polymerase to the exonuclease site occurs prior to translocation;⁴⁰ the pre-translocation state is therefore the branchpoint between the DNA synthesis and editing pathways (Figure 1a). The forward translocation step precedes dNTP binding; the translocation is rectified but not driven by dNTP binding, and dNTP has no influence on the rates across the translocation step (Figure 1a).³⁸ If complementary rNTP escapes initial discrimination and is covalently incorporated, the rNMP residue at the primer terminus can affect the probability of primer strand transfer between the polymerase and exonuclease sites, of the translocation step in the polymerase site, and of subsequent dNTP incorporation after the translocation. Together, the transition rates for these processes determine the net probability of stably incorporating the rNMP.

Figure 1.

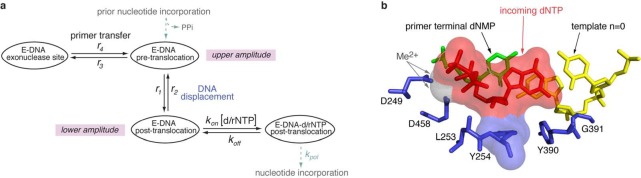
Kinetic and structural determinants of stable dNTP or rNTP incorporation. (a) Model for the kinetic relationships among the steps of translocation, primer strand transfer between the polymerase and exonuclease active sites, and nucleotide triphosphate binding. The kinetic model is fully described by six transition rates: the rates of translocation (r₁, r₂), the rates of primer stand transfer between the pre-translocation state polymerase site and the exonuclease site (r₃, r₄), and the rates of dNTP binding to post-translocation state complexes (k_on[dNTP] and k_off). The mathematical framework based on the model allows us to determine these rates from experimental measurements.^37,38,40 (b) View of the polymerase active site in the Φ29 DNAP–DNA–dNTP, post-translocation state ternary complex from the crystal structure model in PDBID 2PYJ. The structure is from ref (28) and was determined using the D12A/D66A mutant of Φ29 DNAP. Protein residues are blue, the template strand (the n = 0 and n = −1 template residues) are yellow, the primer terminal residue is green, and the incoming dNTP is shown in red. The two active site Me²⁺ ions are rendered as gray spheres. The solvent accessible surfaces of the incoming dNTP and residue Y254, in red and blue, respectively, are shown to highlight the stacking of the deoxyribose sugar of the incoming dNTP on the phenyl ring of residue Y254. Surfaces were rendered in PyMol using a solvent radius of 1.4 Å.

In the B family of DNAPs, the core structure, catalytic mechanisms, and functional properties that contribute to replication fidelity are highly conserved.^28,41−45 Φ29 DNAP serves as an excellent model system for leading strand DNA synthesis catalyzed in more complex replisomes; it catalyzes highly processive DNA synthesis⁴⁶⁻⁴⁸ without the need for accessory proteins such as sliding clamps or helicases, because it remains tightly associated with its DNA substrate and promotes downstream strand displacement during replication.^28,49 The Φ29 DNAP exonuclease active site is located ∼30 Å from the polymerase active site,^28,31 and primer strand transfer between the polymerase and exonuclease sites is an intramolecular process.⁵⁰ In accord with the inefficient editing of rNMPs by replicative DNAPs Pol ε and Pol δ, the probability of exonucleolytic editing of a newly incorporated rNMP by Φ29 DNAP is similar to the basal level observed for complementary dNMP.²² For both Φ29 DNAP and the B-family DNAP from bacteriophage T4, exonucleolytic cleavage of an rNMP residue at the 3′ terminus of a single-stranded substrate is not significantly impaired.^22,51 Thus, it is possible that the inefficient editing observed after complementary rNMP incorporation could occur because the rNMP:dNMP pair is not recognized as incorrect; in this scenario the probability of primer strand transfer from the polymerase to exonuclease site for the complementary rNMP:dNMP pair would not be greater than it is for a complementary dNMP:dNMP pair. But this has not been directly tested, and the contribution of the translocation rates and the dNTP binding rates after translocation to the probability of editing has not been examined.

Φ29 DNAP discriminates against complementary rNTP incorporation by >2 million-fold in steady-state kinetic assays conducted in Mn²⁺.²² In the Φ29 DNAP ternary complex crystal structure, the dNTP is snugly bound, with its deoxyribose moiety stacked upon the phenyl ring of the conserved Y254, leaving no space to accommodate a 2′-OH group on the sugar (Figure 1b),²⁸ leading to the hypothesis that discrimination is due at least in part to steric exclusion of the ribose 2′-OH group. Consistent with this hypothesis, while the Y254F mutation had negligible effects on discrimination between dNTP and rNTP incorporation, introduction of the Y254V mutation decreased the discrimination against rNTP incorporation relative to dNTP incorporation by ∼3 orders of magnitude.²²

Because primer strand transfer from the polymerase site to the exonuclease site precedes translocation,⁴⁰ there is a kinetic competition between primer transfer and the forward translocation. This kinetic competition could be perturbed by a newly incorporated rNMP. Based upon a structural model for the pre-translocation state in which the terminal base pair of the duplex occupies the same configuration that the nascent base pair between the templating base and the incoming dNTP occupies in the post-translocation state ternary complex,²⁸ we hypothesized that the presence of a 2′-OH group at the primer terminus would destabilize the pre-translocation state, due to a structural mechanism of steric exclusion directly analogous to the mechanism that yields discrimination against rNTP binding in the post-translocation state. Specifically, in the structural model for the pre-translocation state, the sugar moiety of the primer terminal residue is predicted to stack on the phenyl ring of Y254, leaving no space to accommodate a primer terminal 2′-OH group. Destabilization of the pre-translocation state following rNTP incorporation could lead to an increase in the rates of both pathways out the pre-translocation state: (i) the transition from the pre-translocation state polymerase site to the exonuclease site (r₃, Figure 1a) and (ii) the transition from the pre-translocation state to the post-translocation state (r₁, Figure 1a). The rates of both of these transitions can directly affect the probability that an incorporated rNMP will be exonucleolytically edited. Furthermore, following the forward translocation, the presence of a 2′-OH group on the primer strand could diminish the probability of binding and incorporating the next dNTP. Because dNTP binds to Φ29 DNAP complexes only after the forward translocation and has no influence on the forward or reverse translocation rates (r₁ and r₂, respectively; Figure 1a),³⁸ a decrease in dNTP binding affinity or in the rate of progression to chemistry (k_pol) caused by a primer terminal rNMP could in turn indirectly affect the probability of transfer to the exonuclease site by increasing the probability of fluctuation back to the pre-translocation state.

In this study, we first examined the kinetic binding mechanisms that govern selection of complementary dNTPs over complementary rNTPs by Φ29 DNAP and by which the Y254V mutation attenuates this discrimination. We then determined the consequences of covalent incorporation of an rNMP residue at the primer terminus on the rates of translocation, the rates of primer strand transfer between the polymerase and exonuclease sites, and the dNTP binding rates. We tested the hypothesis that steric occlusion of a primer terminal 2′-OH group destabilizes the pre-translocation state, which is the branchpoint between the synthesis and editing pathways. The transition rates determined in the study provide insight into the mechanisms that govern the net probability of continuing processive synthesis beyond an rNMP residue, thus stably incorporating it into the nascent strand.

Methods

Enzymes

Wild-type Φ29 DNAP was obtained from Enzymatics (Beverly, MA). The D12A/D66A mutant was obtained from XPol Biotech (Madrid, Spain). Construction, expression, and purification of the Y254V mutant has been described.^22,52 The D12A/D66A-6His mutant was constructed by adding an oligonucleotide coding for six histidines at the carboxyl end of the enzyme to the plasmid containing the D12A/D66A mutation.⁵³ To the resulting plasmid, the Y254V mutation was added to obtain the mutant D12A/D66A/Y254V-6His. The histidine tagged proteins were expressed and purified essentially as described,⁵² with an additional step of a nickel-agarose column. The D12A/D66A and D12A/D66A-6His enzymes were compared in nanopore experiments and the dynamics of complexes formed with the two enzymes were found to be indistinguishable.

DNA substrates

DNA1-H_H, DNA1-H_OH, DNA1-OH_OH, and a version of the DNA1 substrate shortened by one residue at the 3′ end were synthesized at Stanford Protein and Nucleic Acid Facility and purified by denaturing PAGE. DNA1-OH_H was generated from the shortened substrate by incorporating 3′-deoxycytidine-5′-triphosphate (Trilink Biotechnologies) using the D355A/E357A exonuclease-deficient mutant of the Klenow fragment (New England Biolabs) in the presence of Mn²⁺. Reactions were monitored by denaturing PAGE and routinely yielded >95% extended product. The product was purified on Bio-Rad P6 gel filtration spin columns. DNA hairpins were annealed by heating at 90 °C for 4 min followed by snap cooling in ice water.

Nanopore Methods

Nanopore experiments were conducted as described.^{25,36,38,54−56} Briefly, a single α-HL nanopore is inserted in a ∼ 25 μm-diameter lipid bilayer that separates two chambers (cis and trans) containing buffer solution (10 mM K-Hepes, pH 8.0, 0.3 M KCl, and 1 mM EDTA). MgCl₂ and DTT were added to the nanopore cis chamber to final concentrations of 11 mM and 1 mM, respectively. DNA and Φ29 DNAP were added to the cis chamber to final concentrations of 1 and 0.75 μM, respectively. Ionic current was measured with an integrating patch clamp amplifier (Axopatch 200B, Molecular Devices) in voltage clamp mode. Data were sampled using an analog-to-digital converter (Digidata 1440A, Molecular Devices) at 100 kHz in whole-cell configuration and filtered at 5 kHz using a low pass Bessel filter.

Analysis of Ionic Current Time Traces

Each recorded time trace of ionic current amplitude from a captured Φ29 DNAP complex is analyzed in the following series of steps: (i) Determine the centers and relative fractions of the two amplitude clusters. The collection of amplitude samples from each time trace is fitted to a model of two Gaussian modes. The fraction of the upper or lower amplitude mode gives the equilibrium probability of the complex residing at the upper or lower amplitude, respectively. The centers of the upper and lower amplitude modes give approximately the underlying noiseless values of the two amplitude levels. (ii) Extract dwell time samples of each amplitude level from a time trace. We model the measured time trace as a true underlying noiseless time trace plus Gaussian noise. The true underlying noiseless time trace jumps between the two noiseless amplitude levels obtained in step i. Each time the measured amplitudes cross the middle point between the two noiseless amplitude levels, a transition is tentatively detected. To weed out spurious transitions caused by noise, we set a cutoff threshold t_C = 100 μs. A transition from one amplitude to the other is accepted only if the dwell time at the target amplitude level is above the threshold t_C. Transitions with dwell time below the threshold t_C are rejected. All accepted dwell time samples are shifted by t_C; these observed dwell time samples represent the dwell time beyond the threshold t_C. (iii) Determine the intermediate parameters describing the dwell time distribution of each amplitude level. If an amplitude level corresponds to a single kinetic state, the dwell time is exponentially distributed. If an amplitude level corresponds to two kinetic states (see the model diagram in Figure 1a), the dwell time distribution is a combination of two exponential modes (see Supporting Information). The observed dwell time samples of each amplitude level are fitted to their theoretical distribution using the maximum-likelihood estimation (MLE) to determine the intermediate parameters. The two fittings are then corrected to account for the side effects of cutoff threshold t_C = 100 μs. (iv) The intermediate parameters obtained in step iii are used to calculate kinetic transition rates (see Supporting Information). At each experimental condition, we typically have a set of n = 20–30 time traces, which yields a set of n estimated values for each parameter. The final estimation and the associated standard error for each kinetic rate are calculated based on this set of estimated values.

Results and Discussion

In the nanopore experiments, a single α-HL nanopore is inserted into a lipid bilayer that separates two chambers (termed cis and trans) containing buffer solution (Figure 2a). A patch clamp amplifier applies voltage across the bilayer and measures the ionic current that flows through the nanopore, which is carried by K⁺ and Cl^– ions in the buffer. Figure 2b shows a typical ionic current trace that results when an individual binary complex formed between Φ29 DNAP and a DNA substrate (Figure 3a,b(i); DNA1-H_H) is captured atop a nanopore at 180 mV applied potential. The ionic current through the open pore (Figure 2b(i)) drops rapidly when a complex is captured (Figure 2b(ii)). The enzyme is too large to enter the nanopore, and therefore the Φ29 DNAP–DNA complex perches atop the pore. The DNA template strand of the captured complex is suspended through the nanopore lumen, which is just wide enough to accommodate a single strand of DNA. The DNA displacement associated with the translocation is detected by the use of a reporter group comprising five consutive abasic (1′, 2′-H) residues in the template strand (shown as solid red circles in Figure 2b and as red Xs in Figure 3a). When a complex is captured atop the pore, movement of the DNA relative to the enzyme results in a displacement of the template strand reporter group in the nanopore lumen, which, in turn, is manifested as a change in the measured ionic amplitude.

Figure 2.

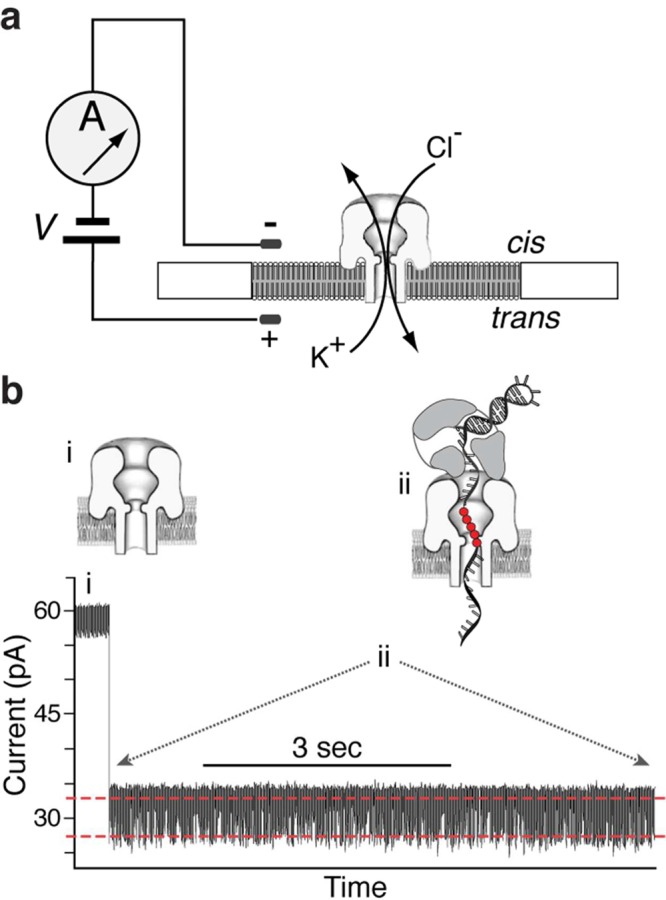
Capturing and measuring individual Φ29 DNAP complexes on the α-HL nanopore. In the nanopore device (a), a single α-HL nanopore is inserted in a ∼25 μm-diameter lipid bilayer separating two chambers (cis and trans) that contain buffer solution. A patch clamp amplifier applies voltage across the bilayer and measures ionic current, which is carried through the nanopore by K⁺ and Cl^– ions. (b) Representative current trace for an individual binary complex of Φ29 DNAP and a DNA substrate (DNA1-H_H, in Figure 3b(i)), formed in the bulk phase in the cis chamber and captured at 180 mV. Cartoons above the current trace illustrate the sequence of events, which is described in the text. In the cartoons, a reporter group of five consecutive abasic (1′, 2′-H) residues is shown as red circles. In the plot of ionic current vs time, the two red dashed lines indicate the two amplitude levels between which the current fluctuates (detailed views of current traces are shown in Figure 3).

Figure 3.

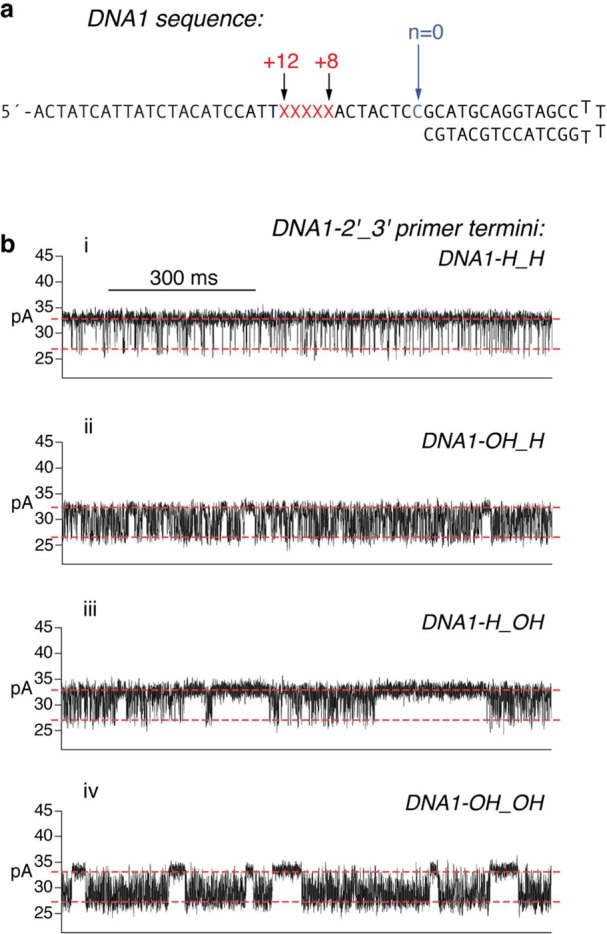
Influence of the DNA substrate primer terminal sugar manifested in ionic current traces for captured Φ29 DNAP complexes. (a) DNA sequence of the hairpin primer–template substrates used in the study. Each substrate features a 14-base pair duplex region and a single-stranded template region of 35 nucleotides. The template strands contain a reporter group of five consecutive abasic (1′,2′-H) residues spanning positions +8 to +12 (indicated as red Xs in the sequence). (b) Ionic current traces for individual binary complexes formed between the D12A/D66A mutant of Φ29 DNAP with (i) DNA1-H_H, which bears a 2′-H, 3′-H primer terminus, (ii) DNA1-OH_H, which bears a 2′-OH, 3′-H primer terminus, (iii) DNA1-H_OH, which bears a 2′-H, 3′-OH (natural deoxyribose) primer terminus, or (iv) DNA1-OH_OH, which bears a 2′-OH, 3′-OH (natural ribose) primer terminus. Complexes were captured at 180 mV.

DNAP–DNA complexes are captured from the bulk phase in the cis chamber, one complex at a time; tens to hundreds of individual complexes are examined, sequentially, in each experiment. Each captured Φ29 DNAP–DNA complex resides atop the nanopore for several seconds (Figure 2b(ii)), during which the measured ionic current fluctuates on the millisond time scale between two amplitude levels (Figures 2b(ii) and 3b). These fluctuations are due to movement of the DNA substrate relative to the enzyme; the distance of this displacement is approximately one nucleotide.³⁶ The observed fluctuations between the two amplitude levels correspond to fluctuations across the translocation step.³⁶ In the complexes formed with DNA1-H_H, at the upper amplitude, the primer–template junction of the DNA substrate is bound in the polymerase active site in the pre-translocation state.³⁶ At 180 mV, the pre-translocation state amplitude is centered at ∼32 pA. At the lower amplitude, the primer–template junction of the DNA substrate resides in the polymerase active site in the post-translocation state.³⁶ The post-translocation state amplitude is centered at ∼26 pA at 180 mV. The amplitude fluctuations continue until the complex dissociates or is ejected, after which another individual complex can be captured.

For binary complexes formed between DNA1-H_H and either the wild-type Φ29 DNAP (Figure 2b) or the exonuclease-deficient mutant D12A/D66A (Figure 3b(i)), the pre-translocation state at the upper amplitude and the post-translocation state at the lower amplitude are discrete kinetic states.³⁷ The transition in each direction across the translocation is a single kinetic step; complexes fluctuate between the two states with two transition rates: r₁, the forward transition from the upper amplitude pre-translocation state to the lower amplitude post-translocation state, and r₂, the reverse transition from the post-translocation state to the pre-translocation state (Figure 1a).³⁷ For complexes formed with DNA1-H_H, the translocation rates r₁ and r₂ for the wild-type enzyme are almost indistinguishable from those of the D12A/D66A mutant.³⁹

The D12A/D66A mutant lacks two of the ligands for the catalytic Me²⁺ ions in the exonuclease active site and thus has negligible exonucleolytic activity,^57,58 permitting us to conduct experiments under conditions in which DNA substrates bearing 3′-OH termini would be degraded if the wild-type enzyme was used.^40,54 When binary complexes are formed between the D12A/D66A mutant and the natural deoxyribose-terminated substrate, DNA1-H_OH, the lower amplitude still corresponds to one kinetic state, the post-translocation state.⁴⁰ But in contrast to complexes formed with DNA1-H_H, in complexes formed with DNA1-H_OH, there is an additional kinetic state at the upper amplitude; the presence of this state can be observed in the time traces as pauses of tens to hundreds of milliseconds that punctuate intervals of rapid fluctuation between the two amplitudes (Figure 3b(iii)) The periods of rapid fluctuation are due to transitions between the pre-translocation and post-translocation states (with rate r₁ for the forward translocation and r₂ for the reverse translocation; Figure 1a), and the pauses in the upper amplitude arise when the primer strand is transferred from the polymerase active site to the exonuclease site (r₃; Figure 1a). When the primer strand is transferred from the exonuclease active site back to the polymerase active site (r₄; Figure 1a), the rapid fluctuations between the pre-translocation and post-translocation states resume.⁴⁰

Discrimination against Complementary rNTP Binding in the Post-translocation State

Wild-type Φ29 DNAP strongly discriminates against complementary rNTP incorporation. In primer extension assays conducted in Mn²⁺, the steady-state kinetic parameter V_max/K_m was >2 million-fold lower for rNTP incorporation than for dNTP incorporation.²² This selective incorporation of dNTPs over rNTPs could be due to a lower binding affinity for rNTPs relative to dNTPs or due to a slower rate of progression to phosphodiester bond formation (k_pol) with rNTP substrates or caused by perturbation of both of these processes. A lower binding affinity may be caused by a lower association rate constant (k_on[rNTP]; Figure 1a), a faster dissociation rate (k_off; Figure 1a), or both. The snug fit of the dNTP bound in the post-translocation state complex observed in the Φ29 DNAP ternary complex crystal structure (Figure 1b)²⁸ indicates that an rNTP residue would not be well accommodated in the polymerase active site; in particular, stacking of the deoxyribose moiety of the incoming dNTP on the phenyl ring of Y254 leaves little space for a 2′-OH group on the sugar. This suggests that the discrimination against complementary rNTP incorporation is at least in part due to ground state binding discrimination.

The 3′-H group at the primer terminus of DNA1-H_H (Figure 3b) significantly inhibits the onset of Φ29 DNAP-catalyzed exonucleolytic digestion of the primer strand.^36,40 This inhibition of exonucleolytic digestion affords protection for DNA in the bulk phase, permitting experiments with wild-type Φ29 DNAP under conditions in which substrates bearing 2′-H, 3′-OH termini are rapidly degraded. In addition, complexes formed with DNA1-H_H support the formation of Φ29 DNAP–DNA–dNTP ternary complexes but not the chemical step of phosphodiester bond formation, allowing the direct comparison of dNTP or rNTP binding affinities and binding rates among complexes.^36,38,39 Complementary dNTP binds with high affinity to complexes in the post-translocation state but has negligible affinity for complexes in the pre-translocation state; the dNTP association and dissociation rates are independent of the applied voltage.^36,38 The transition from the pre-translocation state to the post-translocation state and dNTP binding are sequential (Figure 1a); dNTP can bind to Φ29 DNAP–DNA complexes only after the transition from the pre-translocation state to the post-translocation state, and the transition back to the pre-translocation state cannot occur before the dissociation of dNTP.³⁸

Like complementary dNTP, complementary rNTP stabilizes the post-translocation state in a concentration-dependent manner (Figure 4a and Figure S1c,d, Supporting Information), while having no effect on the dwell time of complexes in the pre-translocation state (Figure S2, Supporting Information). We compared the binding affinity of Φ29 DNAP for complementary dNTP or complementary rNTP in titration experiments, using complexes formed with DNA1-H_H, captured at 180 mV in 10 mM MgCl₂ (Figure 4a). The data are displayed by plotting the normalized p/(1 – p), where p is the probability of post-translocation state occupancy, and the normalized p/(1 – p) is defined as the value of p/(1 – p) in the presence of a given concentration of dNTP or rNTP, divided by the value of p/(1 – p) for the same Φ29 DNAP–DNA complex in the absence of dNTP or rNTP³⁶ (see also Supporting Information). The normalized p/(1 – p) is independent of the transitions between the two translocation states in the absence of dNTP or rNTP; the effect of these transitions is eliminated when p/(1 – p) is normalized by its value measured in the absence of dNTP or rNTP. Based on the model shown in Figure 1a, we derive that (normalized p/(1 – p) – 1) = [d/rNTP]/K_d, where [d/rNTP] refers to the concentration of dNTP or rNTP (see Supporting Information). This theoretical expression predicts that the log–log plot of (normalized p/(1 – p) – 1) vs [d/rNTP] is a straight line with slope =1 and vertical intercept = −log(K_d) at [dNTP] or [rNTP] = 1 μM. K_d is determined from the vertical intercept obtained in fitting observed data points to the theoretical expression. Therefore, the log–log plot of (normalized p/(1 – p) – 1) vs [d/rNTP] allows direct comparison of the post-translocation state binding affinities among the complexes: a higher vertical position in the log–log plot corresponds to a smaller value of K_d (Figure 4a).

Figure 4.

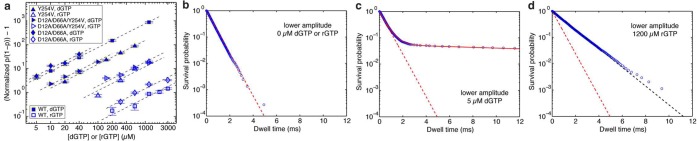
Complementary dNTP or rNTP binding to wild-type Φ29 DNAP and mutants. (a) The normalized p/(1 – p) – 1 is shown in a log–log plot as a function of the concentration of dGTP (filled symbols) or of rGTP (open symbols), for complexes formed between DNA1-H_H and wild-type Φ29 DNAP or mutants. Enzyme identities are indicated by symbol shapes: the wild-type Φ29 DNAP (□), the Y254V mutant (△), the D12A/D66A mutant (◇), or the D12A/D66A/Y254V mutant (▶). The normalized p/(1 – p) is defined as the value of p/(1 – p) in the presence of a given concentration of dNTP or rNTP, divided by the value of p/(1 – p) for the same Φ29 DNAP–DNA complex at 0 μM dNTP or rNTP³⁶where p is the probability of post-translocation state occupancy. Complexes were captured at 180 mV. Error bars show the standard errors. Each data point was determined from 15–30 ionic current time traces for individual captured complexes; each time trace had a duration of 5–10 s. (b–d) Plots of log(survival probability) vs dwell time for the lower amplitude level for complexes formed between wild-type Φ29 DNAP and DNA1-H_H, captured in the presence of (b) 0 μM dGTP or rGTP, (c) 5 μM dGTP, or (d) 1200 μM rGTP. In panels b–d, the dashed red line represents an exponential distribution with rate r₂, which is the constant slope of log(survival probability) at 0 μM dGTP or rGTP and which is obtained by fitting to the data in Figure panel b (see text). The solid red fitting line in panel c shows the fit of the data to a model of two exponential modes. The dashed black fitting line in panel d shows the fit of the data to an exponential distribution. The dwell time samples were extracted from data files collected when complexes were captured at 180 mV; each file yields ∼8000–80000 dwell time samples for each amplitude level. In the plots, while 1 out of every 20 points is shown, the curves are fit to the full set of dwell time samples.

The discrimination by Φ29 DNAP against rNTP incorporation is due at least in part to lower rNTP binding affinity; in complexes formed between the wild-type enzyme and DNA1-H_H, concentration-dependent stabilization of the post-translocation state by complementary rNTP is substantially diminished relative to complementary dNTP (Figure 4a). The K_d for rNTP binding to wild-type complexes is ∼1300-fold greater than the K_d for dNTP binding (Table 1). The D12A/D66A enzyme displays a level of binding discrimination against rNTP similar to the wild-type enzyme; the K_d for rNTP binding to the D12A/D66A enzyme is ∼700-fold larger than the K_d for dNTP binding to this enzyme (Table 1). As we have previously shown, the D12A/D66A mutations themselves yield a modest (<2-fold) increase in complementary dNTP binding affinity, compared with the wild-type enzyme³⁹(Figure 4, Table 1). The D12A/D66A mutations cause an increase in binding affinity of similar magnitude for complementary rNTP, relative to the affinity of the wild-type enzyme for rNTP (Figure 4, Table 1).

Table 1. Complementary dNTP or rNTP Binding Rates for Wild-Type Φ29 DNAP and Mutants^a.

enzyme	DNA	ligand	kon (s–1 μM–1)b	koff (s–1)c	koff (s–1)/kon (s–1 μM–1)	Kd (μM)d
wt	DNA1-H_H	dGTP	21.4 ± 0.6	31.9 ± 0.5	1.49 ± 0.03	1.31 ± 0.04
Y254V	DNA1-H_H	dGTP	19.7 ± 0.9	140 ± 4	7.3 ± 0.3	6.59 ± 0.2
D12A/D66A	DNA1-H_H	dGTP	16.7 ± 0.4	17.7 ± 0.3	1.02 ± 0.02	0.99 ± 0.04
D12A/D66A/Y254V	DNA1-H_H	dGTP	32.4 ± 1.0	126 ± 2.3	3.9 ± 0.2	4.76 ± 0.17
wt	DNA1-H_H	rGTP	>3.2	>5400	e	1702 ± 239
Y254V	DNA1-H_H	rGTP	8.9 ± 1.8	777 ± 16	91 ± 24	83.6 ± 3.6
D12A/D66A	DNA1-H_H	rGTP	>7.1	>4900	e	695 ± 32
D12A/D66A/Y254V	DNA1-H_H	rGTP	12.6 ± 1.9	546 ± 32	45.2 ± 4.2	53.1 ± 1.6
wt	DNA1-OH_H	dGTP	8.9 ± 1.8	526 ± 28	60.8 ± 9.1	59.4 ± 7.3
Y254V	DNA1-OH_H	dGTP	12.7 ± 0.3	1126 ± 39	85.7 ± 1.8	86.4 ± 6.1
D12A/D66A	DNA1-OH_H	dGTP	9.9 ± 0.6	318 ± 26	32 ± 1.0	27.2 ± 1.7
D12A/D66A/Y254V	DNA1-OH_H	dGTP	14.8 ± 0.2	897 ± 19	58.8 ± 1.3	63.4 ± 2.6

^aRates were determined using dwell time samples extracted from ionic current traces (see Methods section) and a three-state kinetic model (consisting of transitions r₁, r₂, k_on and k_off in the model diagram in Figure 1a). Experiments were conducted at 180 mV; k_on[dNTP] and k_off are independent of the applied voltage.³⁸ All values are reported with the standard error.

^bThe dNTP or rNTP association rate constant.

^cThe dNTP or rNTP dissociation rate.

^dK_d values are determined from the vertical intercepts of the fitting lines to the log–log plot of normalized p/(1 – p) – 1 vs [dGTP] or [rGTP], where p is equilibrium probability of the lower amplitude level (see the model diagram in Figure 1a). The plots of normalized p/(1 – p) – 1 vs [dGTP] or [rGTP] are shown in Figures 5 and 7.

^eNot determined.

Introduction of the Y254V mutation partially relieves the discrimination by Φ29 DNAP against rNTP incorporation; the steady-state kinetic parameter V_max/K_m for rNTP incorporation measured in Mn²⁺ was ∼3 orders of magnitude higher for the Y254V mutant than for the wild-type enzyme.²² This partial alleviation of the discrimination against rNTP incorporation by the Y254V mutant is caused in part by an increase in rNTP binding affinity; the K_d for rNTP binding to the post-translocation state of complexes formed with the Y254V mutant was ∼20-fold smaller than the K_d for complexes formed with the wild-type enzyme (Figure 4; Table 1). Similarly, the K_d for rNTP binding for the D12A/D66A/Y254V mutant was ∼13-fold lower than the K_d for complexes with the D12A/D66A enzyme. The presence of the D12A/D66A mutations in the D12A/D66A/Y254V mutant causes a modest increase in binding affinity (decrease in K_d value) for both dNTP and rNTP, relative to the binding affinities for each of these ligands in complexes formed with the Y254V mutant (Figure 4; Table 1).

Y254 is located in the polymerase active site and is directly involved in structural transitions critical to both the translocation and dNTP binding.^28,39,59,60 While the Y254V mutation can relieve the steric clash with rNTP substrates, it does so with the concomitant loss of the stacking interaction with the sugar moiety of the bound nucleotide; the loss of this interaction would be predicted to significantly perturb dNTP binding. When the effects of the Y254V mutant were initially examined in Mn²⁺, the steady-state kinetic parameter V_max/K_m for complementary dNTP incorporation was diminished <2-fold by the presence of the mutation.²² When the effects of introducing the Y254V mutation on dNTP incorporation are examined in Mg²⁺, a more prominent impairment of dNTP incorporation is observed. In the context of a wild-type exonuclease site, the Y254V mutant requires an ∼8-fold higher concentration of dNTPs than is required by the wild-type enzyme to shift the equilibrium between the polymerization and exonucleolytic reactions and achieve a similar primer extension efficiency (Figure S3a, Supporting Information). When measured in an exonuclease-deficient background, the D12A/D66A/Y254V enzyme requires an ∼8-fold higher concentration of dNTPs to support a similar level of primer extension as does the D12A/D66A enzyme (Figure S3b, Supporting Information). In accord with this requirement for a higher concentration of dNTPs, the K_d value for dNTP binding was increased ∼5-fold by the introduction of the Y254V mutation, in both the wild-type and D12A/D66A backgrounds (Figure 4; Table 1). Thus, the Y254V mutation diminishes binding discrimination against rNTP relative to dNTP in two distinct ways: it increases the binding affinity for complementary rNTP while simultaneously decreasing the binding affinity for complementary dNTP.

Kinetic Mechanism of Discrimination against rNTP Binding

The predicted steric occlusion of the 2′-OH group in post-translocation state ternary complexes formed with complementary rNTP²⁸ could yield a decrease in k_on, an increase in k_off, or a change in both rates, relative to complementary dNTP. To understand the kinetic mechanism that yields the low rNTP binding affinity of Φ29 DNAP, we sought to compare k_on and k_off for dNTP and rNTP, calculated from dwell time samples of each amplitude level extracted from measured time traces of ionic current. The calculation of k_on and k_off is based on the mathematical formulation of a three-state model for translocation and nucleotide triphosphate binding, in which r₁, r₂, k_on, and k_off are determined simultaneously from the data.³⁸ We have shown that dNTP has no effect on the translocation rates and that the dNTP association and dissociation rates are independent of the applied voltage (force).³⁸ This three-state model has proven robust for determining dNTP binding rates.^38,39 However, the rNTP binding rates could not be determined for complexes formed between DNA1-H_H and the wild-type enzyme or the D12A/D66A enzyme using this method.

To understand why we could not determine the rNTP binding rates, we examined the effects of complementary rNTP (rGTP) on the observed dwell time samples. We consider the escape problem of exiting from the lower amplitude level. Let S(t) be the probability of dwell time ≥ t (survival probability). Plots of S(t) vs t at various dGTP or rGTP concentrations are shown in Figure 4b–d and in Figure S1a–c, Supporting Information, for complexes formed between DNA1-H_H and the wild-type enzyme. In these plots, the survival probability S(t) is shown in the logarithmic scale. Based on the model in Figure 1a, the slope of log(S(t)) vs t has the expression

where S_post-unbound(t) is the probability of surviving in the lower amplitude level beyond time t and being in the unbound state at time t. The quantity Q(t) = S_post-unbound(t)/S(t) is the fraction of the survival probability in the unbound state. At t = 0, Q(0) = 1. In the presence of dGTP (or rGTP), as t increases, the relative fractions of unbound and bound states reach an equilibrium and Q converges to Q(∞), which is smaller than 1. Correspondingly, the slope of log(S(t)) decreases from r₂ at t = 0 to r₂Q(∞) at large time. For complexes formed between DNA1-H_H and the wild-type enzyme, plots of log(S(t)) are shown for binary complexes (0 μM dGTP or rGTP; Figure 4b) and for complexes captured in the presence of 5 μM dGTP (Figure 4c) or in the presence of 1200 μM rGTP (Figure 4d). The dashed red line in each of the three plots has slope r₂, which is the constant slope of log(S(t)) at 0 μM dGTP or rGTP and is obtained by fitting to the data in Figure 4b. Plots of log(S(t)) at additional concentrations of dGTP or rGTP are shown in Figure S1, Supporting Information. Figure 4c shows clearly the decrease of slope from r₂ to a much smaller value in the plot of log(S(t)) at 5 μM dGTP; the solid red line shows the fitting to a model of two exponential modes. In contrast, in the presence of rGTP, the transition in the slope of log(S(t)) is not observed, as shown for 1200 μM rGTP (Figure 4d). Instead, the observed slope is a constant smaller than r₂; the dashed black line shows a single exponential fitting to the observed dwell time samples.

When k_off ≫ r₂, Q relaxes to equilibrium much faster than the transition rate r₂ and the transition in the slope occurs in a very short time, too short to be resolved in our current experiments. Nevertheless, we can estimate how large k_off has to be given that the transition in the slope is absent in Figure 4d. In extracting dwell time samples, to weed out spurious transitions caused by noise, we set a lower threshold of 100 μs. Transitions with dwell time <100 μs at the target amplitude level are rejected; all accepted dwell time samples are shifted by 100 μs, and these observed dwell time samples represent the dwell time beyond the threshold. Thus, a more precise meaning of S(t) plotted in Figure 4b–d is S(t) = conditional probability of dwell time ≥ t + 100 μs given that dwell time ≥100 μs. In Figure 4d, the observed slope stays at a constant level and is already smaller than r₂. This observation indicates that the transition in slope from r₂ to a smaller value has already occurred within the 100 μs that was cut off. On the other hand, the rate of Q relaxing to equilibrium is bounded by (r₂ + k_on[rGTP]+ k_off), which is the sum of all rates involved in the escape problem of exiting from the lower amplitude level (see Supporting Information). Combining these two results, we obtain

where the factor −log(0.33) reflects the assertion that at least two-thirds (67%) of the transition in slope has occurred in 100 μs. For complexes formed between DNA1-H_H and the wild-type enzyme, r₂ = 1868 s^–1 at 180 mV, and K_d (for rGTP binding) = 1702 μM (Table 1). Figure 4d shows that at 1200 μM rGTP the magnitude of transition in slope is substantial (the difference between the observed constant slope and r₂ is substantial), but the transition is too fast to be observed after the 100 μs cutoff at the lower end. Substituting these values into the inequality above, we arrive at k_off > 5400 s^–1. Accordingly, k_on = k_off/K_d > 3.18 s^–1 μM^–1. These are lower bounds for k_on and k_off. It is reasonable to expect that k_on for rNTP does not exceed k_on for dNTP. For complexes formed between wild-type Φ29 DNAP and DNA1-H_H, k_on = 21.38 ± 0.62 s^–1 μM^–1 for dGTP (Table 1). In the case that k_on for rGTP binding is the same as k_on for dGTP binding and that the increase in K_d value for rGTP relative to dGTP is entirely attributable to the increase in k_off, the dissociation rate for rGTP would be k_off = k_onK_d (for rGTP) = 36346 s^–1, which can be viewed as an upper bound for the rate of dissociation of rGTP from wild-type Φ29 DNAP complexes.

The plots of log(S(t)) vs t for rNTP binding to complexes formed between the D12A/D66A enzyme and DNA1-H_H are very similar to the plots for rNTP binding to wild-type complexes (Figure S2c,d, Supporting Information); the transition in slope from r₂ to a smaller value has already occurred within 100 μs, the cutoff threshold used in extracting dwell time samples. An analysis similar to the one above yields that for rNTP binding to D12A/D66A complexes, k_off > 4900 s^–1. The affinity of rNTP binding to D12A/D66A complexes is K_d = 695 μM (Table 1). Accordingly, for rNTP binding to D12A/D66A complexes, k_on = k_off/K_d > 7.05 s^–1 μM^–1. For complexes formed between the D12A/D66A enzyme and DNA1-H_H, k_on = 16.70 ± 0.4 s^–1 μM^–1 for dGTP (Table 1). In the case that k_on for rGTP binding is the same as k_on for dGTP binding and the increase in K_d value for rGTP relative to dGTP is solely attributable to the increase in k_off, we calculate k_off = k_onK_d (for rGTP) = 11607 s^–1, which can be viewed as an upper bound for the rGTP dissociation rate for the D12A/D66A mutant.

The large increase in k_off suggests that the majority of encounters with rNTP do not progress to phosphodiester bond formation. While we do not have k_pol values for the incorporation of either dNTP or rNTP by Φ29 DNAP, values determined for other B-family DNAPs may provide a plausible range: for dNTP incorporation by T4 DNAP, k_pol = 400 ± 4 s^–1,⁶¹ and for dNTP incorporation by human Pol ε k_pol = 248 ± 6 s^–1.⁶² For the B-family DNAP from bacteriophage RB69, which discriminates against rNTP incorporation by 64000-fold, k_pol = 200 ± 13 s^–1 for dNTP incorporation and k_pol = 0.74 ± 0.2 s^–1 for rNTP incorporation,²¹ a 270-fold decrease in k_pol for rNTP incorporation. It is highly probable that k_pol for rNTP incorporation by Φ29 DNAP is also significantly slower than k_pol for dNTP incorporation; a decrease in k_pol would conspire with the increased rNTP dissociation rate to yield the substantial discrimination exhibited by Φ29 DNAP against rNTP incorporation.

Kinetic Mechanisms by Which the Y254V Mutation Diminishes Discrimination against rNTP Binding

In contrast to complexes formed with the wild-type or D12A/D66A enzymes, for rNTP binding to complexes formed with the Y254V or the D12A/D66A/Y254V mutants, the transition in the slope of log(S(t)) can be resolved in the observed dwell time samples. As a result, the values of k_on and k_off for rGTP binding to these mutants were determined from the data (Table 1). Introduction of the Y254V mutation into either the wild-type or the D12A/D66A background diminishes the discrimination against rNTP binding by causing both an increase in affinity for rNTP and a decrease in affinity for dNTP (Figure 4a; Table 1). The 20-fold increase in the binding affinity of the Y254V mutant for rNTP relative to the wild-type enzyme is primarily due to a decrease in the rNTP dissociation rate. While the plausible range for the rate of rNTP dissociation from the wild-type enzyme is 5400 to ∼36346 s^–1, the rate of rNTP dissociation from the Y254V mutant is k_off = 776.8 ± 16.4 s^–1. Similarly, while the plausible range for the rate of rNTP dissociation from the D12A/D66A enzyme is 4900 to ∼11607 s^–1, the rate of rNTP dissociation from the D12A/D66A/Y254V mutant is k_off = 546.0 ± 31.8 s^–1, indicating that the 13-fold increase in the binding affinity of the D12A/D66A/Y254V mutant for rNTP relative to the D12A/D66A enzyme is also due to a decrease in the rNTP dissociation rate.

In both the wild-type and the D12A/D66A backgrounds, the ∼5-fold decrease in dNTP binding affinity caused by the Y254V mutation is largely due to an increase in the dNTP dissociation rate (Table 1). While there is negligible difference in k_on for dNTP binding attributable to the Y254V mutation, the dNTP dissociation rate of k_off = 140.2 ± 3.9 s^–1 for the Y254V mutant is a ∼4.4-fold increase over k_off = 31.88 ± 0.49 s^–1 for the wild-type enzyme. There is a modest (<2-fold) increase in k_on and an ∼7-fold increase in k_off for dNTP binding to the D12A/D66A/Y254V enzyme relative to the D12A/D66A enzyme. The Y254V mutation may also cause a decrease in k_pol for dNTP, which together with the increase in k_off of the Y254V mutant for dNTP could yield the requirement for a higher concentration of dNTPs to achieve efficient primer extension (Figure S3, Supporting Information).

Kinetic Consequences of Introducing a Primer Terminal 2′-OH Group in the Context of a 3′-H Terminated DNA Substrate

Immediately following covalent incorporation of an rNTP residue, the product occupies the polymerase site in the pre-translocation state. This state is the branchpoint between the DNA synthesis and editing pathways, and we sought to understand the consequences of introducing a ribose sugar at the primer terminus on the fate of Φ29 DNAP binary complexes at this critical juncture. We first examined the effects of introducing a 2′-OH group at the primer terminus by comparing complexes formed with DNA1-OH_H to complexes formed with DNA1-H_H. Inspection of ionic current traces for complexes formed between DNA1-OH_H and the wild-type enzyme or the D12A/D66A enzyme (Figure 3b(ii)) reveals that, in contrast to complexes formed with DNA1-H_H (Figure 3b(i)), intervals of rapid fluctuation between the two amplitudes are punctuated by pauses at the upper amplitude. The pauses are reminiscent of those observed in the time traces for complexes formed between the D12A/D66A enzyme and DNA1-H_OH (Figure 3b(iii)) but appear to be of much shorter duration.

For binary complexes formed between DNA1-OH_H and the wild-type enzyme or the D12A/D66A enzyme, survival probability vs dwell time plots for the lower amplitude fit well to a single exponential distribution (Figure S4d(i,ii), Supporting Information), indicating that, like the complexes formed with DNA1-H_H (Figure S4c(i,ii), Supporting Information), the lower amplitude corresponds to one kinetic state, the post-translocation state. In contrast, survival probability vs dwell time plots of the upper amplitude for complexes formed between DNA1-OH_H and the wild-type enzyme or the D12A/D66A enzyme are inconsistent with a single exponential distribution but are well explained by a model of two exponential modes (Figure S4b(i,ii), Supporting Information). Thus, the pauses at the upper amplitude for the complexes formed with DNA1-OH_H (Figure 3b(ii); Figure S4b(i,ii), Supporting Information), which are not apparent when complexes are formed between DNA1-H_H and either wild-type or D12A/D66A Φ29 DNAP (Figure 3b(i); Figure S4a(i,ii), Supporting Information), correspond to an additional kinetic state. We have shown that this additional kinetic state in the upper amplitude is one in which the primer strand occupies the exonuclease site.⁴⁰

The substantial increase in k_off for complementary rNTP relative to complementary dNTP (Figure 4; Table 1) indicates that in the ground state, the rNTP-bound complex is significantly destabilized relative to the dNTP-bound complex. Based upon a model for the structure of the pre-translocation state in which the terminal base pair of the duplex occupies the same configuration as the nascent base pair does in the post-translocation state ternary complex,²⁸ we therefore hypothesized that an analogous destabilization of the pre-translocation state would be caused by the presence of a 2′-OH group at the primer terminus. This hypothesis predicts that the rates of the transitions out of the pre-translocation state, the forward translocation (r₁) and the primer strand transfer to the exonuclease site (r₃), would increase upon the introduction of a 2′-OH group at the primer terminus. As a first test of this prediction, we compared the dynamic transitions of binary complexes formed with DNA1-H_H or DNA1-OH_H (Figure 5). We used dwell time samples extracted from ionic current traces and a two-state kinetic model³⁷ to determine the translocation rates for complexes formed with DNA1-H_H; we used a three-state model for translocation and primer strand transfer between the polymerase and exonuclease sites⁴⁰ to determine the translocation rates and primer strand transfer rates for complexes formed with DNA1-OH_H.

Figure 5.

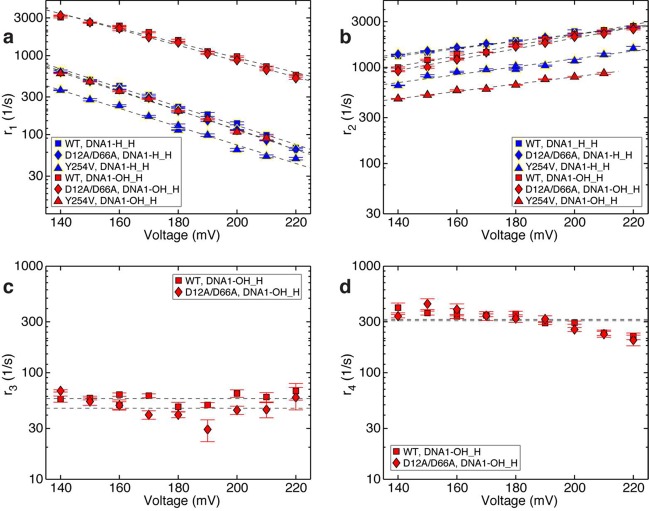
Effects of a 2′-OH, 3′-H primer terminated substrate on the rates of translocation and primer strand transfer between the polymerase and exonuclease sites. Plots of (a) log(r₁) vs voltage, (b) log(r₂) vs voltage, (c) log(r₃) vs voltage, and (d) log(r₄) vs voltage for complexes formed between DNA1-H_H (blue symbols) or DNA1-OH_H (red symbols) and wild-type (■), D12A/D66A (◆), or Y254V (▲) Φ29 DNAP. Rates were determined from dwell time samples extracted from ionic current traces and a three-state kinetic model⁴⁰ consisting of transitions r₁, r₂, r₃, and r₄ in the model diagram in Figure 1a. Errors bars indicate the standard error.

The translocation rates and primer strand transfer rates are plotted as a function of applied voltage (Figure 5). The voltage applies a force along the direction of the translocation, which impedes the rate of the forward translocation (r₁) and increases the rate of the reverse translocation (r₂). The slope of log(r₁) vs voltage is negative and proportional to the distance between the pre-translocation state and the transition state in the translocation step; the slope of log(r₂) vs voltage is positive and proportional to the distance between the transition state and the post-translocation state.³⁷ The rates of primer transfer from the polymerase to the exonuclease site (r₃) and from the exonuclease site to the polymerase site (r₄) do not vary with voltage; this pathway is not associated with a spatial displacement along the direction of the applied force.⁴⁰

The forward (r₁) and reverse (r₂) translocation rates in complexes formed by the wild-type enzyme or the D12A/D66A enzyme with DNA1-H_H are almost indistinguishable,³⁹ and this is also the case for complexes formed with DNA1-OH_H (Figure 5a,b). Consistent with the prediction that the presence of a 2′-OH group at the primer terminus would destabilize the pre-translocation state, r₁ was significantly faster in complexes formed with DNA1-OH_H and the wild-type enzyme or the D12A/D66A enzyme than in complexes formed with DNA1-H_H (Figure 5a). For example, comparing the values at 180 mV for both the wild-type and D12A/D66A enzymes, the presence of the primer terminal 2′-OH caused an ∼7-fold increase in r₁. The primer terminal 2′-OH has modest effects on the magnitude of r₂ (Figure 5b).

In complexes formed with DNA1-OH_H, the rates of primer strand transfer from the polymerase to exonuclease site (r₃; Figure 5c) for the wild-type and D12A/D66A enzymes are very similar. This is also the case for the rates of primer strand transfer from the exonuclease to polymerase site (r₄; Figure 5d). As we have shown for complexes formed with DNA1-H_OH,⁴⁰ in complexes formed with DNA1-OH_H neither r₃ nor r₄ displays a systematic trend with the applied voltage (Figure 5c,d) suggesting that r₃ and r₄ are not affected by the applied force. We therefore treat the data points at individual voltages as independent samples, and calculate the mean and standard error of each rate, for each enzyme. In complexes formed between wild-type Φ29 DNAP and DNA1-OH_H, r₃ = 57.58 ± 2.05 s^–1 and r₄ = 321.6 ± 18.77 s^–1; in complexes formed between the D12A/D66A mutant and DNA1-OH_H, r₃ = 47.65 ± 3.75 s^–1 and r₄ =316.02 ± 25.6 s^–1.

In contrast to the D12A/D66A mutant, the exonuclease site in the wild-type enzyme is catalytically active. Nonetheless, in the complexes formed between the wild-type enzyme and DNA1-OH_H, the rate of primer strand transfer from the exonuclease to polymerase site (r₄) measured when complexes are held atop the pore is for the case when the primer strand is returned to polymerase site uncleaved. The return of the uncleaved primer strand to the polymerase site is indicated by the subsequent resumption of fluctuations between the amplitudes that are characteristic of the pre-translocation and post-translocation states for the intact DNA substrate. Cleavage of the primer strand is rare in the complexes formed between the wild-type enzyme and DNA1-OH_H and, if it occurs, can be readily detected in the ionic current traces. If the primer terminal residue is cleaved, the position of the reporter group in the nanopore lumen is shifted by the distance of one nucleotide, and this yields a new set of two amplitude clusters for the pre-translocation and post-translocation states for the cleaved DNA substrate that is shifted from the set for the substrate before the cleavage.⁴⁰ The transition rates r₃ and r₄ are determined from time traces prior to cleavage of the primer terminal residue, and complexes formed between DNA1-OH_H and the wild-type or the D12A/D66A enzymes have nearly identical values for r₄.

In addition to the increase in r₁ predicted to occur upon introduction of a primer terminal 2′-OH group, the rate of primer strand transfer to the exonuclease site (r₃) is also predicted to increase. Because we cannot reliably detect an upper amplitude dwell time subpopulation corresponding to the state in which the primer strand occupies the exonuclease site for complexes formed with DNA1-H_H (Figure S4 a(i,ii), Supporting Information), we cannot directly compare values of r₃ and r₄ in complexes with DNA1-OH_H to values in complexes with DNA1-H_H. The lack of a separate subpopulation in the upper amplitude dwell time for complexes formed with DNA1-H_H is consistent with the case where r₃/r₄ is very small (either r₃ is small or r₄ is large or both).

Effects of the Y254V Mutation in Complexes Formed with 3′-H Terminated DNA Substrates

While Y254 functions to sterically occlude rNTP binding to post-translocation state complexes, it also participates in dynamic structures in the polymerase active site directly involved in the translocation.²⁸ In the post-translocation state binary complex, the side chains of Y254 and Y390 are stacked; this interaction is presumably disrupted by the Y254V mutation. In the post-translocation state ternary complex, the side chains of Y254 and Y390 are both rotated relative to their positions in the binary complex, which disrupts the stacking interaction between them and allows the deoxyribose sugar of the dNTP to stack on Y254. Thus, in the pre-translocation state binary complex, where the terminal primer strand residue is predicted to occupy the configuration that is occupied by incoming dNTP in the post-translocation state ternary complex, the Y254V mutation would alter the stacking interaction between the Y254 phenyl ring and the primer terminal sugar moiety. Since binary complex interactions in both the pre-translocation state and post-translocation state are perturbed by the Y254V mutation and because of the intimate involvement of Y254 in the active site movements predicted to accompany the translocation displacement,²⁸ it is reasonable to expect that the Y254V mutation would affect the translocation rates. Indeed, introduction of the Y254V mutation in complexes formed with DNA1-H_H causes ∼1.75–2-fold decrease in r₁ (Figure 5a) and ∼1.75–2-fold decrease in r₂ (Figure 5b) relative to the wild-type enzyme. The effects of the Y254V mutant on r₁ and on r₂ are of similar magnitude, yielding little change in the equilibrium across the translocation step in binary complexes.

If the terminal base pair of the duplex occupies the same configuration in the pre-translocation state that the nascent base pair occupies in the post-translocation state ternary complex,²⁸ the destabilization of the pre-translocation state by a primer terminal 2′-OH group would be predicted to be attenuated by the Y254V mutation, via a structural mechanism analogous to the mechanism by which the Y254V mutation increases rNTP binding affinity in the post-translocation state (Figure 4). Consistent with this prediction, when complexes are formed between the Y254V enzyme and DNA1-OH_H, the Y254V mutation almost fully alleviates the ∼7-fold increase in r₁ caused by the introduction of the 2′-OH into complexes formed with the wild-type or D12A/D66A enzymes (Figure 5a); r₁ for complexes of Y254V with DNA1-OH_H is very similar to r₁ for wild-type or D12A/D66A complexes formed with DNA1-H_H. In the complexes formed with DNA1-OH_H, the Y254V mutant yields ∼2-fold decrease in r₂ and a small decrease in the slope of log(r₂) vs voltage, relative to the wild-type or D12A/D66A complexes formed with DNA1-OH_H. These effects of the Y254V mutation on r₂ in complexes formed with DNA1-OH_H are similar to the effects of introducing the mutation in DNA1-H_H complexes.

For complexes formed between the Y254V mutant and DNA1-OH_H, primer strand transition rates (r₃ and r₄) could not be reliably determined. This is reminiscent of complexes formed between Φ29 DNAP with DNA1-H_H, and it is in contrast to complexes of the wild-type or D12A/D66A enzymes with DNA1-H_OH, where a second dwell time cluster at the upper amplitude could be well resolved and r₃ and r₄ could be determined (Figure 5c,d). Inspection of a plot of survival probability vs dwell time for the upper amplitude of complexes formed between the Y254V mutant and DNA1-OH_H shows that while it deviates from a single exponential distribution (Figure S4b(iii), Supporting Information), the second exponential mode that emerged upon the introduction of the 2′-OH in wild-type or D12A/D66A complexes (Figure S4b(i,ii), Supporting Information) is significantly attenuated in the complexes formed with the Y254V mutant, which precludes a reliable estimate of r₃ and r₄ from data.

Kinetic Consequences of Introducing a 2′-OH Group in the Context of a 3′-OH Terminated DNA Substrate

In order to examine the effects of introducing a primer terminal 2′-OH group on the fate of complexes at the branchpoint between synthesis and editing in a context where we can simultaneously detect and quantify the translocation rates (r₁ and r₂ in Figure 1a) and the primer strand transfer rates between the polymerase and exonuclease sites (r₃ and r₄ in Figure 1a), we next compared complexes using DNA substrates with natural deoxyribose (DNA1-H_OH) or ribose (DNA1-OH_OH) primer strand termini, formed with the exonuclease-deficient D12A/D66A mutant. In complexes formed with DNA1-H_H, the translocation rates (r₁ and r₂) for the D12A/D66A enzyme are nearly indistinguishable from those of the wild-type enzyme (ref (39); Figure 5a,b), whereas the primer strand transfer rates r₃ (Figure 5c) and r₄ cannot be determined from the data. For complexes formed with DNA1-OH_H, the D12A/D66A enzyme and the wild-type enzyme yield nearly identical results in the translocation rates, r₁ (Figure 5a) and r₂ (Figure 5b), as well as in the primer strand transfer rates r₃ (Figure 5c) and r₄ (Figure 5d). These data suggest that the wild-type and D12A/D66A enzymes have very similar responses to the introduction of a 2′-OH group at the primer strand terminus. Thus, it is reasonable to expect that the effects on the kinetic rates caused by introducing a primer terminal ribose in D12A/D66A complexes will reflect the effects of introducing a primer terminal ribose in wild-type complexes.

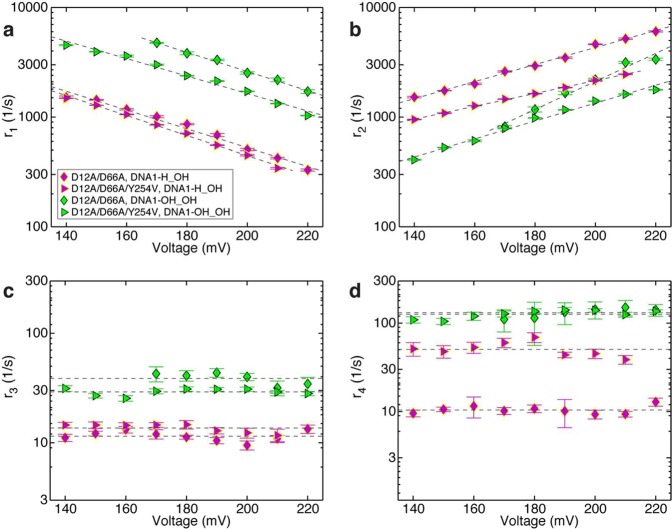
The translocation rates and primer strand transfer rates for complexes formed with DNA1-H_OH (Figure 3b(iii)) or DNA1-OH_OH (Figure 3b(iv)) are plotted as a function of voltage in Figure 6. Consistent with the prediction that a ribose residue at the primer terminus would destabilize the pre-translocation state, in complexes formed between the DNA1-OH_OH and the D12A/D66A enzyme, r₁ was ∼4.8-fold faster than in complexes with DNA1-H_OH (Figure 6a). This is in accord with the increase in r₁ caused by the 2′-OH group in the context of a 3′-H terminated primer strand (Figure 5a). Across the measured voltage range, the ribose-terminated primer strand causes a ∼3.2-fold (lower voltage) to ∼1.8-fold (higher voltage) decrease in r₂ (Figure 6b).

Figure 6.

Effects of a 2′-OH, 3′-OH primer terminated substrate on the rates of translocation and primer strand transfer between the polymerase and exonuclease sites. Plots of (a) log(r₁) vs voltage, (b) log(r₂) vs voltage, (c) log(r₃) vs voltage, and (d) log(r₄) vs voltage for complexes formed between DNA1-H_OH (magenta symbols) or DNA1-OH_OH (green symbols) and D12A/D66A (◆) or D12A/D66A/Y254V (▶) Φ29 DNAP. Rates were determined from dwell time samples extracted from ionic current traces and a three-state kinetic model⁴⁰ consisting of transitions r₁, r₂, r₃, and r₄ in the model diagram in Figure 1a. Errors bars indicate the standard error.

Unlike the case of complexes formed with DNA1-H_H, where rates r₃ and r₄ cannot be reliably estimated, for complexes formed with a natural 3′-OH terminated primer strand, we can directly assess the consequences of introducing a 2′-OH group on the rates of primer transfer between the polymerase and exonuclease sites (Figure 6c,d). Since neither the rate of primer transfer from the polymerase site to the exonuclease site (r₃) nor the rate of primer transfer from the exonuclease site to the polymerase site (r₄) displays a systematic trend with the applied voltage (Figure 6c,d), we treat the data points at individual voltages as independent samples and calculate the mean and standard error for each of these two rates, for each of the two DNA substrates. This yields r₃ = 11.54 ± 0.42 s^–1 for D12A/D66A complexes formed with DNA1-OH_H, the deoxyribose-terminated DNA substrate, and r₃ = 38.86 ± 1.94 s^–1 for D12A/D66A complexes formed with DNA1-OH_OH, the ribose-terminated DNA substrate DNA1-OH_OH. This is a 3.3-fold increase in the rate of primer transfer from the pre-translocation state polymerase site to the exonuclease site, caused by the presence of the 2′-OH group at the primer terminus. Thus, the rates of both pathways out of the pre-translocation state (r₁ and r₃) are increased after the covalent incorporation of an rNTP residue.

The rate of primer strand transfer from the exonuclease to polymerase site was increased >10-fold by the presence of a primer terminal 2′-OH group; r₄ = 10.48 ± 0.38 s^–1 for D12A/D66A complexes formed with DNA1-H_OH, the deoxyribose-terminated substrate, and r₄ = 131.95 ± 6.64 s^–1 for D12A/D66A complexes formed with DNA1-OH_OH, the ribose-terminated substrate. This increase in r₄ for the ribose-terminated primer strand suggests that the 2′-OH group destabilizes primer strand binding in the exonuclease site. While we cannot assess whether this increase in r₄ is of sufficient magnitude to diminish the probability of exonucleolytic cleavage, in experiments that compared exonucleolytic cleavage of single stranded oligonucleotides bearing 3′-terminal deoxyribose or ribose residues conducted with the B family T4 DNAP, as well as with the A family DNAPs, KF and T7 DNAP, cleavage was not impaired for the ribose-terminated substrates.⁵¹ Similarly, the efficiency of exonucleolytic cleavage by wild-type Φ29 DNAP was not impaired by the presence of a ribose residue at the 3′ terminus of a single stranded oligonucleotide substrate.²² These data suggest that the ribose 2′-OH group does not significantly alter the rate of exonucleolytic chemistry. Further, a complementary rNMP residue at the 3′ terminus of the primer strand did not impair cleavage efficiency by wild-type Φ29 DNAP relative to a complementary dNMP residue,²² suggesting that if the increase in r₄ (measured in the nanopore experiments using the exonuclease-deficient D12A/D66A Φ29 DNAP) also occurs when the wild-type enzyme encounters a primer–template substrate with a ribose-terminated primer strand, the 2′-OH group does not render r₄ large enough to compete with the rate of exonucleolytic chemistry.

Effects of the Y254V Mutation in Complexes Formed with 3′-OH Terminated DNA Substrates

In complexes formed between the D12A/D66A/Y254V enzyme and DNA1-H_OH, the DNA substrate with the deoxyribose terminated primer strand, the Y254V mutation causes a small decrease in r₁ (∼1.2-fold), relative to complexes with the D12A/D66A enzyme (Figure 6a). This decrease in r₁ is more modest than the decrease caused by the Y254V mutation in complexes with DNA1-H_H (Figure 5a). We have previously shown that the 3′-OH is a determinant in the energy landscape of the translocation step; r₁ is faster when the primer terminus bears a 3′-OH group than when it bears a 3′-H group.⁴⁰ In the 3′-OH context, the effect of the Y254V mutation on r₁ is not prominently manifested, suggesting that the Y254V mutation does not significantly perturb the effect of the 3′-OH group in increasing r₁.

In the context of complexes formed with DNA1-H_OH, the magnitude of r₂ as well as the dependence of r₂ on opposing force is altered by the Y254V mutation in D12A/D66A/Y254V complexes, relative to D12A/D66A complexes (Figure 6b). Across the measured voltage range, the Y254V mutation causes ∼1.6-fold (lower voltage) to ∼2-fold (higher voltage) decrease in r₂. The decrease in r₂ is similar to the ∼1.75–2-fold decrease in r₂ observed for the Y254 mutation in the context of complexes formed with DNA1-H_H and wild-type or D12A/D66A enzymes (Figure 5b).

The effects of the Y254V mutation on the translocation step are intriguing, since structural predictions can be made that the mutation disrupts the stacking interaction between Y254 and Y390 in the post-translocation state binary complex and disrupts the stacking interaction between Y254 and the sugar moiety of the primer terminal residue in the pre-translocation state binary complex.²⁸ Therefore, the Y254V mutation might be expected to destabilize both the pre-translocation and post-translocation states in binary complexes, leading to increases in r₁ and r₂. Instead, both r₁ and r₂ are decreased when the Y254V mutation is introduced (Figure 5a,b; Figure 6a,b). The loss of the stacking interactions in both of the translocation states makes it implausible that the decreases in both the forward and reverse translocation rates occur because the Y254V mutation lowers the free energy of the pre-translocation or post-translocation state energy wells. It is likely that the Y254V mutation raises the free energy barrier of the transition state by disrupting coordination along the pathway of the translocation step.

The presence of the Y254V mutation has little effect on r₃ in complexes with the deoxyribose-terminated substrate, DNA1-H_OH (Figure 6c); for D12A/D66A/Y254V complexes with DNA1-H_OH r₃ = 13.68 ± 0.42 s^–1 compared with r₃ = 11.54 ± 0.42 s^–1 for D12A/D66A complexes with DNA1-H_OH. In contrast, the Y254V mutation causes ∼5-fold increase in r₄ in complexes formed with the deoxyribose-terminated substrate (Figure 6d); in complexes of the D12A/D66A/Y254V enzyme with DNA1-H_OH, r₄ = 51.16 ± 3.45 s^–1 compared with r₄ = 10.48 ± 0.38 s^–1 for the D12A/D66A enzyme with DNA1-H_OH. We cannot assign a mechanistic cause for this increase in the rate of primer strand transfer from the exonuclease to polymerase site, caused by a mutation located in the polymerase active site. The Y254V mutation may alter the energy landscape across the primer strand transfer pathway, but because the rates across primer strand transfer pathway are insensitive to the force that is applied in the nanopore experimental setup, we cannot directly probe details of the energy landscape.

Consistent with the prediction that the Y254V mutation would attenuate the destabilization of the pre-translocation state by the 2′-OH group, in complexes formed between the D12A/D66A/Y254V mutant and the ribose-terminated substrate DNA1-OH_OH, the rates of both pathways out of the pre-translocation state are modestly decreased relative to the D12A/D66A enzyme with DNA1-OH_OH (Figure 6a). The rate of the pre-translocation to post-translocation state transition, r₁, is decreased ∼1.6-fold, and the rate of primer strand transfer from the polymerase to exonuclease site, r₃, is decreased ∼1.3-fold (for the D12A/D66A enzyme, r₃ = 38.86 ± 1.94 s^–1; for the D12A/D66A/Y254V enzyme, r₃ = 29.22 ± 0.68 s^–1). In contrast to the case with the 3′-H terminated DNA substrates (Figure 5a), in the context of the natural deoxyribose or ribose-terminated DNA substrates, the Y254V mutation only partially alleviates the increase in r₁ caused by introducing the 2′-OH group (Figure 6a).

Finally, while introduction of the Y254V mutation caused an increase in r₄ for complexes formed with DNA1-H_OH, in complexes formed with the ribose-terminated DNA substrate, DNA1-OH_OH, it has negligible effect on r₄; in complexes of D12A/D66A/Y254V, r₄ = 126.54 ± 4.37 s^–1, and in complexes with D12A/D66A, r₄ = 131.95 ± 6.64 s^–1.

The Direct Effect of rNTP Incorporation on the Fate of Complexes at the Branchpoint between the Synthesis and Editing Pathways

The increase in the rate of primer strand transfer from the polymerase to exonuclease site (r₃) elicited by the introduction of a 2′-OH group at the primer terminus (Figure 6c) indicates that a complementary base pair between a primer terminal rNMP and template dNMP (the product of rNTP incorporation) is recognized as incorrect by Φ29 DNAP. The ∼3.3-fold increase in r₃ in complexes formed between D12A/D66A and DNA1-OH_OH relative to DNA1-H_OH is likely modest compared with the increase in r₃ expected for a mismatched (noncomplementary) pair at the primer terminus. Moreover, the increase in r₃ for a newly incorporated rNMP residue is accompanied by an increase in the rate of the forward translocation (r₁). The direct effect of a newly incorporated rNMP residue on the fate of the pre-translocation state complexes can be expressed as the ratio r₁/r₃. For complexes formed with the D12A/D66A enzyme and captured at 180 mV, r₁/r₃ = 76.56 ± 4.28 with the deoxyribose-terminated DNA1-H_OH and r₁/r3 = 93.14 ± 13.10 with the ribose-terminated DNA1-OH_OH. Thus, for Φ29 DNAP complexes formed with both of these DNA substrates, at the branchpoint between the synthesis and editing pathways, the forward transition is more probable, even given that captured complexes are held atop the pore by a force that diminishes the rate of the forward translocation. Further, despite the increased rate of primer strand transfer to the exonuclease site elicited by a newly incorporated rNMP residue, the probability of the forward pathway is slightly increased for a complex bearing a ribose-terminated primer strand, relative to a complex bearing a deoxyribose-terminated primer strand, due to the concomitant increase in the rate of the transition from the pre-translocation to post-translocation state. These findings provide a kinetic basis for the absence of efficient exonucleolytic editing by B-family replicative DNAPs, which likely contributes to the abundant rNMP incorporation in vivo that can be observed prominently in cells that are compromised in RNase H-dependent repair processes.^6,9,34

Effects of a Primer Terminal 2′-OH Group on dNTP Binding after the Translocation

Following the covalent incorporation of complementary rNTP and the forward translocation, complexes attain a state in which they are competent to bind the next incoming dNTP.³⁸ It is reasonable to predict that in the post-translocation state, the presence of a 2′-OH group on the primer terminus could perturb dNTP binding (k_on or k_off), progression to phosphodiester bond formation (k_pol,) or both of these processes. We compared complementary dNTP binding for complexes formed between Φ29 DNAP and DNA1-H_H or DNA1-OH_H. For each of the four Φ29 DNAP enzymes examined (wild-type, D12A/D66A, Y254V, and D12A/D66A/Y254V) introduction of a 2′-OH group at the primer terminus caused a decrease in dNTP binding affinity (Figure 7; Table 1). For the wild-type and D12A/D66A enzymes, the K_d values for dNTP in complexes formed with DNA1-OH_H were increased ∼45-fold and ∼27.5-fold, respectively, relative to complexes formed with DNA1-H_H. The diminished affinity for the wild-type enzyme is caused by ∼2.4-fold decrease in k_on and a larger (∼16.5-fold) increase in k_off. For the D12A/D66A enzyme, the decrease in affinity is due to ∼1.7-fold decrease in k_on and ∼18-fold increase in k_off. The reduction in dNTP binding caused by the primer terminal 2′-OH group is not attenuated by the Y254V mutation (Figure 7; Table 1); rather, in both the wild-type and D12A/D66A backgrounds, this impairment in dNTP binding appears to be roughly additive with the impairment in dNTP binding caused by the Y254V mutation itself (Figure 4; Table 1).

Figure 7.

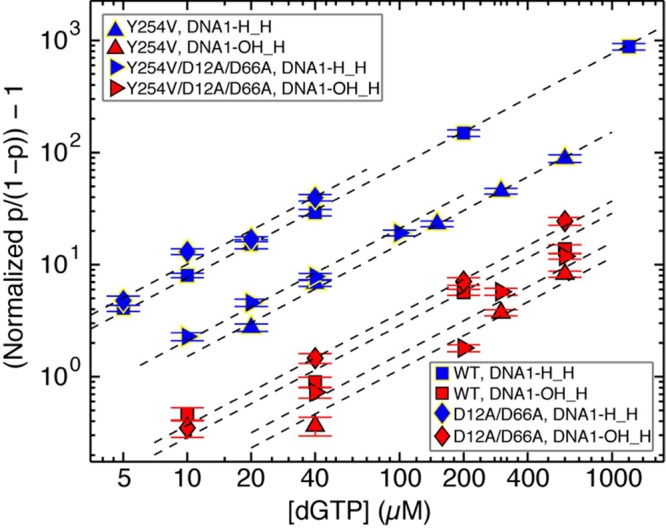
Effects of a primer terminal 2′-OH group on complementary dNTP binding to wild-type Φ29 DNAP and mutants. The (normalized p/(1 – p) – 1) is shown in a log–log plot as a function of the concentration of dGTP for complexes formed between DNA1-H_H (blue symbols) or DNA1-OH_H (red symbols) with the wild-type (■) or Y254V (▲), D12A/D66A (◆), or D12A/D66A/Y254V (▶) Φ29 DNAP. Error bars show the standard errors.

The spatial displacement of translocation separates the state in which dNTP binds from the state in which primer strand transfer from the polymerase to the exonuclease site occurs (Figure 1a); dNTP binds to complexes only after the forward translocation and has no influence on the forward or reverse rates of the translocation, which are inherent to the binary complex.³⁸ Therefore, a decrease in k_on, an increase in k_off, or a decrease in k_pol caused by a primer terminal 2′-OH group will reduce the net probability of the forward synthetic pathway vs the editing pathway after rNTP incorporation by increasing the probability of fluctuating back to the pre-translocation state before the binding of dNTP proceeds to covalent incorporation and carries the complex to the pre-translocation state of the next cycle. Each time a complex fluctuates back to the pre-translocation state, there is a new chance for the primer strand to be transferred to the exonuclease site, with probability governed by the ratio of r₁/r₃.

Once dNTP is covalently added onto the 2′-OH-terminated primer strand, the resulting substrate bears a complementary rNMP:dNMP pair at the −2 position of the duplex. Noncomplementary dNMPs that escape exonucleolytic editing in the −1 position of the primer terminus can continue to exert a strong influence on the probability of editing when they occupy the −2 to −4 positions of the duplex, presumably by increasing the rate of primer transfer to the exonuclease site (refs (63 and 64) and references therein). In a future study, we will examine the influence of complementary rNMP:dNMP pairs in these duplex positions on the net probability of the forward synthetic pathway vs the editing pathway, by determining their effects on the rates of primer strand transfer between the polymerase and exonuclease site, the translocation rates, and the rates of dNTP binding.

Conclusion

The predominant response to the presence of a complementary ribonucleotide in Φ29 DNAP complexes both before and after covalent incorporation is significant destabilization, relative to the presence of a complementary deoxyribonucleotide. This response is exhibited prior to incorporation by the substantially higher dissociation rate for rNTP from post-translocation state complexes (Table 1). Destabilization is also exhibited in the pre-translocation state after rNMP incorporation, as a faster rate of primer strand transfer to the exonuclease site and a faster rate of the forward translocation. When the primer terminus bears a complementary dNMP:dNMP pair, the rate of the forward translocation is much greater than the rate of primer strand transfer to the exonuclease site (Figure 6). While a complementary rNMP:dNMP pair at the primer terminus yields a modest ∼3-fold increase in the rate of transfer to the exonuclease site, the concomitant increase in the forward translocation rate ensures that the probability of exonucleolytic editing is not directly increased by the presence of the incorrect sugar moiety. The net probability of the forward synthetic pathway vs the editing pathway, however, can still be increased indirectly if the presence of the incorrect sugar moiety reduces the probabilities of subsequent forward reactions in the synthetic pathway. Indeed, an example of this is observed when, after incorporation and forward translocation, the presence of a 2′-OH group at the primer terminus also destabilizes the dNTP-bound state.

The findings in this study are in accord with a common structural cause for the destabilization of the rNTP-bound post-translocation state and of the pre-translocation state after rNMP incorporation. They provide strong functional evidence that the polymerase active site configuration surrounding the primer terminal base pair after covalent incorporation, but prior to translocation, resembles the structure of the post-translocation state ternary complex.²⁸ The destabilization that is a consequence of the presence of a ribonucleotide rather than a deoxyribonucleotide in both the pre-translocation and post-translocation states is at least in part due to a steric clash of the 2′-OH group with the phenyl ring of the highly conserved residue Y254; in both translocation states the destabilization is partially alleviated by the Y254V mutation. It is reasonable to predict that other B-family DNAPs, with their conserved polymerase active site structures, have similar responses to complementary ribonucleotides and to further predict that the destabilization of both states may extend to replicative DNAPs from other families. This study thus reveals kinetic mechanisms that contribute to the initial discrimination against rNTPs over dNTPs, kinetic mechanisms that underlie the inefficient editing of newly incorporated rNMPs by replicative DNAPs, and kinetic mechanisms that contribute to the probability that replicative DNAPs will continue synthesis beyond a newly incorporated rNMP and stably incorporate it into the nascent strand.

Supporting Information Available

Mathematical derivations, effects of complementary dNTP or complementary rNTP on the lower amplitude dwell time distributions and the upper amplitude dwell time distributions, effect of the Y254V mutation on the dNTP concentration-dependence of polymerization, and effects of a primer terminal 2′-OH group on dwell time distributions at each of the two amplitude levels for wild-type and mutant Φ29 DNAP binary complexes. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States