Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 2014 Dec 15;111(52):18649–18654. doi: 10.1073/pnas.1321892112

Nonrandom, diversifying processes are disproportionately strong in the smallest size classes of a tropical forest

Peter T Green a,b,1, Kyle E Harms c, Joseph H Connell d
PMCID: PMC4284543  PMID: 25512498

Significance

A long-standing paradigm in forest ecology holds that patterns of relative abundance among a forest’s mature trees are largely set by biotic and abiotic processes that operate most strongly at the earliest life-cycle stages. Although support for this model is implicit in the vast body of research on tropical seedling dynamics, the paradigm has never formally been tested in any forest. Using multidecadal demographic data, we present quantitative evidence for the primacy of early-stage, nonrandom dynamics in forest ecology. This finding corroborates the importance that tropical ecologists have traditionally assigned to early-stage dynamics, and calls for greater and more widespread inclusion of the smallest size classes into large, plot-based tropical forest dynamics projects worldwide.

Keywords: diversity, early life-cycle stages, nonrandom, tropical forest

Abstract

A variety of ecological processes influence diversity and species composition in natural communities. Most of these processes, whether abiotic or biotic, differentially filter individuals from birth to death, thereby altering species’ relative abundances. Nonrandom outcomes could accrue throughout ontogeny, or the processes that generate them could be particularly influential at certain stages. One long-standing paradigm in tropical forest ecology holds that patterns of relative abundance among mature trees are largely set by processes operating at the earliest life cycle stages. Several studies confirm filtering processes at some stages, but the longevity of large trees makes a rigorous comparison across size classes impossible without long-term demographic data. Here, we use one of the world’s longest-running, plot-based forest dynamics projects to compare nonrandom outcomes across stage classes. We considered a cohort of 7,977 individuals in 186 species that were alive in 1971 and monitored in 13 mortality censuses over 42 y to 2013. Nonrandom mortality with respect to species identity occurred more often in the smaller rather than the larger size classes. Furthermore, observed nonrandom mortality in the smaller size classes had a diversifying influence; species richness of the survivors was up to 30% greater than expected in the two smallest size classes, but not greater than expected in the larger size classes. These results highlight the importance of early life cycle stages in tropical forest community dynamics. More generally, they add to an accumulating body of evidence for the importance of early-stage nonrandom outcomes to community structure in marine and terrestrial environments.

Processes that operate nonrandomly with respect to species identity contribute to the structure of natural communities (1–3). Evidence from diverse rain forests includes demographic transitions from seeds to seedlings (4, 5), at the seedling (6, 7) and sapling stages (8) and among large trees (9–12). Although the relative contributions of nonrandom processes at each life cycle stage to determining patterns of abundance and diversity in the mature canopy are unknown, one long-standing paradigm is that community assembly is mediated primarily by events occurring from seed dispersal through seedling germination and small-sapling establishment (13–17). However, despite suggestive patterns (6, 7, 18, 19), evidence is lacking for the comparative strength of early-stage dynamics in determining canopy abundance and diversity.

Numerous studies demonstrate significant interspecific variation in the susceptibility of tropical tree seedlings to postgermination hazards, including natural enemies (20, 21), adverse climatic or edaphic conditions (22), physical damage (23), and the crowding or shared-enemies effects of con- and heterospecific neighbors (24, 25). In other words, the per capita probability of seedling mortality is nonrandom because the probability of death is not the same for all individuals in a local community – it is dependent to some degree on species identity. In plant communities in which generation times are relatively short, experiments have demonstrated that nonrandom mortality through these early transitions can be sufficiently strong to affect the species composition of mature plants (26–29). Such demonstrations are impossible in studies of a few decades or less in duration when generation times are long and even juveniles live for several decades or centuries, such as in many tropical forests. Even so, some hypotheses explicitly identify stressors that affect plants at the earliest life cycle stages (such as pests and pathogens, 13, 14, 30) as disproportionately influential. In addition, some empirical studies find a lack of support for nonrandom processes operating among larger stems (31, 32). Together these hypotheses and observations provide the rationale underpinning the considerable body of research on seed and seedling dynamics in tropical forests worldwide. However, no empirical or experimental assessment has been made of the relative contributions across life cycle stages from nonrandom mortality.

Here, we evaluate the comparative contribution of early-stage dynamics using a multidecadal study of a tropical forest dynamics plot initiated by one of us (J.H.C.) in 1963 at a site in north Queensland, Australia. We considered a cohort of 7,977 individuals in 186 species that were alive on the plot in 1971, from tiny seedlings to large canopy trees, whose fates were monitored in 13 mortality censuses over 42 y to 2013. Individuals were assigned to one of six size classes (Table 1). We used Monte Carlo statistical randomization to test two key predictions: (i) that the degree of nonrandom mortality with respect to species identity in a community of long-lived forest plants is highest among the smallest size classes, which would implicate early stages as especially important; and (ii) observed levels of nonrandom mortality significantly diversify survivors relative to simulated mortality based on purely random expectations.

Table 1.

Demographic summary for the intercensus period from 1971 to 2013

Size class* N in 1971 S in 1971 S in 2013 D in 2013 (% mortality)
SC1 (0-6.0-cm ht) 1,465 91 24 1,421 (97.0)
SC2 (6.1–15.2-cm ht) 1,275 105 47 1,156 (90.7)
SC3 (15.3–36.6-cm ht) 1,291 106 77 965 (74.7)
SC4 (36.7–182.9-cm ht) 1,351 124 101 639 (47.3)
SC5 (183.0-cm ht – 10-cm dbh) 1,208 135 123 330 (27.3)
SC6 (≥10.1-cm dbh) 1,387 122 113 357 (25.7)
Open in a new tab

S, number of species; N, number of stems alive in 1971; D, number of stems that died by 2013; dbh, diameter at breast height.

*

The original units of measurement on this plot were decimal inches and feet. Individuals < 3.2-inches girth have always been measured for height, to the nearest 0.1 ft. The upper height limits of size classes 1–4 are the metric equivalents of 0.2, 0.5, 1.2, and 6.0 ft.

Our analyses proceeded in three stages. First, we determined the percentage, P, of species in each size class dying nonrandomly between 1971 and 13 progressively longer census periods to 2013. A species died nonrandomly within a given size class if the observed number of individuals dying over a census period was significantly different from the number of deaths expected under Monte Carlo simulations (10,000 runs) in which the probability of mortality was random with respect to species identity within the size class (i.e., “expected mortality”). Second, we determined for each census period and size class the effect of nonrandom mortality on the observed species richness of both the stems that survived (SS) and the stems that died (SD). From the simulations we generated means and 95% confidence limits for the expected numbers of survivors for each species in each size class in each census interval. We also calculated means and 95% confidence limits for the expected numbers of deaths for each species in each size class and census interval, as well as the means and 95% confidence limits for expected SS and SD. Third, we investigated frequency-dependent mortality as a potential mechanism explaining departures from expected species richness among observed survivors and the stems that died.

Results

Proportion of Species Dying Nonrandomly.

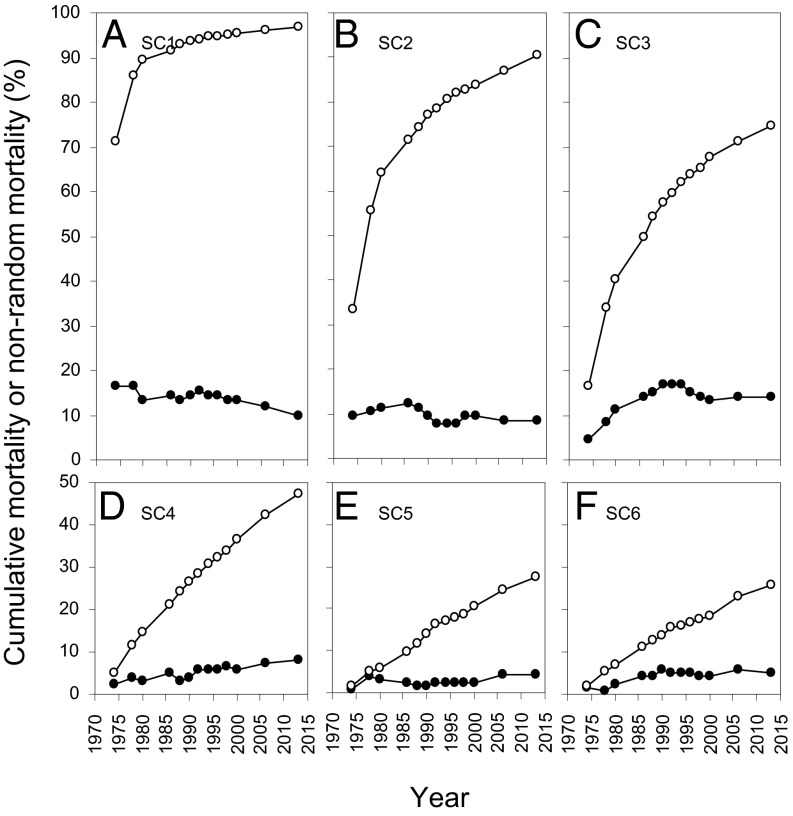
The proportion of species dying nonrandomly (P) varied over time, but for any given census period, P was highest in the three smallest size classes (SCs; SC1–SC3; Fig. 1 A–C), and lowest in the three largest size classes (SC4–SC6; Fig. 1 D–F). In SC1 more than 71% of stems died by the first mortality census after 1971 (i.e., 1974), and 15 of 91 (16.5%) species died nonrandomly. P declined as more stems died over time; by the final mortality census in 2013, 97% of stems had died and 9.9% of species (9 of 91) died nonrandomly. Cumulative mortality in SC2 rose from 33.3% in 1971–90.7% in 2013, and P varied between 8.6% and 12.4%, with the peak occurring in 1986 at 71.4% cumulative mortality. In SC3, cumulative mortality rose from 16.4% in 1971–74.7% in 2013, and P varied between 4.7% and 17.0%, with a sustained peak in the 1990, 1992, and 1994 censuses. In SC4 P peaked in the last (2013) census at 8.1% of species and 47.3% cumulative mortality. Mortality was almost completely random by the time stems had reached about 1.8 m tall, rarely exceeding 5% of species in SC5 and SC6.

Fig. 1.

Fig. 1.

Open in a new tab

Cumulative percent mortality (open circles) and the percentage of species dying nonrandomly (filled circles) for 13 mortality censuses in each of six size classes (SC1, SC2, etc.) between 1971 and 2013. Each panel (A–F) displays one size class; note the truncated y axes for D–F.

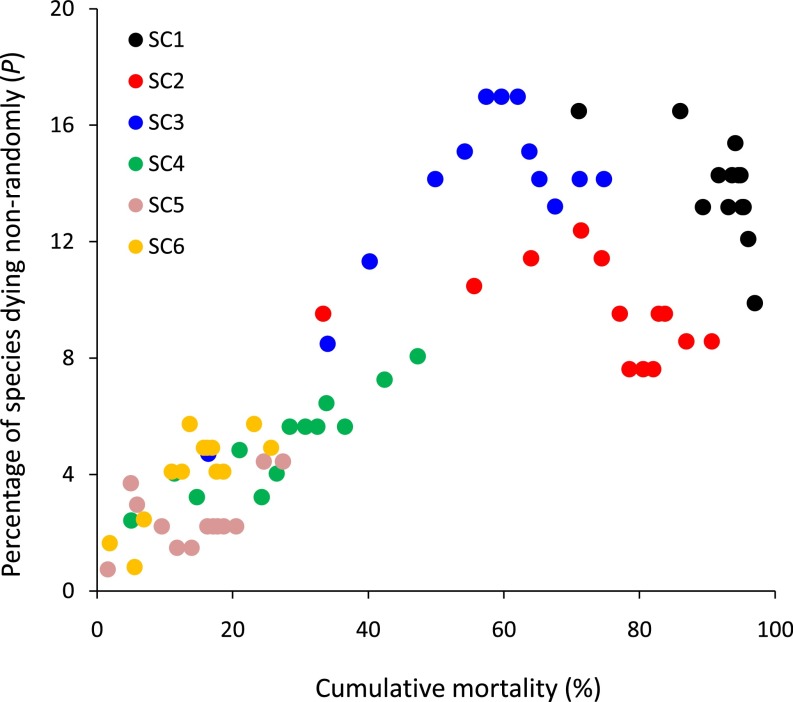
To distinguish differences in intrinsic nonrandom mortality from the influence of cumulative mortality per se, P should be compared among size classes across overlapping parts of their cumulative mortality ranges. For example, there is no indication that P differed among SC4, SC5 and SC6 where their cumulative mortalities overlap to about 25% cumulative mortality (Fig. 2). However, there is clear evidence of greater intrinsic nonrandom mortality among plants in SC1 compared with SC2, where their cumulative mortalities overlap beyond 70% cumulative mortality. Conversely, there is greater intrinsic nonrandom mortality in SC3 than in SC2, where their cumulative mortalities overlap in the range from 33 to 75%. Even though there are few points of comparison, P was larger in SC2 and SC3 relative to SC4 when matched for cumulative mortality.

Fig. 2.

Fig. 2.

Open in a new tab

The percentage of species in each of six size classes dying nonrandomly plotted against percent cumulative mortality, for 13 mortality censuses between 1971 and 2013. Note that, within size classes, the data points are not independent; each represents one census date in a time series that runs from left to right along the x axis.

Effect of Nonrandom Mortality on Species Richness.

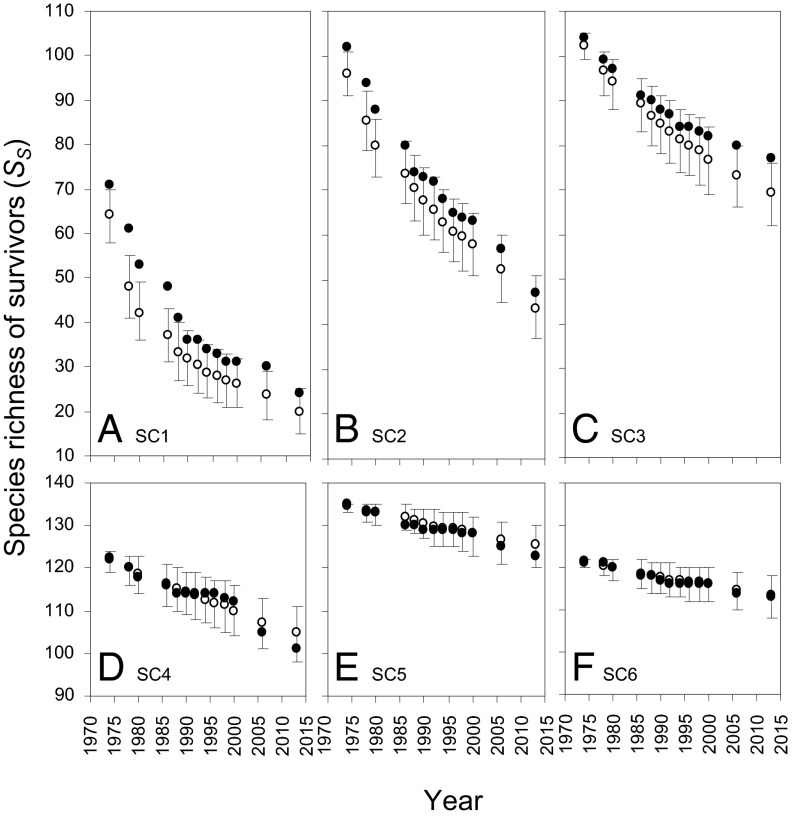
Although some species died nonrandomly in all six size classes, significantly different from expected SS was observed only in the three smallest size classes (Fig. 3 A–C). In SC1, SS was greater than expected in five intercensus periods early in the study; in 1974 there were 71 species in the community of survivors, 6.9 species (10.8%) more than mean expected species richness (Fig. 3A). Furthermore, SS was significantly greater than expected by 13.0 species (27.2%) in 1978, by 10.9 species (25.8%) in 1980, by 11.0 species (29.8%) in 1986, and 7.8 species (23.4%) in 1988. Nonrandom mortality affected SS less often (3 of 13 census periods) and to a lesser degree in SC2, with increases in species richness of 6.1%, 8.4% and 8.1%, respectively, in the first three censuses in 1974, 1978, and 1980. Nonrandom mortality affected species richness in just the last census in SC3, with a significant increase of 11.3% in species richness (Fig. 3C). Nonrandom mortality had no measurable impact on SS in the three larger size classes (Fig. 3 D–F). In all cases in SC1, SC2, and SC3 in which nonrandom mortality had a diversifying impact on the community of survivors, this was mirrored by a complementary, greater than expected reduction in SD over the same time increments (Fig. S1).

Fig. 3.

Fig. 3.

Open in a new tab

Observed (filled circles) and mean expected (open circles) species richness of stems in six size classes (SC1, SC2, etc.) surviving from 1971 to each of 13 mortality censuses thereafter to 2013. Mean expected species richness is plotted with 95% confidence intervals, based on 10,000 randomizations. Each panel (A–F) displays one size class; note the truncated y axes for D–F.

Frequency-Dependent Mortality.

There was no evidence of community-wide frequency-dependent mortality in any size class, but strong evidence in the smallest size classes of positive frequency-dependent mortality (PFDM) among those species showing nonrandom mortality (Table 2). In SC1 and SC2, stems of commoner species were more likely to die than stems of less common species in all 13 periods from 1971, and the same pattern was observed in 12 of 13 periods in SC3. This pattern weakened in SC4 with no relationship between abundance and mortality evident in 4 of 10 analyzable periods, and PFDM in the last 6 periods to 2013. These patterns reversed in the two largest size classes; in SC5, there was significant, negative frequency dependent mortality in 2 of 3 analyzable periods, and in 9 of 10 analyzable periods in SC6.

Table 2.

Frequency dependence among species dying nonrandomly since 1971

SC1 SC2 SC3 SC4 SC5 SC6
Year Slope N Slope N Slope N Slope N Slope N Slope N
1974 pos*** 15 pos*** 10 NS 5
1978 pos*** 15 pos*** 11 pos*** 9 NS 5 NS 5
1980 pos*** 12 pos*** 12 pos*** 12
1986 pos*** 13 pos*** 13 pos*** 15 NS 6 neg*** 5
1988 pos*** 12 pos*** 12 pos*** 16 neg*** 5
1990 pos*** 13 pos*** 10 pos*** 18 NS 5 neg*** 7
1992 pos*** 14 pos*** 8 pos*** 18 NS 7 neg** 6
1994 pos*** 13 pos*** 8 pos*** 18 pos** 7 neg** 6
1996 pos*** 13 pos*** 8 pos*** 16 pos*** 7 NS 6
1998 pos*** 12 pos*** 10 pos*** 15 pos*** 8 neg** 5
2000 pos*** 12 pos*** 10 pos*** 14 pos*** 7 neg** 5
2006 pos*** 11 pos*** 9 pos*** 15 pos*** 9 neg*** 6 neg** 7
2013 pos*** 9 pos*** 9 pos*** 15 pos*** 10 neg*** 6 neg*** 8
Open in a new tab

The slopes are for binomial generalized linear models of log10 abundance in 1971 and percent mortality to each listed census year; “pos” indicates a positive slope (that is, species that were common in 1971 suffered greater mortality, on average, than less common species), and “neg” indicates a negative slope. ***P < 0.001; **P < 0.01; NS, not significant. N is the number of species in each period dying nonrandomly to each listed census year. Binomial glms were calculated only where N ≥ 5. To facilitate comparisons with the figures, instances in which the species richness of survivors was significantly greater than expected are underlined.

In principle, PFDM could have a diversifying effect on the community of survivors, but these data suggest that although a significant increase in SS could be explained by PFDM, this kind of mortality did not always result in significantly greater than expected survivor species richness (Table 2 and Fig. 3). There was PFDM in all 13 census periods to 2013 in the two smallest size classes, but significantly greater than expected survivor species richness in just 5 of these in SC1, and 3 in SC2. Similarly, SS was greater than expected in 1 of 13 census periods in SC3, but there was PFDM in 12 of those periods.

Discussion

Our results support the long-standing but previously untested paradigm in tropical forest ecology that the processes determining abundance and diversity of canopy trees act most strongly on very early-stage individuals (13–17). At Davies Creek, nonrandom mortality was proportionately more common among the smallest plants, and the diversifying effects of this mortality were only apparent among plants to 36-cm tall. As in other tropical forests the processes that contribute toward nonrandom mortality likely include interactions with other organisms and the physical environment. For example, vertebrate exclusion at Davies Creek shifted species composition of seedlings (18). Although untested, other mechanisms such as competition, seed-predation, herbivory, disease, and abiotic variables such as light, water, and soil-nutrient availability likely all play a role at Davies Creek, as they do in other forests (33, 34). Nonrandom mortality due to these and other sources could either enhance or reduce diversity, and the analyses presented here report the net effect.

Why Do Seedlings Show a Greater Propensity to Nonrandom Mortality?

The faster demographic turnover of small stems may be the simplest explanation for why seedlings are more likely to exhibit nonrandom mortality. There would be no detectable nonrandom mortality if no individuals in the community die between censuses, nor if all individuals die, i.e., the extremes along the x axis of Fig. 2. Therefore, an intermediate level of mortality permits the emergence of nonrandom patterns, and should give rise to a hump-shaped relationship or curve relating P to cumulative mortality. Because, broadly speaking, a small stem is more likely to die during a given period than a large stem, differences among size classes in average mortality could explain differences in degrees of observed nonrandom mortality. In other words, for a given intercensus interval, more (but not all) small stems might die than large stems, causing their nonrandom mortality level to be higher. As expected, for any given census P was higher in the three smallest size classes relative to the three largest size classes. Furthermore, as expected by hump-shaped relationships relating P to cumulative mortality within size classes: those size classes whose points mainly fall to the left on Fig. 2 trend positively [SC4, binomial glm significant positive slope (sig. pos.), SC5 slope not significant (NS), SC6 sig. pos.]; those in the middle display unimodal patterns (SC2 NS, SC3 sig. pos.); and the rightmost size class trends negatively (SC1 NS).

In addition to faster demographic turnover of smaller stems, inherent nonrandom dynamics may differ among size classes when matched for cumulative mortality (i.e., using different time slices for the different size classes). Where comparisons were possible, larger stems tended to have higher levels of nonrandom mortality relative to smaller stems (Fig. 2). It is not clear why P should be larger for SC3 than SC2, but stems in those two size classes are all quite small and similar in size (between 6 and 36.6 cm tall).

One hypothesis that could explain greater inherent nonrandom mortality among smaller individuals relative to larger individuals when matched for cumulative mortality is that greater inter- and intraspecific variation in key traits renders seedlings and small saplings more likely to display nonrandom dynamics than larger trees. This could occur if the “trait space” (see ref. 35) occupied by the community contracts as variation in demographically important traits diminishes as the individuals age. For example, specific leaf area spans a 1.7-times greater range of values and exhibits 3-times greater variance for first year seedlings (average height 14 cm) compared with larger (presumably older) saplings (50–250 cm tall) for a matched set of 32 species from Bolivia (data extracted from refs. 36 and 37 for seedlings and saplings, respectively). A larger range in values for key traits among smaller stems could translate into greater among-species differences in demographic performance across environmental conditions. Under this hypothesis, greater nonrandom mortality would be observed among smaller stems for a given level of overall mortality. This mechanism could operate in conjunction with and potentially exacerbate the consequences of faster turnover for nonrandomness in the smallest size classes.

Forest-Wide Cumulative Influence.

The differences we found in levels of nonrandom morality across size classes could amplify as annual rounds of recruitment add individuals to the community. Presumably, these recruits are regularly subjected to the nonrandom effects of a variety of hazards that kill most of them, but conversely, some of them eventually transition nonrandomly into the sapling bank. Accordingly, nonrandom consequences are continuously generated across annual cycles of small-stem recruitment, and accumulate as some individuals transition to larger size classes. For example, of the 44 stems surviving to 2013 in SC1, 2.3% had transitioned to SC2, 18.2% to SC3, 75.0% to SC4, and 4.5% to SC5, but none into the largest size classes. As our analyses show, mortality is close to random with respect to species by the time stems are 36-cm tall (SC4 and larger), so in essence the transition by growth of nonrandom survivors captures the species-compositional influence of small-stem dynamics on overall forest dynamics.

Conclusions

Other studies from larger plots (e.g., Center for Tropical Forest Science plot network) have also found evidence for nonrandom mortality, especially in local neighborhoods. For example, Wills et al. (10) found weak, but diversifying nonrandom mortality in larger size classes [>1-cm dbh (diameter at breast height)] within neighborhoods up to 50 × 50-m. In contrast to the diversifying, nonrandom mortality that we found among seedlings and small saplings, Comita et al. (6) found nonrandom mortality that is not entirely diversifying, i.e., the strength of frequency-dependent mortality was an inverse function of abundance. Whether differences in the strength of nonrandom mortality (regardless of its effect on diversity) across size classes are consistent in other forests has yet to be determined. Accordingly, our results help justify initiatives to incorporate the smallest size classes into several large-scale, long-term forest monitoring projects (38–40), and call for their more widespread inclusion elsewhere. Similar processes are likely to occur in all communities of sessile organisms in which recruitment primarily occurs through dispersed propagules, including marine communities (41).

Methods

The Site.

The site is a 1.7-ha forest dynamics plot at Davies Creek (17° 02' 18.9'' S, 145° 37' 31.3'' E), 25 km southwest of Cairns, in northeastern Australia (these latitude and longitude values update erroneous coordinates published in ref. 42). The plot is in unlogged rainforest at a mean elevation of 830 m, on low-fertility, granitic soils. Mean annual rainfall is ∼3,000 mm, most of which falls in a December–April wet season (for additional details concerning the site, see refs. 42–44). The plot is moderately diverse, with 120 species of trees ≥ 10 cm dbh. The plot has not experienced major cyclonic disturbance since monitoring began in 1963.

Mapping and mensuration were initially conducted using imperial units, but here we use SI units. “Large trees” (≥10-cm dbh) were first tagged, mapped and measured in 1963 across the entire plot. At the same time, “medium trees” (≥2.5-cm dbh but < 10.0-cm dbh) were mapped and tagged along several 6.1-m wide belt transects running through the plot, centered on survey lines 20.1 m apart. In 1965, “small trees” (tiny seedlings to saplings < 2.5-cm dbh), were mapped and tagged along belt transects either 1.8 or 3.6 m wide, centered on the same survey lines used to sample medium trees. Large and medium trees have always been measured for dbh, whereas small trees have been measured for height.

Size Classes.

For the analyses presented here, we considered a single cohort of plants that were alive in 1971. This cohort was divided into six size classes, spanning the full range from tiny seedlings to the largest canopy trees (Table 1). SCs 1–4 are height classes, and were drawn from the original class small trees. SC5 spans the transition from when stems are measured for dbh rather than height, and includes individuals from both the small and medium tree classes. SC6 is a dbh class, drawn from large tree class. Species richness in 1971 varied between 91 and 135 species across the six size classes. The survival of all individuals in these 6 size classes was followed over 42 y to 2013, through 13 mortality censuses in 1974, 1978, 1980, 1986, 1988, 1990, 1992, 1994, 1996, 1998, 2000, 2006, and 2013. Not unexpectedly, the numbers of stems in 1971 were greatest in the smallest size classes, and 42 y mortality to 2013 was highest in SC1 (97.0%) and lowest in the largest size class (SC6; 25.7%). Although surviving stems grew out of the original size classes over time, stems were retained in their 1971 size classes for analyses. By the final census in 2013, 100% of surviving stems in SC1, 98.3% in SC2, 82.8% in SC3, 34.1% in SC4 and 7.6% in SC5 had grown beyond their original size classes. Thus, the greater declines in mortality rates in the three smaller sizes (Fig. 1) are probably due mostly to this growth effect.

Mortality Analyses.

In these analyses, a species died “nonrandomly” if the number of individuals dying between 1971 and a given mortality census (“observed mortality”) was significantly different to the number of individuals that would be expected to have died under simulations in which the probability of mortality was random with respect to species identity (“expected mortality”). For each size class and census period, this was determined as follows. First, the total number of deaths to the mortality census was tallied across all species present in the size class. Next, this same number of individuals was “killed” at random (without replacement) with respect to species from the 1971 cohort, and the number of deaths for each species was recorded. This procedure was repeated for 10,000 runs, generating an expected frequency distribution of the number of deaths for each species. A species died nonrandomly for a given period if its observed number of deaths was either less than the 2.5th percentile, or greater than the 97.5th percentile, of the 10,000 randomly derived numbers of deaths for that species over the same period. The number of species with stems alive in 1971 varied across size classes. To facilitate comparisons, nonrandom mortality was expressed as a percentage (P) of all species present in each size class in 1971.

We assessed the efficacy of our randomization approach by determining the false-positive rate for detecting nonrandom mortality across species within the 6 size-class cohorts and within the 13 intercensus periods. We did this by simulating a community in which there was truly random mortality, and then ran the randomization analysis described above to determine if those analyses introduced any patterns that could have masqueraded as nonrandomness. The rate of these “false positives” was uniformly low (generally <1% of species) and unbiased with respect to size class or intercensus period. All code was written in the R programming language and analyses were conducted using R v. 2.14.1 (45).

Comparisons Across Size Classes and Time Periods.

Our randomization method is less likely to show nonrandom mortality in species represented by singletons or doubletons, and much more likely to show nonrandom mortality, if it is there to be found, in species represented by tens or hundreds of individuals; when species are rare, the 95% confidence intervals of the null model will often overlap the observed value and nonrandom mortality will not be demonstrated. All of the size classes in our study had species that were rare in absolute terms, with one, two, or three individuals only, and our method will probably underestimate the true proportion of species experiencing nonrandom mortality in all size classes. However, it is also possible that this effect is asymmetric across size classes, with some size classes showing a lower proportion of species dying nonrandomly simply because their species-abundance distributions have relatively longer tails of absolutely rare species. We ameliorated the risk of this kind of analytical bias by setting the bounds of the size classes such that they contained similar numbers of individuals, and then checked that the proportion of rare species in each size class did not vary consistently across them (Fig. S2).

It is likely that in any given size class, the number of species dying nonrandomly will depend to some large degree on the amount of mortality over 42 y. In our analyses, if all stems die over the study period then no species can die more or less often than expected by chance. Similarly, if there are very few deaths, then few species will show nonrandom mortality. For this reason, simple comparisons over a single 42-y interval would give a biased indication of differences among size classes; most stems (97.0%) in SC1 died over the study period, whereas few stems (25.7%) in SC6 died. Because of this, we present the proportion of species dying nonrandomly for ever-longer periods from 1971 to each of the 13 subsequent mortality censuses.

Our estimates of nonrandom mortality in the smallest size classes are probably conservative for two reasons. First, over 42 y, many stems transitioned out of their initial size class. More individuals that began in smaller size classes transitioned to larger size classes than did individuals that began in larger size classes and transitioned to even larger size classes during the study period (100% of individuals that began in SC1 in 1971 and survived to 2013 transitioned to a larger size class, whereas 7.6% of individuals surviving in SC5 transitioned to SC6). Under the prediction of size-dependent nonrandom mortality, stems should be less prone to nonrandom mortality as they grow, thereby reducing the observed nonrandom mortality in the smaller size classes that lose the most stems to transitions to larger sizes.

Second, the recruit census immediately preceding our study was done in 1969. Most seedlings at Davies Creek recruit from January through March, so a considerable proportion of seedlings in the smallest size class may have been 18 mo old (survivors from early 1970 recruits) or 6 mo old (early 1971). These individuals would already have passed through the worst of the mortality bottleneck, when they would have been most prone to agents of nonrandom mortality. Future studies that follow the fates of newly germinated seedlings might show an even higher proportion of species dying nonrandomly, especially if seedling censuses explicitly include the very earliest stages.

Species Richness Analyses.

To assess the impact of nonrandom mortality on plant species richness (S) for each size class we compared the actual S of stems surviving (SS) or dying (SD) over the 42-y study period (“observed richness”) against S calculated using the outputs of the 10,000 randomizations (Mortality Analyses, above). Within a size class, SS was greater than expected if it exceeded the 97.5th percentile of the 10,000 randomly generated estimates of survivor S for that size class, and less than expected if it fell below the 2.5th percentile. Similarly, SD over the study period was less than expected if it fell below the 2.5th percentile of the 10,000 randomly generated estimates of dead S, and greater than expected if it exceeded the 97.5th percentile. If nonrandom mortality acts to increase diversity in this community, we predicted that SS should be greater than, and SD less than, expected on the basis of random mortality.

Frequency-Dependence Analyses.

Positive frequency-dependent mortality (PFDM) can have a diversifying effect on the community of survivors. Using binomial generalized linear models, we determined if log10 initial abundance explained any of the cross-species variation in mortality for: (i) all species in each size class; and (ii) those species identified above as having died nonrandomly. For the latter analyses, only those size classes and time periods where ≥5 species died nonrandomly were considered for analysis.

In the absence of demographic stochasticity, any amount of PFDM should diversify a community-wide cohort of individuals. However, demographic stochasticity could mask the deterministic influence of PFDM if the relative influence on the community from stochasticity were to outweigh the community-wide consequences of PFDM. By default our randomizations created variability (i.e., demographic stochasticity) in the outcomes for each species in terms of the number of stems dying, because each confidence interval was created from 10,000 Monte Carlo runs. Confidence intervals could have masked faint deterministic diversifying influences.

Supplementary Material

Supplementary File
pnas.201321892SI.pdf (523.5KB, pdf)

Acknowledgments

We thank Margaret Connell for her support of the Davies Creek Forest Dynamics Project since its inception 50 years ago. Len Webb and Geoff Tracey assisted in setting up the plot, and Geoff Tracey and Meg Lowman spent considerable time over many years identifying plants. Bob Black, Kitty Gehring, Tad Theimer, Steve Swearer, Nicole Barbee, Chris Wills, and two anonymous reviewers provided ideas and suggestions for the manuscript, and Bob Black has been a stalwart member of the field team over many years. Bret Elderd and Tim Paine provided statistical advice. We thank Jessica Eberhard, Suzie Gerrard, and many colleagues at the Australian National University in Canberra and the Commonwealth Scientific and Industrial Research Organization in Atherton for their support of many years, especially Ian Davies, Andrew Graham, Mike Hopkins, Ron Knowlton, Dan Metcalfe, and Ian Noble. We also thank the more than 300 volunteers who over several decades have helped recensus the plot. This research has been funded by the Australian Long Term Ecological Research Network and the United States National Science Foundation (DEB 7301357, 7683013, 8011123, 9220672, 9503217, 9806310).

Footnotes

The authors declare no conflict of interest.

This article is a PNAS Direct Submission.

Data deposition: The data file reported in this paper has been deposited in the DRYAD database, datadryad.org (doi:10.5061/dryad.66v1c).

This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1321892112/-/DCSupplemental.

References

  • 1.Hubbell SP. The Unified Neutral Theory of Biodiversity and Biogeography. Princeton University Press; Princeton, NJ: 2001. [Google Scholar]
  • 2.Chase JM, Leibold MA. Ecological Niches: Linking Classical and Contemporary Approaches. University of Chicago Press; Chicago: 2003. [Google Scholar]
  • 3.Vellend M. Conceptual synthesis in community ecology. Q Rev Biol. 2010;85(2):183–206. doi: 10.1086/652373. [DOI] [PubMed] [Google Scholar]
  • 4.Harms KE, Wright SJ, Calderón O, Hernández A, Herre EA. Pervasive density-dependent recruitment enhances seedling diversity in a tropical forest. Nature. 2000;404(6777):493–495. doi: 10.1038/35006630. [DOI] [PubMed] [Google Scholar]
  • 5.Bagchi R, et al. Pathogens and insect herbivores drive rainforest plant diversity and composition. Nature. 2014;506(7486):85–88. doi: 10.1038/nature12911. [DOI] [PubMed] [Google Scholar]
  • 6.Comita LS, Muller-Landau HC, Aguilar S, Hubbell SP. Asymmetric density dependence shapes species abundances in a tropical tree community. Science. 2010;329(5989):330–332. doi: 10.1126/science.1190772. [DOI] [PubMed] [Google Scholar]
  • 7.Mangan SA, et al. Negative plant-soil feedback predicts tree-species relative abundance in a tropical forest. Nature. 2010;466(7307):752–755. doi: 10.1038/nature09273. [DOI] [PubMed] [Google Scholar]
  • 8.Uriarte M, Condit R, Canham CD, Hubbell SP. A spatially explicit model of sapling growth in a tropical forest: does the identity of neighbours matter? J Ecol. 2004;92:348–360. [Google Scholar]
  • 9.Condit R, Hubbell SP, Foster RB. Mortality rates of 205 neotropical tree and shrub species and the impact of a severe drought. Ecol Monogr. 1995;65:419–439. [Google Scholar]
  • 10.Wills C, et al. Nonrandom processes maintain diversity in tropical forests. Science. 2006;311(5760):527–531. doi: 10.1126/science.1117715. [DOI] [PubMed] [Google Scholar]
  • 11.Newbery DM, Lingenfelder M. Plurality of tree species responses to drought perturbation in Bornean tropical rain forest. Plant Ecol. 2009;201:147–167. [Google Scholar]
  • 12.Curran TJ, et al. Plant functional traits explain interspecific differences in immediate cyclone damage to trees of an endangered rainforest community in north Queensland. Austral Ecol. 2008;33:451–461. [Google Scholar]
  • 13.Janzen DH. Herbivores and the number of tree species in tropical forests. Am Nat. 1970;104:501–528. [Google Scholar]
  • 14.Connell JH. In: Dynamics of Numbers in Populations. Den Boer PJ, Gradwell GR, editors. PUDOC; Wageningen, The Netherlands: 1971. pp. 298–312. [Google Scholar]
  • 15.Grubb PJ. The maintenance of species-richness in plant communities: the importance of the regeneration niche. Biol Rev Camb Philos Soc. 1977;52:107–145. [Google Scholar]
  • 16.Swaine MD. In: The Ecology of Tropical Forest Tree Seedlings. Swaine MD, editor. UNESCO and The Parthenon Publishing Group; Paris, France: 1996. pp. 1–2. [Google Scholar]
  • 17.Whitmore TC. In: The Ecology of Tropical Forest Tree Seedlings. Swaine M, editor. UNESCO and The Parthenon Publishing Group; Paris, France: 1996. pp. 3–39. [Google Scholar]
  • 18.Theimer TC, Gehring CA, Green PT, Connell JH. Terrestrial vertebrates alter seedling composition and richness but not diversity in an Australian tropical rain forest. Ecology. 2011;92(8):1637–1647. doi: 10.1890/10-2231.1. [DOI] [PubMed] [Google Scholar]
  • 19.Metz MR. Does habitat specialization by seedlings contribute to the high diversity of a lowland rain forest? J Ecol. 2012;100:969–979. [Google Scholar]
  • 20.Coley PD, Barone JA. Herbivory and plant defenses in tropical forests. Annu Rev Ecol Syst. 1996;27:305–335. [Google Scholar]
  • 21.Gilbert GS. Evolutionary ecology of plant diseases in natural ecosystems. Annu Rev Phytopathol. 2002;40:13–43. doi: 10.1146/annurev.phyto.40.021202.110417. [DOI] [PubMed] [Google Scholar]
  • 22.Engelbrecht BMJ, et al. Drought sensitivity shapes species distribution patterns in tropical forests. Nature. 2007;447(7140):80–82. doi: 10.1038/nature05747. [DOI] [PubMed] [Google Scholar]
  • 23.Clark DB, Clark DA. The role of physical damage in the seedling mortality regime of a neotropical rain forest. Oikos. 1989;55:225–230. [Google Scholar]
  • 24.Metz MR, Sousa WP, Valencia R. Widespread density-dependent seedling mortality promotes species coexistence in a highly diverse Amazonian rain forest. Ecology. 2010;91(12):3675–3685. doi: 10.1890/08-2323.1. [DOI] [PubMed] [Google Scholar]
  • 25.Bachelot B, Kobe RK. Rare species advantage? Richness of damage types increases with species abundance in a wet tropical forest. J Ecol. 2013;101:846–856. [Google Scholar]
  • 26.Brown JH, Heske EJ. Control of a desert-grassland transition by a keystone rodent guild. Science. 1990;250(4988):1705–1707. doi: 10.1126/science.250.4988.1705. [DOI] [PubMed] [Google Scholar]
  • 27.Hanley ME, Fenner M, Edwards PJ. An experimental field study of the effects of mollusc grazing on seedling recruitment and survival in grassland. J Ecol. 1995;83:621–627. [Google Scholar]
  • 28.Tilman D. Community invasibility, recruitment limitation, and grassland biodiversity. Ecology. 1997;78:81–92. [Google Scholar]
  • 29.Howe HF, Brown JS, Zorn-Arnold B. A rodent plague on prairie diversity. Ecol Lett. 2002;5:30–36. [Google Scholar]
  • 30.Gillett JB. Pest pressure, an underestimated factor in evolution. Syst Ass Pub. 1962;4:37–46. [Google Scholar]
  • 31.Wills C, Condit R. Similar non-random processes maintain diversity in two tropical rainforests. Proc Biol Sci. 1999;266(1427):1445–1452. doi: 10.1098/rspb.1999.0799. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Hubbell SP, et al. Light-Gap disturbances, recruitment limitation, and tree diversity in a neotropical forest. Science. 1999;283(5401):554–557. doi: 10.1126/science.283.5401.554. [DOI] [PubMed] [Google Scholar]
  • 33.Dalling JW, Burslem DFRP. In: Biotic Interactions in the Tropics. Burslem D, Pinard M, Hartley S, editors. Cambridge University Press; Cambridge: 2005. pp. 65–88. [Google Scholar]
  • 34.Turner IM. The Ecology of Trees in the Tropical Rain Forest. Cambridge University Press; Cambridge: 2001. [Google Scholar]
  • 35.Cornwell WK, Schwilk LD, Ackerly DD. A trait-based test for habitat filtering: convex hull volume. Ecology. 2006;87(6):1465–1471. doi: 10.1890/0012-9658(2006)87[1465:attfhf]2.0.co;2. [DOI] [PubMed] [Google Scholar]
  • 36.Markesteijn L, Poorter L. Seedling root morphology and biomass allocation of 62 tropical tree species in relation to drought- and shade-tolerance. J Ecol. 2009;97:311–325. [Google Scholar]
  • 37.Poorter L, Bongers F. Leaf traits are good predictors of plant performance across 53 rain forest species. Ecology. 2006;87(7):1733–1743. doi: 10.1890/0012-9658(2006)87[1733:ltagpo]2.0.co;2. [DOI] [PubMed] [Google Scholar]
  • 38.Wright SJ, Muller-Landau HC, Calderón O, Hernández A. Annual and spatial variation in seedfall and seedling recruitment in a neotropical forest. Ecology. 2005;86:848–860. [Google Scholar]
  • 39.Metz MR, et al. Temporal and spatial variability in seedling dynamics: a cross-site comparison in four lowland tropical forests. J Trop Ecol. 2008;24:9–18. [Google Scholar]
  • 40.Paine CET, et al. Phylogenetic density dependence and environmental filtering predict seedling mortality in a tropical forest. Ecol Lett. 2012;15(1):34–41. doi: 10.1111/j.1461-0248.2011.01705.x. [DOI] [PubMed] [Google Scholar]
  • 41.Sams MA, Keough MJ. Contrasting effects of variable species recruitment on marine sessile communities. Ecology. 2012;93(5):1153–1163. doi: 10.1890/11-1390.1. [DOI] [PubMed] [Google Scholar]
  • 42.Connell JH, Tracey JG, Webb LJ. Compensatory recruitment, growth, and mortality as factors maintaining rainforest tree diversity. Ecol Monogr. 1984;54:141–164. [Google Scholar]
  • 43.Connell JH, et al. In: Tropical Rain Forests: Past, Present, and Future. Bermingham E, Dick CW, Moritz C, editors. University of Chicago Press; Chicago: 2005. pp. 486–506. [Google Scholar]
  • 44.Connell JH, Green PT. Seedling dynamics over thirty-two years in a tropical rainforest tree. Ecology. 2000;81:568–584. [Google Scholar]
  • 45.R Core Team . R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; Vienna, Austria: 2013. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary File
pnas.201321892SI.pdf (523.5KB, pdf)

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES