Abstract
Malaria parasites and immune responses in an infected human interact on a dynamic landscape, in which a population of replicating parasites depletes a population of replenishing red blood cells (RBCs). These underlying dynamics receive relatively little attention, but they offer unique insights into the processes that control most malaria infections. Here, we focus on the observation that three of the four malaria-parasite species that infect humans are restricted to particular age classes of RBC. We explicitly incorporate this observation in models of infection dynamics to distinguish common from species-specific pressures on host immune responses, and we find that age structuring has profound effects on the course of infection. For all four species conditions exist under which the parasites may persist at low densities, or may clear, even in the absence of an immune response. Catastrophic anemia can occur even with the two species that attack only the youngest RBCs, although only a small fraction of cells are parasitized at any point. Furthermore, with these two, compensatory erythropoetic responses in the host accelerate parasite population growth. A “basic reproduction rate” characterizes these differences in outcomes.
Malaria in a human begins with an inoculum of Plasmodium parasites from an Anopheles mosquito. The parasites penetrate liver cells, multiply, then enter the bloodstream, and invade red blood cells (RBCs), where they again multiply and burst the cells, each releasing 8-32 “merozoites” that invade more RBCs and continue the cycle. Almost all malaria pathology is associated with this blood stage replication cycle; it leads to geometric growth in the parasite population and to fevers, anemia, and sometimes death in the host (1).
Parasite population growth is usually constrained by host immune responses. Accordingly, most mathematical models of within-host dynamics have taken the general form of predator-prey models, with the predator a population of immune agents and the prey a population of Plasmodium (2). A few Plasmodium falciparum models attempt to relate the dynamics of the parasite population to those of its prey, the population of RBCs, but none incorporate RBC aging or age-structured susceptibility (3-7).
RBC age appears to be a strong constraint on malaria parasites, however: susceptibility to Plasmodium vivax or Plasmodium ovale invasion is said to be restricted to the very youngest circulating age class of RBCs, the “reticulocytes,” and Plasmodium malariae invasion to the very oldest (8, 9). P. falciparum, the species responsible for almost all the 1-3 million deaths attributed to malaria each year, seems promiscuous with respect to its RBC targets (10). It is widely assumed that these age constraints explain why counts of parasitized RBCs rarely exceed 25,000 per μl with P. vivax, P. ovale, or P. malariae, but may reach 500,000 and beyond with P. falciparum, and thus, in turn, why fatal anemia occurs only in P. falciparum infections (11).
Most malaria infections are not fatal, but the mechanisms involved in their control are notoriously difficult to comprehend. Here, we use mathematical models to identify critical interactions between Plasmodium and RBC populations and indicate effects that immune responses must add (for instance, to counter the unexpectedly strong demands of P. vivax or P. ovale) if system dynamics are to resemble those observed in actual malaria infections.
The Models
RBCs emerge from bone marrow into the circulation, and in uninfected, healthy adults, they are removed by phagocytosis 120 days later (12). A density of ≈5 million RBCs per μl is maintained in adult males. The first 1-2 days of the RBC lifespan are the reticulocyte stage. Compensatory responses to anemia may boost RBC production to several times the basal level (12). We model the rate of RBC production as sensitive to changes in the rate of RBC destruction, with a response time of 48 h, and capped at some maximum given as a parameter value. Here we consider maximum RBC production fixed either at the basal rate [i.e., (5 × 106 RBC per μl)/(120 days) ≈ 1,736 RBC per μl per h] or at twice the basal rate.
Successful invasion of a RBC by a parasite depends on direct contact between the two. We take the contact process itself as random, with contact probabilities proportional to Mer and V, the densities of merozoites and uninfected susceptible RBCs, respectively. On contact, successful invasion depends on the receptor-ligand attachment(s) required for the physical process of invasion, which we model as a binding affinity ζ. Thus, infected RBCs are produced at rate ζ Mer V. The details of RBC receptor usage by different Plasmodium species are not yet clear, in particular with respect to RBC age, but P. vivax invasion is limited to RBCs from Duffy-antigen-positive individuals, and P. falciparum can use multiple receptors (13); nothing is known about P. malariae receptors. Nothing is known about receptors for P. ovale except that they must differ from those for P. vivax; given their shared restriction to reticulocytes, however, we treat P. ovale as identical with P. vivax and refer only to the latter.
Therefore, we model age-structured attacks on RBCs as either (i) a P. vivax-like attack on reticulocytes or (ii) a P. malariae-like attack on senescent RBCs, and set the exact duration of RBC susceptibility in each model as a parameter value. For comparison, we model attacks on RBCs that present appropriate receptors at all ages: a fraction β of RBCs that emerge from marrow has life-long susceptibility; initially, at the start of infection, a fraction β of each RBC age cohort in circulation is susceptible. Hence, we call this attacker a generalist; it is believed β ≈ 1 for P. falciparum (13).
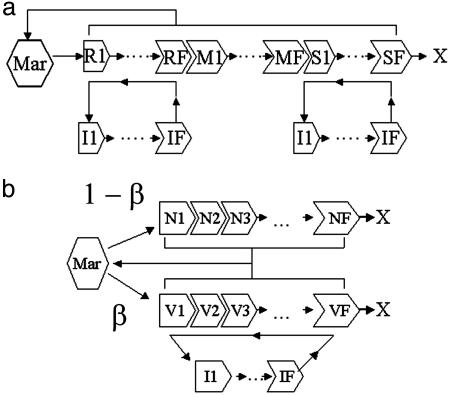
Fig. 1 gives schematic representations of the models, which we formulated as compartmental differential equation systems (CODEs); CODEs allow us to include uncertainty in the duration τ of a process, such as RBC aging or parasite development in a RBC. Variance is set by τ/F1/2, where F is the number of compartments used to describe the process; variances are integral to models' steady-state solutions as well (see supporting information, which is published on the PNAS web site). Each model simulation mimicked 105 h of infection (≈11.4 yr), unless the density of uninfected RBCs declined to 75% of its initial value, which we set as the threshold for catastrophic anemia, in which case the simulation halted. During the first simulated hour 104 merozoites were infused into a total blood volume of 5 liters to mimic primary release from the liver. We take the nominal time τI for a parasite to develop in a RBC as 72 h for P. malariae and 48 h for P. vivax and the generalist, and we use a compartment size of a half-hour. Then, the variance in τI is ≈6 h for P. malariae and ≈4.9 h for P. vivax and the generalist, in line with recent work (3).
Fig. 1.
Schematic of model dynamics. Bone marrow (Mar) is the source of new RBCs. (a) Age-structured models for P. vivax and P. malariae infections. RBC stages R1-RF are reticulocytes, susceptible to P. vivax, and S1-SF are senescent, susceptible to P. malariae;M1-MF are nonsusceptible stages. I1-IF are infected RBCs. (b) Generalist model. V1-VF are the vulnerable subset of RBCs, N1-NF are the nonvulnerable subset; β is the fraction of RBCs produced from marrow that are vulnerable. In all three models, RBC production is regulated by the rate of loss of RBCs by means of normal senescence or infection. Simulations mimic 105 h of infection unless the uninfected RBC count falls to <75% of its initial value (catastrophic anemia). X marks the natural end of the RBC lifespan.
When released from a bursting RBC, a free merozoite will die or be cleared from circulation within a time τMER, believed to be minutes (14). Thus, two competing Poisson processes affect the fate of merozoites: (i) they are removed from the blood at rate 1/τMer; (ii) they attach to RBCs at rate ζV. The probability that a merozoite infects a RBC rather than being cleared is ζVτMER (1 + ζVτMER)-1 (see supporting information). Thus, if τMER << τI, its average number of descendants after a development cycle is
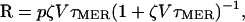 |
1 |
where p is the average number of merozoites released from a bursting RBC. We define R0, the basic reproduction rate, as the value of R at the beginning of the infection. This quantity both determines the initial behavior of an infection and affects its outcome. Nontrivial steady-state solutions exist only if R0 > 1 (see supporting information). Thus, the parasite count ultimately vanishes if R0 < 1, persists at its initial value if R0 = 1, or converges to a larger steady state if R0 > 1, unless the host RBC count is depleted to the point of catastrophic anemia. We stress that R (as opposed to R0) can change during the course of infection as V changes; in particular, R → 1 as a steady state is approached. Note that the existence of a noncatastrophic steady state does not preclude the possibility that catastrophic anemia will occur in the approach.
TINF = 1/ζV = (p - R0)τMER/R0 gives the average time required for a merozoite to contact and invade a RBC. If p = 16 and τMER = 0.1 h, then TINF = 1.35 h, 2 min, or 0 if R0 = 1.1, 12, or 16, respectively. Thus, despite our built-in assumption of free mixing, parasite transmission from RBC to RBC approaches a contact process as R0 → p. The generalist model is not an exact description of P. falciparum because P. falciparum-infected RBCs sequester and rosette with uninfected RBCs, which suggests that many merozoites travel minimal distances to invade RBCs (15). Nor do we consider invasions of a single RBC by multiple merozoites, a relatively rare event that is most frequent with P. falciparum (16). However, because R0 seems to be near p, at least in malaria-naive malaria-therapy patients (3), the behavior of the generalist model for β ≈1 and large R0 may be fairly realistic for P. falciparum.
Here, we set τMer = 0.1 h and p = 16. Calculations with other values of τMer or p do not alter the qualitative conclusions here (see supporting information). Because merozoite counts directly reflect infected RBC counts, we report only the infected RBC counts.
Model Dynamics
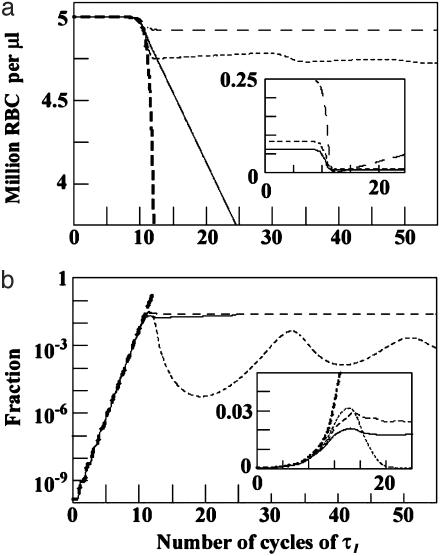
In all three models, the value of R0 determines the infection dynamics until susceptible RBCs are significantly depleted. We would expect this to occur by time TC ≈ τI log(Vo/Mero)/log R0 (see supporting information). At this point the dynamics of the models diverge, as is evident in Fig. 2, which plots four time series: the P. vivax model with reticulocyte stage duration = 36 h, the P. malariae model with senescent RBC duration = 48 h, and the generalist model with β = 0.05 and β = 0.99. For each model, RBC production was held at the basal rate and R0 set to 80/13 (≈6.15). Note that all four models are initially in lockstep, with parasite density growing exponentially for the first 9-12 cycles of τI (as expected from the TC formula). After the first few weeks of the β = 0.99 generalist infection, the density of uninfected RBCs quickly collapses and the fraction of RBCs infected soars. For the β = 0.05 generalist and P. malariae infections, the density of uninfected RBCs is only mildly affected and the fraction of RBCs infected never exceeds ≈3%. The P. vivax infection leads to catastrophic anemia, however, although the maximum fraction of RBCs infected is ≈2%. The initial fraction of RBCs susceptible to P. vivax is only 36 h/120days = 0.0125, but P. vivax attack has more drastic clinical consequences than the β = 0.05 generalist, because targeted culling of reticulocytes ensures that few remain to mature and replenish the older RBCs.
Fig. 2.
Time course of infection. The time since primary release (horizontal axis) is shown as multiples of τI (3 days for P. malariae and 2 days for the others). In each case ζ is set so that R0 = 80/13 (or ≈6.15). Lines are coded as:—, P. vivax with reticulocyte duration = 36 h; - -, P. malariae with senescent RBC duration = 48 h; - - -, generalist with β = 0.05; - - -, generalist with β = 0.99. (a) Uninfected RBC count. (Inset) The count of vulnerable RBCs for the P. vivax, P. malariae, and generalist β = 0.05 models. (b) The fraction of RBCs that are infected. (Inset) Enlargement of the region around 10 τI, showing the structure in the “hump.” Note the linear (instead of log) vertical scale of Inset.
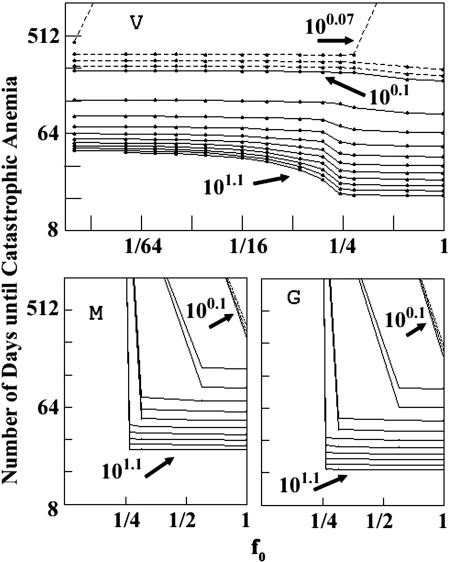
Differences in model dynamics are also apparent in Fig. 3, which, for a range of R0 values >1, plots the time until the onset of catastrophic anemia as a function of f0, the fraction of RBCs initially susceptible (β for the generalist, and the susceptible-stage duration/120 days for the other two models; f0 = 0.0125 and 0.0167, respectively, for the P. vivax 36-h and P. malariae 48-h examples in Fig. 2). In the generalist and P. malariae models, the density of uninfected RBCs declines to 75% of its initial value, our threshold for catastrophic anemia, only if f0 > 0.25. In the P. vivax model, however, catastrophic anemia can occur even with f0 ≈ 0.01 and R0 barely >1. Even with a reticulocyte duration of just 18 h (f0 = 0.00625) and R0 = 100.06 (≈1.15), catastrophic anemia would occur in ≈450 days; the peak infected RBC count would be 2.1 × 104 per μl, so the fraction of RBCs infected would never exceed (2.1 × 104)/(3.75 × 106 + 2.1 × 104) ≈ 0.6%. With a 36-h reticulocyte duration and R0 = 10, the fraction of RBCs infected would never exceed ≈3%, but catastrophic anemia would occur within 45 days.
Fig. 3.
Time to catastrophic anemia as a function of f0, the initial fraction of RBCs susceptible to infection. (Upper) P. vivax.(Lower Left) P. malariae.(Lower Right) Generalist. The solid curves are contours of R0 from 100.1 to 101.1, spaced so that log R0 changes by 0.1. The dotted lines are contours for R0 < 0.1, spaced so that log R0 changes by 0.01.
P. vivax model behaviors begin to resemble those of the other two models if the reticulocyte duration expands to encompass > ≈30% of the RBC lifespan; mature RBCs constitute a smaller fraction of the total RBC count, so choking off their predecessor reticulocytes has less effect. This is especially evident for R0 near 1, as can be seen in Fig. 3 and in the steady state (see supporting information).
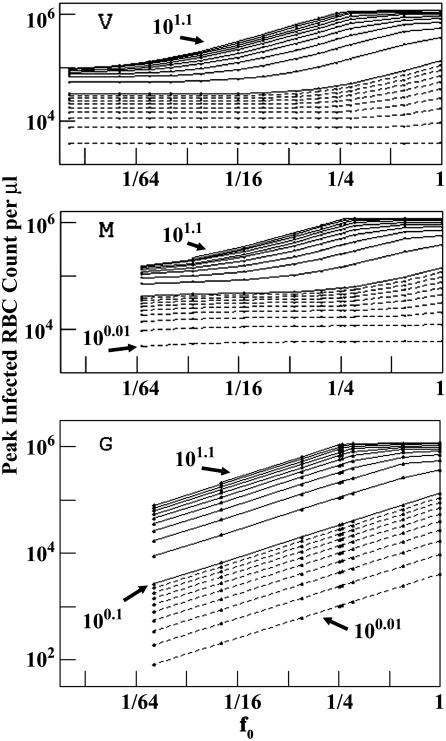
Fig. 4 shows the peak infected RBC counts, IPK, corresponding to Fig. 3. Age-structured attacks produce striking differences: for a given R0 and f0, IPK is higher in P. vivax and P. malariae models than in the generalist model. All RBCs emerging from bone marrow reach the stage susceptible to P. vivax or P. malariae, whatever the value of f0, either immediately (P. vivax) or after aging (P. malariae). For the generalist, however, only a fraction β of new RBCs enters the susceptible pool. IPK curves for the generalist approach those of the other two models as f0 → 1. Age-structured attacks also differ in their steady-state values (see supporting information).
Fig. 4.
Peak count of infected RBCs, IPK, as a function of f0. (Top) P. vivax. (Middle) P. malariae. (Bottom) Generalist. Contours are as in Fig. 3.
For R0 < 1, all three models effectively have the same stiff but analytically solvable ordinary differential equation (ODE) system. As R0 → 1, to a very good approximation the time required for the initial parasite population to decrease by 1/e (the e-folding time) is -τI/ln R0.If τI = 48 h, the e-folding time is ≈19 days for R0 = 0.9 and ≈199 days for R0 = 0.99. Thus nonsustainable infections with R0 just below the threshold of persistence could linger, at undetectable densities, with the host vulnerable to increases in p or ζ.
Integrated Parasite Count
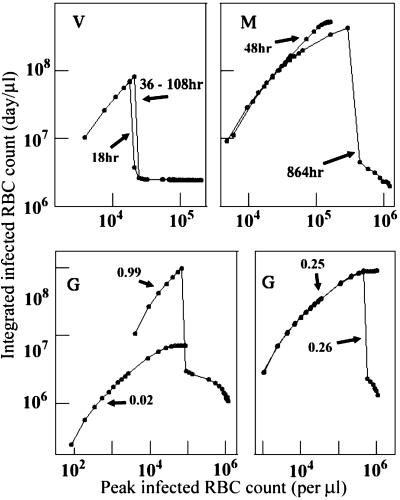
As a proxy for the cumulative number of parasites produced in an infection, we define the integrated infected RBC count IINT = (average infected RBC count) × (duration of simulated infection). Fig. 5 plots IINT vs. IPK for key values of f0. R0 varies from 100.01 to 101.1 along each curve, tracking IPK. The maximum IINT for each model occurs at a distinct combination of R0 and f0 values, e.g., a relatively small R0 (1.17) and large f0 (0.99) for the generalist, large R0 (>12) and intermediate f0 (0.25) for P. malariae. With small f0 values in the generalist or P. malariae models, IINT is monotonic in IPK, but large f0 values lead to catastrophic anemia: IINT abruptly collapses with increased IPK as f0 exceeds 0.25. Again, the P. vivax model differs dramatically: the IINT vs. IPK curve is relatively insensitive to reticulocyte duration, and the largest values of IINT occur with IPK < 30,000 per μl, an order of magnitude lower than with the P. malariae or generalist models.
Fig. 5.
Integrated parasite count, IINT, vs. peak parasite count, IPK, for representative values of susceptible-stage duration (P. vivax in Upper Left and P. malariae in Upper Right)or β (generalist in the two Lower sections). On each curve, the points correspond to values of R0 used in Figs. 3 and 4, from 100.01 on the left to 101.1 on the right.
Compensatory Responses to Anemia
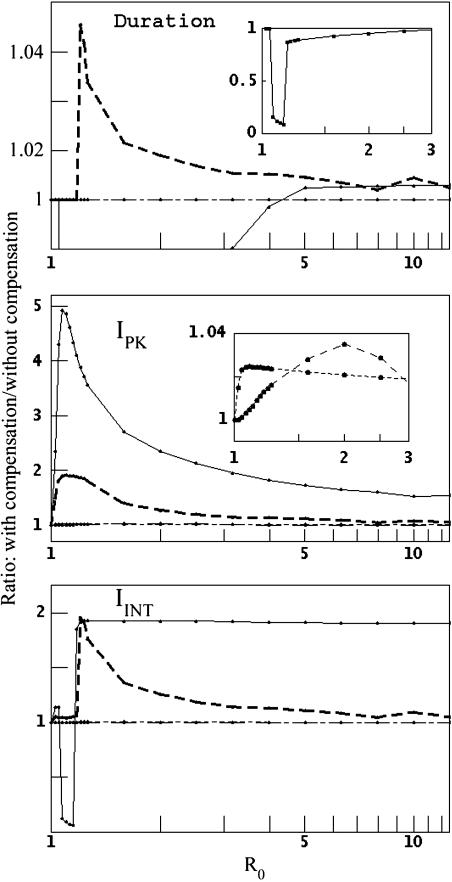
The preceding results assume that RBC production remains fixed at the basal rate throughout a malaria infection; in fact, significant RBC loss usually stimulates enhanced or accelerated production. The particular mechanisms involved are still poorly understood (17), but one recent analysis reported an average 37% increase in RBC production in adult first-time P. falciparum patients (18). Here, we allow RBC production to match RBC depletion, up to a maximum of twice the basal rate (Eq. 5). Fig. 6 shows the effects of compensatory responses, with varying R0, in four model situations: P. vivax with 36-h reticulocyte duration, P. malariae with 48-h senescent RBC duration, and the generalist with β = 0.05 or 0.99.
Fig. 6.
Changes in dynamics when RBC production increases with RBC depletion. This figure compares the ratios of model results with compensation (i.e., the RBC production rate matches the RBC depletion rate, up to twice the basal rate) to those without compensation (basal rate only). Lines are coded as in Fig. 2. (Top, Duration) Time to catastrophic anemia. (Middle, IPK) Peak count of infected RBCs. (Bottom,IINT) Integrated parasite count. (Upper Inset) Demonstration that compensation substantially accelerates the onset of catastrophic anemia in P. vivax infection with R0 < 2. (Middle Inset) Demonstration that compensation has relatively little effect on peak density in P. malariae or β = 0.05 generalist infections.
In the P. vivax model, the host gains little or no benefit from compensatory response. For R0 < 100.6 (≈4), increased RBC production actually speeds the onset of catastrophic anemia. In contrast, compensation slightly delays the onset in the β = 0.99 generalist model. Compensation boosts peak parasite counts in all models, but most dramatically in the P. vivax model for R0 < 100.4 (≈2.5). Consider the P. vivax model with R0 = 100.05 ≈1.122, for instance: doubling the rate of RBC production quickly doubles the reticulocyte count, the instantaneous reproduction rate R becomes nearly twice R0 (2.097; Eq. 1), and a nonlethal P. vivax infection becomes lethal. Compensation also boosts the integrated count, with the notable exception of P. vivax with R0 (≈1.25), the regime in which nonlethal infections turn lethal. If infection reduces RBC production rates, the onset of catastrophic anemia with P. vivax is delayed, and IPK decreases, consistent with a reduction of R (see supporting information).
Discussion
Our results show that age-restricted RBC susceptibility strongly influences the dynamics of Plasmodium infection and thus the imperatives for host immune response. They conform to clinical observations: if we limit susceptibility to the small fraction of RBCs that are senescent, infections are relatively benign, as is P. malariae. They suggest that compensatory RBC production usually aggravates infections; in fact, it may be functionally suppressed in chronically exposed patients (17). However, our results argue against the belief that, because only a small fraction of RBCs are reticulocytes, P. vivax and P. ovale are intrinsically less dangerous than P. falciparum: attacks on reticulocytes choke off the supply of mature RBCs and lead to catastrophic anemia; control demands aggressive reactions.
Insights into RBC dynamics should aid in assessing interventions, most obviously exchange transfusion (19), but also drugs or potential vaccines. With age-restricted susceptibility, uninfected RBCs can graduate into or out of a susceptible class, but depletion of that class depletes older ones. Future work must identify more precise age-associated RBC characteristics that govern susceptibility, however. Because circulating RBCs are anucleate and cannot synthesize new surface molecules, receptors that decay cannot be replaced; reticulocyte susceptibility to P. vivax may be related to higher Duffy-antigen density, for instance (20). If RBC susceptibility to P. malariae is related to senescence markers, the accelerated senescence of uninfected RBCs reported with P. falciparum (21) should greatly affect mixed-species infections (22). The common portrayal of P. falciparum as a generalist is complicated by evidence of a seeming preference for young RBCs (23), but more detailed resolution is needed here as well: our model shows that the proportion of RBCs that is in young age classes increases as an infection proceeds.
Similarities and differences in immune response to different Plasmodium species remain obscure partly due to preoccupation with P. falciparum. Duffy, sickle-cell and other RBC polymorphisms indicate that malaria has shaped human immunity in more than the usual, proximate sense of the term, however. The four species that infect humans diverged long ago, their histories with non-human hosts differ, and comparing their traits should be informative (24). For instance, in humans, P. vivax induces fever at much lower densities than P. falciparum (25), which suggests accelerated activation of innate responses; the relatively slow growth of P. malariae may allow more reliance on the agents of acquired responses (26).
Our results show that, in the absence of immune responses, direct parasite-induced hemolysis can cause anemia. In some malaria patients a “bystander” effect may contribute to anemia: increased macrophage activity removes uninfected and infected RBCs, destroying perhaps 8.5 uninfected RBCs for each bursting infected RBC (18). Diserythropoesis may also contribute to anemia (17). Although we do not explore any effects of immune responses here, we crudely mimicked these effects in simulations, and, as expected, the usual result was accelerated onset of catastrophic anemia (see supporting information). However, it should be clear that in their current form our models cannot resolve the debate about which factor is the major cause of sustained anemia in actual P. falciparum infections (3, 18). Our results show that age-structured RBC susceptibility is an important, previously unappreciated determinant of malaria infection dynamics, to be considered in future work.
We do not consider parasite synchronization, which is likely immune-mediated (27), but note that it would probably benefit the host of a P. vivax infection were reticulocyte susceptibility <48 h. We also do not consider the blood stages transmissible to mosquitoes; their production entails complex trade-offs between density, persistence, pathogenesis, and transmission (28, 29), but these should not alter the qualitative conclusions given here. Here, any correlates of the peak infected RBC count would be maximized simply by maximizing R0 and f0; larger R0 values also lead more quickly to catastrophic anemia, however, and correlates of the integrated infected RBC count would be maximized by species-specific balances between R0 and f0. Finally, although our results are scaled on a per-microliter basis, we note that any given number of parasites represents a higher proportion of the RBC total in a child than in an adult, which may add to response imperatives.
Mathematical Formalism
We model the infection dynamics with systems of CODEs. The notation is as in Fig. 1. The CODEs for the infected RBCs are:
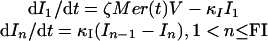 |
2 |
where FI is the number of compartments and κI = FI/τI. Given its short duration, we use a single ODE for the merozoite:
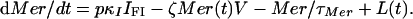 |
3 |
V is the total count of vulnerable RBCs. L(t) describes the primary infusion of merozoites from the liver into the blood, the details of which are unknown beyond that it occurs quickly (≈1 h), with just 104-105 parasites released (1). We took a tent form for L(t), which allows for some control in the time profile of release:
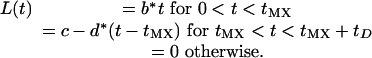 |
4 |
The release is at its maximum rate at t = tMX and concludes at t = tD. Parameters b, c, and d are fixed uniquely for a given tMX and tD by requiring L(t) to be continuous with time integral equal to 104/(5 × 106 mm). Details of L(t) had little effect on model dynamics, because the number released is small and tD is no more than a few hours (results not shown). For simulations reported here, tMX = 0.5 h and tD = 1 h.
The RBC source has its own ODE:
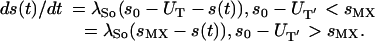 |
5 |
λSo is the rate of response of the source to changes in the RBC count. We took 1/λSo = 2 days (12). UT is the time rate of change in the total count of uninfected RBCs, s0 is the normal rate of new RBC production, and sMX is the maximum rate.
The CODEs for the susceptible (R) and nonsusceptible (M) RBCs in the P. vivax model are:
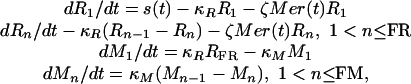 |
6 |
where κR = FR/τR, and τR is the average reticulocyte duration. Based on what is known about RBC development (12), we took FR = 21 so that the variance in the reticulocyte stage duration is ≈0.22τR (or ≈8 h if τR = 36 h). κM = FM/τM, and τM is the nominal duration of the nonvulnerable stage (120 days - τR). We choose FM so that 1/κM = 18 h. The total count of the susceptible cells is V = Σn = 1, FR Rn.
The CODEs in the P. malariae model are:
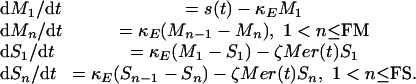 |
7 |
FM/κE is the nominal duration of the nonvulnerable RBC stage, and FS/κE is the nominal duration of the senescent stage. We chose FM + FS so that 1/κE = 12 h, for a RBC lifespan of 120 days. Here V = Σn = 1, FR Sn.
The CODEs in the generalist model are:
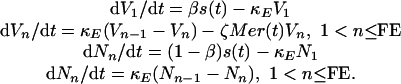 |
8 |
We took 1/κE = 12 h for both nonsusceptible and susceptible cells, and V = Σn = 1, FR Vn.
If at any point the merozoite count or the infected, susceptible or nonsusceptible RBC total drop to <1 for the whole volume of blood (here 5 × 106 μl), all the compartments that contribute to that particular total are reset to zero. All ODE systems were solved by using the fifth-order Runge-Kutta-Fehlberg algorithm, which incorporates an embedded fourth-order Runge-Kutta algorithm for adaptive stepsize control of the time integration (30, 31).
Supplementary Material
Acknowledgments
We thank David L. Smith, Barbara C. Sorkin, and an anonymous reviewer for critical comments.
This paper was submitted directly (Track II) to the PNAS office.
Abbreviations: CODE, compartmental differential equation system; ODE, ordinary differential equation.
References
- 1.White, N. J. & Breman, J. G. (2001) in Harrison's Principles of Internal Medicine, eds. Braunwald, E., Fauci, A. S., Isselbacher, K. J., Kasper, D. L., Hauser, S. L., Longo, D. L. & Jameson, J. L. (McGraw-Hill, New York) pp. 1203-1213.
- 2.Molineaux, L. & Dietz, K. (1999) Parassitologia 41, 221-231. [PubMed] [Google Scholar]
- 3.Gravenor, M. B., McLean, A. R. & Kwiatkowski, D. (1995) Parasitology 110, 115-122. [DOI] [PubMed] [Google Scholar]
- 4.Hetzel, C. & Anderson, R. M. (1996) Parasitology 113, 25-38. [DOI] [PubMed] [Google Scholar]
- 5.Hoshen, M. B., Heinrich, R., Stein, W. D. & Ginsburg, H. (2000) Parasitology 121, 227-235. [DOI] [PubMed] [Google Scholar]
- 6.Gravenor, M. B., Lloyd, A. L., Kremsner, P. G., Missinou, M. A., English, M., Marsh, K. & Kwiatkowski, D. (2002) J. Theor. Biol. 217, 137-148. [DOI] [PubMed] [Google Scholar]
- 7.Haydon, D. T., Matthews, L., Timms, R. & Colegrave, N. (2003) Proc. R. Soc. London Ser. B 270, 289-298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.McKenzie, F. E., Jeffery, G. M. & Collins, W. E. (2001) J. Parasitol. 87, 626-637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.McKenzie, F. E., Jeffery, G. M. & Collins, W. E. (2002) J. Parasitol. 88, 521-535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Gilles, H. M. (1993) in Bruce-Chwatt's Essential Malariology, eds. Gilles, H. M. & Warrell, D. A. (Edward Arnold, London), pp. 12-34.
- 11.Krogstad, D. J. (1995) in Principles and Practice of Infectious Diseases, eds. Mandell, G. L., Bennett, J. E. & Dolin, R. (Churchill Livingstone, New York), pp. 2415-2427.
- 12.Rapaport, S. I. (1987) Introduction to Hematology (Lippincott, Philadelphia).
- 13.Miller, L. H., Baruch, D. I., Marsh, K. & Doumbo, O. K. (2002) Nature 415, 673-679. [DOI] [PubMed] [Google Scholar]
- 14.Johnson, J. G., Epstein, N., Shiroishi, T. & Miller, L. H. (1980) Parasitology 80, 539-550. [DOI] [PubMed] [Google Scholar]
- 15.Davis, T. M. E., Krishna, S., Looareesuwan, S., Supanaranond, W., Pukrittayakamee, S., Attatamsoonthom, K. & White, N. J. (1990) J. Clin. Invest. 86, 793-800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Simpson, J. A., Silamut, K., Chotivanich, K., Pukrittayakamee, S. & White, N. J. (1999) Trans. R. Soc. Trop. Med. Hyg. 93, 165-168. [DOI] [PubMed] [Google Scholar]
- 17.Wickramasinghe, S. N. & Abdalla, S. H. (2000) Baillieres Best Pract. Res. Clin. Haematol. 13, 277-299. [DOI] [PubMed] [Google Scholar]
- 18.Jakeman, G. N., Saul, A., Hogarth, W. L. & Collins, W. E. (1999) Parasitology 119, 127-133. [DOI] [PubMed] [Google Scholar]
- 19.Wilkinson, R. J., Brown, J. L., Pasvol, G., Chiodini, P. L. & Davidson, R. N. (1994) Q. J. Med. 87, 553-557. [PubMed] [Google Scholar]
- 20.Woolley, I. J., Hotmire, K. A., Sramkoski, R. M., Zimmerman, P. A. & Kazura, J. W. (2000) Transfusion 40, 949-953. [DOI] [PubMed] [Google Scholar]
- 21.Omodeo-Sale, M. F., Motti, A., Basilico, N., Parapini, S., Olliaro, P. & Taramelli, D. (2003) Blood 102, 705-711. [DOI] [PubMed] [Google Scholar]
- 22.McKenzie, F. E. & Bossert, W. H. (1997) J. Parasitol. 83, 593-600. [PMC free article] [PubMed] [Google Scholar]
- 23.Pasvol, G., Weatherall, D. J. & Wilson, R. J. M. (1980) Br. J. Haematol. 45, 285-295. [DOI] [PubMed] [Google Scholar]
- 24.Paul, R. E. L., Ariey, F. & Robert, V. (2003) Ecol. Lett. 6, 866-880. [Google Scholar]
- 25.Kitchen, S. F. (1949) in Malariology, ed. Boyd, M. F. (Saunders, Philadelphia) pp. 1027-1045.
- 26.Mason, D. P. & McKenzie, F. E. (1999) Am. J. Trop. Med. Hyg. 61, 367-374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Rouzine, I. M. & McKenzie, F. E. (2003) Proc. Natl. Acad. Sci. USA 100, 3473-3478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.McKenzie, F. E. & Bossert, W. H. (1998) J. Theor. Biol. 193, 419-428. [DOI] [PubMed] [Google Scholar]
- 29.McKenzie, F. E. & Bossert, W. H. (1998) Am. J. Trop. Med. Hyg. 58, 763-767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Cash, J. R. & Karp, A. H. (1990) ACM Trans. Math. Soft 16, 201-222. [Google Scholar]
- 31.Press, W. H., Teukolskky, S. A., Vettering, W. T. & Flannery, B. P. (1992) Numerical Recipes in C (Cambridge Univ. Press, Cambridge, U.K.).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.