Algorithms for Quantitative Quasi-static Elasticity Imaging using Force Data

Abstract

Quasi-static elasticity imaging can improve diagnosis and detection of diseases that affect the mechanical behavior of tissue. In this methodology images of the shear modulus of the tissue are reconstructed from the measured displacement field. This is accomplished by seeking the spatial distribution of mechanical properties that minimizes the difference between the predicted and the measured displacement fields, where the former is required to satisfy a finite element approximation to the equations of equilibrium. In the absence of force data, the shear modulus is determined only up to a multiplicative constant. In this manuscript we address the problem of calibrating quantitative elastic modulus reconstructions created from measurements of quasi-static deformations. We present two methods that utilize the knowledge of the applied force on a portion of the boundary. The first involves rescaling the shear modulus of the original minimization problem to best match the measured force data. This approach is easily implemented but neglects the spatial distribution of tractions. The second involves adding a force-matching term to the original minimization problem and a change of variables, wherein we seek the log of the shear modulus. We present numerical results that demonstrate the usefulness of both methods.

1. INTRODUCTION

Elasticity imaging, or more generally biomechanical imaging, has emerged as an important new modality for the detection and diagnosis of different type of diseases including breast and prostate cancer [1, 2], atherosclerosis [3, 4], liver cirrhosis [5], and disorders of the brain [6, 7]. Further, since it involves generating maps of the mechanical properties of tissue in-vivo, it may also be used to create patient-specific, predictive models of tissue deformation which find applications in surgical planning and training.

In elasticity imaging the deformation field within the tissue in response to an external or internal excitation is measured, and this field in conjunction with the equations of equilibrium and an assumed stress-strain law is used to determine the spatial distribution of the material parameters in that law [8]. One may classify elasticity imaging by considering whether the time scale of the excitation is fast enough so that inertia of the tissue is significant [9]. If this is the case, it is often possible to estimate absolute (also referred to as quantitative) estimates of the material properties. This is because given the displacement history, the inertia term, which is a product of the tissue density and acceleration, can be estimated easily. Here it is assumed that the density of soft tissues is known and does not vary significantly. This provides a calibrated body force term on the right hand side of the equations of motion, which in turn permits the quantitative estimation of the elasticity parameters. We remark that quantitative estimates of material properties are useful because (a) they can be used to monitor the progression of a disease or a treatment (think of a tumor becoming less stiff following chemotherapy), (b) they are needed in creating patient-specific models for surgical planning and training, (c) in some cases they may be used to stage a disease (liver fibrosis, for example [5, 10, 11, 12, 13, 14]) and perhaps most importantly, (d) they provide an objective means to compare results across operators, imaging systems, and time.

In another class of elasticity imaging applications, the tissue is deformed slowly, and the displacements are measured typically using ultrasound. In these applications the time scale of excitation is slow so that inertia plays no role. We refer to this as quasi-static elasticity imaging. In quasi-static elasticity imaging, one typically has at most a measured quasi-static displacement field. From such data, then even in the most optimistic modeling case, one can determine the shear modulus of the tissue only up to a multiplicative constant [15, 16, 17, 18]. This is because in the equations of motion, there is no term on the right-hand-side in order to calibrate the material parameters (see Equation (1) in the following section). This is a shortcoming of quasi-static elasticity imaging which is overcome by other advantages such as simpler experimental set up and higher resolution. Thus there has been effort in recent years in making quasi-static elasticity imaging quantitative [19].

One approach to quantitative quasi-static elasticity imaging has focused on using a calibrated layer or stand-off pad on the surface of the tissue that is being compressed [19, 20, 21]. Techniques that use calibration layers must ensure that the layer and the tissue are compatible both in terms of their acoustic and elastic properties. Further the coupling between the ultrasound transducer and the calibration layer, as well as between the calibration layer and the tissue has to be tight.

As an alternative, such restrictions may be avoided by measuring the contact force between the ultrasound probe and the body, as for example, described in [22, 23, 24]. We consider two approaches for making use of force data. The first uses force data as a post-processing step once the relative modulus distribution has been determined using displacement data only. This method is simple and easy to implement, however it does not make use of the force data measured in several spatial locations in order to improve the estimate of the spatial distribution of the shear modulus. The second approach overcomes this limitation by appending to the original minimization problem a force matching term (in addition to a displacement matching and a regularization term). Through simple analysis and numerical examples we demonstrate that a naive implementation of this approach fails due to the conflicting requirements of minimizing the force matching and regularization terms. We propose a simple remedy to this problem by solving for the Jeffrey’s parameter [25], which is the natural log of the modulus instead of the modulus itself. We demonstrate its efficacy through analysis and numerical experiments.

The layout of this paper is as follows. We begin with defining the forward and inverse elasticity problems in Section 2. Thereafter in Section 3 we quantify the indeterminacy of the shear modulus based on pure displacement data. We also demonstrate that when the inverse problem is solved as a minimization problem the regularization term forces the modulus distribution toward the smallest possible value. In Section 4 we describe two approaches for quantitative elasticity reconstructions using force data, and in Section 5 we verify their numerical performance. In Section 6 we extend the application of these methods to a pure Dirichlet problem and end with conclusions in Section 7.

2. FORWARD AND INVERSE PROBLEMS

2.1. Equation of equilibrium and constitutive model

The equation of equilibrium in the current configuration is,

$$\mathit{\text{div}}(\mathit{\sigma })=\mathbf{0}\mathit{\text{in}}\mathrm{\Omega }.$$ (1)

The Cauchy stress tensor is given by,

$$\mathit{\sigma }=\frac{1}{J}\mathit{F}\mathit{S}{\mathit{F}}^{\mathit{T}},$$ (2)

where J is the Jacobian or the determinant of the deformation gradient F = 1 + ∇u, where u is the displacement field, and S is the second Piola-Kirchhoff stress tensor which may be obtained from any valid strain energy density function as

$$\mathit{S}=-pJ{\mathit{C}}^{-1}+2\frac{\partial W}{\partial \mathit{C}}$$ (3)

Here p is the pressure and W is the strain energy density function that depends on the invariants of the Cauchy-Green strain tensor C = F^TF. In the above equation we have assumed that the material is incompressible.

We utilize the Blatz [26] strain energy density function given by

$$W=\frac{\mu }{2\gamma }(e^{\gamma (J^{-\frac{2}{3}}{I}_1-3)}-1).$$ (4)

Here μ is the shear modulus at zero strain, γ is a nonlinear parameter that determines the nonlinearity of the material response, and I₁ = trace(C) is the first principal invariant of the Cauchy Green tensor. This strain energy density function and the resulting stress-strain relation has an exponential functional form (see [27] for more details). Using (4) in (3) and (2) we arrive at

$$\mathit{\sigma }=-p\mathbf{1}+\mu \mathit{A}[\mathit{u}],$$ (5)

where

$$\mathit{A}[\mathit{u}]=J^{-\frac{5}{3}}(\mathit{F}{\mathit{F}}^T-\frac{1}{3}{I}_1\mathit{I})e^{\gamma (J^{-\frac{2}{3}}{I}_{1-3})}.$$ (6)

We note that we have explicitly written A as a function of the displacement.

The equation of equilibrium (1) above is appended by boundary conditions. We consider displacements that are prescribed on a portion of the boundary,

$$\mathit{u}=\mathit{g},\text{on}{\mathrm{\Gamma }}_g.$$ (7)

Further, we assume that some portion of the boundary may be traction-free. That is,

$$\mathit{\sigma }\mathit{n}=\mathbf{0},\text{on}{\mathrm{\Gamma }}_h.$$ (8)

Together Γ_g and Γ_h must cover the entire boundary, that is ∂Ω = Γ_g ∪ Γ_h. We also assume that at least some portion of the boundary is traction-free, that is Γ_h ≠ ∅.

Forward problem

Together (1), (5), (7) and (8) define a well posed forward problem: given the material parameters μ and γ, and the boundary data g, determine the displacements u and the pressure p everywhere in Ω. In this manuscript, when solving the inverse problem, we will consider a sequence of forward problems where g and γ will be fixed, and μ will be varied. In that case we may write the solution to the forward problem as {u, p} = {û, p̂}[μ] to indicate that for every field μ we have a corresponding set of displacement and pressure fields. We also denote the Cauchy stress constructed using these fields as σ = σ̂[μ].

Inverse problem

In elasticity imaging, we wish to solve the inverse problem: given the displacement field u everywhere in Ω determine the material parameters μ and γ. There are several important remarks to be made here:

1. The pressure field is typically not measured in elasticity imaging, and is therefore unknown when solving the inverse problem. However, once the material parameters have been determined it can be recovered from (5), after recognizing that the material parameters and the displacement fields are both known. Hence the pressure field may be thought of as a useful by-product of the inverse problem.

2. In order to solve for both the shear modulus μ and the nonlinear parameter γ, it is necessary to measure a displacement field at small strains (|∇u| ≪ 1) and another at a finite value of strain [17]. The first displacement field is then used to determine the shear modulus μ, while fixing γ to a small constant (say 1) throughout the domain. The second displacement field in then used to determine γ everywhere. This procedure works, because the linearization of (5), obtained assuming small strains (|∇u| ≪ 1), reduces to

   $$\mathit{\sigma }=-p\mathbf{1}+2\mu \mathit{\epsilon }.$$ (9)

   Here $\epsilon =\frac{1}{2}(\nabla \mathit{u}+{\mathit{u}}^T)$ is the infinitesimal strain tensor, and remarkably the nonlinear parameter does not appear in the expression for the stress. Thus the nonlinear parameter does not influence the displacement at small strains. In this paper we will focus on this first step of solving the nonlinear elasticity problem. That is, we will assume that γ is fixed and we are interested in determining a quantitative estimate of μ.

3. When the inverse problem is solved using only displacement data (the set up described above) the shear modulus is determined only up to a multiplicative factor. In order to determine the absolute value of the shear modulus some force measurement is necessary. This statement is made precise in the following section.

Minimization problem

The inverse problem is typically solved as a minimization problem [28, 29, 30], where the shear modulus μ* is given by

$${\mu }^{*}=\underset{\mu \ge \mathrm{\mu ̅}}{\text{argmin}}\pi [\mu ]\equiv 𝒟[\mu ]+\alpha ℛ[\mu ]$$ (10)

In the expression above 𝒟[μ] is the displacement matching term defined as,

$$𝒟[\mu ]=\frac{1}{2}{\int }_{\mathrm{\Omega }}{|\mathit{û}[\mu ]-\mathit{U}|}^{2}d\mathit{x},$$ (11)

where U is the measured displacement field, and û[μ] is the displacement field corresponding to a shear modulus distribution μ. The goal is to find the shear modulus distribution that yields a displacement field u, which minimizes π. Also, in the equation above ℛ[μ] represents the regularization term, and α the corresponding parameter. The regularization term imposes prior beliefs on the reconstructed shear modulus distribution while at the same time regularizing the inverse problem. In elasticity imaging, where the goal is to identify regions with sharp variations in material properties, one popular choice for the regularization term is the total variation term [31, 27], given by

$$ℛ[\mu ]={\int }_{\mathrm{\Omega }}\sqrt{|\nabla \mu |+{\beta }^2}d\mathit{x}.$$ (12)

This term penalizes the total variation in μ without regard for the steepness of the variation. Further, β ≪ |∇μ|, is a parameter than ensures that this term has continuous derivatives with respect to μ at ∇μ = 0.

3. INDETERMINACY OF THE SHEAR MODULUS

In this section we demonstrate that given only displacement data it is possible to determine the shear modulus only up to a multiplicative constant. We do so by proving three propositions that shed light on the solution obtained by solving the inverse problem defined in (10). Throughout this section μ₀ is an arbitrary positive constant.

Proposition 1

We claim that

$$\{\mathit{û},\mathrm{p̂}\}[{\mu }_0\mu (\mathit{x})]=\{\mathit{û},{\mu }_0\mathrm{p̂}\}[\mu (\mathit{x})].$$ (13)

That is let {u, p, μ} be a solution to the forward problem, then {u, μ₀p, μ₀μ} is also a solution to the forward problem.

Proof

In order to prove this we have to prove that the set {u, μ₀p, μ₀μ} satisfies the equation of equilibrium and the boundary conditions given that the set {u, p, μ} satisfies the equation of equilibrium and the boundary conditions.

Since the displacement field is unaltered between the two sets the Dirichlet boundary condition is automatically satisfied.

We denote the Cauchy stress for the sets {u, μ₀p, μ₀μ} and {u, p, μ} by σ₀ and σ, respectively. Then

$${\mathit{\sigma }}_0=-{\mu }_{0}p\mathbf{1}+{\mu }_0\mu \mathit{A}[\mathit{u}]={\mu }_0\mathit{\sigma }\text{from}(5).$$ (14)

As a result,

$$\nabla ·{\mathit{\sigma }}_0={\mu }_0\nabla ·\mathit{\sigma }=\mathbf{0},\text{from}(1).$$ (15)

and on Γ_h,

$${\mathbf{\sigma }}_0\mathit{n}={\mu }_0\mathbf{\sigma }\mathit{n}=\mathbf{0},\text{from}(8).$$ (16)

Hence we conclude that the set {u, μ₀p, μ₀μ} is a solution to the forward problem.

Proposition 2

Let μ* be the solution of the minimization problem (10), then 𝒟[μ₀μ*] = 𝒟[μ*]. That is any other shear modulus field constructed by multiplying μ* with a positive real number yields the same value for the displacement matching term.

Proof

From the definition of the displacement matching term, we have

$$𝒟[{\mu }_0{\mu }^{*}]=\frac{1}{2}{\int }_{\mathrm{\Omega }}|\mathit{û}[{\mu }_0{\mu }^{*}]-\mathit{U}{|}^{2}d\mathit{x}=\frac{1}{2}{\int }_{\mathrm{\Omega }}|\mathit{û}[{\mu }^{*}]-\mathit{U}{|}^{2}d\mathit{x},\text{from}(13)=𝒟[{\mu }^{*}].$$ (17)

Proposition 3

Let μ* be the solution of the minimization problem (10), and let ${\mu }_l=\underset{\mathit{x}\in \mathrm{\Omega }}{\text{min}}(\mu *(\mathit{x}))$, then μ_l = μ̄.

Proof

This proposition states that minimizer μ* must attain the lower bound somewhere. To prove this we assume the contrary, that is μ_l > μ̄, and construct the shear modulus field $\frac{\mathrm{\mu ̄}}{{\mu }_l}{\mu }^{*}$. Next we evaluate

$$\pi [\frac{\mathrm{\mu ̄}}{{\mu }_l}{\mu }^{*}]=𝒟[\frac{\mathrm{\mu ̄}}{{\mu }_l}{\mu }^{*}]+\alpha ℛ[\frac{\mathrm{\mu ̄}}{{\mu }_l}{\mu }^{*}]=𝒟[{\mu }^{*}]+\alpha ℛ[\frac{\mathrm{\mu ̄}}{{\mu }_l}{\mu }^{*}],\text{from}(13)=𝒟[{\mu }^{*}]+\alpha {\int }_{\mathrm{\Omega }}\sqrt{{(\frac{\mathrm{\mu ̄}}{{\mu }_l})}^2{|\nabla {\mu }^{*}|}^2+{\beta }^2}d\mathit{x},\text{from}(12)<𝒟[{\mu }^{*}]+\alpha {\int }_{\mathrm{\Omega }}\sqrt{({|\nabla {\mu }^{*}|}^2+{\beta }^2}d\mathit{x},=\pi [{\mu }^{*}].$$ (18)

However, this violates our assumption that μ* is the minimizer. Hence we conclude that μ_l = μ̄.

Taken together the propositions above tell us the following about μ*, the solution to the minimization problem:

1. Any field μ₀μ*, where μ₀ is a positive real number, is an equally viable field in that it yields the same value for the displacement matching term as μ*.

2. Of all these possible fields the TV regularization selects the one whose minimum is equal to the specified lower bound.

3. By solving the inverse problem, while we can expect some information in the contrast of the shear modulus, we cannot get any information about its magnitude. In the following section we demonstrate how we recover the magnitude by using measured force data.

4. USING FORCE DATA

In this section we demonstrate how force data may be used to tackle the indeterminacy in evaluating the shear modulus. We assume that on multiple surface patches of the boundary Γ_g the normal force has been measured. We denoted the set of points on each patch by Γ⁽ⁱ⁾ and the measured normal force by $F_n^{(i)}$, where i = 1, ⋯, M.

We consider two approaches. The first is a post-processing method in which the inverse problem is first solved without accounting for any force information, and the thereafter the shear modulus is rescaled using the force data. In the second approach the force data is incorporated in the data matching term while solving the inverse problem. The post-processing approach is easier to implement, however it is limited in that it does not make effective use of multiple force measurements in evaluating the spatial distribution of the shear modulus. The second approach overcomes this short coming but at the expense of solving a more complicated problem. In addition we will observe that in order for the second approach to work we will need to modify the form of the minimization problem posed in (10).

Post-processing method

We assume that the inverse problem has been solved using displacement matching data, and the resulting displacement field, pressure, shear modulus and Cauchy stress fields are denoted by u*, p*, μ* and σ*. In the previous section we have demonstrated that any shear modulus field μ₀μ* is an equally likely solution in that it will also minimize the displacement matching term to the same extent as μ*. Further, in Proposition 1 we have shown that the corresponding displacement, pressure and stress fields will be given by u*, μ₀p* and μ₀σ*. We now determine the optimal value of μ₀ by matching the measured and predicted forces,

$$F_n^{(i)}={\int }_{{\mathrm{\Gamma }}^{(i)}}{\mu }_0{\sigma }_{nn}^{*}d\mathit{x}={\mu }_0{\int }_{{\mathrm{\Gamma }}^{(i)}}{\sigma }_{nn}^{*}d\mathit{x},$$ (19)

$$\Rightarrow {\mu }_0=F_n^{(i)}/{\int }_{{\mathrm{\Gamma }}^{(i)}}{\sigma }_{nn}^{*}d\mathit{x}$$ (20)

We note that the force term on the right hand side of (20) is measured and integral of the Cauchy stress can be evaluated once the reconstruction with the displacement matching term is done. Using these two pieces of data we can estimate μ₀. With μ₀ known, we can estimate the actual modulus distribution as μ(x) = μ₀μ*(x).

If more than one force measurements are available (M > 1), we will have M estimates of μ₀. In this case we may solve (19) in a least-squares sense in order to determine μ₀.

Force-matching method

The second approach involves appending to the original objective function a force matching term so that optimal shear modulus distribution is given by

$${\mu }^{*}=\underset{\mu \ge \mathrm{\mu ̄}}{\text{argmin}}{\pi }_1[\mu ]\equiv 𝒟[\mu ]+\alpha ℛ[\mu ]+{\alpha }_fℱ[\mu ].$$ (21)

Here α_f is a penalty parameter that determines the relative importance of the force matching term which is denoted ℱ[μ] and is equal to

$$ℱ[\mu ]=\frac{1}{2}\sum _{i=1}^M{(F_n^{(i)}-{\int }_{{\mathrm{\Gamma }}^{(i)}}{\sigma }_{nn}[\mu ]d\mathit{x})}^2.$$ (22)

We now discuss a drawback associated with using this from of the objective function. It is related to the opposing tendencies of the regularization and the force matching terms, and leads to poor modulus reconstructions as shown in the following section. In the previous section we demonstrated that the displacement matching term is unchanged when the target modulus is changed from μ(x) to μ₀μ(x), where μ₀ is a positive constant. We also proved that out of all possible μ₀’s the regularization term will select one for which the shear modulus attains the lower bound somewhere in the domain. However, in contrast to this, the force matching term is minimized when the value of μ₀ (for a single force measurement) is given by

$${\mu }_0=F_n^{(i)}/{\int }_{{\mathrm{\Gamma }}^{(i)}}{\sigma }_{nn}[\mu ]d\mathit{x}.$$ (23)

Depending on the value of μ and $F_n^{(i)}$ this may lead to a very large value of μ₀. More importantly it can be much larger than μ̄, the lower bound on μ. As a result the force matching term will act in direct opposition to the regularization term. While the force matching will try to converge to a larger value of μ₀, the regularization term will try and lower it so that the total variation is minimized. A direct consequence of this is the appearance of artifacts in the reconstructions when the displacement field is corrupted with even a small amount of noise (see Section 5).

This difficulty can be avoided by introducing a variable transformation ψ = ln μ and a new objective function such that the optimal distribution of ψ is given by

$${\psi }^{*}=\underset{\psi }{\text{argmin}}{\pi }_2[\psi ]\equiv 𝒟[e^{\psi }]+\alpha ℛ[\psi ]+{\alpha }_fℱ[e^{\psi }].$$ (24)

In this new setting as the shear modulus is changed from μ to μ₀μ the log-modulus changes from ψ to ψ₀ + ψ, where ψ₀ = ln μ₀. Consequently the value of the objective function changes to

$${\pi }_2[{\psi }_0+\psi ]=𝒟[e^{{\psi }_0}{e}^{\psi }]+\alpha ℛ[{\psi }_0+\psi ]+{\alpha }_fℱ[e^{{\psi }_0}{e}^{\psi }]=𝒟[e^{\psi }]+\alpha ℛ[\psi ]+{\alpha }_fℱ[e^{{\psi }_0}{e}^{\psi }].$$ (25)

In deriving the above we have made use of the relations 𝒟[μ₀μ] = 𝒟[μ] (the result of Proposition 2) and the fact the total variation of ψ, which depends only on ∇ψ, is unchanged by the addition of a constant to ψ. Now the only term that is affected by adding a constant to ψ, and hence multiplying μ with a constant, is the force matching term. The displacement matching and the regularization terms are unchanged. As a result the force-matching term determines the value of this constant with no “interference” from the other terms.

We note that a similar transformation to the log of conductivity is also described in [32] when solving the inverse heat conduction problem. However, in that case the motivation is to transform the minimization with bounds to one with no bounds. This is because while the conductivity needs to be bounded away from zero, there is no such requirement on its logarithm.

5. NUMERICAL RESULTS

We now consider two numerical examples that demonstrate the utility of the methods discussed in the previous section. In both examples the specimen is a cube with edge length L = 20 and is subject to the loading sketched in Figure 1. The top surface is fixed in the vertical direction and is traction free in all other directions while the bottom surface is compressed by a strain ε₀ = 1% in the vertical direction and is traction free in all other directions. This level of strain represents a typical value at which displacement data is estimated in practice. Further, by restricting the strain to a small value we are avoiding the confounding nonlinear elastic effects. All other surfaces are traction free. In order to eliminate the rigid body modes, the corner of the specimen that is coincident with the origin is fixed in all directions and the corner at (0, L, 0) is fixed in the x and the z directions.

Figure 1.

Schematic of the numerical examples.

The specimen is treated as an isotropic incompressible hyperelastic material with a strain energy density given by (4). In this expression the value of γ is set to 0.1, implying that the stress response is mostly linear in the range of the prescribed deformation. The value of μ varies depending on the problem considered.

The displacement field within the specimen is “measured” by solving the forward problem using stabilized finite elements [33, 34] on tetrahedral mesh with 20³ elements and then adding 1% Gaussian white noise to the displacement field. In addition the force on the bottom surface (the one that is compressed) is also measured and is corrupted by 1% noise. The shear modulus is reconstructed using these measurements on the same mesh. We avoid the “inverse crime” by adding noise to both the displacement and force data.

Sandwich problem

In this problem the specimen is comprised of three layers of equal thickness with μ_top = μ_bottom = 1 and μ_middle = 10 (see Figure 2(a)).

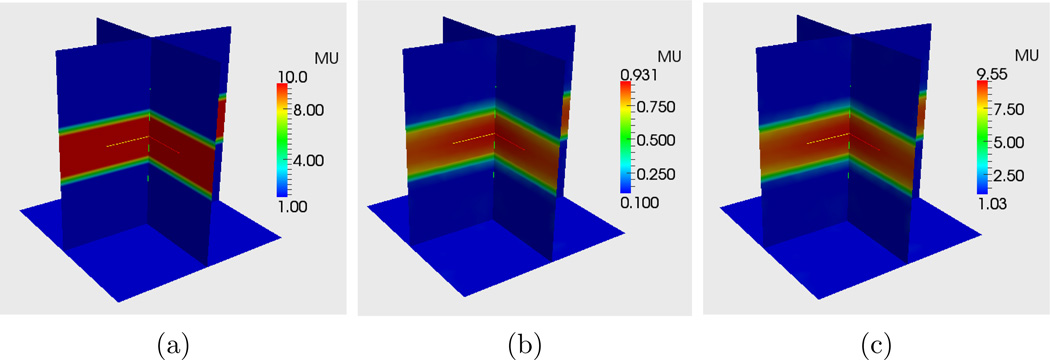
Figure 2.

Shear modulus distributions for the sandwich problem: (a) Exact μ, (b) Reconstruction of μ with displacement matching only, (c) Reconstruction of μ after post-processing for the measured force

First, we solve for the shear modulus field using only the displacement data and produce a relative modulus reconstruction. We set the lower bound for μ at 0.1 and use μ = 0.1 as an initial guess over the entire domain. We solve the inverse problem using this algorithms described in [27]. The resulting reconstruction is shown in Figure 2(b). We note that the TV regularization has caused the softer layers to attain the lower bound, and that the contrast between the soft and the stiff layers is 9.31, which is quite close to the correct value. We obtain the quantitative reconstruction from this image by employing the post-processing approach described in Section 4. The result is shown in Figure 2(c). We note that the modulus has now been re-scaled so that its distribution is quite close to the absolute modulus distribution.

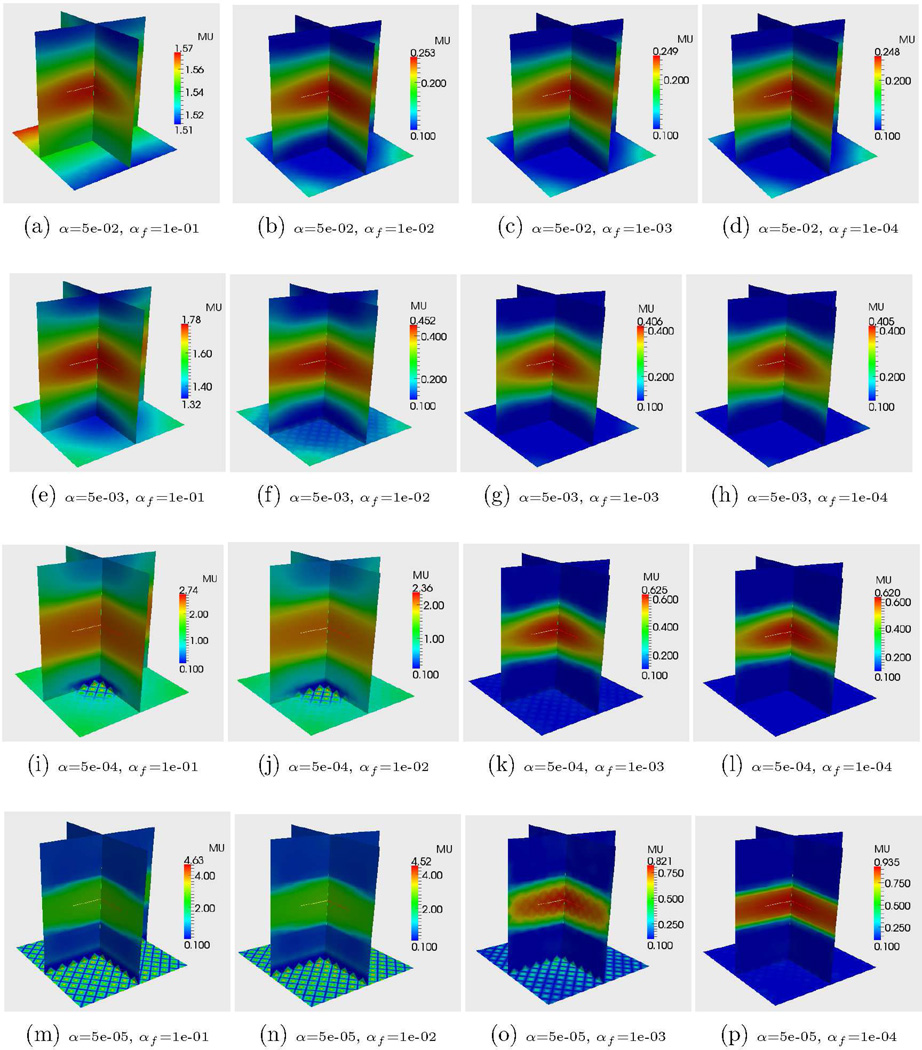
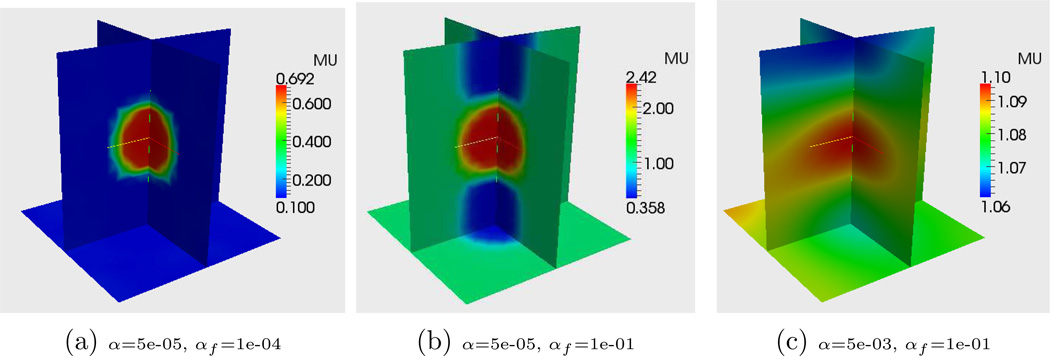
We also solve for the shear modulus distribution by adding the force matching term to the displacement matching term. The objective function for this formulation is given by (21). We note that we have to select α (the regularization parameter) and α_f (the force-matching parameter) for this problem. We vary these over several orders of magnitude and obtain the results displayed in Figure 3. In this array of figures the regularization parameter α increases going from bottom to top, while the force matching parameter α_f increases going from right to left.

Figure 3.

Reconstruction of μ through displacement and force matching terms.

From this figure we observe that there is no choice of these parameters that results in a viable reconstruction for μ. When α_f is small (right-most column in the figure), there is a value of the regularization parameter, α, that produces a reconstruction with the right contrast and no oscillations (subfigure 3(p)). However, the value of α_f is so small that the force matching term plays no role and this reconstruction is essentially the same as that for the pure displacement matching term. As a result we recover a good relative modulus distribution but not a quantitative one.

The way to enhance the effect of the force matching term is to increase α_f. Once this is done we are lead to reconstruction like those in subfigure 3(m). Here the average value of shear modulus on the face where the force is measured (the bottom face) approaches the correct answer μ = 1, however away from the face it quickly drops down to the lower bound in order to minimize the regularization term. This leads to a spurious “boundary layer” in the reconstruction. Furthermore, the oscillations in μ on the face indicate that the regularization term is too small. However, once this term is increased we are lead to results like subfigure 3(e). Now the regularization term appears to overwhelm both the force and displacement matching terms. Consequently, the average shear modulus on the bottom face is significantly smaller than 1, and the contrast within the specimen is also much smaller than 10. The conclusion therefore is that in the α, α_f parameter space there is no value that leads to an accurate quantitative reconstruction. As discussed in the previous section the reason for this is the conflict between the force matching and regularization terms.

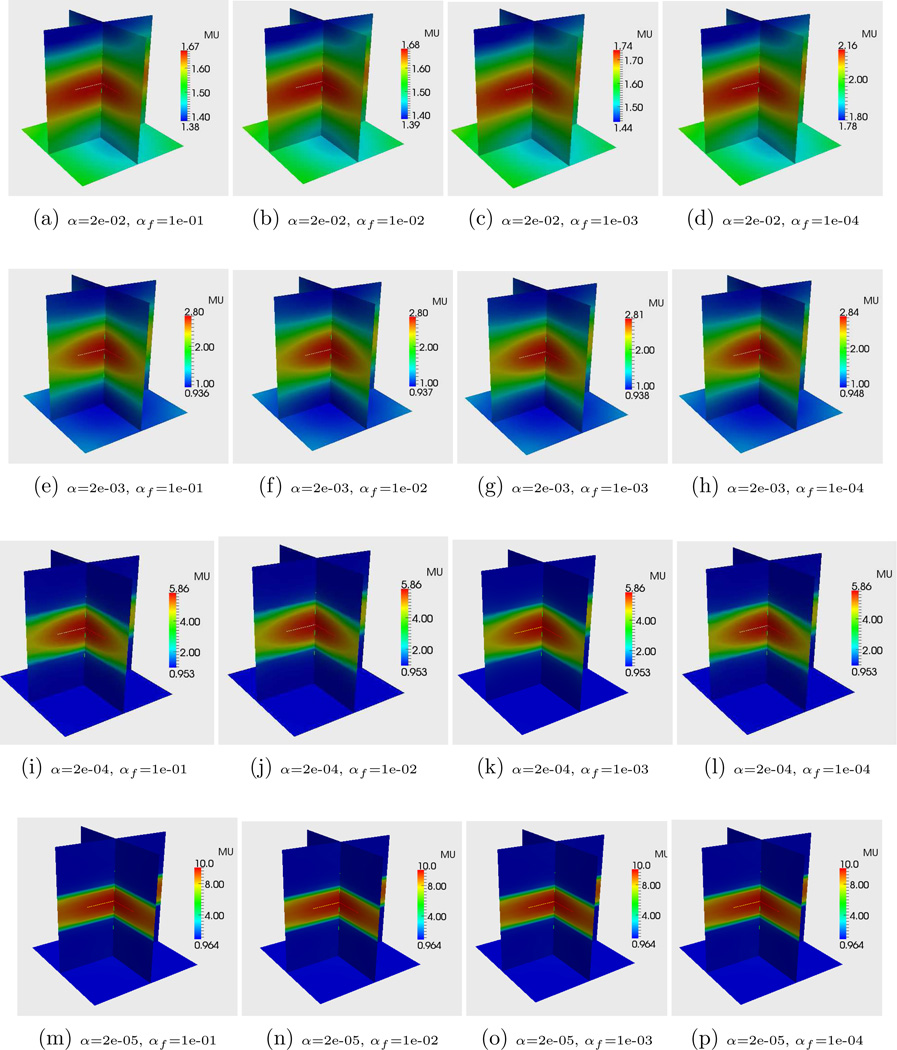
Finally, we solve for the shear modulus by including the displacement and force matching terms and by using the transformation ψ = log μ (see Section 4). This formulation also includes the two parameters, α and α_f, and the reconstructions obtained by varying these parameters are shown in Figure 4. In contrast to the previous case (Figure 3) where there was no value of these parameters that lead to accurate quantitative reconstructions, we now observe that there is a range of values of α and α_f for which accurate quantitative reconstructions are obtained. In particular, all the reconstructions in subfigures (m) to (p) within Figure 4 are accurate. In particular, when the regularization parameter is small enough so as to recover the contrast in the modulus, there is a large range of force-matching parameter (O(10³)) within which we recover accurate quantitative reconstructions. As discussed in Section 4, this is due to the fact that in this formulation the force matching term alone determines the absolute value of μ and the displacement matching and the regularization terms are unchanged when μ is altered by a multiplicative constant.

Figure 4.

Reconstruction of μ through displacement and force matching terms and using the variable transformation ψ = log μ.

Inclusion problem

In this problem the specimen is comprised of a hard spherical inclusion of diameter =(2/5)L placed at the center with μ_inclusion = 10 in a soft background with μ_background = 1 (see Figure 5(a)). All the other parameters are the same as in the sandwich problem.

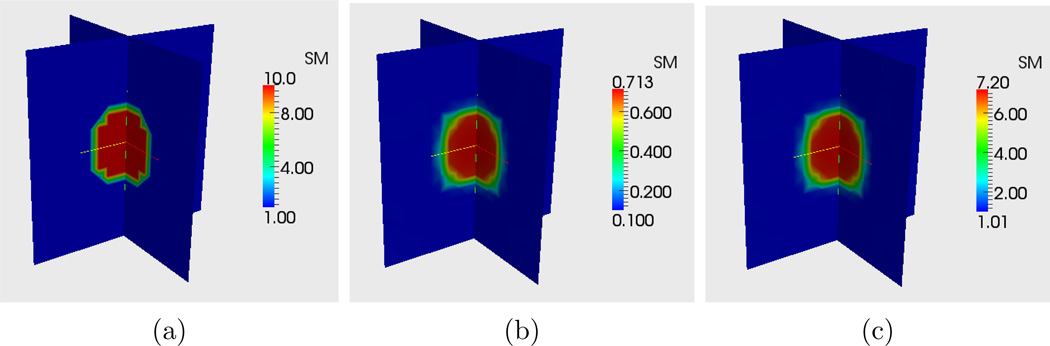
Figure 5.

Shear modulus distributions for the inclusion problem: (a) Exact μ, (b) Reconstruction of μ with displacement matching only, (c) Reconstruction of μ after post-processing for the measured force.

we solve for the shear modulus field using only the displacement data and produce a relative modulus reconstruction. We set the lower bound for μ at 0.1 and use μ = 0.1 as an initial guess over the entire domain. The resulting reconstruction is shown in Figure 5(b). We note that the TV regularization has caused the background to attain the lower bound, and that the contrast between the background and the inclusion is 7.13, which is close to the correct value. We obtain the quantitative reconstruction from this image by employing the post-processing approach described in Section 4.

The result is shown in Figure 5(c). We note that the modulus has now been re-scaled so that its distribution is quite close to the absolute modulus distribution.

We also solve for the shear modulus distribution by adding the force matching term to the displacement matching term. The objective function for this formulation is given by (21). Similar to the previous problem we have varied the parameters α and α_f over several orders of magnitude. Of these, some representative results are shown in Figure 6.

Figure 6.

Reconstruction of μ using force matching and displacement matching term.

When α_f is small there is a value of the regularization parameter, α, that produces a reconstruction with the right contrast and no oscillations (Figure 6(a)). However, the value of α_f is so small that the force matching term plays no role and this reconstruction is essentially the same as that for the pure displacement matching term. As a result we recover a good relative modulus distribution but not a quantitative one.

When α_f is increased we are lead to reconstructions like those in Figure 6(b). Here the average value of shear modulus on the face where the force is measured (the bottom face) approaches the correct answer μ = 1, however we can clearly see a spurious region of low modulus below the inclusion on this face. The low value of shear modulus in this region ensures that the total variation of the reconstructed modulus remains small even in the presence of the contrast in the modulus, which develops in order to reduce the displacement matching term. The net result is a reconstruction which is very different from the actual distribution.

When the regularization parameter is increased in order to force the reconstruction on the bottom face to be more uniform, we obtain results like those in Figure 6(c). Now the regularization term appears to overwhelm the displacement matching term. The average shear modulus on the bottom is close to 1, however the contrast is severely diminished. Thus even for this example, the conclusion therefore is that in the α, α_f parameter space there is no value that leads to an accurate quantitative reconstruction.

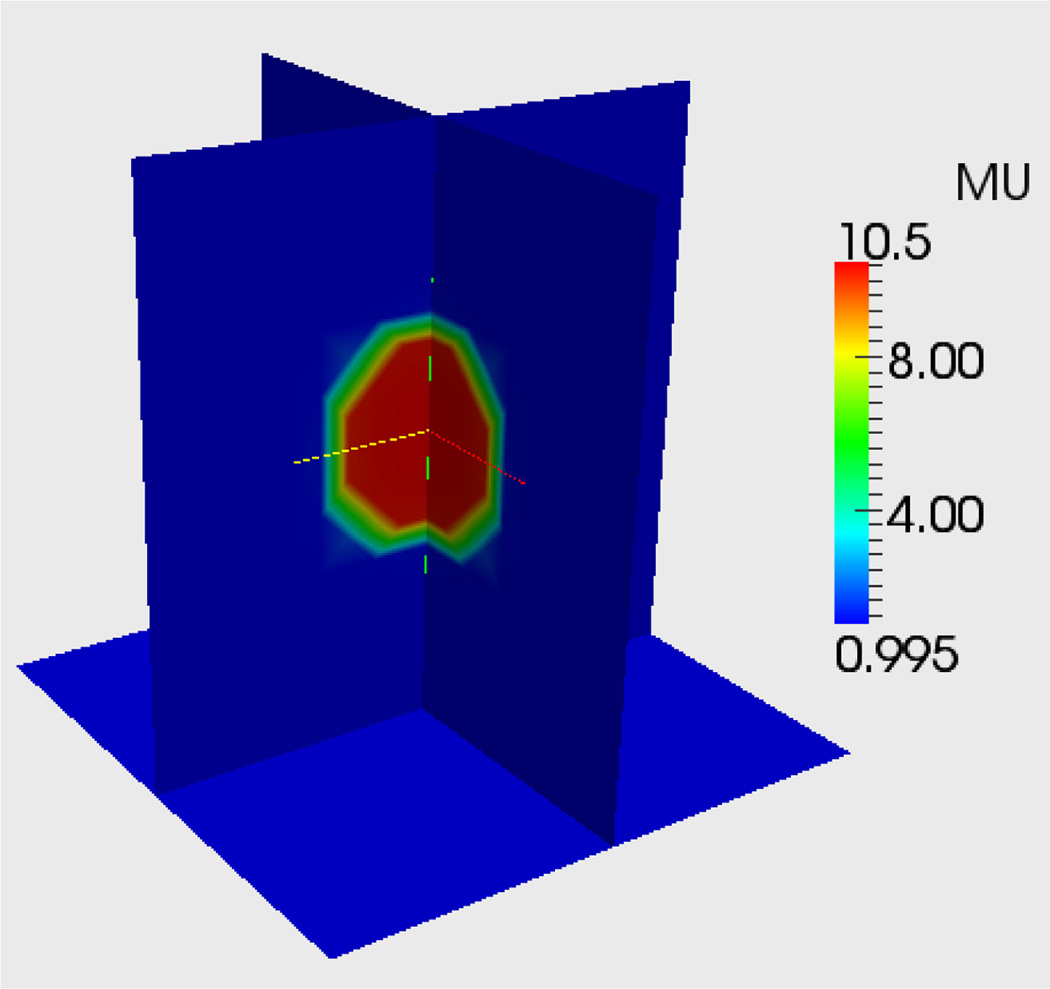
Finally, we solve for the shear modulus by including the displacement and force matching terms and by using the transformation ψ = log μ (see Section 4). In this case for a given value of the regularization parameter, there is a large range of values for the force-matching parameter that leads to results to accurate results. One such result is shown in Figure 7, where we note that the reconstruction has the correct absolute value and contrast.

Figure 7.

Reconstruction of μ using force matching and displacement matching term and variable transformation ψ = log μ with α=2e-06, α_f =1e-04.

6. EXTENSION TO A PURE DIRICHLET PROBLEM

Up to this point, we used knowledge of the (non-zero) applied force on one face, and the fact that we know another face to be traction free. In some instances it may not be feasible to assume that one of the boundaries is traction free. This would happen when none of the boundaries in the ultrasound image is close to an unconstrained physical boundary. In this section, the approach developed in this article for utilizing force data to reconstruct quantitative modulus estimates, is extended to such problems. To do so, we assume that we know the (non-zero) applied force on two or more faces. As such, this may be thought of as an extension of the previous case where the applied force on a second face is zero, to one where the applied force on a second face is non-zero but known.

In the pure Dirichlet case Γ_h = ∅ and the boundary condition (7) does not apply. The forward problem for the pressure is unique up to an additive constant. In order to make the problem unique it is assumed that the average value of the sought pressure is zero, that is,

$${\int }_{\mathrm{\Omega }}pd\mathit{x}=0.$$ (26)

We note that this choice is arbitrary and the average pressure can be set to any finite-valued constant without changing the displacement field. The solution to (1), (5), (7) and (26) given all the data is now unique. Since we are interested how this solution varies with variation in the shear modulus, we may once again denote it by {u, p} = {û, p̂}[μ] to indicate that for every field μ we have a corresponding set of displacement and pressure fields.

It is easy to verify that for this forward problem (the solution to (1), (5), (7) and (26)) also the three propositions of Section 2 hold. As a result with only displacement data we can determine μ by solving (10) up to a multiplicative constant. Further the pressure is known only up to an additive constant since the constraint (26) is arbitrary. Thus there are two arbitrary constants μ₀ and p₀ that are left undetermined and may be computed using measured force data.

Post-processing method

We assume that the inverse problem (10) has been solved using displacement matching data, and the resulting displacement field, pressure, shear modulus and Cauchy stress fields are denoted by u*, p*, μ* and σ*.We note that any shear modulus field μ₀μ* is an equally likely solution in that it will also minimize the displacement matching term to the same extent as μ*, and that the pressure is only determined up to an additive constant. The corresponding displacement, pressure and stress fields will be given by u*, μ₀p* + p₀ and μ₀σ* − p₀1. Note that in comparison to the traction-free boundary case, we have an additional unknown p₀. We now determine the values of μ₀ and p₀ by matching the measured and predicted forces,

$$F_n^{(i)}={\int }_{{\mathrm{\Gamma }}^{(i)}}{\sigma }_{nn}d\mathit{x}={\int }_{{\mathrm{\Gamma }}^{(i)}}({\mu }_0{\sigma }_{nn}^{*}-p_0)d\mathit{x}={\mu }_0{\int }_{{\mathrm{\Gamma }}^{(i)}}{\sigma }_{nn}^{*}d\mathit{x}-p_0{A}^{(i)},$$ (27)

where A⁽ⁱ⁾ is the area of the surface on which the force is measured. In the last line of the equation above A⁽ⁱ⁾ and ${\int }_{{\mathrm{\Gamma }}^{(i)}}{\sigma }_{nn}^{*}dx$ are known. Consequently, we arrive at a linear system of equations for the unknowns μ₀ and p₀. These can be solved once two force measurements are available. Alternatively, for more than two force measurements, these can be solved in a least-squares sense to determine the optimal values of μ₀ and p₀.

Force-matching method

We now consider modifying the inverse problem in order to account for the measured force data, and using this to determine a quantitative estimate of the shear modulus and the pressure. Based on our experience of simply adding a force matching term to the objective function for the case when one boundary condition is traction free (see Section 4), we anticipate a difficulty due to the opposing tendencies of the force matching and regularization terms. In oder to overcome this, we propose a change of variables from μ to ψ = ln μ and propose solving the following inverse problem in order to determine the log-shear modulus field ψ*(x) and the additive pressure parameter $p_0^{*}$:

$$\{{\psi }^{*},p_0^{*}\}=\underset{\psi ,p_0}{\text{argmin}}{\pi }_3[\psi ,p_0]\equiv 𝒟[e^{\psi }]+\alpha ℛ[\psi ]+{\alpha }_fℱ[e^{\psi },p_0].$$ (28)

where the displacement matching and regularization terms are given by (11), and (12), respectively, and the forcing matching term is given by

$$ℱ[\mu ,p_0]=\frac{1}{2}\sum _{i=1}^M{(F_n^{(i)}+p_0{A}^{(i)}-{\int }_{{\mathrm{\Gamma }}^{(i)}}{\sigma }_{nn}[\mu ]d\mathit{x})}^2.$$ (29)

For the inverse problem described in (28):

1. In the displacement matching term for a given value of ψ (and hence μ = e^ψ), the displacement field is determined by solving the forward problem given through equations (1), (5), (7) and (26).

2. Both the displacement matching and the regularization terms are unchanged if the log shear modulus is altered by an additive constant and the constant pressure p₀ is changed. The only term that determines these values is the force matching term. Hence we anticipate that similar to the case with some traction-free surface, this inverse problem will yield accurate results in the presence of noise.

7. CONCLUSIONS

We have considered the quasi-static elasticity imaging problem of determining the shear modulus distribution in the interior of a specimen from a measurement of the interior displacement field. We have demonstrated that in the absence of any force data the shear modulus is undetermined up to a multiplicative constant. When this problem is solved by minimizing a displacement matching term in conjunction with total variation regularization, the regularization term automatically selects this constant to be the one that minimizes the total variation while conforming to the lower bound set on the shear modulus.

When some force data is available, there are two options of determining this constant and hence a quantitative estimate of the shear modulus. The first involves post-processing the results of the original minimization problem in order to rescale the shear modulus so as to best match the measured force data. This approach is easy to implement but may not make the best use of distributed force measurements. The second involves adding a force-matching term to the original minimization problem, and has the potential to make use of distributed force data. However, it suffers from a direct conflict between the force-matching term and the regularization term, leading to erroneous reconstructions in the presence of noise. This difficulty is circumvented by a simple change of variables, wherein we seek to determine the log of the shear modulus instead of the shear modulus itself, and minimize its total variation. Using log μ as an optimization variable removes the conflict between the force matching and regularization terms. The force matching term works by rescaling the shear modulus by a multiplicative constant in order to best match the measured force, which is the same as adding a constant to log μ. The addition of a constant has no effect on the regularization term, which only involves the gradient of log μ. Hence using log μ instead of μ effectively decouples the force matching and regularization terms.

We have applied and tested both the approaches (post-processing and force-matching) to a problem where a portion of the boundary is assumed to be traction free and force data is measured on some other portion. Numerical tests have verified our claims and the benefit of working the log of the shear modulus. In addition, we have extended these approaches to the case where no surface on the specimen is assumed to be traction-free.

In summary the methods described in this paper provide two alternate approaches for including force data in elasticity imaging that lead to quantitative estimates of the shear modulus. Similar extensions to other elastic properties will be considered in the future.