Abstract
Heavy-tailed high-dimensional data are commonly encountered in various scientific fields and pose great challenges to modern statistical analysis. A natural procedure to address this problem is to use penalized quantile regression with weighted L1-penalty, called weighted robust Lasso (WR-Lasso), in which weights are introduced to ameliorate the bias problem induced by the L1-penalty. In the ultra-high dimensional setting, where the dimensionality can grow exponentially with the sample size, we investigate the model selection oracle property and establish the asymptotic normality of the WR-Lasso. We show that only mild conditions on the model error distribution are needed. Our theoretical results also reveal that adaptive choice of the weight vector is essential for the WR-Lasso to enjoy these nice asymptotic properties. To make the WR-Lasso practically feasible, we propose a two-step procedure, called adaptive robust Lasso (AR-Lasso), in which the weight vector in the second step is constructed based on the L1-penalized quantile regression estimate from the first step. This two-step procedure is justified theoretically to possess the oracle property and the asymptotic normality. Numerical studies demonstrate the favorable finite-sample performance of the AR-Lasso.
Keywords and phrases: Adaptive weighted L1, High dimensions, Oracle properties, Robust regularization
1. Introduction
The advent of modern technology makes it easier to collect massive, large-scale data sets. A common feature of these data sets is that the number of covariates greatly exceeds the number of observations, a regime opposite to conventional statistical settings. For example, portfolio allocation with hundreds of stocks in finance involves a covariance matrix of about tens of thousands of parameters, but the sample sizes are often only in the order of hundreds (e.g., daily data over a year period (Fan et al., 2008)). Genome-wide association studies in biology involve hundreds of thousands of single-nucleotide polymorphisms (SNPs), but the available sample size is usually in hundreds too. Data-sets with large number of variables but relatively small sample size pose great unprecedented challenges, and opportunities, for statistical analysis.
Regularization methods have been widely used for high-dimensional variable selection (Bickel and Li, 2006; Bickel et al., 2009; Efron et al., 2007; Fan and Li, 2001; Lv and Fan, 2009; Tibshirani, 1996; Zhang, 2010; Zou, 2006). Yet, most existing methods such as penalized least-squares or penalized likelihood (Fan and Lv, 2011) are designed for light-tailed distributions. Zhao and Yu (2006) established the irrepresentability conditions for the model selection consistency of the Lasso estimator. Fan and Li (2001) studied the oracle properties of nonconcave penalized likelihood estimators for fixed dimensionality. Lv and Fan (2009) investigated the penalized least-squares estimator with folded-concave penalty functions in the ultra-high dimensional setting and established a nonasymptotic weak oracle property. Fan and Lv (2008) proposed and investigated the sure independence screening method in the setting of light-tailed distributions. The robustness of the aforementioned methods have not yet been thoroughly studied and well understood.
Robust regularization methods such as the least absolute deviation (LAD) regression and quantile regression have been used for variable selection in the case of fixed dimensionality. See, for example, Li and Zhu (2008); Wang, Li and Jiang (2007); Wu and Liu (2009); Zou and Yuan (2008). The penalized composite likelihood method was proposed in Bradic et al. (2011) for robust estimation in ultra-high dimensions with focus on the efficiency of the method. They still assumed sub-Gaussian tails. Belloni and Chernozhukov (2011) studied the L1-penalized quantile regression in high-dimensional sparse models where the dimensionality could be larger than the sample size. We refer to their method as robust Lasso (R-Lasso). They showed that the R-Lasso estimate is consistent at the near-oracle rate, and gave conditions under which the selected model includes the true model, and derived bounds on the size of the selected model, uniformly in a compact set of quantile indices. Wang (2012) studied the L1-penalized LAD regression and showed that the estimate achieves near oracle risk performance with a nearly universal penalty parameter and established also a sure screening property for such an estimator. van de Geer and Müller (2012) obtained bounds on the prediction error of a large class of L1 penalized estimators, including quantile regression. Wang et al. (2012) considered the nonconvex penalized quantile regression in the ultra-high dimensional setting and showed that the oracle estimate belongs to the set of local minima of the nonconvex penalized quantile regression, under mild assumptions on the error distribution.
In this paper, we introduce the penalized quantile regression with the weighted L1-penalty (WR-Lasso) for robust regularization, as in Bradic et al. (2011). The weights are introduced to reduce the bias problem induced by the L1-penalty. The exibility of the choice of the weights provides exibility in shrinkage estimation of the regression coefficient. WR-Lasso shares a similar spirit to the folded-concave penalized quantile-regression (Wang et al., 2012; Zou and Li, 2008), but avoids the nonconvex optimization problem. We establish conditions on the error distribution in order for the WR-Lasso to successfully recover the true underlying sparse model with asymptotic probability one. It turns out that the required condition is much weaker than the sub-Gaussian assumption in Bradic et al. (2011). The only conditions we impose is that the density function of error has Lipschitz property in a neighborhood around 0. This includes a large class of heavy-tailed distributions such as the stable distributions, including the Cauchy distribution. It also covers the double exponential distribution whose density function is nondifferentiable at the origin.
Unfortunately, because of the penalized nature of the estimator, WR-Lasso estimate has a bias. In order to reduce the bias, the weights in WR-Lasso need to be chosen adaptively according to the magnitudes of the unknown true regression coefficients, which makes the bias reduction infeasible for practical applications.
To make the bias reduction feasible, we introduce the adaptive robust Lasso (AR-Lasso). The AR-Lasso first runs R-Lasso to obtain an initial estimate, and then computes the weight vector of the weighted L1-penalty according to a decreasing function of the magnitude of the initial estimate. After that, AR-Lasso runs WR-Lasso with the computed weights. We formally establish the model selection oracle property of AR-Lasso in the context of Fan and Li (2001) with no assumptions made on the tail distribution of the model error. In particular, the asymptotic normality of the AR-Lasso is formally established.
This paper is organized as follows. First, we introduce our robust estimators in Section 2. Then, to demonstrate the advantages of our estimator, we show in Section 3 with a simple example that Lasso behaves sub-optimally when noise has heavy tails. In Section 4.1, we study the performance of the oracle-assisted regularization estimator. Then in Section 4.2, we show that when the weights are adaptively chosen, WR-Lasso has the model selection oracle property, and performs as well as the oracle-assisted regularization estimate. In Section 4.3, we prove the asymptotic normality of our proposed estimator. The feasible estimator, AR-Lasso, is investigated in Section 5. Section 6 presents the results of the simulation studies. Finally, in Section 7 we present the proofs of the main theorems. Additional proofs, as well as the results of a genome-wide association study, are provided in the supplementary Appendix (Fan et al., 2013).
2. Adaptive Robust Lasso
Consider the linear regression model
| (2.1) |
where y is an n-dimensional response vector, X = (x1, …, xn)T = (x̃1, ···, x̃p) is an n × p fixed design matrix, β = (β1,…, βp)T is a p-dimensional regression coefficient vector, and ε = (ε1, …, εn)T is an n-dimensional error vector whose components are independently distributed and satisfy P(εi ≤ 0) = τ for some known constant τ ∈ (0, 1). Under this model, is the conditional τth-quantile of yi given xi. We impose no conditions on the heaviness of the tail probability or the homoscedasticity of εi. We consider a challenging setting in which log p = o(nb) with some constant b > 0. To ensure the model identifiability and to enhance the model fitting accuracy and interpretability, the true regression coefficient vector β* is commonly imposed to be sparse with only a small proportion of nonzeros (Fan and Li, 2001; Tibshirani, 1996). Denoting the number of nonzero elements of the true regression coefficients by sn, we allow sn to slowly diverge with the sample size n and assume that sn = o(n). To ease the presentation, we suppress the dependence of sn on n whenever there is no confusion. Without loss of generality, we write , i.e. only the first s entries are non-vanishing. The true model is denoted by
and its complement, , represents the set of noise variables.
We consider a fixed design matrix in this paper and denote by S = (S1, ···, Sn)T = (x̃1, ···, x̃s) the submatrix of X corresponding to the covariates whose coefficients are non-vanishing. These variables will be referred to as the signal covariates and the rest will be called noise covariates. The set of columns that correspond to the noise covariates is denoted by Q = (Q1, ···, Qn)T = (x̃s+1, ···, x̃p). We standardize each column of X to have L2-norm .
To recover the true model and estimate β*, we consider the following regularization problem
| (2.2) |
where ρτ (u) = u(τ − 1{u ≤ 0}) is the quantile loss function, and pλn(·) is a nonnegative penalty function on [0, ∞) with a regularization parameter λn ≥ 0. The use of quantile loss function in (2.2) is to overcome the difficulty of heavy tails of the error distribution. Since P(ε ≤ 0) = τ, (2.2) can be interpreted as the sparse estimation of the conditional τth quantile. Regarding the choice of pλn(·), it was demonstrated in Lv and Fan (2009) and Fan and Lv (2011) that folded-concave penalties are more advantageous for variable selection in high dimensions than the convex ones such as the L1-penalty. It is, however, computationally more challenging to minimize the objective function in (2.2) when pλ(·) is folded-concave. Noting that with a good initial estimate of the true coefficient vector, we have
Thus, instead of (2.2) we consider the following weighted L1-regularized quantile regression
| (2.3) |
where d = (d1, ···, dp)T is the vector of non-negative weights, and ∘ is the Hadamard product, i.e., the componentwise product of two vectors. This motivates us to define the weighted robust Lasso (WR-Lasso) estimate as the global minimizer of the convex function Ln(β) for a given non-stochastic weight vector:
| (2.4) |
The uniqueness of the global minimizer is easily guaranteed by adding a negligible L2-regularization in implementation. In particular, when dj = 1 for all j, the method will be referred to as robust Lasso (R-Lasso).
The adaptive robust Lasso (AR-Lasso) refers specifically to the two-stage procedure in which the stochastic weights for j = 1, ···, p are used in the second step for WR-Lasso and are constructed using a concave penalty pλn(·) and the initial estimates, , from the first step. In practice, we recommend using R-Lasso as the initial estimate and then using SCAD to compute the weights in AR-Lasso. The asymptotic result of this specific AR-Lasso is summarized in Corollary 1 in Section 5 for the ultra-high dimensional robust regression problem. This is a main contribution of the paper.
3. Suboptimality of Lasso
In this section, we use a specific example to illustrate that, in the case of heavy-tailed error distribution, Lasso fails at model selection unless the non-zero coefficients, , have a very large magnitude. We assume that the errors ε1, ···, εn have the identical symmetric stable distribution and the characteristic function of ε1 is given by
where α ∈ (0, 2). By Nolan (2012), E|ε1|p is finite for 0 < p < α, and E|ε1|p = ∞ for p ≥ α. Furthermore as z → ∞,
where is a constant depending only on α, and we use the notation ~ to denote that two terms are equivalent up to some constant. Moreover, for any constant vector a = (a1, ···, an)T, the linear combination aTε has the following tail behavior
| (3.1) |
with ||·||α denoting the Lα-norm of a vector.
To demonstrate the suboptimality of Lasso, we consider a simple case in which the design matrix satisfies the conditions that STQ = 0, , the columns of Q satisfy |supp(x̃j)| = mn = O(n1/2) and supp(x̃k) ∩ supp(x̃j) = Ø for any k ≠ j and k, j ∈ {s + 1, ···, p}. Here, mn is a positive integer measuring the sparsity level of the columns of Q. We assume that there are only fixed number of true variables, i.e., s is finite, and that maxij |xij| = O(n1/4). Thus, it is easy to see that p = O(n1/2). In addition, we assume further that all nonzero regression coefficients are the same and .
We first consider R-Lasso, which is the global minimizer of (2.4). We will later see in Theorem 2 that by choosing the tuning parameter
R-Lasso can recover the true support
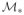 = {1, ···, s} with probability tending to 1. Moreover, the signs of the true regression coefficients can also be recovered with asymptotic probability one as long as the following condition on signal strength is satisfied
= {1, ···, s} with probability tending to 1. Moreover, the signs of the true regression coefficients can also be recovered with asymptotic probability one as long as the following condition on signal strength is satisfied
| (3.2) |
Now, consider Lasso, which minimizes
| (3.3) |
We will see that for (3.3) to recover the true model and the correct signs of coefficients, we need a much stronger signal level than that is given in (3.2). By results in optimization theory, the Karush–Kuhn–Tucker (KKT) conditions guaranteeing the necessary and sufficient conditions for β̃ with
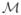 = supp(β̃) being a minimizer to (3.3) are
= supp(β̃) being a minimizer to (3.3) are
where
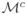 is the complement of
is the complement of
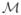 ,
,
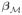 is the subvector formed by entries of β with indices in
is the subvector formed by entries of β with indices in
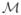 , and
, and
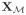 and
and
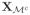 are the submatrices formed by columns of X with indices in
are the submatrices formed by columns of X with indices in
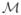 and
and
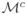 , respectively. It is easy to see from the above two conditions that for Lasso to enjoy the sign consistency, sgn(β̃) = sgn(β*) with asymptotic probability one, we must have these two conditions satisfied with
, respectively. It is easy to see from the above two conditions that for Lasso to enjoy the sign consistency, sgn(β̃) = sgn(β*) with asymptotic probability one, we must have these two conditions satisfied with
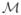 =
=
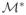 with probability tending to 1. Since we have assumed that QTS = 0 and n−1STS = I, the above sufficient and necessary conditions can also be written as
with probability tending to 1. Since we have assumed that QTS = 0 and n−1STS = I, the above sufficient and necessary conditions can also be written as
| (3.4) |
| (3.5) |
Conditions (3.4) and (3.5) are hard for Lasso to hold simultaneously. The following proposition summarizes the necessary condition, whose proof is given in the supplementary material (Fan et al., 2013).
Proposition 1
In the above model, with probability at least 1 − e−c̃0, where c̃0 is some positive constant, Lasso does not have sign consistency, unless the following signal condition is satisfied
| (3.6) |
Comparing this with (3.2), it is easy to see that even in this simple case, Lasso needs much stronger signal levels than R-Lasso in order to have a sign consistency in the presence of a heavy-tailed distribution.
4. Model Selection Oracle Property
In this section, we establish the model selection oracle property of WR-Lasso. The study enables us to see the bias due to penalization, and that an adaptive weighting scheme is needed in order to eliminate such a bias. We need the following condition on the distribution of noise.
Condition 1
There exist universal constants c1 > 0 and c2 > 0 such that for any u satisfying |u| ≤ c1, fi(u)’s are uniformly bounded away from 0 and ∞ and
where fi(u) and Fi(u) are the density function and distribution function of the error εi, respectively.
Condition 1 implies basically that each fi(u) is Lipschitz around the origin. Commonly used distributions such as the double-exponential distribution and stable distributions including the Cauchy distribution all satisfy this condition.
Denote by H = diag{f1(0), ···, fn(0)}. The next condition is on the sub-matrix of X that corresponds to signal covariates and the magnitude of the entries of X.
Condition 2
The eigenvalues of are bounded from below and above by some positive constants c0 and 1/c0, respectively. Furthermore,
Although Condition 2 is on the fixed design matrix, we note that the above condition on κn is satisfied with asymptotic probability one when the design matrix is generated from some distributions. For instance, if the entries of X are independent copies from a sub-exponential distribution, the bound on κn is satisfied with asymptotic probability one as long as ; if the components are generated from sub-Gaussian distribution, then the condition on κn is satisfied with probability tending to one when .
4.1. Oracle Regularized Estimator
To evaluate our newly proposed method, we first study how well one can do with the assistance of the oracle information on the locations of signal covariates. Then, we use this to establish the asymptotic property of our estimator without the oracle assistance. Denote by the oracle regularized estimator (ORE) with and 0 being the vector of all zeros, which minimizes Ln(β) over the space { }. The next theorem shows that ORE is consistent, and estimates the correct sign of the true coefficient vector with probability tending to one. We use d0 to denote the first s elements of d.
Theorem 1
Let with C1 > 0 a constant. If Conditions 1 and 2 hold and , then there exists some constant c > 0 such that
| (4.1) |
If in addition , then with probability at least 1−n−cs,
where the above equation should be understood componentwisely.
As shown in Theorem 1, the consistency rate of in terms of the vector L2-norm is given by γn. The first component of γn, , is the oracle rate within a factor of log n, and the second component C1λn||d0||2 reflects the bias due to penalization. If no prior information is available, one may choose equal weights d0 = (1, 1, ···, 1)T, which corresponds to R-Lasso. Thus for R-Lasso, with probability at least 1 − n−cs, it holds that
| (4.2) |
4.2. WR-Lasso
In this section, we show that even without the oracle information, WR-Lasso enjoys the same asymptotic property as in Theorem 1 when the weight vector is appropriately chosen. Since the regularized estimator β̂ in (2.4) depends on the full design matrix X, we need to impose the following conditions on the design matrix to control the correlation of columns in Q and S.
Condition 3
With γn defined in Theorem 1, it holds that
where ||A||2,∞ = supx≠0 ||Ax||∞/||x||2 for a matrix A and vector x, and . Furthermore, log(p) = o(nb) for some constant b ∈ (0, 1).
To understand the implications of Condition 3, we consider the case of f1(0) = ⋯ = fn(0) ≡ f(0). In the special case of QT S = 0, Condition 3 is satisfied automatically. In the case of equal correlation, that is, n−1XTX having off-diagonal elements all equal to ρ, the above Condition 3 reduces to
This puts an upper bound on the correlation coefficient ρ for such a dense matrix.
It is well known that for Gaussian errors, the optimal choice of regularization parameter λn has the order (Bickel et al., 2009). The distribution of the model noise with heavy tails demands a larger choice of λn to filter the noise for R-lasso. When , γn given in (4.2) is in the order of . In this case, Condition 3 reduces to
| (4.3) |
For WR-Lasso, if the weights are chosen such that and ||d1||∞ = O(1), then γn is in the order of , and correspondingly, Condition 3 becomes
This is a more relaxed condition than (4.3), since with heavy-tailed errors, the optimal γn should be larger than . In other words, WR-Lasso not only reduces the bias of the estimate, but also allows for stronger correlations among the signal and noise covariates. However, the above choice of weights depends on unknown locations of signals. A data-driven choice will be given in Section 5, in which the resulting AR-Lasso estimator will be studied.
The following theorem shows the model selection oracle property of the WR-Lasso estimator.
Theorem 2
Suppose Conditions 1 – 3 hold. In addition, assume that minj≥s+1 dj > c3 with some constant c3 > 0,
| (4.4) |
and , where κn is defined in Condition 2, γn is defined in Theorem 1, and c is some positive constant. Then, with probability at least 1− O(n−cs), there exists a global minimizer of Ln(β) which satisfies
β̂2 = 0;
.
Theorem 2 shows that the WR-Lasso estimator enjoys the same property as ORE with probability tending to one. However, we impose non-adaptive assumptions on the weight vector . For noise covariates, we assume minj>s dj > c3, which implies that each coordinate needs to be penalized. For the signal covariates, we impose (4.4), which requires ||d0||2 to be small.
When studying the nonconvex penalized quantile regression, Wang et al. (2012) assumed that κn is bounded and the density functions of εi’s are uniformly bounded away from 0 and ∞ in a small neighborhood of 0. Their assumption on the error distribution is weaker than our Condition 1. We remark that the difference is because we have weaker conditions on κn and the penalty function (See Condition 2 and (4.4)). In fact, our Condition 1 can be weakened to the same condition as that in Wang et al. (2012) at the cost of imposing stronger assumptions on κn and the weight vector d.
Belloni and Chernozhukov (2011) and Wang (2012) imposed the restricted eigenvalue assumption of the design matrix and studied the L1-penalized quantile regression and LAD regression, respectively. We impose different conditions on the design matrix and allow flexible shrinkage by choosing d. In addition, our Theorem 2 provides a stronger result than consistency; we establish model selection oracle property of the estimator.
4.3. Asymptotic Normality
We now present the asymptotic normality of our estimator. Define Vn = (STHS)−1/2 and Zn = (Zn1, ⋯, Znn)T = SVn with Znj ∈ Rs for j = 1, ⋯, n.
Theorem 3
Assume the conditions of Theorem 2 hold, the first and second order derivatives and are uniformly bounded in a small neighborhood of 0 for all i = 1, ⋯, n, and that , maxi ||H1/2Zni||2 = o(s−7/2(log s)−1), and . Then, with probability tending to 1 there exists a global minimizer of Ln(β) such that β̂2 = 0. Moreover,
where c is an arbitrary s-dimensional vector satisfying cTc = 1, and d̃0 is an s-dimensional vector with the jth element .
The proof of Theorem 3 is an extension of the proof on the asymptotic normality theorem for the LAD estimator in Pollard (1990), in which the theorem is proved for fixed dimensionality. The idea is to approximate Ln(β1, 0) in (2.4) by a sequence of quadratic functions, whose minimizers converge to normal distribution. Since Ln(β1, 0) and the quadratic approximation are close, their minimizers are also close, which results in the asymptotic normality in Theorem 3.
Theorem 3 assumes that maxi ||H1/2Zni||2 = o(s−7/2(log s)−1). Since by definition , it is seen that the condition implies s = o(n1/8). This assumption is made to guarantee that the quadratic approximation is close enough to Ln(β1, 0). When s is finite, the condition becomes maxi ||Zni||2 = o(1), as in Pollard (1990). Another important assumption is , which is imposed to make sure that the bias 2−1nλncTVnd0 caused by the penalty term does not diverge. For instance, using R-Lasso will create a non-diminishing bias and thus cannot be guaranteed to have asymptotic normality.
Note that we do not assume a parametric form of the error distribution. Thus, our oracle estimator is in fact a semiparametric estimator with the error density as the nuisance parameter. Heuristically speaking, Theorem 3 shows that the asymptotic variance of is . Since Vn = (ST HS)−1/2 and Zn = SVn, if the model errors εi are i.i.d. with density function fε(·), then this asymptotic variance reduces to . In the random design case where the true covariate vectors are i.i.d. observations, n−1STS converges to as n → ∞, and the asymptotic variance reduces to . This is the semiparametric efficiency bound derived by Newey and Powell (1990) for random designs. In fact, if we assume that (xi, yi) are i.i.d., then the conditions of Theorem 3 can hold with asymptotic probability one. Using similar arguments, it can be formally shown that is asymptotically normal with covariance matrix equal to the aforementioned semiparametric efficiency bound. Hence, our oracle estimator is semiparametric efficient.
5. Properties of the Adaptive Robust Lasso
In previous sections, we have seen that the choice of the weight vector d plays a pivotal role for the WR-Lasso estimate to enjoy the model selection oracle property and asymptotic normality. In fact, conditions in Theorem 2 require that minj≥s+1 dj > c3 and that ||d0||2 does not diverge too fast. Theorem 3 imposes an even more stringent condition, , on the weight vector d0. For R-Lasso, and these conditions become very restrictive. For example, the condition in Theorem 3 becomes λn = O(n−1/2), which is too low for a thresholding level even for Gaussian errors. Hence, an adaptive choice of weights is needed to ensure that those conditions are satisfied. To this end, we propose a two-step procedure.
In the first step, we use R-Lasso, which gives the estimate β̂ini. As has been shown in Belloni and Chernozhukov (2011) and Wang (2012), R-Lasso is consistent at a near-oracle rate
and selects the true model
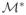 as a submodel (in other words, R-Lasso has the sure screening property using the terminology of Fan and Lv (2008)) with asymptotic probability one, namely,
as a submodel (in other words, R-Lasso has the sure screening property using the terminology of Fan and Lv (2008)) with asymptotic probability one, namely,
We remark that our Theorem 2 also ensures the consistency of R-Lasso. Compared to Belloni and Chernozhukov (2011), Theorem 2 presents stronger results but also needs more restrictive conditions for R-Lasso. As will be shown in latter theorems, only the consistency of R-Lasso is needed in the study of AR-Lasso, so we quote the results and conditions on R-Lasso in Belloni and Chernozhukov (2011) with the mind of imposing weaker conditions.
In the second step, we set d̂ = (d̂1, ···, d̂p)T with where pλn(|·|) is a folded concave penalty function, and then solve the regularization problem (2.4) with a newly computed weight vector. Thus, vector d̂0 is expected to be close to the vector under L2-norm. If a folded concave penalty such as SCAD is used, then will be close, or even equal, to zero for 1 ≤ j ≤ s and thus the magnitude of ||d̂0||2 is negligible.
Now, we formally establish the asymptotic properties of AR-Lasso. We first present a more general result and then highlight our recommended procedure, which uses R-Lasso as the initial estimate and then uses SCAD to compute the stochastic weights, in Corollary 1. Denote by with . Using the weight vector d̂, AR-Lasso minimizes the following objective function
| (5.1) |
We also need the following conditions to show the model selection oracle property of the two-step procedure.
Condition 4
With asymptotic probability one, the initial estimate satisfies with some constant C2 > 0.
As discussed above, if R-Lasso is used to obtain the initial estimate, it satisfies the above condition. Our second condition is on the penalty function.
Condition 5
is non-increasing in t ∈ (0, ∞) and is Lipschitz with constant c5, that is,
for any β1, β2 ∈ R. Moreover, for large enough n, where C2 is defined in Condition 4.
For the SCAD (Fan and Li, 2001) penalty, is given by
| (5.2) |
for a given constant a > 2, and it can be easily verified that Condition 5 holds if .
Theorem 4
Assume conditions of Theorem 2 hold with d = d* and γn = an, where
with some constant C3 > 0, and . Then, under Conditions 4 and 5, with probability tending to one, there exists a global minimizer of (5.1) such that β̂2 = 0 and .
The results in Theorem 4 are analogous to those in Theorem 2. The extra term in the convergence rate an, compared to the convergence rate γn in Theorem 2, is caused by the bias of the initial estimate β̂ini. Since the regularization parameter λn goes to zero, the bias of AR-Lasso is much smaller than that of the initial estimator β̂ini. Moreover, the AR-Lasso β̂ possesses the model selection oracle property.
Now we present the asymptotic normality of the AR-Lasso estimate.
Condition 6
The smallest signal satisfies . Moreover, it holds that for any .
The above condition on the penalty function is satisfied when the SCAD penalty is used and where a is the parameter in the SCAD penalty (5.2).
Theorem 5
Assume conditions of Theorem 3 hold with d = d* and γn = an, where an is defined in Theorem 4. Then, under Conditions 4 – 6, with asymptotic probability one, there exists a global minimizer β̂ of (5.1) having the same asymptotic properties as those in Theorem 3.
With the SCAD penalty, conditions in Theorems 4 and 5 can be simplified and AR-Lasso still enjoys the same asymptotic properties, as presented in the following corollary.
Corollary 1
Assume with a the parameter in the SCAD penalty, and κn = o(n1/4s−1/2(log n)−3/2(log p)1/2). Further assume that with C4 some positive constant. Then, under Conditions 1 and 2, with asymptotic probability one, there exists a global minimizer of L̂n(β) such that
If in addition, maxi ||H1/2Zni||2 = o(s−7/2(log s)−1), then we also have
where c is an arbitrary s-dimensional vector satisfying cTc = 1.
Corollary 1 provides sufficient conditions for ensuring the variable selection sign consistency of AR-Lasso. These conditions require that R-Lasso in the initial step has the sure screening property. We remark that in implementation, AR-Lasso is able to select the variables missed by R-Lasso, as demonstrated in our numerical studies in the next section. The theoretical comparison of the variable selection results of R-Lasso and AR-Lasso would be an interesting topic for future study. One set of (p, n, s, κn) satisfying conditions in Corollary 1 is log p = O(nb1), s = o(n(1−b1)/2) and κn = o(nb1/4(log n)−3/2) with b1 ∈ (0, 1/2) some constant. Corollary 1 gives one specific choice of λn, not necessarily the smallest λn, which makes our procedure work. In fact, the condition on λn can be weakened to . Currently, we use the L2-norm to bound this L∞-norm, which is too crude. If one can establish for an initial estimator , then the choice of λn can be as small as , the same order as that used in Wang (2012). On the other hand, since we are using AR-Lasso, the choice of λn is not as sensitive as R-Lasso.
6. Numerical Studies
In this section we evaluate the finite sample property of our proposed estimator with synthetic data. Please see the supplementary material (Fan et al., 2013) for a real life data set analysis, where we provide results of an eQTL study on the CHRNA6 gene.
To assess the performance of the proposed estimator and compare it with other methods, we simulated data from the high-dimensional linear regression model
where the data had n = 100 observations and the number of parameters was chosen as p = 400. We fixed the true regression coefficient vector as
For the distribution of the noise, ε, we considered six symmetric distributions: Normal with variance 2 (
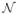 (0, 2)), a scale mixture of Normals for which
with probability 0.9 and
otherwise (MN1), a different scale mixture model where
and σi ~ Unif(1, 5) (MN2), Laplace, Student’s t with degrees of freedom 4 with doubled variance (
) and Cauchy. We take τ = 0.5, corresponding to L1-regression, throughout the simulation. Correlation of the covariates, Σx were either chosen to be identity (i.e. Σx = Ip) or they were generated from an AR(1) model with correlation 0.5, that is Σx(i,j) = 0.5|i−j|.
(0, 2)), a scale mixture of Normals for which
with probability 0.9 and
otherwise (MN1), a different scale mixture model where
and σi ~ Unif(1, 5) (MN2), Laplace, Student’s t with degrees of freedom 4 with doubled variance (
) and Cauchy. We take τ = 0.5, corresponding to L1-regression, throughout the simulation. Correlation of the covariates, Σx were either chosen to be identity (i.e. Σx = Ip) or they were generated from an AR(1) model with correlation 0.5, that is Σx(i,j) = 0.5|i−j|.
We implemented five methods for each setting:
L2-Oracle, which is the least squares estimator based on the signal covariates.
Lasso, the penalized least-squares estimator with L1-penalty as in Tibshirani (1996).
SCAD, the penalized least-squares estimator with SCAD penalty as in Fan and Li (2001).
R-Lasso, the robust Lasso defined as the minimizer of (2.4) with d = 1.
AR-Lasso, which is the adaptive robust lasso whose adaptive weights on the penalty function were computed based on the SCAD penalty using the R-Lasso estimate as an initial value.
The tuning parameter, λn, was chosen optimally based on 100 validation data-sets. For each of these data-sets, we ran a grid search to find the best λn (with the lowest L2 error for β) for the particular setting. This optimal λn was recorded for each of the 100 validation data-sets. The median of these 100 optimal λn were used in the simulation studies. We preferred this procedure over cross-validation because of the instability of the L2 loss under heavy tails.
The following four performance measures were calculated:
L2 loss, which is defined as ||β* − β̂||2.
L1 loss, which is defined as ||β* − β̂||1.
Number of noise covariates that are included in the model, that is the number of false positives (FP).
Number of signal covariates that are not included, i.e. the number of false negatives (FN).
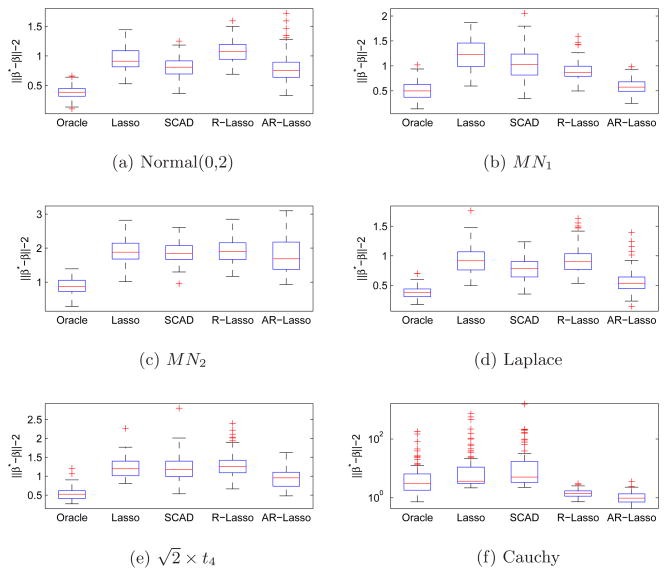
For each setting, we present the average of the performance measure based on 100 simulations. The results are depicted in Tables 1 and 2. A boxplot of the L2 losses under different noise settings is also given in Figure 1 (the L2 loss boxplot for the independent covariate setting is similar and omitted). For the results in Tables 1 and 2, one should compare the performance between Lasso and R-Lasso and that between SCAD and AR-Lasso. This comparison reflects the effectiveness of L1-regression in dealing with heavy-tail distributions. Furthermore, comparing Lasso with SCAD, and R-Lasso with AR-Lasso, shows the effectiveness of using adaptive weights in the penalty function.
Table 1.
Simulation Results with Independent Covariates
| L2 Oracle | Lasso | SCAD | R-Lasso | AR-Lasso | |||
|---|---|---|---|---|---|---|---|
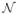 (0, 2) (0, 2) |
L2 loss | 0.833 | 4.114 | 3.412 | 5.342 | 2.662 | |
| L1 loss | 0.380 | 1.047 | 0.819 | 1.169 | 0.785 | ||
| FP, FN | - | 27.00, 0.49 | 29.60, 0.51 | 36.81, 0.62 | 17.27, 0.70 | ||
|
| |||||||
| MN1 | L2 loss | 0.977 | 5.232 | 4.736 | 4.525 | 2.039 | |
| L1 loss | 0.446 | 1.304 | 1.113 | 1.028 | 0.598 | ||
| FP, FN | - | 26.80, 0.73 | 29.29, 0.68 | 34.26, 0.51 | 16.76, 0.51 | ||
|
| |||||||
| MN2 | L2 loss | 1.886 | 7.563 | 7.583 | 8.121 | 5.647 | |
| L1 loss | 0.861 | 2.085 | 2.007 | 2.083 | 1.845 | ||
| FP, FN | - | 20.39, 2.28 | 23.25, 2.19 | 24.64, 2.29 | 11.97, 2.57 | ||
|
| |||||||
| Laplace | L2 loss | 0.795 | 4.056 | 3.395 | 4.610 | 2.025 | |
| L1 loss | 0.366 | 1.016 | 0.799 | 1.039 | 0.573 | ||
| FP, FN | - | 26.87, 0.62 | 29.98, 0.49 | 34.76, 0.48 | 18.81, 0.40 | ||
|
| |||||||
|
|
L2 loss | 1.087 | 5.303 | 5.859 | 6.185 | 3.266 | |
| L1 loss | 0.502 | 1.378 | 1.256 | 1.403 | 0.951 | ||
| FP, FN | - | 24.61, 0.85 | 36.95, 0.76 | 33.84, 0.84 | 18.53, 0.82 | ||
|
| |||||||
| Cauchy | L2 loss | 37.451 | 211.699 | 266.088 | 6.647 | 3.587 | |
| L1 loss | 17.136 | 30.052 | 40.041 | 1.646 | 1.081 | ||
| FP, FN | - | 27.39, 5.78 | 34.32, 5.94 | 27.33, 1.41 | 17.28, 1.10 | ||
Table 2.
Simulation Results with Correlated Covariates
| L2 Oracle | Lasso | SCAD | R-Lasso | AR-Lasso | |||
|---|---|---|---|---|---|---|---|
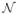 (0, 2) (0, 2) |
L2 loss | 0.836 | 3.440 | 3.003 | 4.185 | 2.580 | |
| L1 loss | 0.375 | 0.943 | 0.803 | 1.079 | 0.806 | ||
| FP, FN | - | 20.62, 0.59 | 23.13, 0.56 | 22.72, 0.77 | 14.49, 0.74 | ||
|
| |||||||
| MN1 | L2 loss | 1.081 | 4.415 | 3.589 | 3.652 | 1.829 | |
| L1 loss | 0.495 | 1.211 | 1.055 | 0.901 | 0.593 | ||
| FP, FN | - | 18.66, 0.77 | 15.71, 0.75 | 26.65, 0.60 | 13.29, 0.51 | ||
|
| |||||||
| MN2 | L2 loss | 1.858 | 6.427 | 6.249 | 6.882 | 4.890 | |
| L1 loss | 0.844 | 1.899 | 1.876 | 1.916 | 1.785 | ||
| FP, FN | - | 15.16, 2.08 | 14.77, 1.96 | 18.22, 1.91 | 7.86, 2.71 | ||
|
| |||||||
| Laplace | L2 loss | 0.803 | 3.341 | 2.909 | 3.606 | 1.785 | |
| L1 loss | 0.371 | 0.931 | 0.781 | 0.927 | 0.573 | ||
| FP, FN | - | 19.32, 0.62 | 21.60, 0.38 | 24.44, 0.46 | 12.90, 0.55 | ||
|
| |||||||
|
|
L2 loss | 1.122 | 4.474 | 4.259 | 4.980 | 2.855 | |
| L1 loss | 0.518 | 1.222 | 1.201 | 1.299 | 0.946 | ||
| FP, FN | - | 20.00, 0.76 | 18.49, 0.91 | 23.56, 0.79 | 13.40, 1.05 | ||
|
| |||||||
| Cauchy | L2 loss | 31.095 | 217.395 | 243.141 | 5.388 | 3.286 | |
| L1 loss | 13.978 | 31.361 | 36.624 | 1.461 | 1.074 | ||
| FP, FN | - | 25.59, 5.48 | 32.01, 5.43 | 20.80, 1.16 | 12.45, 1.17 | ||
Fig. 1.
Boxplots for L2 Loss with Correlated Covariates
Our simulation results reveal the following facts. The quantile based estimators were more robust in dealing with the outliers. For example, for the first mixture model (MN1) and Cauchy, R-Lasso outperformed Lasso, and AR-Lasso outperformed SCAD in all of the four metrics, and significantly so when the error distribution is the Cauchy distribution. On the other hand, for the light-tail distributions such as the normal distribution, the efficiency loss was limited. When the tails get heavier, for instance for the Laplace distribution, quantile based methods started to outperform the least-squares based approaches, more so when the tails got heavier.
The effectiveness of weights in AR-Lasso is self-evident. SCAD outperformed Lasso and AR-Lasso outperformed R-Lasso in almost all of the settings. Furthermore, for all of the error settings AR-Lasso had significantly lower L2 and L1 loss as well as a smaller model size compared to other estimators.
It is seen that when the noise does not have heavy tails, that is for the normal and the Laplace distribution, all the estimators are comparable in terms of L1 loss. As expected, estimators that minimize squared loss worked better than R-Lasso and AR-Lasso estimators under Gaussian noise, but their performances deteriorated as the tails got heavier. In addition, in the two heteroscedastic settings, AR-Lasso had the best performance among others.
For Cauchy noise, least squares methods could only recover 1 or 2 of the true variables on average. On the other hand, L1-estimators (R-Lasso and AR-Lasso) had very few false negatives, and as evident from L2 loss values, these estimators only missed variables with smaller magnitudes.
In addition, AR-Lasso consistently selected a smaller set of variables than R-Lasso. For instance, for the setting with independent covariates, under the Laplace distribution, R-Lasso and AR-Lasso had on average 34.76 and 18.81 false positives, respectively. Also note that AR-Lasso consistently outperformed R-Lasso: It estimated β* (lower L1 and L2 losses), and the support of β* (lower averages for the number of false positives) more efficiently.
7. Proofs
In this section, we prove Theorems 1, 2 and 4 and provide the lemmas used in these proofs. The proofs of Theorems 3 and 5 and Proposition 1 are given in the supplementary Appendix (Fan et al., 2013).
We use techniques from empirical process theory to prove the theoretical results. Let . Then . For a given deterministic M > 0, define the set
Then, define the function
| (7.1) |
Lemma 1 in Section 7.4 gives the rate of convergence for Zn(M).
7.1. Proof of Theorem 1
We first show that for any with ,
| (7.2) |
for sufficiently large n, where c is the lower bound for fi(·) in the neighborhood of 0. The intuition follows from the fact that β* is the minimizer of the function Evn(β) and hence in Taylor’s expansion of E[vn(β) − vn(β*)] around β*, the first order derivative is zero at the point β = β*. The left-hand side of (7.2) will be controlled by Zn(M). This yields the L2-rate of convergence in Theorem 1.
To prove (7.2), we set
. Then, for β ∈
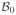 (M),
(M),
Thus if , by E1{εi ≤ 0} = τ, Fubini’s theorem, mean value theorem, and Condition 1 it is easy to derive that
| (7.3) |
where the o(1) is uniformly over all i = 1, ···, n. When , the same result can be obtained. Furthermore, by Condition 2,
This together with (7.3) and the definition of vn(β) proves (7.2).
The inequality (7.2) holds for any , yet may not be in the set. Thus, we let , where
which falls in the set
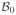 (M). Then, by the convexity and the definition of
,
(M). Then, by the convexity and the definition of
,
Using this and the triangle inequality we have
| (7.4) |
By the Cauchy-Schwarz inequality, the very last term is bounded by .
Define the event . Then by Lemma 1,
| (7.5) |
On the event
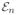 , by (7.4), we have
, by (7.4), we have
Taking
. By Condition 2 and the assumption
, it is easy to check that
. Combining these two results with (7.2), we obtain that on the event
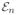 ,
,
which entails that
Note that
implies
. Thus, on the event
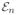 ,
,
The second result follows trivially.
7.2. Proof of Theorem 2
Since defined in Theorem 1 is a minimizer of Ln(β1, 0), it satisfies the KKT conditions. To prove that is a global minimizer of Ln(β) in the original Rp space, we only need to check the following condition
| (7.6) |
where for any n-vector u = (u1, ···, un)T with . Here, denotes the vector . Then the KKT conditions and the convexity of Ln(β) together ensure that β̂ is a global minimizer of L(β).
Define events
where γn is defined in Theorem 1 and
Then by Theorem 1 and Lemma 2 in Section 7.4, P(A1 ∩ A2) ≥1 − o(n−cs). Since β̂ ∈
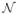 on the event A1, the inequality (7.6) holds on the event A1 ∩ A2. This completes the proof of Theorem 2.
on the event A1, the inequality (7.6) holds on the event A1 ∩ A2. This completes the proof of Theorem 2.
7.3. Proof of Theorem 4
The idea of the proof follows those used in the proof of Theorems 1 and 2. We first consider the minimizer of L̂n(β) in the subspace { }. Let , where with , ||v1||2 = C, and C > 0 is some large enough constant. By the assumptions in the theorem we have . Note that
| (7.7) |
where and with for any vector u = (u1, ···, un)T. By the results in the proof of Theorem 1, , and moreover, with probability at least 1 − n−cs,
Thus, by the triangle inequality,
| (7.8) |
The second term on the right side of (7.7) can be bounded as
| (7.9) |
By triangle inequality and Conditions 4 and 5, it holds that
| (7.10) |
Thus, combining (7.7)–(7.10) yields
Making ||v1||2 = C large enough, we obtain that with probability tending to one, L̂n(β*+ ãnv) − L̂n(β*) > 0. Then, it follows immediately that with asymptotic probability one, there exists a minimizer β̂1 of L̂n(β1, 0) such that with some constant C3 > 0.
It remains to prove that with asymptotic probability one,
| (7.11) |
Then by KKT conditions, is a global minimizer of L̂n(β).
Now we proceed to prove (7.11). Since for all j = s + 1, ···, p, we have that . Furthermore, by Condition 4, it holds that with asymptotic probability one. Then, it follows that
Therefore, by Condition 5 we conclude that
| (7.12) |
From the conditions of Theorem 2 with γn = an, it follows from Lemma 2 (inequality (7.20)) that, with probability at least 1 − o(p−c),
| (7.13) |
Combining (7.12)–(7.13) and by the triangle inequality, it holds that with asymptotic probability one,
Since the minimizer β̂1 satisfies with asymptotic probability one, the above inequality ensures that (7.11) holds with probability tending to one. This completes the proof.
7.4. Lemmas
This subsection contains Lemmas used in proofs of Theorems 1,2 and 4.
Lemma 1
Under Condition 2, for any t > 0, we have
| (7.14) |
Proof
Define ρ(s, y) = (y−s)(τ − 1{y− s ≤ 0}). Then, vn(β) in (7.1) can be rewritten as . Note that the following Lipschitz condition holds for ρ(·; yi)
| (7.15) |
Let W1, ···, Wn be a Rademacher sequence, independent of model errors ε1, ···, εn. The Lipschitz inequality (7.15) combined with the symmetrization theorem and Concentration inequality (see, for example, Theorems 14.3 and 14.4 in Büuhlmann and van de Geer (2011)) yields that
| (7.16) |
On the other hand, by the Cauchy-Schwarz inequality
By Jensen’s inequality and concavity of the square root function, E(X1/2) ≤ (EX)1/2 for any non-negative random variable X. Thus, these two inequalities ensure that the very right hand side of (7.16) can be further bounded by
| (7.17) |
Therefore, it follows from (7.16) and (7.17) that
| (7.18) |
Next since n−1STS has bounded eigenvalues, for any ,
Combining this with the Lipschitz inequality (7.15), (7.18), and applying Massart’s concentration theorem (see Theorem 14.2 in Bühlmann and van de Geer (2011)) yields that for any t > 0,
This proves the Lemma.
Lemma 2
Consider a ball in Rs around with some sequence γn → 0. Assume that minj>s dj > c3, , n1/2λn(log p)−1/2 → ∞, and . Then under Conditions 1–3, there exists some constant c > 0 such that
where .
Proof
For a fixed j ∈ {s + 1, ···, p} and , define
where is the i-th row of the design matrix. The key for the proof is to use the following decomposition
| (7.19) |
We will prove that with probability at least 1 − o(p−c),
| (7.20) |
| (7.21) |
| (7.22) |
Combining (7.19)–(7.22) with the assumption minj>s dj > c3 completes the proof of the Lemma.
Now we proceed to prove (7.20). Note that I1 can be rewritten as
| (7.23) |
By Condition 1,
where F(t) is the cumulative distribution function of εi, and . Thus, for any j > s,
This together with (7.23) and Cauchy-Schwartz inequality entails that
| (7.24) |
where H = diag{f1(0, ···, fn(0))}. We consider the two terms on the right hand side of (7.24) one by one. By Condition 3, the first term can be bounded as
| (7.25) |
By Condition 1, . This together with Condition 2 ensures that the second term of (7.24) can be bounded as
Since β ∈
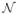 , it follows from the assumption
that
, it follows from the assumption
that
Plugging the above inequality and (7.25) into (7.24) completes the proof of (7.20).
Next we prove (7.21). By Hoeffding’s inequality, if with c is some positive constant, then
Thus, with probability at least 1 − O(p−c), (7.21) holds.
We now apply Corollary 14.4 in Bühlmann and van de Geer (2011) to prove (7.22). To this end, we need to check conditions of the Corollary. For each fixed j, define the functional space Γj = {γβ,j : β ∈
 }. First note that E[γβ,j(xi, yi)] = 0 for any γβ,j ∈ Γj. Second, since the
function is bounded, we have
}. First note that E[γβ,j(xi, yi)] = 0 for any γβ,j ∈ Γj. Second, since the
function is bounded, we have
Thus, .
Third, we will calculate the covering number of the functional space Γj, N(·, Γj, ||·||2). For any and , by Condition 1 and the mean value theorem,
| (7.26) |
where F(t) is the cumulative distribution function of εi, and a1i lies on the segment connecting and . Let κn = maxij |xij|. Since fi(u)’s are uniformly bounded, by (7.26),
| (7.27) |
where C > 0 is some generic constant. It is known (see, for example, Lemma 14.27 in Bühlmann and van de Geer (2011)) that the ball
 in Rs can be covered by (1 + 4γn/δ)s balls with radius δ. Since
can only take 3 different values {−1, 0, 1}, it follows from (7.27) that the covering number of Γj is
. Thus, by calculus, for any 0 ≤ k ≤ (log2
n)/2,
in Rs can be covered by (1 + 4γn/δ)s balls with radius δ. Since
can only take 3 different values {−1, 0, 1}, it follows from (7.27) that the covering number of Γj is
. Thus, by calculus, for any 0 ≤ k ≤ (log2
n)/2,
Hence, conditions of Corollary 14.4 in Bühlmann and van de Geer (2011) are checked and we obtain that for any t > 0,
Taking with C > 0 large enough constant we obtain that
Thus if , then with probability at least 1 − o(p−c), (7.22) holds. This completes the proof of the Lemma.
Supplementary Material
Acknowledgments
The authors sincerely thank the Editor, Associate Editor, and three referees for their constructive comments that led to substantial improvement of the paper.
References
- Belloni A, Chernozhukov V. 1-penalized quantile regression in high-dimensional sparse models. Ann Statist. 2011;39:82–130. [Google Scholar]
- Bickel PJ, Li B. Regularization in statistics (with discussion) Test. 2006;15:271–344. [Google Scholar]
- Bickel PJ, Ritov Y, Tsybakov A. Simultaneous analysis of lasso and dantzig selector. Ann Statist. 2009;37:1705–1732. [Google Scholar]
- Bradic J, Fan J, Wang W. Penalized composite quasi-likelihood for ultrahigh-dimensional variable selection. J Roy Statist Soc Ser B. 2011;73:325–349. doi: 10.1111/j.1467-9868.2010.00764.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bühlmann P, van de Geer S. Statistics for High-Dimensional Data: Methods, Theory and Applications. New York: Springer; 2011. [Google Scholar]
- Candés EJ, Tao T. The Dantzig selector: statistical estimation when p is much larger than n (with discussion) Ann Statist. 2007;35:2313–2351. [Google Scholar]
- Efron B, Hastie T, Tibshirani R. Discussion of the “dantzig selector”. Ann Statist. 2007;35(6):2358–2364. [Google Scholar]
- Fan J, Fan Y, Barut E. Supplement to “Adaptive Robust Variable Selection”. 2013 doi: 10.1214/13-AOS1191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan J, Fan Y, Lv J. High dimensional covariance matrix estimation using a factor model. J Econometrics. 2008;147:186–197. [Google Scholar]
- Fan J, Li R. Variable selection via nonconcave penalized likelihood and its oracle properties. J Amer Statist Assoc. 2001;96:1348–1360. [Google Scholar]
- Fan J, Lv J. Sure independence screening for ultrahigh dimensional feature space (with discussion) J Roy Statist Soc Ser B. 2008;70:849–911. doi: 10.1111/j.1467-9868.2008.00674.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan J, Lv J. Non-concave penalized likelihood with np-dimensionality. IEEE Trans Inform Theory. 2011;57:5467–5484. doi: 10.1109/TIT.2011.2158486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan J, Peng H. On non-concave penalized likelihood with diverging number of parameters. Ann Statist. 2004;32:928–961. [Google Scholar]
- Li Y, Zhu J. L1-norm quantile regression. J Comput Graph Statist. 2008;17:163–185. [Google Scholar]
- Lv J, Fan Y. A unified approach to model selection and sparse recovery using regularized least squares. Ann Statist. 2009;37:3498–3528. [Google Scholar]
- Meinshausen N, Bühlmann B. Stability selection. J Roy Statist Soc Ser B. 2010;72:417–473. [Google Scholar]
- Newey WK, Powell JL. Efficient Estimation of Linear and Type I Censored Regression Models under Conditional Quantile Restrictions. Econometric Theory. 1990;3:295–317. [Google Scholar]
- Nolan JP. Stable Distributions - Models for Heavy Tailed Data. Birkhauser; 2012. (In progress, Chapter 1 online at academic2.american.edu/~jpnolan) [Google Scholar]
- Pollard D. Asymptotics for least absolute deviation regression estimators. Econometric Theory. 1990;7:186–199. [Google Scholar]
- Tibshirani R. Regression shrinkage and selection via the Lasso. J Roy Statist Soc Ser B. 1996;58:267–288. [Google Scholar]
- van de Geer S, Müller P. Quasi-likelihood and/or robust estimation in high dimensions. Stat Sci. 2012;27:469–480. [Google Scholar]
- Wang H, Li G, Jiang G. Robust regression shrinkage and consistent variable selection through the LAD-Lasso. J Bus Econom Statist. 2007;25:347–355. [Google Scholar]
- Wang L. L1 penalized LAD estimator for high dimensional linear regression. Tentatively accepted by Journal of Multivariate Analysis 2012 [Google Scholar]
- Wang L, Wu Y, Li R. Quantile regression for analyzing heterogeneity in ultrahigh dimension. Journal of American Statistical Association. 2012;107:214– 222. doi: 10.1080/01621459.2012.656014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Y, Liu Y. Variable selection in quantile regression. Statist Sin. 2009;37:801–817. [Google Scholar]
- Zhang CH. Nearly unbiased variable selection under minimax concave penalty. Ann Statist. 2010;38:894–942. [Google Scholar]
- Zhao P, Yu B. On model selection consistency of lasso. J Mach Learn Res. 2006;7:2541–2563. [Google Scholar]
- Zou H. The adaptive lasso and its oracle properties. J Amer Statist Assoc. 2006;101:1418–1429. [Google Scholar]
- Zou H, Li R. One-step sparse estimates in nonconcave penalized likelihood models (with discussion) Ann Statist. 2008;36(4):1509–1533. doi: 10.1214/009053607000000802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou H, Yuan M. Composite quantile regression and the oracle model selection theory. Ann Statist. 2008;36:1108–1126. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.