Abstract
Motivation: RNA-seq has become a routine technique in differential expression (DE) identification. Scientists face a number of experimental design decisions, including the sample size. The power for detecting differential expression is affected by several factors, including the fraction of DE genes, distribution of the magnitude of DE, distribution of gene expression level, sequencing coverage and the choice of type I error control. The complexity and flexibility of RNA-seq experiments, the high-throughput nature of transcriptome-wide expression measurements and the unique characteristics of RNA-seq data make the power assessment particularly challenging.
Results: We propose prospective power assessment instead of a direct sample size calculation by making assumptions on all of these factors. Our power assessment tool includes two components: (i) a semi-parametric simulation that generates data based on actual RNA-seq experiments with flexible choices on baseline expressions, biological variations and patterns of DE; and (ii) a power assessment component that provides a comprehensive view of power. We introduce the concepts of stratified power and false discovery cost, and demonstrate the usefulness of our method in experimental design (such as sample size and sequencing depth), as well as analysis plan (gene filtering).
Availability: The proposed method is implemented in a freely available R software package PROPER.
Contact: hao.wu@emory.edu, zhijin_wu@brown.edu.
Supplementary information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
RNA-sequencing has become a routine technique to study the whole transcriptome (Mortazavi et al., 2008). In addition to the initial excitements of the extraordinary power of the technology such as being able to detect novel transcripts and alternative splicing patterns (Djebali et al., 2012), more and more researchers use RNA-seq as a replacement of gene expression microarrays to quantify and compare expression levels under distinct biological contexts, for example, to identify differentially expressed (DE) genes. It has been well recognized now that technology improvements do not eliminate biological variability (Hansen et al., 2011), thus replication is still necessary in establishing statistical significance in the identification of DE. However, the number of replicates needed in RNA-seq, a key issue in experimental design, remains a challenge owing to the complexities of the experiment and the nature of RNA-seq data.
In classical sample size determination involving a single-hypothesis test, one typically starts with a few quantities that one can make reasonable assumptions on: the minimum effect size, which is scientifically meaningful, the variance (which can be estimated from historical data), an acceptable type I error rate, usually in the form of P-value, etc. The statistical power also has a clear definition: the probability of rejecting the null hypothesis under the alternative model. Based on these assumptions, one can then study the relationship between the statistical power and the sample size.
In high-throughput experiments (such as identifying DE genes from microarray or RNA-seq) where many statistical tests are performed simultaneously, several factors complicate the sample size calculation. The first one is the need to deal with multiple testing. False discovery rate (FDR) is often a preferred control of type I error over family-wise error rate. For microarray studies, several sample size calculation methods have been proposed based on controlling FDR. For example, Liu and Hwang (2007) built a connection between FDR and power, and derived algorithms for power calculation based on t- or F-test.
Second, we note that the power analysis for RNA-seq is even more complicated than that in microarray data. The baseline expression level is not of interest in microarray data, and can often be assumed to be zero without loss of generality, as it does not affect type I or II error in the DE detection. This is because the preprocessed expression values can be modeled as Gaussian distribution, where the mean and variance are unrelated. Thus, the baseline expression level does not affect the test statistics in microarray data. However, in RNA-seq, gene expressions are measured as counts and often modeled as Poisson or negative binomial distributions (Anders and Huber, 2010; Robinson et al., 2010; Wu et al., 2013). The variation in gene expression measurements comes from both the biological variation and the sequencing counting error. The relative importance of the counting error depends on the expression level: for genes with low counts, the variation owing to the counting process dominates the variance, whereas for genes with high counts, it is negligible. As a result, the power in DE detection is affected by expression level. For example, there is power bias toward longer genes because more reads are generated from longer transcripts (Oshlack and Wakefield, 2009). Further, as coverage depends on sequencing efficiency as well as expression level, genes with modest counts are not necessarily expressed at low levels. Thus, these may still be of interest even if we want to focus on genes that are above a certain level of expression.
Another issue often overlooked in existing methods of sample size determination for DE experiments is the wide application of empirical Bayes approach in DE detection (Anders and Huber, 2010; Robinson et al., 2010; Smyth, 2004; Tusher et al., 2001; Wu et al., 2013). Because of the limited sample size in many experiments, the gene-specific biological variance is often estimated with some shrinkage by borrowing strength across genes. This helps stabilizing the variance estimates and leads to better ranking of true DE genes, but in the meantime also creates dependency among genes, which affects the validity of some error-control procedures in multiple testing. Though all methods report type I error (either as P-value, FDR/q-value or both), the type I error may be computed from a parametric test of which assumptions are not all met, and the reported FDR is often obtained via simple conversion from nominal P-values using Benjamini–Hochberg methods (Anders and Huber, 2010; Robinson et al., 2010). The resulting nominal error rate can be rather different from actual error rate (Wu et al., 2013).
Finally, the flexibility of sequencing experiments gives scientists more freedom in experimental design: for the same amount of sequencing, one may choose to seek deeper coverage of a small collection of samples, or to obtain more samples with modest coverage. This is an additional factor not encountered in microarrays.
There are several methods for calculating the sample size for RNA-seq data in recent literature. These include methods for single-gene differential expression analysis based on likelihood ratio or Wald test (Fang and Cui, 2011), or on score test from negative binomial model (Hart et al., 2013). These methods, however, are not directly applicable to simultaneously testing thousands of genes profiled from one RNA-seq experiment because they do not come with a procedure that deals with multiple comparisons. Li et al. (2013b) proposed an analytical method based on Poisson model to determine sample size for both single gene and multiple gene comparisons with adjustment for FDR. This method has been further extended to negative binomial model in Li et al. (2013a). However, to make calculations attainable, the authors suggested setting a common value for parameters including fold change, dispersion, and average read count for all the genes. In reality, these parameters vary a lot between genes, and this method is not flexible enough to fully capture the complex characteristics of RNA-seq data. Although one can choose common conservative values for these parameters, it will overestimate the sample size and increase the cost of the experiments.
We argue, because of the complexities of RNA-seq experiments, it is no longer feasible to rely on one simple power versus sample size curve while treating all other factors as fixed input and holding strong assumptions such as exchangeability between genes and equating nominal error rate as actual error rate. We advocate prospective power evaluation in the context of RNA-seq, i.e. evaluating power in a comprehensive manner under various scenarios of sample size and sequencing depth. We use the word ‘prospective’ to emphasize our choice to assess and visualize power in multiple forms and maintain its high-dimensional nature, instead of specifying a fixed level of one particular form of power to determine the sample size. We demonstrate that, in addition to the sample size and the other usual suspects in power analysis (namely, effect size and within-group variance), there are other factors (such as the distribution of mean expression level) and other choices (such as sequencing depth and gene filtering) that influence the power of DE detection. We propose a simulation-based power evaluation, as the accumulation of RNA-seq data allows us to construct in silico datasets that well resemble real RNA-seq data, and the increasing computing efficiency allows us to evaluate actual error rate. Moreover, we demonstrate that conditional power, i.e. power stratified by coverage or biological variation, is more informative than overall (marginal) power in both experimental design and analysis plan.
2 METHODS
We propose to evaluate how experimental design affects power completely based on simulation. Our proposed method consists of two separate components. First, we provide a flexible semi-parametric simulation module that generates count tables resembling actual RNA-seq data in many aspects: marginal distribution of average expression, marginal distribution of biological dispersion, conditional relationship between dispersion and expression level, etc. Then, in a separate component, we evaluate power and error rates on the simulated dataset, emphasizing the concepts of stratified power and false discovery cost (FDC). We keep these two components separate so a user may choose an entirely different simulation scheme and still apply the same power assessment tools.
2.1 Data generation
We provide a negative binomial model-based simulation scheme, for using the power evaluation part of our method. The negative binomial model is the most widely used model for RNA-seq count data for its simplicity, flexibility and interpretability. It can be seen as a gamma-Poisson mixture, with the gamma layer capturing biological variation conditioning on covariates, and the Poisson distribution capturing the sequencing counting error. Let Ygi be the observed count for gene g, replicate i, we assume that . Here, μg and represent the mean and dispersion for gene g, respectively. si represents the normalizing factor, such as the library size. We begin by simulating a baseline expression level μg for each gene. This can be drawn from a parametric distribution, or re-sampled non-parametrically using the empirical average expressions estimated from an existing dataset. Unless there is a good justification for the choice of a parametric distribution of a transcriptome, we recommend re-sampling, as coverage is important in detecting DE and the dynamic range for RNA-seq is rather wide. This is one major difference from microarray, where often the mean expression (in log scale) can be simulated as 0 without loss of generality, as it does not affect DE detection.
Next we simulate a dispersion parameter that captures a gene’s biological variation. This dispersion parameter, referred to as the squared biological coefficient of variance (Anders and Huber, 2010; McCarthy et al., 2012), is closely related to the standard deviation in log transformed microarray data, which represents the biological variation of gene expression between replicates (Wu et al., 2013). Again, the parameter can be drawn from a parametric distribution or re-sampled based on empirical sample dispersions from a real dataset of the user’s choice. An important option here is provided: can be drawn independently, or a functional relationship between and μg can be preserved as suggested by previous data. Though there is no simple biological explanation for the dependence between biological variation and mean expression, this trend has been reported in many studies (Anders and Huber, 2010; Robinson et al., 2010).
In the third step, we set the effect sizes. This is the most difficult assumption to make, as we rarely know the amount of differential expression that is biologically relevant, nor do we know the proportion of genes with that level of difference. In the literature, several settings have been used. The first is a mixture: let zg be the indicator that gene g is differentially expressed, the proportion of gene with DE is . We have the effect size βg satisfying and . As there is a point mass at zero, i.e. , we refer to this asa zero-inflated normal distribution for βg. Another option is to allow be uniform over a user-defined range. Moreover, we can also choose to investigate the power of detecting specific effect sizes, by setting βg at multiple constant levels with the greatest point mass at 0, reflecting the general assumption that DE is present in only a small subset of genes in most experiments.
Many genes with zg = 1 are by definition differentially expressed, but may not be biologically interesting, as is small or even essentially 0. We should expect little power detecting these genes. Thus, we may be interested in defining DE of interest—an indicator if or , and investigate the power of detecting these genes. We let the user decide the ‘meaningful effect size’. The user can also simply provide a vector of , with paring indicators whether each βg is considered a true positive.
2.2 DE detection
After generating the simulated read counts, existing software developed for count-based RNA-seq is applied to detect DE genes. We implemented interface for calling edgeR (Robinson et al., 2010), DESeq (Anders and Huber, 2010) and DSS (Wu et al., 2013). Users can define other DE detection methods and plug into the procedure. Each method reports test statistics, P-values and FDR for all genes. These results are used for downstream power assessment. The simulations (data generation and DE detection) are performed under different sample sizes (number of replicates in each biological condition). Each simulation is repeated for a number of times, and the power assessments are averaged to provide the final results.
2.3 Power assessment and visualization
We consider genes that can potentially fall into three categories: (i) non-DE where the null hypothesis is true; (ii) with low DE that is not biologically relevant; and (iii) with DE high enough that we are most interested in identifying. The total number of genes in each categories are represented by and , respectively. Let Dg be the decision on gene g (), with Dg = 1 declaring DE (discovery) and Dg = 0 declaring non-DE, we summarize the decisions in Table 1, where V represents the total number of type I errors. Though any gene with is differentially expressed, thus failing to discover it is a type II error, we argue that we care less about a gene with low DE that does not achieve a user-defined relevance level. The power we care about is the ability of detecting genes in the third category, i.e. power associated with Sb. We call it the targeted power. In the rest of this article, we will focus on the assessment of the targeted power. In the software, we provide options to define biologically interesting genes by or . For illustration purpose, we focus only on results from the former definition throughout this manuscript.
Table 1.
DE detection and potential errors
| zg | Discovery? |
Total | |||
|---|---|---|---|---|---|
| (Dg = 1) | (Dg = 0) | ||||
| 0 | 0 | ||||
| 1 | 0 | ||||
|
|
1 |
1 |
|
|
|
| Total | |||||
The family-wise type I error rate is , and the FDR is . We introduce a concept that we referred to as FDC, defined as . The interpretation is straightforward: for every discovery that we care about ( when Dg = 1), the expected number of false discoveries. Thus, FDC represents the cost of false discoveries we expect to identify each true discovery we aim for. We are still testing the null . If we called a gene with as DE, it is not a false discovery, but simply that we would not mind as much if we fail to discover it.
Statistical power in gene expression experiments has complex meanings. The ‘family-wise power’, that is the probability of detecting all true DE genes, can be small in most studies, especially when many DE genes have small magnitude of differences or low baseline expression levels. This means that is often small. However, it is rarely the goal to detect every single DE gene in an RNA-seq experiment. We may be interested in the proportion of true DE genes detected: when there are a small set of true DE genes, we may wish to detect the majority of these. If the tests for DE are independent, the expected proportion is the same as average power: .
In other cases, especially in hypothesis-generating experiments, we may simply aim for a number of leads, even if that is a small proportion of all DE genes. That is, the power of interest is , or the expected number (as opposed to proportion) of true discoveries. Finally, as mentioned above, regardless of proportion or absolute number of discoveries, we may only care about the power of detecting DE of a certain size, i.e. of a medical or a biological relevance.
With these considerations, we advocate comprehensive power evaluation by visualizing its relationship with a number of factors, including but not limited to sample size, instead of pre-specifying a desired power level, as we recognize that power in a high-throughput setting could have more than one definition. We refer to this as prospective power evaluation, in contrast to sample size determination with preselected power definition and level. We compute the following quantities from each simulation when discoveries are made with a user-defined type I error control (at a nominal P-value or FDR/q-value) and a user-defined magnitude of relevant effect size Δ. We report the averages of these quantities from a number of simulations as our empirical values for error rates and power.
- Empirical marginal type I error rate:
- Empirical marginal FDR:
- Empirical marginal targeted power: the proportion of biologically meaningful DE genes detected at the nominal type I error
If one is interested in detecting DE of any size, defining Δ = 0 will reduce the targeted power to the classical definition of average power.
- Empirical marginal FDC:
- Empirical stratified targeted power by coverage: for genes with average coverage: () in the stratum
- Empirical stratified targeted power by dispersion: for genes with dispersions in the stratum
Empirical stratified FDC, FDR and type I error rate by coverage or dispersion: similar to the definition of the stratified targeted power.
For experimental design, we provide a comprehensive view of the statistical power as a function of not only sample size, but also coverage, biological dispersion, proportion and magnitude of DE. We also provide the empirical error rates to alert the user that the nominal type I error, either in the form of raw P-value or FDR, may not be valid. Our stratified view of both type I error and power shows the gain and loss in different subsets of a transcriptome, aiding the investigators in both experimental design (choosing number of samples and sequencing depth, for example) and analysis plan (setting filters and choosing a reasonable control for error rate).
2.4 Power reassessment
One challenge in the sample size determination in high-throughput experiment is the choice of type I error control. Classical sample size calculation often assumes a valid test is available, which is often the case when asymptotic properties can be assumed in large samples. In high-throughput experiments with multiple testing, FDR is often a preferred choice over family-wise type I error for its balance between false positive and power. However, we face a 2-fold difficulty here. First, there is no conventional guidance for FDR cutoff, as the level of acceptable FDR often depends on the number of discoveries. With 10 total discoveries, a 20% FDR may be reasonable, but this may be considered too high if the total discoveries reach 100. Second, many DE analysis methods report an FDR that is a rough estimate and relies on assumptions such as independence and exchangeability. Thus, the reported FDR may not reflect the actual FDR. Therefore, we often want to evaluate power at several nominal FDR levels, and assess the power as well as the validity of error control.
For each simulation study, we thus keep all settings for data generation, and save the necessary simulation results, including the nominal P-value, reported FDR and observed average expression and dispersion. When we would like to reassess the power under a different choice of type I error control, desired effect size, or choose a different stratification of genes, we do not need to rerun the entire simulation. That greatly reduces the computational burden.
2.5 Implementation
We implemented the proposed methods in an open-source R package PROPER, standing for PROspective Power Evaluation for RNAseq. The software is currently available at
http://web1.sph.emory.edu/users/hwu30/PROPER.html, and being prepared to submit to Bioconductor (Gentleman et al., 2004). A vignette is distributed with the package, which contains detailed instruction and examples of using the package, interpreting the results and an example of sample size justification for grant proposal.
The computational efficiency of PROPER depends on the DE detection software and the scale of the simulation. For the ones presented in Section 3 (50 000 genes, five different sample sizes and using edgeR), each simulation takes around 10 s on a MacPro laptop with 2.7Ghz i7 CPU and 16 G RAM, which translates to 17 min for 100 simulations.
3 RESULTS
3.1 Simulation setup
To illustrate the power evaluation in various forms, we generated results using two public datasets as our basis for simulation. The Cheung data (Cheung et al., 2010) quantifies the expressions of lymphoblastoid cell lines from 41 CEU individuals in International HapMap Project (The International HapMap Consortium, 2003). The samples are from unrelated individuals, and the expressions show large biological variations overall. The Bottomly data (Bottomly et al., 2011) includes 21 striatum samples from two strains of inbred mice (C57BL/6J and DBA/2J). The expressions in this dataset show much smaller biological variations. These two datasets, one involving a random sample from a human population and the other involving animals from model organisms, represent experiments with large and small biological variations. Most of the other datasets we examined, including almost all datasets on reCount (Frazee et al., 2011) and 80% of experiments in Barcode (McCall et al., 2011), have biological variation that falls between these two examples.
In all simulations, we use 50 000 genes and assume 5% of them are DE. For each simulation, the read counts are generated according to the steps described in Section 2. To be specific, the baseline expression level μg and the dispersion parameter are resampled independently from the real data. The effect size is set to be 0 for non-DE genes, and is randomly sampled from normal distribution for DE genes. This choice of the effect size is only for illustration purpose. The software provides an option for user-defined effect sizes. In practice, we recommend users obtain effect sizes from historical data under similar biological context.
Under each simulation scenario, we evaluate power at replicate numbers 2, 3, 5, 7 and 10. We apply edgeR for DE detection to identify DE genes, then compare the results with the truth to evaluate both type I error control and various metrics of power. The results presented below are averaged >100 simulations. The aim of our method is not to compare performance of different DE analysis methods, which often depends on simulation setting. We choose edgeR as the illustrative method for its popularity and speed. For all results presented below, we use to define biologically meaningful DE genes.
3.2 Simulation results with independent mean and dispersion
As an overall summary, we present a table that compares the marginal targeted power as well as the actual type I error rate at the user-specified control of nominal type I error. The measurement of power in the form of the proportion of true DE genes identified and the average number of DE genes identified are both provided.
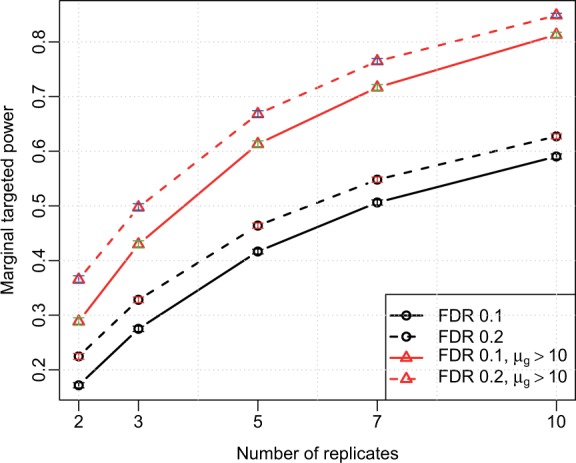
Table 2A is an example using Cheung data as the source for simulation, at a nominal FDR at 0.1. As expected, the targeted power increases with sample size. In a classical multiple testing situation with exchangeable tests, one would expect that a valid control of FDR would mean that the ratio of true and false discoveries is maintained as sample size increases, and the increase in targeted power results from more true discoveries. However, Table 2 shows that the actual FDR is quite different from the nominal FDR. Under the same nominal FDR control, we obtain less false discoveries and more true discoveries as sample size increases, thus the actual FDR decreases. Overall, the nominal FDR mostly underestimates the true FDR in our simulation settings. The FDC also decreases with larger sample size, meaning that it is cheaper to detect DE genes when there are more replicates. Table 2B shows the result from a similar simulation based on Bottomly data, which are from inbred animals with much smaller biological variances. Results show that the DE detection is easier in these data: the powers are considerably higher and the FDCs are lower under the same sample size. These imply that compared with the Cheung data, it would require less replicates here to achieve the same level of power.
Table 2.
Marginal targeted power analysis results from simulations when DE are declared with nominal FDR 0.1
| N | FDRn | FDRo | power | FDC | ||
|---|---|---|---|---|---|---|
| Cheung data | ||||||
| 2 | 0.10 | 0.59 | 0.17 | 66.02 | 95.93 | 1.45 |
| 3 | 0.10 | 0.48 | 0.27 | 107.00 | 100.75 | 0.94 |
| 5 | 0.10 | 0.31 | 0.41 | 165.26 | 73.73 | 0.45 |
| 7 | 0.10 | 0.22 | 0.49 | 205.10 | 58.19 | 0.28 |
| 10 | 0.10 | 0.15 | 0.58 | 244.62 | 45.06 | 0.18 |
| Bottomly data | ||||||
| 2 | 0.10 | 0.28 | 0.53 | 343.70 | 136.64 | 0.40 |
| 3 | 0.10 | 0.24 | 0.62 | 407.79 | 130.35 | 0.32 |
| 5 | 0.10 | 0.15 | 0.72 | 482.79 | 85.16 | 0.18 |
| 7 | 0.10 | 0.11 | 0.77 | 519.17 | 67.61 | 0.13 |
| 10 | 0.10 | 0.08 | 0.80 | 547.04 | 53.71 | 0.10 |
N: number of replicates in each group. FDRn: nominal FDR. FDRo: observed FDR. : average number of true discoveries. : average number of false discoveries.
FDR is often a preferred measure of type I error over the raw P-value, owing to concerns of excessive multiple testing and the over-conservativeness of Bonferroni correction. However, there is no conventional cutoff of FDR as the classical significance level of 0.05/0.01 for P-values. An acceptable FDR may depend on the number of discoveries. Thus, we let the user reevaluate the targeted power at a different nominal FDR level. The summary tables for nominal FDR at 0.2 are provided in the Supplementary Table S1.
At the first glance, the targeted power from the Cheung data-based simulation appears rather low: only 0.58, when there are 10 replicates in each group. This is disappointing especially when we observe that the actual FDR can be higher than the nominal FDR. However, we strongly recommend viewing the stratified targeted power as shown in Figure 1. Here the genes are stratified by the average counts. Clearly larger sample size leads to better power at all strata, as expected. But for all sample sizes, including n = 10, there is little power for the genes with low coverage (average counts up to 10). This is not surprising because even if there is true DE, when the expression level is so low (that is, at current sequencing depth, only a few reads from the gene are sequenced), the Poisson counting error shadows the real biological difference and we do not have high probabilities of detecting these DE genes while controlling for FDR. When the average counts become moderately large (average counts greater than 10), the gain of targeted power is significant with increased sample size. For example, the stratified targeted power for genes with read counts between 10 and 20 increases from 0.33 to 0.73 when the number of replicates increases from 3 to 10. Moreover, for this simulation, the stratified targeted power increases sharply past the first stratum, but further increases are modest after the average count goes beyond 20.
Fig. 1.
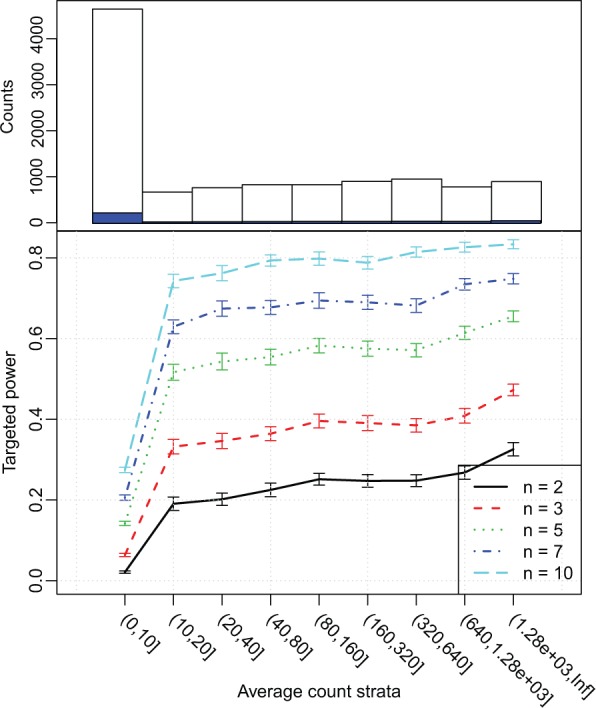
Top: Histogram of genes stratified by average counts. Open histogram is for total number of genes and blue histogram is the counts of DE genes. Bottom: Targeted power stratified by average counts, under different sample sizes. Results are averaged from 100 simulations based on Cheung data. n: the number of replicates in each group in a two-class comparison
When the average targeted power is the goal and the stratified targeted power varies a lot as seen in Figure 1, we may decide to simply filter out genes with low counts: we give up the possibility of detecting DE in this stratum knowing there is little power, but at the same time we avoid making any false discovery as well. For the rest of the genes, we can achieve a much higher marginal power, as seen in Figure 2. It shows that if one discards genes with <10 average counts, the marginal targeted power will increase to 0.8 (from 0.58) when the sample size is 10, using FDR <0.1 to define DE genes. The significant gains in power after filtering are achieved from two sources: (i) reduced size of the true positive set, and (ii) reduced number of simultaneous tests. These simulation results demonstrate that filtering genes with low counts make it easier to achieve significance for the remaining genes. The software package allows users to specify strata. Additional results from using a different set of strata are provided in the Supplementary Section S6 and Supplementary Figure S7. We recommend users explore the results under different strata to choose proper stratification and filtering strategy.
Fig. 2.
Marginal targeted power versus sample sizes, with and without filtering out genes with average counts lower than 10, averaged from 100 simulations based on Cheung data
To maximize our gain, that is, to obtain the most true discoveries with the same cost of false discovery, we recommend viewing ‘false discovery cost’ plot (Fig. 3) for the choice of filtering. The FDC has a simple interpretation: at the current cutoff for declaring DE, the expected number of false discovery (cost) for each true discovery. For example, Figure 3 shows that when there are three replicates in each group, to detect every true positive gene with average counts between 0–10, one can expect to detect 1.3 false–positive findings. Overall, these results show that using more replicates will decrease FDC for all strata, and genes with greater expression levels have lower associated FDC (so it is ‘cheaper’ to detect the highly expressed DE genes).
Fig. 3.
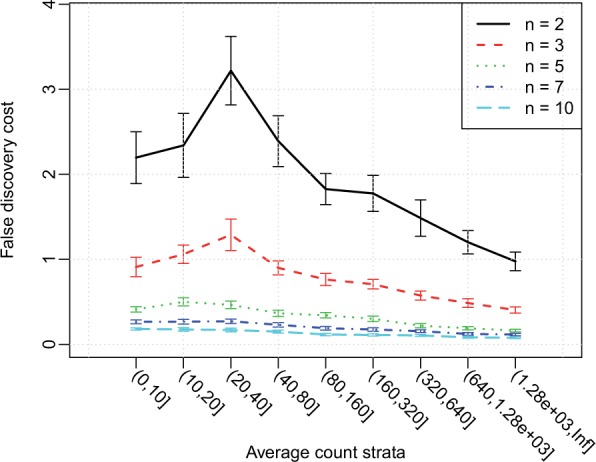
False discovery cost stratified by average counts, under different sample sizes, averaged from 100 simulations based on Cheung data
The stratified visualization of targeted power, as seen in Figures 1 and 3 above, sends a rather different message than the marginal targeted power. This demonstrates that we should not consider power as a single numeric value. We recommend viewing several other figures simultaneously, especially when the power we target is not the average power. For example, in hypothesis-generating studies, our goal may be identifying a number of leads for further study. In this case, the number of discoveries, rather than the proportion of discoveries, is more important. We show the average number of true discoveries in each stratum of average gene counts in Figure 4. Results based on the two different targeted power definitions, as seen in Figures 1 and 4, are seemingly contradictory at the first glance. This is because genes are not evenly distributed across the strata. The actual number of discoveries is a product of the total number of true DE genes and the average power, thus a higher value in either quantity can increase the number of discoveries. Though the sensitivity of a DE detection is low in certain strata, a small fraction of a big collection of genes can still yield a considerable number. For example, in Figure 1, genes in the first stratum has power several folds lower than other strata, but there are >4000 genes in this stratum, 200 of which have DE. Thus a small sensitivity at can still lead to >40 discoveries when n = 10, as shown in Figure 4. RNA-seq data reflect the wide dynamic range of expression levels across the transcriptome, and often a large fraction of genes are covered with modest counts. Thus, it is common that power in absolute number of discoveries versus power in fraction of true DEs discovered may send different messages. Whether one should focus on the fraction of true DE genes (Figure 1) or the actual number of true DE genes detected (Fig. 4) depends on the purpose of the experiment. If one aims to recover most of the transcriptomic response to a treatment, the average power is a better guide. If one aims to identify a number of hits in a hypothesis generating exercise to lead further study, the actual number of true DE genes identified is more useful. We leave this judgement to the users.
Fig. 4.
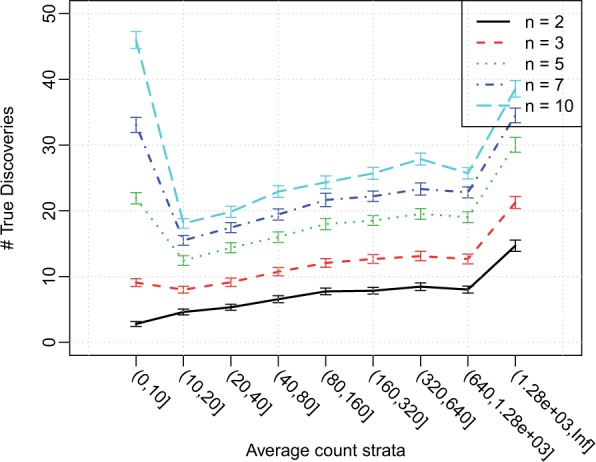
Number of true discoveries stratified by average counts, under different sample sizes, averaged from 100 simulations based on Cheung data
Realizing that genes with low coverage have low power of DE detection and high FDC, we may consider increasing the sequencing depth as an alternative to increasing the sample size. Using the same amount of resources (total number of sequencing reads), which choice benefits us more? We provide a table that compares the targeted power at various sequencing depth, so the user can decide on a desirable combination of sequencing depth and sample size. Table 3 shows the result based on Cheung data at deeper and shallower sequencing. In this example, increasing the sequencing depth does not help as much as increasing the number of replicates. Specifically, using five replicates in each group and double the coverage depth in Cheung data produces marginal targeted power of 0.45. Using the same number of total reads, one can double the sample size (to 10 replicates per group), and use the same coverage depth as in Cheung data. That will provide a marginal targeted power of 0.58, greatly improved compared with the other strategy. These results agree with the conclusion in Liu et al. (2014), i.e. using more replicate is more beneficial than sequencing deeper. In real applications, we suggest the users reproduce the table based on their simulation choices, especially when the simulation is based on a different dataset, as both the baseline expression level and the distribution of DE magnitudes can have strong impact on statistical power.
Table 3.
Effect of changing sequencing depth on marginal targeted power in simulations based on Cheung data at nominal FDR 0.1
| Relative coverage | 2 reps | 3 reps | 5 reps | 7 reps | 10 reps |
|---|---|---|---|---|---|
| 0.2 | 0.13 | 0.22 | 0.34 | 0.43 | 0.51 |
| 0.5 | 0.15 | 0.25 | 0.38 | 0.47 | 0.56 |
| 1 | 0.17 | 0.27 | 0.42 | 0.49 | 0.58 |
| 2 | 0.19 | 0.30 | 0.45 | 0.54 | 0.62 |
| 5 | 0.22 | 0.34 | 0.49 | 0.58 | 0.66 |
| 10 | 0.24 | 0.36 | 0.52 | 0.61 | 0.69 |
All figures presented above are based on the Cheung data. The same set of figures for the Bottomly data is provided in the Supplementary Materials (Supplementary Fig. S2). Owing to smaller biological variations in inbred animals, the DE detection is easier in Bottomly data under similar effect sizes and sequencing depths. We observe, as expected, higher powers and lower FDCs for DE detection in Bottomly data. The general conclusions from the analyses are otherwise consistent with the Cheung data.
For all results presented above, we use to define biologically meaningful DE genes. Users may choose different Δ values to define DE genes. We present a set of results from using Δ = 1 in Supplementary Materials (Supplementary Table S2, Supplementary Figs S3 and S4). As expected, greater values of Δ lead to better targeted power because the effect sizes are larger. On the other hand, this also leads to decreased number of true discoveries, which could be undesirable if the primary goal of DE detection is to generate a set of target genes. It is advisable for users to try different options based on these simulation results and select proper experimental design and analysis plan.
We also provide functionality for computing the power-related metrics stratified by biological coefficient of variation (through dispersion). Those results are provided in the Supplementary materials (Supplementary Figs S5 and S6). In general, genes with greater dispersion have lower power and higher FDC, and larger sample size helps DE detection.
Furthermore, we compared the power assessment results from PROPER and ssize.fdr, the R package based on method by Liu and Hwang (2007) for microarray data. In general, we found that ssize.fdr over-estimates power (Supplementary Section 7 and Supplementary Fig. S8). That is because ssize.fdr does not take into account the sequencing depth information, and assumes that the power of detecting DE genes only depends on the effect sizes. The comparison demonstrate that power calculation method developed for microarray data is not applicable for RNA-seq data and may lead to erroneous results.
3.3 Simulation results with dispersion–mean dependency
Although its biological explanation remains elusive, dependency between and μg has been reported in many studies (Anders and Huber, 2010; Robinson et al., 2010), with low expression genes often associated with higher dispersion. We performed simulation when the dependence of dispersion and mean expression is preserved based on the Cheung data. To be specific, we first estimate μg and for all genes, then sample μg and in pairs, thus their correlation is preserved in simulation. There is a strong negative correlation between μg and , e.g. genes with higher expressions show lower biological variations.
Figure 5 shows the power analysis results. Both targeted power and FDC increase sharply as average count increases. Compared with the results in Section 3.2, the dependence of targeted power and FDC on average count is stronger: the sharp increase retains even after the average count goes beyond 20. This is because genes with lower counts now suffer from higher dispersion, in addition to under higher influence of Poisson counting error. In contrast, highly expressed genes benefit from lower dispersion. In situations like these, filtering out genes with low counts may provide even more benefit. Moreover, in the presence of dispersion–mean dependence, it will be even more difficult to derive a sample size formula analytically, so the proposed method will be more important and practically useful.
Fig. 5.
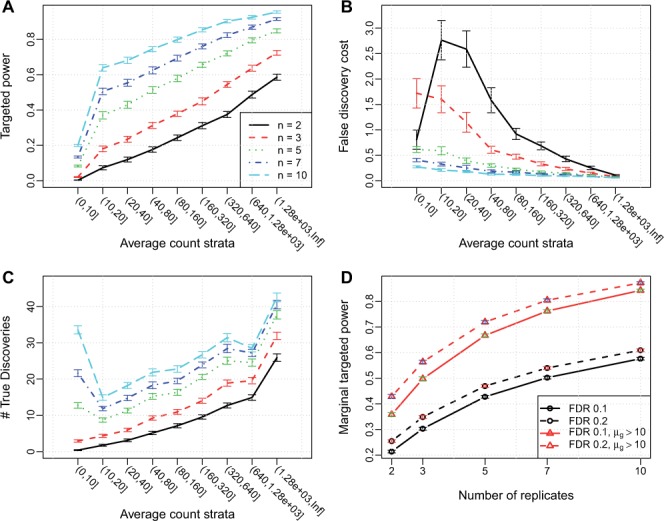
Simulation results based on the Cheung data, with dispersion–mean dependency
4 DISCUSSION
Statistical power and sample size determination are the most common questions we face in experimental design. In high-throughput experiments that involve a large number of in-exchangeable tests, statistical power is not as tractable as in classical hypothesis testing. We demonstrate that in a RNA-seq study, more factors affect the sample size determination in addition to the effect size and variance, including the distribution of the baseline expression level (what proportion of genes have high coverage in the sequencing), the distribution of the biological variation and the proportion of genes having DE. Asking a biologist to provide specific numbers for all the above factors, and/or to confirm that a particular parametric distribution is reasonable for some parameter, seems unrealistic. On the other hand, assuming the overall behavior of a factor to resemble that in some existing dataset eases the communication. Thus, we prefer semi-parametric simulation settings as described in Section 2.
The definition of power itself can vary in RNA-seq experiments: we may be interested in average marginal power as the proportion of all DE genes identified, or targeted power as the proportion of DE genes identified from a subset of genes, or we may be interested in the number instead of proportion of DE genes identified. For these reasons, we advocate sample size decision based on a comprehensive evaluation of statistical power as well as actual type I error, over a range of sample sizes, based on simulation studies. We refer to this as prospective power evaluation, as compared with fixing one set of assumptions on effect sizes/type I error control/expression level/sequencing depth and then compute a minimum sample size to achieve a certain level of power, for a particular type of power. The user visualizes the relationship between various types of power and sample size, expression level and biological variation, and understands the cost of false discovery in different strata of genes. The power evaluation thus assist the decision on sequencing depth, analysis plan (filtering or not, choice of nominal error rate), and then based on these decisions, the user can select a sample size that provides acceptable power.
Filtering certainly comes with sacrifice: we discard the power completely on the genes we filter out. But the power evaluation allows us an informative decision: we would know how much power we give up, and make this decision before real data are analyzed, so we reduce the number of tests, hence not having to adjust for the tests never performed.
The fact that statistical power depends on the baseline expression level and the dispersion level has several consequences. The first consequence is that power for Δ = 0 (i.e., ) is often biased toward highly expressed genes. Sometimes it may be beneficial to filter out genes with counts too low, as discussed above. The second consequence is that simulation results based on one RNA-seq dataset may not be generalizable to experiments involving another tissue/cell type with a different expression distribution across genes. For this reason we provide options using several public RNA-seq datasets as simulation sources. We also let the user substitute with their choice of baseline expression.
One way of increasing power is to increase sequencing depth. This is apparent from the stratified power plot: when we sequence deeper, genes with average counts in lower strata will move to higher strata and be associated with higher sensitivity at the same type I error control. However, based on Figure 1, there is a sharp increase of power when the genes average count goes >10, but remains relatively flat thereafter. If there are many genes whose expression level is lower than but near 10, increasing the sequencing depth may help, but there is little gain on DE detection sensitivity for those genes that already have high power. Thus, the impact of sequencing depth also depends on the expression pattern of the transcriptome under study. If the transcriptome consists of a smaller fraction of the genes with similar level of expression, then with modest depth, most of the genes may already reside in middle expression strata with acceptable power.
Funding: H.W. was partially supported by the National Center for Advancing Translational Sciences of the National Institutes of Health under Award Number UL1TR000454. Z.W. was partially supported by the National Science Foundation award DBI1054905 and the National Institutes of Health under Award Number R01 GM067862.
Conflict of interest: none declared.
Supplementary Material
REFERENCES
- Anders S, Huber W. Differential expression analysis for sequence count data. Genome Biol. 2010;11:R106. doi: 10.1186/gb-2010-11-10-r106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bottomly D, et al. Evaluating gene expression in c57bl/6j and dba/2j mouse striatum using RNA-seq and microarrays. PloS One. 2011;6:e17820. doi: 10.1371/journal.pone.0017820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheung VG, et al. Polymorphic cis-and trans-regulation of human gene expression. PLoS Biol. 2010;8:e1000480. doi: 10.1371/journal.pbio.1000480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Djebali S, et al. Landscape of transcription in human cells. Nature. 2012;489:101–108. doi: 10.1038/nature11233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fang Z, Cui X. Design and validation issues in RNA-seq experiments. Brief. Bioinformatics. 2011;12:280–287. doi: 10.1093/bib/bbr004. [DOI] [PubMed] [Google Scholar]
- Frazee AC, et al. Recount: a multi-experiment resource of analysis-ready rna-seq gene count datasets. BMC Bioinformatics. 2011;12:449. doi: 10.1186/1471-2105-12-449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gentleman RC, et al. Bioconductor: open software development for computational biology and bioinformatics. Genome Biol. 2004;5:R80. doi: 10.1186/gb-2004-5-10-r80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen KD, et al. Sequencing technology does not eliminate biological variability. Nat. Biotechnol. 2011;29:572–573. doi: 10.1038/nbt.1910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hart SN, et al. Calculating sample size estimates for RNA sequencing data. J. Comput. Biol. 2013;20:970–978. doi: 10.1089/cmb.2012.0283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li C-I, et al. Sample size calculation based on exact test for assessing differential expression analysis in RNA-seq data. BMC Bioinformatics. 2013a;14:357. doi: 10.1186/1471-2105-14-357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li C-I, et al. Sample size calculation for differential expression analysis of RNA-seq data under poisson distribution. Int. J. Comput. Biol. Drug Des. 2013b;6:358–375. doi: 10.1504/IJCBDD.2013.056830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu P, Hwang JG. Quick calculation for sample size while controlling false discovery rate with application to microarray analysis. Bioinformatics. 2007;23:739–746. doi: 10.1093/bioinformatics/btl664. [DOI] [PubMed] [Google Scholar]
- Liu Y, et al. RNA-seq differential expression studies: more sequence or more replication? Bioinformatics. 2014;30:301–304. doi: 10.1093/bioinformatics/btt688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCall MN, et al. The gene expression barcode: leveraging public data repositories to begin cataloging the human and murine transcriptomes. Nucleic Acids Res. 2011;39(Suppl. 1):D1011–D1015. doi: 10.1093/nar/gkq1259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCarthy DJ, et al. Differential expression analysis of multifactor RNA-seq experiments with respect to biological variation. Nucleic Acids Res. 2012;40:4288–4297. doi: 10.1093/nar/gks042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mortazavi A, et al. Mapping and quantifying mammalian transcriptomes by RNA-seq. Nat. Methods. 2008;5:621–628. doi: 10.1038/nmeth.1226. [DOI] [PubMed] [Google Scholar]
- Oshlack A, Wakefield MJ. Transcript length bias in RNA-seq data confounds systems biology. Biol. Direct. 2009;4:14. doi: 10.1186/1745-6150-4-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson MD, et al. edger: a bioconductor package for differential expression analysis of digital gene expression data. Bioinformatics. 2010;26:139–140. doi: 10.1093/bioinformatics/btp616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smyth GK. Linear models and empirical bayes methods for assessing differential expression in microarray experiments. Stat. Appl. Genet. Mol. Biol. 2004;3:3. doi: 10.2202/1544-6115.1027. [DOI] [PubMed] [Google Scholar]
- The International HapMap Consortium. The international hapmap project. Nature. 2003;426:789–796. doi: 10.1038/nature02168. [DOI] [PubMed] [Google Scholar]
- Tusher VG, et al. Significance analysis of microarrays applied to the ionizing radiation response. Proc. Natl Acad. Sci. USA. 2001;98:5116–5121. doi: 10.1073/pnas.091062498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu H, et al. A new shrinkage estimator for dispersion improves differential expression detection in RNA-seq data. Biostatistics. 2013;14:232–243. doi: 10.1093/biostatistics/kxs033. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


