Quantifying the cost in power of ignoring continuous covariate imbalances in clinical trial randomization

Abstract

Motivated by potentially serious imbalances of continuous baseline covariates in clinical trials, we investigated the cost in statistical power of ignoring the balance of these covariates in treatment allocation design for a logistic regression model. Based on data from a clinical trial of acute ischemic stroke treatment, computer simulations were used to create scenarios varying from best possible baseline covariate balance to worst possible imbalance, with multiple balance levels between the two extremes. The likelihood of each scenario occurring under simple randomization was evaluated. Power of the main effect test for treatment was examined. Our simulation results show that the worst possible imbalance is highly unlikely, but it can still occur under simple random allocation. Also, power loss could be nontrivial if balancing distributions of important continuous covariates were ignored even if adjustment is made in analysis for important covariates. This situation, although unlikely, is more serious for trials with a small sample size and for covariates with large influence on primary outcome. These results suggest that attempts should be made to balance known prognostic continuous covariates at the design phase of a clinical trial even when adjustment is planned for these covariates at the analysis.

1. Introduction

Randomization in clinical trials is fundamental to study design. It provides validity of statistical analyses of trial results by incorporating randomness, and it promotes comparable treatment groups with respect to allocation numbers and baseline covariate distributions. Simple randomization ensures independence among subject treatment assignments and prevents potential selection biases associated with baseline covariates, but it cannot guarantee balance in covariate distributions across treatment groups [1, 2]. The expected level of imbalance under simple randomization is zero, but this is only an average over an infinite number of imbalances. A clinical trial is only a single realization of a random phenomenon, and it cannot be assumed that the observed imbalance across treatment groups will be zero for any single trial. This paper illustrates that simple random allocation has the potential to result in large levels of covariate imbalances across treatment groups.

Constrained randomization designs have been used in clinical trials to balance the allocation across treatment groups, including permuted block, biased coin [3], and urn designs [4, 5]. Stratification and minimization [6, 7] are used together with these constrained randomization methods to combat imbalances in baseline covariate distributions. However, these methods only apply to categorical covariates, and they lack the capacity to control imbalance in continuous baseline covariates. Optimal designs developed by Begg, Iglewicz [8], and Atkinson [9] have the ability to control imbalances in continuous covariates, but their properties have not been fully explored and they have yet to be implemented in clinical trials [1]. Aickin [10], Nishi and Takaichi [11], Endo, et al [12], Frane [13], and Greevy [14] have also illustrated continuous covariate balancing techniques.

In clinical trial practice, however, continuous baseline covariates are traditionally categorized, and their imbalance is controlled with stratification or minimization. This strategy is limited because of the large number of potential strata which result in a small average stratum size, reducing the effectiveness of the constrained randomization method [1, 15]. Lack of publicity for practical methods for continuous covariate balancing and lack of knowledge on the cost of failing to balance continuous covariates results in a common phenomenon, whereby continuous covariates are excluded from the randomization plan in clinical trials. Leaving important continuous covariates outside of the randomization scheme could lead to selection bias when an investigator has both knowledge of the covariate and influence on recruitment. Additionally, uncontrolled imbalances in continuous covariates may affect the statistical analysis of the trial outcome.

The purpose of this research is to explore both ends of the balance-imbalance spectrum and quantify the effect of imbalance in continuous covariate distributions on power in a nonlinear setup. We propose a visual method and a mathematical expression for measuring imbalance in continuous covariate distributions across two treatment groups. Computer simulation attempts to determine the imbalance distribution under several allocation scenarios. The next section provides motivation and background for this study. Section 3 outlines the simulation methods, followed by results in Section 4. The last section discusses overall conclusions from this simulation study and explains what remains to be explored.

2. Motivation

Partly due to baseline disease severity and age imbalances across treatment groups, the National Institutes of Neurological Disorders and Stroke (NINDS) tissue plasminogen activator (tPA) study [16] for the treatment of acute ischemic stoke has been the source of controversy [17–20]. The randomization scheme implemented in the NINDS trial was the permuted block design, stratified by time from stroke onset (0–90 min, 91–180 min) and clinical site. This randomization scheme balances the number of subjects between the two treatment arms within each time-from-onset stratum in each site. Age and baseline National Institutes of Health Stroke Scale (NIHSS) score were not included in the randomization scheme, although both variables are known predictors of the trial’s primary outcome, the three month functional outcome following ischemic stroke [17, 21].

Insignificant statistical test results comparing mean or median covariate values across treatment groups does not necessarily suggest that there is little need for concern about covariate imbalance and its impact on the trial results. We propose a tool to assess the imbalance in the entire continuous variable distribution between two treatment groups.

Let F(x, j) be the number of subjects randomized to treatment arm j (j = 1,2) with the covariate value less than or equal to x. Then D(x) = F(x,1) − F(x,2) represents the distribution of cumulative imbalances between the two treatment arms. Ideally, an imbalance at one value (or in a small region) of the covariate can be compensated by another imbalance in the opposite direction at a nearby point (or small region). In this case, the curve of D(x) would frequently cross the zero line in the entire range of the covariate, indicating a nearly balanced distribution of that covariate between the two treatment arms.

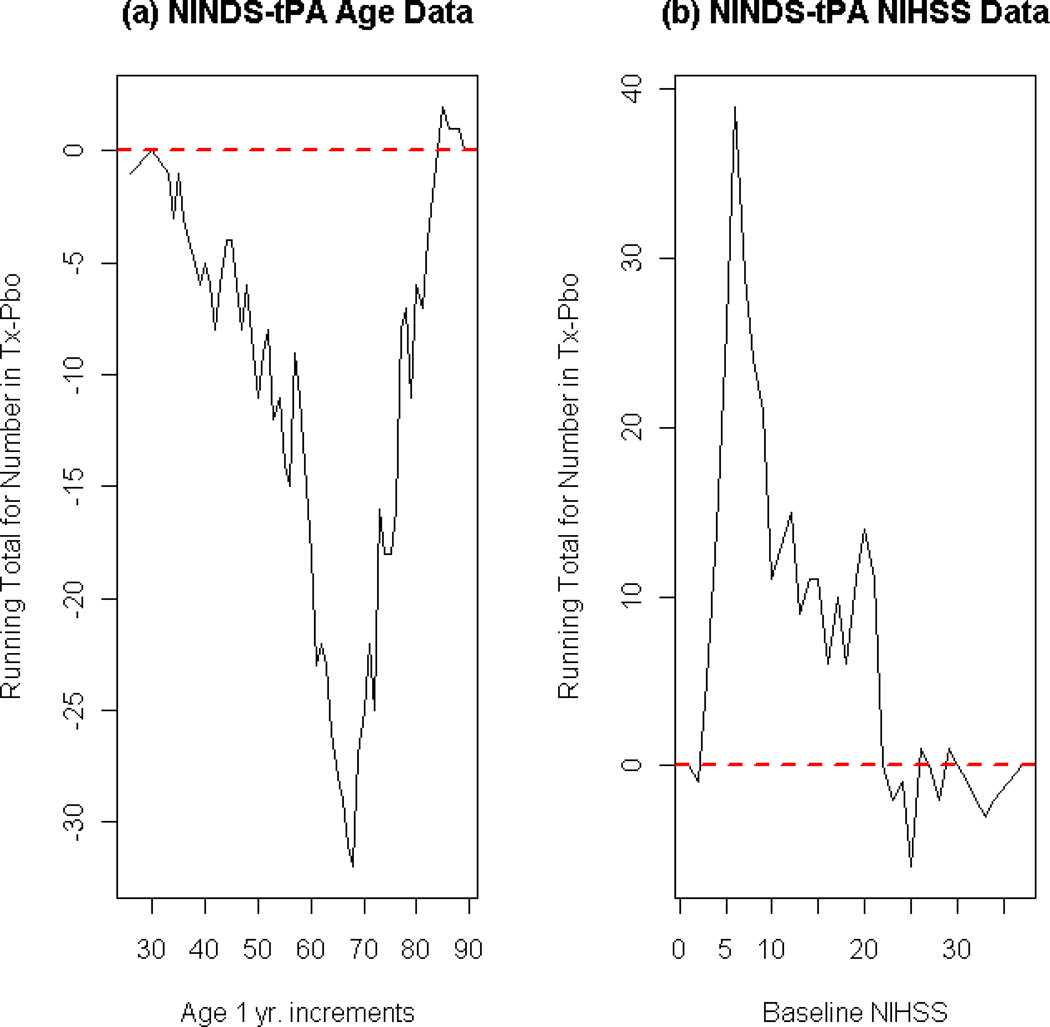
In the NINDS tPA Trial, the mean baseline age differed by two years (p-value=0.03) between the treatment arms, and the mean baseline NIHSS score across treatment groups differed by only one unit (p-value=0.14). A closer look at the distribution of cumulative differences of both variables across treatment groups reveals major imbalances that cannot be seen by examining the means alone. Figure 1 illustrates plots of the cumulative imbalances, D(x), for age and NIHSS. It is evident from these plots that the cumulative imbalance for each variable strays far from zero, suggesting large amounts of distributional imbalance. With such large baseline imbalances in these known predictors, the randomization design in the NINDS trial is questionable.

Figure 1. Baseline covariate imbalances in NINDS tPA dataset.

These plots represent the cumulative sum of imbalance as measured by the difference in the number of subjects in each treatment groups at each level of the respective covariate. Let F(x,j) be the number of subjects randomized to treatment arm j (j = 1,2) with the covariate value less than or equal to x. Then these plots illustrate D(x)=F(x,1)−F(x,2), the distribution of cumulative imbalances between the two treatment arms. Ideally, the curve of D(x) would frequently cross the zero (red, dotted) line in the entire range of the covariate, indicating a nearly balanced distribution of that covariate between the two treatment arms. (Tx: Treatment group receiving tPA, Pbo: Placebo group). (a)Cumulative sum of imbalances by level of age (1 year increments). Older subjects were assigned to treatment group. (b)Cumulative sum of imbalances by level of baseline NIHSS, which ranges from 0 to 42. Subjects with less severe strokes were assigned to treatment (tPA) group.

In addition to the NINDS tPA clinical trial, there have been several other controversial clinical trials whose criticism stems from baseline covariate imbalances. For example, the Breast Cancer Erythropoietin Trial (BEST) terminated early as a result of an observed higher mortality rate in the group treated with erythropoietin (Eprex) compared to the placebo group [22]. Upon termination, this trial had enrolled 939 patients across 139 sites in 20 different countries. Despite the increased death rates observed in the active treatment group, Leyland-Jones explains that the results of this trial are inconclusive as this group also showed an increased incidence of disease progression, increased incidence of thrombotic and vascular events (TVEs), higher average age, lower overall performance status, and increased incidence of other risk factors for TVEs when compared to the placebo group [22].

Furthermore, results from the Heart Outcomes Prevention Evaluation (HOPE) study [23] have also been criticized as a result of baseline covariate imbalances [24]. The study showed a decreased risk in cardiovascular events in subjects treated with angiotensin-converting-enzyme (ACE) inhibitor when compared to those in the placebo group. However, Taylor points out that the placebo group contained more subjects with cardiovascular risk factors including peripheral vascular disease, previous myocardial infarction, angina, previous cerebrovascular disease, and raised total cholesterol [24]. Thus, the results of this trial must also be interpreted with caution. In response to these comments, Sleight et al state that the observed imbalances are not statistically significant [25], but statistically insignificant imbalances in prognostic covariates can have a substantial effect on outcome [26].

Finally, it has been suggested that baseline imbalances may have effected overall study results in a clinical trial for efficacy and safety of recombinant activated factor VII for acute intracerebral hemorrhage (FAST) [27]. The purpose of the FAST study was to confirm previous findings from another study in which recombinant activated factor VII (rFVIIa) reduced growth of hematoma and improved survival and functional outcomes following intracerebral hemorrhage. In this study therapy with rFVIIa resulted in decreased hematoma growth, but no improvement was observed in survival or functional outcome. The authors state that “potentially important randomization imbalances were present.” Namely, larger proportions of patients with intraventricular hemorrhage, coma, and left ventricular hypertrophy were observed in the active treatment arm(s) compared to the placebo group at baseline. Imbalance in total lesion volume was also observed at baseline in this trial. The results of this trial were, therefore, not confirmatory, and further research is needed in this area [27]. An extensive list of controversial clinical trials can be found in Berger’s Selection Bias and Covariate Imbalances in Randomized Clinical Trials [28].

It is a common practice to include important baseline covariates in the final analysis model for a clinical trial to account for potential confounding, but the hope that any imbalances observed can simply be “adjusted away is no more than wishful thinking” [29]. The magnitude of the benefit in achieving baseline balance in the distributions of important continuous (or ordinal) predictors in a logistic regression setting is unclear. This research uses computer simulations in an attempt to quantify the effect on statistical power of detecting a treatment effect in a logistic regression model accounting for important baseline covariates with varying levels of imbalances across treatment groups in clinical trials.

3. Methods

3.1. Simulation assumptions

The NINDS tPA dataset served as a source for this simulation study and parameter values were obtained from the NINDS tPA descriptive statistics. The two covariates of interest were age and NIHSS. For the purposes of this simulation study, these were the only two covariates included in a simple logistic regression model for successful outcome at three months, defined as a Modified Rankin Scale (MRS) score of 0 or 1 [30, 31].

Standardized (mean centered, divided by standard deviation) NIHSS and age values from the NINDS tPA Trial data were used to model the overall response rate. The following simple logistic regression model was obtained by modeling success at three months in terms of the standardized variables and treatment. This model was used to simulate successful response in the simulation algorithm:

$$\text{log}({\mathit{\text{odds}}}_{\mathit{\text{success}}})=-1.3-0.3x_1-1.2x_2+0.8I(tPA),$$ (1)

where x₁ corresponds to age, x₂ corresponds to NIHSS, and I (tPA) is an indicator variable for active treatment (tPA). All simulations assumed only two treatment groups and for each subject simulated, two covariates were sampled from a standard normal distribution. If a sampled value was outside 3 standard deviations from the mean, it was resampled from the standard normal until a sampled value within 3 standard deviations was obtained. This was done to ensure that a valid range for the covariate of interest was obtained for each sample. Equation (1) was used to generate a probability of successful response. Adjustment was made for these two covariates in the analysis of each simulation dataset.

3.2. Measurement of imbalance

Imbalance in the sampled covariates of interest was measured by a rank-sum ratio (RSR). Within each sample, the values of each of the covariates were ranked from 1 to N, where N is the total sample size. Then, the ratio of the sum of the ranks in the treatment group to the sum of the ranks in the placebo group was calculated as the measurement of imbalance. For example, to calculate the RSR for the age variable in a clinical trial with 2 treatment groups, a total sample size of 100, and 50 subjects per treatment arm, we would first rank all age values in order from 1 to 100. Let r_ij be the rank for individual i (i=1,…,50) in treatment group j (j=1,2). Then, the rank-sum ratio for age can be calculated as

$$RS{R}_{\mathit{\text{age}}}=\left(\sum _{i=1}^{50}{r}_{i1}\right)/\left(\sum _{i=1}^{50}{r}_{i2}\right).$$ (2)

Ideally, this value would stay close to 1, but large imbalances correspond to large deviations from 1.

This measurement of imbalance was chosen for continuous covariates since it does not require any distributional assumptions, and it is analogous to several nonparametric test statistics [32]. It can be shown that if the two treatment groups have equal sample sizes, the worst case scenario (i.e. the lowest/highest 50% of values belong to the treatment group) imbalance for a single variable approaches 3 or 1/3 (depending on which 50% of values are in the treatment group) as the overall sample size approaches infinity. In this research the RSR was calculated using the ranks of the active treatment group in the numerator and the ranks of the placebo in the denominator. This means that for a covariate negatively associated with outcome, a RSR greater than 1 suggests an imbalance that “favors” the placebo group or results in a poorer baseline prognosis for the active treatment group.

3.3 Simulation algorithms

All simulations were conducted in R (version 2.10.0) and simulated a clinical trial involving two treatment arms. The scenarios investigated in these simulations were the worst case scenario, simple random allocation, randomized block allocation to ensure equal sample sizes, and an ideal scenario that attempted to achieve perfect balance across treatment and placebo groups. Sample sizes of N=50, 100, and 300 were investigated under each of these scenarios. Additional scenarios that allowed for varying levels of influence on outcome for the variable corresponding to NIHSS (x₂) were also investigated.

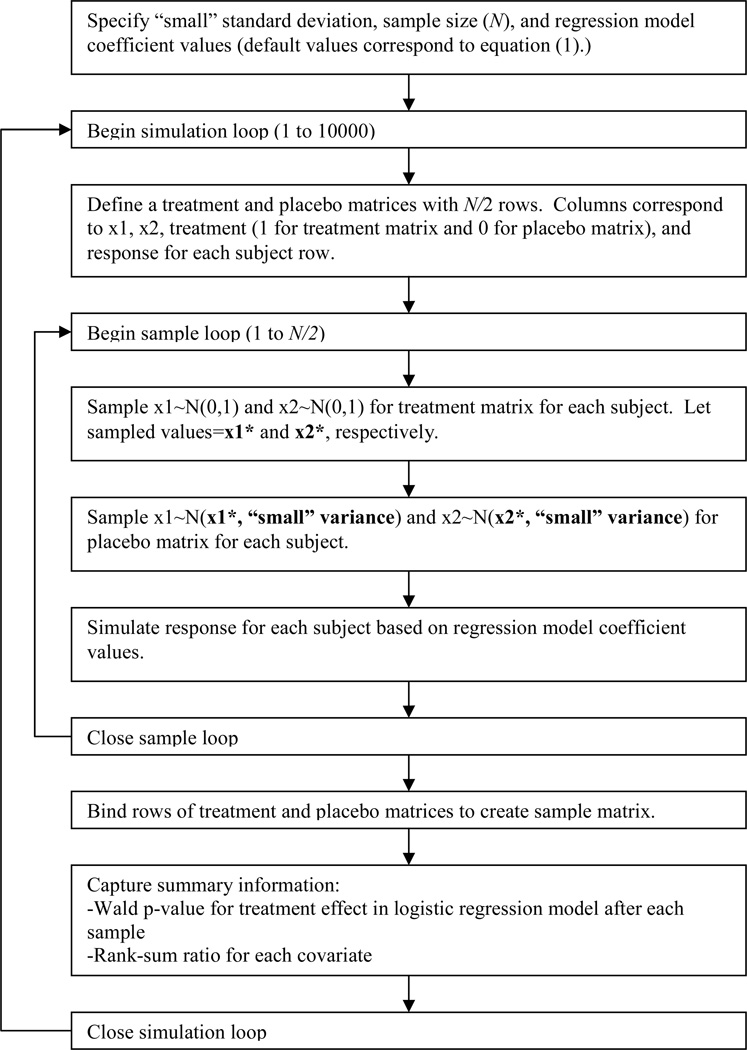
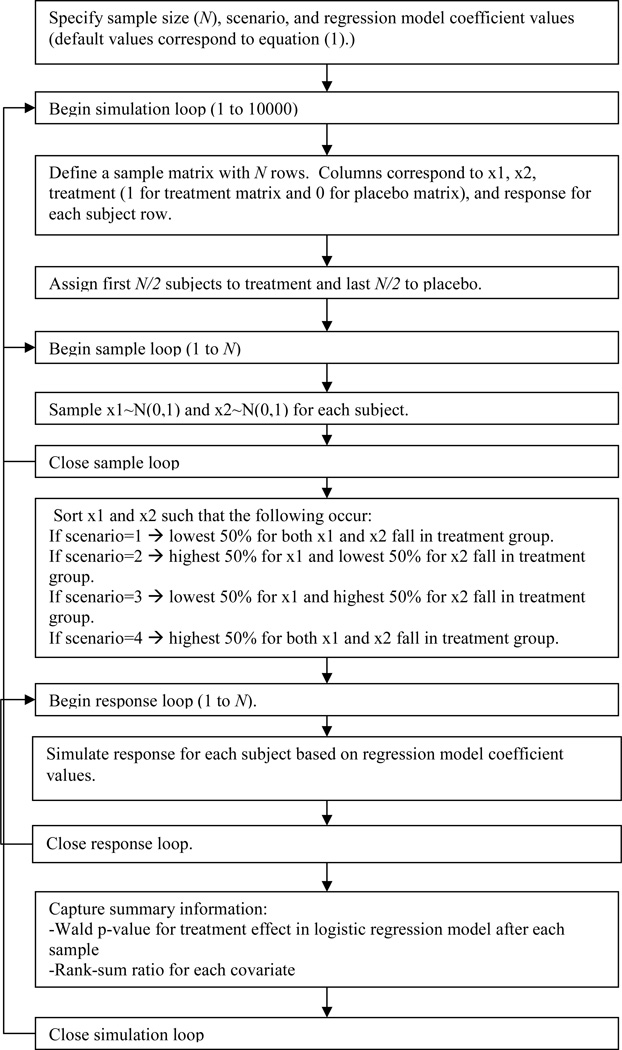
Flow charts of the simulation algorithms for the ideal scenario as well as the worst case scenario can be found in Figures 2 and 3, respectively. For the ideal scenario, both covariates were sampled from a standard normal distribution for the treatment group. The placebo group values were sampled from normal distributions centered at the corresponding treatment sample realizations with very small variance (standard deviation=0.001) so as to essentially match treatment and placebo groups while still allowing for slight variation. For the worst case scenarios, both covariates were again sampled from standard normal distributions. Then the sampled values were ranked from 1 to N, and, depending on the scenario, the upper or lower 50% of these values were placed in the treatment group, and the remainders were placed in the placebo group.

Figure 2. Simulation flow chart for the ideal scenario.

This flow chart explains the basic logic in the computer algorithm that ensured the ideal level of balance in covariates of interest. Note that a trivial level of variation between treatment and placebo groups was allowed to exist.

Figure 3. Simulation flow chart for the worst case scenario.

This flow chart explains the basic logic in the computer algorithm that ensured the worst case imbalance in covariate distributions of interest. Note that there were four possible scenarios since there were two baseline covariates of interest.

The simple random allocation algorithm simply assigned each subject to treatment or placebo with 50% probability, and the randomized block allocation used a blocking scheme to ensure equal sample sizes across treatment groups. The next section presents the simulation results for each of the simulation scenarios investigated.

4. Results

4.1. Rank-sum ratio and its distribution

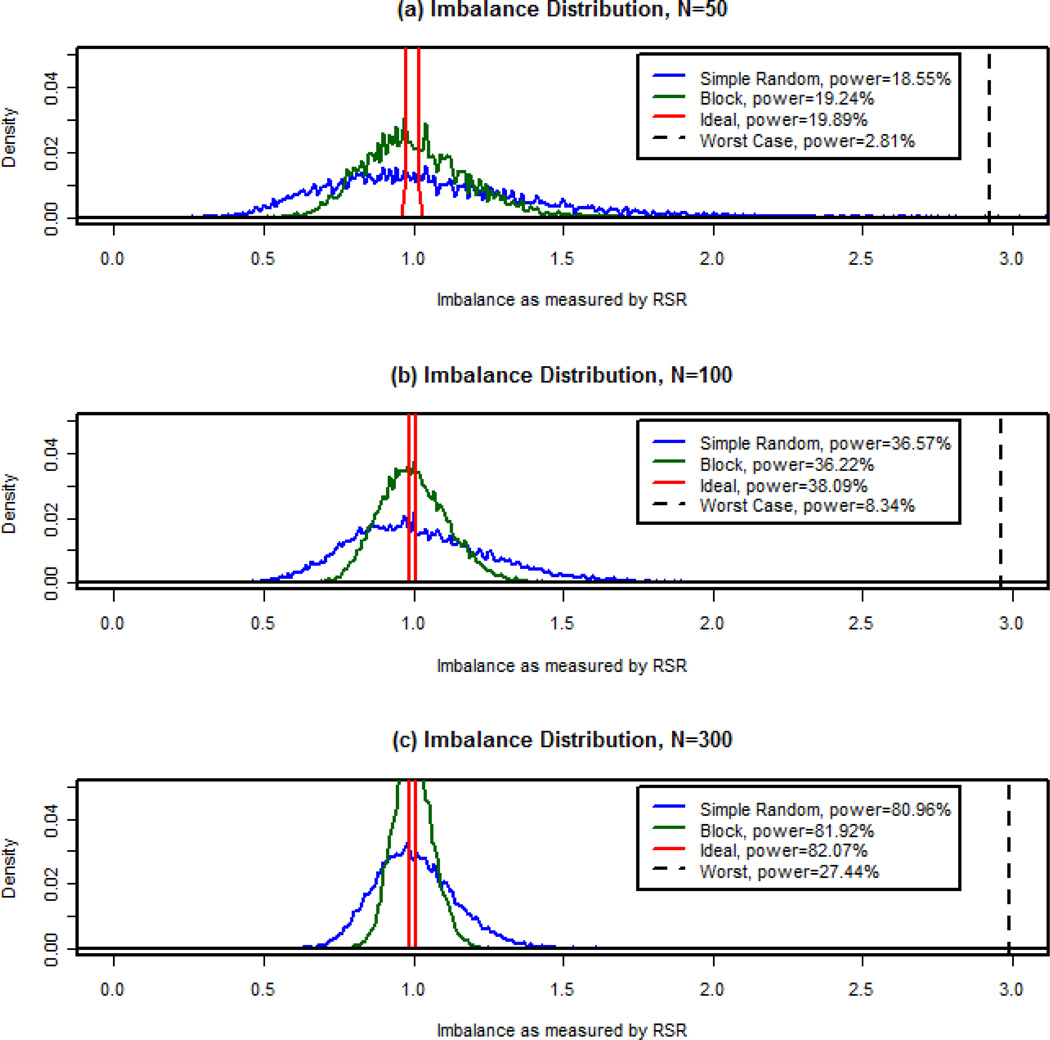
Figure 4 shows empirical imbalance densities across 10,000 simulations for each scenario examined for the variable corresponding to NIHSS. Among the four worst case scenarios examined (see Figure 3), the worst performing scheme in terms of power occurred when the lower 50% of the first covariate (the less influential variable, corresponding to age) and the highest 50% of the second covariate (the more influential variable, corresponding to NIHSS) fell in the treatment group; this is the worst case scenario illustrated in Figure 4. The number of successful treatment effect detections as determined by a Wald p-value less than 0.05 out of the 10,000 simulated samples was used to estimate statistical power of treatment effect detection. These values are reported in the legend for this figure. The greatest power was achieved in the ideal scenario, and the smallest power was achieved in the worst case scenario for each sample size.

Figure 4. Distribution of imbalance.

These plots show the empirical probability densities for the imbalance measurement as determined by the RSR (rank-sum ratio) for each simulated allocation scenario (simple random allocation, blocked, ideal, and worst case) based on 10,000 simulations. The estimated power for the main effect of treatment is shown in the legend for each scenario. Sample sizes of (a)50, (b)100, and (c)300 are shown here.

The ideal scenario RSR showed very slight deviations from 1, implying nearly perfect covariate balance across treatment groups. The maximum values under this scenario for sample sizes of 50, 100, and 300 were 1.033, 1.010, and 1.002, respectively. On the other hand, since the simple random allocation scheme does not ensure equal sample sizes, it is possible for the imbalance measure to exceed that of the worst case scenario (which assumed equal sample sizes across treatment groups). For a sample size of 50, this occurred 18 out of 10,000 times (or 0.18% of the time). As the sample size increased, the probability of simple randomization resulting in imbalance greater than or equal to that observed under the worst case scenario quickly diminished (0.01% of the time for sample size of 100). In fact, once sample size reached 300, an imbalance of this magnitude was never observed. Under the random block allocation scheme, the worst case imbalance never occurred in these simulations. From this information and the plots in Figure 4, it is evident that as sample size increased, the distribution of the RSR remained more closely centered around 1.

4.2 Power analyses

Recall that ideal scenario had the largest power for all sample sizes while the worst case scenario had the smallest power for all sample sizes. Since both of these designs are impractical and simple random allocation is not commonly used, it may be more appropriate to examine the random block scenario that ensures equal sample size (as long as all blocks are filled at the end of the trial). Also, recall that the simulations assumed the treatment effect was detected successfully if the Wald p-value for a particular simulation was less than 0.05. Thus, one could argue that the smaller the p-value, the larger the power.

In order to better characterize the distribution of the imbalance measure (i.e. to simulate a larger number of extreme RSR values), an additional one million simulations were run using the blocked randomization scheme to ensure equal sample size. Sample sizes of 50, 100, 300, and 500 were used to simulate one million clinical trials with varying levels of influence for x₂, the variable representing NIHSS. The distributional results for the Wald p-value for treatment effect and power associated with each scenario can be found in Table 1. The magnitude of influence for this variable is defined by the logistic regression coefficient associated with this variable in generating a positive response for each simulated subject. In the model dataset, this coefficient value was −1.2 as shown in equation (1). Coefficient values of −2.4 and −0.5 were also used to simulate response in order to examine the impact of the influence level for the variable of interest on power. The results under each level of influence can be seen in Table 1.

Table 1.

Distribution of p-value and Power Estimates Based on 1 million Simulations in Random Block Scenario.

Sample Size	Influence Levela	10th Percentile	Median	90th Percentile	Power Estimate
50	0.5	0.018	0.206	0.785	22.14%
50	1.2	0.022	0.229	0.801	19.64%
100	0.5	0.004	0.079	0.586	41.44%
100	1.2	0.005	0.100	0.638	36.92%
100	2.4	0.011	0.154	0.731	28.05%
300	0.5	<0.001	0.003	0.076	86.34%
300	1.2	<0.001	0.005	0.111	81.77%
300	2.4	<0.001	0.015	0.235	68.98%
500	0.5	<0.001	<0.001	0.008	97.66%
500	1.2	<0.001	<0.001	0.016	95.96%
500	2.4	<0.001	0.002	0.057	88.92%

^aInfluence level is measured by the absolute value of the magnitude of the logistic regression coefficient for the variable corresponding to NIHSS in the model used to simulated response. In the model dataset the regression coefficient was −1.2 as seen in equation (1). Values of −0.5 and −2.4 were also examined (The value of −2.4 is not reported here for sample size of 50 due to convergence issues in the analysis model for these simulations). It should be noted that the effect of this covariate is in the opposite direction of the treatment effect.

As one may expect, the level of influence of the variable of interest had a substantial impact on power. The purpose of Table 1 is to illustrate that for a given sample size, the power estimate decreased as the level of influence for the covariate of interest increased. Similarly, the distribution of the p-values shifted in a positive direction as the level of magnitude of influence increased.

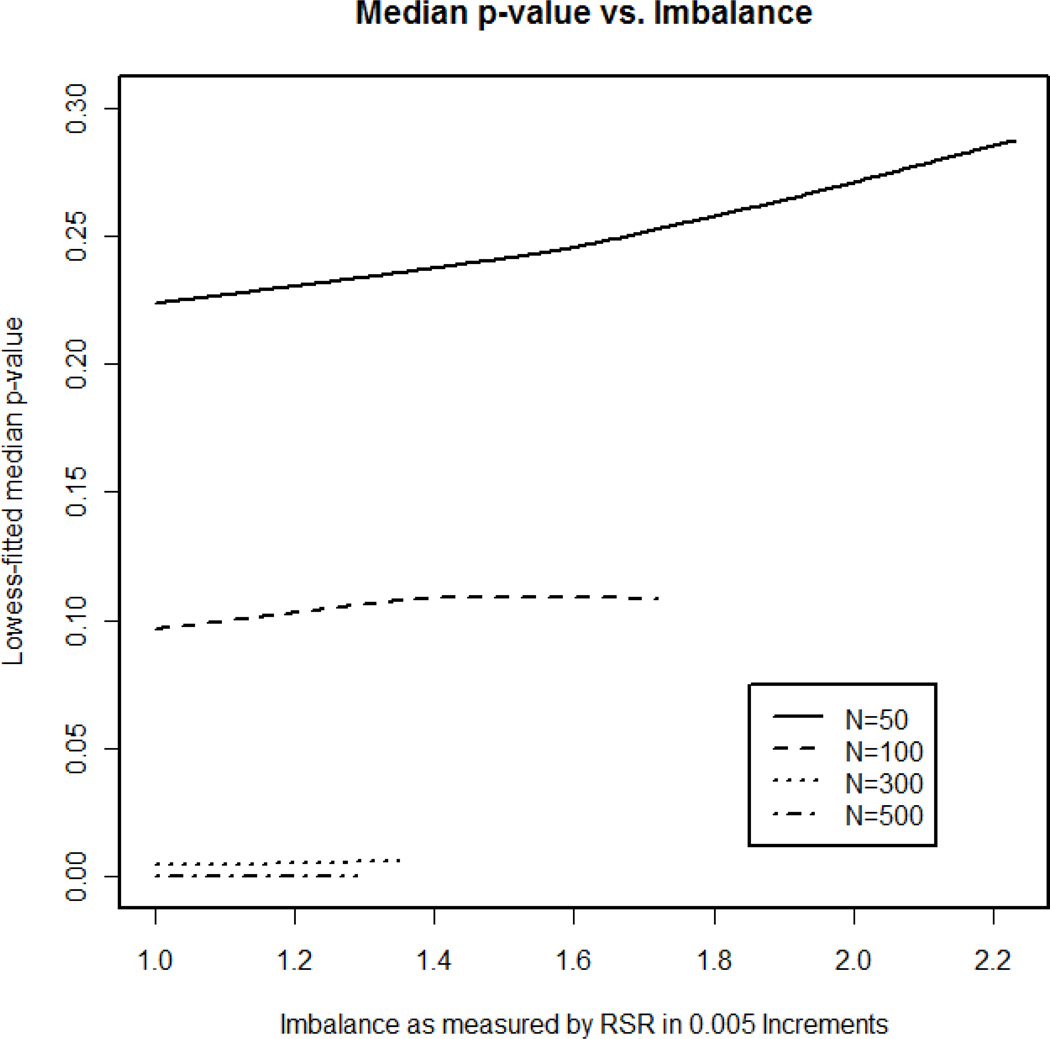
In order to determine whether imbalance can predict power, separate datasets were created in each scenario for the imbalance measure (RSR) in increments of 0.005, ranging from 1 to the maximum imbalance observed for that scenario. The median p-value in each of these datasets was calculated and plotted versus the RSRs to illustrate the impact of RSR on power. Figure 5 illustrates the lowess smoothing line [33] for median p-value versus level of imbalance for these newly created datasets for each sample size, using the magnitude of influence observed in the model dataset (logistic regression coefficient for x₂ is −1.2 as in equation (1)). As imbalance increased (i.e. as RSR strayed from 1), the median p-value for detecting treatment effect increased (i.e. power decreased), but the slope of the lowess line in Figure 5 appears to approach zero as sample size increases. Therefore, as sample size grew, the magnitude of the effect of imbalance on power decreased. It should be noted that the number of observations in each of these datasets quickly diminished as RSRs deviated from 1. Although the additional million simulations were conducted to combat this issue of sparse data for large imbalances, greater variation was observed in the median p-values for datasets representing extreme imbalance. For this reason, the plot in Figure 5 should be interpreted with caution for extreme levels of imbalance.

Figure 5. Median p-value versus imbalance.

The data in these plots come from the 1 million simulations under the blocked scenario to ensure equal sample sizes. The 1 million simulations were divided by rank-sum ratio (RSR) increments of 0.005, ranging from 1 (the minimum) to the maximum value observed under each sample size. The lowess-fitted median Wald p-values for detection of a treatment effect are plotted for each imbalance level. The sample sizes explored were N=50, N=100, N=300, and N=500. The lines illustrate a definite positive trend. As imbalance increases, the predicted median p-value observed also increases, and this will in turn correspond to a decrease in power. It should be noted that the most extreme levels of imbalance must be interpretted with caution due to the scarcity in RSR observations at these values. As sample size increases, magnitude of the effect or RSR on median p-value decreases as the lowess lines for N=300 and N=500 are nearly horizontal.

For a sample size of 100, all simulations were combined into a single dataset to model successful detection of treatment effect given β (“beta”), the logistic regression coefficient for x₂, and RSR. The following model was developed:

$$\text{log}({\text{odds}}_{\text{detection}})=-0.803+0.136\mathrm{\beta }-0.036{\mathrm{\beta }}^2+1.147(\mathrm{R}\mathrm{S}\mathrm{R})-0.568{(\mathrm{R}\mathrm{S}\mathrm{R})}^2-0.074\mathrm{\beta }(\mathrm{R}\mathrm{S}\mathrm{R})$$ (3)

The Hosmer-Lemeshow goodness of fit test [34] shows marginal evidence against goodness of fit for this model (p-value=0.04), but each term is highly significant (i.e. p-value<2E–16). This model can be used to determine an estimate for power given a RSR and a particular level of influence for x₂ assuming a sample size of 100.

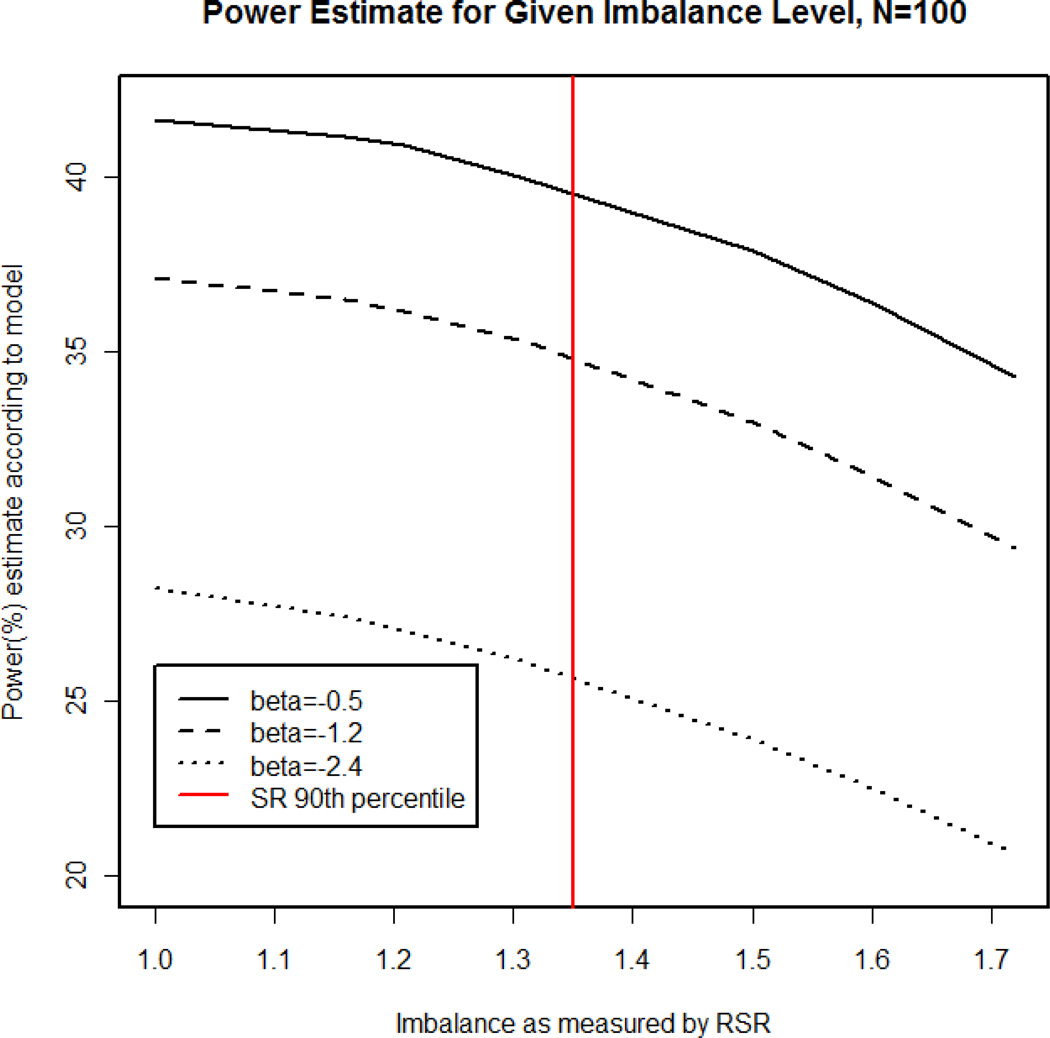
Figure 6 illustrates the power estimates based on this model for a given level of imbalance (i.e. RSR) at each β value explored in these simulations. From this figure it is evident that as RSR moves away from 1, the estimated power of treatment effect detection (according to the model) decreases for every level of covariate influence examined in these simulations. In addition, Figure 6 shows the 90^th percentile value under the simple random scenario. According to this model, for a β = −1.2 (as in the model NINDS tPA Trial dataset), simple random allocation had a 10% chance of exhibiting an imbalance of 1.350 or larger, corresponding to an estimated 2.2 % decrease in power when compared to the ideal scenario (RSR=1.0). The maximum level of imbalance observed in the 1 million simulations under the block scenario was 1.719. The probability of simple random allocation resulting in an imbalance this large was 1% in these simulations, and this corresponds to a 7.74% decrease in power.

Figure 6. Power estimate based on generalized linear model for a given imbalance level.

Using equation (3) from the Results section, the power estimates were calculated for several levels of imbalance as measured by RSR (rank-sum ratio) and plotted here for varying levels of influence for the covariate of interest (logistic coefficient or “beta”=−0.50, −1.2, and −2.4). The 90^th percentile for the simple random (SR) allocation scheme is also indicated here for reference.

5. Discussion

Balancing baseline covariates across treatment groups is important not only for face validity, but it also decreases excess noise in clinical trial data to allow for increased likelihood of detecting the treatment effect. This simulation study explored the magnitude of this effect on power for the logistic model framework even when adjustment is planned for these covariates. Balance in covariate distributions becomes important in clinical trials with sequential subject enrollment in case of early stopping, interim analyses, and to ensure maximal power in primary and secondary outcome analyses [15]. It is true that failure to include any known important covariates in a logistic regression model for final primary outcome results in biased treatment effect estimates [35], and regardless of observed imbalance or balance of important covariates, these variables should always be included in logistic regression models for primary outcome in order to prevent bias and achieve maximal power [35–37]. This simulation study has shown that the ideal level of balance in continuous prognostic factors, although impractical, may result in increases in power even when adjustment is made for these variables in analysis. On the other hand, the worst-case level of imbalance, although extremely rare, could occur when the covariate is excluded from the randomization scheme, and it has a potential to result in large loss in power. Therefore, every effort should be made to balance known important covariates at baseline in order to ensure that the rare case of severe imbalance does not occur and to protect from power loss.

The balance in the distribution of a covariate across treatment arms is controlled by the randomization only when the covariate is included in the randomization scheme. The most commonly implemented methods including covariates in the randomization scheme are stratification and minimization [15]. Stratification controls covariate imbalance via the balancing of treatment allocation within each stratum formed based on covariate categories. Minimization controls the imbalances at each margin of covariate categories. Both methods require categorization if the covariate is continuous. Atkinson has shown that these methods result in substantial statistical loss when the stratified covariates do not come from truly discrete distributions, and their balancing ability quickly approaches that of simple randomization when categorizing highly skewed covariate distributions [38]. Developments from Begg, Iglewicz [8], and Atkinson [9] include optimal techniques based on linear models that have the capacity to account for continuous covariate distributions, but these designs have not been explored fully (especially for nonlinear relationships) and remain unpopular today [1, 15].

Greevy, et al. have outlined an allocation method involving optimal matching that accounts for categorical and continuous covariates when all subjects for a clinical trial are available at once [14]. In the authors’ simulation study, average efficiency for optimally matched samples was about 7% larger than unmatched samples, equating to a 7% increase in sample size in the linear model framework at no additional cost. This method does not apply to sequential clinical trials.

Some less well-known treatment allocation algorithms have been developed to tackle continuous covariate balancing in sequential trials, but they have gained little recognition. Endo, et al. have attempted to tackle the issue of continuous covariate balancing for sequential clinical trials using Kullback-Leibler Divergence (KLD) [12], but this method, like the optimal designs, remains to be explored theoretically and implemented in clinical trials. Nishi and Takaichi have also proposed a minimization method that minimizes a weighted sum of the differences in means and standard deviations of continuous prognostic covariates between treatment groups [11]. To the authors’ knowledge, this method has not been implemented. In addition, Frane has suggested an adaptation to the biased coin design for continuous covariates. This procedure favors allocation to the treatment group assignment resulting in the largest p-values for t-tests and analysis of variance (ANOVA) comparing continuous variables across treatment groups [13]. A method similar to this was actually implemented in the design of the controlled rosuvastatin multinational study in heart failure (CORONA) [39, 40]. Although detail of the treatment allocation algorithm was not included in the article(s) reporting the study results, this information was provided by an anonymous referee. Similarly, Aickin explains an allocation algorithm in which logistic regression models for treatment assignment (given all important covariates of interest) are fit under each potential treatment assignment for an entering subject. The treatment allocation chosen for the current subject is that corresponding to the logistic regression model with the smallest likelihood [10]. The algorithms discussed here to control continuous covariate imbalance at baseline have had very little publicity when compared to the popular stratified block and minimization designs.

To our knowledge, a randomization scheme based on RSR (rank-sum ratio) minimization has not been developed or implemented in practice. However, Stigsby and Taves have recently proposed a similar method of rank-minimization as a simple and effective allocation method for controlling imbalance in covariate distributions [41]. This method has yet to be explored in terms of power advantages or disadvantages as well as balancing capabilities in comparison to the optimum designs. Further research in this area involves development of a RSR minimization algorithm and comparison with the rank-minimization method of Stigsby and Taves as well as comparison with additional continuous covariate balancing algorithms.

As the treatment allocation scheme shifts away from complete randomization toward constrained and/or covariate-adaptive designs, standard methods of statistical analysis may no longer be valid. Most statistical analyses for a clinical trial assume independence between subjects, but this assumption is not necessarily valid in these sequential allocation schemes as each subject’s treatment assignment depends on the previous assignments. Friedman, Furberg, and DeMets [2] suggest using simulation studies to determine an appropriate significance level for the statistical tests to be conducted in clinical trials using constrained or covariate-adaptive allocation schemes. The authors suggest analysis of covariance (ANCOVA) when minimization or adaptive stratification allocation schemes have been used, and failure to adjust overall significance level would result in an error on the conservative side for clinical trial analysis with the exception of non-inferiority trials [2]. In any case, adjustment should be made in the final analysis for those covariates controlled at the design phase as well as any known influential covariates.

The majority of research in the topic of randomization has focused on continuous outcome variables and the effect that various treatment allocation schemes have on power and efficiency. Several authors have explored the effects of currently available allocation schemes on efficiency and power for continuous outcome variables [8, 9, 14, 38, 42], and the overall consensus is that better balance in covariates across treatment groups implies increased power. Rosenberger and Sverdlov have pointed out that balance in covariate distributions does not necessarily imply increased power over the imbalanced scenario in nonlinear models (e.g. when the outcome is binary) [43]. Little work has been done to examine the magnitude of the effect of balance or imbalance in important baseline covariates in a logistic regression setup. In this simulation study, better baseline covariate balance resulted in increased estimated power, and the effect on power was more substantial for small sample sizes and highly influential variables. It should be noted that this effect was only seen after running a very large number of simulations (millions) in several scenarios and combining all data into one extremely large dataset. The large numbers of simulations were conducted in order to better characterize the imbalance distribution at extreme values, but it is unclear whether the “highly significant” decrease in power predicted by the model presented in Section 4 is truly nontrivial or if it simply a result of an over-powered model as the dataset was so large.

Nonetheless, in a small to moderately sized clinical trial (N=50 or N=100), ignoring imbalances that may be observed as a result of pure random assignment has the potential to result in the worst case scenario level of imbalance in covariate distributions, and this imbalance may be associated with substantial loss in power. However, as sample size increased, the magnitude of the effect of imbalance on power diminished. Thus, it can be concluded that some attempt should be made to balance highly influential continuous covariates, especially in small sample sized clinical trials. As McEntegart and Greevy, et al. have pointed out, allocation schemes that control imbalance in baseline covariates can be seen as a “low-cost insurance policy” [15] against “rare disasters” that can be observed in a single realization of a random phenomenon[14].