Lagrangian postprocessing of computational hemodynamics

Abstract

Recent advances in imaging, modeling and computing have rapidly expanded our capabilities to model hemodynamics in the large vessels (heart, arteries and veins). This data encodes a wealth of information that is often under-utilized. Modeling (and measuring) blood flow in the large vessels typically amounts to solving for the time-varying velocity field in a region of interest. Flow in the heart and larger arteries is often complex, and velocity field data provides a starting point for investigating the hemodynamics. This data can be used to perform Lagrangian particle tracking, and other Lagrangian-based postprocessing. As described herein, Lagrangian methods are necessary to understand inherently transient hemodynamic conditions from the fluid mechanics perspective, and to properly understand the biomechanical factors that lead to acute and gradual changes of vascular function and health. The goal of the present paper is to review Lagrangian methods that have been used in post-processing velocity data of cardiovascular flows.

1 Introduction

The practical motivations for computational hemodynamics are to better understand blood flow in a particular region of the vasculature to (1) improve diagnosis of a cardiovascular problem, (2) better understand the hemodynamic underpinnings of cardiovascular disease initiation or progression, (3) evaluate and possibly improve how an intervention or device alters blood flow, or (4) gain more fundamental understanding of native cardiovascular function. These motivations are broad and have significant overlap.

The circulation serves to transport and exchange matter and energy throughout the body. The arteries and veins mostly serve a mechanical role in distributing blood between the heart and various microvascular beds where exchange processes take place. We restrict our discussion to the heart and larger vessels where inertial effects of blood flow are important and, in concert with local vascular morphology, can promote complex flow structures. Computational hemodynamics serves as a tool to probe such complex conditions for the purposes described above. From the physical perspective, disturbances in blood flow influence biology in two fundamental ways, (1) by imparting forces on cellular elements in the vessel wall or in the blood, and (2) by enhancing or suppressing transport to and from various regions. Quantitative analysis of spatially resolved hemodynamics data has largely focused on determining the fluid mechanic forces imparted on the vessel wall – and namely wall shear stress for its role in endothelial function [36] and growth and remodeling [64]. Quantitative analysis of transport is less common. This is not because it is less important, but because transport is an emergent, spatiotemporal phenomenon that is difficult to quantify.

The hemodynamics in larger vessels are typically studied using computational fluid dynamics (CFD), and particularly using an image-based framework [144]. After verification and validation, an important question that arises is how to properly use, or postprocess, the resulting data. CFD can provide highly resolved spatial and temporal velocity and pressure field information. However, the purpose of computing is insight, not numbers. Image-based simulations usually deal with complex domains and pulsatile unsteady flow. From the fluid mechanics standpoint, the inherent complexity of the flow makes interpretation difficult, which is confounded by uncertainty in what about the flow is meaningful–either from the clinical, biological or even numerical perspective. Moreover, modeling or measuring fluid flow often amounts to deriving velocity data, u(x, t). Not surprisingly, this predisposes the analysis of fluid mechanics to visualization of the velocity field, or closely related instantaneous measures. So while fluid flow, and especially blood flow, is traditionally analyzed in terms of instantaneous Eulerian fields, these measures often fail in conveying the integrated fluid behavior because their viewpoint is both frame-dependent and localized in time.

The scope of this paper is a discussion of methods used to postprocess hemodynamics velocity field data for purposes of understanding transport. It is biased to Lagrangian post-processing, which more naturally captures the spatiotemporal behavior of fluid flow than rate-of-change measures, especially when the flow topology is changing with time as is the case in most investigations of hemodynamics. The discussion mostly coincides with modeling blood as a homogeneous fluid, where blood is treated as a continuum in deriving the governing dynamics, which when solved typically provide velocity (and pressure) field information. This discussion also applies to measured velocimetry data. We do not discuss Lagrangian-based methods for modeling blood flow dynamics per se, e.g. methods that inherently model blood as a suspension and directly solve particle dynamics as part of the governing equations for blood flow [47]. Modeling blood as a suspension is mostly limited to very small scales and low Reynolds numbers, e.g. modeling flow in the microcirculation, where the hemodynamics are quite different than the flow in heart, arteries and veins.

2 Modeling advection from velocity data

The velocity field is the primitive variable used to describe fluid mechanics, including blood flow, and ostensibly describes how a parcel of blood, or an element carried by the blood, is transported. However, the velocity field is largely a mathematical construct, representing the instantaneous and differential change in a fluid element’s position with time. For unsteady flows, it is easy to misinterpret the physical behavior of the flow from inspection of the velocity data. Namely, the spatial and temporal variation of the velocity field can be simple and predictable, yet the motion of fluid elements integrated according to the velocity field alone can be surprisingly chaotic. This realization is important because it is the transport of blood elements over space and time, not the velocity field per se, that is more biologically relevant. Likewise, the relevance of other instantaneous fields derived from the velocity, or more commonly the velocity gradient (including most methods to identify “vortical” structures), to the integrated flow behavior is tenuous because a sequence of snapshots often fails to capture the emergent behavior of the integrated effect. Namely, it is challenging to characterize something that is always changing.

2.1 Eulerian approach

We refer to the motion of fluid elements according to the velocity field as advection. There are two main approaches for studying advection. The continuum approach models advection by a partial differential equation (PDE) and each fluid element is assumed to transport some property or concentration, which might not be strictly invariant due to flux on the sub-element scale (diffusion). This viewpoint commonly leads to the advection-diffusion (AD) equation modeling the transport of the scalar field c(x, t) according to

$$\frac{\partial c}{\partial t}+\mathbf{u}·\nabla c=\nabla ·(\mathbf{K}·\nabla c)+s,$$ (1)

where u(x, t) is the velocity field that is assumed known, K is the diffusivity tensor, and an arbitrary source/sink (or reaction) term s has been added for generality. The material derivative on the left hand side can be thought of as an artifact of using an Eulerian viewpoint to describe the variable c. Therefore, we view the AD equation as an Eulerian approach to studying transport.

Non-dimensionalizing Eq. (1) using a characteristic length L, velocity magnitude u₀ and corresponding (advective) time L/u₀, along with dropping the source term and assuming isotropic diffusion (K → κ), the AD equation can be written in familiar form

$$\frac{\partial c}{\partial t}+\mathbf{u}·\nabla c=\frac{1}{Pe}\nabla ·\nabla c,$$ (2)

where Pe = u₀L/κ is the Peclet number. For red blood cells, platelets and most macro-molecules transported in blood κ is less than (10⁻⁷ cm²/s) [27, 147]. For blood flow in vessels where the velocity field is typically computed or measured, u₀ = (1–10 cm/s) and L = (0.1–1 cm), yielding Peclet numbers generally larger than (10⁶). Recalling that Pe can be interpreted as the ratio of the diffusion response time (L²/κ) to the advection response time (L/u₀) it is clear that transport in larger vessels is heavily advection dominated and the right hand side can often be ignored.

Eq. (2) models the evolution of a scalar field, not discrete elements or particle trajectories. Although not common, the Eulerian approach can be used to compute the trajectories of individual fluid elements. We can “label” each material point in the domain by its initial location at some arbitrary (initial) time t₀. More formally, consider a point (x, t) ∈ Ω × I ⊂ ℝ³ × ℝ in space-time, which corresponds to a material point whose position as a function of time is denoted x(t), with x₀ ≐ x(t₀). Then we can define a labeling l : (x, t) ↦ x₀. This labeling is unique (by uniqueness of solutions) and invariant under the flow (by definition of a material point), and thus satisfies

$$\frac{\partial \mathbf{l}}{\partial t}+\mathbf{u}·\nabla \mathbf{l}=0.$$ (3)

This advection equation can then be solved and individual trajectories can be obtained as the intersection of level sets l_i(x, t) = x_0i for i = 1, 2, 3 in extended phase space, where l = (l₁, l₂, l₃) and x₀ = (x₀₁, x₀₂, x₀₃).

2.2 Lagrangian particle tracking

The alternative approach to studying advection is a (discrete) Lagrangian approach. Using this viewpoint, the position of a material point or tracer may be governed by the ordinary differential equation (ODE)

$$\stackrel{.}{\mathbf{x}}(t)=\mathbf{u}(\mathbf{x},t);\mathbf{x}(t_0)={\mathbf{x}}_0,$$ (4)

where the velocity field u(x, t) is assumed known and (x, t) ∈ Ω × I. Eq. (4) can be integrated to obtain the position of a tracer at a desired time

$$\mathbf{x}(t)=\mathbf{x}(t_0)+{\int }_{t_0}^t\mathbf{u}(\mathbf{x}(s),s)\mathrm{d}s,$$ (5)

using an appropriate numerical method.

The term Lagrangian particle tracking is often used to describe integration of tracers. However, the term “particle” is also often used to refer to objects with non-negligible size and mass (inertial particles), as modeled using dynamic relationships (force balances) rather than the direct kinematic equation of motion above (cf. §2.3). Regardless, there are generally two main objectives in Lagrangian particle tracking. The first is to better understand the transport topology by visualization or geometric quantification of particle paths. The second is to quantify the exposure of particles to some influence as they move through the domain, such as the level of shear stress or chemical exposure experienced by a cellular or sub cellular element (e.g. platelet).

Lagrangian particle tracking has been used in several cardiovascular applications to study transport. Ehrlich and Friedman [41] performed one of the first computational particle tracking studies in blood flow using an idealized 2D bifurcation model to determine a measure of stasis as the (normalized) distance traveled by a particle over one cardiac cycle. Perktold et al. [110, 112, 113] studied pathlines inside idealized aneurysms and observed complicated whirling motions hypothesized to promote thrombosis. More generically, the flow inside curved vessels has been studied by constructing trajectories traced from the inlet of the vessel to demonstrate recirculating and helical flow features [149, 56]. The carotid bifurcation is a common focus for hemodynamics research, due to the compelling correlations between atherosclerosis and separated blood flow in this region, and different studies have used particle tracking to better understand flow features in this region [111, 137, 139, 142, 92]. The effect of non-Newtonian blood rheology on tracer paths has been investigated in a 2D stenosis model [20], and in a 2D slice of an aneurysm where velocities were obtained from particle image velocimetry (PIV) [37]. Lagrangian particle tracking has also been used in evaluating surgical and device design, including optimal flow distribution in the design for the Fontan surgery [91, 157, 156]. Figure 1 shows an example of Lagrangian particle tracking for evaluating how blood is distributed in a surgery to treat congenital heart defects.

Figure 1.

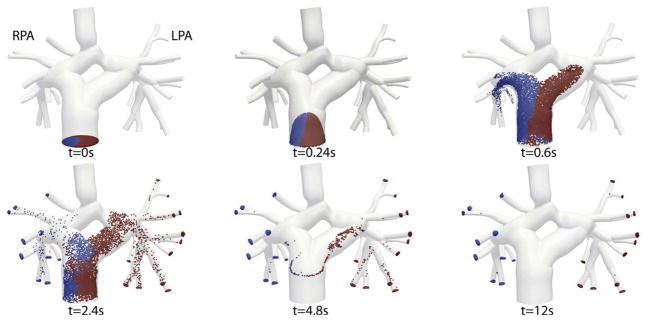
Lagrangian particle tracking in a Y-graft model used to quantify inferior vena cava flow distribution to the left (LPA) and right (RPA) pulmonary arteries. Figure from Yang et al. [157] with permission.

2.2.1 Comments on pathlines and trajectories

Note that solutions x(t) can be viewed as tracing out curves in Ω or in Ω × I; we refer to the former as pathlines and the later as trajectories. In this sense, a pathline is the projection of a trajectory. An implication is that pathlines of two material points may intersect each other or themselves, but trajectories do not intersect due to uniqueness of solution. We also tend to refer to the motion of a material point’s position x(t) in Ω as its trajectory–the duality being that a trajectory can be identified as a curve in Ω × I, or as a moving point in Ω when viewed over time.

As far as visualization, it is known that for unsteady flows streamlines are of questionable utility (or even misleading) since nothing physically flows along them. Direct integration of particle trajectories is needed to better understand how material is transported through the domain. This is achieved by visualizing pathlines or viewing trajectories of particles over time, however both approaches typically provide an intertwined mess that is difficult to interpret. This is perhaps why streamlines are commonly visualized even for unsteady applications; while nothing actually flows along them, they are visually appealing since they do not intersect. While trajectories in space-time do not intersect, visualization of curves in space-time (where time is a coordinate) is unintuitive and difficult to graph.

Pathlines are often plotted to visualize the flow structure of unsteady hemodynamics data. However, the flow structure revealed is highly specific to when the pathlines are initialized – a fact that is often overlooked. The path traced out by x(t) depends explicitly on its location at some “initial” time. Hence, the initial position(s) and time(s) particles are seeded in the domain can play a pivotal role in what is revealed about the flow. One way to consider this is to recall pathlines as the projections of trajectories. The trajectory lives in Ω × I, and hence projecting to some hyperplane (physical 3D space), which we denote Ω_t0, gives the pathlines seeded at t₀. These projections can look completely different as the projection hyperplane Ω_t0 varies with t₀. Moreover, we can have fundamentally different trajectories leading to the same pathlines.

These are not problems in steady flow, where points can be seeded and integrated forward and backward in time to map out the flow. The same is not true for pathlines for unsteady flow. Hence, pathlines in unsteady flows are inherently not as useful as pathlines (streamlines) in steady flows. As an aside, from the dynamical systems perspective, the flow generated by Eq. (4) is a one-parameter family : x₀ ↦ x(t; x₀) when u is independent of t; otherwise the flow is a two-parameter family ${\mathcal{F}}_{t_0}^t:{\mathbf{x}}_0\mapsto \mathbf{x}(t;t_0,{\mathbf{x}}_0)$ for time dependent u. One can map out the flow in space as integral curves parameterized by t for steady flows; such parameterized curves (pathlines) do not encode the flow for unsteady u since the extra parameter t₀ is not accommodated.

2.3 Inertial particle tracking

It is often desirable to model transport of particles in the cardiovascular system whose size and mass cannot be readily ignored. Embolic particles are an important example. Fundamental work into particle transport has a rich background in fluid mechanics, as reviewed by Michaelides [97]. The works of Maxey and Riley [95] and Gatignol [51] derive the following dynamical equation

$$m_p\frac{d\mathbf{v}}{dt}=m_f\frac{D\mathbf{u}}{Dt}+(m_p-m_f)\mathbf{g}-\frac{m_f}{2}\left[\frac{d\mathbf{v}}{dt}-\frac{D}{dt}\left[\mathbf{u}-\frac{a^2}{10}\mathrm{\Delta }\mathbf{u}\right]\right]-6\pi a\mu \left[\mathbf{v}-\mathbf{u}-\frac{a^2}{6}\mathrm{\Delta }\mathbf{u}\right]-\frac{6\pi a^2\mu }{\sqrt{\pi \nu }}{\int }_0^t\frac{1}{\sqrt{t-\tau }}\left[\frac{d\mathbf{v}}{d\tau }-\frac{D}{Dt}\left[\mathbf{u}-\frac{a^2}{10}\mathrm{\Delta }\mathbf{u}\right]\right]d\tau ,$$ (6)

where m_p and m_f are the mass of the (spherical) particle and displaced fluid respectively; g is the acceleration due to gravity; v and u are the velocity of the particle and fluid; a is the particle radius; and μ and ν are the dynamic and kinematic viscosities of the fluid, and $\frac{D}{Dt}$ and $\frac{d}{dt}$ are the material derivatives following the fluid and particle. The first term on the right is the sum of the hydrodynamic forces an equivalent fluid sphere would experience. Including this term and neglecting the rest would model the particle as a fluid element, equivalent to using Eq. (4). The next term is the buoyancy force. The remaining three terms are essentially drag forces: the first is the added mass effect, the next is the steady (Stokes) drag, and the last (Boussinesq/Basset/history) term accounts for diffusion of vorticity. These last three terms include the Δu Faxen corrections, which account for local non-uniformity of the velocity field.

Equation (6) can be derived by assuming the relative Reynolds number, based on the difference between the particle velocity and the fluid velocity, is small, and that the particle is small compared to the length scale of the background flow. The application of Eq. (6) is often extended beyond these realms [97]. To a first order approximation, most emboli can be considered spherical in shape, but Eq. (6) can also be used to understand the motion of irregular particles. In such cases, the irregular particle can be modeled in terms of a equivalent diameter particle. Alternatively, if more information is known about the shape, e.g. discoid or spheroid, a theoretical or empirical correction can be added as appropriate [30, 73]. Eq. (6) does not account for hydrodynamic lift, which can be added accordingly [96, 73] such as in locations of high shear (Saffman lift) or for rotating (Magnus lift) or non spherical particles.

An early computational study simulating inertial particle dynamics in a steady, 2D bifurcating artery was performed by Nazemi & Kleinstreue [105], and looked at impact locations of cellular (dia = 5μm sphere) particles in the bifurcation. Kleinstreuer et al. [65, 66, 21] later used the same methods in 3D geometries to correlate various wall shear stress (WSS) metrics to particle deposition sites. Basciano et al. [11] similarly looked into the transport of inertial particles inside an abdominal aortic aneurysm (AAA) with relation to stagnation and thrombus formation. These studies assumed deposition occurred when the distance of the center of the particle from the wall was within a specified threshold. Since chemical or biophysical affinity of the vessel wall and particle are likely crucial parameters for wall deposition, a more refined deposition model was proposed by Kim et al. [72] in the context of inertial particle tracking. Other modeling of inertial particle dynamics employed in the study of blood flow includes modeling the separation of different blood constituents [33].

Many studies including the above have primarily focused on modeling the transport of blood cells as inertial particles in large artery flows. This sets up inherent inconsistencies that are difficult to reconcile. Prior to applying Eq. (6), or a similar one-way coupled particle dynamics model, blood is modeled as a fluid, i.e. a continuum, to derive the velocity field u(x, t). In most large vessels, blood is a dense suspension, but when endowed with a proper rheology, blood can be modeled as a homogeneous fluid and the macroscopic mechanical behavior can be effectively recovered. However, this does not reasonably imply one can go back and use the flow field to model the dynamics of cellular elements as a dilute solution surrounded by a homogeneous fluid. Unlike in dilute suspensions, there is not a compelling expectation that individual cells of blood are dominated by fluid forces as described by Eq. (6). Rather intercellular collision and adhesion forces are likely as dominant, if not more dominant, than inertial and drag forces on this scale. Moreover, the fluid mechanics is not being resolved on the micron scale per se, since blood cannot be modeled as homogeneous on this scale. It is perhaps more consistent to assume cellular elements are advected by the velocity field, and possibly with diffusive (not necessarily Brownian) motion superimposed, as in e.g. [114]. That is, modeling cells as experiencing more “sub-element” effects versus “super-element” effects.

For particles whose size is large compared to that of a blood cell, blood may effectively be treated as a homogeneous fluid from the particle’s perspective, which imposes hydrodynamic forces according to Eq. (6), or similar dynamical model. This may be relevant in modeling of embolic particles, which has previously been performed to model thromboemboli [107, 28]. The Stokes number (characteristic time of a particle to characteristic time of the flow) of cellular elements is typically < 0.001 in larger arteries and hence cells can be treated as material points. The Stokes number for thromboemboli can easily become close to 1. Hence an important consideration is how might the transport of inertial particles, especially to different locations in the circulation, differ from the distribution of blood flow. This is especially true for particles originating from the heart, which are a leading cause of stroke and whose possible destination is less obvious or consequential than for particles originating elsewhere in the circulation. Carr et al. [28], demonstrated that the transport of inertial particles from the heart to the cerebral arteries can vary markedly from the distribution of blood flow, and the relationship to particle size is not monotonic as one might expect. Fig. 2 is a visualization of inertial particle tracking through an aortic coarctation that differentiates between particle to the upper aortic branch arteries and the descending aorta.

Figure 2.

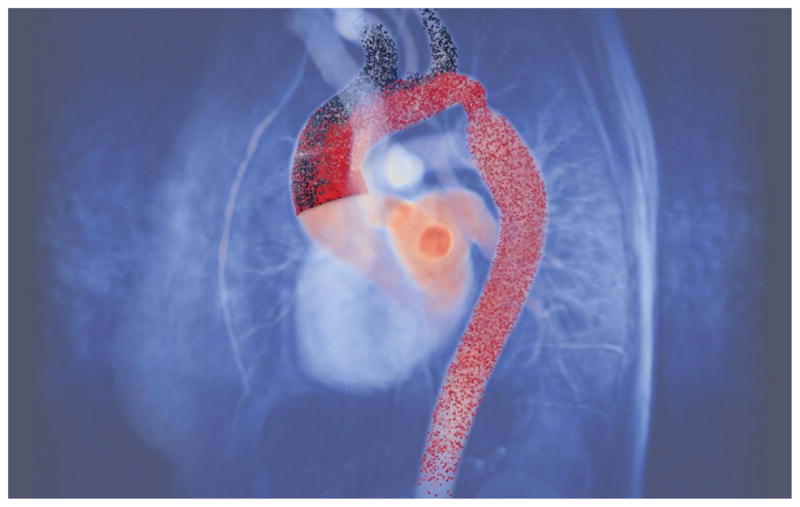
Tracking inertial particles from the aortic valve through an aortic coarctation model. Particles are colored according to whether they are transported to the descending aorta or aortic arch branch arteries using methods described in [28].

As consistent with the scope of this paper, Eq. 6 employs a one-way coupling whereby the particles are assumed to not affect the velocity field (and particle-particle interactions are ignored as reasonable for low particle concentrations). Whether a one way coupling is a reasonable assumption or not depends on the particular application. There are several variations in how, and to what extent, the fluid and particle dynamics may be more fully coupled. Given the complexity of cardiovascular flow modeling, few studies have investigated fully-coupled particle dynamics simulations in comparison with one-way coupling. However, in a recent study, a two-way coupling approach was used to track the distribution of particles of different size and density in circle of Willis [44], which reported a slight change in velocity contours between one- and two-way coupled methods, but did not report how that influenced particle distributions.

2.4 Lagrangian Helicity

The number of flow descriptors that have been used to characterize fluid mechanics from velocity field, or its derivatives, are too numerous to discuss. However, one descriptor that has seen repeated use in cardiovascular applications is Lagrangian helicity. Helical motion of blood flow is often observed in arteries. Helicity density is defined as the inner product of velocity u(x, t) and vorticity ω(x, t) = ∇ × u(x, t) [98]. Grigioni et al. [56] introduced the local normalized helicity

$$\text{LNH}(\mathbf{x},t)=\frac{\mathbf{u}(\mathbf{x},t)·\omega (\mathbf{x},t)}{\Vert \mathbf{u}(\mathbf{x},t)\Vert \Vert \omega (\mathbf{x},t)\Vert }.$$ (7)

They integrated this measure along tracers to measure Lagrangian helicity

$${\mathit{hfi}}_k=\frac{1}{T}{\int }_{t_0}^{t_0+T}\mid {\text{LNH}}_k(s)\mid \mathrm{d}s,$$ (8)

where the calculation is done for the k’th tracer. Repeating the calculation for different tracers a mean quantity called the helical flow index (HFI) was obtained

$$\text{HFI}=\frac{1}{N_p}\sum _{k=1}^{N_p}{\mathit{hfi}}_{k}0\le \text{HFI}\le 1,$$ (9)

where N_p is the total number of tracers. Morbiducci et al. used this approach to quantify helicity in bypass grafts [101], aorta [103, 104], and carotid bifurcations [100, 99]. A comparison of helical and traditional artery bypass grafts has also been done with this method [150, 162].

2.5 Simulated particle tracking for experimental data

Phase contrast (PC) magnetic resonance imaging (MRI), also referred to as PC cardiovascular magnetic resonance (CMR), is a non-invasive flow imaging technique capable of providing 3D time-resolved velocity in all three directions for large arteries in vivo. With the advances made in imaging techniques in the past years PCMRI has become an emerging tool in studying blood flow in major arteries [90, 159, 61].

The velocity field obtained by PCMRI has been commonly used for visualizing pathlines. The earliest studies have shown the feasibility of this methodology, applying it to various major arteries by forward and backward integration of velocity [23, 24]. The construction of pathlines in the aorta [16, 17, 88, 89], heart [151, 49, 18, 42, 19], heart valves [74], pulmonary artery [10], and aortic aneurysms [62, 48] has been used to visualize in vivo flow features. Figure 3 demonstrates pathlines emanating from the heart obtained from in vivo PCMRI data, created by releasing tracers in left and right ventricles.

Figure 3.

Pathline visualization of systolic blood flow from the heart obtained by releasing tracers in the left and right ventricles during isovolumic contraction. The pathlines are computed from in vivo PCMRI velocity data by the methods described in Eriksson et al. [42]. Figure courtesy of Dr. Tino Ebbers.

MRI is subject to inherent measurement errors and artifacts that arise especially in complex flows. Numerical simulation of MRI has been used to understand these imaging errors. This process uses velocity data obtained from CFD to perform particle tracking of spins (magnetic moments) to reconstruct the MR image with appropriate equations. This approach has been used in studying the signal loss in magnetic resonance angiography [131], and imaging artifacts in black blood MR [138].

3 Tracking cellular damage

Thrombosis stemming from alterations in blood flow is a primary concern with nearly all major cardiovascular diseases, surgeries, and devices. Platelet activation is a critical step in the cascade of events that lead to thrombosis, and platelets can become activated chemically, or by exposure to high levels of shear (mechanical activation). Therefore, it is no surprise that velocity data from computational hemodynamics simulations has been extensively used to better understand the chemical or shear exposure of platelets as they are transported in a variety of cardiovascular flows.

Platelets are 2–4 μm in diameter. In larger artery flows, platelets have very high Peclet numbers and very small Stokes numbers, so it is reasonable to assume they are transported as material points. The exposure of platelets to pathological stresses in disturbed (high shear) flow conditions, such as through heart valves, devices and stenoses, has been of significant interest. By tracking platelets through the flow domain as discrete particles, it is common to define an activation potential (AP) as the integrated stress that the particle experiences. E.g. the activation potential defined in [127] was

$$\text{AP}({\mathbf{x}}_0,t_0;T)={\int }_0^T{\Vert \mathbf{e}(\mathbf{x}(t),t)\Vert }_F\mathrm{d}t,$$ (10)

where e is the rate of strain tensor (obtained from the velocity field gradient), T is the integration length (exposure time of platelets). Alternatively, the deviatoric stress tensor σ could be used in place of e; the two are related by the viscosity. Some studies only incorporate “shear stress” in this definition, however experiments suggest that activation can also occur from normal stress [116]. The above AP measures both the duration that a particle remains in the domain and the level of stress that it has sustained during that time.

As noted in Sec. 2, the AP, like most Lagrangian measures, depends on the initial time and location when particles are seeded. To alleviate this problem, particles may be uniformly seeded initially, and then released at the inlet of the domain proportional to flow rate (in space and time) as to simulate a uniform density of particles continuously released and integrated through the domain, which is more or less what occurs physiologically with the seeding of platelets (ignoring the fact that platelets are thought to have higher near wall density, which may be of questionable relevance in complex flows). Regardless, since the initial location and time one starts to accumulate stress is arbitrary, one may interpret results as representing the local contribution to mechanical activation, or assuming some initial activation potential, as well as assuming only stresses above some threshold contribute to the activation potential [143].

Equation (10) quantifies the stress acting on a particle by the (Frobenius) norm of the stress tensor. Most experimental studies that have measured a stress threshold for platelet activation are based on a simple shear experiment. However, in reality all the components of the stress tensor are involved in deforming fluid elements (and potentially cellular elements). Based on Von-Mises yield criteria, setting the work done in deforming an element in a simple shear flow equal to that done by a full 3D stress tensor one obtains [3]

$${\sigma }_{\nu }=\frac{1}{\sqrt{3}}\sqrt{{\sigma }_{xx}^2+{\sigma }_{yy}^2+{\sigma }_{zz}^2-{\sigma }_{xx}{\sigma }_{yy}-{\sigma }_{xx}{\sigma }_{zz}-{\sigma }_{yy}{\sigma }_{zz}+3({\sigma }_{xy}^2+{\sigma }_{xz}^2+{\sigma }_{yz}^2)}.$$ (11)

Therefore, σ_ν could be used in Eq. (10) alternatively. This has been used in several computational studies to calculate AP [9, 1, 133]. It should be noted however that for incompressible flow, ${\sigma }_{\nu }=\sqrt{2}\mu {\mathbf{e}}_F$, and the two measures provide equivalent results. Some experimental studies have suggested that stress and exposure time should not be “weighted equally,” but AP is better expressed as a power law of stress and exposure time [53, 2, 55, 106], which has been applied in several computational studies [9, 1, 102, 153, 132, 133, 12, 93].

Mechanical heart valves (MHV) have represented an important application of this type of study. Thrombosis and thromboembolism are the major complications of these devices, mainly due to mechanical platelet activation. Bluestein et al. [14, 13] have studied the vortex shedding phenomena behind MHVs, showing that platelets initially exposed to high shear get trapped in the formed vortices, consequently contributing to a higher AP level, similarly shown in [134]. Performance of bileaflet and monoleaflet MHVs have been compared showing higher AP levels for the bileaflet MHVs [158, 9]. The AP levels of different commercial bilieaflet MHVs has also been compared [39, 154, 160]. Different phases of MHV closure have been studied by comparison of vorticity, shear stress, and AP [76, 54]. Morbiducci et al. [102] have shown that spanwise vorticity has a greater effect on platelet activation in MHVs than the streamwise vorticity. The levels of AP in bioprosthetic heart valves (BHV) have also been studied [133].

PIV is another method to obtain highly resolved velocity data to calculate AP[12], and has been compared to CFD predictions of AP giving good agreement [117]. The influence of helical flow on platelet activation has been studied in a stenosed carotid bifurcation [93]. Shadden and Hendabadi [127] have shown that AP is generally maximized near the distinguished material surfaces of the flow that control the transport mechanism (see Sec 5).

Another important application tracking cellular damage is the study of hemolysis. High levels of mechanical stress on blood cells can cause cell rupture, which leads to the release of its contents into the surrounding medium. The mechanical modeling of hemolysis is similar to platelet activation but requiring much higher levels of stress thresholds (referred to as blood damage index or hemolysis index in this context). Similar to platelet activation potential, different models have been proposed to study hemolysis taking the exposure time and stress level into account [57]. Ventricular assist devices (blood pumps) [3, 135, 136, 152, 153, 109], and MHVs [34, 132, 35, 63] have been common applications of hemolysis studies.

4 Flow Stagnation

Regions of the vasculature that are diseased or surgically-altered, and regions where vascular disease often initiates, commonly harbor flow stagnation and recirculation (e.g. aneurysms, stenosis, bifurcation zones, arterial bends, etc.). Increased residence time of atherogenic compounds, coupled with endothelial dysfunction from reduced wall shear in these locations, may be an important factor stimulating plaque formation and atherosclerosis [161]. Moreover, flow stagnation can lead to the accumulation of antagonistic compounds, platelet and blood cell aggregation, and reduced transport of natural inhibitors, leading to intravascular thrombosis. Flow stagnation is inherently a transport phenomena and hence important application of Lagrangian methods.

Particle residence time (PRT) is a common measure readily computed from particle trajectory data. A simple field definition for PRT is the minimum amount of time that a tracer with initial position x₀ at time t₀ requires to leave a domain of interest (Γ)

$$\text{PRT}({\mathbf{x}}_0,t_0;\mathrm{\Gamma })=min(t)\in (0,\infty )\mathrm{s}.\mathrm{t}.\mathbf{x}({\mathbf{x}}_0,t_0+t)\notin \mathrm{\Gamma },$$ (12)

where the tracer position x(x₀, t₀ + t) is given by Eq. (5). The calculation of PRT requires a region Γ to be specified, which can be a subset of the computational domain. A main problem with the above definition is that it does not account for the nominal unidirectionality of blood flow, and hence locations further upstream become biased to generally higher PRT values.

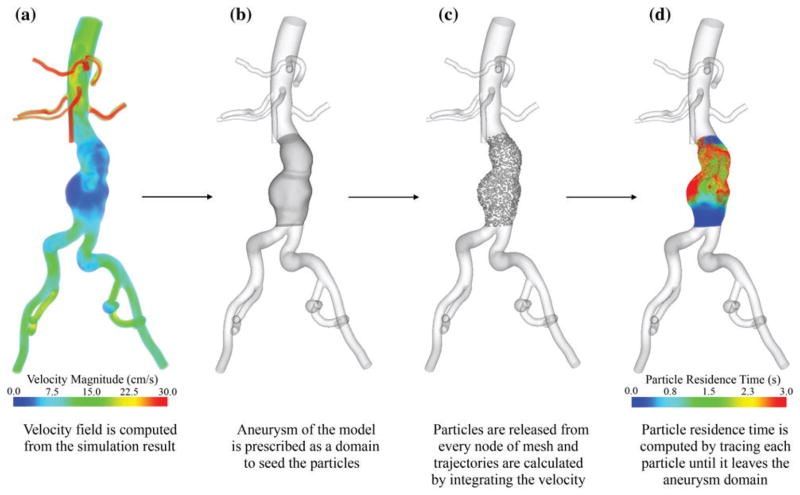
Buchanan et al. [22] normalized PRT by the values calculated from a steady flow with the same mean Reynolds number to study the transient effects induced by changing the Womersley number in a stenosis. The effect of continuous flow from ventricular assist devices on PRT has also been evaluated [121, 115, 46]. Aneurysms are an important application of flow stagnation and recirculation. PRT in an internal carotid artery with two aneurysms has been investigated [25], as well as for abdominal aortic aneurysms (AAA). In AAA, the expansion of the aneurysm bulge together with retrograde flow induced by the renal arteries creates stagnant conditions, which have long been thought to promote aggregation of platelets and intraluminal thrombus formation (a major complication of most AAAs). Suh et al. [140, 141] computed PRT for several patient specific AAA demonstrating a considerable decrease in PRT during lower limb exercise due to increase in infrarenal flow rate. Arzani et al. [5] quantified the overall level of residence time inside different AAAs for rest and exercise conditions. Experimental techniques have also been used to evaluate PRT [69, 26, 71, 146, 45]. Figure 4 shows the procedures used for obtaining a PRT field in a AAA.

Figure 4.

The procedure used in computation of particle residence time (PRT). Tracers are released in a region of interest and integrated using the velocity data until they exit the prescribed domain. The time that each tracer takes to exit the domain is mapped to its initial location of release, resulting in the PRT field. Figure from Suh et al. [140] with permission.

Another problem with PRT measures is that tracers that have been seeded at a particular location might get trapped later on in another location. Hence high PRT at a particular location does not necessarily reveal where stagnation/recirculation happens. To overcome this issue, the mean exposure time (MET) has been proposed [86], similar to that in [77] (termed volumetric residence time therein). MET is defined for each element or voxel e of the domain, and measures the accumulated amount of time that tracers entering the model spend inside this subset, as

$$\begin{array}{c}\text{MET}(e)=\frac{1}{N_e\sqrt[3]{V_e}}\sum _{p=1}^{N_t}{\int }_0^{\infty }{H}_e(p,t)\mathrm{d}t\\ H_e=\{\begin{array}{c}1\text{if}{\mathbf{x}}_p(t)\in e\\ 0\text{if}{\mathbf{x}}_p(t)\notin e\end{array},\end{array}$$ (13)

where N_e is the number of encounters of a tracer into the element e, V_e is the volume of the element, x_p(t) is the position of the tracer, H_e is the indicator function of the element e, and N_t is the total number of particles released. The particle release is usually done constantly at the inlet of the domain of interest. Because of the N_e normalization, MET weighs recirculation (tracers re-entering the element) lower than stagnation (tracers staying inside the element). Similar measures without this normalization have been proposed [122]. The $\sqrt[3]{V_e}$ scaling is most reasonable for small elements, where the time spent passing through an element is proportional to length, not volume. One shortcoming of the MET measure is that it requires a high resolution of Lagrangian tracers to be released in order to sample all the computational elements sufficiently. Therefore, it is not advisable to use the flow solver elements e, but instead larger elements that are more commensurate with the features of interest. That is, stagnation/recirculation is something that happens over space and time and hence requires some finite-spatial scale of interest. Making elements too small renders the information rather useless–becoming effectively an inverse measure of flow speed at each location.

Gundert et al. computed MET for different stent designs [58]. MET has been calculated in patient specific AAAs to relate flow stagnation and progression of the aneurysm [7]. Duvernois et al. developed methods to perform Lagrangian postprocessing on deformable grids, demonstrating that PRT and MET calculations from deformable and rigid wall models produced similar results [40].

Longest et al. [83, 79] have proposed a measure to quantify near-wall residence time (NWRT) as

$$\text{NWRT}=\frac{Q_{av}}{N_t{V}_{NW}}\sum _{p=1}^{N_e}{\int }_{\text{path},p}{\left(\frac{a_p}{h_p}\right)}^s\frac{1}{\Vert {\mathbf{u}}_p\Vert }\mathrm{d}\mathbf{r},$$ (14)

where N_t is the total number of particles released, N_e is the total number of particles passing through a near wall volume (V_NW ), Q_av is the average flow rate of the model used to nondimensionalize the measure, a_p is the radius of the particle, h_p is the distance between particle center and the wall, s represents an exponent set to match experimental data (set to 0 for massless particles), ||u_p|| is the magnitude of the particle velocity, and the integration is done along particle path (r). This group has used this measure to quantify stagnation in the near wall region for different applications such as grafts [83, 80, 79, 81, 82, 84], monocyte and platelet deposition [85, 78], and diseased carotid artery surgery [67]. Recently, NWRT has been used to evaluate monocyte deposition in AAAs [59].

5 Lagrangian coherent structures (LCS)

The computation of LCS seeks to overcome some important pitfalls of standard approaches to analyze flow topology. As mentioned above, characterization of unsteady flow is often performed by seeding the domain with particles and visualizing their motion. The complexity of the resulting motion and dependence on seeding strategy obscures interpretation and fundamental details of the flow. Alternatively, one can compute a scalar field of interest (residence time, helicity, vorticity, λ₂ criterion, etc.) and visualize this field. These measures can be derived from instantaneous rate of change information, or Lagrangian statistics, but in either case the field typically does little to retain/convey mechanistic understanding of transport. While in some cases the scalar field has direct clinical or biological meaning, in many cases the measure is more or less ad hoc, and interpretation depends on arbitrary color mapping or thresholding.

The reason that a simple Lagrangian tracking technique loses its capabilities in complex flows is the chaotic behavior of fluid motion. Fluid is a substance that is constantly busy getting out of its own way. However, even when viewing complex fluid motion, coherent structures can be observed. By definition, there is something “special” about these material objects, as by definition they have some persistent organizing behavior on the flow. Thus, if we restrict ourselves to viewing the fluid evolution directly, not some mathematical construct, rather than track material points at random (whose motion ends up looking random), one may seek to identify core material surfaces organizing tracer advection – which we identify as LCS.

Fluid, whether compressible or not, wants to behave as incompressible when it moves – i.e. it rather get out of its own way than bunch up. This sets up inherent saddle type hyperbolicity for fluid elements, and the elements whose direction and strength of attraction and repulsion remain most persistent are organizing features in the flow. (E.g. when “flow visualization” experiments are performed, dye is essentially used to highlight the most persistently attracting material structures.) With this viewpoint, LCS can be defined as material surfaces that are most strongly attracting or repelling – the later are hidden from dye visualization but are nonetheless important. This can be done using the right Cauchy-Green strain tensor $C({\mathbf{x}}_0;t_0,t)=\nabla {{\mathcal{F}}_{t_0}^t}^{\top }·\nabla {\mathcal{F}}_{t_0}^t$, where : x₀ ↦ x(t) is the flow map obtained e.g. from Eq. (5).

The most common method to visualize LCS is by computation of the finite time Lyapunov exponent (FTLE) field. The FTLE is essentially a scaling of the largest eigenvalue of the right Cauchy-Green strain tensor, [129] as

$$\sigma ({\mathbf{x}}_0;t_0,t)=\frac{1}{\mid t-t_0\mid }ln\sqrt{{\lambda }_{max}C({\mathbf{x}}_0;t_0,t)}.$$ (15)

The natural log tends to highlight “exponential” separation and the 1/|t − t₀| make the measure an average growth rate but is mostly unnecessary in identifying LCS. FTLE measures the exponential rate of separation of nearby trajectories, a common feature of chaos. To compute the tensor field C(x₀; t₀, t), a grid of tracers is placed in the domain of interest and integrated forward, and the strain tensor can be computed by e.g. finite differencing nearby paths. In general, the integration length is dependent on the time scales of the flow structures. Consult [124] for a comprehensive review on FTLE/LCS calculations. Repelling LCS can be obtained from forward FTLE (choosing T > 0), and attracting LCS can be obtained from backward FTLE (T < 0). These structures have been used to extract vortex boundaries (combination of attracting and repelling LCS), flow separation (from attracting LCS) or reattachment profiles (from repelling LCS), boundaries of stagnant flow (from repelling LCS), partitions of fluid going to different downstream vessels (from repelling LCS), and mixing mechanisms (stretching and folding marked by repelling LCS and attracting LCS respectively).

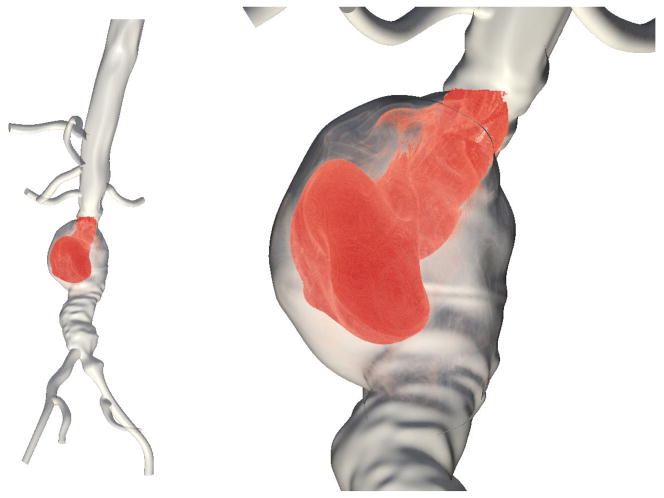
These methods were first applied to cardiovascular flows in [130], who demonstrated the capabilities of this approach to track evolution of flow separation (in a carotid bifurcation), evolution of vortex boundaries (in an idealized AAA), complex mixing patterns (in a patient specific AAA), and how the partitioning of blood to downstream vessels can be mapped out (left and right pulmonary arteries in a total cavopulmonary connection). AAA represents an important application where highly complex blood flow typically occurs, which is difficult to analyze with traditional methods. Arzani and Shadden [6] used LCS to understand the detailed flow topology in several patient specific AAA showing that in all the patients the jet penetrating into the aneurysm bulge forms a vortex ring in systole, and not only the propagation of this vortex ring determines the transport topology during diastole, but also the diastole flow field dictates the fate of the penetrating vortex. An LCS capturing a large coherent vortex in a AAA model is shown in Fig. 5. Arzani et al. [5] extended this analysis to study the effects of exercise and the complexities it adds to the flow topology in AAA.

Figure 5.

An attracting LCS delineates a large coherent vortex ring formed in an aortic aneurysm. This material surface defines the leading edge of the vortex [126, 128].

The transport of blood in the left ventricle (LV) during the heart filling in diastole is another interesting application of LCS. The formation of a vortex ring inside LV enhances the optimal transport and it is correlated with ejection fraction [52]. LCS can be used as an objective method to quantify the volume of the vortex. Espa et al. [43] used experimental data from a heart pump to compute LCS and study the flow structures formed inside LV. LCS has also been computed from in-vivo LV PCMRI data of healthy and diseased patients [145, 29], and used to quantify the volume of the vortex ring [145]. Hendabadi et al. [60] computed LCS from LV Doppler-echocardiography data of healthy and diseased patients. They used attracting LCS to identify the boundaries of injection and repelling LCS as boundaries of ejection. The combination of these information was further used in their study to quantify residence time. Figure 6 contrasts characterization of flow topology using streamlines versus LCS in the LV using methods described in [60], revealing important flow structures not easily observed using traditional flow visualization.

Figure 6.

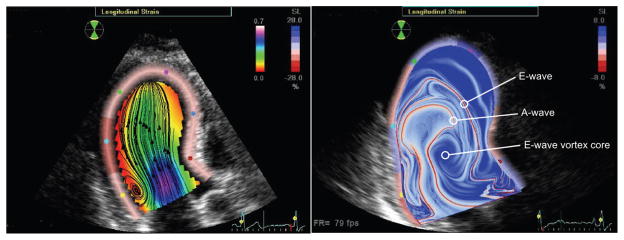
Comparison of streamlines (left) and FTLE (right) from velocity field data reconstructed from Doppler echocardiography data at end of diastole. Distinct LCS revealed in the FTLE field denote the boundaries and evolution of E-wave and A-wave filling, along with respective vortex interaction.

Other studies have used this method to study transport in different aortic flows. FTLE/LCS has been computed for steady flow measured from PIV in a carotid artery showing the recirculating structures, and the increase in complexity of the structures with increase in Reynolds number [148]. LCS has been used in aortic valves to delineate the boundaries and area of the jet formed downstream of the valve [125, 8], used to quantify the severity of aortic stenosis. Xu et al. [155] used LCS to study blood flow during clot formation and determined regions of blood that were delivered to the clot. Duvernois et al. [40] computed FTLE on a deformable grid from a TCPC patient and observed little difference of the emerging LCS compared to the rigid grid. Krishnan et al. [75] developed a method by FTLE computations to extract vessel boundaries from PCMRI data, exploiting the fact that PCMRI gives random (noisy) velocity data for regions outside the vessel wall that lead to high FTLE values.

Schelin et al. [118, 120, 119] studied the chaotic advection of blood flow in idealized stenosis and aneurysm models. They used the concept of fractal dimension and Lyapunov exponents to quantify the chaotic behavior of flow. They argued that the creation of fractal structures by the chaotic flow can lead to an increase in exposure time of platelets along these structures, and the high stretching induced by these regions can enhance platelet activation. Parshar et al. [108] quantified chaos with Lyapunov exponents in an idealized aneurysm for different Reynolds number. Maiti et al. [87] looked at the effect of blood rheology corresponding to different hematocrit concentrations on the chaotic flow in a stenosis.

6 Mixing

Although LCS (Sec 5) can be effective to understand the mechanisms underlying mixing, they do not (directly) provide quantitative information on mixing or mixedness. In this section other Lagrangian approaches used to evaluate mixing are discussed. Whether mixing in cardiovascular flows is beneficial or not is not an easy question. Laminar flow in a straight tube is unidirectional with poor mixing, however this is generally the preferred state in arteries. The situation can become more complex for diseased arteries. For example, high mixing in AAA is thought to be favorable. If there is a high global mixing in the aneurysm, platelets near the wall that are subject to aggregation and thrombosis due to stasis have a higher chance of being advected away from the wall and flushed out of the aneurysm. On the other hand, it is possible to have a region relatively cut off from the rest of the flow, but that maintains rather good mixing within itself. This is generally adverse though and can enhance thrombosis by maintaining relative stasis. Likewise, in the heart (e.g. left ventricle) an efficient momentum exchange of fluid from the inflow (mitral valve) to outflow (aortic valve) is considered beneficial, but on the other hand the heart is not emptied when it contract, and thus mixing of the residual blood volume with the injection and ejection volumes is needed. In short, secondary flow structures are beneficial for mixing, but also lead to low WSS, recirculation, pressure loss, and other undesirable characteristics.

The simplest way to evaluate mixing by Lagrangian methods is to use particle tracking and qualitatively evaluate the mixing behavior of tracers. Doorly et al. [38] studied the effect of vortices on mixing. They assumed that for short time intervals viscous effects can be ignored, therefore vortex lines are advected by the flow. They placed two ring of tracers aligned with the vorticity, one close to the wall and another near the axis, and tracked their evolution by particle tracking. The interaction of these two rings as they were advected by the flow was used to reveal some of the mixing features in a graft flow. The complex distribution of PRT and basins of attraction of tracers has been related to complex mixing patterns [25]. Avrahami et al. [9] used particle tracking to investigate the role of mixing in wash out properties of ventricular assist devices with different MHVs and the relation to thrombus formation. Combining two helical tubes with different diameters has been proposed to increase mixing in bypass grafts and arteriovenous shunts with only small pressure drops [32]. Bockman et al. [15] investigated the mixing of two streams of tracers from the left and right vertebral arteries into the basilar artery. Seo and Mittal [123] studied the mixing in the left ventricle by tracking tracers coming from the mitral valve, and tracers residing in the ventricle at the beginning of diastole. They sampled the domain into small volumes, and by using the standard deviation of the concentration of mitral tracers during end of diastole, and the standard deviations of unmixed, and perfect mixing conditions, they defined a mixing quality index used to quantify mixing.

Realizing that mixing is an increase in disorder of a system, the entropy concept could be used in quantification of mixing. Shannon introduced information entropy as the amount of information that a message carries (see [70])

$$S=-\sum _{x_i\in X}P(x_i)ln(P(x_i)),$$ (16)

where P represents a probability measure, and the sum is over the set of all the realizations where the probability is defined on. Cookson et al. [31] used an alternative description of Shannon entropy and used particle tracking to quantify entropy in helical tubes such as bypass grafts. Namely,

$$S=-\sum _{i=1}^{N_c}\left(w_i\sum _{k=1}^{N_s}(n_{i,k}log{n}_{i,k})\right),$$ (17)

where N_c is the number of cells (used to discretize the domain), N_s is the number of species (different sets of particles whose mixing property is desired), i and k are cell and species index respectively, n_i,k is the fraction of the k’th species in the i’th cell, and w_i is a weighting factor set to zero if the cell has no particles, or only single type particles. Equation 17 has also been used in quantifying mixing of bypass grafts with an Eulerian approach (advection-diffusion equation) [50].

The concept of Shannon entropy has been applied in dynamical systems, referred to Kolmogorov-Sinai entropy as an objective measure [68, 4]. It can be shown that under specific conditions the Kolmogorov-Sinai entropy is the spatial integral of the Lyapunov exponents of the dynamical system. In other words it measures the spectrum of all the Lyapunov exponents, and could be thought of as a measure quantifying chaotic behavior of all degrees of freedom of a system. Consequently, the close relation between chaotic transport and mixing could be observed as explained in Sec 5.

There are examples of transformations that have zero entropy but can mix specific scalar fields, furthermore the entropy measure is independent of initial configuration of the scalar field, therefore the concept of mix-norm and mix-variance has been introduced [94]. The idea is to integrate the square of the averaged values of a given scalar field over a set of subdomains (densely contained in the entire domain) to quantify mixing across all the scales. In other words, mix-norm parametrizes all the sub-domains and takes the root mean square of the average values of the scalar field across these sub-domains. Mix-variance has the same formulation but the mean of the scalar field is subtracted from the scalar field. This idea was used quantify mixing in AAAs during rest and exercise conditions in [5], by introducing two sets of tracers: fresh blood penetrating into the aneurysm, and old blood that is initially inside the aneurysm. By defining the scalar field as the concentration of fresh blood they quantified mix-norm and mix-variance and found higher and more uniform mixing during exercise. In their formulation mix-norm represents the overall percentage of fresh blood at different subdomains and mix-variance represents the overall variation in mixing at different subdomains.

7 Conclusions

Computational hemodynamics provides a powerful tool for modeling in vivo hemodynamics. Blood flow in large vessels can have fascinatingly complex behavior and understanding the nature of this complexity is one of the important challenges in hemodynamics research. Lagrangian postprocessing methods are essential in quantifying and better elucidating important features of complicated pulsatile flows. Most of these methods are based on Lagrangian particle tracking for direct visualization or geometric quantification of trajectories, or as Lagrangian framework to quantify the exposure of blood borne element as they are transported to various influences – the fluid mechanic stresses exerted on cellular elements being an important example.

While visualization of Lagrangian particle tracking alone can provide more insight into the flow topology than the velocity field or common flow characterization measures, the complex nature of trajectory data makes interoperation difficult. Quantification of broader transport behavior such as flow separation, mixing, stagnation, recirculation, etc., is often achieved by defining suitable Lagrangian-based measures that can be plotted as scalar fields. Such an approach is usually ad hoc and the scalar field of interest depends closely on the specific application, and ultimately shrouds the mechanistic behavior leading to the particular field values. LCS computation seeks a compromise by defining a scalar field from trajectory data with physical meaning, but retaining the ability to convey explicit geometric information about how fluid elements are transported.