Stabilizing the false vacuum: Mott skyrmions

Abstract

Topological excitations keep fascinating physicists since many decades. While individual vortices and solitons emerge and have been observed in many areas of physics, their most intriguing higher dimensional topological relatives, skyrmions (smooth, topologically stable textures) and magnetic monopoles emerging almost necessarily in any grand unified theory and responsible for charge quantization remained mostly elusive. Here we propose that loading a three-component nematic superfluid such as ²³Na into a deep optical lattice and thereby creating an insulating core, one can create topologically stable skyrmion textures. The skyrmion's extreme stability and its compact geometry enable one to investigate the skyrmion's structure, and the interplay of topology and excitations in detail. In particular, the superfluid's excitation spectrum as well as the quantum numbers are demonstrated to change dramatically due to the skyrmion, and reflect the presence of a trapped monopole, as imposed by the skyrmion's topology.

Topological excitations and defects emerge and play a key role in almost any area of physics where spontaneous symmetry breaking occurs. Domain walls, besides being the necessary ingredients of magnetic recording media, also emerge in cosmology, string theory¹, and constitute basic quasiparticles in 1+1 dimensional field theories². Line defects such as vortices belong today to our basic understanding of superfluidity and superconductivity³,⁴,⁵, and dislocations have a central impact on the elastic properties of materials and on melting and fracture⁶.

Topological point defects and excitations such as monopoles⁷,⁸,⁹,¹⁰ and skyrmions may be even more fascinating than vortices and domain walls. Skyrmions, originally proposed to describe hadronic particles¹¹,¹², emerge as smooth, localized, and topologically protected textures of some vector field (order parameter). Their gauge theoretical counterparts, the 't Hooft-Polyakov monopoles appear to be necessary ingredients of almost any grand unified theories, and are needed to explain charge quantization. While planar or line-like topological defects are abundant in condensed matter, observing topological point defects in the laboratory proved to be very hard, since only peculiar order parameters support their existence. Moreover, as shown by Derrick¹³, skyrmions are generally doomed to shrink to a point or to expand to infinity and vanish in a homogeneous system in the absence of non-trivial external gauge fields¹⁴. It is in fact only very recently that the existence of monopoles has been convincingly demonstrated in spin ice materials such as Dy₂Ti₂O₇¹⁵,¹⁶, and that the spontaneous formation of skyrmion lattice textures, displaying the celebrated topological Hall effect¹⁷,¹⁸,¹⁹, has been reported in certain magnetic materials²⁰,²¹,²², holding the promise of next-generation spintronic devices²³.

The advent of ultracold atoms opened new perspectives to creating and manipulating individual skyrmions and monopoles. It has been noticed very early that certain spin F = 1 multicomponent superfluids such as ²³Na or ⁸⁷Rb support magnetic phases²⁴,²⁵,²⁶,²⁷,²⁸,²⁹,³⁰,³¹,³²,³³, which – combined with an inhomogeneous trap geometry³⁴ – were argued to give rise to stable skyrmion and monopole configurations³³,³⁵. In a nematic superfluid such as ²³Na, in particular, the superfluid order parameter Ψ(r) = (Ψ_x, Ψ_y, Ψ_z) takes a remarkably simple form,

with 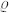denoting the superfluid density, φ the superfluid phase, and 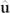a real unit vector. From equation (1) we can identify the topological structure of the nematic order parameter space as 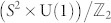, with the unit sphere S² corresponding to the orientation of the vector 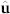and the U(1) symmetry associated with the phase degree of freedom, φ. The curious 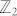factorization is a consequence of the fact that phase changes φ → φ + π are equivalent to flipping the orientation of the vector, 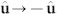. Due to this structure, topologically nontrivial and thus topologically stable hedgehog-like field configurations 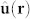exist (see Fig. 1) and can give rise to skyrmion and monopole structures in two and three dimensions, respectively.

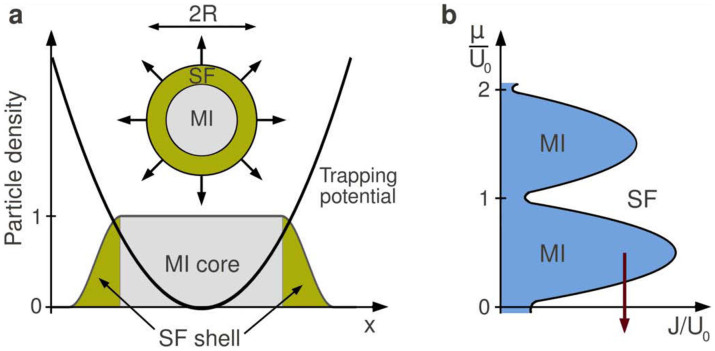
Figure 1. Schematic structure of the Mott skyrmion.

(a) A Mott insulator (MI) core is surrounded by a superfluid (SF) shell with a skyrmion spin structure. Arrows denote the orientation of the nematic order parameter, 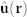in equation (1). The MI core stabilizes the skyrmion by keeping it from drifting out from the trap. (b) Schematic finite temperature phase diagram of strongly interacting bosons in an optical lattice. The red arrow shows the chemical potential as one moves from the center of the trapped skyrmion towards its edge. The MI has no magnetic structure at the temperatures considered.

Unfortunately however, topological excitations trapped in usual cold atomic setups turned out to be much more unstable than initially thought; monopoles and skyrmions generically slip out of the trap³⁵ or they simply gradually unwind and disappear within a short time³⁶,³⁷. Therefore – so far – only unstable skyrmion configurations have been imprinted and observed experimentally³⁶,³⁸. While the application of external artificial non-Abelian gauge fields could stabilize skyrmions¹⁴,³⁹, the realization of such complex gauge fields is beyond the reach of current experiments.

Here we propose to stabilize the skyrmion states geometrically by generating a non-superfluid core at the center of a trapped nematic superfluid. We suggest to achieve this by placing the nematic superfluid into a deep optical lattice, and thus driving the atoms at the center into a Mott insulating state (see Fig. 1). In this way a closed two-dimensional superfluid shell is created, which – unlike open shell configurations – supports topologically stable skyrmions, anchored by the Mott insulating core. We compute the free energy of this strongly interacting ‘Mott skyrmion’ system numerically, and demonstrate that the skyrmion texture is indeed stable.

In the skyrmion configuration the superfluid order parameter acquires a non-trivial, topologically protected texture, generated virtually by a monopole at the center of the trap. As predicted by Jackiw and Rebbi and Hasenfratz and 't Hooft⁴⁰,⁴¹, the presence of a monopole can influence the quantum numbers of the excitations around the monopole – and turns bosonic excitations to fermions, a phenomenon termed ‘spin from isospin’ mechanism. As we show by detailed calculations, somewhat similarly to the ‘spin from isospin’ mechanism, the presence of the monopole changes drastically the excitation spectrum of the superfluid (see also⁴²), and removes a pseudospin quantum number, present in the ‘skyrmionless’ ground state. Given the exceptional stability of the ‘Mott skyrmion’, and its peculiar compact geometry, the predicted change in the excitation spectrum becomes experimentally accessible. The effect of the ground state topology on the excitation spectrum is a general phenomenon, having deep mathematical origins, and has been studied theoretically in a large variety of topological excitations across all fields of physics. Our proposal provides a unique way to observe in an experimentally realizable system for the first time, how topology leads to significant changes in the excitation spectrum of an individual three-dimensional topological excitation.

We describe a balanced mixture of interacting spin F = 1 bosons using the lattice Hamiltonian 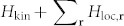with the kinetic and local parts defined as

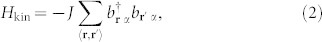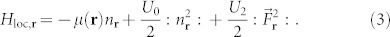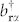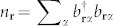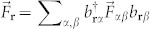Here the operators create a boson of spin component α (α = x, y, z) at the lattice site r, and and denote their density and magnetic moments, respectively. The F^j stand for the usual angular momentum matrices in the α = x, y, z basis, 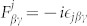, and : … : refers to normal ordering. The hopping J sets the kinetic energy of the bosons, while the effect of trapping potential 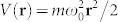is incorporated in the effective position dependent chemical potential, µ(r) ≡ µ − V(r). The (normal ordered) interaction term U₀ describes the strong repulsion between lattice-confined bosons, while the second, much weaker interaction term U₂ accounts for the magnetic interaction between them. It is this second term, U₂ > 0, which for ²³Na forces the superfluid order parameter Ψ_α ∝ 〈b_α〉 to stay within the nematic phase, 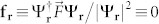(a condition implying equation (1)), once the superfluid density 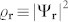becomes finite.

In the following we focus our attention onto the regime zJ/U₀ ≈ 0.2 with z = 6 the number of nearest neighbors. Here, increasing the chemical potential at the center of the trap beyond some critical value (or equivalently, making the trap tighter), the density at the center increases and finally reaches the first Mott lobe (see Fig. 1b). For ²³Na, in particular, we estimate U₀ ≈ 250 nK and U₂ ≈ 9 nK in this regime of interest, and zJ ≈ 50 nK, as shown in Supplementary Note 1. We also assume that the temperature is already low enough (T < zJ) to forming a superfluid around the Mott core with typical radius R, albeit it is well above the magnetic ordering temperature of the Mott insulating core, T_C ~ 0.1 T (with T_C ~ zJ²/U₀), in accordance with the temperature range of current experiments. Thus the core is essentially non-magnetic, and the interplay between the magnetism in the Mott core and superfluidity can be ignored (see also our discussion in subsection ‘Excitation spectrum’).

I. Results

Stable skyrmion configuration

First, to verify the stability of the skyrmion, we introduced local order parameter fields by performing a Hubbard-Stratonovich transformation, b_r → Ψ_r ≈ 〈b(r)〉 (see Methods), and traced out the original boson fields numerically to obtain the free energy functional

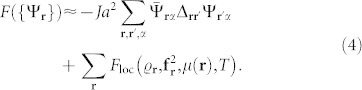Here a denotes the lattice constant, and Δ_rr′ stands for the discrete Laplace operator. The first term describes the stiffness of the superfluid order parameter, while the second term incorporates the effect of the interaction as well as that of the confining potential, and has been determined numerically for each lattice point (see Methods). Its structure follows from the obvious O(3) rotational symmetry and U(1) gauge symmetry of the underlying Hamiltonian, equations (2, 3).

To find the minimum of F({Ψ_r}) we used the imaginary time equations of motions,

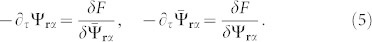The dynamics generated by equation (5) drives the field configuration {Ψ_r} towards the minima of the free energy functional. In particular, for appropriate parameters, starting from a configuration with a skyrmion texture imprinted, the field Ψ_r is found to relax to a configuration

with 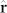denoting the radial unit vector. We verified by adding a random component to the initial field configuration that this final state is indeed a robust local minimum of the free energy, as anticipated.

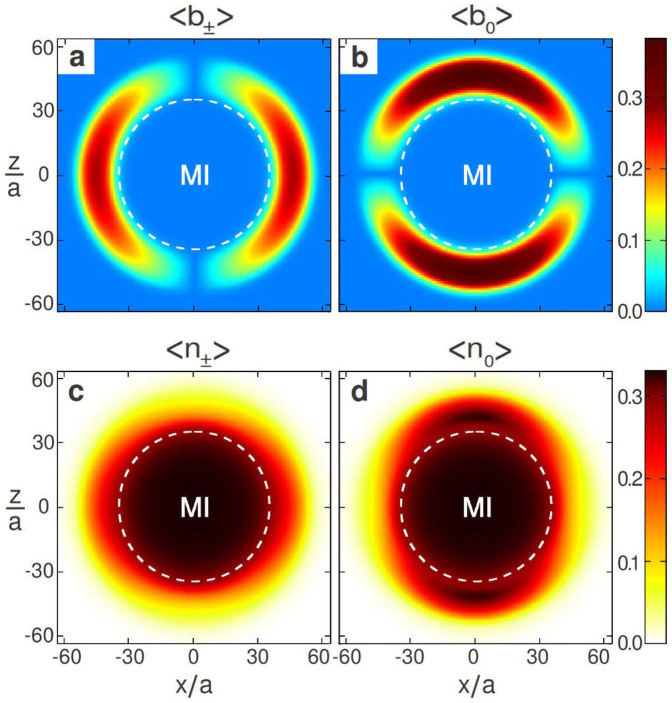
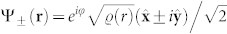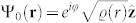Fig. 2 displays the superfluid and total densities across the trap in the usual hyperfine spin basis, F^z = ±1 and F^z = 0, where the amplitudes of the various superfluid components read as , and . The superfluid density is clearly suppressed at the center of the trap, where the stabilizing Mott insulating core is formed, and it lives on a two dimensional shell around this core. The components Ψ_± form vortices around the equator, while the Ψ₀ component behaves as a dark soliton, localized at the north and south poles. The total density of the components of the superfluid is also distorted and reflects the structure of the order parameters; the density of 〈b₀〉 ~ 〈b_z〉 is elongated along the z-axis, while that of the other two spin components, 〈b_±〉 ~ 〈b_x〉 ± i〈b_y〉 is squeezed along it (see Fig. 2 bottom).

Figure 2. Inner structure of the skyrmion in the (x, z) plane.

(a) In-trap SF densities of the |+1〉 (|−1〉) bosons form a vortex (antivortex) around the equator, whereas that of the |0〉 condensate in (b) creates a dark soliton at the poles. (c,d) show in-trap particle densities. SF order of one of the spin components leads to a local increase of the component's particle density at the expense of those of the other two components, leading to a specific density structure characterizing the skyrmion (bottom). This structure gets significantly more pronounced at lower temperatures. [Physical parameters of the plot: T/U₀ = 0.05, U₂/U₀ = 0.025, zJ/U₀ = 0.18, chemical potential in the middle µ_mid/U₀ = 0.36, and at the edge µ_edge/U₀ = −0.09.].

Creation

A possible way to create the skyrmion is to imprint diabatically a vortex, an antivortex and a dark soliton into the three spin components⁴³, and then stabilize the vortex state by turning on a deep optical optical lattice. Starting with a superfluid with all atoms in the |−1〉 state, as a first step, a fraction of the atoms could be transferred into a vortex state in component |1〉 using a so-called Λ transition. This is possible by applying a diabatic pulse of a pair of counter-propagating σ⁻, σ⁺ Raman beams of first order Laguerre-Gaussian (LG⁻¹) and Gaussian density profiles, respectively³⁸. This vortex could then be transferred to state |0〉 by a simple RF π-shift. As a next step, the creation of an antivortex in component |1〉 could be achieved by changing the chirality of the Laguerre-Gaussian beam from LG⁻¹ to LG⁺¹. Finally, another laser, perpendicular to the quantization axis, would be used to imprint the dark soliton into the remaining atoms in state |−1〉⁴⁴.

An alternative and maybe even simpler way to create the skyrmion could be to imprint three dark solitons in the x, y, and z directions, respectively, and then mixing them using an RF π/2-shift.

Excitation spectrum

To study the excitation spectrum of the superfluid shell, we constructed a two-dimensional effective field theory for the superfluid order parameter ψ(r), by assuming a thin superfluid shell of radius R. We also neglected the penetration of the nematic order into the Mott insulator, which is expected to decay abruptly within a few atomic layers⁴⁵, leading to slight renormalization of the parameters of our model, and presumably negligible dissipation. Thus, we can describe the superfluid by the Lagrange density

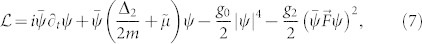generating the following equations of motion for the order parameter field,

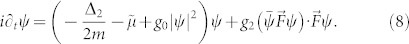Here Δ₂ denotes the two dimensional Laplace operator on the sphere, 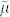the effective chemical potential of the superfluid shell, and and g₀ and g₂ stand for the effective couplings. All of these parameters depend on the precise width of the superfluid shell as well as on the lattice parameters. We estimated them from our lattice computations, as explained in more detail in Supplementary Note 3.

The excitation spectrum of the condensate is obtained by linearizing equation (8) around the ground state field configuration, and then solving the resulting coupled differential equations. Equivalently, we can treat the field ψ as a quantum field, and obtain the corresponding Bogoliubov spectrum of the condensate (see Methods and Supplementary Note 4). For a uniform, ‘skyrmionless’ configuration, 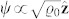, we find that the density (phase) and spin excitations decouple and the spectrum can be obtained analytically, similarly to the case of a spatially homogeneous systems⁴⁶. In the limit of large trap radii compared to the superfluid and magnetic healing lengths, defined through 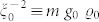and 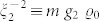, we obtain the spectrum

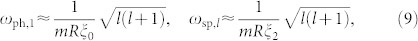with l = 0, 1, .. the angular momentum quantum number. Since the spin coupling is much smaller than the density coupling, 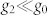, and thus 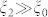, spin excitations dominate the low energy excitation spectrum of the condensate. For a spherical trap every excited state in the spin sector has a (2l + 1) × 2-fold orbital degeneracy. The (2l + 1)-fold degeneracy is due to spherical symmetry and is accidental in the sense that it is lifted once the trap is distorted, and spherical symmetry is broken. The other, two-fold degeneracy is, however, a consequence of the residual O(2) symmetry of the vector part of the order parameter, and can be interpreted as a spin degeneracy of the Bogoliubov quasiparticles in the spin sector. Notice that this spin degeneracy is absent in the phase sector, where excitations have only a (2l + 1)-fold angular momentum degeneracy for a spherical trap. In addition to the finite energy excitations, three zero-energy excitations (Goldstone modes) are found with quantum numbers l = 0, corresponding to global phase and spin rotations, respectively (see Fig. 3).

Figure 3. Excitation spectrum.

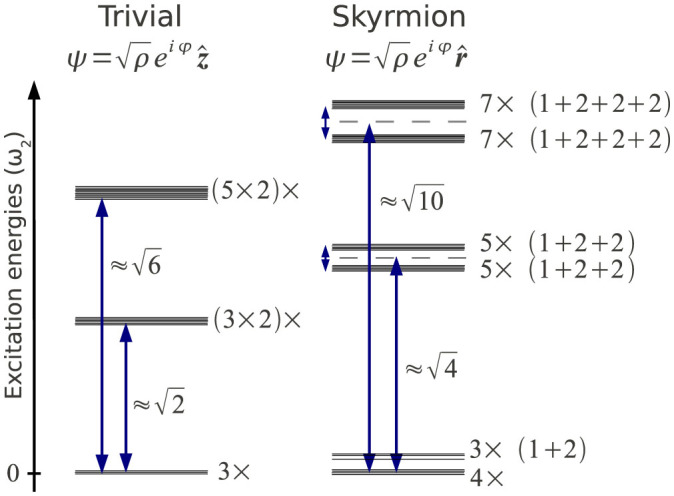
The left (right) panel visualizes the low energy part of the excitation spectrum above the trivial (skyrmion) ground states in units of ω₂ = 1/(mRξ₂), with the magnetic healing length 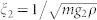. Due to the rotational symmetry of the trivial state around 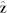, each excited state has a 2-fold spin degeneracy in addition to the (2l + 1)-fold orbital degeneracy. In contrast, spin degeneracy splits, and only orbital (rotational) degeneracies survive in the skyrmion sector. The trivial and skyrmion states exhibit different number of zero modes (Goldstone modes) as well. Apart from the phase degree of freedom, only two zero modes exist in the trivial case, since rotations around 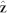in configuration space leave this state invariant. In the skyrmion state, however, the number of zero modes increases by one, since rotations around all three spin axes provide a zero mode on top of the phase mode.

Excitations in the skyrmion sector are more complicated, since spin and density fluctuations couple to each other due to the spatial winding of the skyrmion texture⁴⁷. Furthermore, the spherical symmetry is found to be spontaneously broken, and the skyrmion slightly distorts into a randomly selected direction (see Supplementary Note 4). Here we find four skyrmionic zero-energy Goldstone modes and three more excitations of almost zero energy, associated with the spontaneous symmetry breaking. The rest of the excitations have energies ω ~ 1/(m R ξ₂), and they come in groups of (2l + 1) almost degenerate excitations, split into l states of degeneracy 2 and a non-degenerate state, as induced by the spontaneous cylindrical distortion of the superfluid. The skyrmion's excitation spectrum is sketched in Fig. 3. Notice that the structure of the excitation spectrum is completely different from that of the ‘skyrmionless’ sector, the spin degeneracy of the spin excitations completely disappears.

The above mentioned coupling between density and spin fluctuations leads to a clear fingerprint of the skyrmion state in lattice modulation experiments. Modulation of the atom tunneling, J, excites oscillations in the amplitude of the superfluid order parameter, which are coupled to the low energy spin excitations of the skyrmion. Thus, even though these modulations do not couple directly to spin degrees of freedom, the topological winding of the skyrmion texture gives rise to an indirect coupling to spin excitations, leading in effect to ‘spin-orbit coupling’. Specifically we consider modulation of the tunneling along one axis by varying the intensity of the optical lattice. This corresponds to perturbation in the l = 0 and l = 2 angular momentum channels, and excites the lower l = 2 branch of excitations of the skyrmion texture in Fig. 3 (see Supplementary Note 5). In contrast to the skyrmion case, spin and density fluctuations are completely decoupled in the trivial sector, and modulation of the tunneling cannot excite any of the low energy spin modes of this state. Similarly, modulation of the trapping potential along one direction leads to excitations of the low energy spectrum of the skyrmion state, but no excitation of the trivial configuration. We thus find, that the trivial and skyrmion configurations are clearly distinguishable through analyzing the low energy spectrum of modulation experiments.

For typical parameters we find that the energies of the superfluid excitation are in the order of 10 Hz (see Supplementary Note 3). It would be essentially impossible to study these excitations in previous unstable skyrmion configurations, however, the extreme stability of our ‘Mott skyrmion’, should now allow to access them and to study their dynamics.

Detection

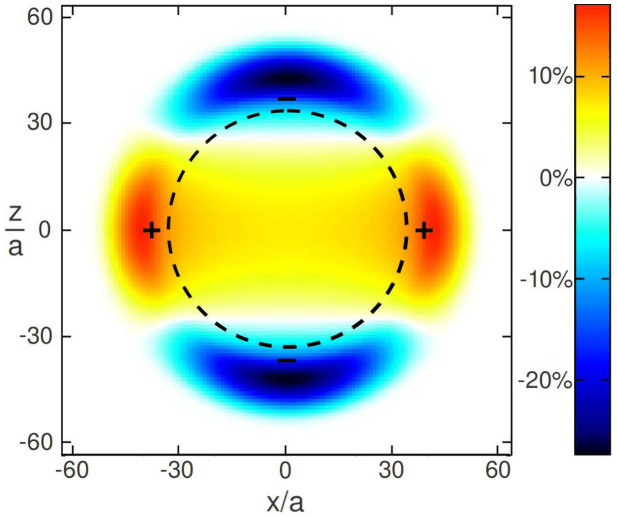
The skyrmion texture can be detected in many ways. Although the change in the density of the components is moderate, their in trap density difference is rather pronounced and is clearly detectable through absorption imaging (see Fig. 4).

Figure 4. Difference of in-trap absorption images of the components |±1〉 and |0〉, taken along the y axis.

Due to the non-trivial SF configurations of the skyrmion, |±1〉 (|0〉) bosons have higher densities along the equator (poles), see also Fig. 2. [Densities are shown as percentages of the largest value of the absorption image of component |0〉. Physical parameters: identical to the ones in Fig. 2.].

The skyrmion texture can also be easily detected through time-of-flight (ToF) measurements, imaging the momentum distribution of the trapped atoms⁴⁸. The ToF image of the atoms with spin component α at time t is approximately proportional to⁴⁹

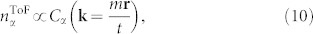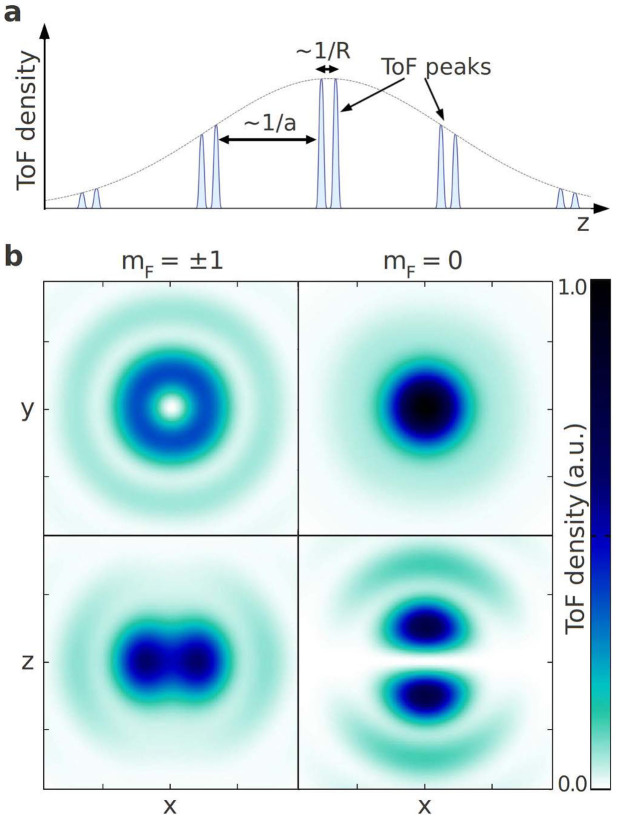
with C_α(k) denoting the Fourier transform of the correlation function , and is approximately given by 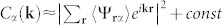. As we show in Fig. 5, the ToF image consists of Bragg peaks —- fingerprints of the underlying optical lattice. Each Bragg peak, however, displays a fine structure at a momentum scale k ~ 1/R, characteristic of the skyrmion texture of the superfluid³²,³⁷. The ToF image of the m = 0 component, e.g., displays a circular structure when imaged from the z direction, while a clear double peak structure should be detected under imaging from the x or y directions.

Figure 5. Time of flight characteristics of the skyrmion.

(a) Schematic picture of time of flight (ToF) peaks located at the reciprocal lattice vectors in momentum space, with an additional fine structure (~ 1/R) reflecting the spatial SF correlations of the skyrmion of spatial extent R. (b) Structure of the doughnut (double peak) shaped ToF peaks of component |±1〉 (|0〉), on the left (right), taken along the z (y) axes, top (bottom). [Color code and axes: arbitrary but identical units. Physical parameters: identical to those in Fig. 2.].

II. Methods

Free energy

The thermodynamic partition function, Z, of the lattice system is given by the functional integral 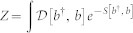, where the action reads as

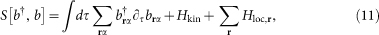with H_kin and H_loc,r defined in equations (2, 3). The hopping term is decoupled by a Hubbard-Stratonovich transformation⁵⁰ after introducing the superfluid order parameter Ψ as

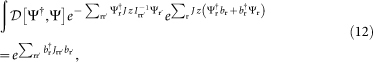with the hopping term expressed as J_rr′ = Jz I_rr′, with z = 6 the number of nearest neighbors. Its inverse can be rewritten for small kinetic energies using 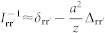. Within the saddle point approximation, the functional integral in b can be carried out exactly, leading to the free energy F[Ψ^†, Ψ] = −T log Z[Ψ^†, Ψ] in equation (4) with

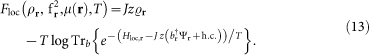Numerical minimization of the free energy

We use a modified version of the imaginary time minimization algorithm implemented in⁵¹. The imaginary time dynamics of the fields in equation (5) lead to a continuous decrease in the free energy

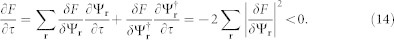In order to speed up our numerics, we separate the kinetic part from the remaining onsite contributions, 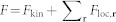. F_kin is calculated using a fast Fourier transform, whereas we use numerical interpolation in parameter space to calculate F_loc,r at each site. For additional details, see Supplementary Note 2.

Excitation spectrum

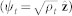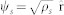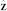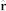We analyze excitations around the trivial and skyrmion () configurations, assuming uniform ground state densities on the sphere. Here and denote unit vectors in the z and radial directions, respectively. We determine the two dimensional superfluid densities by using the saddle point approximation for the two dimensional effective Lagrangian 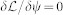, yielding ρ_t = µ/g₀ and ρ_s = (µ − 1/mR²)/g₀, with R the radius of the sphere. In the latter case, the chemical potential becomes renormalized by the −1/mR² curvature term, due to the winding of the ground state, leading to a slight depletion of the superfluid.

In the trivial state ψ_t the fluctuations parallel (δψ_||) and perpendicular (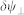) to the ground state decouple, and their equations of motion take on the simple form

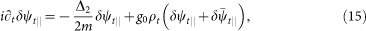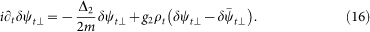The interaction term g₀ sets the velocity of the fluctuations of the superfluid phase and density, whereas the spin interaction g₂ determines the velocity of the perpendicular fluctuations. In the skyrmion state, ψ_s, however, the kinetic parts in equations (15, 16) acquires geometrical terms due to the curvature of the ground state configuration. The Laplace operator is replaced by

with 1/mR² a curvature term shifting the kinetic energy of fluctuations, and the covariant derivative D = ∇ + iA, defined using the non-Abelian vector-potential A, mixing the components 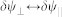. These geometrical terms shift the spectrum and lead to the splitting of the excitation energies. Further details of this calculation are presented in Supplementary Note 4.

Author Contributions

M.K.-N. carried out the analytical and numerical calculations; G.Z. conceived the project, carried out part of the calculations and supervised them; G.Z. and M.K.-N. prepared the manuscript; M.K.-N. and G.Z. proposed the creation and detection schemes; E.A.D. proposed the experimental system; G.Z. and E.A.D. coordinated the work; B.D. participated in the stability analysis of the skyrmion. All authors took part in discussions and commented on the manuscript.

Supplementary Material

Supplementary Information

Supplementary Information