Evolutionary tipping points in the capacity to adapt to environmental change

Significance

Environmental variation is becoming more frequent and unpredictable as a consequence of climate change, yet we currently lack the tools to evaluate the extent to which organisms may adapt to this phenomenon. Here we develop a model that explores these issues and use it to study how changes in the timescale and predictability of environmental variation may ultimately affect population viability. Our model indicates that, although populations can often cope with fairly large changes in these environmental parameters, on occasion they will collapse abruptly and go extinct. We characterize the conditions under which these evolutionary tipping points occur and discuss how vulnerability to such cryptic threats may depend on the genetic architecture and life history of the organisms involved.

Abstract

In an era of rapid climate change, there is a pressing need to understand how organisms will cope with faster and less predictable variation in environmental conditions. Here we develop a unifying model that predicts evolutionary responses to environmentally driven fluctuating selection and use this theoretical framework to explore the potential consequences of altered environmental cycles. We first show that the parameter space determined by different combinations of predictability and timescale of environmental variation is partitioned into distinct regions where a single mode of response (reversible phenotypic plasticity, irreversible phenotypic plasticity, bet-hedging, or adaptive tracking) has a clear selective advantage over all others. We then demonstrate that, although significant environmental changes within these regions can be accommodated by evolution, most changes that involve transitions between regions result in rapid population collapse and often extinction. Thus, the boundaries between response mode regions in our model correspond to evolutionary tipping points, where even minor changes in environmental parameters can have dramatic and disproportionate consequences on population viability. Finally, we discuss how different life histories and genetic architectures may influence the location of tipping points in parameter space and the likelihood of extinction during such transitions. These insights can help identify and address some of the cryptic threats to natural populations that are likely to result from any natural or human-induced change in environmental conditions. They also demonstrate the potential value of evolutionary thinking in the study of global climate change.

Understanding how organisms cope with and adapt to changes in their environments is a central theme in evolutionary ecology (1). However, we currently lack the tools to predict the most likely evolutionary responses to changes in environmental conditions (2), including those currently experienced through global change (3, 4). Evolutionary responses to within- and among-year fluctuation in ecological parameters like ambient temperature or precipitation can be highly informative about the process of adaptation to environmental change, as well as about the potential consequences of the recently accelerated rates of global change and the associated increase in climatic variability and unpredictability (5–8). Earlier work indicates that some organisms face environmental uncertainty by hedging their bets with a strategy that minimizes fitness variance across all possible environmental conditions (conservative bet-hedging) (9), whereas others have evolved a mix of strategies to take advantage of alternative environmental scenarios in a probabilistic fashion (diversification bet-hedging) (9). In still other cases, organisms cope with environmental variation through phenotypic plasticity, which is the ability to respond to environmental cues through the adjustment of genotypic expression either during early development (irreversible or developmental plasticity) (10) or throughout life (reversible plasticity) (11). Finally, environmental variation is also known to result in correlated variation in mean population traits, as natural selection favors different phenotypes over evolutionary time (adaptive tracking) (12). Although an increasing amount of attention has been recently devoted to the conditions that promote these different forms of evolutionary response to environmental variation (hereafter “response modes”) (2, 9, 13–18), most studies have considered only one or a small subset of response modes (16, 17), and few have explored the general conditions under which one (or more) may be selected above the others (2, 18). Addressing these issues will be critical for improving our ability to predict whether and how populations will adapt to both natural and human-induced environmental change.

Here we develop a theoretical model that considers the joint evolution of a comprehensive range of evolutionary responses to environmental variation. Although we illustrate our model by exploring the effects of temperature, the principles we describe apply to other naturally fluctuating environmental variables (e.g., precipitation). We use the term insulation, I, as a broad descriptor of morphological (e.g., coat thickness) (19), behavioral (e.g., huddling), or physiological (e.g., sweating) characteristics that help counter thermal stress. To investigate the dynamics of adaptation to environmental variation, we use individual-based evolutionary simulations in which the pattern of variation in genotypic expression across a range of environmental conditions (i.e., the reaction norm of the genotype) (14) is assumed to be heritable and subject to mutation and natural selection. We begin by testing the consistency of evolutionary response to different types of environmental change and then use this general framework to explore how systems react to disruption in the nature of environmental oscillations. A nontechnical description of how our model can inform issues related to global change is included in the SI Text.

Results

Environmental variation includes both deterministic (i.e., climate) and stochastic (i.e., weather) components. For example, temperatures oscillate deterministically from cold winters to hot summers, but the actual values experienced in a given day vary stochastically from the seasonally expected average. We modeled these components as

$$E_t=A\mathrm{\cdot }\sin \left(2\mathrm{\pi }t/LR\right)+B\mathrm{\cdot \epsilon },$$

where t is time, L is the number of time steps per generation (i.e., lifespan), R is the relative timescale of environmental variation (i.e., number of generations per environmental cycle), ε is a stochastic error term, and A and B are scaling constants reflecting the relative importance of deterministic and stochastic factors. This equation describes a simple sinusoidal oscillation in environmental conditions when R is intermediate or small and approximates a slow directional change when R is very large. Because R is a relative metric, the findings presented below are easily applicable to organisms with different lifespans.

In nature, changes in environmental conditions are often preceded by correlated changes in photoperiod, barometric pressure, or other environmental cues. For example, day length variation tends to be well correlated with seasonal temperature variation in temperate regions. Thus, we model the predictability of environmental conditions, P, by altering the degree to which an environmental cue, C, is correlated with future temperature values (SI Text and Fig. S1). When temperatures and cues are perfectly correlated, the environment is completely predictable, P = 1, and when they are not correlated at all, it is completely unpredictable, P = 0. In the simulations presented here, cues are provided to individuals before experiencing any changes in their environment (Methods).

Simulation runs in our model proceed in discrete time steps with nonoverlapping generations and individual lifespans of L = 5 time steps. Individuals possess seven genetic traits—loci h, s, a, I₀, ${I\prime }_0$, b, and b′—that determine the amount of insulation to be produced under different environmental cues. Every genotype specifies two different reaction norms: one encoded by I₀ and b, and another one encoded by ${I\prime }_0$ and b′. Loci I₀ and ${I^{\prime }}_0$ determine baseline degrees of insulation, whereas loci b and b′ determine the degree to which insulation is made dependent on environmental cues. Each individual in our model expresses only one of these reaction norms through life: the one based on I₀ and b′ is chosen at birth with probability h, whereas the one based on ${I\prime }_0$ and b′ is chosen with probability 1 − h. In practice, this implies that locus h enables individuals with the same genotype to respond to environmental variation in two completely different ways (as in diversifying bet-hedging). Locus s is a genetic switch that determines whether the organism makes its insulation dependent on environmental cues (i.e., whether it allows for phenotypic plasticity; s > 0.5) or not (s ≤ 0.5). Nonplastic individuals ignore environmental cues and exhibit a fixed insulation phenotype encoded by the baseline loci I₀ or ${I\prime }_0$. Plastic individuals adjust their insulation phenotypes, I, to the environmental cues they perceive using linear norms of reaction such that, $I=I_0+b\mathrm{\cdot }C$ or $I={I\prime }_0+b^{\prime }\mathrm{\cdot }C$. Locus a determines whether this cue dependence is only happening during ontogeny (irreversible or developmental plasticity) or also throughout the individual’s lifetime (reversible phenotypic plasticity). In practice, this means that individuals with a = 0 respond to environmental cues only during development—and therefore exhibit a single phenotype throughout life—whereas those with a > 0 alter their phenotypes with probability a at each time step after development. As in earlier studies (14), we assume that phenotypic plasticity is costly both during and after development. Thus, plastic individuals pay a one-time developmental cost, k_d, and each phenotypic adjustment after development is assumed to incur in an additional cost of k_a.

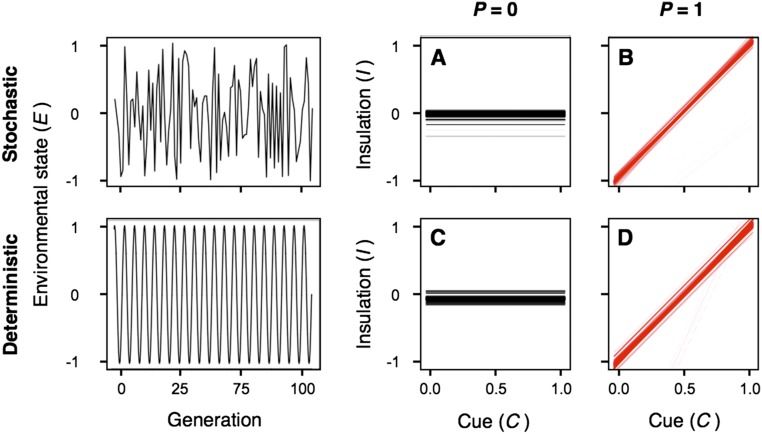
To establish a baseline for comparison, we began by evaluating the effects of environments with a constant temperature. As expected, this simple scenario led to the evolution of nonplastic insulation strategies with a mean population value that approximately matched the temperature experienced. We then considered completely stochastic environments (A = 0 and B = 1), where individuals had no information about the potential state of the environment (P = 0). Under these conditions, populations evolved to ignore uninformative cues, producing instead a fixed phenotype at the average environmental condition (I = 0; Fig. 1A). In contrast, when we allowed these same stochastic environments to be completely predictable (P = 1), the resulting reaction norms led to insulation levels that varied with the intensity of environmental cues (Fig. 1B). In completely deterministic environments (A = 1 and B = 0) with rapid environmental variation (logR = 0), we observed that phenotypic plasticity also evolved only when individuals were able to anticipate environmental changes (Fig. 1 C and D). This result highlights a key aspect of adaptation to environmental change: the way in which environments vary (i.e., whether the pattern of environmental oscillations appears to be stochastic or deterministic) is less important to evolution than the degree to which individuals can anticipate the future state of the environment (20). Thus, the remaining simulations focus on the effects of predictability of environmental variation and assume, for simplicity, that A = 1 and B = 0 (SI Text).

Fig. 1.

Effects of environmental stochasticity on the evolution of thermal strategies when environments are either completely unpredictable (A and C) or completely predictable (B and D). Stochastic environmental variation (A and B) was modeled by setting the value of weighting constants to A = 0 and B = 1. Conversely, comparable deterministic variation (C and D) was modeled through A = 1, B = 0, and R = 1. The norm of reaction plots depict the strategies of 5,000 individuals at generation 50,000 in representative replicate simulation runs. Darker colors indicate that a higher number of individuals share a given response to a particular environmental cue. Comparison of the top and bottom panels indicates that the way in which environments vary, stochastically vs. deterministically, is less important to evolution than the degree to which individuals can anticipate such variation.

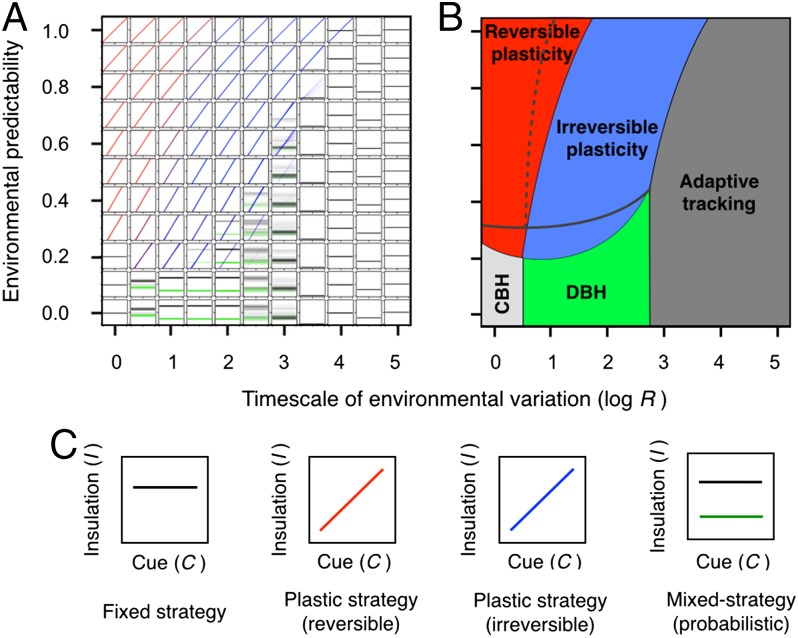
We proceeded to explore evolutionary outcomes at different predictability levels and across a comprehensive range of timescales of variation (Fig. 2). For each set of conditions, we performed 100 replicated simulations. Each subplot in Fig. 2A depicts the 100 evolved mean reaction norms at generation 50,000 (e.g., $I=\overline{b}\mathrm{\cdot }C+\overline{I_0}$, where $\overline{b}$ and $\overline{I_0}$ correspond to the mean population values for b and I₀). Overall, we find that evolution results in remarkably consistent outcomes for the majority of parameter combinations (Fig. 2A, SI Text, and Fig. S2) and that different response modes occur largely in nonoverlapping regions of parameter space (Fig. 2B, Table S1, SI Text, and Fig. S3). These findings are robust to the implementation of density- and frequency-dependent selection, as well as to alternative coding schemes for genotype-to-phenotype mapping (SI Text and Fig. S4). In cases where environmental variation within a generation is both predictable and fast (P is large, R is small; upper left corner of Fig. 2B), each subplot in Fig. 2A shows a single cluster of reaction norms. This indicates that (i) similar reaction norms evolved in all 100 replicate simulations at that parameter combination, (ii) the evolved populations exhibit a high degree of plasticity (i.e., $\overline{s}\hspace{0.17em}\mathrm{>}\hspace{0.17em}0.5$ and $\overline{b}\hspace{0.17em}\mathrm{\approx }\hspace{0.17em}1$), and (iii) individuals in these populations often adjust their phenotypes after development ($\overline{a}\hspace{0.17em}\mathrm{\approx }\hspace{0.17em}1$; Table S1). As R becomes larger, locus a quickly evolves to $\overline{a}\hspace{0.17em}\mathrm{\approx }\hspace{0.17em}0$ (depicted in blue in Fig. 2A) because the diminishing benefits of avoiding thermal mismatches no longer surpass the costs of phenotypic adjustment (13, 21, 22). We label this strategy irreversible plasticity because individuals in these populations exhibit plasticity exclusively during development. The transition from reversible to irreversible plasticity occurs at progressively shorter timescales in less predictable environments because the expected benefits of phenotypic adjustment decrease with higher potential for errors in anticipating environmental change.

Fig. 2.

Evolutionary response to environmental variation under different levels of predictability (P) and relative timescale of environmental variation (R). At each parameter combination in A, the 100 mean population reaction norms that evolved at generation 50,000 in different replicate simulations are depicted as in Fig. 1 with environmental cues on the x axis and the resulting insulation phenotypes on the y axis (labels omitted for simplicity). If only one reaction norm is visible, this is an indication that the same response evolved in all replicates. As illustrated in C, reaction norms are depicted in black when $\overline{s}\le 0.5$ (see Table S1 for details). In such a case, phenotypic plasticity does not occur (a is not expressed) and the reaction norm is flat. In case of a plastic response ($\overline{s}>0.5$), reaction norms are depicted in a color gradient ranging from red when $\overline{a}=1$ (reversible plasticity) to blue when $\overline{a}=0$ (irreversible plasticity). For simplicity, secondary reaction norms are depicted in green with intensity proportional to how often they are used (i.e., they are not visible if $\overline{h}=1$). (B) The consistency of outcomes across replicates in A suggests that different regions in parameter space favor different modes of response. Conservative and diversifying bet-hedging are identified in B as CBH and DBH, respectively. Dashed gray lines in B depict changes in the boundaries between different adaptive regions when adjustment costs, k_a, are doubled from 0.01 to 0.02, and solid gray lines depict changes when the cost of development, k_d, is doubled from 0.02 to 0.04.

When environmental conditions are fairly unpredictable, the rate at which environments change determines the resulting evolutionary outcome. If R is large (lower right corner of Fig. 2B), the slow rate of environmental change allows for beneficial mutations in I₀ to appear and approach fixation. The resulting pattern is a gradual change of the mean phenotype that tends to lag behind the change in environmental conditions (adaptive tracking in Fig. S5A). However, at faster timescales (lower center and lower left in Fig. 2B), environmental change is too fast to be tracked by mutation and too unpredictable to be addressed through plasticity. Consistent with previous studies (9, 16), this extreme form of uncertainty forces individuals to hedge their bets. When individuals experience all possible conditions with similar probability (e.g., very low R), we observe the evolution of fixed phenotypes at I ∼ 0. Although this insulation value rarely matches the actual conditions experienced, it matches the average environment and therefore minimizes overall thermal mismatch across the entire range of potential environmental conditions (Table S1). Thus, this strategy resembles conservative bet-hedging (9) in that it minimizes the variance in fitness among selection events and across individuals that share the same genotype. In contrast, when individuals of a given genotype experience only a fraction of the environmental cycle (e.g., logR = 0.5), we observe the evolution of mixed strategies that produce alternative phenotypes with either heavy or light insulation in a probabilistic fashion (green in Fig. 2A). This strategy resembles the phenotypic polymorphism of diversification bet-hedging (9) (Table S1), because the different phenotypes produced by a single genotype minimize thermal mismatch in different scenarios (i.e., the larger I phenotype does best when experiencing disproportionally more of the upper than the lower half of the environmental cycle, and the smaller I phenotype does best in the opposite situation).

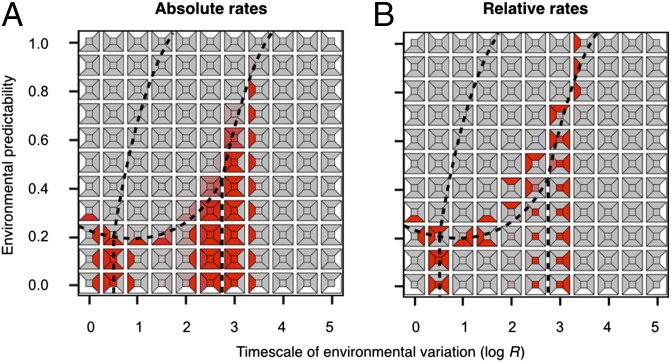
Having determined the most likely evolutionary outcomes under a comprehensive range of parameter combinations, we proceeded to explore how populations are affected by changes in the predictability or timescale of environmental variation (i.e., in the signature of their environment). The well-defined response mode regions observed in Fig. 2 allowed us to make a simple but important a priori prediction: changes in environmental signatures that require the evolution of an entirely different mode of response may be harder to cope with than those that do not. To test this hypothesis, we abandoned the assumption of a constant population size in our model and linked reproductive output to absolute rather than relative fitness (Methods). By relaxing this assumption, we were able to assess the demographic consequences (e.g., changes in population size and risk of extinction) of different environmental challenges. In this eco-evolutionary version of our model, maximal fecundity, q, was defined as the average number of offspring that an individual produces when it pays no plasticity costs and is able to exactly match its environment at every time step of its life. Thus, the mean fecundity of individual i, ${\overline{F}}_i$, is determined by the fraction of the maximum payoff that it is able to achieve, such that ${\overline{F}}_i=q\hspace{0.17em}\mathrm{\cdot }\hspace{0.17em}{W}_i/W_{\max }$(Methods). Fig. 3 depicts the potential for extinction at each parameter combination (inner squares), as well as during transitions between adjacent combinations in parameter space when q = 2.2 (see Fig. S6 for alternative values of q). Each of the four possible transitions to an adjacent cell is depicted using trapezoids. For example, the color of the upper trapezoid within a given subplot indicates the effects of transitioning from that particular parameter combination to the one above it. As predicted, we found that the potential for extinction during these transitions is considerably higher when populations are forced into a different response mode region (a result that holds even if much larger changes in P or R are attempted).

Fig. 3.

Rates of extinction when transitioning into nearby regions of parameter space when q = 2.2. Each subplot within each panel depicts the baseline level of extinction at a given parameter combination (inner square), and the extinction rates associated with transitioning into the nearest parameter combination to the top, bottom, left, and right of that cell (trapezoids). The boundaries between response mode regions in Fig. 2B are presented as dashed lines. (A) We use a color gradient from gray (0%) to red (100%) to depict absolute extinction rates (i.e., the proportion of simulations that went extinct during 100 replicate transition runs). (B) Relative rates were computed as (TR − BR)/BR, where TR = transition rate of extinction, and BR = baseline rate of extinction at the target parameter combination (i.e., where the population is moving into). The color scale for these rates ranges from blue (≤−100%) to red (≥100%). The absence of blue trapezoids in B indicates that, in practice, transition rates were always similar or greater than their corresponding baselines.

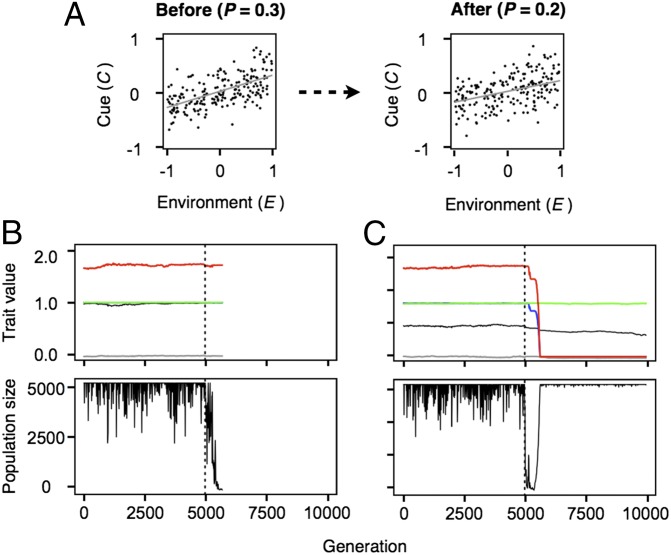
The nonuniformity of transitional extinction rates in our model is driven by at least two different mechanisms. First, some transitions imply moving into regions of parameter space that are particularly challenging for adaptation. For example, when environmental oscillations are quick and unpredictable (i.e., the bet-hedging region), baseline levels of extinction are high, particularly at lower q values (Fig. S6). Thus, any population that is suddenly forced into this region will also be expected to have a high likelihood of extinction (Fig. 3A). The second contributor to extinction relates to the complexity of genetic changes required for adaptation during transition and is more readily observable after accounting for potential differences in baseline levels of extinction in the new environments. For example, when relative extinction rates are considered (Fig. 3B), we find that extinction is only more likely than expected when populations move into a different response mode region (even if this transition involves moving into regions of parameter space that appear to be easier for adaptation, such as into more predictable environments). The reason for the increased risk of extinction during these tipping point transitions is that adapting to a completely new strategy for phenotypic development often requires a radical restructuring of the genome, which can be particularly difficult to achieve as populations collapse. For example, in the transition from phenotypic plasticity to bet-hedging, plastic strategies become maladapted (i.e., their expected number of offspring, W, is less than 1) and population decline is swift (Fig. 4). Thus, given that adaptation to the new environment requires in this case resetting developmental switches (s and a) and adjusting almost every other locus in the virtual genome, the stochastic nature of mutation supply and the reduced standing genetic variation of declining populations are more likely to result in extinction (Fig. 4A) than in evolutionary rescue (Fig. 4B). Conversely, the relative extinction rates for the reverse transition are also high because the fitness of fixed strategies is low compared with that of plastic ones, and because many of the mutations that can potentially transform a fixed strategy into a plastic one will, in the absence of other necessary genetic changes, result in maladapted phenotypes. Another case with high relative rates of extinction during tipping point transitions is the change from conservative to diversifying bet-hedging, which involves similarly extensive genetic changes, including the resetting of h, I₀, ${I\prime }_0$, b, and b′. In contrast, when genomic changes are relatively simple, as in the case of the transition between reversible and irreversible plasticity, the likelihood of adaptation during transition is much higher (Fig. 3).

Fig. 4.

Representative examples of population dynamics during transitions through evolutionary tipping points in our model. (A) In the simulations depicted here, populations were forced to move from the region of reversible plasticity into that of bet-hedging by lowering P from 0.3 to 0.2 at log R = 0 (all other model parameters as in the main text). (Top) Change in the correlation between cues and environmental values. (Middle) Evolution of traits before and after the transition (black = s, blue = a, green = h, gray = I₀, and red = b; the time of transition is depicted by a dashed vertical line at generation 5,000). (Bottom) Associated changes in population size over time. (A) Even though the change in predictability is barely visible to the naked eye, populations immediately decline after predictability is reduced. (B) In most situations, populations become extinct because the mutations required to adapt to the new environment fail to arise. (C) However, in cases where beneficial mutations arise on time, these traits tend to reach fixation quickly and evolutionary rescue is complete.

Discussion

Our model suggests that evolutionary response to environmental variation may be more predictable than previously anticipated. Through evolutionary simulations, we showed that fundamentally different adaptive responses consistently evolve under different timescales and predictabilities of environmental variation. The response mode regions predicted by our model are largely consistent with a variety of empirical findings in a range of biological systems. For example, reversibly plastic adaptations like torpor (23) and hibernation (24) have been shown to occur in response to frequent (i.e., daily or yearly) and predictable changes in environmental conditions. In some examples of reversible phenotypic changes, such as the seasonal change in coat coloration in temperate mammals, there is even evidence that the increasing unpredictability of relevant environmental parameters is currently exerting strong selection on natural populations (e.g., snow cover for snowshoe hares) (25). Another potential example of reversible plasticity is cognitive ability, particularly given its role in enabling behavioral flexibility (26). Consistent with our predictions, the evolution of cognitive enhancement appears to be driven in many systems by the exposure to intense, short-term, and only moderately predictable environmental variation (27–29). In contrast, most well-documented examples of developmental (i.e., irreversible) plasticity occur when environmental features remain constant during a lifetime but vary among individuals. For example, the short-lived Daphnia cucullata only develops costly and life-long protective helmets if coexisting with predatory fish (30). Empirical examples of conservative (e.g., cooperative breeding behavior) (31), and diversifying bet-hedging [e.g., maternal adjustment of variance in offspring traits (32) or fimbriae expression in bacteria (33)] also conform to our predictions as they all involve responses to highly unpredictable environmental conditions. Over much longer timescales, where our model predicts adaptive tracking, we see congruence with empirical examples like the slow changes in breeding and migration dates in birds (34) or even the rise of arid-adapted African mammals—including hominids—in response to increased aridity in East Africa during the Pliocene and early Pleistocene (35).

A key insight from our model is that adaptive capacity to environmental change is likely to be subject to evolutionary tipping points (36), where most environmental changes will be relatively innocuous but some—even very small ones—can have disproportionate and dramatic effects. Specifically, the potential for adaption to changes in the predictability or timescale of environmental change appears to depend more on the location of parameter space that populations are moving into than on the magnitude of the change itself. For example, our simulations indicate that evolution can easily accommodate rather large changes in environmental signatures if the same general strategy for phenotypic expression is appropriate before and after the change. However, it also shows that populations will decline rapidly and tend to go extinct whenever they are forced into situations where their current strategy is no longer appropriate (i.e., when crossing boundaries into different response mode regions; Fig. 3). These observations have important implications in the context of global climate change because they suggest that even species that appear to be coping well with current changes in environmental signatures (3) may become vulnerable to extinction if a tipping point is crossed. Thus, an empirical characterization of evolutionary tipping point dynamics could be of major importance for a better understanding of otherwise cryptic threats to natural populations and for a proper design and implementation of conservation strategies.

Several aspects of the natural history of an organism are likely to influence the location and intensity of tipping points in parameter space. For example, species that pay higher costs of plasticity may move across an evolutionary tipping point much sooner than others, because the boundaries between plastic and nonplastic response mode regions occur at higher predictability values when k_a and k_d increase (Fig. 2). Similarly, organisms with slow life histories that do not reproduce often or that produce low numbers of progeny during each breeding attempt (modeled here as low values of q) are likely to be more vulnerable to environmental oscillations and tipping point transitions because of their potentially lower supply of beneficial mutations and their decreased ability to rebound from population bottlenecks (Fig. S6). In addition, our model indicates that the potential for extinction during tipping point transitions depends critically on the genetic architecture of relevant traits (37) and in particular on the number or magnitude of mutations required to achieve the genotypic optimum for the new selection regime. For example, we expect that populations will be more likely to go extinct when the strategy that needs to be evolved requires either de novo evolution (or loss) of complex organs and structures or a major readjustment of basic physiological/developmental pathways. Conversely, we expect lower vulnerability to extinction when the desired new strategy after transition is achievable through the evolution of simple genetic changes that do not interfere with major body plans.

In conclusion, our model provides a unifying theoretical framework for predicting evolutionary responses to environmental change and leads to a series of testable predictions regarding organismal capacity to adapt to natural or human induced changes in the environment. These predictions can be tested through experimental evolution of microorganisms or through comparative analyses of populations or species distributed along a gradient of environmental variation. Ultimately, evolutionary models like the one we present here can aide in determining the specific type of adaptation that organisms may use to cope with specific environmental changes, thereby improving our understanding of how populations and species may respond to either global change or other environmental challenges.

Methods

Norms of Reaction.

The tendency of a genotype to be systematically expressed as different phenotypes across a range of environmental conditions is known as the genotype’s norm of reaction. Our model assumes that the effects of heat and cold stress are symmetric and that selection favors phenotypes that match the environmental condition in which they are expressed (see below). These simplifying assumptions imply that if individuals have perfect information about the environment, then they can maximize their returns with I = E. Accordingly, we have parameterized reaction norms in our model as linear functions. Thus, I = I₀ + b⋅C (or $I={I\prime }_0+b^{\prime }\mathrm{\cdot }C$ with probability 1 − h), where I₀ is the insulation level produced at C = 0, and b is a slope that determines the degree to which insulation levels change as a function of changes in environmental cues (for alternative genotype-phenotype mapping schemes, see SI Text and Fig. S3).

Fitness.

Every individual in our model lives for L = 5 time steps. Each time step proceeds in a defined order. First, environmental conditions are updated and environmental cues are computed from E_t and P as described above. Then, individuals have access to the cue and are given the opportunity to develop or adjust their phenotype accordingly. Finally, individuals are exposed to selection by computing their phenotypic mismatch, M, with the condition experienced such that

$$M_{i,t}=\left|E_t\mathrm{-}{I}_{i,t}\right|,$$

where E_t is the current environmental state and I_i,t is the individual's current phenotype. At the end of a generation, a nonplastic individual’s lifetime payoff, W_i, is computed as a function of the sum total of phenotypic mismatches throughout life, such that

$$W_i=\exp \left(\mathrm{-}\tau \mathrm{\cdot }{\displaystyle \sum _{t=0}^L{M}_{i,t}}\right),$$

where τ is a constant that determines the strength of fitness decay as a function of total phenotypic mismatch. For plastic individuals (i.e., s > 0.5)

$$W_i=\exp \left(\mathrm{-}\tau \mathrm{\cdot }{\displaystyle \sum _{t=0}^L{M}_{i,t}}\right)\mathrm{-}{k}_d\mathrm{-}n\mathrm{\cdot }{k}_a,$$

where n is the total number of times an individual adjusts its phenotype during its lifetime.

Individual-Based Simulations.

Our evolutionary model is based on populations of 5,000 individuals exposed to mutation and natural selection for 50,000 discrete, nonoverlapping generations (simulation runs were replicated 100 times at each parameter combination). Reproduction occurs only at the end of each generation and is proportional to the payoffs accumulated during each individual’s lifetime (W_i). Thus, the number of offspring for individual i is drawn from a Poisson distribution with mean $W_i/\overline{W}$, where $\overline{W}$ is the mean cumulative payoff for that generation. As a consequence, the average number of offspring per individual is equal to one and the size of the offspring population is very similar to that of the parent population. To compensate for the occasional differences between these two population sizes, we randomly removed or replicated offspring when needed to maintain a population of 5,000. All offspring in our model inherit the alleles at each locus from their parents, with a per locus mutation probability of μ = 0.001 and mutational steps drawn from a normal distribution with a mean of zero and an SD of 0.05. The loci that encode slopes in the reaction norms (b and b′) and reversibility in plasticity (a) are only allowed to mutate if individuals are plastic (i.e., when s > 0.5). Otherwise, these traits are set to zero and subsequently ignored unless s evolves a value greater than 0.5.

Simulating Transitions to Different Regions of Parameter Space.

To include the possibility of varying population sizes into our model, we replaced relative with absolute fitness so that reproductive output was directly tied to how well individuals were able to match their environment. To this end, we modified the algorithm of our basic model so that the number of offspring for individual i was drawn from a Poisson distribution with mean q ⋅ W_i/W_max, where W_max is the maximum possible payoff (i.e., the payoff an individual would accrue if it paid no costs and were able to match the exact temperature of its environment every time step of its life). Because individual payoffs were compared here to an absolute standard, W_max, rather than to each other, the average number of offspring was no longer equal to one and population size was able to change over time (e.g., everybody attained low fitness when all strategies in the population did poorly compared with W_max). To prevent population size from exploding in cases where fecundity was large, we applied an upper boundary constraint in these simulations at a population carrying capacity of 5,000 individuals; because increasing carrying capacity did not change qualitatively our results, we maintained the population size used in the constant population size simulations. We then took the final population of each replicate simulation in Fig. 2 and allowed it to evolve under different values of P and/or R for 1,000 additional generations. In transition simulations where R remained the same, we simply extended the environmental cycle from the time it was left off at the end of the initial simulation. When R changed, we adjusted the phase of the new environmental cycle to prevent abrupt discontinuities in the direction or magnitude of E.

Parameter Settings.

All simulations reported above are based on the following parameters unless otherwise stated: L = 5, k_d = 0.02, k_a = 0.01, τ = 0.25, and q = 2.2. In every replicate, with the exception of transition simulations, the starting population was initialized by setting h = 1 (i.e., assuming that genomes only code for one norm of reaction), and by drawing the remaining traits for each individual at random from uniform distributions on [0, 1] for a and s; [−1, 1] for I₀ and ${I\prime }_0$; and [−2, 2] for b and b′. Subsequent evolution was completely unbounded and determined solely by mutation and natural selection.