Merging molecular mechanism and evolution: theory and computation at the interface of biophysics and evolutionary population genetics

Abstract

The variation among sequences and structures in nature is both determined by physical laws and by evolutionary history. However, these two factors are traditionally investigated by disciplines with different emphasis and philosophy—molecular biophysics on one hand and evolutionary population genetics in another. Here, we review recent theoretical and computational approaches that address the critical need to integrate these two disciplines. We first articulate the elements of these integrated approaches. Then, we survey their contribution to our mechanistic understanding of molecular evolution, the polymorphisms in coding region, the distribution of fitness effects (DFE) of mutations, the observed folding stability of proteins in nature, and the distribution of protein folds in genomes.

Introduction

In this review, we highlight the recent results from the theoretical and computational models being developed at the interface of biophysics and evolutionary population genetics. These models integrate the tools from molecular biophysics that have been developed to determine and design properties of proteins, our emerging knowledge of the genotype-phenotype relationship (GPR), and established approaches population genetics. Because these models are built bottom-up, integrating insights from biophysics and cell biology, they provide a robust and mechanistic understanding of the origin of observed genetic and structural variation.

This field is still in its infancy. However, it already offers new insights into the molecular determinants of the rate of protein evolution, the genetic variation in coding regions, the distribution of fitness effects of mutations, and the observed thermodynamic and structural properties of proteins in nature.

Bottom-up and multiscale evolutionary models: the basic elements

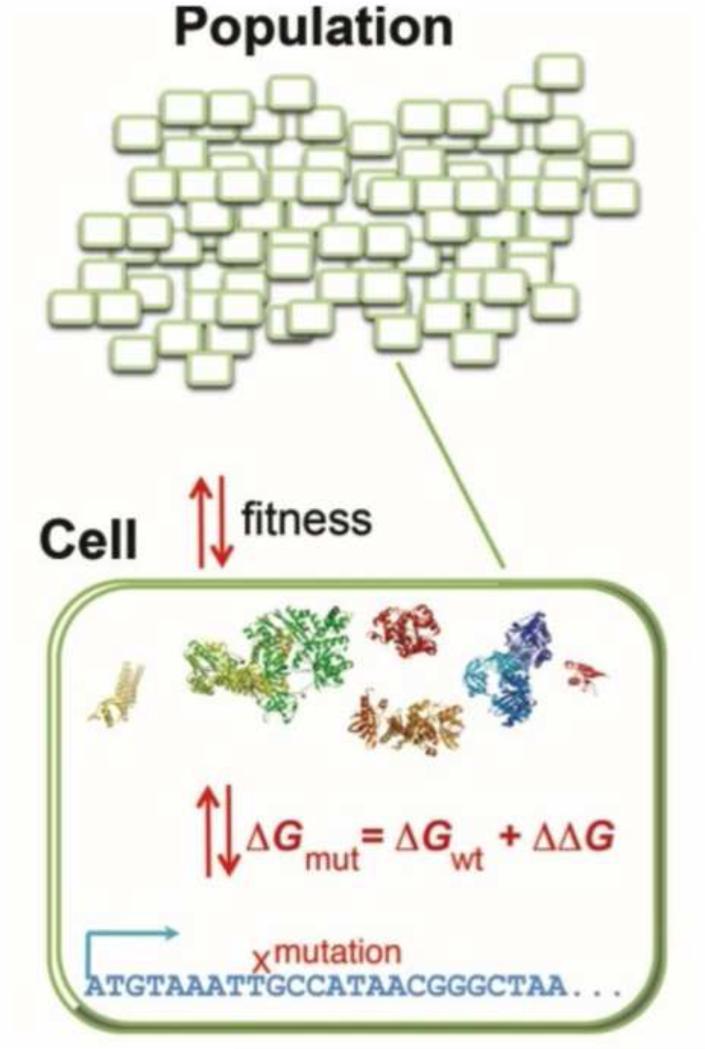
The underlying motivation for these multiscale models is to integrate our accumulated understanding of the mechanism in biological systems and evolutionary population dynamics. There are four elements to these models: (i) the genotype-phenotype relationship (GPR), (ii) the representation of the genomes and the protein products, (iii) the sources of genetic variation either by mutation or recombination, and (iv) the population dynamics and demographic model (Figure 1).

Figure 1. Schema of a bottom-up and multi-scale evolutionary models.

A model population consists of N organisms each with explicit genomes that encode proteins. The fitness of an organism is proportional to the folding stability of the proteins in the cytoplasm. The protein products are represented by their 3D structures from the protein databank (PDB)[16*]. When a random mutation occurs in the genome, tools in protein engineering and the 3D structure are used to estimate its effect on folding stability and, consequently, fitness. Alternatively, the proteins can be represented by 3D lattice models that allows for the exact calculation of biophysical properties [65] or for the possibility of a change in fold. The entire population is subject to mutation, drift, and purifying selection.

Traditional models in evolutionary biology assume the distribution of fitness effects (DFE) and then infer the possible dynamics [1,2], or assume the possible dynamics and then infer the DFE [3-5]. Both approaches have potential limitations because demography and the DFE are intrinsically coupled [6]. In contrast, in the bottom-up approach (Figure 1), the DFE is not an assumption but a consequence of the model. The integrated approach also builds on tools in protein folding and engineering, which have matured in the past decade, to estimate the effects of random mutations on proteins. Lastly, the bottom-up approach adds molecular realism to the traditional models in genetics (e.g., site-independence, 2-allele, etc.) by its explicit representation of the genes.

Contribution of biophysics to population and evolutionary genetics: The distribution of fitness effects of mutations in coding regions

In order to function, most proteins (with the obvious exception of intrinsically disordered domains) must maintain their native 3D structure. This requires folded proteins to be sufficiently stable against thermal fluctuations in the cellular environment. Protein folding stability, or the free energy difference between folded and unfolded states is a well-defined measurable sequence-dependent molecular property of proteins [7-9]. Folding stability determines the amount of folded (active) proteins according to the Boltzmann relation in statistical mechanics and it further modulates the protein abundance in cytoplasm by affecting turnover rates [10**]. The GPRs in these models are motivated by the selection for abundance of folded proteins[11,12], toxicity of misfolding proteins [13-15] and metabolic flux [16*]. In all these GPR, folding stability therefore is a key molecular parameter of fitness because it determines the total abundances of unfolded or folded proteins. The main quantity that defines the fate of arising mutations in population genetics is the selection coefficient s:

$$s=\frac{b_{after}-b_{before}}{b_{before}}$$

where b_before and b_after are the finesses of an organism (often defined in terms of growth or division rates) before and after the mutation respectively [17]. The selection coefficient quantifies the effect of a mutation on the fitness of an organism. In GPR based on protein folding stability, and under the assumption that the protein folding thermodynamics is two-state [7,8,18], the selection coefficient upon a mutation can be approximately expressed as [11,12,15]

$$s\approx e^{\beta \Delta G_{wildtype}}\left(1-e^{\beta \Delta \Delta G}\right)$$ (1)

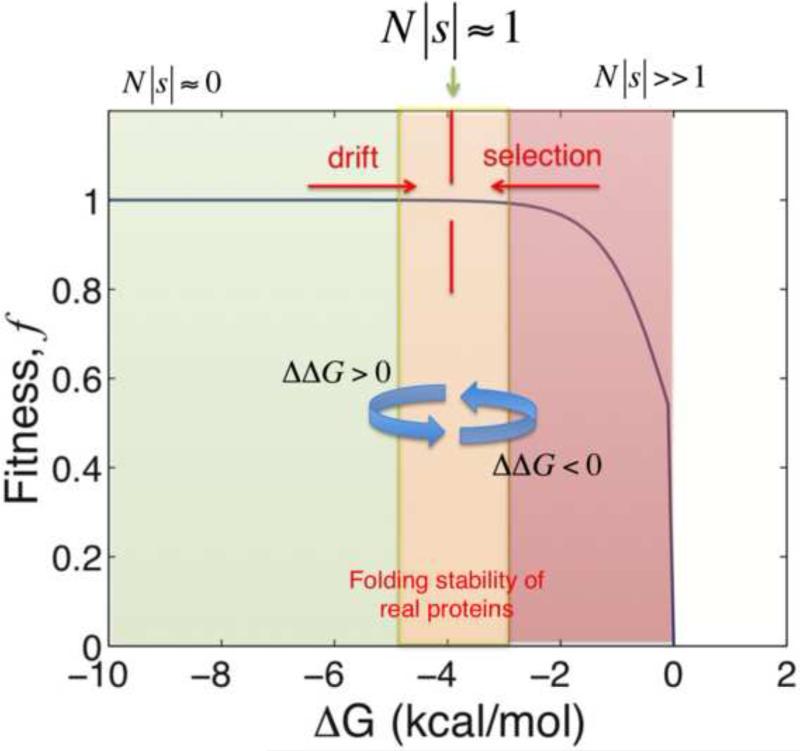
where ΔG_wildtype is the folding stability of the protein prior to the mutation, and ΔΔG = ΔG_mutant − ΔG_wildtype is the change in protein folding stability due to the mutation. The factor β = 1/k_BT (where k_BT=0.593 kcal/mol at room temperature). This non-linear expression provides a mechanistic interpretation of epistasis in proteins (Fig. 2). The effect of a specific arising random mutation ΔΔG is modulated by the pre-mutation (“background” or wild type) folding stability ΔG.

Figure 2. Fitness effects of mutations on a protein folding thermodynamic landscape.

The integrated biophysics-population dynamics models typically assume that the fitness of the model organism is proportional to the total number of folded (functional) proteins in the cytoplasm. That is, fitness f ∝1/(1+e^βΔG). Under this assumption, equation 2 defines how molecular changes (ΔΔG) map to fitness effect (s) [11,12,15]. In the regime of very stable proteins, the factor e^βΔG → 0, thus N|s| ≈ 0 even if ΔΔG values are nonzero. Additionally, because arising mutations are predominantly destabilizing, most mutations that fix in this regime are destabilizing giving rise to a mutational drift of ΔG towards the less stable regime. Conversely, in the regime of unstable proteins, N|s| > > 1 and selection dominates. Hence, in the unstable regime, mutations that fix are predominantly stabilizing. Mutation-selection balance occurs at the folding stability value where N|s| ≈ 1. Altogether, the epistatic interactions mutations on the thermodynamic fitness landscape results in the near neutrality of the fitness effects of fixed substitutions even if their molecular effects (ΔΔG) are non-neutral.

To be more quantitative, we provide an example of the fitness effect values realized from actual simulations[16*]. In the particular simulation, the population size was N=10³. A destabilizing mutation of ΔΔG =1 kcal/mol occurring in genes with ΔG_pre-mutation = −8 kcal/mol has a fitness effect of _251658240 Ns ≈ −10⁻⁴ however, the same mutation occurring in genes with ΔG_pre-mutation = −0.5 could be lethal. A stabilizing mutation of ΔΔG = −1 kcal/mol occurring in genes with ΔG_pre-mutation = −8 kcal/mol has a fitness effect of _251658240 Ns ≈ +10⁻⁴; however, if it occurs in genes with ΔG_pre-mutation = −0.5 kcal/mol, the mutation is extremely beneficial _251658240 Ns ≈ +10². Thus, in the regime where proteins are very stable, both destabilizing and stabilizing mutations have Ns < < 1; however, because of the larger supply of destabilizing than stabilizing mutations, most mutations that fix are destabilizing. This imbalance gives rise to a mutational drift of ΔG towards less stable proteins and away from the flatter part of the fitness landscape. In the regime where proteins are less stable, selection for stabilizing and against destabilizing mutations lead to the fixation of a larger fraction of stabilizing mutations. Mutation-selection balance occurs at the folding stability value where stabilizing and destabilizing mutations have equal likelihood of fixation[16*]. This balance indeed occurs in the regime of moderate protein folding stability and gives rise to the observation that proteins are “marginally” stable [19,20]. It is important to note the common misconception that selection for stability must result in very stable proteins and that the observed modest stabilities of proteins (in comparison for example with de novo designed ones [21]) therefore implies a “stability-activity tradeoff’’ [22] or provides the evidence against selection for stability altogether [23*]. As discussed here and in [9,11,19,20,24,25*,26*], selection for folding stability should not lead to most stable proteins. Rather, it is balanced by mutational drift towards destabilization resulting in a mutation selection balance that establishes observable distributions of protein stabilities.

We note that the distribution for the parameters on the right hand side of Eq. 1, ΔG_wildtype and ΔΔG, has been well-established experimentally [27]. The distribution of effects of random mutations on folding stability has also been estimated to be universal across several classes of protein folds[28]. Stability-centric models successfully reproduced experimentally observed distributions of protein stabilities [9,24,26*,29] and distribution of fitness effects in viruses [11]. Thus, the distribution of fitness effect s (DFE) of arising random mutations is in principle the convolution of the well-established distributions of ΔG_wildtype and ΔΔG.

While the DFE has been measured for viruses [30], its measurement in living organisms is difficult and resolution-limited [31]. Thus, studies on the DFE have largely relied on Bayesian maximum-likelihood approaches to fit population dynamic and demographic models to patterns of polymorphisms and amino acid differences between species [32-35]. A consensus result is that the DFE is characteristically skewed and can be described by a gamma distribution [32,34,35]. To arrive at a more mechanistic understanding of the DFE and polymorphisms, a recent work extended these biophysics-based evolutionary models to the polyclonal regime[16*]. The authors assumed that fitness is proportional to the total metabolic flux of a prototypical metabolic pathway and the total number of misfolded proteins. The PDB structures of proteins representing a prototypical glycolysis pathways were used in model cells in [16*]. They could keep track of all arising mutations, their history, and biophysical properties. More importantly, they could also mimic “population-wide deep sequencing” and compare with real SNPs [16*,36].

A major contribution from this work is its recapitulation “from first principles” of the DFE derived using the maximum Bayesian approaches. The DFE observed in simulations is skewed and can be well fitted to a gamma distribution, in agreement with empirical studies that estimated the DFE using maximum likelihood methods in human [32,34,35] and in flies[37] .

The near-neutrality of the resulting DFE from this mechanistic approach also shows that the near neutral theory of Ohta [38] should not be taken simply as a postulate, but rather as a robust consequence of the interplay between biophysics and evolutionary dynamics. Additionally, this mechanistic models shows that the patterns of polymorphisms, when framed in very direct observables such as changes in folding stability, supports the argument for a predominantly non-adaptive tempo of evolution at least for the coding region of the human genome (see Fig. 6 in ref. [16*]).

Contribution of population genetics to molecular biophysics: Environmental determinants of the evolution of protein folding stability

Under the assumption of mutation-selection balance, the selection coefficient of fixed mutations would be N|s|~1 (Fig. 2) [39]. Specifically, under the assumption that proteins are under selection to avoid the cytotoxic effects of misfolding, the selection coefficient is s ≈ Ae^{βΔG_pre-mutation} (Eq. 2, ref. [40]) where A stands for the protein copy number in cytoplasm. This expression for s translates to (ref. [40])

$$\Delta G\propto -k_{B}T\ln N_e-k_{B}T\ln A-k_{B}T\ln \left(\frac{1}{k_{B}T}\frac{\Delta \Delta G_{sd}^2}{\Delta \Delta G_{mean}}\right)$$ (Eq. 2)

Equation 2 is significant because it quantifies the direct effect of Darwinian selection on folding stability through its dependence on the effective population size N_e [11,40]. In particular, weak selection in low population sizes is predicted to lead to the evolution of less stable proteins; conversely, stronger selection in large population sizes will lead to the evolution of more stable proteins. Equation 2 also quantitatively defines the contribution of protein cellular abundance (A) on folding stability. Highly abundant proteins are predicted to be more stable than proteins with low copy number in the cell. The third term in Equation 2 gives the distribution of changes on protein folding stability (ΔΔG) due to random mutations. This distribution is approximately a Gaussian with mean ΔΔG_mean=1 kcal/mol and standard deviation ΔΔG_sd = 1.7 kcal/mol [9]. Both parameters are estimated from empirical measurements of folding stability changes due to single point mutations (ProTherm database[27]). Altogether, Equation 2 quantifies the direct and nonnegligible contribution of non-biophysical parameters (population size and abundance) on the evolution of protein folding stability.

The magnitude of the contribution of different selection and cellular factors can be quantified in terms of resulting statistical variation of protein stabilities suggested by Eq.2. Protein cellular abundances span ~10 to ~10⁶ copies per cell (as shown in yeast [41] and E. coli [42]), which is equivalent to variation of ~7 kcal/mol in protein stability (Eq[2]). Effective population sizes in nature range from 10⁴ (vertebrates) to 10⁹ (bacteria)[43], which could impose a ~6 kcal/mol spread in folding stability. Thus, the variation of protein folding stability in nature could be largely due to protein abundance and population size, however, this requires more proteomic measurements to prove.

Meanwhile, the range in abundance should systematically manifest itself in the structural properties of proteins across a genome. The observation that highly abundant, slow evolving proteins and proteins from thermophilic bacteria share similar amino acid composition [44] lends support to the dependence of stability on abundance. To demonstrate this prediction more unambiguously, it was shown that protein domains in yeast that are highly abundant in the cell show more favorable van der Waals interaction energy and more extensive hydrogen bond network [40].

As noted in [11,25*,45] population size may affect the cellular distribution of important signatures of folding stabilities such that organisms with small effective population sizes (e.g., endosymbiotic parasites that undergo episodic bottle-necking) will evolve less thermodynamically stable proteins, simply because deleterious mutations will fix at a higher probability in smaller population sizes. On the contrary, organisms with higher population sizes, which experience stronger purifying selection, are predicted to evolve more stable proteins. Additionally, assuming that all other things are equal, vertebrates (with effective population sizes of 10⁴–10⁵ [46] are predicted by Eq. 2 to evolve proteins that are on average 6 kcal/mol less stable than proteins in prokaryotes (whose population sizes are ~10⁸ [46]). Interestingly, protein structures of viruses, which undergo episodic bottlenecking (and hence have a low effective population size), show weak van der Waals interaction and low hydrogen-bond contact densities [47]. Large variations in effective population sizes also occur even among closely related species. In bacteria, species that are endosymbiotic have lower effective population sizes compared to the free-living counterparts. Mendez and co-workers argued that the bias towards higher AT (adenine and thymine) content among obligate endosymbiotic bacteria could be the response against less effective purifying selection against protein misfolding [48]. These bioinformatic studies strongly support the coupling between biophysical properties and evolutionary population variables, but a systematic survey of biophysical properties of proteins (such as folding stability) in genomes should be an exciting subject of future experimental work.

A recent bioinformatics analysis highlighted the important role of selection for protein stability [49*]. In this work the adaptation in catecaens to changing environment was linked to molecular events in evolution of their Myoglobins (Mb) through ancestor sequence reconstruction on the branches of the Mb phylogenetic tree. Seven positively selected sites were identified which contribute to protein stability according to experimental measurements and computational predictions. Furthermore, the authors noted correlated evolution of stability and abundance of Mb lending empirical support to GPR assumptions of integrated evolutionary models. A recent study [50*] provided a similar phylogenetic analysis of evolution of stability and activity for another important protein RUBISCO - a classic model to study chaperonin-dependent folding [51].

Application of the integrated approaches to the evolution of protein folds

The explosion of genomics data also led to notable observations of the distribution of protein folds in nature. First, it is finite and small, numbering only less than 10,000 [52]. Second, some folds are highly represented while others are rare, giving rise to a distribution of usage of protein folds in a genome that is skewed and uneven [53]. This uneven distribution resembles a power law [54,55], an observation that is robust to the details associated with defining protein folds. The universality of the power law distribution suggests fundamental features of protein and genome evolution.

The models that explain the power law distribution can be broadly classified into two classes. First class of models posits that observed distributions of protein folds reflects certain biophysical properties of proteins such as, e.g. their designability [56-58], propensity to participate in protein-protein interactions [59*,60] or folding rates [61]. Another class of models posits that the observed distribution is simply a consequence of the duplication-divergence dynamics of emergence of new folds without biases due to individual properties of proteins [55,62]. Nevertheless, certain biases are introduced in phenomenological duplication and divergence models just to fit the empirical observations. Additionally, these models should be cognizant of the fact that selection acts at the level of populations of organisms and not individual genes or proteins. This detail is crucial because numerous observations in the genome architecture (beyond the distribution of protein folds), could also be explained by a largely nonadaptive mode of evolution [63,64]; in this view, population size is a crucial parameter.

Many of these works have been recently reviewed [65-67]. Thus, here we instead focus on the studies to reconcile these two classes of models. These models also need to be consistent with evolutionary dynamics arising from neutral drift and Darwinian selection. Indeed, a more robust understanding of fold evolution can only arise by providing molecular and mechanistic details to the phenomenological duplication and divergence schemes.

Zeldovich et al. explicitly modeled the emergence of new folds in a multiscale model with explicit representation of proteins and selection acting at the organism level[68]. Their model cells contained variable number of genes that encoded model lattice proteins. They assumed that the fitness of the organism is a function of the folding stability of the encoded proteins; in particular, the death rate of the organism is a function of the least stable protein in the cell. From simulations that started with random sequences, they observed that once favorable sequence–structure combinations are discovered, the population grows exponentially, and the initially diverse structural repertoire collapses into limited number of selected fold architectures. This repertoire remained stable and abundant at timescales greater than organismal lifetime. The emergence of protein families and superfamilies and ensuing power law distributions that match distributions for real proteins arise as a consequence of properties of the physical model, which suggests new folds from dominant folds by satisfying energetically favored native conformations. Cuypers et al. [69] also modeled genome evolution using a population of virtual cells evolving to maintain homeostasis. Although the work was not aimed at explaining fold distributions (no details on the protein folds is included), they nonetheless observed that an initial rapid expansion of the genome was followed by a prolonged phase of mutational load reduction. This load reduction was achieved by the deletion of redundant genes, generating a streamlining pattern. This integrated biophysics-population dynamics model of fold evolution could potentially explain the dependence of the power law exponent on genome size, [70,71]. We note that there is a well-known correlation between genome size and population size [43], and that the decreasing power-law exponent could be partly due to the population size variation. This conjecture remains to be proven explicitly.

Conclusion and Outlook

We have shown in this review that an approach that integrates molecular biophysics and evolutionary population genetics provides more mechanistic insights into the origin of protein fold and sequence variation in nature. These works have largely focused on protein folding stability for reasons that are both scientific (folding stability is the most universal of protein biophysical properties) and pragmatic (there are available biophysical tools to estimate the effects of random mutations on protein folding stability). In the near future, together with developments in protein folding and engineering and drug discovery, we will be able to include in the evolutionary models the effects of random mutations on enzymatic activity or protein-protein interactions using realistic protein structures. Additionally, because the approach is bottom-up, it can be coupled to the current efforts that build comprehensive cellular model of the genotype-phenotype relationship [72]. Lastly, in very well defined biological systems such as viral evolution and development of antibiotic resistance, this integrated molecular biophysics and population dynamics approach offers the possibility of predicting near term evolutionary trajectories.

An important direction of current and future research is to establish more realistic and robust GPR. The progress towards this goal requires synergistic experimental and theoretical efforts. “Top down’’ directed evolution approaches aim to evolve a particular phenotype first and subsequently determine a genomic variation that caused phenotypic changes. However the major challenge here is to establish a causal link between the evolved phenotype and genomic changes given ensuing massive genomic variation (the “passenger-driver problem’’ [73]). An alternative approach is “bottom up’’ where genetic variation is introduced either rationally by genomic editing [10**][74] or via targeted random or saturating mutagenesis [75**,76] with subsequent analysis of fitness changes. The latter can be evaluated either from competition assays or direct measurements of growth rates [10**,74] or through deep sequencing approaches [76-78]. The “bottom up’’ approach provides, in principle, a direct link between mutational changes in molecular properties of proteins and phenotypic change. In practice the relation can be quite complex due to many intervening factors such as protein homeostatsis in cellular milieu mitigating the molecular effects of mutations [10**,79-81]. With the advent of new CRISPR-based [82] and other new tools of genomic editing we will witness major progress in our understanding of GPR in many organisms which in turn will lead to the development of new generation of more accurate and predictive microscopic multiscale evolutionary models.

Highlights.

1. The natural variation of proteins is a consequence of both biophysics and population dynamics.

2. Recent theoretical and computational efforts integrate biophysics and evolutionary population biology.

3. These integrated approaches provide more mechanistic insights into fundamental questions in biophysics and evolution.