To what extent does anti-mullerian hormone contribute to a better prediction of live birth after IVF?

Abstract

Objective

We assessed the predictive value added by Anti-Mullerian Hormone (AMH) to currently validated live birth (LB) prediction models.

Methods

Based on recent data from our center, we compared the external validity of the Templeton Model (TM) and its recent improvement (TMA) to select our model of reference. The added predictive value of AMH was assessed in testing the likelihood ratio significance and the Net Reclassification Index (NRI). The surrogate utility of AMH was tested by conducting an exploratory stepwise logistic regression.

Results

Based on 715 cycles, the original TM had poor performances (auROC C = 0.61 [0.58, 0.66], improving by fitting TM to our data (C = 0.71[0.66, 0.75]. TMA fitting proved better (C = 0.76; 95 %CI: 0.71, 0.80) and was selected as model of reference. Adding AMH to TMA or TM had no effect on discrimination (C = 0.76; 95 %CI: 0.72, 0.80), the likelihood ratio test was significant (p = 0.023), but the NRI was not (6.7 %; p = 0.055). A stepwise exploratory logistic regression identified the effects of age, previous IVF resulting in LB, time trend and AMH, leading to a prediction model reduced to four predictors (C = 0.75 [0.70, 0.81]).

Conclusion

The added predictive value of AMH is limited. A possible surrogate/simplifying effect of AMH was found in eliminating 9/13 predictors from the model of reference. We conclude that whereas AMH does not add significant predictive value to the existing model, it contributes to simplifying the equation to reliable, easy to collect, and available in all databases predictors: age, AMH, time trend and female previous fertility history.

Introduction

Determining which baseline characteristics are associated with the highest chance of achieving a live birth (LB) after IVF/ICSI has received much attention in the assisted reproduction technology (ART) literature. Prediction models are essentially designed to help ART experts counsel their patients and to decide whether or not to offer them IVF. The historical development of these models has highlighted the difficulties encountered in developing a model with sufficient precision for use in routine practice. Numerous approaches have been proposed, the best-known of which is the Templeton Model (TM) [1]. Other approaches include Bancsi (2), Commenges-Ducos [3], Ferlitsch [4], Hunault [5], Lintsen [6], Minaretzis [7], Nelson [8], Ottosen [9], Smeenk [10], and Stolwijk [11]. A methodological comparison of these models suggested that TM was most predictive of LB [12]. Although a more recent comparison between the Templeton and Nelson models [13] found equal overall performance in a primary infertility setting, the external validity of TM was confirmed on a wider basis [15] and a suggested improvement, the addition of three further predictors, resulted in higher discrimination (Templeton Model modified by Arvis, TMA [14], auROC = 0.75), although this model was not yet validated externally.

Despite these improvements, prediction remains insufficiently precise and requires improvement. Anti-Mullerian Hormone (AMH) is a dimeric glycoprotein and member of the transforming growth factor-beta superfamily, which includes growth and differentiation factors such as activins and inhibins, was recently suggested as a potential prediction marker of LB. Data from studies on women undergoing ovarian stimulation suggest that AMH is secreted in the serum mainly from small antral follicles and ceases to be produced when these follicles reach the dominance stage [15, 16]. In the human ovary, AMH expression is highest in follicles <4 mm in diameter and absent in follicles > 8 mm [17]. The utility of this expression as a marker for ovarian response has been suggested in numerous studies [15, 17–21]. Compared with the Antral Follicle Count (AFC), AMH is measurable throughout the menstrual cycle and in all patients, even those with ovarian cysts limiting AFC measurement; AMH also has low intra- and inter-cycle variability, although instability has been reported in some circumstances (n = 5006) [22].

Some studies have suggested that AMH has predictive value for LB after adjustment for age [23–25]; however none of these studies compared the predictive value with currently validated models such as TM, nor did they provide evidence of the higher predictive value offered when AMH was added to the model of reference. Our objective was to explore the extent to which the addition of AMH to TM increases the predictive value for LB. As a secondary objective, we assessed another possible usefulness of AMH: irrespective of its added predictive value, AMH may also exert a surrogate effect, eliminating existing predictors in the original model thus reducing their number, making the model simpler and easier to interpret.

Methods

Data collection

Our study was limited to the data available at our centre. All the IVF/ICI cycles prior to December 2010 and for which LB information was available, including those with early interruption at any stage, were included. We documented female age, male age, duration of sub-fertility, pregnancy history (primary/secondary infertility), cause of infertility (tubal infertility (TbI), male infertility, ovulatory dysfunctions, endometriosis and unexplained sub-fertility), uterus abnormality, BMI (weight/height²), basal FSH (IU/L), number of previous failed cycles (NFC), smoking habits of women and partners (Yes/No), previous number of miscarriages, duration of sub-fertility, previous IVF pregnancies resulting in LB (ILB), previous IVF pregnancies not resulting in LB (INB), previous Non-IVF pregnancies resulting in LB (NLB), previous Non-IVF pregnancies not resulting in LB (NNB), Antral Follicle Count (AFC) and AMH blood levels (ng/mL). Only baseline variables were used, any variables collected during or post down-regulation were disregarded at this stage. AMH was measured at cycle baseline using either the Immunotech–Beckman Coulter (AMH Gen II ELISA, Beckman Coulter, Inc., Brea, CA, USA), ELISA or the Diagnostic System Laboratories test (DSL, Active MIS/AMH ELISA; Diagnostic Systems Laboratories, Webster, TX, USA). AMH values in SI units (pmol/L) were converted to ng/mL by a factor of 7.14. Log-transformed AMH values were systematically used in the analyses.

Statistical analysis

In a first stage, we compared the external validity of TM and TMA to select our reference model before assessing the added predictive value of AMH. Discrimination was evaluated by the area under the curve of a ROC curve (auROC), a model considered to have poor, fair or good performance when the AuROC exceeds 0.7, 0.8 or 0.9, respectively [26]. Model calibration was assessed by the Hosmer goodness-of-fit test [27] and by testing the departure of the fitted line between observed and predicted frequencies [31]. For all the model fits, we used a bootstrapping technique for estimation of CIs, a shrinkage factor to reduce the model over-fit and obtain relatively unbiased estimates [28]. We tested and compared three models sequentially: TM original formulation, and TM and TMA fitted to our data. We compared models by their discrimination (auROC), and pairwise comparisons in which each tested model included an intercept and an offset term of the log odds of LB calculated by the control model.

The selected model was considered as our model of reference on which we assessed the added predictive value of AMH for LB: a) By adding AMH to the predictor list, we tested the significance of the added term by a Chi-square Likelihood ratio Test LRT between the two nested models. b) We evaluated the net benefit in comparing old and new classifications [29], net reclassification improvement (NRI) constitutes the net effect on reclassification tables constructed separately for participants with and without LB, and quantifies the correct movement in categories upwards for events and downwards for non-events. The integrated discrimination improvement (IDI) focuses on differences between sensitivity and specificity for models with and without the new predictors.

Our secondary objective was the extent to which, independently of its added predictive value, AMH may help simplify the model by eliminating a subset of existing predictors. To this end, we conducted an exploratory stepwise algorithm on our data by considering as potential predictors all the variables included into TM and TMA, and adding AMH. The final model was found by using bootstrapping (n = 5000) and testing several variable selection strategies (forward, backward and stepwise).

To account for more than one cycle for the same patient, the prediction model was fitted by using a non-linear mixed model featuring a logistic model in which the patient was considered as a random factor. The main and interaction effects were tested at the 0.05 and 0.1 two-sided confidence levels, respectively. All the statistical analyses were carried out using the R statistical software package (R, version 2.12.2).

Results

A total of 723 IVF cycles were included according to our initial selection principles (Table 1): In summary, these patients were characterized by a median age of 35.1 [Interquartile Q = 31.1,38.7], mean BMI of 23.4 ± 4.2 kg/m2, mean number of 2.15 ± 1.2 unsuccessful IVF attempts, mean AMH of 3.84 ± 3.17 ng/L and 11.7 % tubal infertility. 56 % of patients were treated with a GnRH long protocol agonist, and ICSI was applied in 42 %. No missing data was found on LB, 1.4 % missing data were found in the predictor variables, prompting exclusion of 8 cycles leading to a final study sample of 715 cycles. 108 (15.1 %) of the 715 cycles studied resulted in live births.

Table 1.

Sample description, mean ± SD or median [interquartile], (count) and percentage (%)

Parameter	Value
Age - Median [interquartile]	35.1 [31.1, 38.7]
BMI - mean ± SD	23.44 ± 4.20
FSH - mean ± SD	7.45 ± 3.38
LH (UI/L) - mean ± SD	3.22 ± 2.52
E2 (pg/ml) - mean ± SD	52.17 ± 39.14
E2 Triggering - mean ± SD	2301 ± 1326
AMH - mean ± SD	3.84 ± 3.17
Number of Attempts - mean ± SD	2.15 ± 1.58
Infertility duration - mean ± SD	23.18 ± 9.09
ICSI application (Count)	(305) 42.7 %
GnRH antagonist (Count)	(401) 56.1 %
Previous LB after IVF (Count)	(173) 24.2 %
Previous Non-LB after IVF (Count)	(100) 14.0 %
Previous non-IVF LB (Count)	(113) 15.8 %
Previous non-IVF non-LB (Count)	(103) 14.4 %
Diagnosis (Count):
Unexplained	(135) 29.2 %
Tubal	(54) 11.7 %
IUI failure	(30) 6.5 %
Endometriosis	(33) 7.1 %
Age > 40	(45) 9.7 %
Multiple	(165) 35.7 %

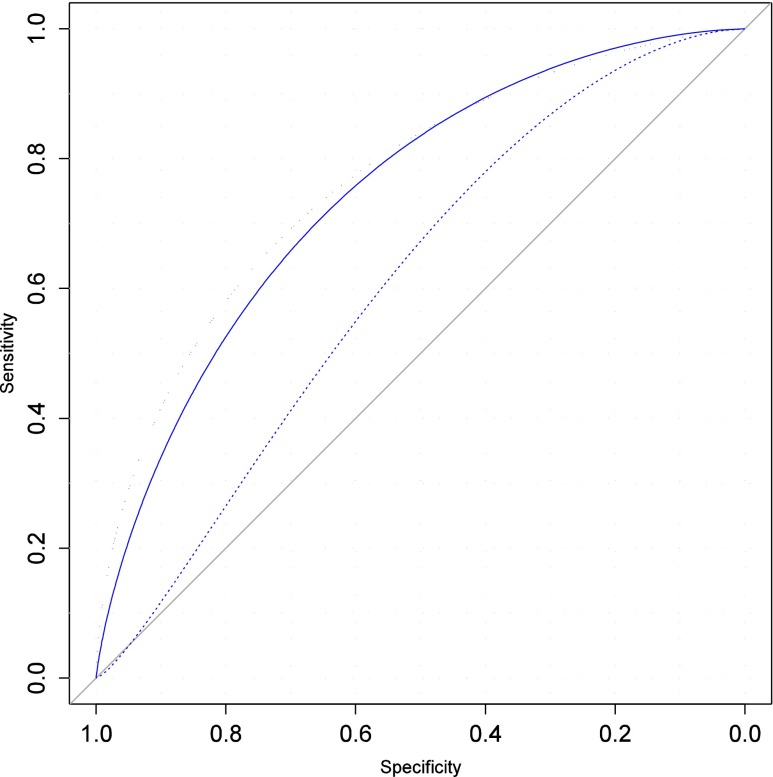
Three models were compared to select the model of reference: the original TM model led to poor discrimination (auROC = 0.61, [0.58; 0.66], Fig. 1), irrespective of whether the woman’s age at the first or current IVF cycle was used. Calibration assessment highlighted underestimated prediction of 16 % corresponding to higher observed rates (Fig. 2, Hosmer Test, p = 0.008). Discrimination significantly increased when TM was fitted to our data (auROC = 0.71, [0.66; 0.75]), and a further significant increase was observed when TMA was fitted (auROC = 0.76, [0.71; 0.80], Fig. 1), with almost perfect calibration (Fig. 2) expressed as a maximum difference of 1.9 % between the true and predicted values (Fig. 2), and the fitted line coinciding with the diagonal (slope = 0.93, [-0.47; 1.35]).

Fig. 1.

Discrimination measured by the Area under the ROC curve (AuROC), for the three models considered: strict Templeton model (auROC = 0.61, 95%CI 0.54, 0.56, dashed curve), Templeton-Arvis TMA model (AuROC = 0.76, [0.71, 0.80], dotted line), and simplified model using AMH (auROC = 0.75, [0.70, 0.80], solid line)

Fig. 2.

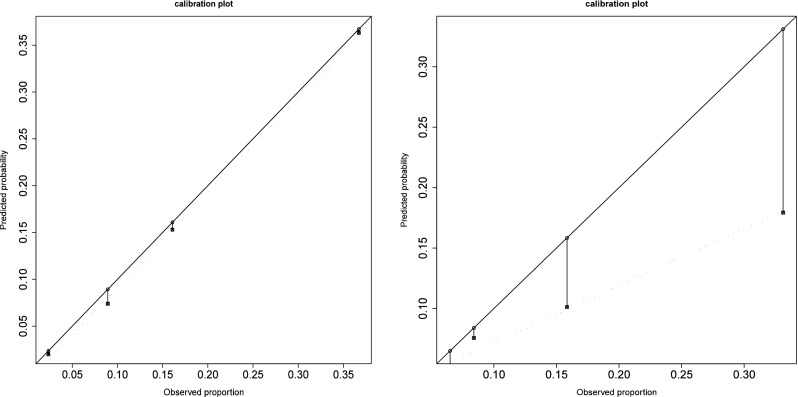
Calibration plot for the original TM model (right) and TMA fitted model (left). Ordinates and abscises represent the predicted and observed live birth probabilities, respectively, the solid line is the ideal line (meaning coincidence between observed and predicted probabilities) and the dotted line is the linear fitting based on the quartiles of the distribution observed

The TM fitted to our data was compared to the original TM by including an intercept and an offset term of the log odds of LB calculated using the original TM: only the intercept was found to be significant (p < 0.001). The same comparison between the fitted TMA versus the fitted TM highlighted four highly significant terms (p < 0.001): intercept, trend in time, FSH and BMI.

TMA fitted to our data was selected as our model of reference to evaluate the added predictive value of AMH: a) When adding AMH to this model, the discrimination remained unchanged; b) A significant contribution was found in adding AMH to the TMA (df = 1, LRT = 5.37,p = .023); c) In cycles leading to a live birth, the net gain in sensitivity was 4/108 = 2.77 %, whereas for non-responders, the gain in specificity was 24/607 = 3.95 %, the overall Net Gain being NRI = 6.73 % (SE = 3.45 %, p = 0.055) whereas the estimated IDI was 0.0167 (p < 0.001).

Instead of TMA, we also evaluated the added predictive value of AMH on TM, as TM was more used and externally validated. Adding AMH to TM modified the auROC from .71 to .713, a significant contribution of AMH was found (df = 1, LRT = 6.31,p = .039), and the overall Net Gain was NRI = 7.2 % (SE = 4.01 %, p = 0.048)

Our secondary objective was to assess the capacity of AMH to simplify the existing model of reference. We conducted a stepwise exploratory Logistic regression by taking LB as the dependent variable and all the available baseline variables of TM, TMA, to which we added AMH. Across bootstrapping and several strategies of variable selection, a consistent model was identified limited to 4 significant predictors (Table 2): the linear and quadratic effect of age (Odds Ratio OR = 1.15/year, [1.04; 1.27]) and OR = 0.98/year² [0.96; 0.99]), at least one previous IVF resulting in Live birth (OR = 4.03, [2.57;6.32], Time Trend (OR = 1.22 [1.07; 1.39] and AMH (log-transformed value, OR = 2.27 [1.37; 3.67]), with an observed auROC discrimination of 0.76 [0.71; 0.80].

Table 2.

Summary of model findings The final simplified model based on stepwise regression analysis is reported in the third column

.	Templeton (TM)			Templeton-Arvis (TMA)				Final Simplified ModeI
	OR(3)	95 %CI	Est(2)	OR(3)	95 %	CI	Est(2)	OR(3)	95%CI	Est(2)
Intercept(6)(age = 30)	0.17	0.15, 0.20	−1.77	0.23	0.07,	0.72	−1.48	0.29	0.17,	0.49	−1.24
Age (1)	1.01	1.01, 1.007	0.005	1.17	1.05,	1.30	0.15	1.15	1.04,	1.27	0.14
Age2 (1)	1.00	1.00, 1.000	−0.0002	0.98	0.96,	0.98	−0.02	0.98	0.96,	0.99	−0.02
Infertility duration:				0.97	0.95,	1.01	−0.02
1 Year	1.19	.68,1.73	0.171
4 years	0.88	0.55, 1.39	−0.012
7 years	0.78	0.54, 1.37	−0.248
13 years	0.61	0.25, 0.99	−0.494
Number of attempts	0.87	0.71, 1.29	−0.013	0.85	0.73,	1.01	−0.15
Tubal Infertility	0.76	0.67, 1.39	−0.271	0.40	0.13,	1.19	−0.90
ILB (8)	2.01	1.65, 2.76	0.698	3.97	2.52,	6.25	1.38	4.03	2.57,	6.32	1.39
INB(8)	1.34	0.89, 2.55	0.292	0.76	0.39,	1.45	−0.27
NLB(8)	1.21	0.77, 1.57	0.190	0.89	0.48,	1.65	−0.11
NNB(8)	1.02	0.54, 1.41	0.019	0.84	0.43,	1.65	−0.17
Year (from 2011)				1.23	1.07,	1.40	0.21	1.22	1.07,	1.39	0.20
FSH >10				1.84	0.90,	3.79	0.61
BMI > 26 or <18				1.77	1.01,	3.12	0.57
AMH				1.18	0.67, 1.85	0.16	2.28	1.376,	3.768	0.731
C (Strict Model)(4)	0.61	0.58, 0.66
C (Fitted model) (5)	0.71	0.66, 0.75	R2 = .067 (7)	0.76	0.71, 0.80	R2 = .14 (7)	0.75	0.71, 0.80	R2 = .14(7)

¹⁾ Age and Age2 are polynomial components of age. ⁽²⁾ Est reports the parameter estimates of the logistic regression. ⁽³⁾ Odds Ratio (OR) and 95%CI calculated as exp(est), p values <0.001 are in bold underlined. ⁽⁴⁾ C = area under the ROC curve and 95%CI calculated on the strict model (no fitting). ⁽⁵⁾ C = area under the ROC curve and 95%CI calculated on the fitted model. ⁽⁶⁾ The intercept of the model depends on the selected reference in coding the predictors, and corresponds to age of 30 years. ⁽⁷⁾ Nagelkerke Determination (R²) coefficient of the Logistic model. ⁽⁸⁾ Female fertility history: ILB: previous IVF pregnancies resulting in LB, INB: previous IVF pregnancies not resulting in LB, NLB: previous Non-IVF pregnancies resulting in LB, NNB: previous Non-IVF pregnancies not resulting in LB

Compared with this final model, the simple model restrained to Age and AMH was characterized by a significantly lower auROC of .67. The coefficients of determination were R² = .14 and .05, for our model and the Age + AMH model respectively.

Discussion

Main objectives

Our primary objective was to assess the predictive value of AMH for LB prediction. The a priori relevance of AMH in this setting is justified as it is a marker of ovarian reserve, which may in turn influence LB. After selection of a reference prediction model, we tested the added predictive value of AMH in the model in several independent ways: By using TM or TMA. the discrimination (auROC) remained virtually unchanged, and although the likelihood ratio of the two nested models was significant, we identified a modest but non-significant net gain classification of 6.7 and 7.2 % compared with and without AMH for TMA and TM, respectively. We conclude that the added predictive value of AMH is limited.

We also assessed the ability of AMH to simplify the prediction model using a stepwise regression algorithm based on all the available potential predictors involved in the existing validated prediction models. Four significant effects consistently emerged, including AMH and three contained in the original TM and TMA models (linear and quadratic effect of age, time trend and previous IVF resulting in Live birth). The corresponding auROC value (0.75 [0.70, 80]) remained virtually unchanged compared with the TMA model based on 13 covariates, and very close of the value found for TMA in another centre [14]. This result provides evidence of a significant surrogate effect of AMH: Using AMH, the model becomes substantially simpler: 9 out of the 13 original covariates of TMA are eliminated, i.e. duration of infertility, number of attempts, previous live or not live (still)births, FSH level and BMI. Our model confirms the independent effects of AMH and age, as already suggested elsewhere [24]; however, in accounting for the nonlinear effect of age, previous IVF history (existence of a previous LB), and the improvement in LB over time, the discrimination significantly improved and the percentage of explained variance (R²) more than doubled.

A cluster analysis on the correlations between the predictors helped in understanding the simplification effect of AMH. In this analysis, we found an important group of correlated predictors: FSH, AMH, infertility duration, number of attempts, and age. Almost all these variables were eliminated from the model except age. AMH, a strong predictor of ovarian reserve removed all these variables appearing as indirect and less determinant predictors of ovarian reserve. Although unknown when Templeton model was published, AMH is now widely available and advantageously substitutes for indirect measures of ovarian reserve.

Secondary objectives

Before assessing the added predictive value of AMH, our preliminary objective was to select the best prediction model. External validation is a key step before deciding to adopt a prediction model. Although in many other pathologies, fitting a model to a particular centre generally constitutes a licit approach, in the ART context, a model fitted in one centre and assessed in other centres will likely demonstrate poor validity due to the paramount centre effect overriding the patient mix effect [14, 30]. As has already been reported in previous external validations of TM [10, 31], the performance of TM and TMA original formulations were very poor, although these results were easily predictable. Instead of fitting the original centre-specific formulation of a model to another centre, a model must be first fitted to the data of the centre studied to estimate, at the very least, the model intercept. In such cases, if no other significant effect is found, the model tested is de-facto considered to be externally valid in adjusting for the intercept which measures center performance. By this analysis, we suggest a statistical technique adapted to predicting models in ART, taking into account higher differences between centers. We also provide some evidence of the improvement of the TMA compared with TM by confirming the added predictive values of FSH, BMI and time trend. Smoking habits, another additional variable included in the TMA but not TM, was not considered as significant.

Limitations

There are several limitations in this study. Firstly, our suggested external validation technique based on fitting the data to the center is based on a simplified hypothesis that the center performance and the mix coefficients (patient specific variables) are separable, which in particular supposes the absence of interaction between the center and specific women variables.

Templeton and Nelson models were fitted on the basis of very large sample sizes. Data were collected from legal sources and issued by many centers. Our study is based on a small sample size, and has no ambition of competing with these models. Our results are based on one center, and need to be generalized across other centers. The small sample size underpowered the results particularly in the stepwise regression. A multicenter investigation involving a larger sample and allowing center-mix interaction testing could be required.

Other important limitations remain before LB prediction models can be considered as applicable. Despite adding a new marker like AMH to the existing models, the predictive potential remains poor. Even in the best conditions in fitting a model to a specific center, never a sufficient discrimination was reached (maximum values of 0.78 were found, which is considered as fair, but not good). Calibration has been suggested as a more important characteristic than discrimination (32). We admit that a bias-free estimate irrespective of the magnitude of the prediction is useful; however, such a prediction without knowledge of the precision of the prediction remains somewhat unsatisfactory, in particular because the precision is not constant and depends on the value of the predictors. A more pressing concern is when a predictive model is used to predict the outcome of a specific individual. In this case, even the confidence interval of the probability is no longer relevant and tolerance interval must be used instead (33). However, tolerance values essentially depend on the determination coefficient of the model (R²), rarely documented in the studies, except in the present case in which the maximum R² was 0.14. These limitations are beyond the scope of this paper, but necessitate further research before a predictive model can be utilized on a regular basis in IVF applications.