Abstract
We present a method to tune the resonance frequency and the Q-factor of micro and nano-metric mechanical oscillators. A counteracting loop drives a capacitive force applied to the oscillator. The proportional and differential gains are used to shift the resonance frequency up to 75% and to tune the Q-factor of the oscillator, by changing its effective stiffness and damping ratio. The oscillator position is monitored in a large bandwidth with a fiber-optic based interferometer. We applied this simple operational scheme with different oscillators for modifying easily their dynamical properties. Compared to alternative methods requiring external fields, our method can either increase or decrease the resonance frequency in a frequency range much more extended. This opens up a wide range of applications, from force sensors with extremely low elastic constants but high quality factor to tunable energy harvesters or to high-frequency tuning of radio frequency filters. The control scheme can work in different media, and is then suitable to be applied to biological sensors and actuators.
Micro and Nano Mechanical systems (MMO and NMO) are devices that are suitable to a wide array of applications spanning a broad frequency range: mass sensing1,2, detection of biological activities3, Scanning Probe Microscopy4, high-frequency displacement transducers5 and many others6. Usually these devices can be considered as simple mechanical harmonic oscillators.
The control of the dynamic properties of Micro and Nano Mechanical Oscillators is a necessary way to extend their range of utilization. The full control of the oscillator parameters is a key element in the mentioned applications. For instance, the increase of the stiffness of the oscillator is useful to avoid the jump to contact mechanism, but its decrease, coupled with a high Q-factor, is fundamental to increase the resolution in force sensors. In another example, low-frequency, tunable resonators are being developed for harvesting vibrational energy in order to power portable wireless electronics, used in a multitude of applications today7,8. Meanwhile, tunable NMOs are a possibility for the control of Radio-Frequency mechanical filters. NMO's are also used in the detection of biological activity in solution. Here, extensive research has been made to maximize the quality factor of the oscillators, and different approaches have been followed2,9,10.
The tuning of MMOs and NMOs is usually done taking into account that the surrounding environment highly affects MMO and NMO behavior. In particular, a shift in the first eigen-mode is observed in presence of external fields11 or when working in extremely damped media12. Several operational schemes have been suggested for tuning the first resonance in these devices, ranging from the insertion of the oscillators in external force gradient11 to the thermal tune of phase transition based devices13,14. In analogy, several approaches have been followed to tune the oscillators Q-factor. At first, there has been an interest in increasing the Q-factor, leading to the development of active Q-control6,15,16 and parametric excitation17,18. On a different approach, an active damping of the resonator has been implemented to decrease its relaxation time, allowing faster Atomic Force Microscopy scanning speed19 or for damping its thermal vibration20. However, most of the solutions7,8,11,13,21 provide only a monodirectional moderate shift of the first resonance of the oscillator, in the range of ±2–10%, and can only exceed these values for low frequency applications. Even then, the values reported in literature do not exceed ±20% of the natural frequency of the oscillator.
We propose a method to tune the dynamical properties of a MMO for controlling, simultaneously and independently, its resonance frequency and Q-factor in a large frequency range, with bi-directionality. The operational scheme is based on the measurement of the instantaneous position of the MMO in a large bandwidth with a fiber optic based interferometer22. Effectively, this methodology is similar to the one proposed for a very specific probe21 where the excitation of the oscillator is carried out by a signal partially proportional to the position and partially to the speed of the oscillator. Moreover, harmonic oscillators have been controlled by PID loops in a wide range of applications, ranging from Music and Acoustics23 to nanotechnology24. Here we propose this method to tune the resonance micro and nanomechanical oscillators in a large bandwidth.
In our case, the position is kept constant by a PID loop which drives a capacitive force acting on any generic MMO and NMO. One plate of the capacitor is the MMO itself, whereas the second plate is an optical fiber on which we have deposited a thin gold layer. A scheme is shown in Fig. 1. This operational scheme allows to artificially increase or decrease the stiffness of the oscillator, leading to first resonance shifts two orders of magnitude higher than the shifts due to conventional external static force gradients11. Although the static capacitive force between the plates is attractive, it is possible to shift up the resonance to frequencies higher than the unperturbed resonance, which is not possible in presence of solely static attractive force gradients. Together with the shift of the resonance, we implement an active Q-control of the resonator by tuning the differential gain of the counteracting loop, sweeping the Q-factor of different cantilevers by several times the unperturbed oscillator's value. The PID counteracting loop is integrated in a FPGA.
Figure 1. Operational scheme used to shift the dynamical parameters of the cantilever in air.
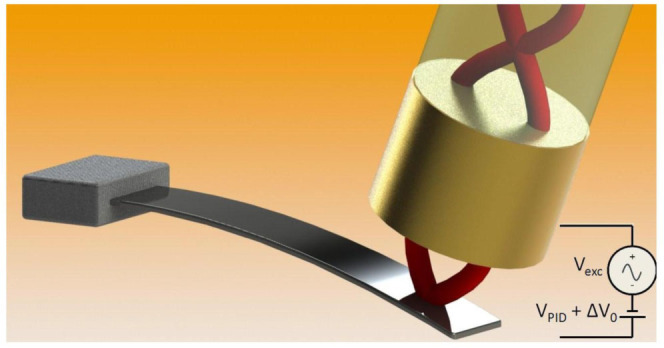
The free end of the optical fiber is coated with 30 nm of gold. A capacitive Fcontrol is imposed to the oscillator by applying a voltage VPID between the fiber and the backside of the cantilever. The harmonic excitation is employed to monitor the changes of the oscillator transfer function.
At first, we show that the method works in air. Then, we additionally use it for tuning the dynamical properties of an oscillator in liquid, in this case substituting the capacitive actuation with a phothermal one.
The Force Feedback control theory based on a fast PID counteracting loop of AFM cantilevers has already been reported25,26 and its capabilities have already been shown in a large number of works24,27,28,29. We will now consider AFM cantilevers as MMO and NMO devices. The loop gains can be included in the harmonic oscillator equation:
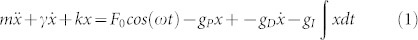 |
where x is the position of the free end of the oscillator and 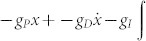 is the feedback force imposed by the PID with gP, gI and gD the proportional, differential and integral gains, respectively. F0 is the harmonic stimulus used to test the oscillator response. We measured the cantilever end position with a fiber-optic based interferometer which is described in the Methods section. Equation (1) implies that the presence of the loop affects the dynamic response of the harmonic oscillator. We can define a new stiffness kC = k + gP and a new damping γC = γ + gD.
is the feedback force imposed by the PID with gP, gI and gD the proportional, differential and integral gains, respectively. F0 is the harmonic stimulus used to test the oscillator response. We measured the cantilever end position with a fiber-optic based interferometer which is described in the Methods section. Equation (1) implies that the presence of the loop affects the dynamic response of the harmonic oscillator. We can define a new stiffness kC = k + gP and a new damping γC = γ + gD.
The controlled oscillator has now different dynamical properties. In particular, we can define its resonance frequency26
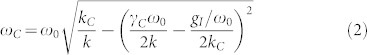 |
where gI is the integral gain. We can define the Q-factor
 |
where 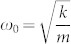 is the natural frequency of the unperturbed cantilever.
is the natural frequency of the unperturbed cantilever.
Results
The methodology has been tested on three different oscillators in air, considering the different possible applications that could be addressed: besides a regular tapping-mode cantilever, we tested a low-frequency MMO to verify the possibility of tuning an extremely soft oscillator, and finally we analyzed a high-frequency NMO, that could cover a wide range of applications. Table 1 shows the geometrical properties and the stiffness of each oscillator.
Table 1. Nominal parameters (dimensions and elastic constant) of the different cantilevers used in the experiments.
| Oscillator | L × W × T (µm) | k (N/m) |
|---|---|---|
| Olympus BL-AC40TS | 38 × 16 × 0.2 | 0.09 |
| Bruker MLCT - D | 225 × 20 × 0.55 | 0.03 |
| Olympus BL-AC10DS-A2 | 9 × 2 × 0.13 | 0.1 |
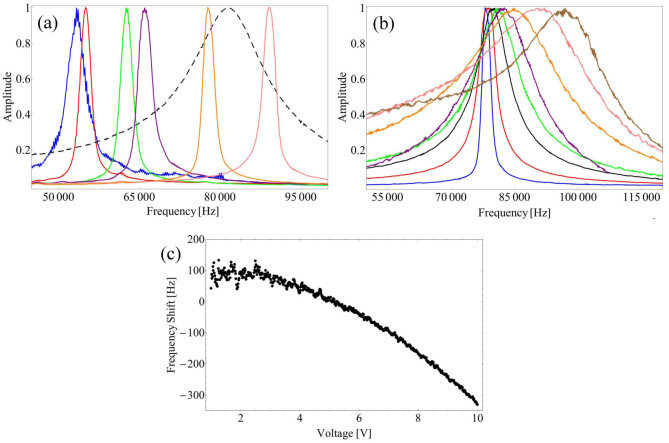
We focus first on the Olympus BL-AC40TS. Following equations 2 and 3, it is possible to freely tune the frequency and Q-factor of the oscillator by changing the control parameters gP and gD. To check this behavior, several frequency sweeps were performed on the cantilever employing the Lock-In amplifier. Figure 2, (a) and (b), present the change of the controlled oscillator transfer function for different control gains.
Figure 2.
(a) Normalized frequency response of the MMO for an ensemble of control gains. Black (dashed): the response of the cantilever in absence of control. (b) Effect of the differential gain on the normalized transfer function of the cantilever. (c) Dependence of the frequency shift sweeping the static voltage between the oscillator and the optical fiber. The frequency shift obtained applying a static field is two orders of magnitude lower than the one obtained with the PID control.
We were able to obtain relevant shifts of the resonant frequency and quality factor of the cantilever over several tens of kHz for the frequency (a shift corresponding to the interval from 0.66ω0 to 1.18ω0) and for Q-factor changes over one order of magnitude around Q (0.75Q0 to 10.37Q0). These results compare, and even exceed, other results obtained with and without using active control, and they are limited only by the maximum controller gains that keep the system stable, and ultimately by the elastic constant of the cantilever in use. We have already discussed the maximum attainable gains dependence on the external PID actuation in a previous work26, while the dependence on the bandwidth of the actuator has been discussed elsewhere25. Figure 1(c) shows the resonant frequency of the oscillator as a function of the static field applied V0, with the feedback loop then turned off. The frequency shift is measured with a Phase Locked Loop. The maximum frequency shift obtained by changing the static field is two orders of magnitude lower than the shift obtained with the active control, indicating that the effect of the feedback is indeed the key factor in changing the resonant frequency of the cantilever.
The setup is suited for different oscillators: a micro-sized oscillator that resonates at a lower frequency (15 kHz) and a NMO resonating at 1.25 MHz. The results are shown in Figure 3. Figure 3 (a) shows the change of the oscillator's transfer function. A gigantic shift (±75%ω0) is observed for the oscillator and, surprisingly, we observe that, when shifting the resonance at low frequencies (3–4 kHz), it is possible to keep a relatively high Q factor compared to the unperturbed value evaluated from the black dashed curve.
Figure 3. Normalized frequency response for the (a) low-frequency and (b) high-frequency cantilevers, for different sets of control gains.
In the black curves the controller is off.
Figure 3 (b) shows the change of the transfer function of the NMO. In this case, in order to provide high bandwidth to the control loop, an analog Proportional-Derivative controller was custom-made for this experiment. The dynamic range of the loop is between 0 V and 10 V. The Integral part of the controller was provided at low frequency by an additional low-bandwidth Proportional-Integral control loop. In this experiment ΔV0 has been fixed to 60V in order to compensate the reduction of the force gradient due to the reduced cantilever size. This provides an effective Fcontrol per Volt equal to 2.5nN/V, comparable to the one employed in previous experiments. Figure 1S in the supplementary section presents the frequency shift induced by a sweep of the static voltage applied between the fiber and the cantilever starting from 60V. Over the static method, we can gain three orders of magnitude in terms of frequency shift imposed to the oscillator when using fast PID control. The observed shift is about 25%ω0. There is however an asymmetry with regard to ω0, since the positive shift is about 4 times smaller than the observed shift to lower frequencies. We consider this to be a result of the custom-made PID's bandwidth not being high enough to provide a full range of actuation around the natural frequency of the resonator.
These results show that this method works for very different oscillators. Besides the full control of low frequency oscillators, the results for the fast cantilever prove that this method is also viable for high frequency NMOs. To resume, Table 2 summarizes the different dynamic parameters obtained for all the oscillators.
Table 2. Resume of the different dynamic properties throughout the experiments.
| k (Nominal, N/m) | 0.09 | 0.01 | 0.1 |
| ω0 (kHz) | 82.479 | 14.7 | 1254.8 |
| Q | 7.1 | 4.5 | 43.8 |
| ωCmin (kHz) | 54.2 | 3.9 | 995.2 |
| ωCmax (kHz) | 97.2 | 25.5 | 1323.5 |
| QCmin | 5.3 | 0.8 | 4.72 |
| QCmax | 73.6 | 34.6 | 226.8 |
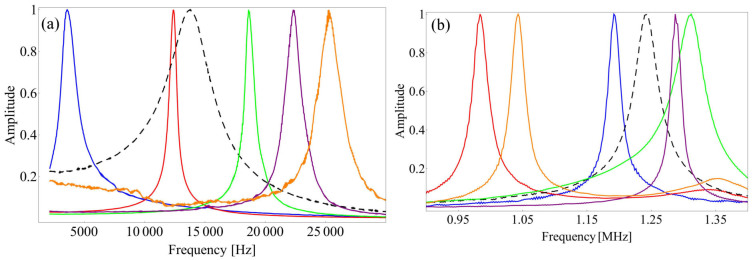
To demonstrate the flexibility of this methodology, we tested the behavior of the NMS when actuated in water, as it would be necessary for addressing life-science applications. Due to the nature of the capacitive interaction it was impossible to obtain the same force gradients applied to the cantilever in this medium. We circumvented this fact by exciting the NMO with a photothermal excitation of a commercial Atomic Force Microscope, with the power of the excitation laser controlled by the sum of the AC excitation signal with the custom-made high-frequency Proportional amplifier output. The derivative part of the control signal was done employing regular Q-control provided by the AFM. Figure 4 presents the NMO's transfer function when employing different proportional gains.
Figure 4.
(a) Operational scheme used to shift the dynamical properties in liquid, employing a photothermal actuation at the oscillator base. An optical beam deflection scheme employs a red laser to measure the oscillator deflecting angle. The PID loop keeps the cantilever deflecting angle constant by driving the power of the blue laser focused at the oscillator base. (b) Frequency response of the NMO in water for different control parameters. The dashed curve presents the unperturbed response, while the remaining experiments are done keeping the Q-control/derivative gain constant, and applying a negative (green) and positive (red) or null (blue) Proportional gain.
Despite the non linearity in frequency of the photothermal actuation, resulting in a higher excitation at low frequencies, the observations clearly demonstrate the effectiveness of the actuation method in changing the oscillator's parameters. The presence of a peak in every experiment for ω → 0 is due to photothermal excitation technique providing an excitation force not constant with frequency, attenuating high-frequency signals30. The experiment proves that the operation scheme can be used, not only in different media, but also with different actuation procedures.
Discussion
We have analyzed the validity of the model concerning the change of the dynamical behavior with the control gains on the Olympus BL-AC40TS oscillator. For this purpose, we have swept gP from -0.023 N/m to 0.023 N/m. gD was changed between different values, positive and negative, limited the controller's actuation range. For each pair of gP and gD the frequency response was acquired. The results are presented in Fig. 5. Fitting equation 3 to the measured Q-factor dependence, we retrieved the actual differential gains used in the experiments. This to account the fact that: i) the differential gain is multiplied with the proportional one ending up in a non-linear dependence of this parameter, and ii) the FPGA actuation is itself not linear, making difficult the comparison with the adopted model. Note that these equations are only valid for a low-damping regime26, and for this reason we fitted only the data for which gD < 0. With this analysis we are able to infer that the differential gains used for the lower damping experiments were in the range of 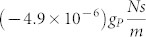 to
to 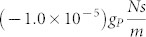 . It is thus natural a deviation from the model for increasingly negative values of gP. In addition to the experimental points, Figure 5 presents the curves derived from model equations once the fitted parameters are inserted. The data is in good agreement with the model, considering that the obtained values for gD provide a good explanation of both the frequency and Q-factor behavior simultaneously.
. It is thus natural a deviation from the model for increasingly negative values of gP. In addition to the experimental points, Figure 5 presents the curves derived from model equations once the fitted parameters are inserted. The data is in good agreement with the model, considering that the obtained values for gD provide a good explanation of both the frequency and Q-factor behavior simultaneously.
Figure 5. Change of resonant frequency and Q-factor as a function of the proportional and differential gains.
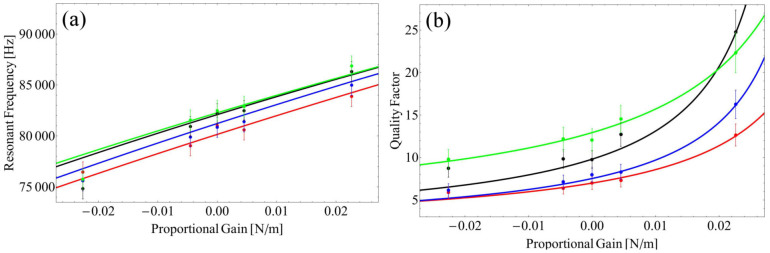
Measured and model data for gD < 0. (a) Resonant frequency versus proportional gain. Different curves correspond to different differential gains; (b) Quality factor versus proportional gain. Different curves correspond to different differential gains: green: 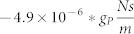 , black:
, black: 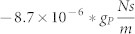 , blue:
, blue: 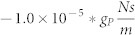 and red:
and red: 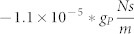 .
.
Conclusion
In this work we introduced a novel method capable of reproducibly tuning the resonant frequency and quality factor of a MMO. By applying a feedback control on the oscillation of a microsized cantilever we are able to tune its dynamic properties in a broad range. The proposed actuation model fits well the experiments. The method can effectively work for any type of NEMS, provided the actuation to be high enough respect to the oscillator stiffness and applied in a large bandwidth. Compared to previous works, it provides a larger range for the observed shifts, bi-directionality (absent in static fields), room temperature operating conditions, and fairly simple instrumentation. The method can tune the resonant frequency and quality factor of a nanomechanical oscillator in the MHz regime with an effective shift of the resonant frequency which is between 2 and 3 orders of magnitude higher than the one obtained with a static force gradient. We also showed that the method is independent of the type of actuation and works well with operation in liquids, opening up a wide range of applications when concerning biological matter analysis.
Methods
Interferometry
We used a Shafter + Kirchhoff 51nanoFI as laser source. The photodetctor is a Thorlabs DET36A and the transimpedance amplifier is a FEMTO DHPCA-100 providing a bandwidth of 3.5 MHz for a gain of 106.
Due to the small size of the NMO, the alignment of the optic fiber and the oscillator has been performed after having turned upside down the chip holding the NMO. This solution permitted to approach the fiber in close vicinity with the NMO, at 10/μm distance, avoiding the mechanical contact of the fiber with the chip.
Capacitive actuation
Our actuation is capacitive, employing the optical fiber and the cantilever backside as plates, with their separation, z0, kept constant to a few µm. Thus, the force applied on the oscillator is given by the gradient of the electrostatic energy of the 2-plates capacitor, which means
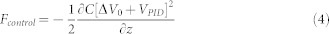 |
where C is the capacitance, z = z0 + x(t) and ΔV0 + VPID the potential difference between the plates. ΔV0 has been fixed to 5 Volts in our experiments, whereas VPID is the output of PID controller which keeps constant the cantilever end position. Assuming VPID ≪ ΔV0
x(t) ≪ z0 and 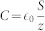 , equation 4 leads in a first order approximation to a linear dependence of the force on the voltage applied VPID.
, equation 4 leads in a first order approximation to a linear dependence of the force on the voltage applied VPID.
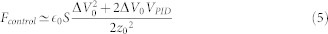 |
where S is the surface of the plates and z the cantilever-optical fiber distance. Applying a PID control, i.e. a voltage proportional to the instant position, its derivative, and its integral, gives:
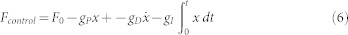 |
The cantilever end position is controlled with a custom made PID implemented inside a Xilinx Virtex-5 LX50 FPGA. We have coated the bottom of the optical fiber with 30 nm of gold and its borders with 300 nm of gold. The optical fiber functions as an electrode. We used a SPECS Nanonis Lock-In amplifier.
Photothermal actuation
The excitation in liquid was provided by the blueDrive™ phototermal excitation of a commercial Cypher™ Asylum Research - Oxford Instruments Atomic Force Microscope. The Q-control is included in the electronics of the Cypher™ AFM.
Author Contributions
L.C. conceived this research. M.S.R. provided the theoretical background. M.V.V. and L.C. performed the measurements. S.C. performed preliminary measurements. A.P. conceived and fabricated the high-speed proportional-integral-derivative controller. M.V.V., M.S.R. and L.C. contributed to prepare this manuscript.
Supplementary Material
Supplementary Information
Acknowledgments
Mario S. Rodrigues acknowledges financial support from Fundação para a Ciência e Tecnologia SFRH/BPD/69201/2010. Luca Costa acknowledges Nicola Manca for discussions. The authors thank Joël Chevrier and Fabio Comin for their support and for fruitful discussions. This work was performed at the Surface Science Laboratory of the ESRF.
References
- Jensen K., Kwanpyo K. & Zettl A. An atomic-resolution nanomechanical mass sensor. Nat. Nanotechnol. 3, 533–537 (2008). [DOI] [PubMed] [Google Scholar]
- Burg T. P. et al. Weighing of biomolecules, single cells and single nanoparticles in fluid. Nature 446, 1066–1069 (2007). [DOI] [PubMed] [Google Scholar]
- Longo G. et al. Rapid detection of bacterial resistance to antibiotics using afm cantilevers as nanome-chanical sensors. Nat. Nanotechnol. 8, 522–526 (2013). [DOI] [PubMed] [Google Scholar]
- Li M., Tang X. H. & Roukes M. L. Ultra-sensitive nems-based cantilevers for sensing, scanned probe and very high-frequency applications. Nat. Nanotechnol. 2, 114–120 (2007). [DOI] [PubMed] [Google Scholar]
- Ekinci K. L., Yang Y. T., Huang X. M. H. & Roukes M. L. Balanced electronic detection of displacement in nanoelectromechanical systems. Appl. Phys. Lett. 81, 2253–2255 (2002). [Google Scholar]
- Ekinci K. L. & Roukes M. L. Nanoelectromechanical systems. Rev. Sci. Instrum. 76, 061101 (2005). [Google Scholar]
- Peters C., Maurath D., Schock W., Mezgerl F. M. & Manoli Y. A closed-loop wide-range tunable mechanical resonator for energy harvesting systems. J. Micromech. Microeng. 19, 094004 (2009). [Google Scholar]
- Tang L., Yang Y. & Soh C. K. Toward broadband vibration-based energy harvesting. J. Intel. Mat. Syst. Str. 21, 1867–1897 (2010). [Google Scholar]
- Agache V., Blanco-Gomez G., Cochet M. & Caillat P. Suspended nanochannel in mems plate resonator for mass sensing in liquid. Paper presented at Micro Electro Mechanical Systems (MEMS): IEEE 24th International Conference, Cancun: IEEE (2011). [Google Scholar]
- Braun T. et al. Micromechanical mass sensors for biomolecular detection in a physiological environment. Phys. Rev. E 72, 031907 (2005). [DOI] [PubMed] [Google Scholar]
- Unterreithmeier Q. P., Weig E. M. & Kotthaus J. P. Universal transduction scheme for nanomechanical systems based on dielectric forces. Nature 458, 1001–1004 (2009). [DOI] [PubMed] [Google Scholar]
- Siria A. et al. Viscous cavity damping of a microlever in a simple fluid. Phys. Rev. Lett. 102, 254503 (2009). [DOI] [PubMed] [Google Scholar]
- Manca N. et al. Programmable mechanical resonances in mems by localized joule heating of phase change materials. Adv. Mater. 25, 6430–6435 (2013). [DOI] [PubMed] [Google Scholar]
- Merced E. et al. Photothermal actuation of v o 2 :cr-coated microcantilevers in air and aqueous media. Smart Mater. Struct. 21, 105009 (2012). [Google Scholar]
- Holscher H., Ebeling D. & Schwarz U. D. Theory of q-controlled dynamic force microscopy in air. J. Appl. Phys. 99, 084311 (2006). [Google Scholar]
- Ebeling D., Holscher H., Fuchs H., Anczykowski B. & Schwarz U. D. Imaging of biomaterials in liquids: a comparison between conventional and q -controlled amplitude modulation (‘tapping mode’) atomic force microscopy. Nanotechnology 17, S221 (2006). [DOI] [PubMed] [Google Scholar]
- Moreno-Moreno M., Raman A., Gomez-Herrero J. & Reifenberger R. Parametric resonance based scanning probe microscopy. Appl. Phys. Lett. 88, 193108 (2006). [Google Scholar]
- Prakash G., Raman A., Rhoads J. & Reifenberger R. G. Parametric noise squeezing and parametric resonance of microcantilevers in air and liquid environments. Rev. Sci. Instrum. 83, 065109 (2012). [DOI] [PubMed] [Google Scholar]
- Sulchek T. et al. High-speed tapping mode imaging with active q control for atomic force microscopy. Appl. Phys. Lett. 76, 1473–1475 (2000). [Google Scholar]
- Rugar D. & Grütter P. Mechanical parametric amplification and thermomechanical noise squeezing. Phys. Rev. Lett. 67, 699–702 (1991). [DOI] [PubMed] [Google Scholar]
- Orun B., Necipoglu S., Basdogan C. & Guvenc L. State feedback control for adjusting the dynamic behavior of a piezoactuated bimorph atomic force microscopy probe. Rev. Sci. Instrum. 80, 063701 (2009). [DOI] [PubMed] [Google Scholar]
- Rugar D., Mamin H. J., Erlandsson R., Stern J. E. & Terris B. D. Force microscope using a fiber-optic displacement sensor. Rev. Sci. Instrum. 59, 2337–2340 (1988). [Google Scholar]
- Berdahl E. J., Smith J. O. & Freed A. Active damping of a vibrating string. Paper presented at Active, Adelaide, Australia. (2006)
- Rodrigues M. S., Costa L., Chevrier J. & Comin F. Why do atomic force microscopy force curves still exhibit jump to contact? Appl. Phys. Lett. 101, 203105 (2012). [Google Scholar]
- Kato N., Kikuta H., Nakano T., Matsumoto T. & Iwata K. System analysis of the force-feedback method for force curve measurements. Rev. Sci. Instrum. 70, 2402–2407 (1999). [Google Scholar]
- Rodrigues M. S., Costa L., Chevrier J. & Comin F. System analysis of force feedback microscopy. J. Appl. Phys. 115, 054309–054309-5 (2014). [Google Scholar]
- Jarvis S., Yamada H., Yamamoto S.-I., Tokumoto H. & Pethica J. Direct mechanical measurement of interatomic potentials. Nature 384, 247–249 (1996). [Google Scholar]
- Goertz M. & Moore N. Mechanics of soft interfaces studied with displacement-controlled scanning force microscopy. Prog. Surf. Sci. 85, 347–397 (2010). [Google Scholar]
- Yamamoto S., Yamada H. & Tokumoto H. Precise force curve detection system with a cantilever controlled by magnetic force feedback. Rev. Sci. Instrum. 68, 4132–4136 (1997). [Google Scholar]
- Ramos D., Tamayo J., Mertens J. & Calleja M. Photothermal excitation of microcantilevers in liquids. J. Appl. Phys. 99, 124904–124904-8 (2006). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Information