Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2015 Jan 20;5:7907. doi: 10.1038/srep07907

Spin pumping in Ferromagnet-Topological Insulator-Ferromagnet Heterostructures

A A Baker 1,2, A I Figueroa 2, L J Collins-McIntyre 1, G van der Laan 2, T Hesjedal 1,a
PMCID: PMC4298741  PMID: 25601364

Abstract

Topological insulators (TIs) are enticing prospects for the future of spintronics due to their large spin-orbit coupling and dissipationless, counter-propagating conduction channels in the surface state. However, a means to interact with and exploit the topological surface state remains elusive. Here, we report a study of spin pumping at the TI-ferromagnet interface, investigating spin transfer dynamics in a spin-valve like structure using element specific time-resolved x-ray magnetic circular dichroism, and ferromagnetic resonance. Gilbert damping increases approximately linearly with increasing TI thickness, indicating efficient behaviour as a spin sink. However, layer-resolved measurements suggest that a dynamic coupling is limited. These results shed new light on the spin dynamics of this novel material class, and suggest great potential for TIs in spintronic devices, through their novel magnetodynamics that persist even up to room temperature.

The exciting physics of topological insulators (TIs) has been under intense study since their theoretical prediction1 and experimental verification2,3,4. Recently, they were shown to display the quantum anomalous Hall effect after doping with magnetic impurities5, and are proposed to host image magnetic monopoles and the giant magneto-optical effect6,7,8,9. In the prototypical three-dimensional TI Bi2Se3 a large spin-orbit interaction leads to a band inversion in the bulk and the formation of a topologically protected surface state (TSS), with fully spin-polarised counter-propagating conduction channels that are robust against scattering from non-magnetic impurities10. Figure 1a shows a diagram of the bandstructure of a TI. Spin-momentum locking suggests the possibility of very long spin-flip scattering lifetimes and the ability to generate ultra-high spin-orbit torques11,12,13. It has been predicted that the TSS can exert a torque on spins in a neighbouring ferromagnet (FM) through exchange coupling14. However, in order to realise these prospects the magnetodynamics of the TSS must be studied and such TI-FM heterostructures fabricated. While angle-resolved photo-emission spectroscopy has been extremely successful at identifying TIs3,4, transport measurements have met with limited success due to large bulk conductivities that make unambiguously identifying the surface state challenging15,16. It is therefore highly desirable to apply a wider range of techniques to the study of TIs, aiming to focus more closely on the spin degrees of freedom present in the TSS.

Figure 1. Schematic of the FM-TI-FM heterostructure and key concepts of spin pumping.

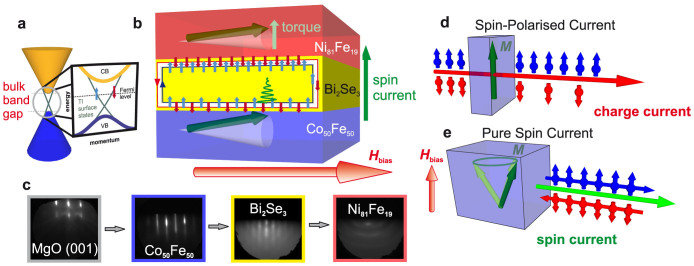
Figure 1

Open in a new tab

(a), Bandstructure of a TI, showing the valence (blue) and conduction (orange) bands, with the spin-locked surface state crossing the bulk bandgap. (b), Schematic of the device structure, showing the TI Bi2Se3 placed between two FM layers. The surface state is indicated by up- and down-arrows, representing counter-propagating spin-momentum locked conduction. The precession of magnetisation excited around the static bias field drives a pure spin current from the Co50Fe50 through the Bi2Se3 into the Ni81Fe19, exerting a spin transfer torque. (c), RHEED images of the growth of each layer. (d),(e), Illustration of the difference between a spin polarised current and a pure spin current. Note the similarity between counter-propagation of spins in a pure spin current and the counter propagating conduction channels in the TSS.

A key focus of spintronic research in recent years has been the phenomenon of spin pumping17,18, whereby the ferromagnetic resonance (FMR) generates a pure spin current that enters adjacent layers19. Such non-local spin dynamics manifest as an additional damping term in the Landau-Lifshitz-Gilbert (LLG) equation for magnetodynamics20, broadening the measured resonance. Furthermore, spin pumping through a nonmagnetic spacer into a second FM affects the phase and amplitude of precession21, allowing direct confirmation of the presence of a coherent pure spin current. The application of this technique to TIs is quite naturally suggested by the similarity between the spin-locked surface state of a TI and the separation of angular momentum and charge flow that takes place in a pure spin current. Recently, studies of such exciting effects have begun to emerge through electrical transport and inverse spin-hall effect measurements13,22,23, demonstrating the great potential of TIs for incorporation into spintronic devices such as spin valves.

In this letter we use FMR and time-resolved x-ray magnetic circular dichroism (TR-XMCD) to study the spin pumping in FM-TI-FM heterostructures. TR-XMCD allows element- (and thus layer-) specific detection of precession of magnetisation21,24,25. The phase of precession across magnetic resonances is highly sensitive to spin transfer phenomena. The ability of a TI to absorb and transfer a pure spin current is probed, determining the spin mixing conductance. We find that the TI interlayer functions as an excellent spin sink, dramatically increasing the Gilbert damping of magnetodynamics in the FM layers. However, there is only weak evidence of spin transfer through the TI to a second FM, which could be explained either by dynamic exchange or by a short range coupling between surface states that is suppressed with increasing TI thickness.

In the classical limit the dynamics of magnetization can be described by the LLG equation of motion, which represents the precessional torque arising due to an effective internal field, Heff, and the damping due to the phenomenological Gilbert torque, α. Gilbert damping includes energy loss mechanisms such as spin-flip scattering and the excitation of phonons. This equation can be readily modified to include spin pumping; for a trilayer structure with only one layer, i, on resonance, the motion of magnetisation mi, is18:

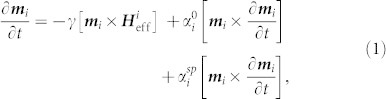graphic file with name srep07907-m1.jpg

where the subscript denotes the magnetic layer number, γ is the gyromagnetic ratio, α0 the intrinsic Gilbert damping parameter and αsp additional damping due to spin pumping. The third term represents increased damping in layer i due to spin pumping. If the second layer is allowed to precess an anti-damping (or accelerating) torque from the STT induced by momentum transfer from layer j is also present, but this vanishes if the resonances are well separated in frequency-field space. This assumption is valid in all samples considered here, as confirmed by the TR-XMCD measurements. The additional damping associated with spin pumping can be written as21:

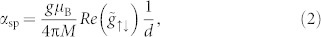graphic file with name srep07907-m2.jpg

where g is the Landé g-factor, μB the Bohr magneton, M the magnetisation of the magnetic layer, d the layer thickness and 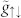Inline graphic the spin mixing conductance, which controls spin-selective transport across the interface17. Spin pumping across a non-magnetic barrier usually decays exponentially, as scattering of the pure spin current leads to a loss of angular momentum and backflow into the on-resonance layer. This is in effect a simultaneous damping and anti-damping of motion, for thinner barriers the second ferromagnet absorbs the spin current and minimises backflow, while for thicker barriers spin pumping is reduced as more electrons are scattered. See the Supplementary Information for more theory of spin pumping in normal metals and TIs.

A schematic of the heterostructure is shown in Fig. 1b. Samples were prepared by molecular beam epitaxy, on MgO(001) substrates. Growth was monitored using in-situ reflection high energy electron diffraction (RHEED), see Fig. 1c. First, 30 nm of Co50Fe50 were deposited and annealed to form an epitaxial ferromagnetic layer. Next, Bi2Se3 was deposited, with thickness ranging from 4 nm to 20 nm. 30 nm of Ni81Fe19 were then deposited at room temperature (300 K) forming a polycrystalline layer, as demonstrated by rings in the RHEED pattern. This is important in order to prevent damage to the TI due to Se out-diffusion or Fe intercalation. See Supplementary Information for more details.

Vector network analyser (VNA) FMR measurements were performed in the frequency range 0.5–20 GHz for samples mounted on a coplanar waveguide (CPW). The forces acting on a ferromagnet undergoing FMR are shown in Fig. 2a. Real and imaginary components of the microwave transmission parameter, S12, were measured as a function of bias field for multiple frequencies. Figure 2b shows a typical field-frequency-transmission map. The linewidth of the resonance is frequency (f) dependent and relates to the damping as26:

graphic file with name srep07907-m3.jpg

where ΔH is the full width at half maximum of the resonance, ΔH0 the inhomogeneous broadening arising from non-Gilbert damping mechanisms such as lattice defects and α = α0 + αsp the Gilbert damping, including contributions related to coupling to the lattice (such as spin flip scattering, phonon drag or spin pumping).

Figure 2. Gilbert damping increases as a function of TI interlayer thickness.

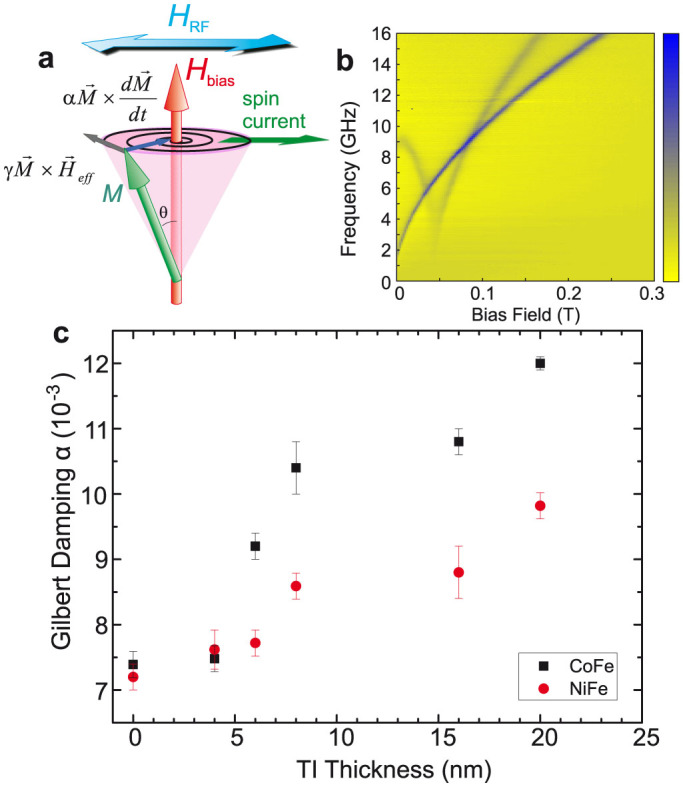
Figure 2

Open in a new tab

(a), Diagram of the forces acting on the magnetisation of a material undergoing FMR, showing excitation field (HRF), static bias field (HB) and precessing magnetisation vector (M). M × Heff acts as the driving force of precession, while 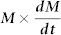Inline graphic “brakes” the magnetisation back towards the equilibrium condition according to the total damping, α. (b), Field-frequency-transmission map showing on-resonance absorption of the heterostructure. Blue indicates high absorption, when the resonance condition is met. The bias field is applied parallel to the [100] axis of Co50Fe50, an in-plane hard axis, so the lower branch of the Kittel curve corresponds to magnetisation canted along the in-plane easy axis, the upper branch to the magnetisation collinear with the bias field. (c), Calculated damping factor as a function of thickness of the TI interlayer for Co50Fe50 (black) and Ni81Fe19 (red) layers. Error bars represent the uncertainty on linear fits to linewidth as a function of frequency.

Figure 2c shows the measured damping parameter, α, for the Ni81Fe19 and Co50Fe50 layers as a function of the thickness of the TI interlayer. A linear increase is observed up to 20 nm, wherein the spin pumping component represents a significant fraction of the total damping, indicating a large transfer of angular momentum to the TI. It is important to compare this result with other materials. Damping in trilayers normally drops exponentially with spacer thickness27, as scattering within the non-magnetic (NM) layer is a much less efficient sink for angular momentum than absorption by a second ferromagnet. Here, however, damping increases with TI thickness, suggesting not only that the TI is a very efficient spin-sink, but that the pure spin current can penetrate some distance into the TI, at least 8 nm (compared to ~ 3 nm in Si or <1 nm in Ta21,28).

As a spin current is driven into the TSS a spin imbalance develops, which is converted to a charge current13. The scattering of such conduction electrons within the bulk of the TI could then provide a mechanism for efficient absorption of pumped angular momentum.

It is instructive to analyse the spin pumping results in the analytical framework of the STT in normal metals. Equation 2 can be rearranged to yield the spin mixing conductance, 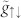Inline graphic. Considering, for example, the case of the Ni81Fe19 (Ms = 0.906 × 106 A/m) layer in the tTI = 20 nm sample, the spin pumping damping can be extracted by comparison with a bare Ni81Fe19 layer, yielding αsp = (2.6 ± 0.3) × 10−3. The spin mixing conductance is then 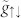Inline graphic = (4.2 ± 0.5) × 1015 cm−2. Performing the same calculation for the Co50Fe50 layer in this sample (Ms = 1.76 × 106 A/m) gives 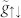Inline graphic = (2.49 ± 0.1) × 1015 cm−2. The discrepancy between the results for the two layers points towards dissimilar interfaces. This most likely arises due to the requirement for low temperature deposition of the Ni81Fe19 layer, in order to preserve crystal quality within the Bi2Se3 layer.

Since the damping does not completely saturate these value should be regarded only as a lower limit on the effective spin mixing conductance available in FM/TI heterostructures. These values are comparable to the spin mixing conductances calculated by Jamali et al. from their inverse spin Hall effect measurements29. They are greater than previous reports for even a good spin conductor such as Ag, where 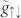Inline graphic ≈ 2 × 1015 cm−2 30. Note that the calculation does not separate pumping into the bulk and surface state, which display very different spin dynamics. The value should therefore be considered only as a rough estimate of the effective spin mixing conductance that is available in TI heterostructures.

TR-XMCD allows element specific measurement of the precession of magnetisation within each ferromagnetic layer through polarisation dependence of x-ray absorption at the L2,3 edges31. A resolution of several picoseconds is achieved through synchronisation of x-ray bunch arrival with the RF driving precession. The layer-specific phase of precession is determined with high precision by analysing the amplitude of the XMCD signal, making it a powerful tool to study the subtle effects of coupling through the TI. Figure 3a shows a schematic of the measurement geometry.

Figure 3. Time-resolved precession of magnetisation of Ni.

Figure 3

Open in a new tab

(a), Illustration of the experimental configuration for the measurement of TR-XMCD. The sample is placed face-down on a CPW and incident circularly polarised x-rays pass through a hole in the signal line. The magnetisation of the stack about Hbias is driven by the RF field, HRF. The cone angle of precession is exaggerated for clarity; the typical magnitude of precession is ~ 1°. (b), TR-XMCD data for Ni81Fe19 continuously driven at 4 GHz for the Co50Fe50(30)/Bi2Se3(8)/Ni81Fe19(30) sample (thicknesses in nm). Varying static bias field indicated by colour of lines, offset for clarity, showing increase in amplitude and phase shift across resonance at 14 mT. Solid lines are sine curve fits to the data.

Precession of Ni magnetisation is shown in Fig. 3b for the Co50Fe50(30)/Bi2Se3(8)/Ni81Fe19(30) sample (thicknesses in nm). The increase in amplitude of precession and phase shift is clearly visible across the resonant field of 14 mT. Fitting sine curves to the precession yields amplitude and phase, which allows study of the coupling of the two layers.

Figure 4 shows the phase of precession determined in this way for three different thicknesses of interlayer. In a traditional spin valve, coupling of the two magnetic layers is mediated by the passage of a pure spin current through the spacer, leading to off resonance precession and a phase shift. Such features can be seen in the Ni81Fe19 layer for tTI = 8 nm (Fig. 4b) and the Co50Fe50 layer for tTI = 4 nm (Fig. 4a). However, this effect is rather weak, suggesting a suppression of spin pumping due to spin-flip scattering. Measurements on a sample with 20 nm Bi2Se3 (not shown) showed no evidence of coupling, suggesting complete absorption of the pumped spin angular momentum. This confirms that the weak dynamic coupling of the two layers is suppressed at this thickness, suggesting that the pumped spin current is scattered by the maximum thickness measured. We note that good conductors such as Cu, Ag or Au can have a spin coherence length of tens of nanometres27, while trivial insulators such as MgO or heavy metals such as Ta suppress spin pumping after just a few nm21,32. Suppression of spin pumping in insulators was recently studied by Du et al.28, who showed that there was a characteristic decay length of under 1 nm for SrTiO3, Sr2GaTaO6 and Sr2CrNbO6. Amorphous silicon also suppressed spin pumping for films 3 nm thick. As a heavy element bulk bandgap insulator Bi2Se3 might therefore be expected to suppress spin pumping, absorbing angular momentum.

Figure 4. Phase variation across resonance.

Figure 4

Open in a new tab

Phase of precession of magnetisation for Ni81Fe19 (red circles) and Co50Fe50 (black squares) layers at 4 GHz driving frequency for tTI = 4 nm and 8 nm ((a),(b), respectively). Dashed lines show the positions of the resonance amplitude peak The drop and recovery in phase across the Co mode is caused by the superposition of the two modes, corresponding to canted and collinear magnetisation, as can be seen in Fig. 2b. Error bars arise from uncertainty on fits to the time-resolved precession, see Fig. 3b.

The TR-XMCD results must therefore be considered alongside the VNA-FMR measurements. First, it is important to consider the distinction between the two techniques: VNA-FMR measures increased damping due to spin pumping out of a FM, while TR-XMCD allows detection of modified precessional dynamics induced by spin pumping into a FM. The increase of damping parameter with TI thickness suggests that the TI functions as an excellent spin sink, but transfer of the spin current is less efficient. The weak coupling observed in the TR-XMCD could be attributed to transmission of a pure spin current, with a decay length on the order of 8 nm. While the current can persist within the TI (as demonstrated by continued increase of Gilbert damping with TI thickness), its passage across the FM/TI interface and the topological surface state is suppressed. The dissimilar interfaces indicated by the calculated values of 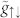Inline graphic suggest that this transmission could be improved (and even higher values of 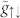Inline graphic obtained) if the quality of the interface in future devices can be improved.

An alternative explanation could arise from the proximity coupling of 'top' and 'bottom' surface states that takes place in ultrathin TIs. As shown by Zhang et al.33, for Bi2Se3 thicknesses beneath 6 nm the surface state at the two interfaces can interfere, disrupting the bandstructure. In this instance, direct communication between top and bottom surface should be possible, without passing through the bulk. If the TSS at each surface in these samples have retreated by ~ 1 nm due to FM proximity or surface roughness34, then this could explain the coupling observed for 4 nm and 8 nm, while the distinct states at 20 nm do not allow this. The VNA-FMR experiments then probe the spin sink properties of the bulk, which has great capacity to absorb angular momentum, arising from its large spin-orbit coupling.

In summary, these experimental results demonstrate that TIs hold great promise for the field of spintronics. They display an unusual thickness dependence to their Gilbert damping, demonstrating a high capacity to absorb angular momentum, and – if the process is reversed – to generate a significant spin transfer torque. TR-XMCD experiments reveal that transfer of angular momentum between ferromagnetic layers in a spin valve structure is possible, either through conventional spin pumping or possibly through a direct coupling of the topological surface state. As these effects can be observed at room temperature and low magnetic fields, TIs are particularly well suited to future device applications, as well as being a fertile ground for investigation of fundamental physical phenomena.

Methods

Ferromagnetic Resonance Measurements

VNA-FMR measurements were performed using a Rhode and Schwartz ZVB20 vector network analyser. Samples were mounted face-down on a coplanar waveguide of characteristic impedance 50 Ω and placed in an octupole electromagnet, capable of applying a field of up to 0.5 T in any direction. Real and imaginary components of the microwave transmission parameter, S12, were measured as a function of field vector (strength and angle) and frequency. The resulting resonances were fitted using asymmetric Lorentzians to extract resonance frequency and linewidth. All measurements were performed at room temperature.

Time Resolved X-ray Magnetic Circular Dichroism

TR-XMCD measurements were performed on beamline I10 at Diamond Light Source (UK) and beamline 4.0.2 at the Advanced Light Source (US). TR-XMCD offers an element (and thus layer-) specific time-resolved measurement of magnetisation alignment, allowing mapping of the precessional dynamics of each FM layer on the picosecond timescale. The sample is mounted on a CPW and driven by an applied RF field while under a DC bias field. The XMCD effect is then used as an element specific probe of magnetisation, as the size of the effect scales as the cosine of the angle between the incident x-ray helicity vector and the magnetisation alignment. By synchronising the driving RF with a multiple of the master oscillator clock of the synchrotron, the magnitude of the XMCD can be probed as a function of delay between RF excitation (pump) and x-ray bunch arrival (probe). The x-ray absorption in transmission was detected using luminescence of the MgO substrate. All TR-XMCD measurements were performed at the Ni and Co L3 edges.

Author Contributions

A.A.B., G.v.d.L. and T.H. conceived the idea and A.A.B., L.C.M. and T.H. fabricated the device structure. G.v.d.L. and A.I.F. developed the TR-XMCD instrumentation. A.A.B. and A.I.F. performed the VNA-FMR measurements, all authors took part in the TR-XMCD experiments, A.A.B. and A.I.F. analysed the data. A.A.B. and T.H. wrote the paper with comments and input from all authors. All authors contributed to the discussions.

Supplementary Material

Supplementary Information

Supplementary material

srep07907-s1.pdf (231.1KB, pdf)

Acknowledgments

We thank G.B.G. Stenning and L.R. Shelford for technical assistance during the TR-XMCD measurements. This publication arises from research funded by the John Fell Oxford University Press Research Fund. We thank Diamond Light Source for beamtime on I10 (under proposal number SI-9210) and the Advanced Light Source for beamtime on 4.0.2 (Magnetic Spectroscopy), as well as the Research Complex at Harwell for their hospitality. A.A.B. acknowledges funding from Diamond Light Source through a joint studentship and Wadham College through a senior scholarship. A.A.B. and L.C.M. acknowledge support from the EPSRC through doctoral training awards.

References

  1. Kane C. L. & Mele E. J. Z2 topological order and the quantum spin hall effect. Phys. Rev. Lett. 95, 146802 (2005). [DOI] [PubMed] [Google Scholar]
  2. Bernevig B. A., Hughes T. L. & Zhang S.-C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 314, 1757–1761 (2006). [DOI] [PubMed] [Google Scholar]
  3. Chen Y. et al. Experimental realization of a three-dimensional topological insulator, Bi2Te3. Science 325, 178–181 (2009). [DOI] [PubMed] [Google Scholar]
  4. Chen Y. et al. Massive Dirac fermion on the surface of a magnetically doped topological insulator. Science 329, 659–662 (2010). [DOI] [PubMed] [Google Scholar]
  5. Chang C.-Z. et al. Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator. Science 340, 167–170 (2013). [DOI] [PubMed] [Google Scholar]
  6. Qi X.-L., Li R., Zang J. & Zhang S.-C. Inducing a magnetic monopole with topological surface states. Science 323, 1184–1187 (2009). [DOI] [PubMed] [Google Scholar]
  7. Tse W.-K. & MacDonald A. H. Giant magneto-optical Kerr effect and universal Faraday effect in thin-film topological insulators. Phys. Rev. Lett. 105, 057401 (2010). [DOI] [PubMed] [Google Scholar]
  8. Williams J. et al. Unconventional Josephson effect in hybrid superconductor-topological insulator devices. arXiv,1202.2323 (2012). [DOI] [PubMed]
  9. Kong D. et al. Ambipolar field effect in the ternary topological insulator (BixSb1−x)2Te3 by composition tuning. Nature Nanotech. 6, 705–709 (2011). [DOI] [PubMed] [Google Scholar]
  10. Moore J. E. The birth of topological insulators. Nature 464, 194–198 (2010). [DOI] [PubMed] [Google Scholar]
  11. Fischer M. H., Vaezi A., Manchon A. & Kim E.-A. Large spin torque in topological insulator/ferromagnetic metal bilayers. arXiv ,1305.1328 (2013). [Google Scholar]
  12. Fan Y. et al. Magnetization switching through giant spin–orbit torque in a magnetically doped topological insulator heterostructure. Nature Mater. 13, 699–704 (2014). [DOI] [PubMed] [Google Scholar]
  13. Shiomi Y. et al. Bulk topological insulators as inborn spintronics detectors. arXiv,1312.7091 (2013).
  14. Yokoyama T., Zang J. & Nagaosa N. Theoretical study of the dynamics of magnetization on the topological surface. Phys. Rev. B 81, 241410 (2010). [Google Scholar]
  15. Ren Z., Taskin A., Sasaki S., Segawa K. & Ando Y. Large bulk resistivity and surface quantum oscillations in the topological insulator Bi2Te2Se. Phys. Rev. B 82, 241306 (2010). [Google Scholar]
  16. Li C. et al. Electrical detection of charge-current-induced spin polarization due to spin-momentum locking in Bi2Se3. Nature Nanotech. 9, 218–224 (2014). [DOI] [PubMed] [Google Scholar]
  17. Tserkovnyak Y., Brataas A., Bauer G. E. & Halperin B. I. Nonlocal magnetization dynamics in ferromagnetic heterostructures. Rev. Mod. Phys. 77, 1375 (2005). [Google Scholar]
  18. Heinrich B. et al. Dynamic exchange coupling in magnetic bilayers. Phys. Rev. Lett. 90, 187601 (2003). [DOI] [PubMed] [Google Scholar]
  19. Brataas A., Tserkovnyak Y., Bauer G. E. W. & Halperin B. I. Spin battery operated by ferromagnetic resonance. Phys. Rev. B 66, 060404 (2002). [Google Scholar]
  20. Tserkovnyak Y., Brataas A. & Bauer G. E. Spin pumping and magnetization dynamics in metallic multilayers. Phys. Rev. B 66, 224403 (2002). [Google Scholar]
  21. Marcham M. et al. Phase-resolved x-ray ferromagnetic resonance measurements of spin pumping in spin valve structures. Phys. Rev. B 87, 180403 (2013). [Google Scholar]
  22. Tian J. et al. Topological insulator based spin valve devices: evidence for spin polarized transport of spin-momentum-locked topological surface states. Solid State Commun. 191, 1–5 (2014). [Google Scholar]
  23. Mellnik A. et al. Spin-transfer torque generated by a topological insulator. Nature 511, 449–451 (2014). [DOI] [PubMed] [Google Scholar]
  24. Bailey W. et al. Detection of microwave phase variation in nanometre-scale magnetic heterostructures. Nat. Commun. 4, 2025 (2013). [DOI] [PubMed] [Google Scholar]
  25. Guan Y., Bailey W., Vescovo E., Kao C.-C. & Arena D. Phase and amplitude of element-specific moment precession in Ni81Fe19. J. Magn. Magn. Mater. 312, 374–378 (2007). [Google Scholar]
  26. Kalarickal S. S. et al. Ferromagnetic resonance linewidth in metallic thin films: Comparison of measurement methods. J. Appl. Phys. 99, 093909 (2006). [Google Scholar]
  27. Kardasz B. & Heinrich B. Ferromagnetic resonance studies of accumulation and diffusion of spin momentum density in Fe/Ag/Fe/GaAs (001) and Ag/Fe/GaAs (001) structures. Phys. Rev. B 81, 094409 (2010). [Google Scholar]
  28. Du C. et al. Probing the spin pumping mechanism: Exchange coupling with exponential decay in Y3Fe5O12/Barrier/Pt heterostructures. Phys. Rev. Lett. 111, 247202 (2013). [DOI] [PubMed] [Google Scholar]
  29. Jamali M. et al. Room temperature spin pumping in topological insulator Bi2Se3. arXiv,1407.7940 (2014).
  30. Sánchez J. R. et al. Spin-to-charge conversion using Rashba coupling at the interface between non-magnetic materials. Nat. Commun. 4, 2944 (2013). [DOI] [PubMed] [Google Scholar]
  31. van der Laan G. Applications of soft x-ray magnetic dichroism J. Phys.: Conf. Ser. 430, 012127 (2013). [Google Scholar]
  32. Mosendz O., Pearson J., Fradin F., Bader S. & Hoffmann A. Suppression of spin-pumping by a MgO tunnel-barrier. Appl. Phys. Lett. 96, 022502 (2010). [DOI] [PubMed] [Google Scholar]
  33. Zhang Y. et al. Crossover of the three-dimensional topological insulator Bi2Se3 to the two-dimensional limit. Nature Phys. 6, 584–588 (2010). [Google Scholar]
  34. Wu G. et al. Tuning the vertical location of helical surface states in topological insulator heterostructures via dual-proximity effects. Sci. Rep 3, 1233 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary material

srep07907-s1.pdf (231.1KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES