Q- and A-learning Methods for Estimating Optimal Dynamic Treatment Regimes

Abstract

In clinical practice, physicians make a series of treatment decisions over the course of a patient’s disease based on his/her baseline and evolving characteristics. A dynamic treatment regime is a set of sequential decision rules that operationalizes this process. Each rule corresponds to a decision point and dictates the next treatment action based on the accrued information. Using existing data, a key goal is estimating the optimal regime, that, if followed by the patient population, would yield the most favorable outcome on average. Q- and A-learning are two main approaches for this purpose. We provide a detailed account of these methods, study their performance, and illustrate them using data from a depression study.

1. INTRODUCTION

An area of current interest is personalized medicine, which involves making treatment decisions for an individual patient using all information available on the patient, including genetic, physiologic, demographic, and other clinical variables, to achieve the “best” outcome for the patient given this information. In treating a patient with an ongoing disease or disorder, a clinician makes a series of decisions based on the patient’s evolving status. A dynamic treatment regime is a list of sequential decision rules formalizing this process. Each rule corresponds to a key decision point in the disease/disorder progression and takes as input the information on the patient to that point and outputs the treatment that s/he should receive from among the available options. A key step toward personalized medicine is thus finding the optimal dynamic treatment regime, that which, if followed by the entire patient population, would yield the most favorable outcome on average.

The statistical problem is to estimate the optimal regime based on data from a clinical trial or observational study. Q-learning (Q denoting “quality,” Watkins, 1989; Watkins and Dayan, 1992; Nahum-Shani et al., 2010) and advantage learning (A-learning, Murphy, 2003; Robins, 2004; Blatt, Murphy and Zhu, 2004) are two main approaches for this purpose and are related to reinforcement learning methods for sequential decision-making in computer science. Q-learning is based roughly on posited regression models for the outcome of interest given patient information at each decision point and is implemented through a backwards recursive fitting procedure that is related to the dynamic programming algorithm (Bather, 2000), a standard approach for deducing optimal sequential decisions. A-learning involves the same recursive strategy, but requires only posited models for the part of the outcome regression representing contrasts among treatments and for the probability of observed treatment assignment given patient information at each decision point. As discussed later, this may make A-learning more robust to model misspecification than Q-learning for consistent estimation of the optimal treatment regime.

Examples of the use of Q- and A-learning and alternative methods to deduce optimal strategies for treatment of substance abuse, psychiatric disorders, cancer, and HIV infection and for dose adjustment in response to evolving patient status have been presented (Rosthøj et al., 2006; Murphy et al., 2007a,b; Zhao, Kosorok and Zeng, 2009; Henderson, Ansell and Alshibani, 2010). Relevant work includes Thall, Millikan and Sung (2000), Thall, Sung and Etsey (2002), Robins (2004), Moodie, Richardson and Stephens (2007), Thall et al. (2007), van der Laan and Petersen (2007), Robins, Orellana and Rotnitzky (2008), Almirall, Ten Have and Murphy (2010), Orellana, Rotnitzky and Robins (2010), Zhang et al. (2012a,b), Zhao et al. (2012), Zhang et al. (2013) and Zhao et al. (2013).

The objective of this article is to provide readers interested in an introduction to estimation of optimal dynamic treatment regimes with a self-contained, detailed description of an appropriate statistical framework in which to define formally an optimal regime, of some of the operational and philosophical considerations involved, and of Q- and A-learning methods. Section 2 introduces the statistical framework, and Sections 3 and 4 discuss the form of the optimal regime. We describe and contrast Q- and A-learning in Section 5 and present systematic empirical studies of their relative performance and the effects of misspecification of the postulated models involved in Section 6. The methods are demonstrated using data from the Sequenced Treatment Alternatives to Relieve Depression (STAR*D, Rush et al., 2004) study in Section 7.

2. FRAMEWORK AND ASSUMPTIONS

Consider the setting of K prespecified, ordered decision points, indexed by k = 1,…, K, which may be times or events in the disease or disorder process that necessitate a treatment decision, where, at each point, a set of treatment options is available. Assume that there is a final outcome Y of interest for which large values are preferred. The outcome may be ascertained following the Kth decision, as with CD4 T-cell count at a prespecified follow-up time in HIV infection (Moodie et al., 2007); or may be a function of information accrued over the entire sequence of decisions, as in Henderson et al. (2010), where the outcome is the overall proportion of time a measure of blood clotting speed is kept within a target range in dosing of anticoagulant agents.

In order to define an optimal treatment regime and discuss its estimation based on data from an observational study or clinical trial, we define a suitable conceptual framework. For simplicity, our presentation is heuristic. Imagine that there is a superpopulation of patients, denoted by Ω, where one may view an element ω ∈ Ω as a patient from this population. We assume that patients in the population have been treated according to routine clinical practice for the disease or disorder prior to the first treatment decision. Consequently, immediately prior to this first decision, patient ω would present to the decision-maker with a set of baseline information (covariates) denoted by the random variable S₁, discussed further below. Thus, S₁(ω) is the value of his/her information immediately prior to decision 1, taking values s₁, say, in a set 𝒮₁. Assume that, at each decision point k = 1,…, K, there is a finite set of all possible treatment options 𝒜_k, with elements a_k. We do not consider the case of continuous treatment and henceforth restrict attention to a finite set of options. Denote by ā_k = (a₁, …, a_k) a possible treatment history that could be administered through decision k, taking values in 𝒜̄_k = 𝒜₁ × … × 𝒜_k, the set of all possible treatment histories ā_K through all K decisions.

We then define the potential outcomes (Robins, 1986)

$$W^{*}=\{S_2^{*}(a_1),S_3^{*}({\overline{a}}_2),\dots ,S_k^{*}({\overline{a}}_{k-1}),\dots ,S_K^{*}({\overline{a}}_{K-1}),Y^{*}({\overline{a}}_K)\text{for all}{\overline{a}}_K\in {\overline{𝒜}}_K\}.$$ (1)

In (1), $S_k^{*}({\overline{a}}_{k-1})(\omega )$ denotes the value of covariate information that would arise between decisions k − 1 and k for a patient ω ∈ Ω in the hypothetical situation that s/he were to have received previously treatment history ā_k−1, taking values s_k in a set 𝒮_k, k = 2, …, K. Similarly, Y*(ā_K)(ω) is the hypothetical outcome that would result for ω were s/he to have been administered the full set of K treatments in ā_K. This notation implies that, for random variables such as $S_k^{*}({\overline{a}}_{k-1}),{\overline{a}}_{k-1}$ is an index representing prior treatment history. Write ${\overline{S}}_k^{*}({\overline{a}}_{k-1})=\{S_1,S_2^{*}(a_1),\dots ,S_k^{*}({\overline{a}}_{k-1})\},k=1,\dots ,K$ , where ${\overline{S}}_k^{*}({\overline{a}}_{k-1})(\omega )$ takes values s̄_k in 𝒮̄_k = 𝒮₁ × … × 𝒮_k; this definition includes the baseline covariate S₁ and is taken equal to S₁ when k = 1. The elements of the ${\overline{S}}_k^{*}({\overline{a}}_{k-1})\text{and}{Y}^{*}({\overline{a}}_K)$ may be discrete or continuous; in what follows, for simplicity, we take these random variables to be discrete, but the results hold more generally.

A dynamic treatment regime d = (d₁, …, d_K) is a set of rules that forms an algorithm for treating a patient over time; it is “dynamic” because treatment is determined based on a patient’s previous history. At the kth decision point, the kth rule d_k(s̄_k, ā_k−1), say, takes as input the patient’s realized covariate and treatment history prior to the kth treatment decision and outputs a value a_k ∈ Ψ_k (s̄_k, ā_k−1) ⊆ 𝒜_k; for k = 1, there is no prior treatment (a₀ is null), and we write d₁(s₁) and Ψ₁(s₁). Here, Ψ_k(s̄_k, ā_k−1) is a specified set of possible treatment options for a patient with realized history (s̄_k, ā_k−1), discussed further below. Accordingly, although we suppress this in the notation for brevity, the definition of a dynamic treatment regime we now present depends on the specified Ψ_k(s̄_k, ā_k−1), k = 1, …, K. Because d_k(s̄_k, ā_k−1) ∈ Ψ_k(s̄_k, ā_k−1), ⊆ 𝒜_k, d_k need only map a subset of 𝒮̄_k × 𝒜̄_k−1 to 𝒜_k. We define these subsets recursively as

$${\mathrm{\Gamma }}_k=\{({\overline{s}}_k,{\overline{a}}_{k-1})\in {\overline{𝒮}}_k\times {\overline{𝒜}}_{k-1}\text{satisfying}(\mathrm{i})a_j\in {\mathrm{\Psi }}_j({\overline{s}}_j,{\overline{a}}_{j-1}),j=1,\dots ,k-1,\text{and}(\text{ii})\text{pr}\{{\overline{S}}_k^{*}({\overline{a}}_{k-1})={\overline{s}}_k\}>0\},k=1,\dots ,K,$$ (2)

determined by Ψ = (Ψ₁, …, Ψ_K). The Γ_k contain all realizations of covariate and treatment history consistent with having followed such Ψ-specific regimes to decision k. Define the class 𝒟 of (Ψ-specific) dynamic treatment regimes to be the set of all d for which d_k, k = 1,…, K, is a mapping from Γ_k into 𝒜_k satisfying d_k (s̄_k, ā_k−1) ∈ Ψ_k (s̄_k, ā_k−1) for every (s̄_k, ā_k−1) ∈ Γ_k.

Specification of the Ψ_k (s̄_k, ā_k−1), k = 1,…, K, is dictated by the scientific setting and objectives. Some treatment options may be unethical or impossible for patients with certain histories, making it natural to restrict the set of possible options for such patients. In the context of public health policy, the focus may be on regimes involving only treatment options that are less costly or widely available unless a patient’s condition is especially serious, as reflected in his/her covariate information. In what follows, we assume that a particular fixed set Ψ is specified, and by an optimal regime we mean an optimal regime within the class of corresponding Ψ-specific regimes.

An optimal regime should represent the “best” way to intervene to treat patients in Ω. To formalize, for any d ∈ 𝒟, writing d̄_k = (d₁,… ,d_k), k = 1, …, K, d̄_K = d, define the potential outcomes associated with d as $\{S_2^{*}(d_1),\dots ,S_k^{*}({\overline{d}}_{k-1}),\dots ,S_K^{*}({\overline{d}}_{K-1}),Y^{*}(d)\}$ such that, for any ω ∈ Ω, with S₁(ω) = s₁,

$$d_1(s_1)=u_1,S_2^{*}(d_1)(\omega )=S_2^{*}(u_1)(\omega )=s_2,d_2({\overline{s}}_2,u_1)=u_2,\dots ,d_{K-1}({\overline{s}}_{K-1},{\overline{u}}_{K-2})=u_{K-1},S_K^{*}({\overline{d}}_{K-1})(\omega )=S_K^{*}({\overline{u}}_{K-1})(\omega )=s_K,d_K({\overline{s}}_K,{\overline{u}}_{K-1})=u_K,Y^{*}(d)(\omega )=Y^{*}({\overline{u}}_K)(\omega )=y.$$ (3)

The index d̄_k−1 emphasizes that $S_k^{*}({\overline{d}}_{k-1})(\omega )$ represents the covariate information that would arise between decisions k − 1 and k were patient ω to receive the treatments sequentially dictated by the first k − 1 rules in d. Similarly, Y*(d)(ω) is the final outcome that ω would experience if s/he were to receive the K treatments dictated by d.

With these definitions, the expected outcome in the population if all patients with initial state S₁ = s₁ were to follow regime d is E{Y*(d)|S₁ = s₁}. An optimal regime, d^opt ∈ 𝒟, say, satisfies

$$\mathrm{E}\{Y^{*}(d)|S_1=s_1\}\le \mathrm{E}\{Y^{*}(d^{\text{opt}})|S_1=s_1\}\text{for all}d\in 𝒟\text{and all}{s}_1\in {𝒮}_1.$$ (4)

Because (4) is true for any fixed s₁, in fact E{Y*(d)} ≤ E{Y*(d^(1)opt)} for any d ∈ 𝒟. In Section 3, we give the form of d^opt satisfying (4).

Alternative specifications of Ψ may lead to different classes of regimes across which the optimal regime may differ. We emphasize that the definition (4) is predicated on the particular set Ψ, and hence class 𝒟, of interest. In principle, the class 𝒟 of interest is conceived based on scientific or policy objectives without reference to data available from a particular study.

Of course, potential outcomes for a given patient for all d ∈ 𝒟 are not observed. Thus, the goal is to estimate d^opt in (4) using data from a study carried out on a random sample of n patients from Ω that record baseline and evolving covariate information and treatments actually received. Denote these available data as independent and identically distributed (i.i.d.) time-ordered random variables (S_1i, A_1i, …, S_Ki, A_Ki, Y_i), i = 1, …, n, on Ω. Here, S₁ is as before; S_k, k = 2, …, K, is covariate information recorded between decisions k − 1 and k, taking values s_k ∈ 𝒮_k; A_k, k = 1, …, K, is the recorded, observed treatment assignment, taking values a_k ∈ 𝒜_k; and Y is the observed outcome, taking values y ∈ 𝒴. As above, define S̄_k = (S₁, …. S_k) and Ā_k = (A₁, …, A_k), k = 1, …, K, taking values s̄_k ∈ 𝒮̄_k and ā_k ∈ 𝒜̄_k.

The available data may arise from an observational study involving n participants randomly sampled from the population; here, treatment assignment takes place according to routine clinical practice in the population. Alternatively, the data may arise from an intervention study. A clinical trial design that has been advocated for collecting data suitable for estimating optimal treatment regimes is that of a so-called sequential multiple-assignment randomized trial (SMART, Lavori and Dawson, 2000; Murphy, 2005). In a SMART involving K pre-specified decision points, each participant is randomized at each decision point to one of a set of treatment options, where, at the kth decision, the randomization probabilities may depend on past realized information s̄_k, ā_k−1.

In order to use the observed data from either type of study to estimate an optimal regime, several assumptions are required. As is standard, we make the consistency assumption (e.g., Robins, 1994) that the covariates and outcomes observed in the study are those that potentially would be seen under the treatments actually received; that is, $S_k=S_k^{*}({\overline{A}}_{k-1}),k=2,\dots ,K$, and Y = Y*(Ā_K). We also make the stable unit treatment value assumption (Rubin, 1978), which ensures that a patient’s covariates and outcome are unaffected by how treatments are allocated to her/him and other patients. The critical assumption of no unmeasured confounders, also referred to as the sequential randomization assumption (Robins, 1994), must be satisfied. A strong version of this assumption states that A_k is conditionally independent of W* in (1) given {S̄_k, Ā_k−1}, k = 1,…,K, where A₀ is null, written A_k ⫫ W*|S̄_k, Ā_k−1. In a SMART, this assumption is satisfied by design; in an observational study, it is unverifiable from the observed data. The strong version is sufficient for identification of the distribution of not only Y*(ā_K) but of the joint distribution of Y*(ā_K) and ${\overline{S}}_K^{*}({\overline{a}}_{K-1})$ and allows the results of Section 4 to hold. Although in the population patients and their providers may make decisions based only on past covariate information available to them, the issue is whether or not all of the information that is related to treatment assignment and future covariates and outcome is recorded in the S_k; see Robins (2004, Sections 2–3) for discussion and a relaxation of the version of the sequential randomization assumption given here. We assume henceforth that these assumptions hold.

Whether or not it is possible to estimate d^opt from the available data is predicated on the treatment options in Ψ_k (s̄_k, ā_k−1), k = 1,…, K, being represented in the data. For a prospectively-designed SMART, ordinarily, Ψ defining the class 𝒟 of interest would dictate the design. At decision k, subjects would be randomized to the options in Ψ_k (s̄_k, ā_k−1), satisfying this condition. If the data are from an observational study, all treatment options in Ψ_k (s̄_k, ā_k−1) at each decision k must have been assigned to some patients. That is, if we define recursively ${\mathrm{\Gamma }}_1^{\text{max}}=\{s_1\in {𝒮}_1:\text{pr}(S_1=s_1)>0\},{\mathrm{\Psi }}_1^{\text{max}}(s_1)=\{a_1\in {𝒜}_1:\text{pr}(A_1=a_1|S_1=s_1)>0\text{for all}{s}_1\in {\mathrm{\Gamma }}_1^{\text{max}}\},{\mathrm{\Gamma }}_k^{\text{max}}=[({\overline{s}}_k,{\overline{a}}_{k-1})\in {\overline{𝒮}}_k\times {\overline{𝒜}}_{k-1}$ satisfying (i) $a_j\in {\mathrm{\Psi }}_j^{\text{max}}({\overline{s}}_j,{\overline{a}}_{j-1}),j=1,\dots ,k-1$, and (ii) $\text{pr}\{{\overline{S}}_k^{*}({\overline{a}}_{k-1})={\overline{s}}_k\}>0],{\mathrm{\Psi }}_k^{\text{max}}({\overline{s}}_k,{\overline{a}}_{k-1})=\{a_k\in {𝒜}_k:\text{pr}(A_k=a_k|{\overline{S}}_k={\overline{s}}_k,{\overline{A}}_{k-1}={\overline{a}}_{k-1})>0\text{for all}({\overline{s}}_k,{\overline{a}}_{k-1})\in {\mathrm{\Gamma }}_k^{\text{max}}\},k=2,\dots ,K$, we must have ${\mathrm{\Psi }}_k({\overline{s}}_k,{\overline{a}}_{k-1})\subseteq {\mathrm{\Psi }}_k^{\text{max}}({\overline{s}}_k,{\overline{a}}_{k-1}),k=1,\dots ,K$. The class of regimes dictated by ${\mathrm{\Psi }}^{\text{max}}=({\mathrm{\Psi }}_1^{\text{max}},\dots ,{\mathrm{\Psi }}_K^{\text{max}})$ is the largest that can be considered based on the data, sometimes referred to as the class of “feasible regimes” (Robins, 2004). If this inclusion condition does not hold for all k = 1, …, K, d^opt cannot be estimated from the data, and the class of regimes 𝒟 of interest must be reevaluated or another data source found.

3. OPTIMAL TREATMENT REGIMES

Q- and A-learning are two approaches to estimating d^opt satisfying (4) under the foregoing framework. Both involve recursive fitting algorithms; the main distinguishing feature is the form of the underlying models. To appreciate the rationale, one must understand how d^opt is determined via dynamic programming, also known as backward induction. We demonstrate the formulation of d^opt in terms of the potential outcomes and then show how d^opt may be expressed in terms of the observed data under assumptions including those in Section 2. We sometimes highlight dependence on specific elements of quantities such as ā_k, writing, for example, ā_k as (ā_k−1, a_k).

At the Kth decision point, for any s̄_K ∈ 𝒮̄_K, ā_K−1 ∈ 𝒜̄_K−1 for which (s̄_K, ā_K−1) ∈ Γ_K, define

$$d_K^{(1)\text{opt}}({\overline{s}}_K,{\overline{a}}_{K-1})=\text{arg}\underset{a_K\in {\mathrm{\Psi }}_K({\overline{s}}_K,{\overline{a}}_{K-1})}{\text{max}}\mathrm{E}\{Y^{*}({\overline{a}}_{K-1},a_K)|{\overline{S}}_K^{*}({\overline{a}}_{K-1})={\overline{s}}_K\},$$ (5)

$$V_K^{(1)}({\overline{s}}_K,{\overline{a}}_{K-1})=\underset{a_K\in {\mathrm{\Psi }}_K({\overline{s}}_K,{\overline{a}}_{K-1})}{\text{max}}\mathrm{E}\{Y^{*}({\overline{a}}_{K-1},a_K)|{\overline{S}}_K^{*}({\overline{a}}_{K-1})={\overline{s}}_K\}.$$ (6)

For k = K − 1, …, 1 and any s̄_k ∈ 𝒮̄_k, ā_k−1 ∈ 𝒜̄_k−1 for which (s̄_k, ā_k−1) ∈ Γ_k, which clearly holds if (s̄_K, ā_K−1) ∈ Γ_K, let

$$d_k^{(1)\text{opt}}({\overline{s}}_k,{\overline{a}}_{k-1})=\text{arg}\underset{a_k\in {\mathrm{\Psi }}_k({\overline{s}}_k,{\overline{a}}_{k-1})}{\text{max}}\mathrm{E}[V_{k+1}^{(1)}\{{\overline{s}}_k,S_{k+1}^{*}({\overline{a}}_{k-1},a_k),{\overline{a}}_{k-1},a_k\}|{\overline{S}}_k^{*}({\overline{a}}_{k-1})={\overline{s}}_k],$$ (7)

$$V_k^{(1)}({\overline{s}}_k,{\overline{a}}_{k-1})=\underset{a_k\in {\mathrm{\Psi }}_k({\overline{s}}_k,{\overline{a}}_{k-1})}{\text{max}}\mathrm{E}[V_{k+1}^{(1)}\{{\overline{s}}_k,S_{k+1}^{*}({\overline{a}}_{k-1},a_k),{\overline{a}}_{k-1},a_k\}|{\overline{S}}_k^{*}({\overline{a}}_{k-1})={\overline{s}}_k];$$ (8)

thus, for $s_1\in {𝒮}_1,d_1^{(1)\text{opt}}(s_1)={\text{arg max}}_{a_1\in {\mathrm{\Psi }}_1(s_1)}\mathrm{E}[V_2^{(1)}\{s_1,S_2^{*}(a_1),a_1\}|S_1=s_1],V_1^{(1)}(s_1)={\text{max}}_{a_1\in {\mathrm{\Psi }}_1(s_1)}\mathrm{E}[V_2^{(1)}\{s_1,S_2^{*}(a_1),a_1\}|S_1=s_1]$. Conditional expectations are well-defined by (2)(ii).

Clearly, $d^{(1)\text{opt}}=(d_1^{(1)\text{opt}},\dots ,d_K^{(1)\text{opt}})$ is a treatment regime, as it comprises a set of rules that uses patient information to assign treatment from among the options in Ψ. The superscript (1) indicates that d^(1)opt provides K rules for a patient presenting prior to decision 1 with baseline information S₁ = s₁; Section 4 considers optimal treatment of patients presenting at subsequent decisions after receiving possibly sub-optimal treatment at prior decisions. Note that d^(1)opt is defined in a backward iterative fashion. At decision K, (5) gives the treatment that maximizes the expected potential final outcome given the prior potential information, and (6) is the maximum achieved. At decisions k = K − 1,…, 1, (7) gives the treatment that maximizes the expected outcome that would be achieved if subsequent optimal rules already defined were followed henceforth. In Section A.1 of the supplemental article [Schulte et al. (2012)], we show that d^(1)opt defined in (5)–(8) is an optimal treatment regime in the sense of satisfying (4).

The foregoing developments express optimal regimes in terms of the distribution of potential outcomes. If an optimal regime is to be identifiable, it must be possible under the assumptions in Section 2 to express d^(1)opt in terms of the distribution of the observed data. To this end, define

$$Q_K({\overline{s}}_K,{\overline{a}}_K)=\mathrm{E}(Y|{\overline{S}}_K={\overline{s}}_K,{\overline{A}}_K={\overline{a}}_K),$$ (9)

$$d_K^{\text{opt}}({\overline{s}}_K,{\overline{a}}_{K-1})=\text{arg}\underset{a_K\in {\mathrm{\Psi }}_K({\overline{s}}_K,{\overline{a}}_{K-1})}{\text{max}}{Q}_K({\overline{s}}_K,{\overline{a}}_{K-1},a_K),$$ (10)

$$V_K({\overline{s}}_K,{\overline{a}}_{K-1})=\underset{a_K\in {\mathrm{\Psi }}_K({\overline{s}}_K,{\overline{a}}_{K-1})}{\text{max}}{Q}_K({\overline{s}}_K,{\overline{a}}_{K-1},a_K),$$ (11)

and for k = K − 1,…, 1, define

$$Q_k({\overline{s}}_k,{\overline{a}}_k)=\mathrm{E}\{V_{k+1}({\overline{s}}_k,S_{k+1},{\overline{a}}_k)|{\overline{S}}_k={\overline{s}}_k,{\overline{A}}_k={\overline{a}}_k\}$$ (12)

$$d_k^{\text{opt}}({\overline{s}}_k,{\overline{a}}_{k-1})=\text{arg}\underset{a_k\in {\mathrm{\Psi }}_k({\overline{s}}_k,{\overline{a}}_{k-1})}{\text{max}}{Q}_k({\overline{s}}_k,{\overline{a}}_{k-1},a_k),$$ (13)

$$V_k({\overline{s}}_k,{\overline{a}}_{k-1})=\underset{a_k\in {\mathrm{\Psi }}_k({\overline{s}}_k,{\overline{a}}_{k-1})}{\text{max}}{Q}_k({\overline{s}}_k,{\overline{a}}_{k-1},a_k).$$ (14)

.

The expressions in (9)–(14) are well-defined under assumptions we discuss next. In (9) and (12), Q_k(s̄_k,ā_k) are referred to as “Q-functions,” viewed as measuring the “quality” associated with using treatment a_k at decision k given the history up to that decision and then following the optimal regime thereafter. The “value functions” V_k(s̄_k, ā_k−1) in (11) and (14) reflect the “value” of a patient’s history s̄_k, ā_k−1 assuming that optimal decisions are made in the future. We emphasize that the $d_k^{\text{opt}},k=1,\dots ,K$, defined (9)–(14) may not be optimal unless the sequential randomization, consistency, and positivity assumptions hold.

As in Section 2, the treatment options in Ψ must be represented in the data, i.e., ${\mathrm{\Psi }}_k({\overline{s}}_k,{\overline{a}}_{k-1})\subseteq {\mathrm{\Psi }}_k^{\text{max}}({\overline{s}}_k,{\overline{a}}_{k-1}),k=1,\dots ,K$, in order to estimate an optimal regime. Formally, this implies that

$$\text{pr}(A_k=a_k|{\overline{S}}_k={\overline{s}}_k,{\overline{A}}_{k-1}={\overline{a}}_{k-1})>0\text{if}({\overline{s}}_k,{\overline{a}}_{k-1})\in {\mathrm{\Gamma }}_k\text{and}{a}_k\in {\mathrm{\Psi }}_k({\overline{s}}_k,{\overline{a}}_{k-1})$$ (15)

for all k = 1,…, K. In Section A.2 of the supplemental article [Schulte et al. (2012)], under the consistency and sequential randomization assumptions and the positivity assumption (15), we show that, for any (s̄_k, ā_k−1) ∈ Γ_k and a_k ∈ Ψ_k (s̄_k, ā_k−1), k = 1,…, K,

$$\text{pr}({\overline{S}}_k={\overline{s}}_k,{\overline{A}}_k={\overline{a}}_k)>0,$$ (16)

$$\text{pr}(S_{k+1}=s_{k+1}|{\overline{S}}_k={\overline{s}}_k,{\overline{A}}_k={\overline{a}}_k)=\text{pr}\{S_{k+1}^{*}({\overline{a}}_k)=s_{k+1}|{\overline{S}}_k={\overline{s}}_k,{\overline{A}}_{k-1}={\overline{a}}_{k-1}\}$$ (17)

$$=\text{pr}\{S_{k+1}^{*}({\overline{a}}_k)=s_{k+1}|{\overline{S}}_j={\overline{s}}_j,{\overline{A}}_{j-1}={\overline{a}}_{j-1},S_{j+1}^{*}({\overline{a}}_j)=s_{j+1},\dots ,S_k^{*}({\overline{a}}_{k-1})=s_k\},$$ (18)

for j = 1,…, k, where (18) with j = k is the same as the right-hand side of (17), S_K+1 = Y and $S_{K+1}^{*}({\overline{a}}_K)=Y^{*}({\overline{a}}_K)$, and when j = 1 the conditioning events do not involve treatment. By (16), the quantities in (9)–(14) are well-defined. Under (17)–(18), the conditional distributions of the observed data involved in (9)–(14) are the same as the conditional distributions of the potential outcomes involved in (5)–(8). It follows that

$$d_k^{(1)\text{opt}}({\overline{s}}_k,{\overline{a}}_{k-1})=d_k^{\text{opt}}({\overline{s}}_k,{\overline{a}}_{k-1}),V_k^{(1)}({\overline{s}}_k,{\overline{a}}_{k-1})=V_k({\overline{s}}_k,{\overline{a}}_{k-1}),$$ (19)

for (s̄_k, ā_k−1) ∈ Γ_k, k = 1, …, K. The equivalence in (19) shows that, under the consistency, sequential randomization, and positivity assumptions, an optimal treatment regime in the (Ψ-specific) class of interest 𝒟 may be obtained using the distribution of the observed data.

There may not be a unique d^opt. At any decision k, if there is more than one possible option a_k maximizing the Q-function, then any rule $d_k^{\text{opt}}$ yielding one of these a_k defines an optimal regime.

4. OPTIMAL “MIDSTREAM” TREATMENT REGIME

In Section 3, we define a (Ψ-specific) optimal treatment regime starting at decision point 1 and elucidate conditions under which it may be estimated using data from a clinical or observational study collected through all K decisions on a sample from the patient population. The goal is to estimate the optimal regime and implement it in new such patients presenting at the first decision.

In routine clinical practice, however, a new patient may be encountered subsequent to decision point 1. For definiteness, suppose a new patient presents “midstream,” immediately prior to the ℓth decision point, ℓ = 2,…, K. A natural question is how to treat this patient optimally henceforth. For such a patient, the first ℓ − 1 treatment decisions presumably have been made according to routine practice, and s/he has a realized past history that may be viewed as realizations of random variables $(S_1^{(P)},A_1^{(P)},\dots ,S_{\ell -1}^{(P)},A_{\ell -1}^{(P)},S_{\ell }^{(P)})$. Here, $A_k^{(P)},k=1,\dots ,\ell -1$, represent the treatments received by such a patient according to the treatment assignment mechanism governing routine practice; and $S_k^{(P)},k=1,\dots ,\ell -1$, denote covariate information collected up to the ℓth decision. Write ${\overline{A}}_k^{(P)}=(A_1^{(P)},\dots ,A_k^{(P)}),k=1,\dots ,\ell -1\text{and}{\overline{S}}_k^{(P)}=(S_1^{(P)},\dots ,S_k^{(P)}),k=1,\dots ,\ell$.

As 𝒜_k denotes the set of all possible treatment options at decision k, ${\overline{A}}_{\ell -1}^{(P)}$ takes on values ā_ℓ−1 ∈ 𝒜̄_ℓ−1. To define Ψ-specific regimes starting at decision ℓ, at the least, $S_k^{(P)}$ must contain the same information as S_k in the data, k = 1, …,ℓ. Because the available data dictate the covariate information incorporated in the class of regimes 𝒟, if $S_k^{(P)}$ contains additional information, it cannot be used in the context of such regimes. We thus take $S_k^{(P)}$ and S_k to contain the same information, stated formally as the consistency assumption $S_k^{(P)}=S_k^{*}({\overline{A}}_{k-1}^{(P)}),k=1,\dots ,\ell$. Moreover, we can only consider treating new patients with realized histories (s̄_ℓ, ā_ℓ−1) that are contained in Γ_ℓ; that is, that could have resulted from following a Ψ-specific regime through decision ∓ − 1. If the data arise from a SMART including only a subset of the treatments employed in practice, this may not hold.

We thus desire rules $d_k^{(\ell )}({\overline{s}}_k,{\overline{a}}_{k-1}),k=\ell ,\ell +1,\dots ,K$, say, that dictate how to treat such midstream patients presenting with realized past history $({\overline{S}}_{\ell }^{(P)},{\overline{A}}_{\ell -1}^{(P)})=({\overline{s}}_{\ell },{\overline{a}}_{\ell -1})$. In the following, we regard (s̄_ℓ, ā_ℓ−1) as fixed, corresponding to the particular new patient. Let ${\mathrm{\Gamma }}_k^{(\ell )}$ be all elements of Γ_k with (s̄_ℓ, ā_ℓ−1) fixed at the values for the given new patient. Write $d^{(\ell )}=(d_{\ell }^{(\ell )},d_{\ell +1}^{(\ell )},\dots ,d_K^{(\ell )})$ to denote regimes starting at the ℓth decision point, and define the class 𝒟^(ℓ) of all such regimes to be the set of all d^(ℓ) for which $d_k^{(\ell )}({\overline{s}}_k,{\overline{a}}_{k-1})=a_k$ for $({\overline{s}}_k,{\overline{a}}_{k-1})\in {\mathrm{\Gamma }}_k^{(\ell )}$ and a_k ∈ Ψ_k (s̄_k, ā_k−1) for k = ℓ,…, K. Then, by analogy to (4), we seek d^(ℓ)opt satisfying

$$\mathrm{E}\{Y^{*}({\overline{a}}_{\ell -1},d^{(\ell )})|{\overline{S}}_{\ell }^{(P)}={\overline{s}}_{\ell },{\overline{A}}_{\ell -1}^{(P)}={\overline{a}}_{\ell -1}\}\le \mathrm{E}\{Y^{*}({\overline{a}}_{\ell -1},d^{(\ell )\text{opt}})|{\overline{S}}_{\ell }^{(P)}={\overline{s}}_{\ell },{\overline{A}}_{\ell -1}^{(P)}={\overline{a}}_{\ell -1}\}$$ (20)

for all d^(ℓ) ∈ 𝒟^(ℓ) and s̄_ℓ ∈ 𝒮̄_ℓ, ā_ℓ−1 ∈ 𝒜̄_ℓ−1 for which $\text{pr}({\overline{S}}_{\ell }^{(P)}={\overline{s}}_{\ell },{\overline{A}}_{\ell -1}^{(P)}={\overline{a}}_{\ell -1})>0$. Viewing this as a problem of making K − ℓ+1 decisions at decision points ℓ, ℓ +1,…, K, with initial state ${\overline{S}}_{\ell }^{(P)}={\overline{s}}_{\ell },{\overline{A}}_{\ell -1}^{(P)}={\overline{a}}_{\ell -1}$, by an argument analogous to that in Section A.1 of the supplemental article [Schulte et al. (2012)] for ℓ = 1 and initial state S₁ = s₁ letting ${𝒱}_{\ell ,k}=\{{\overline{S}}_{\ell }^{(P)}={\overline{s}}_{\ell },{\overline{A}}_{\ell -1}^{(P)}={\overline{a}}_{\ell -1},S_{\ell +1}^{*}({\overline{a}}_{\ell })=s_{\ell +1},\dots ,S_k^{*}({\overline{a}}_{k-1})=s_k\}$, it may be shown that d^(ℓ)opt satisfying (20) is given by

$$d_K^{(\ell )\text{opt}}({\overline{s}}_K,{\overline{a}}_{K-1})=\text{arg}\underset{a_K\in {\mathrm{\Psi }}_K({\overline{s}}_K,{\overline{a}}_{K-1})}{\text{max}}\mathrm{E}\{Y^{*}({\overline{a}}_{K-1},a_K)|{𝒱}_{\ell ,K}\},$$ (21)

$$V_K^{(\ell )}({\overline{s}}_K,{\overline{a}}_{K-1})=\underset{a_K\in {\mathrm{\Psi }}_K({\overline{s}}_K,{\overline{a}}_{K-1})}{\text{max}}\mathrm{E}\{Y^{*}({\overline{a}}_{K-1},a_K)|{𝒱}_{\ell ,K}\}$$ (22)

for any s̄_K ∈ 𝒮̄_K, ā_K−1 ∈ 𝒜̄_K−1 for which $({\overline{s}}_K,{\overline{a}}_{K-1})\in {\mathrm{\Gamma }}_K^{(\ell )}$; and, for k = K − 1,… ℓ,

$$d_k^{(\ell )\text{opt}}({\overline{s}}_k,{\overline{a}}_{k-1})=\text{arg}\underset{a_k\in {\mathrm{\Psi }}_k({\overline{s}}_k,{\overline{a}}_{k-1})}{\text{max}}\mathrm{E}[V_{k+1}^{(\ell )}\{{\overline{s}}_k,S_{k+1}^{*}({\overline{a}}_{k-1},a_k),{\overline{a}}_{k-1},a_k\}|{𝒱}_{\ell ,k}],$$ (23)

$$V_k^{(\ell )}({\overline{s}}_k,{\overline{a}}_{k-1})=\underset{a_k\in {\mathrm{\Psi }}_k({\overline{s}}_k,{\overline{a}}_{k-1})}{\text{max}}\mathrm{E}[V_{k+1}^{(\ell )}\{{\overline{s}}_k,S_{k+1}^{*}({\overline{a}}_{k-1},a_k),{\overline{a}}_{k-1},a_k\left\}\right|{𝒱}_{\ell ,k}]$$ (24)

for any s̄_k ∈ 𝒮̄_k, ā_k−1 ∈ 𝒜̄_k−1 for which $({\overline{s}}_k,{\overline{a}}_{k-1})\in {\mathrm{\Gamma }}_k^{(\ell )}$, so that

$$d_{\ell }^{(\ell )\text{opt}}({\overline{s}}_{\ell },{\overline{a}}_{\ell -1})=\text{arg}\underset{a_{\ell }\in {\mathrm{\Psi }}_{\ell }({\overline{s}}_{\ell },{\overline{a}}_{\ell -1})}{\text{max}}\mathrm{E}[V_{\ell +1}^{(\ell )}\{{\overline{s}}_{\ell },S_{\ell +1}^{*}({\overline{a}}_{\ell -1},a_{\ell }),{\overline{a}}_{\ell -1},a_{\ell }\}|{\overline{S}}_{\ell }^{(P)}={\overline{s}}_{\ell },{\overline{A}}_{\ell -1}^{(P)}={\overline{a}}_{\ell -1}].$$

Comparison of (5)–(8) to (21)–(24) shows that the ℓth to Kth rules of the optimal regime d^(1)opt that would be followed by a patient presenting at the first decision are not necessarily the same as those of the optimal regime d^(ℓ)opt that would be followed by a patient presenting at the ℓth decision. In particular, noting that the conditioning sets in (5)–(8) are 𝒱_1,K and 𝒱_1,k, the rules are ℓ-dependent through dependence of the conditioning sets 𝒱_ℓ,k, ℓ = 1, …, K, k = ℓ,…, K, on ℓ. However, we now demonstrate that these rules coincide under certain conditions.

Make the consistency, sequential randomization, and positivity (15) assumptions on the available data required to show (19) in Section 3, along with the consistency assumption on the $S_k^{(P)}$ above and the sequential randomization assumption $A_k^{(P)}⫫W^{*}|{\overline{S}}_k^{(P)},{\overline{A}}_{k-1}^{(P)},k=1,\dots ,\ell -1$, which ensures that the ${\overline{S}}_k^{(P)}$ include all information related to treatment assignment and future covariates and outcome up to decision ℓ. Note that (21)–(24) are expressed in terms of the conditional distributions $\text{pr}\{S_{k+1}^{*}({\overline{a}}_k)=s_{k+1}|{\overline{S}}_{\ell }^{(P)}={\overline{s}}_{\ell },{\overline{A}}_{\ell -1}^{(P)}={\overline{a}}_{\ell -1},S_{\ell +1}^{*}({\overline{a}}_{\ell })=s_{\ell },\dots ,S_k^{*}({\overline{a}}_{k-1})=s_k\},k=\ell ,\dots ,K$. We can then use (18) with j = ℓ to deduce that these conditional distributions can be written equivalently as $\text{pr}\{S_{k+1}^{*}({\overline{a}}_k)=s_{k+1}|{\overline{S}}_k^{*}({\overline{a}}_{k-1})={\overline{s}}_k\},k=\ell ,\dots ,K$, so solely in terms of the distribution of the potential outcomes. By (17) and (18) with j = 1, this can be written as pr(S_k+1 = s_k+1| S̄_k = s̄_k, Ā_k = ā_k). This shows that (21)–(24) can be reexpressed in terms of the observed data, so that, for (s̄_k, ā_k−1) ∈ Γ_k for ℓ = 1,…, K and k = ℓ,…, K,

$$d_k^{(\ell )\text{opt}}({\overline{s}}_k,{\overline{a}}_{k-1})=d_k^{\text{opt}}({\overline{s}}_k,{\overline{a}}_{k-1}),V_k^{(\ell )}({\overline{s}}_k,{\overline{a}}_{k-1})=V_k({\overline{s}}_k,{\overline{a}}_{k-1}).$$ (25)

Note that (25) subsumes (19) when ℓ = 1. The equivalence in (25) not only demonstrates that an optimal treatment regime can be obtained using the distribution of the observed data but also that the corresponding rules dictating treatment do not depend on ℓ under these assumptions. Thus, the single set of rules $d^{\text{opt}}=(d_1^{\text{opt}},\dots ,d_k^{\text{opt}})$ defined in (10) and (13) is relevant regardless of when a patient presents. That is, treatment at the ℓth decision point for a patient who presents at decision 1 and has followed the rules in d^opt to that point would be determined by $d_{\ell }^{\text{opt}}$ evaluated at his/her history up to that point, as would treatment for a subject presenting for the first time immediately prior to decision ℓ. See Robins (2004, pages 305–306) for more discussion.

5. Q- AND A-LEARNING

5.1 Q-Learning

From (10), (13) and (19), an optimal (Ψ-specific) regime d^opt may be represented in terms of the Q-functions (9), (12). Thus, estimation of d^opt based on i.i.d. data (S_1i, A_1i,…, S_Ki, A_Ki, Y_i), i = 1,…, n, may be accomplished via direct modeling and fitting of the Q-functions. This is the approach underlying Q-learning. Specifically, one may posit models Q_k(s̄_k,ā_k;ξ_k), say, for k = K,K − 1,…, 1, each depending on a finite-dimensional parameter ξ_k. The models may be linear or nonlinear in ξ_k and include main effects and interactions in the elements of s̄_k and ā_k.

Estimators ξ̂_k may be obtained in a backward iterative fashion for k = K, K −1,…, 1 by solving suitable estimating equations [e.g., ordinary (OLS) or weighted (WLS) least squares]. Assuming the latter, for k = K, letting Ṽ_(K+1)i = Y_i one would first solve

$$\sum _{i=1}^n\frac{\partial Q_K({\overline{S}}_{Ki},{\overline{A}}_{Ki};{\xi }_K)}{\partial {\xi }_K}{\mathrm{\Sigma }}_K^{-1}({\overline{S}}_{Ki},{\overline{A}}_{Ki})\{{\tilde{V}}_{(K+1)i}-Q_K({\overline{S}}_{Ki},{\overline{A}}_{Ki};{\xi }_K)\}=0$$ (26)

in ξ_K to obtain ξ̂_K, where Σ_K(s̄_K, ā_K) is a working variance model. Substituting the model Q_K (s̄_K, ā_K; ξ_K) in (10) and accordingly writing $d_K^{\text{opt}}({\overline{s}}_K,{\overline{a}}_{K-1};{\xi }_K)$, substituting ξ̂_K for ξ_K yields an estimator for the optimal treatment choice at decision K for a patient with past history S̄_K = s̄_K, Ā_K−1 = ā_K−1. With ξ̂_K in hand, one would form for each i, based on (11), Ṽ_Ki = max_{aK∈ΨK(S̄Ki,Ā(K−1)i)} Q_K(S̄_Ki,Ā_(K−1)i,a_K;ξ̂_K). To obtain ξ̂_K−1, setting k = K − 1, based on (12) and letting Σ_k(s̄_k, ā_k) be a working variance model, one would then solve for ξ_k

$$\sum _{i=1}^n\frac{\partial Q_k({\overline{S}}_{ki},{\overline{A}}_{ki};{\xi }_k)}{\partial {\xi }_k}{\mathrm{\Sigma }}_k^{-1}({\overline{S}}_{ki},{\overline{A}}_{ki})\{{\tilde{V}}_{(k+1)i}-Q_k({\overline{S}}_{ki},{\overline{A}}_{ki};{\xi }_k)\}=0.$$ (27)

The corresponding $d_{K-1}^{\text{opt}}({\overline{s}}_{K-1},{\overline{a}}_{K-2};{\widehat{\xi }}_{K-1})$ yields an estimator for the optimal treatment choice at decision K − 1 for a patient with past history S̄_K−1 = s̄_K−1, Ā_K−2 = ā_K−2, assuming s/he will take the optimal treatment at decision K. One would continue this process in the obvious fashion for k = K − 2,…, 1, forming Ṽ_ki = max_{ak∈Ψk(S̄ki,Ā(k−1)i)} Q_k(S̄_ki,Ā_(k−1)i,a_k;ξ̂_k), and solving equations of form (27) to obtain ξ̂_k and corresponding $d_k^{\text{opt}}({\overline{s}}_k,{\overline{a}}_{k-1};{\widehat{\xi }}_k)$.

We may now summarize the estimated optimal regime as ${\widehat{d}}_Q^{\text{opt}}=({\widehat{d}}_{Q,1}^{\text{opt}},\dots ,{\widehat{d}}_{Q,K}^{\text{opt}})$, where

$${\widehat{d}}_{Q,1}^{\text{opt}}(s_1)=d_1^{\text{opt}}(s_1;{\widehat{\xi }}_1),{\widehat{d}}_{Q,k}^{\text{opt}}({\overline{s}}_k,{\overline{a}}_{k-1})=d_k^{\text{opt}}({\overline{s}}_k,{\overline{a}}_{k-1};{\widehat{\xi }}_k),k=2,\dots ,K.$$ (28)

It is important to recognize that, even under the sequential randomization assumption, the estimated regime (28) may not be a consistent estimator for the true optimal regime unless all the models for the Q-functions are correctly specified.

We illustrate the approach for K = 2, where at each decision there are two possible treatment options coded as 0 and 1; i.e., Ψ₁(s₁) = 𝒜₁ = {0,1} for all s₁ and Ψ₂(s̄₂, a₁) = 𝒜₂= {0,1} for all s̄₂ and a₁ ∈ {0,1}. Let ${\mathscr{H}}_1={(1,s_1^T)}^T\text{and}{\mathscr{H}}_2={(1,s_1^T,a_1,s_2^T)}^T$. As in many modeling contexts, it is standard to adopt linear models for the Q-functions; accordingly, consider the models

$$Q_1(s_1,a_1;{\xi }_1)={\mathscr{H}}_1^T{\beta }_1+a_1({\mathscr{H}}_1^T{\psi }_1),Q_2({\overline{s}}_2,{\overline{a}}_2;{\xi }_2)={\mathscr{H}}_2^T{\beta }_2+a_2({\mathscr{H}}_2^T{\psi }_2),$$ (29)

where ${\xi }_k={({\beta }_k^T,{\psi }_k^T)}^T,k=1,2$. In (29), Q₂(s̄₂, ā₂; ξ₂) is a model for E(Y|S̄₂ = s̄₂, Ā₂ = ā₂), a standard regression problem involving observable data, whereas Q₁(s₁, a₁;ξ₁) is a model for the conditional expectation of V₂(s̄₂, a₁ = max_a2∈{0,1} E(Y|S̄₂ = s₂, A₁ = a₁, A₂ = a₂) given S₁ = s₁ and A₁ = a₁, which is an approximation to a complex true relationship; see Section 5.3. Under (29), $V_2({\overline{s}}_2,a_1;{\xi }_2)={\text{max}}_{a_2\in \{0,1\}}{Q}_2({\overline{s}}_2,a_1,a_2;{\xi }_2)={\mathscr{H}}_2^T{\beta }_2+({\mathscr{H}}_2^T{\psi }_2)I({\mathscr{H}}_2^T{\psi }_2>0)$ and $V_1(s_1;{\xi }_1)={\text{max}}_{a_1\in \{0,1\}}{Q}_1(s_1,a_1;{\xi }_1)={\mathscr{H}}_1^T{\beta }_1+({\mathscr{H}}_1^T{\psi }_1)I({\mathscr{H}}_1^T{\psi }_1>0)$. Substituting the Q-functions in (29) in (10) and (13) then yields $d_1^{\text{opt}}(s_1;{\xi }_1)=I({\mathscr{H}}_1^T{\psi }_1>0)$ and $d_2^{\text{opt}}({\overline{s}}_2,a_1;{\xi }_2)=I({\mathscr{H}}_2^T{\psi }_2>0)$.

We have presented (26) and (27) in the conventional WLS form, with leading term in the summand $\partial /\partial {\xi }_k{Q}_k({\overline{S}}_{ki},{\overline{A}}_{ki};{\xi }_k){\mathrm{\Sigma }}_k^{-1}({\overline{S}}_{ki},{\overline{A}}_{ki})$; taking Σ_k to be a constant yields OLS. At the Kth decision, with responses Y_i, standard theory implies that this is the optimal leading term when var(Y|S̄_K = s_K, Ā_K = a_K) = Σ_K(s̄_K, ā_K), yielding the (asymptotically) efficient estimator for ξ_K. For k < K, with “responses” Ṽ_(k+1)i, this theory may no longer apply; however, deriving the optimal leading term involves considerable complication. Accordingly, it is standard to fit the posited models Q_k (s̄_k, ā_k; ξ_k) via OLS or WLS; some authors define Q-learning as using OLS (Chakraborty, Murphy and Strecher, 2010). The choice may be dictated by apparent relevance of the homoscedasticity assumption on the Ṽ_(k+1)i, k = K, K − 1, …, 1, and whether or not linear models are sufficient to approximate the relationships may also be evaluated, but see Section 5.3.

5.2 A-Learning

Advantage learning (A-learning, Blatt et al., 2004) is a term used to describe a class of alternative methods to Q-learning predicated on the fact that the entire Q-function need not be specified to estimate the optimal regime. For simplicity, we consider here only the case of two treatment options coded as 0 and 1 at each decision; i.e., Ψ_k(s̄_k, ā_k−1) = 𝒜_k = {0,1}, k = 1,…, K.

To fix ideas, consider (29). Note that $d_1^{\text{opt}}(s_1;{\xi }_1)$ implied by (29) depends only on ${\mathscr{H}}_1^T{\psi }_1=Q_1(s_1,1;{\xi }_1)-Q_1(s_1,0;{\xi }_1)$; likewise, $d_2^{\text{opt}}({\overline{s}}_2,a_1;{\xi }_2)$ depends only on ${\mathscr{H}}_2^T{\psi }_2=Q_2({\overline{s}}_2,a_1,1;{\xi }_2)-Q_2({\overline{s}}_2,a_1,0;{\xi }_2)$. This reflects the general result that, for purposes of deducing the optimal regime, for each k = 1,…, K, it suffices to know the contrast function C_k(s̄_k, ā_k−1) = Q_k(s̄_k, ā_k−1, 1) − Q_k(s̄_k, ā_k−1, 0). This can be appreciated by noting that any arbitrary Q_k(s̄_k, ā_k) may be written as h_k(s̄_k, ā_k−1) + a_kC_k(s̄_k, ā_k−1), where h_k(s̄_k, ā_k−1) = Q_k(s̄_k, ā_k−1, 0), so that Q_k(s̄_k, ā_k−1, a_k) is maximized by taking a_k = I{C_k(s̄_k, ā_k−1) > 0}; and the maximum itself is the expression h_k(s̄_k, ā_k−1) + C_k(s̄_k, ā_k−1)I{C_k(s̄_k, ā_k−1) > 0}. In the case of two treatment options we consider here, the contrast function is also referred to as the optimal-blip-to-zero function (Robins, 2004; Moodie et al., 2007). Murphy (2003) considers the expression C_k(S̄_k, Ā_k−1)[I{C_k(S̄_k, Ā_k−1) > 0} − A_k], referred to as the advantage or regret function, as it represents the “advantage” in response incurred if the optimal treatment at the kth decision were given relative to that actually received (or, equivalently, the “regret” incurred by not using the optimal treatment). See Robins (2004) and Moodie et al. (2007) for discussion of the relationship between regrets and optimal blip functions in this and settings other than binary treatment options.

We discuss here an A-learning method based on explicit modeling of the contrast functions, which we refer to as contrast-based A-learning. This approach is implemented via recursive solution of certain estimating equations given below developed by Robins (2004), often referred to as g-estimation. See Moodie et al. (2007) and the supplementary material to Zhang et al. (2013) for details. Contrast-based A-learning is distinguished from the regret-based A-learning methods of Murphy (2003) and Blatt et al. (2004), which rely on direct modeling of the regret functions and are implemented using a different estimating equation formulation called Iterative Minimization for Optimal Regimes by Moodie et al. (2007).

All of these methods are alternatives to Q-learning, which involves modeling the full Q-functions. For k = K − 1,…, 1, the Q-functions involve possibly complex relationships, raising concern over the consequences of model misspecification for estimation of the optimal regime. As identifying the optimal regime depends only on correct specification of the contrast or regret functions, A-learning methods may be less sensitive to mismodeling; see Sections 5.3 and 6.

Although we consider these methods only in the case of binary treatment options here, they may be extended to more than two treatments at the expense of complicating the formulation; see Robins (2004) and Moodie et al. (2007).

Contrast-based A-learning proceeds as follows. Posit models C_k(s̄_k, ā_k−1; ψ_k), k = 1,…, K, for the contrast functions, depending on parameters ψ_k. Consider decision K. Let π_K(s̄_K, ā_K−1) = pr(A_K = 1|S̄_K = s̄_K, Ā_K−1 = ā_K−1) be the propensity of receiving treatment 1 in the observed data as a function of past history and Ṽ_(K+1)i = Y_i. Robins (2004) showed that all consistent and asymptotically normal estimators for ψ_K are solutions to estimating equations of the form

$$\sum _{i=1}^n{\lambda }_K({\overline{S}}_{Ki},{\overline{A}}_{(K-1)i})\{A_{Ki}-{\pi }_K({\overline{S}}_{Ki},{\overline{A}}_{(K-1)i})\}\times \{{\tilde{V}}_{(K+1)i}-A_{Ki}{C}_K({\overline{S}}_{Ki},{\overline{A}}_{(K-1)i};{\psi }_K)-{\theta }_K({\overline{S}}_{Ki},{\overline{A}}_{(K-1)i})\}=0$$ (30)

for arbitrary functions λ_K(s̄_K, ā_K−1) of the same dimension as ψ_K and arbitrary functions θ_K(s̄_K, ā_K−1). Assuming that the model C_K(s̄_K, ā_K−1; ψ_K) is correct, if var(Y|S̄_K = s_k, Ā_K−1 = a_k−1) is constant, the optimal choices of these functions are given by λ_K(s̄_K, ā_K−1; ψ_K) = ∂/∂ψ_K C_K(s̄_K, ā_K−1; ψ_K) and θ_K (s̄_Ki, ā_(K−1)i) = h_K (s̄_K, ā_K−1); otherwise, if the variance is not constant, the optimal λ_K is complex (Robins, 2004).

To implement estimation of ψ_K via (30), one may adopt parametric models for these functions. Although A-learning obviates the need to specify fully the Q-functions, one may posit models for the optimal θ_K, h_K(s̄_K, ā_K−1; β_K), say. Moreover, unless the data are from a SMART study, in which case the propensities π_K(s̄_K, ā_K−1) are known, these may be modeled as π_K(s̄_K, ā_K−1; ϕ_K) (e.g., by a logistic regression). These models are only adjuncts to estimating ψ_K; as long as at least one of these models is correctly specified, (30) will yield a consistent estimator for ψ_K, the so-called double robustness property. In contrast, Q-learning requires correct specification of all Q-functions; see Section 5.3 and Section A.5 of the supplemental article [Schulte et al. (2012).]

Substituting these models in (30), one solves (30) jointly in ${({\psi }_K^T,{\beta }_K^T,{\varphi }_K^T)}^T$ with

$$\sum _{i=1}^n\frac{\partial h_K({\overline{S}}_K,{\overline{A}}_{K-1};{\beta }_K)}{\partial {\beta }_K}\{{\tilde{V}}_{(K+1)i}-A_{Ki}{C}_K({\overline{S}}_{Ki},{\overline{A}}_{(K-1)i};{\psi }_K)-h_K({\overline{S}}_{Ki},{\overline{A}}_{(K-1)i};{\beta }_K)\}=0$$

and the usual binary regression likelihood score equations in ϕ_K. We then have $d_K^{\text{opt}}({\overline{s}}_K,{\overline{a}}_{K-1};{\psi }_K)=I\{C_K({\overline{s}}_k,{\overline{a}}_{K-1};{\psi }_K)>0\}$; as in Q-learning, substituting ψ̂_K yields an estimator for the optimal treatment choice at decision K for a patient with past history S̄_K = s_K, Ā_K−1 = ā_K−1.

With ψ̂_K in hand, the contrast-based A-learning algorithm proceeds in a backward iterative fashion to yield ψ̂_k, k = K − 1,…, 1. At the kth decision, given models h_k(s̄_k, ā_k−1;β_k) and π_k(s̄_k, ā_k−1; ϕ_k), one solves jointly in ${({\psi }_K^T,{\beta }_K^T,{\varphi }_K^T)}^T$ a system of estimating equations analogous to those above. The kth set of equations is based on “optimal responses” Ṽ_(k+1)i, where, for each i, Ṽ_ki estimates V_k(S̄_ki, Ā_(k−1),i). It may be shown (see Section A.3 of the supplemental article [Schulte et al. (2012)]) that E(V_k+1(S̄_k+1, Ā_k) + C_k(S̄_k, Ā_k−1)[I{C_k(S̄_k, Ā_k−1) > 0} − A_k]| S̄_k, Ā_k−1) = V_k(S̄_k, Ā_k−1). Accordingly, define recursively Ṽ_ki = Ṽ_(k+1)i+C_k(S̄_ki, Ā_(k−1)i; ψ̂_k)[I(C_k(S̄_ki, Ā_(k−1)i;ψ̂_k) > 0}− A_ki], k = K,K − 1,…1, Ṽ_(K+1)i = Y_i. The equations at the kth decision are then

$$\sum _{i=1}^n{\lambda }_k({\overline{S}}_{ki},{\overline{A}}_{(k-1)i};{\psi }_k)\{A_{ki}-{\pi }_k({\overline{S}}_{ki},{\overline{A}}_{(k-1)i};{\varphi }_k)\}\times \{{\tilde{V}}_{(k+1)i}-A_{ki}{C}_k({\overline{S}}_{ki},{\overline{A}}_{(k-1)i};{\psi }_k)-h_k({\overline{S}}_{ki},{\overline{A}}_{(k-1)i};{\beta }_k)\}=0,\sum _{i=1}^n\frac{\partial h_k({\overline{S}}_k,{\overline{A}}_{k-1};{\beta }_k)}{\partial {\beta }_k}\{{\tilde{V}}_{(k+1)i}-A_{ki}{C}_k({\overline{S}}_{ki},{\overline{A}}_{(k-1)i};{\psi }_k)-h_k({\overline{S}}_{ki},{\overline{A}}_{(k-1)i};{\beta }_k)\}=0,$$ (31)

for a given specification λ_k(s̄_k, ā_k−1; ψ_k), solved jointly with the maximum likelihood score equations for binary regression in ϕ_k. It follows that $d_k^{\text{opt}}({\overline{s}}_k,{\overline{a}}_{k-1};{\widehat{\psi }}_k)=I\{C_k({\overline{s}}_k,{\overline{a}}_{k-1};{\widehat{\psi }}_k)>0\}$. As above, the optimal λ_k is complex (Robins, 2004); taking λ_k(s̄_k, ā_k−1; ψ_k) = ∂/∂ψ_k C_k(s̄_k, ā_k−1; ψ_k) is reasonable for practical implementation.

Summarizing, the estimated optimal regime ${\widehat{d}}_A^{\text{opt}}=({\widehat{d}}_{A,1}^{\text{opt}},\dots ,{\widehat{d}}_{A,K}^{\text{opt}})$ is

$${\widehat{d}}_{A,1}^{\text{opt}}(s_1)=d_1^{\text{opt}}(s_1;{\widehat{\psi }}_1),{\widehat{d}}_{A,k}^{\text{opt}}({\overline{s}}_k,{\overline{a}}_{k-1})=d_k^{\text{opt}}({\overline{s}}_k,a_{k-1};{\widehat{\psi }}_k),k=2,\dots ,K,$$ (32)

How well ${\widehat{d}}_A^{\text{opt}}$ estimates d^opt and hence d^(1)opt depends on how close the posited C_k(s̄_k, ā_k−1;ψ_k) are to the true contrast functions as well as correct specification of the functions h_k or π_k.

Henceforth, for brevity, we suppress the descriptor “contrast-based” and refer to the foregoing approach simply as A-learning.

5.3 Comparison and Practical Considerations

When K = 1, the Q-function is a model for E(Y|S₁ = s₁, A₁ = a₁). If in Q-learning this model and the variance model Σ₁ in (26) are correctly specified, then, as above, the form of (26) is optimal for estimating ξ₁. Accordingly, even if C₁(s₁;ψ₁) and h₁(s₁;β₁) are correctly modeled, (31) with K = 1 is generally not of this optimal form for any choice λ₁(s₁;ψ₁), and hence A-learning will yield relatively inefficient inference on ψ₁ and the optimal regime. However, if in Q-learning the Q-function is mismodeled, but in A-learning C₁(s₁;ψ₁) and π₁(s₁;ϕ₁) are both correctly specified, then A-learning will still yield consistent inference on ψ₁ and hence the optimal regime, whereas inference on ξ₁ and the optimal regime via Q-learning may be inconsistent. We assess the trade-off between consistency and efficiency in this case in Section 6. For K > 1, owing to the complications involved in specifying optimal estimating equations for Q- and A-learning, relative performance is not readily apparent; we investigate empirically in Section 6.

In special cases, Q- and A-learning lead to identical estimators for the Q-function (Chakraborty et al., 2010). For example, this holds if the propensities for treatment are constant, as would be the case under pure randomization at each decision point, and certain linear models are used for C₁(s₁;ψ₁) and h₁(s₁;β₁); Section A.4 of the supplemental article [Schulte et al. (2012)] demonstrates when K = 1 and pr(A₁ = 1|S₁ = s₁) does not depend on s₁. See Robins (2004, page 1999) and Rosenblum and van der Laan (2009) for further discussion.

As we have emphasized, for Q-learning, while modeling the Q-function at decision K is a standard regression problem with response Y, for decisions k = K − 1,…, 1, this involves modeling the estimated value function, which at decision k depends on relationships for future decisions k + 1,…, K. Ideally, the sequence of posited models Q_k(s̄_k, ā_k; ξ_k) should respect this constraint. However, this may be difficult to achieve with standard regression models. To illustrate, consider (29), and assume S₁, S₂ are scalar, where the conditional distribution of S₂ given S₁ = s₁, A₁ = a₁ is Normal $({𝒦}_1^T\gamma ,{\mathrm{\sigma }}^2)$, say, 𝒦₁ = (1, s₁, a₁)^T. Recall that $V_2({\overline{s}}_2,a_1;{\xi }_2)={\mathscr{H}}_2^T{\beta }_2+({\mathscr{H}}_2^T{\psi }_2)I({\mathscr{H}}_2^T{\psi }_2>0)$, where ${\mathscr{H}}_2^T{\beta }_2={𝒦}_1^T{\beta }_{21}+s_2{\beta }_{22}\text{and}{\mathscr{H}}_2^T{\psi }_2={𝒦}_1^T{\psi }_{21}+s_2{\psi }_{22}$. Then, if the model Q₂ in (29) were correct, from (12), ideally, Q₁(s₁, a₁) = E{V₂(s₁, S₂, a₁; ξ₂)|S₁ = s₁, A₁ = a₁}. Letting φ(·) and Φ(·) be the standard normal density and cumulative distribution function, respectively, it may be shown (see Section A.5 of the supplemental article [Schulte et al. (2012)]) that

$$Q_1(s_1,a_1)=\mathrm{E}\{V_2(s_1,S_2,a_1;{\xi }_2)|S_1=s_1,A_1=a_1\}={𝒦}_1^T({\beta }_{21}+\gamma {\beta }_{22})+({𝒦}_1^T{\psi }_{21})\{1-\mathrm{\Phi }(\eta )\}+{\psi }_{22}\{\mathrm{\sigma }\phi (\eta )+({𝒦}_1^T\gamma )\{1-\mathrm{\Phi }(\eta )\}\},\eta =-{𝒦}_1^T({\psi }_{21}/{\psi }_{22}+\gamma )/\mathrm{\sigma },$$ (33)

taking ψ₂₂ > 0. The true Q₁(s₁, a₁) in (33) is clearly highly nonlinear and likely poorly approximated by the posited linear model Q₁(s₁, a₁; ξ₁) in (29). For larger K, this incompatibility between true and assumed models would propagate from K − 1,…, 1. Thus, while using linear models for the Q-functions is popular in practice, the potential for such mismodeling should be recognized.

An approach that may mitigate the risk of mismodeling is to employ flexible models for the Q-functions; Zhao, Kosorok and Zeng (2009) use support vector regression models. Developments in statistical learning suggest a large collection of powerful regression methods that might be used. Many of these methods must be tuned in order to balance bias and variance, a natural approach to which is to minimize the cross-validated mean squared error of the Q-functions at each decision point. An obvious downside is that the final model may be difficult to interpret, and clinicians may not be willing to use “black box” rules. One compromise is to fit a simple, interpretable model, such as a decision tree, to the fitted values of the complex model in order explore the factors driving the recommended treatment decisions. This simple model can then be checked against scientific theory. If it appears sensible, then clinicians may be willing to use predictions from the complex model. For discussion, see Craven and Shavlik (1996).

A-learning represents a middle ground between Q-learning and these approaches in that it allows for flexible modeling of the functions h_k(s̄_k, ā_k−1) while maintaining simple parametric models for the contrast functions C_k(s̄_k, ā_k−1). Thus, the resulting decision rule, which depends only on the contrast function, remains interpretable, while the model for the response is allowed to be nonlinear. This is also appealing in that it may be reasonable to expect, based on the underlying science, that the relationship between patient history and outcome is complex while the optimal rule for treatment assignment is dependent, in a simple fashion, on a small number of variables. The flexibility allowed by a semi-parametric model also has its drawbacks. Techniques for formal model building, critique, and diagnosis are well understood for linear models but much less so for semi-parametric models. Consequently, Q-learning based on building a series of linear models may be more appealing to an analyst interested in formal diagnostics.

A-learning may have certain advantages for making inference under the null hypothesis of no effect of any treatment regime in 𝒟 on outcome. For example, in a SMART, the propensities are specified by design, and under the null, the contrast functions are identically zero and hence correctly specified. Thus, A-learning will yield consistent estimators for the parameters defining the contrast function. See Robins (2004) and the references in Section 8.

6. SIMULATION STUDIES

We examine the finite sample performance of Q- and A-learning on a suite of simple test examples via Monte Carlo simulation. We emphasize that the methods are straightforward to implement in more complex settings than those here. To illustrate trade-offs between the methods, we begin with correctly specified models and systematically introduce misspecification of the Q-function, the propensity model, and both. We focus here on situations where the contrast function is correctly specified to gain insight into impact of other model components. Scenarios with a misspecified contrast model can be constructed to include or exclude the target d^opt, precluding generalizable conclusions. See Section A.9 of the supplemental article [Schulte et al. (2012)], Zhang et al. (2012a,b), and Zhang et al. (2013) for simulations involving misspecified contrast functions and Robins (2004, Section 9) for discussion.

In all scenarios, 10,000 Monte Carlo replications were used, and, for each generated data set, ${\widehat{d}}_Q^{\text{opt}}\text{and}{\widehat{d}}_A^{\text{opt}}$ in (28) and (32) were obtained using the Q- and A-learning procedures in Sections 5.1 and 5.2. For simplicity, we consider one (K = 1) and two (K = 2) decision problems, where, at each decision point, there are two treatment options coded as 0 and 1. In all cases, we used Q-functions of the form Q₁(s₁, a₁;ξ₁) = h₁(s₁; β₁) + a₁C₁(s₁; ψ₁) and Q₂(s̄₂, ā₂; ξ₂) = h₂(s̄₂; ā₁; β₂) + a₂,C₂(s̄₂, a₁; ψ₂) to represent both true and assumed working models. With the contrast functions correctly specified, ψ_k, k = 1,2, dictate the optimal regime. Thus, as one measure of performance, we focus on relative efficiency of the estimators of components of ψ_k as reflected by the ratio of Monte Carlo mean squared errors (MSEs) given by MSE of A-learning/MSE of Q-learning, so that values greater than 1 favor Q-learning. Recognizing that E(Y*(d^opt)} is the benchmark achievable outcome on average, as a second measure, we consider the extent to which the estimated regimes ${\widehat{d}}_Q^{\text{opt}}\text{and}{\widehat{d}}_A^{\text{opt}}$ achieve E(Y*(d^opt)} if followed by the population. Specifically, for regime d indexed by ψ₁ (K = 1) or ${({\psi }_1^T,{\psi }_2^T)}^T(K=2)$, let H(d) = E{Y*(d)}, a function of these parameters. Then H(d^opt) = E{Y*(d^opt)} is this function evaluated at the true parameter values, and H(d̂^opt) is this function evaluated the estimated parameter values for a given data set, where d̂^opt is ${\widehat{d}}_Q^{\text{opt}}\text{or}{\widehat{d}}_A^{\text{opt}}$. Define R(d̂^opt) = E{H(d̂^opt)}/H(d^opt), where the expectation in the numerator is with respect to the distribution of the estimated parameters in d̂^opt. We refer to R(d̂^opt) as the v-efficiency of d̂^opt, as it reflects the extent to which d̂^opt achieves the “value” of the true optimal regime. In Section A.6 of the supplemental article [Schulte et al. (2012); we discuss calculation of R(d̂^opt).

6.1 One Decision Point

In this and the next section, n = 200. Here, the observed data are (S_1i,A_1i,Y_i), i = 1,…, n. With expit(x) = e^x/(1 + e^x), we used the class of generative models

$$S_1~\text{Normal}(0,1),A_1|S_1=s_1~\text{Bernoulli}\{\text{expit(}{\varphi }_{10}^0+{\varphi }_{11}^0{s}_1+{\varphi }_{12}^0{s}_1^2)\},Y|S_1=s_1,A_1=a_1~\text{Normal}\{{\beta }_{10}^0+{\beta }_{11}^0{s}_1+{\beta }_{12}^0{s}_1^2+a_1({\psi }_{10}^0+{\psi }_{11}^0{s}_1),9\},$$ (34)

indexed by ${\varphi }^0={({\varphi }_{10}^0,{\varphi }_{11}^0,{\varphi }_{12}^0)}^T,{\beta }^0={({\beta }_{10}^0,{\beta }_{11}^0,{\beta }_{12}^0)}^T,{\psi }^0={({\psi }_{10}^0,{\psi }_{11}^0)}^T$, so that $d^{\text{opt}}=d_1^{\text{opt}},d_1^{\text{opt}}(s_1)=I({\psi }_{10}^0+{\psi }_{11}^0{s}_1>0)$. For A-learning, we assumed models h₁(s₁; β₁) = β₁₀ + β₁₁s₁, C₁(s₁;ψ₁) = ψ₁₀ + ψ₁₁s₁, and π₁(s₁;ϕ₁) = expit(ϕ₁₀ + ϕ₁₁s₁), and for Q-learning we used Q₁(s₁, a₁;ξ₁) = h₁(s₁;β₁) + a₁C₁(s₁;ψ₁). These models involve correctly specified contrast functions and are nested within the true models, with h₁(s₁; β₁), and hence the Q-function, correctly specified when ${\beta }_{12}^0=0$. The propensity model π₁(s₁; ϕ₁) is correctly specified when ${\varphi }_{12}^0=0$. To study the effects of misspecification, we varied ${\beta }_{12}^0\text{and}{\varphi }_{12}^0$ while keeping the others fixed, considering parameter settings of the form ${\varphi }^0={(0,-2,{\varphi }_{12}^0)}^T,{\beta }^0={(1,1,{\beta }_{12}^0)}^T,{\psi }^0={(1,0.5)}^T$.

Correctly specified models

As noted in Section 5.3, when all working models are correctly specified, Q-learning is more efficient than A-learning, which for (34) occurs when ${\beta }_{12}^0\text{=}{\varphi }_{12}^0=0$. Here, the efficiency of Q-learning relative to A-learning is 1.06 for estimating ${\psi }_{10}^0$ and 2.74 for ${\psi }_{11}^0$. Thus, Q-learning is a modest 6% more efficient in estimating ${\psi }_{10}^0$ but a dramatic 174% more efficient in estimating ${\psi }_{11}^0$. Interestingly, the v-efficiency of the decision rules produced by the methods is similar, with $R({\widehat{d}}_Q^{\text{opt}})=0.97\text{and}R({\widehat{d}}_A^{\text{opt}})=0.95$, so that inefficiency in estimation of ψ₁ via A-learning does not translate into a regime of poorer quality than that found by Q-learning.

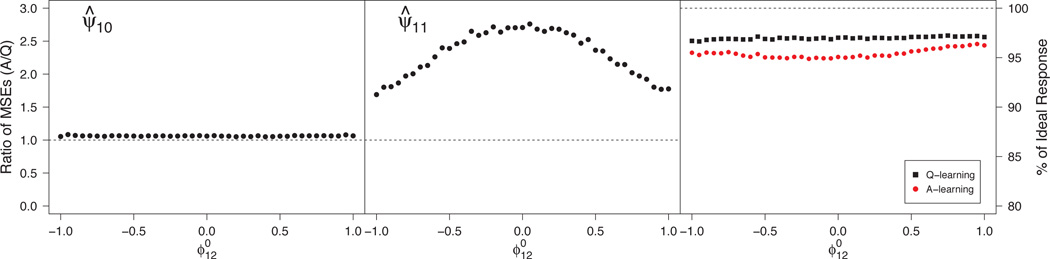
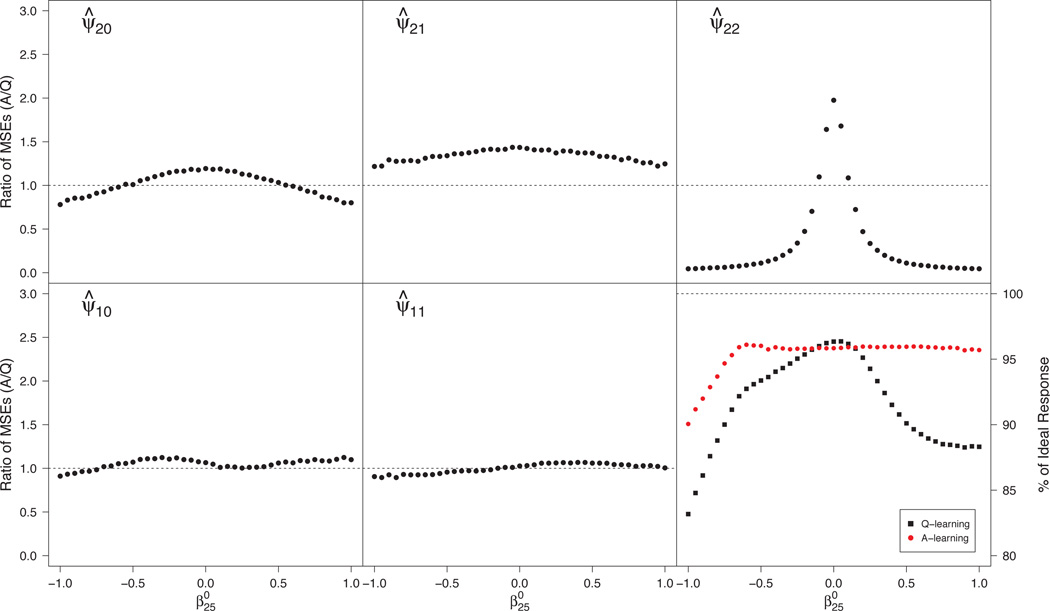
Misspecified propensity model

Under (34), this situation corresponds to ${\beta }_{12}^0=0$ and nonzero ${\varphi }_{12}^0$. An appeal of A-learning is the double robustness property noted in Section 5.2, which implies that ψ₁ is estimated consistently when the propensity model is misspecified provided that the Q-function is correct. In contrast, Q-learning does not depend on the propensity model, so its performance is unaffected. Figure 1 shows the relative efficiency in estimating ${\psi }_{10}^0\text{and}{\psi }_{11}^0$ and the efficiency of ${\widehat{d}}_Q^{\text{opt}}\text{and}{\widehat{d}}_A^{\text{opt}}\text{as}{\varphi }_{12}^0$ varies from −1 to 1. The leftmost panel shows that there is minimal efficiency gain by using Q-learning instead of A-learning in estimation of ${\psi }_{10}^0$. From the center panel, Q-learning yields substantial gains over A-learning for estimating ${\psi }_{11}^0$. Interestingly, the gain is largest when ${\varphi }_{12}^0=0$, which corresponds to a correctly specified propensity model. Letting ${\pi }^0(s_1;{\varphi }_1^0)$ be the true propensity, ${\varphi }_1^0={({\varphi }_{10}^0,{\varphi }_{11}^0,{\varphi }_{12}^0)}^T$, a possible explanation for this seemingly contradictory result in this scenario is that, as $\left|{\varphi }_{12}^0\right|$ gets larger, $\text{logit}\{{\pi }^0(S_1;{\varphi }_1^0\}={\varphi }_{10}^0+{\varphi }_{11}^0{s}_1+{\varphi }_{12}^0{s}_1^2$ becomes more profoundly quadratic. Consequently, the estimator for ϕ₁₁ in the posited model π₁(s₁; ϕ₁) = expit(ϕ₁₀ + ϕ₁₁s₁) approaches zero, so that the estimated posited propensity approaches a constant. Because Q- and A-learning are algebraically equivalent under constant propensity here, substituting an estimated propensity that is nearly constant leads to an estimator very similar to that from Q-learning. Consequently, empirical efficiency gains decrease as $\left|{\varphi }_{12}^0\right|\to \infty$. The right panel of Figure 1 shows a small gain in v-efficiency of ${\widehat{d}}_Q^{\text{opt}}\text{over}{\widehat{d}}_A^{\text{opt}}$; both achieve good performance.

Fig 1.

Monte Carlo MSE ratios for estimators of components of ψ₁ (left and center panels) and efficiencies $R({\widehat{d}}_Q^{\text{opt}})\text{and}R({\widehat{d}}_A^{\text{opt}})$ for estimating the true d^opt (right panel) under misspecification of the propensity model. MSE ratios > 1 favor Q-learning

See Section A.9 of the supplemental article [Schulte et al. (2012)] for evidence demonstrating this behavior of the propensity score and for further summaries reflecting the relative efficiency of the estimated regimes in all scenarios in this and the next section.

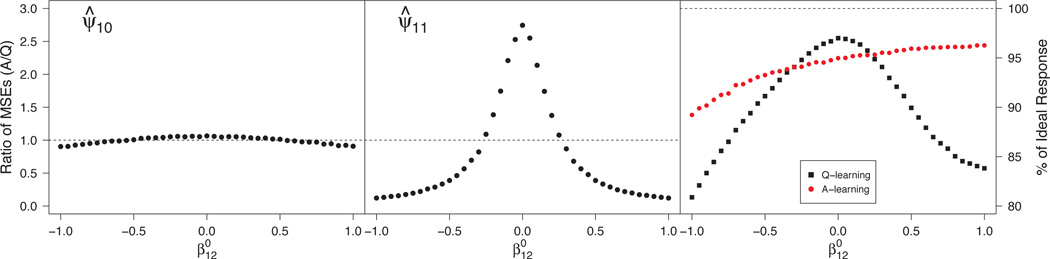
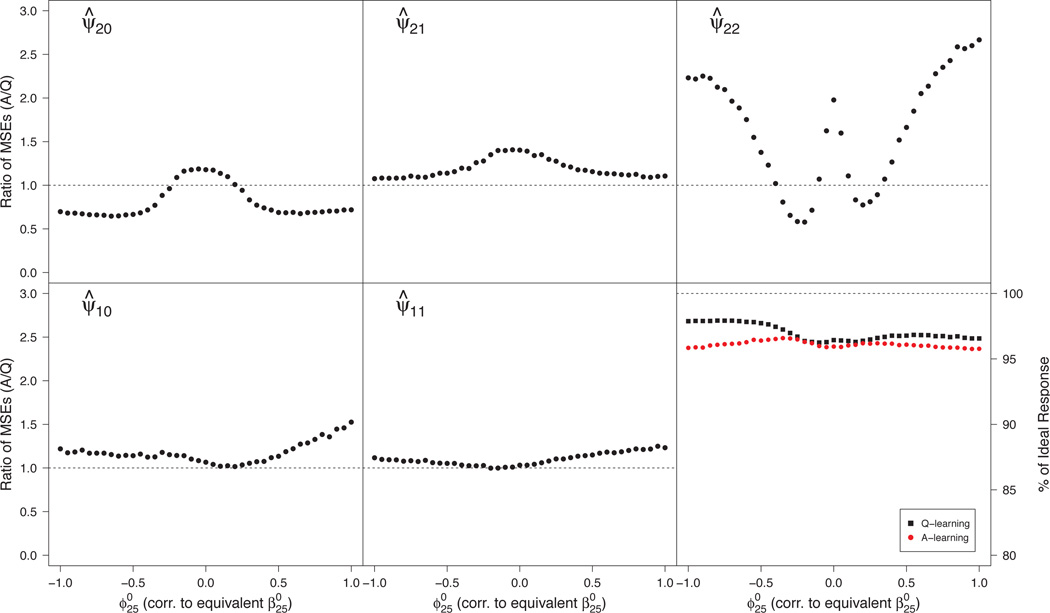
Misspecified Q-function

This scenario examines the second aspect of A-learning’s double-robustness, characterized in (34) by ${\varphi }_{12}^0=0$ and nonzero ${\beta }_{12}^0$. Here, A-learning leads to consistent estimation while Q-learning need not. The left panel of Figure 2 shows that the gain in efficiency using A-learning is minimal in estimating ${\psi }_{10}^0$. The center panel illustrates the bias-variance trade-off associated with Q- versus A-learning. For ${\beta }_{12}^0$ far from zero, bias in the misspecified Q-function dominates the variance, and A-learning enjoys smaller MSE while, for small values of ${\beta }_{12}^0$, variance dominates bias, and Q-learning is more efficient. The right panel shows that large bias in the Q-function can lead to meaningful loss (~10%) in v-efficiency of ${\widehat{d}}_Q^{\text{opt}}$ relative to ${\widehat{d}}_A^{\text{opt}}$.

Fig 2.

Monte Carlo MSE ratios for estimators of components of ψ₁ (left and center panels) and efficiencies $R({\widehat{d}}_Q^{\text{opt}})\text{and}R({\widehat{d}}_A^{\text{opt}})$ for estimating the true d^opt (right panel) under misspecification of the Q-function. MSE ratios > 1 favor Q-learning

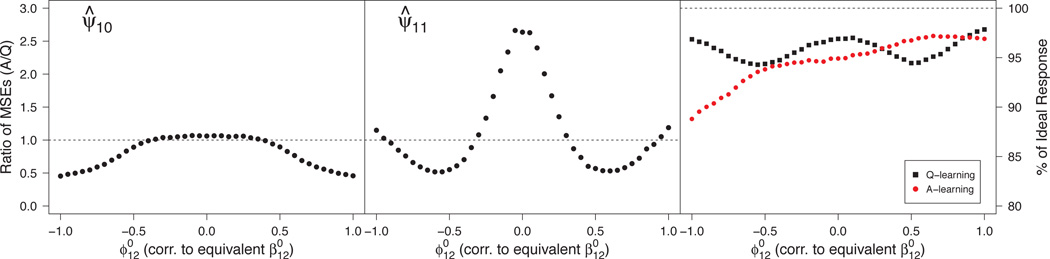
Both propensity model and Q-function misspecified

In our class of generative models (34), this corresponds to nonzero values of both ${\beta }_{12}^0\text{and}{\varphi }_{12}^0$. Rather than vary both values, (e.g., over a grid), we varied one and chose the other so that it is “equivalently misspecified.” In particular, for a given value of ${\varphi }_{12}^0$, we selected ${\beta }_{12}^0={\beta }_{12}^0({\varphi }_{12}^0)$ so that the t-statistic associated with testing ${\varphi }_{12}^0=0$ in the logistic propensity model and the t-statistic associated with testing ${\beta }_{12}^0=0$ in the linear Q-function would be approximately equal in distribution. Consequently, across data sets, an analyst would be equally likely to detect either form of misspecification. Details of this construction are given in Section A.7 of the supplemental article [Schulte et al. (2012)].

As in the preceding scenario, Figure 3 illustrates the bias-variance trade-off associated with Q- and A-learning. For large misspecification, A-learning provides a large enough reduction in bias to yield lower MSE; for small misspecification, Q-learning incurs some bias but reduces the variance enough to yield lower MSE. From the right panel of the figure, bias seems to translate into a larger loss in v-efficiency of the estimators of d^opt than variance.

Fig 3.

Monte Carlo MSE ratios for estimators of components of ψ₁ (left and center panels) and efficiencies $R({\widehat{d}}_Q^{\text{opt}})\text{and}R({\widehat{d}}_A^{\text{opt}})$ for estimating the true d^opt (right panel) under misspecification of both the propensity model and the Q-function. MSE ratios > 1 favor Q-learning

6.2 Two Decision Points

For K = 2, the observed data available to estimate $d^{\text{opt}}=(d_1^{\text{opt}},d_2^{\text{opt}})$ are (S_1i, A_1i, S_2i, A_2i, Y_i), i = 1,…, n. For these scenarios, we used a class of true generative data models that differs from those of Chakraborty et al. (2010), Song et al. (2010), and Laber et al. (2010) only in that S₂ is continuous instead of binary; as the model at the first stage is saturated, this allows correct specification of the Q-function at decision 1. The generative model is

$$S_1~\text{Bernoulli}(0.5),A_1|S_1=s_1~\text{Bernoulli}\{\text{expit(}{\varphi }_{10}^0+{\varphi }_{11}^0{s}_1)\},S_2|S_1=s_1,A_1=a_1~\text{Normal}({\delta }_{10}^0+{\delta }_{11}^0{s}_1+{\delta }_{12}^0{a}_1+{\delta }_{13}^0{s}_1{a}_1,2),A_2|S_1=s_1,S_2=s_2,A_1=a_1~\text{Bernoulli}\{\text{expit(}{\varphi }_{20}^0+{\varphi }_{21}^0{s}_1+{\varphi }_{22}^0{a}_1+{\varphi }_{23}^0{s}_2+{\varphi }_{24}^0{a}_1{s}_2+{\varphi }_{25}^0{s}_2^2)\},Y|S_1=s_1,S_2=s_2,A_1=a_1,A_2=a_2~\text{Normal}\{m(s_1,s_2,a_1,a_2),10\},m(s_1,s_2,a_1,a_2)={\beta }_{20}^0+{\beta }_{21}^0{s}_1+{\beta }_{22}^0{a}_1+{\beta }_{23}^0{s}_1{a}_1+{\beta }_{24}^0{s}_2+{\beta }_{25}^0{s}_2^2+a_2({\psi }_{20}^0+{\psi }_{21}^0{a}_1+{\psi }_{22}^0{s}_2).$$

The model is indexed by ${\varphi }_1^0={({\varphi }_{10}^0,{\varphi }_{11}^0)}^T,{\delta }_1^0={({\delta }_{10}^0,{\delta }_{11}^0,{\delta }_{12}^0,{\delta }_{13}^0)}^T,{\varphi }_2^0={({\varphi }_{20}^0,{\varphi }_{21}^0,{\varphi }_{22}^0,{\varphi }_{23}^0,{\varphi }_{24}^0,{\varphi }_{25}^0)}^T,{\beta }_2^0={({\beta }_{20}^0,{\beta }_{21}^0,{\beta }_{22}^0,{\beta }_{23}^0,{\beta }_{24}^0,{\beta }_{25}^0)}^T,\text{and}{\psi }_2^0={({\psi }_{20}^0,{\psi }_{21}^0,{\psi }_{22}^0)}^T$, with true $h_2^0(s_1,s_2,a_1)={\beta }_{20}^0+{\beta }_{21}^0{s}_1+{\beta }_{22}^0{a}_1+{\beta }_{23}^0{s}_1{a}_1+{\beta }_{24}^0{s}_2+{\beta }_{25}^0{s}_2^2$ and contrast function $C_2^0(s_1,s_2,a_1)={\psi }_{20}^0+{\psi }_{21}^0{a}_1+{\psi }_{22}^0{s}_2$, say. Because A₁ and S₁ are binary, the true functions $h_1^0(s_1)={\beta }_{10}^0+{\beta }_{11}^0{s}_1\text{and}{C}_1^0(s_1)={\psi }_{10}^0+{\psi }_{11}^0{s}_1$ are linear in $s_1;{\beta }_{10}^0,{\beta }_{11}^0,{\psi }_{10}^0,\text{and}{\psi }_{10}^0$ are derived in terms of parameters indexing the generative model in Section A.8 of the supplemental article [Schulte et al. (2012)]. Thus, the true optimal regime has $d_1^{\text{opt}}(s_1)=I({\psi }_{10}^0+{\psi }_{11}^0{s}_1>0)\text{and}{d}_2^{\text{opt}}(s_1,s_2,a_1)=I({\psi }_{20}^0+{\psi }_{21}^0{a}_1+{\psi }_{22}^0{s}_2>0)$.

We assumed working models for A-learning of the form h₁(s₁;β₁) = β₁₀ + β₁₁s₁, C₁(s₁;ψ₁) = ψ₁₀ + ψ₁₁s₁, π₁(s₁; ϕ₁) = expit(ϕ₁₀ + ϕ₁₁s₁), h₂(s₁, s₂, a₁; β₂) = β₂₀ + β₂₁s₁ + β₂₂a₁ + β₂₃s₁a₁ + β₂₄s₂, C₂(s₁,s₂, a₁;ψ₂) = ψ₂₀ + ψ₂₁a₁ + ψ₂₂s₂, and π₂(s₁,s₂, a₁;ϕ₂) = expit(ϕ₂₀ + ϕ₂₁s₁ + ϕ₂₂a₁ + ϕ₂₃s₂ + ϕ₂₄a₁s₂); and, similarly, Q-functions Q₁(s₁, a₁; ξ₁) = h₁(s₁;β₁) +a₁C₁(s₁;ψ₁) and Q₂(s₁,s₂, a₁, a₂;ξ₂) = h₂(s₁,s₂, a₁;β₂) + a₂C₂(s₁,s₂, a₁;ψ₂) for Q-learning, so that the contrast functions are correctly specified in each case. Comparison of the working and generative models shows that the former are correctly specified when ${\varphi }_{25}^0\text{and}{\beta }_{25}^0$ are both zero and are misspecified otherwise. Thus, we systematically varied these parameters to study the effects of misspecification, leaving all other parameter values fixed, taking ${\varphi }_1^0={(0.3,-0.5)}^T,{\delta }_1^0={(0,0.5,-0.75,0.25)}^T,{\varphi }_2^0={(0,0.5,0.1,-1,-0.1,{\varphi }_{25}^0)}^T,{\beta }_2^0={(3,0,0.1,-0.5,-0.5,{\beta }_{25}^0)}^T,\text{and}{\psi }_2^0={(1,0.25,0.5)}^T$.

Correctly specified models

This occurs when ${\varphi }_{25}^0={\beta }_{25}^0=0$. As discussed previously, Q-learning is efficient when the models are correctly specified. Efficiencies of Q- learning relative to A-learning for estimating ${\psi }_{10}^0,{\psi }_{11}^0,{\psi }_{20}^0,{\psi }_{21}^0,\text{and}{\psi }_{22}^0$ are 1.07, 1.03, 1.19, 1.44, and 1.98, respectively. Hence, Q-learning is markedly more efficient in estimating the second stage parameters but only modestly so for first stage parameters. More efficient estimators of the parameters do not translate into greater v-efficiency of the estimated regimes in this scenario, as $R({\widehat{d}}_Q^{\text{opt}})=0.96\text{and}R({\widehat{d}}_A^{\text{opt}})=0.96$.

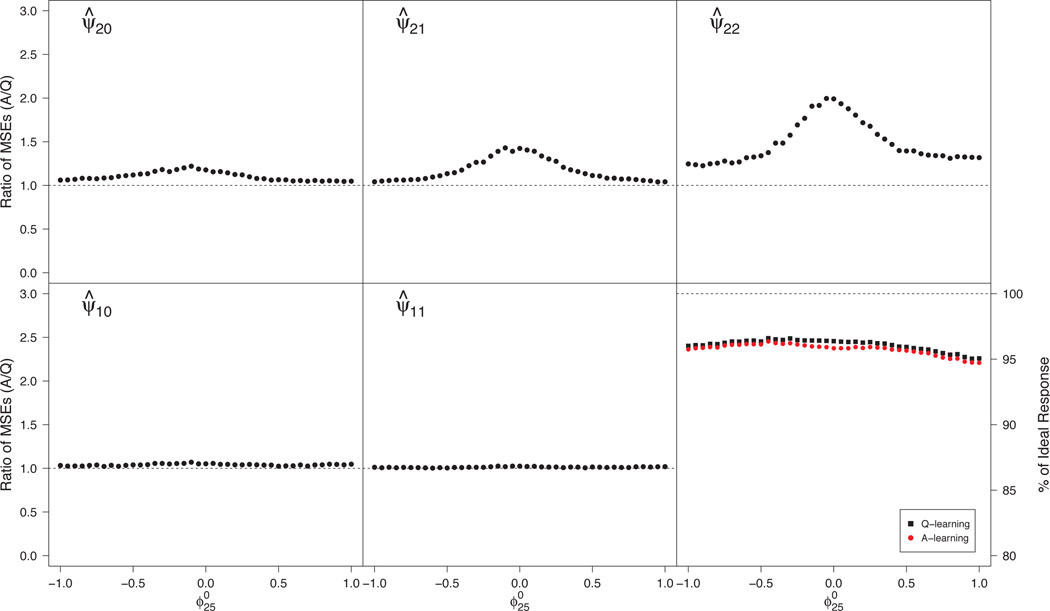
Misspecified propensity model

The propensity model at the second stage is misspecified when ${\varphi }_{25}^0$ is nonzero. To isolate the effects of such misspecification, we set ${\beta }_{25}^0=0$ and varied ${\varphi }_{25}^0$ between −1 and 1. From Figure 4, Q-learning is more efficient than A-learning for estimation of all parameters in ψ₁ and ψ₂, and, as in the one decision case, the efficiency gain is largest when ${\varphi }_{25}^0=0$, corresponding to a correctly specified propensity model. From the lower right panel, there appears to be little difference in v-efficiency of ${\widehat{d}}_Q^{\text{opt}}\text{and}{\widehat{d}}_A^{\text{opt}}$.

Fig 4.

Monte Carlo MSE ratios for estimators of components of ψ₂ and ψ₁ (upper row and lower row left and center panels) and efficiencies $R({\widehat{d}}_Q^{\text{opt}})\text{and}R({\widehat{d}}_A^{\text{opt}})$ for estimating the true d^opt (lower right panel) under misspecification of the propensity model. MSE ratios > 1 favor Q-learning

Misspecified Q-function

Under our class of generative models, the Q-function is misspecified when ${\beta }_{25}^0$ is nonzero. We set ${\varphi }_{25}^0=0$ to focus on the effects of such misspecification. Figure 5 shows that, for the first stage parameters ${\psi }_{10}^0\text{and}{\psi }_{11}^0$, there is little difference in efficiency between Q- and A-learning. The upper panels illustrate varying degrees of the bias-variance trade-off between the methods. In particular, in estimating ${\psi }_{22}^0$, a small amount of misspecification leads to significant bias, and hence A-learning produces a much more accurate estimator, while, for ${\psi }_{20}^0$ the bias-variance trade-off is present but attenuated, and there is little difference between Q- and A-learning. In estimation of ${\psi }_{21}^0$, variance appears to dominate bias, and Q-learning is preferred for the chosen range of ${\beta }_{25}^0$ values. From the lower right panel, relative efficiency for estimating ${\psi }_{22}^0$ weakly tracks the relative efficiencies of the estimated regimes ${\widehat{d}}_Q^{\text{opt}}\text{and}{\widehat{d}}_A^{\text{opt}}$, suggesting that the efficiency gain for A-learning in estimating ${\psi }_{22}^0$ leads to improved estimation of d^opt.

Fig 5.

Monte Carlo MSE ratios for estimators of components ofψ₂ and ψ₁ (upper row and lower row left and center panels) and efficiencies $R({\widehat{d}}_Q^{\text{opt}})\text{and}R({\widehat{d}}_A^{\text{opt}})$ for estimating the true d^opt (lower right panel) under misspecification of the Q-functions. MSE ratios > 1 favor Q-learning

Both the propensity model and Q-function misspecified

This scenario corresponds to nonzero values of ${\beta }_{25}^0\text{and}{\varphi }_{25}^0$. Analogous to the one decision case, we chose pairs $({\beta }_{25}^0,{\varphi }_{25}^0)$ that are “equivalently misspecified;” see Section A.7 of the supplemental article [Schulte et al. (2012)]. From Figure 6, there is no general trend in efficiency of estimation across parameters that might recommend one method over the other. Furthermore, from the lower right panel, there is little difference in v-efficiency of the estimated regimes. One should not expect to draw broad conclusions, as neither Q- nor A-learning need be consistent here. Interestingly, despite misspecification of both models, ${\widehat{d}}_Q^{\text{opt}}\text{and}{\widehat{d}}_A^{\text{opt}}$ still enjoy high v-efficiency in this scenario.

Fig 6.

Monte Carlo MSE ratios for estimators of components of ψ₂ and ψ₁ (upper row and lower row left and center panels) and efficiencies $R({\widehat{d}}_Q^{\text{opt}})\text{and}R({\widehat{d}}_A^{\text{opt}})$ for estimating the true d^opt (lower right panel) under misspecification of both the propensity models and Q-functions. MSE ratios > 1 favor Q-learning

6.3 Moodie, Richardson, and Stephens Scenario

The foregoing simulation scenarios deliberately involve simple models for the Q-functions in order to allow straightforward interpretation. To investigate the relative performance of the methods in a more challenging setting, we generated data from a scenario similar to that in Moodie et al. (2007) in which the true contrast functions are simple yet the Q-functions are complex.

The data generating process used mimics a study in which HIV-infected patients are randomized to receive antiretroviral therapy (coded as 1) or not (coded as 0) at baseline and again at six months, where the randomization probabilities depend on baseline and six month CD4 counts. Specifically, we generated baseline CD4 count S₁ ~ Normal(450, 150²), and baseline treatment A₁ was then assigned according to $A_1|S_1=s_1~\text{Bernoulli}\{\text{expit(}{\varphi }_{10}^0+{\varphi }_{11}^0{s}_1)\}$. We generated six month CD4 count S₂, distributed conditional on S₁ = s₁, A₁ = a₁ as Normal(1.25s₁,60²). Treatment A₂ was then generated according to $A_2|S_1=s_1,A_1=a_1,S_2=s_2~\text{Bernoulli}\{\text{expit(}{\varphi }_{20}^0+{\varphi }_{21}^0{s}_2)\}$. In contrast to the scenario in Moodie et al. (2007), this allows all possible treatment combinations. The outcome Y is CD4 count at one year; following Moodie et al. (2007), Y was generated as $Y=Y^{\text{opt}}-{\mu }_1^0(S_1,A_1)-{\mu }_2^0(S_1,S_2,A_1,A_2)$, where Y^opt|S₁ = s₁, A₁ = a₁, S₂ = s₂, A₂ = a₂ ~ Normal(400 + 1.6s₁, 60²). Here, ${\mu }_1^0(S_1,A_1)\text{and}{\mu }_2^0(S_1,S_2,A_1,A_2)$ are the true advantage (regret) functions; we took $C_1^0(s_1)={\psi }_{10}^0+{\psi }_{11}^0{s}_1\text{and}{C}_2^0(s_1,s_2,a_1)={\psi }_{20}^0+{\psi }_{21}^0{s}_2$ to be the true contrast functions, so that, from Section 5.2,

$${\mu }_1^0(S_1,A_1)=({\psi }_{10}^0+{\psi }_{11}^0{S}_1)\{I({\psi }_{10}^0+{\psi }_{11}^0{S}_1>0)-A_1\},$$ (35)

$${\mu }_2^0(S_1,S_2,A_1,A_2)=({\psi }_{20}^0+{\psi }_{21}^0{S}_2)\{I({\psi }_{20}^0+{\psi }_{21}^0{S}_2>0)-A_2\}.$$ (36)

It follows that the optimal treatment regime $d^{\text{opt}}=(d_1^{\text{opt}},d_2^{\text{opt}})$ has $d_1^{\text{opt}}(s_1)=I({\psi }_{10}^0+{\psi }_{11}^0{s}_1>0)$ and $d_2^{\text{opt}}({\overline{s}}_2,a_1)=I({\psi }_{20}^0+{\psi }_{21}^0{s}_1>0)$. While the true contrast functions are linear in ${\psi }_k^0,k=1,2$, the true implied $h_1^0(s_1)\text{and}{h}_2^0(s_1,a_1,s_2)$ are nonsmooth and possibly complex.

Following Moodie et al. (2007), for A-learning, we assumed working models h₁(s₁;β₁) = β₁₀ + β_11s1, C₁(s₁;ψ₁) = ψ₁₀ + ψ₁₁s₁, h₂(s₁, s₂, a₁; β₂) = β₂₀ + β₂₁s₁ + β₂₂a₁ + β₂₃s₁a₁ + β₂₄s₂, and C₂(s₁, s₂, a₁; ψ₂) = ψ₂₀ + ψ₂₁s₂, and propensity models π₁(s₁;ϕ₁) = expit(ϕ₁₀ + ϕ₁₁s₁) and π₂(s₁, s₂, a₁; ϕ₂) = expit(ϕ₂₀ + ϕ₂₁s₂). For Q-learning, we analogously assumed Q-functions Q₁(s₁, a₁; ξ₁) = h₁(s₁; β₁) + a₁C₁(s₁; ψ₁) and Q₂(s₁, s₂, a₁, a₂; ξ₂) = h₂(s₁, s₁, a₁; β₂) + a₂C₂(s₁, s₂, a₁;ψ₂). Note that the contrast functions in each case are correctly specified, as are the propensity models; however, the Q-functions are misspecified, as the linear models h₁(s₁; β₁) and h₂(s₁, s₁, a₁; β₂) are poor approximations to the complex forms of the true $h_1^0(s_1)\text{and}{h}_2^0(s_1,s_2,a_1)$.

We report results for n = 1000 with ${\varphi }_1^0={({\varphi }_{10}^0,{\varphi }_{11}^0)}^T={(2.0,-0.006)}^T,{\varphi }_2^0={({\varphi }_{20}^0,{\varphi }_{21}^0)}^T={(0.8,-0.004)}^T,{\psi }_1^0={({\psi }_{10}^0,{\psi }_{11}^0)}^T={(250,-1.0)}^T,\text{and}{\psi }_2^0={({\psi }_{20}^0,{\psi }_{21}^0)}^T={(720,-2.0)}^T$ in Table 1. Because the Q-functions are misspecified, the Q-learning estimators for ${\psi }_1^0\text{and}{\psi }_2^0$ are biased, while those obtained via A-learning are consistent owing to the double robustness property. This leads to the dramatic relative inefficiency of Q-learning reflected by the MSE ratios. Under the assumed models, the estimated optimal regime for Q-learning dictates that, at baseline, therapy be given to patients with baseline CD4 count less than 199.7, while that estimated using A-learning gives treatment to those with baseline CD4 count less than 249.1, almost perfectly achieving the true optimal CD4 threshold of 250. Under the data generative process, using the baseline decision rule estimated via Q-learning may result in as many as 4.4% of patients who would receive therapy at baseline under the true optimal regime being assigned no treatment. Similarly, at the second decision, the estimated optimal regimes obtained by Q- and A-learning dictate that therapy be given to patients with six month CD4 count less than 320.2 and 360.1, respectively. Again, A-learning yields an estimated threshold almost identical to the optimal value of 360. Although that obtained via Q-learning is lower, 4.3% of patients who should receive therapy at six months would not if the estimated six month rule from Q-learning were followed by the population.

Table 1.

Monte Carlo average (standard deviation) of estimates obtained via Q- and A-learning and ratio of Monte Carlo MSE for the Moodie and Richardson scenario; MSE ratios > 1 favor Q-learning

Parameter (true value)	Q-learning	A-learning	MSE ratio
${\psi }_{10}^0=250$	154.8 (23.2)	249.1 (18.7)	0.036
${\psi }_{11}^0=-1.0$	−0.775 (0.052)	−0.998 (0.041)	0.032
${\psi }_{20}^0=720$	507.3 (49.2)	720.3 (48.4)	0.050
${\psi }_{21}^0=-2.0$	−1.584 (0.092)	−2.001 (0.085)	0.040

By Section A.6 of the supplemental article [Schulte et al. (2012)], H(d^opt) = 1120, whereas $\mathrm{E}\{H({\widehat{d}}_Q^{\text{opt}})\}\approx 1117.1$ (estimated standard error 1.3) and $\mathrm{E}\{H({\widehat{d}}_A^{\text{opt}})\}\approx 1119.9(0.3)$, so that $R({\widehat{d}}_Q^{\text{opt}})\text{and}R({\widehat{d}}_A^{\text{opt}})$ are virtually equal to one. Thus, although Q-learning yields poor estimation of parameters in the contrast functions, loss in v-efficiency of the estimated optimal regime is negligible. A possible explanation is as follows. For (35) and (36), some patients near the true treatment decision boundary would have $C_k^0({\overline{S}}_k,{\overline{A}}_{k-1}),k=1,2$, close to zero. Thus, even if a regime improperly assigns treatment to these patients, they would experience only a small loss in outcome and hence have little effect on the overall average. For other patients for whom the true contrast is not close to zero, improper assignment could result in considerable degradation of outcome. Because the proportion of patients receiving improper assignment is small in this scenario, the effect of these latter patients on the overall expected outcome is not substantial, leading to the relatively good expected outcome under the estimated Q-learning regime.

7. APPLICATION TO STAR*D

Sequenced Treatment Alternatives to Relieve Depression (STAR*D) was a randomized clinical trial enrolling 4041 patients designed to compare treatment options for patients with major depressive disorder. The trial involved four levels, where each level consisted of a 12 week period of treatment, with scheduled clinic visits at weeks 0, 2, 4, 6, 9, 12. Severity of depression at any visit was assessed using clinician-rated and self-reported versions of the Quick Inventory of Depressive Symptomatology (QIDS) score (Rush et al., 2003), for which higher values correspond to higher severity. At the end of each level, patients deemed to have an adequate clinical response to that level’s treatment did not move on to future levels, where adequate response was defined by 12-week clinician-rated QIDS score ≤ 5 (remission) or showing a 50% or greater decrease from the baseline score at the beginning of level 1 (successful reduction). During level 1, all patients were treated with citalopram. Patients continuing to level 2 due to inadequate response, conferring with their physicians, expressed preference to (i) switch or (ii) augment citalopram and within that preference were randomized to one of several options: (i) switch: sertraline, bupropion, venlafaxine, or cognitive therapy, or (ii) augment: citalopram plus one of either bupropion, buspirone, or cognitive therapy. Patients randomized to cognitive therapy (alone or augmented with citalopram) were eligible, in the case of inadequate response, to move to a supplementary level 2A and be randomized to switch to bupropion or venlafaxine. All patients without adequate response at level 2 (or 2A) continued to level 3 and, depending on preference to (i) switch or (ii) augment, were randomized within that preference to (i) switch: mirtazepine or nortriptyline or (ii) augment with either: lithium or triiodothyronine. Patients without adequate response continued to level 4, requiring a switch to tranylcypromine or mirtazepine combined with venlafaxine (determined by preference). Thus, although the study involved randomization, it is observational with respect to the treatment options switch or augment. For a complete description see Rush et al. (2004); see Section A.10 of the supplemental article [Schulte et al. (2012)] for a schematic of the design.

To demonstrate formulation of this problem within the framework of Sections 2 and 3, we take level 2A to be part of level 2 and consider only levels 2 and 3, calling them stages (decision points) 1 and 2, respectively (K = 2). Some patients in stage 1 without adequate response dropped out of the study without continuing to stage 2. Hence, we analyze complete case data, excluding dropouts, from 795 patients entering stage 1; 330 of these subsequently continued to stage 2. Let A_k, k = 1, 2, be the treatment at stage k, taking values 0 (augment) or 1 (switch); both options are feasible for all eligible subjects. Let S₁₀ denote baseline (study entry) QIDS score and S₁₁ denote the most recent QIDS score at the beginning of stage 1, respectively, so that S₁ = (S₁₀, S₁₁)^T is information available immediately prior to the first decision. Similarly, let S₂ be the information available immediately prior to stage 2; here, S₂ is the most recent QIDS score at the end of stage 1/beginning of stage 2. Finally, let T be QIDS score at the end of stage 2. Because some patients exhibited adequate response at the end of stage 1 and did not progress to stage 2, we define the outcome of interest to be −S₂ (negative QIDS score at the end of stage 1) for patients not moving to stage 2 and −(S₂ + T)/2 (average of negative QIDS scores at the end of stages 1 and 2) otherwise. Thus, writing L₀ = max(5, S₁₀/2), Y = −S₂I(S₂ ≤ L₀) − (S₂ + T)I(S₂ > L₀)/2, the cumulative average negative QIDS score. Thus, this demonstrates the case where outcome is a function of accrued information over the sequence of decisions.

From (9), Q₂(s̄₂, ā₂) = E(Y|S̄₂ = s̄₂, Ā₂ = ā₂) = −s₂{I{s₂ ≤ l₀) + I(s₂ > l₀)/2} + E(−T|S̄₂ = s̄₂, Ā₂ = ā₂, S₂ > l₀)I(s₂ > l₀)/2, so that V₂(s̄₂, a₁) = −s₂I(s₂ ≤ l₀) + {−s₂ + U₂(s̄₂, a₁)}I(s₂ > l₀)/2, where U₂(s̄₂, a₁) = max_a2 E(−T|S̄₂ = s̄₂, Ā₁ = ā₁, A₂ = a₂, S₂ > l₀). Thus, from (12),

$$Q_1(s_1,a_1)=E[-S_{2}I(S_2\le l_0)+\{-S_2+U_2({\overline{s}}_2,a_1)\}I(S_2>l_0)/2|S_1=s_a,A_1=a_1].$$

We describe implementation for Q-learning. At the second decision point, we must posit a model for Q₂(s̄₂, ā₂). From the form of Q₂(s̄₂, ā₂), we need only specify a model for E(−T|S̄₂ = s̄₂, Ā₂ = ā₂, S₂ > l₀); given the form of the conditioning set, this may be carried out using only the data from patients moving to stage 2. Based on exploratory analysis, defining s₂₂ to be the slope of QIDS score over stage 1 based on s₁₁ and s₂, we took this model to be of the form β₂₀ + β₂₁s₂ + β₂₂s₂₂ + ψ₂₀a₂, so that the posited Q-function is

$$Q_2({\overline{s}}_2,{\overline{a}}_2;{\xi }_2)=-s_2\{I(s_2\le l_0)+I(s_2>l_0)/2\}+I(s_2>l_0)({\beta }_{20}+{\beta }_{21}{s}_2+{\beta }_{22}{s}_{22}+{\psi }_{20}{a}_2)/2,$$ (37)

ξ₂ = (β₂₀, β₂₁, β₂₂, ψ₂₀)^T. Under (37), V₂(s̄₂, a₁;ξ₂) = −s₂{I(s₂ ≤ l₀) + I(s₂ > l₀)/2} + I(s₂ > l₀){β₂₀ + β₂₁s₂ + β₂₂s₂₂ + ψ₂₀I(ψ₂₀ > 0)}/2, and the “responses“ Ṽ_2,i for use in (27) may then be formed by substituting the estimate for ξ₂. Based on exploratory analysis, we took the posited Q-function at the first stage to be Q₁(s₁, a₁; ξ₁) = β₁₀ + β₁₁ s₁₁ + β₁₂s₁₂ + a₁ (ψ₁₀ + ψ₁₁s₁₂), where s₁₂ is the slope of QIDS score prior to stage 1 based on s₁₀ and s₁₁; and ξ₁ = (β₁₀, β₁₁, β₁₂, ψ₁₀, ψ₁₁)^T. For A-learning, we posited models for the functions h_k(s̄_k, ā_k−1) and C_k(s̄_k, ā_k−1), k = 1,2, in the obvious way analogous to those above, and we took the propensity models to be of the form π₂(s̄₂, a₁; ϕ₂) = expit(ϕ₂₀ + ϕ₂₁s₂ + ϕ₂₂s₂₂ + ϕ₂₃a₁) and π₁(s₁; ϕ₁) = expit(ϕ₁₀ + ϕ₁₁s₁₁ + ϕ₁₂s₁₂). Section A.11 of the supplemental article [Schulte et al. (2012)] presents model diagnostics.

The results are given in Table 2. To describe implementation, we consider interactions significant based on a test at level α = 0.10. At the first stage, Q-learning suggests a treatment switch for those with QIDS slope prior to stage 1 greater than −1.09 (obtained by solving 1.11 + 1.02S₁₂ = 0); A-learning assigns a treatment switch for those with this QIDS slope greater than −1.66. At stage 2, the results suggest that all patients should switch and not augment their existing treatments.

Table 2.

STAR*D data analysis results

	Q-learning			A-learning
Parameter	Estimate	95% CI	p-value	Estimate	95% CI	p-value
Stage 2
β20	−1.46	(−3.47 , 0.55)		−1.47	(−3.49 , 0.54)
β21	−0.75	(−0.88 , −0.61)	*	−0.75	(−0.88 , −0.61)	*
β22	1.17	(0.52 , 1.81)	*	1.17	(0.52 , 1.81)	*
ψ20	1.10	(0.02 , 2.19)	*	1.12	(0.03 , 2.22)	*
Stage 1
β10	−0.62	(−1.94 , 0.70)		−0.30	(−1.69 , 1.09)
β11	−0.54	(−0.62 , −0.45)	*	−0.55	(−0.64 , −0.46)	*
β12	−0.08	(−0.60 , 0.45)		0.10	(−0.46 , 0.66)
Ψ10	1.11	(0.28 , 1.94)	*	0.73	(−0.18 , 1.65)
ψ11	1.02	(−0.08 , 2.11)	*	0.44	(−0.83 , 1.72)

Asterisks indicate evidence at level of significance 0.05 (0.10) that the main effect (treatment contrast) parameter is non-zero

8. DISCUSSION

We have provided a self-contained account of Q- and A-learning methods for estimating optimal dynamic treatment regimes, including a detailed discussion of the underlying statistical framework in which these methods may be formalized and of their relative merits. Our discussion of A-learning is limited to the case of two treatment options at each decision. Our simulation studies suggest that, while A-learning may be inefficient relative to Q-learning in estimating parameters that define the optimal regime when the Q-functions required for the latter are correctly specified, A-learning may offer robustness to such misspecification. Nonetheless, Q-learning may have practical advantages in that it involves modeling tasks familiar to most data analysts, allowing the use of standard diagnostic tools. On the other hand, A-learning may be preferred in settings where it is expected that the form of the decision rules defining the optimal regime is not overly complex. However, A-learning increases in complexity with more than two treatment options at each stage, which may limit its appeal. Interestingly, in the simulation scenarios we consider, inefficiency and bias in estimation of parameters defining the optimal regime does not necessarily translate into large degradation of average performance of the estimated regime for either method.

Although our simple simulation studies provide some insight into the relative merits of these methods, there remain many unresolved issues in estimation of optimal treatment regimes. Approaches to address the challenges of high-dimensional information and large numbers of decision points are required. Existing methods for model selection focusing on minimization of prediction error may not be best for developing models optimal for decision-making. When K is very large, the number of parameters in the models required for Q- and A-learning becomes unwieldy. The analyst may wish to postulate models in which parameters are shared across decision points; see Robins (2004), Robins et al. (2008), Orellana et al. (2010) and Chakraborty and Moodie (2012).

In our development, we have invoked a strong version of the sequential randomization assumption to simplify supporting arguments. Richardson and Robins (2013) allow identification of potential outcomes under possibly weaker assumptions via graphical representations. These authors also extend the notion of a dynamic treatment regime.

Formal inference procedures for evaluating the uncertainty associated with estimation of the optimal regime are challenging due to the nonsmooth nature of decision rules, which in turn leads to nonregularity of the parameter estimators; see Robins (2004), Chakraborty et al. (2010), Laber et al. (2010), Moodie and Richardson (2010), Song et al. (2010), and Laber and Murphy (2011).

We have discussed sequential decision-making in the context of personalized medicine, but many other applications exist where, at one or more times in an evolving process, an action must be taken from among a set of plausible actions. Indeed, Q-learning was originally proposed in the computer science literature with these more general problems in mind; see Shortreed et al. (2010).