Large-Scale Identification of Single-Feature Polymorphisms in Complex Genomes

Abstract

We have developed a high-throughput genotyping platform by hybridizing genomic DNA from Arabidopsis thaliana accessions to an RNA expression GeneChip (AtGenome1). Using newly developed analytical tools, a large number of single-feature polymorphisms (SFPs) were identified. A comparison of two accessions, the reference strain Columbia (Col) and the strain Landsberg erecta (Ler), identified nearly 4000 SFPs, which could be reliably scored at a 5% error rate. Ler sequence was used to confirm 117 of 121 SFPs and to determine the sensitivity of array hybridization. Features containing sequence repeats, as well as those from high copy genes, showed greater polymorphism rates. A linear clustering algorithm was developed to identify clusters of SFPs representing potential deletions in 111 genes at a 5% false discovery rate (FDR). Among the potential deletions were transposons, disease resistance genes, and genes involved in secondary metabolism. The applicability of this technique was demonstrated by genotyping a recombinant inbred line. Recombination break points could be clearly defined, and in one case delimited to an interval of 29 kb. We further demonstrate that array hybridization can be combined with bulk segregant analysis to quickly map mutations. The extension of these tools to organisms with complex genomes, such as Arabidopsis, will greatly increase our ability to map and clone quantitative trait loci (QTL).

[Supplemental material is available online at www.genome.org.]

Identifying the molecular basis of natural phenotypic variation will reveal answers to several long-standing evolutionary questions, as well as many important practical problems, not the least of which is the complex genetics of human disease. With the genomics tools now available we have an increased ability to identify functional variants responsible for phenotypic diversity. So far, most complete genome sequences are from model organisms, usually represented by just a single strain. As a consequence, tools such as microarrays are usually designed for that single reference strain. To identify the causes of intraspecific phenotypic variation, we must look beyond reference strains at the whole genome level. By understanding the molecular nature of this diversity we will gain insights into the mechanisms of evolution and discover genes responsible for natural variation. New genomics approaches, applicable to all organisms and strains, need to be developed to assess natural genetic variation at the whole-genome level, allowing us to tap into the diversity that exists outside a handful of laboratory strains.

Variation in nature usually takes a continuous quantitative form, contrary to discrete qualitative phenotypes that are typical of laboratory mutations. Quantitative trait locus (QTL) analysis has been used to dissect the polygenic nature of complex traits (Mackay 2001; Mauricio 2001; Doerge 2002). To perform QTL mapping, individuals must be genotyped along all chromosomes. This is often times the limiting step. A method to quickly genotype progeny at high resolution would allow new genes to be mapped from new populations in rapid fashion.

An attractive complement to QTL mapping of inbred lines is linkage disequilibrium (LD) mapping. LD mapping ties particular ancestral haplotypes to variation in quantitative traits. To be able to recognize these haplotypes, substantial disequilibrium must exist and a sufficient number of polymorphisms must be typed in order to reveal this disequilibrium. To perform whole genome LD mapping, many markers at very high resolution must be identified from many different individuals. LD mapping may identify much smaller intervals as a result of the greater amount of historical recombination than in experimental crosses; however, a disadvantage is the many unknown population genetic parameters.

Once linkage between markers and quantitative traits is found, either by QTL mapping or LD mapping, candidate genes must be identified. A method to identify changes in coding regions and insertion/deletion polymorphisms at the whole genome level will improve the candidate gene selection process, and provide a detailed characterization of within-species variation. Such an approach would complement global transcription analysis, allowing variation at the DNA level to be accounted for.

Both LD and QTL analyses have traditionally depended on scoring markers such as amplified fragment length polymorphisms (Vos et al. 1995), simple sequence length polymorphisms (Bell and Ecker 1994), and single nucleotide polymorphisms (SNPs; Alderborn et al. 2000). These methods require individual markers to be amplified by polymerase chain reaction (PCR) from individual progeny. The genotypes of each amplified marker are then read serially, usually by gel electrophoresis. New methods have been developed for genotyping hundreds to thousands of markers in parallel. Such methods take advantage of oligonucleotide arrays (SNP arrays), which contain hundreds of thousands of unique 25-base pair (bp) oligonucleotides, termed features. Though an improvement over conventional methods, the disadvantage is that each marker needs to be PCR-amplified and prior knowledge of the polymorphism is required before the SNP array can be produced (Wang et al. 1998; Cho et al. 1999). Variation detection arrays (VDAs), which tile every bp along the chromosome, have also been used effectively to identify and genotype variation, but in this case a vast number of features are required (eight for each bp), making this approach enormously expensive in organisms with complex genomes (Halushka et al. 1999; Patil et al. 2001).

Oligonucleotide arrays designed for expression analysis have been used to detect and score allelic variation in yeast via direct hybridization of labeled genomic DNA (Winzeler et al. 1998). A QTL for high temperature growth in yeast was recently fine-mapped and cloned using this procedure (Steinmetz et al. 2002). Many expression-level polymorphisms were also mapped subsequent to expression array genotyping in yeast (Brem et al. 2002). Whether such a simple method could be used to detect and score allelic variation in a more complex genome has been a matter of debate. Here, we show that even though the 120-Mb Arabidopsis genome is ten times more complex than the S. cerevisiae genome, we are still able to identify 3806 SFPs with high confidence between two accessions using direct genomic DNA hybridization. In addition, we use this method for genome-wide genotyping of an RIL and for mapping of a morphological mutation via bulk segregant analysis. Finally, a linear cluster algorithm was used to identify potential deletions in 111 genes, which, along with coding region SFPs, define excellent candidate genes for causes of natural phenotypic variation.

RESULTS

Arabidopsis Expression Array Feature Analysis

The AtGenome1 array, manufactured by Affymetrix, was designed for gene expression monitoring before completion of the Arabidopsis thaliana genome sequence. Features are clustered at the 3′ end of known and predicted genes. This array, contains 285,186 PM (perfect match) and MM (mismatch) features, 103,860 of which are specific to a single region of the genome with high stringency. Due to overlap in the array design, 92,924 of these features map to unique positions separated by at least 4 bp (Suppl. Table 1 and Methods).

In order to determine whether or not such an array could be used to detect allelic variation in Arabidopsis, DNA was isolated independently from three Col and three Ler (Ler) plants, fragmented, end-labeled, and hybridized to six AtGenome1 arrays (see Methods). Since A. thaliana has a high selfing rate, most of the variation is expected to be between Col and Ler with very little variation within accessions. The arrays were scanned and mean intensity of each feature was calculated from raw pixel data using Affymetrix MicroArray Suite software version 4. We occasionally noticed sporadic regions on an array with generally faint signals due to causes other than specific feature hybridization signal. A smudge, for example, could reduce the signal in a general area, but not completely mask the signal from an individual feature below the smudge. To systematically account for spatial artifacts, we calculated the mean intensity of sliding windows (see Methods) along the array. A false color image of the spatial correction from three independent replicate arrays is shown in Figure 1. Applying the spatial correction always improved the correlation between replicates and, importantly, increased the difference between genotypes. This need for spatial correction is recognized in the computation of gene expression indices. For example, the program dChip (Li and Wong 2001) accounts for spatial artifacts by excluding potential problem areas from further analysis or allowing the user to identify regions to be corrected (Schadt et al. 2000, 2001).

Figure 1.

Spatial correction of hybridization signals. The spatial correction applied to three replicate arrays is shown in false color (A–C). Some prominent spatial artifacts can be seen. Pairwise scatter plots (D) compare the log intensity of each feature between replicate arrays. Before spatial correction (bottom left three scatter plots), a shoulder can be seen mainly due to the large smudge on rep.2. After spatial correction (top right three scatter plots), this shoulder is almost completely removed, increasing the replicate correlation.

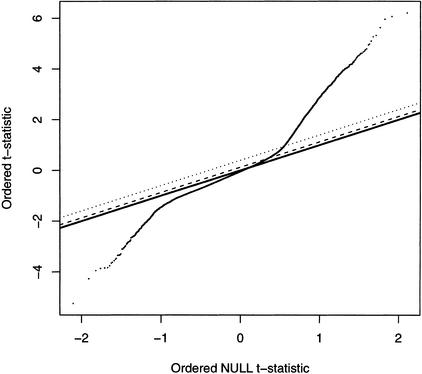
After the spatial correction was applied, data from the three replicates of Col were compared to three replicates of Ler using a modified t-test to index the relative difference for each feature (see Methods). Our procedure is quite similar to that used in Significance Analysis of Microarrays (SAM) where the difference between the mean feature intensity of Col and Ler is divided by the pooled variance within the three Col and three Ler replicates. In addition, a small constant is added to the variance (Tusher et al. 2001). Ranked t-statistics for the Col/Ler comparison are plotted in Figure 2. For each of the 92,924 features, a separate t-statistic was calculated. We needed a method to evaluate the overall significance that would account for the large number of comparisons and the specifics of our experiment. Thus permutation testing was applied according to SAM; three replicates and two genotypes allow 20 possible permutations. This includes the original test of three Col versus three Ler arrays and the reverse test switching all three Ler arrays for Col arrays. The 92,924 scores from each permutation were sorted and averaged to obtain an expected null distribution of t-statistics. The distribution of the nonpermuted (original) data was then compared to the expected null distribution (Fig. 2). A FDR was calculated by dividing the average number of features exceeding the threshold for each permutation by the number of features exceeding the threshold in the nonpermuted data at different thresholds (Table 1). Using this procedure, 3806 SFPs were identified at a 5% FDR. In this study, we only consider SFPs where the Col (reference genome) allele has higher hybridization intensity, thereby insuring the correct genomic location of each SFP. An interactive chromosome browser containing positions of all SFPs can be found at http://naturalvariation.org/sfp.

Figure 2.

Distribution of t-statistics. The 92924 Col/Ler observed t-statistics are plotted against the expected “null” distribution (thick line). The dotted line represents a 5% FDR threshold. The dashed line represents an 18% FDR threshold.

Table 1.

SAM Threshold and False Discovery Rate

SAM threshold	Original data	Permuted data	Difference	FDR
0.10	13,113	3757	9356	28.6%
0.13	10,627	1894	8733	17.8%
0.15	9191	1300	7891	14.1%
0.20	7088	718	6370	10.1%
0.30	4837	294	4543	6.1%
0.40	3806	179	3627	4.7%
0.50	3170	129	3041	4.1%

The number of features exceeding a given threshold in the original data and the average number of features exceeding the threshold in the permuted data set is shown. This is used to calculate the difference and the false discovery rate (FDR) at different thresholds according to SAM (Tusher et al. 2001).

Sequence Confirmation

To further confirm the SFPs, we compared our results to available sequence data in public databases. The sequenced reference strain of Arabidopsis thaliana is Col (The Arabidopsis Genome Initiative 2000). Two shotgun sequencing projects have released data on Ler sequence. The Institute for Genome Research (TIGR) has made available the sequence of 4300 short contigs. Alignment of TIGR Ler sequence and AtGenome1 feature sequences to the full Col genome identified 477 features that were not polymorphic between Col and Ler. A more extensive Ler shotgun sequence project, by Cereon Genomics, has released 55,921 candidate polymorphisms. Upon alignment, 358 AtGenome1 features overlapped the Cereon candidate polymorphisms (Methods and Table 2).

Table 2.

SFP and Sequence Polymorphism Comparison

Independent SFP false discovery rates were determined at different SAM thresholds by comparison with available sequence data. Sensitivity rates were calculated using Cereon candidate polymorphisms, assuming different levels of accuracy (see Results and Methods). False Discovery Rate (FDR), Chi square test statistic (Chisq).

The TIGR and Cereon data sets allowed us to independently estimate the FDR, in a manner analogous to sequence confirming randomly chosen SFPs. Of the 3806 SFPs that we had identified, sequence information was available for 121 of them. All but four were found to be polymorphic by sequence analysis (Table 2). This indicates a 3% FDR, which is similar to that obtained by permutation testing (5%), and suggests that a permutation distribution can be used to set a reasonable threshold in the absence of sequence data.

The Cereon candidate polymorphism data also allowed us to ask an alternative question that could not be addressed had we just sequenced some SFPs. That is, of the potential polymorphisms identified by sequence analysis, how many did we detect on the array? This question addresses the sensitivity and estimates how many of the total SFPs are detectable using this technology. In this analysis, we were limited by the quality of the candidate polymorphisms, since sequence errors cause the prediction of polymorphisms that cannot be detected by array hybridization. We identified 117 SFPs out of 340 candidate polymorphisms (Table 2). Some identifiable SFPs were likely missed at this threshold because we required a low FDR. Table 2 also shows that 197 of the potential Cereon polymorphisms can be identified at a less stringent threshold (18% FDR). A second explanation for the low sensitivity is that some of the candidate polymorphisms are incorrect. We calculated sensitivities for our array genotyping method allowing different accuracies for Cereon markers (see Methods). Better sensitivities were obtained (Table 2). A third explanation is that the position of the polymorphism within the 25 bp is important. Cereon candidate polymorphism data was again used for this analysis. Suppl. Figure 1 shows that polymorphisms near the central base are more often detected as SFPs than polymorphisms near the edge of the 25 bp feature. Of course with our method, a simple and straightforward way to improve both the sensitivity and FDR is to increase the number of replicate arrays.

We also evaluated whether the data from the MM feature was useful in predicting SFPs. A perfect match–mismatch (PM–MM) model, a MM alone model, and a PM together with MM model were evaluated (Suppl. Table 2 and description). Each model was effective at detecting SFPs, but none were more accurate than the PM alone model. We see no benefit for including a MM feature.

Feature Properties

We next asked if there were particular classes of sequences that would show higher rates of SFPs. We examined three properties of each feature. First, we investigated nucleotide repeats. Microsatellites are highly abundant repeat regions found in animals and plants (Morgante et al. 2002). We searched through the list of 92,924 features for ones that contained stretches of polynucleotides (N_4–6). We also categorized the length of di-, tri-, and tetranucleotide repeats within each 25 bp feature. Table 3 shows that features that contain longer stretches of polynucleotides are more likely to be markers. This was also true of di-, tri-, and tetranucleotide repeats. In addition, poly-, di-, and tetranucleotide repeats were found most often in untranslated regions (UTRs), whereas trinucleotide repeats were nearly evenly distributed between coding regions and UTRs. Second, we determined if features corresponded to coding or UTRs. As expected, features detecting coding regions of genes were less likely to be polymorphic than those detecting UTRs (P < 0.0004, see Methods). Third, the copy number of each gene was investigated to test whether features in genes present at higher copy numbers were more likely to be polymorphic. Copy number was determined by aligning the entire DNA sequence of genes detected by AtGenome1 with a database containing all the genes (see Methods). The number of high stringency matches was taken as the gene copy number. Keep in mind that each individual 25 bp feature is unique and can easily distinguish between gene family members. Table 3 also shows that features in genes present at ten or greater copies had a three times higher polymorphism rate than features in single copy genes, suggesting that duplicated genes are less constrained and accumulate more polymorphisms.

Table 3.

Properties of Features That Are SFPs

	Polynucleotide
	N,NN,NNN 0	NNNN 4	NNNNN 5	NNNNNN 6
SFPs	2999	654	130	23
nonSFPs	73,761	13.080	2053	224
	3.9%	4.8%	6.0%	9.3%
Chisq = 59, df = 3, p-value = 1.1e-12

	Gene copy number
	1	2	3	4	5	6	7	8	9	10
SFPs	1216	921	491	244	205	124	85	85	72	338
nonSFPs	37,552	23,137	10,426	5142	2990	2045	1338	1219	896	3387
	3.1%	3.8%	4.5%	4.5%	6.4%	5.7%	6.0%	6.5%	7.4%	9.1%
Chisq = 453, df = 9, p-value < 2.2e-16

Features that contain polynucleotide repeats or that are in duplicated gene have higher levels of polymorphism. 3806 SFPs were scored at a 5% FDR threshold.

Potential Deletions

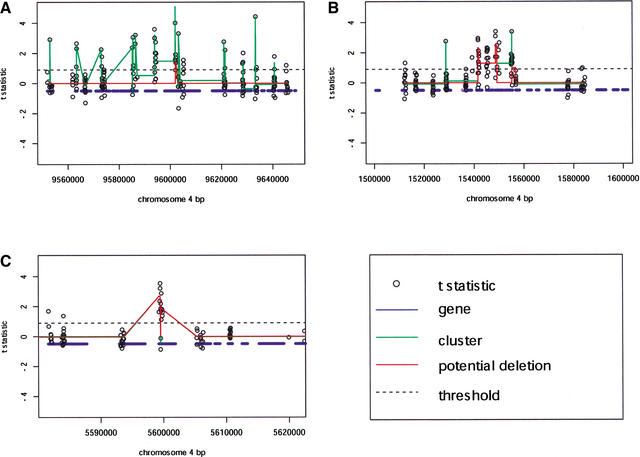
We next investigated whether clusters of adjacent markers had elevated t-statistics, which would indicate deletions rather than small (less than 25 bp) SFPs. We used a linear clustering algorithm, lcluster (http://hacuna.ucsd.edu/lcluster), to join adjacent t-statistics that had similar values. Most features were not markers and clustered together with an average t-statistic of nearly 0. SFPs stood out from this background. Occasionally, adjacent features from an entire gene or genes all had large t-statistics and clustered together (Fig. 3).

Figure 3.

Loci containing potential deletions. (A) A cluster of disease resistance-like genes shows high rates of polymorphism and contains potential gene deletions. (B) Other regions containing genes of unknown function are also highly polymorphic and contain potential gene deletions. (C) A potential deletion in a single RPS2-like disease resistance gene. Plots of the entire genome can be viewed at http://naturalvariation.org/sfp.

We calculated the mean statistic, the number of features, and cluster length in bp for 2000 clusters from the 5 chromosomes. Potential deletions were defined as clusters that contained at least four features, had a total cluster length of at least 100 bp and were supported by at least one feature every 350 bp to avoid long unsupported clusters from being included. In addition, for a cluster to represent a potential deletion it had to have a mean t-statistic above a significance threshold. We counted the number of potential deletions among the 2000 clusters for the real data set and the permuted data sets at different thresholds (Suppl. Table 3). This identified 105 potential deletions covering 111 genes at a 5% FDR. If all 92,924 t-statistics are shuffled with respect to chromosome position prior to cluster analysis, then 0 potential gene deletions are found in 2000 clusters at a 0.2 threshold, illustrating the stringent requirements we have set for potential gene deletions. Furthermore, 45 deletions were confirmed by sequence analysis using Cereon data–partial Ler shotgun sequence (Suppl. Table 4).

We then examined the types of genes in these clusters (Suppl. Table 4). Transposon encoding genes were by far the largest class of genes among those potentially deleted; 23 of the 111 potentially deleted genes (21%) were transposons. The entire array of 7098 genes only has 114 genes encoding transposons (1.6%), thus many more transposons have been deleted than would be expected by chance. Given the relatedness of the two accessions and the high level of transposon variation, it seems likely that many mobile elements are still active.

Disease resistance-like genes (R genes) were also among the potentially deleted genes. R genes are sometimes found in tandem arrays that are highly polymorphic between accessions (Noel et al. 1999). We found increased polymorphism rates and potential gene deletions in a 100-kb region spanning five R genes on chromosome 4 (Fig. 3A). However, not all polymorphic R genes occur in tandem arrays (Grant et al. 1995). We found a single RPS2-like resistance gene to be potentially deleted at 5,600 kb on chromosome 4 (Fig. 3C, Suppl. Table 4). Chromosome regions with increased polymorphism rates containing potential gene deletions were not limited to clusters of R genes. Figure 3B shows a region of potentially deleted genes encoding proteins of unknown function on chromosome 4.

Genes involved in secondary metabolism were also found among the list of potentially deleted genes (Suppl. Table 4). Polymorphisms between accessions in genes involved in secondary metabolism are responsible for variation in insect resistance between accessions (Kliebenstein et al. 2001a,b,c; Lambrix et al. 2001). In addition, genes present at higher copy numbers were more likely to be deleted (P < 2e-16) which partially explains why a larger proportion of SFPs were detected in these genes (Table 3).

Genotyping a Recombinant Inbred Line

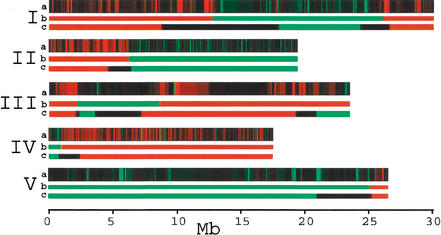
An important test for SFPs is segregation analysis, as physically linked SFPs should cosegregate. We hybridized DNA from a recombinant inbred line (RIL CL-33) to a single GeneChip and determined the genotype at 3806 previously identified SFPs. Each SFP was assigned a likelihood of being either Col or Ler (Fig. 4, chromosome a). The 3806 SFPs are not equally distributed along all chromosomes as AtGenome1 was designed prior to completion of the Arabidopsis genome. Chromosome 2 and chromosome 4 are well covered and contain 1371 and 1275 SFPs respectively. Chromosomes 1, 3, and 5 contain 779, 155, and 226 SFPs (unequally distributed), making the prediction of breakpoints on these chromosomes less accurate. Linear clustering was used to group the adjacent markers and predict the recombination breakpoints (Fig. 4, chromosome b). The breakpoint on chromosome 2 could be localized to within 29 kb (P = 3.3e-7; see Methods). The high resolution-genotype of the RIL CL-33, as determined by array hybridization, matches that of the published low-resolution genotype (Fig. 4, chromosome c, 74 PCR markers) except for the end of chromosome 3 where very few features are present.

Figure 4.

Genotype of RIL CL-33. The genotypes of 3806 SFPs were evaluated via chip hybridization as being Col (green), Ler (red), or unknown (black) for the RIL shown in the a chromosome. Color intensity represents the likelihood of each genotype (see Methods). A clustering algorithm was applied to determine the precise location of the recombination events according to the likelihood of each genotype. This is shown in bright green or red, b chromosome. Recombination breakpoints are clearly defined for chromosomes 2 and 4 because they are well covered on AtGenome1. The c chromosome shows the genotypes obtained from low-resolution PCR genotyping with 74 markers (www.natural-eu.org) for comparison. The unknown locations of the recombination events are shown in black, c chromosome.

We also performed array hybridization with a single F2 plant and determined that Col, Ler, and heterozygous genotypes could easily be scored (data not shown). Array hybridization with a single F1 plant gave uniform heterozygous genotypes; no blocks of Col and Ler genotypes were observed. Heterozygous genotypes have a hybridization intensity that is approximately the average of the Col and Ler intensity and were quite reproducible (data not shown).

Bulk Segregant Analysis

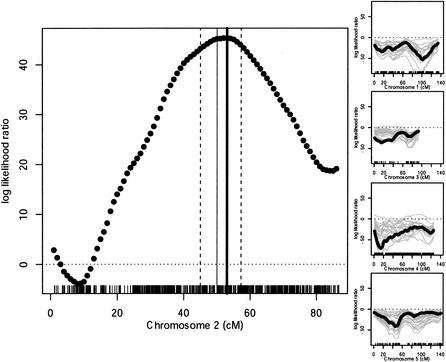
Since many SFPs throughout the genome could easily be identified using this method, we turned our attention to mapping. The erecta mutation is a recessive mutation in Ler. Its phenotype is easily identified in segregating Ler/Col F2 plants. ERECTA maps to a region on chromosome 2, which is well covered on this array, making it an ideal test case. Equal amounts of leaf tissue from 15 Col/Ler F2 plants showing the erecta phenotype and 15 wild-type Col/Ler F2 plants were combined into mutant and wild-type samples. DNA from each pooled sample was extracted, fragmented, labeled, and hybridized to a single expression array. Markers should be enriched for the Ler genotype at the ERECTA locus in the mutant pool and enriched for the Col genotype in the wild-type pool. Other loci, not linked to ERECTA are expected to show no bias toward Ler or Col genotypes since both pools should contain roughly equal numbers of Ler and Col chromosomes. The 3806 SFPs were scored by a single hybridization with DNA from erecta and wild-type pools and evaluated using ChipMap, scripts that implement a likelihood model that accounts for both variance in F2 pools and array variation (see Methods). The log likelihood ratio (LLR) test statistic was evaluated at 1-cM intervals across all chromosomes (Fig. 5). The maximum LLR was at 53 cM on chromosome 2. Simulation studies determined that the maximum location was between 45 and 57 cM in 95% of trials when the position of ERECTA was as estimated 53 cM. Two LOD support intervals also gave a similar 12-cM confidence interval (not shown). The actual position of the ERECTA gene is 50 cM inside the estimated confidence limits.

Figure 5.

Bulk segregant analysis. Hybridization of F2 pools was used to determine the predicted location of the erecta mutation. (Left) Solid circles show the LLR statistic at each cM. The maximum LLR (thick vertical line), is 3 cM away from the ERECTA gene (thin vertical line) on chromosome 2. Simulations were used to determine that the 95% confidence interval spanned 12 cM (dashed vertical lines). LLR scores on unlinked chromosomes (black solid circles). Most LLR scores are negative on unlinked chromosomes. Gray lines show the variation in LLR scores produced by simulations.

SFP Discovery in Other Accessions

To further verify this method of marker discovery and to estimate SFP allele frequencies, we expanded our analysis to other Arabidopsis accessions. DNA from the Ws-2, Nd-1, Tsu-1, and Cvi accessions was isolated, fragmented, labeled, and hybridized to three arrays each (two arrays for Cvi). Each accession was compared to Col and the same threshold (as determined for Ler) was applied. This allowed us to again identify 3806 SFPs, this time specific to Col and the particular accession being tested. From all five accessions a total of 12,487 unique SFPs were identified. 7774 of these were polymorphic in a single accession, and 4713 were polymorphic in multiple accessions when compared to Col (3438 in two accessions, 836 in three, 323 in four, and 116 in five accessions). SFPs with moderate allele frequencies are generally more useful for mapping in crosses between other accessions and have a much smaller false positive rate. As such, these SFPs will be the most informative. SFPs from all accessions are available (http://naturalvariation.org/sfp).

DISCUSSION

We have used an Affymetrix GeneChip designed for RNA expression analysis for highly parallel genotyping in an organism with a complex genome. Our method tests the hybridization intensity of each feature for a statistical difference between the accession in question and the reference strain. The statistical power comes from the use of independent replicates, which can account for random variation at the level of the organism, DNA preparation, fragmentation, and labeling, as well as array hybridization. This technique has not been used so far for analysis of genomes larger than that of S. cerevisiae. We have used total genomic DNA, eliminating the need to amplify specific loci by PCR. In contrast to anonymous genetic markers, the physical location of each SFP is known. Our method is comparable to VDA genotyping (Halushka et al. 1999); however, far fewer features are required (six replicate observations of one 25 bp feature, vs. one observation of 200 features covering 25 bp). In addition, error rates for our method can be improved by simply increasing the number of replicates.

We have previously used specifically designed SNP arrays to type known polymorphisms, however only 163 of 412 markers were robust enough to be used across multiple accessions (Nordborg et al. 2002). DNA hybridization to expression arrays is both a polymorphism discovery and genotyping platform, eliminating the need for different array designs, furthermore, the array can be utilized efficiently for two purposes: expression studies and polymorphism detection. Full genome expression arrays for Arabidopsis (ATH1) are now available ($400) that contain 211,561 PM features. We expect to be able to identify and type more than 8000 SFPs between any accession and the reference strain in highly parallel fashion. Identification will require six arrays (∼$0.30 per SFP), and typing will require one array ($0.05 per SFP), making the individual marker costs very competitive.

Our method also offers considerable advantages for QTL mapping studies. In traditional QTL analysis, recombination breakpoints are inferred between markers using interval mapping. However, as shown in this study, array hybridization precisely defines recombination breakpoints, allowing QTL to be defined by intervals. Such a dense marker set is clearly an advantage for large RIL populations (Dupuis and Siegmund 1999). An additional advantage is that a single RI line can be completely genotyped with one hybridization; multiple loci do not need to be independently assayed. As the price of GeneChips decrease, the benefits of increased resolution and higher throughput will make expression array genotyping very attractive for QTL mapping.

We have effectively used expression array genotyping to map a known mutation in Arabidopsis using bulk segregant analysis. Here two arrays were hybridized with DNA made from pooled F2 plants that had been sorted according to mutant or wild-type phenotypes. Larger bulk segregant pool sizes (>200 plants), with two replicates of both wild-type and mutant hybridizations, will increase the mapping precision to less than 5cM (J. Borevitz and C. Berry, unpubl.). Full genome expression arrays will be effective tools to map new mutations in segregating populations. An extension of this approach to quantitative traits would allow the simultaneous mapping of multiple loci with unknown dominance effects. Bulk segregant analysis coupled with extreme mapping (Tanksley 1993) could quickly determine if new large effect QTL are segregating in a particular F2 cross.

We have previously surveyed LD in Arabidopsis and found it to decay variably throughout the genome, on the order of 50–250 kb in worldwide samples (Nordborg et al. 2002). It was clear from this study that many more markers would be needed to describe a complete LD map from a worldwide sample of Arabidopsis accessions. Using the GeneChip genotyping technology described here, we identified 4499 markers on chromosome 2 from five accessions. The average inter-marker distance is 4.4 kb. As more accessions are surveyed, additional markers will be discovered further increasing the resolution. This same level of resolution could be attained on all chromosomes using a full genome array. Expression array hybridization data from many accessions may describe a genome wide LD map for Arabidopsis from which association mapping could be performed without prior knowledge of candidate loci.

We have identified 3806 SFPs between the Ler accession and the Col reference strain. Cluster analysis grouped 801 of these into 105 potential deletions in 111 genes. A similar analysis could also be used to define the precise lesion(s) generated by fast neutron mutagenesis when the hybridization differences between wild type and mutant are directly compared. Furthermore, this approach could be applied to identify the precise chromosomal duplications and deletions that occur in tumor cells, an improvement from current BAC array methods (Pinkel et al. 1998; Pollack et al. 1999). An alternative algorithm for microarray deletion analysis was effectively used in Mycobacterium tuberculosis (Salamon et al. 2000; Kato-Maeda et al. 2001).

We identified a number of potential naturally occurring deletions. Of them, transposon-encoding genes were the largest single class to be identified. Potential deletions were found in disease resistance-like genes present in both single copies and in highly polymorphic clusters (Fig. 3). Genes involved in secondary metabolism were also identified. High levels of variation in genes, or gene clusters, may suggest some functional role in natural variation, and many of the naturally occurring deletions will be excellent candidates for QTL. Candidate gene selection, subsequent to QTL analysis, can be guided with the knowledge of potential deletions combined with the vast number of coding region SFPs. The power of this approach has been confirmed by the detection of a potential deletion in a transcription factor gene that maps to the location of a flowering time QTL (J. Werner, J. Maloof, G. Trainer, J. Borevitz, J. Chory, and D. Weigel, unpubl.). Finally, genes present at high copy numbers were more polymorphic (Table 3) and contained potential deletions, providing evidence that duplicated genes may be under less functional constraints.

Our discoveries that ∼4% of features on the expression arrays are polymorphic between two accessions, and that ∼1%–2% of genes may be deleted, have implications for transcription analysis when different accessions are compared. If relatively few expression differences (<5%) are found, care should be taken as to whether hybridization changes instead of expression differences are the cause. To remedy this problem, the DNA hybridization pattern could be used as a background for expression analysis, or polymorphic features could be removed prior to expression comparisons.

Our method emphasizes that only a significant difference in hybridization intensity is needed to define a SFP. Knowledge about the exact sequence change is not necessary. In this regard genomic DNA from any organism could be hybridized to an expression array to identify SFPs. When DNA is used from more complex genomes, such as from human, the number of replicates can be increased to improve quality. Cross species comparisons could also be effective, however the physical location of SFPs will be unknown. A high density genetic map can be constructed by array genotyping segregating populations. We have hybridized two subspecies of Brassica oleracea to Arabidopsis expression arrays and found many significant SFPs (J. Borevitz, unpubl.).

Four years have passed since DNA hybridization to expression arrays was first demonstrated to be effective in yeast (Winzeler et al. 1998). We have now analyzed Arabidopsis DNA using an improved statistical algorithm that included permutation tests, and a spatial correction. Repetitive and overlapping features have been removed and we have shown that the MM feature provided no additional information. Steinmetz et al. (2002) recently cloned three genes from one locus responsible for high temperature growth, a quantitative trait in yeast. They were greatly assisted by the use of DNA hybridization to expression arrays. Our work indicates that these approaches can now be extended to organisms with more complex genomes. We look at quantitative trait locus analysis with renewed excitement.

METHODS

All raw data, analysis scripts, and a table with the marker state and descriptions of 92,924 features are provided at http://naturalvariation.org/sfp.

DNA Methods

Total genomic DNA was extracted individually from separate plants (5g fresh weight (FW) leaf tissue), using a 2X CTAB buffer (2% CTAB, 1.4 M NaCl, 20 mM EDTA, 100 mM TrisHCl, pH 8.0, 10 mg/L RNAse). Tissue was frozen in liquid N₂, ground to a fine powder, thawed in 5 mL CTAB buffer, incubated at 65°C for 1/2 h, chloroform extracted, and isopropanol precipitated. To avoid precipitation of carbohydrates, centrifugation was limited to 30 sec during the isopropanol precipitation. Thirty μg of genomic plant DNA with 2.5 ng each Bio B, Bio C, Bio D, and Cre control bacterial DNA were fragmented with 1 U DNAse1 (Promega) for 4 min at 37°C in 1X one-phor-all buffer with 1.5 mM Cobalt Chloride in 35 μL. DNAse1 was added to the lid of each tube; digestion was simultaneously initiated via a quick spin. After heat inactivation for 10 min at 95°C, equal digestion was confirmed on agarose gels by the presence of sheared products centered at ∼25–50 bp. The labeling reaction was performed by adding 20 U terminal deoxynucleotidyl transferase and 1 μL (1 mM) Biotin N⁶-ddATP to the fragmentation reaction and incubating for 1 h at 37°C. Hybridization was subsequently carried out using standard Affymetrix protocols for RNA, specifically, overnight hybridization at 45°C was followed by the Eukaryotic wash protocol that includes antibody staining.

Feature Sequence Analysis

Each of the 131,822 PM features on the Arabidopsis expression array (http://www.netaffx.com) was blasted against the 5 Arabidopsis pseudo-chromosomes (ftp://ftp.tigr.org/pub/data/a_thaliana/ath1/SEQUENCES/ATH1_chr_all.5con, release 1/7/2002) using a stringency of e = 0.004. The positions of 103,860 features with exactly one match were extracted using a perl script, “cleanblast.pl”. Analysis was performed on 92,924 independent features (see Suppl. Table 1). These features were then blasted to the ATH1.cds (coding sequences) and ATH1.seq (mRNA sequence) databases to determine whether a feature was in a coding region or in an untranslated region. Gene copy number was evaluated by blasting the sequence of genes which were detected on the Affymetrix expression array (http://www.netaffx.com) with the ATH1.seq database at a stringency of e = 0.000004. The number of matches from one to ten and greater was recorded using “blast.affy.copy.num.pl”. Features that contained mini-microsatellites were evaluated using “microsat.pl”. Random Ler genomic sequences from TIGR (ftp://ftp.tigr.org/pub/data/a_thaliana/Ler/Ler_20010523.tar) and 40 bp flanking putative Ler markers from CEREON (http://www.arabidopsis.org/Cereon/index.html) were blasted to the pseudochromosomes to identify locations. “myan” and “tdnalign” (H. Chen and J. Ecker, unpubl.) software was used to filter blast results and compare the Ler sequence positions for overlap with AtGenome1 features.

Spatial Correction

All statistical analysis was performed in the freely available statistical package R (http://www.r-project.org; Ihaka and Gentleman 1996). After individual “.cel” files were read into R, a matrix corresponding to the original scan of 534 by 534 features was recreated. Intensities were log transformed. The mean log intensity of a 37 by 37 feature sliding-window was calculated at each coordinate. Only data from the unique 103,860 and corresponding MM features were used for spatial correction. This matrix of window means was subtracted from the original matrix of log intensities, yielding a spatially corrected feature intensity for each unique feature. Other window sizes gave similar results.

SFP Identification

Analysis was performed in a manner very similar to SAM (Tusher et al. 2001) written in R. When features overlapped, by 22, 23, 24, 25 bp, they were included in the model as multiple observations of a feature; however, overlapping features were allowed to have different mean intensities. For groups of features a single t-statistic for the Col/Ler difference was derived by regression. Features with low intensities can have large t-statistics if the error is correspondingly small. To avoid these spuriously large t-statistics we added a small positive constant (s₀) in the denominator as suggested by SAM. We used the median standard deviation of log feature intensity for s₀. s₀ was fixed and not recalculated for each permutation.

Sequence Confirmation

To independently determine the FDR for SFPs we compared our results with available sequence data. Since some markers in the CEREON database may be sequencing artifacts, we calculated error rates for array genotyping allowing different accuracies of CEREON markers. The array error rates were calculated as a function of the data in Table 2 and assumed error rates for the sequence databases using this model:

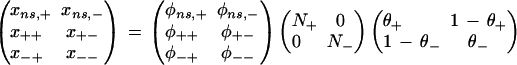where the left-hand side contains the expected counts corresponding to the sum of the cells in Table 2, φ_ij is the probability of sequence classification “i” given the true polymorphism status “j,” N_i are the actual counts of polymorphic and nonpolymorphic sites, and θ_i is the probability that the statistical classification is correct given the actual status is “i”. Further, values are given for the probability that a sequence classification is correct when the sequences are the same,

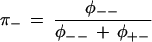and for when they are different

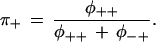This last value is always taken as 1.0, since it is exceedingly unlikely that a sequencing error could make two different sequences of 25 bp appear to be the same sequence. Finding values for the unknowns to yield expected counts, χ_ij, equal to the observed counts requires solution of a system of nonlinear equations, which was carried out in R (Ihaka and Gentleman 1996).

Properties of Features That Are Markers

To assess whether the length of a mini-microsatellite, feature location within a gene, or gene copy number was a predictor of the feature t-statistic and thus marker state, we used regression. For each single, di, tri, and tetra repeats we regressed the SFP t-statistic against length of the repeat (as an unordered categorical variable) in four separate analyses. The SFP t-statistic was significantly different from 0 (P < 0.0004), indicating higher rates of polymorphism, for features with single nucleotide repeats of length four or greater, di-nucleotide repeat length three or greater and tri and tetra nucleotide repeats of length two or greater. Features that correspond to noncoding regions also had t-statistics significantly different than 0 (P < 0.0004), again indicating higher rates of polymorphism. Lastly, the SFP t-statistic was also regressed on gene copy number (as an unordered categorical variable). t-statistics of genes with copy numbers of three or greater were significantly different than 0 (P < 0.0004). Table 3 shows the proportion of features identified as markers at different lengths of single-nucleotide repeats and different gene copy numbers. χ² tests were also highly significant (Table 3).

Linear Clustering

To identify clusters of markers that might represent potential gene deletions, we applied a linear clustering method called lcluster. lcluster is an add-on package to R that is available at (http://hacuna.ucsd.edu/lcluster). lcluster operates on 92,924 ordered features along the 5 chromosomes. Adjacent markers with similar t-statistics were joined and scores averaged, with the most similar ones (according to a total residual sum of squares criterion) being joined first until all features had been joined. Any fixed number of clusters could be identified in this hierarchy; we chose to examine 2000 clusters based on a preliminary inspection of the data; however, 1000 and 5000 clusters gave similar results. Clusters were then assessed for potential gene deletions as described in the results.

RIL Genotyping

The genotypes for RIL CL-33 were scored at each of 3806 SFPs by calculating a log likelihood ratio (LLR) test-statistic. The likelihood of a CL-33 feature representing a Col genotype was divided by likelihood of a CL-33 feature representing a Ler genotype. The standard deviation + small positive constant, s₀, was used when testing each marker. The log of this likelihood ratio was plotted in Figure 4 (top chromosome). Log ratios were truncated at 7 and −7, which correspond to green or red; intermediate log ratios have intermediate colors. Linear clustering (lcluster) was then applied to the truncated log ratio data from each chromosome to identify the recombination breakpoints. Chromosomes 1, 2, and 4 were cut into four clusters. Log ratios for chromosomes 3 and 5 were first truncated at 4 and −4 and then seven clusters were identified, because the number of features from chromosomes 3 and 5 on AtGenome1 is much lower than chromosomes 1, 2, 4 (Suppl. Table 1). The number of clusters exceeded the number of expected recombination events for each chromosome. “Positive cluster” means indicated Col genotype and “negative cluster” means indicated Ler genotype, as shown in color (Fig. 4, bottom chromosome). On chromosome 2, the recombination breakpoint was delimited to an interval of 29 kb (P = 3.3e-7 for larger than 29 kb) by examining the likelihood ratios of markers adjacent to the breakpoint. Three markers to the right gave an odds ratio of 289/1 for Col, and seven markers to the left gave an odds ratio of 1/10474 for the Ler genotype P = 1/(2898*10474) = 3.3e-7.

Bulk Segregant Analysis

A brief description of the likelihood model in the ChipMap R package is given here. The model accounts for variance and covariance from segregation in the F2 pools as well as variance due to array genotyping. We modeled a single recessive mutation by assuming a Gaussian distribution for M marker values with parent Ler and Col means given by vectors of α + β and α − β. Bulk segregant “mutant” and “wild-type” pools (N_mut and N_wt) were modeled as having and lacking the recessive trait with variance matrices having diagonal elements Σ_ii = ς² + φ² and off-diagonal elements Σ_ij = φ². The likelihood for measurements from a single replicate of each marker array, based on N_mut and N_wt F2 plants, is a finite mixture of Gaussians that is asymptotically Gaussian with mean vectors

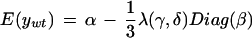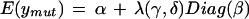and the variances are

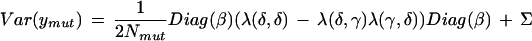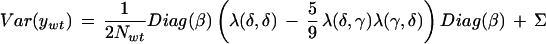Under the null hypothesis, the common expectation vector is E(y) = α and the variance matrices are

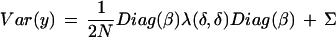with N = N_wt or N_mut. Here the M marker locations on the chromosome are δ = (d₁,d₂,…,d_M) in Haldane map distance, the putative location of a gene is γ, and λ(x,y) = 1 −2r(x,y), where r(x,y) is the recombination fraction between locations xand y. λ(δ,δ) is an M by M array of such values, that is, the lengths of the vector arguments determine the row and column dimensions of λ(·,·).

Our implementation of mapping using this likelihood uses the observed averages over three arrays in each parent line to find α and β and their residuals to estimate ς² and φ². Map locations are assigned to the midpoints of 1-cM-wide bins. The log likelihood ratio statistic is given by

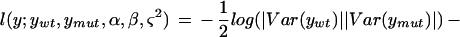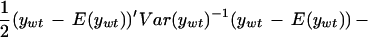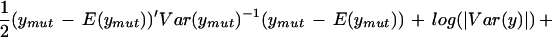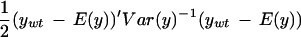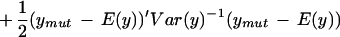F2 plants were simulated and then pooled according to whether they were erecta (Ler homozygous) or wild-type (heterozygous or Col homozygous) at 53 cM on chromosome 2. The true genotype signal in the pool is the mean genotype of each of the 15 mutant or 15 wild-type simulated plants. Array noise was then added to the true genotype signal that was proportional to the variation in observed SFPs. The bulk segregant likelihood model was applied to identify the location of the mutation. This was simulated 500 times to determine the distribution of maximum LLR scores and estimate confidence limits.

WEB SITE REFERENCES

http://naturalvariation.org/sfp; Is the Single Feature Polymorphism section of Natural Variation.

http://hacuna.ucsd.edu/lcluster; This site describes the lcluster algorithm.

http://www.netaffx.com; Data analysis section of Affymetrix.

http://www.arabidopsis.org/Cereon/index.html; Access to Cereon Ler sequence.

http://www.r-project.org; Site of the R package for statistical computing.

http://www.natural-eu.org; European Union site for Natural Variation in Arabidopsis thaliana.