Slower recovery in space before collapse of connected populations

Abstract

Slower recovery from perturbations near a tipping point and its indirect signatures in fluctuation patterns have been suggested to foreshadow catastrophes in a wide variety of systems^1,2. Recent studies of populations in the field and in the laboratory have used time-series data to confirm some of the theoretically predicted early warning indicators, such as an increase in recovery time or in the size and timescale of fluctuations^3–6. However, the predictive power of temporal warning signals is limited by the demand for long-term observations. Large-scale spatial data are more accessible, but the performance of warning signals in spatially extended systems^7–10 needs to be examined empirically^3,11–13. Here we use spatially extended yeast populations, an experimental system displaying a fold bifurcation⁶, to evaluate early warning signals based on spatio-temporal fluctuations and to identify a novel warning indicator in space. We found that two leading indicators based on fluctuations increased before collapse of connected populations; however, the magnitude of increase was smaller than that observed in isolated populations, possibly because local variation is reduced by dispersal. Furthermore, we propose a generic indicator based on deterministic spatial patterns, “recovery length”. As the spatial counterpart of recovery time¹⁴, recovery length is defined as the distance for connected populations to recover from perturbations in space (e.g. a region of poor quality). In our experiments, recovery length increased substantially before population collapse, suggesting that the spatial scale of recovery can provide a superior warning signal before tipping points in spatially extended systems.

Positive feedback is widespread in nature, ranging from cellular circuits to population growth to the melting of ice sheets. There is growing evidence that positive feedback leads to alternative stable states and tipping points (i.e. fold bifurcations) in various ecological systems^15–18. Closer to a tipping point an ecosystem becomes less resilient and more likely to shift to an alternative state¹⁹ such as the collapse of fish stocks, eutrophication of lakes, and loss of vegetation²⁰. Predicting these undesirable transitions may sound like an impossible task because of the inherent complexity underlying these systems. However, recent advances incorporating ideas from nonlinear dynamical systems theory suggest that there may be signatures of “critical slowing down” in the vicinity of tipping points^1,2. At the brink of these sudden transitions, the recovery of a system after perturbations should slow down¹⁴, also leading to changes in the pattern of fluctuations²¹. Thus, a set of indicators related to critical slowing down may provide advance warning of an impending transition. Empirical tests in the field⁴ and in the laboratory^3,5,6 have revealed some of the early warning signals based on fluctuations in time series, such as temporal variation and autocorrelation.

However, our understanding of early warning signals in spatially extended systems is still limited^1,2. The studies in time series typically ignore spatial interactions; in reality the spatial coupling between habitat patches (e.g. dispersal of populations or exchange of biomass) is common and may affect the performance of some warning signals²². Moreover, temporal warning signals rely on data from long-term observations, which are scarce and difficult to obtain. Large-scale spatial data, such as satellite-derived data sets¹⁷, could be more readily available. Spatial data not only provide a greater quantity of information, they also allow us to study features of the system that are not available through time series. Statistical indicators based on spatial fluctuations have been proposed^7–10 but empirical studies are limited^3,11,12; testing these indicators in replicated experiments, which avoid the bias introduced by selective sampling²³, are lacking. In addition, previous studies of vegetation systems discovered emerging spatial patterns preceding transitions^24,25. However, the vegetation patterns are often specific to the system studied; identifying generic spatial warning signals would add a powerful tool in the analysis of ecosystem stability. Here we address these questions using an experimental system of spatially extended yeast populations with alternative stable states and a tipping point leading to population collapse.

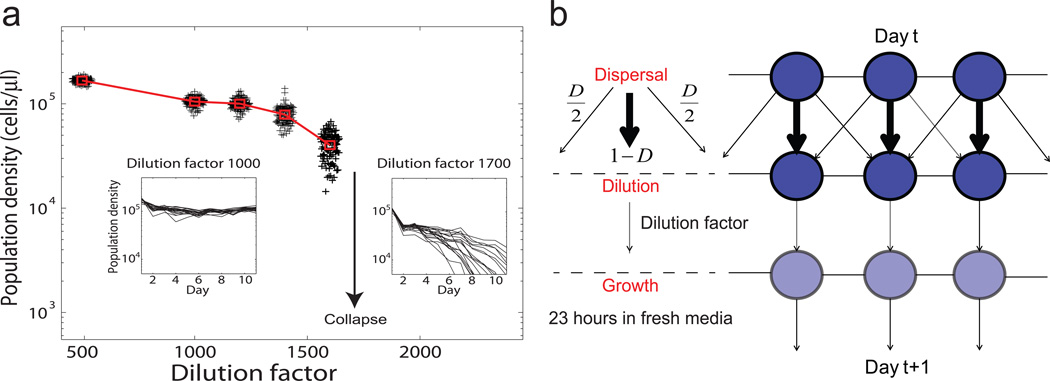
We grew laboratory populations of the budding yeast Saccharomyces cerevisiae in sucrose and performed daily dilution into fresh media. During the daily dilution, a fraction (e.g. 1 in 500 for dilution factor 500) of the cells were transferred to fresh media. This is a well characterized system with an experimentally mapped fold bifurcation⁶. Yeast cells grow cooperatively in sucrose by sharing the hydrolysis products²⁶, creating positive feedback between cells that leads to bistability and a tipping point (Supplementary Fig. 1). By increasing the dilution factor (equivalent to an increase in the mortality rate), we could drive isolated yeast populations to collapse upon crossing the tipping point (Fig. 1a).

Figure 1. Yeast populations with a tipping point: an experimental system to study collapse of connected populations.

a, Isolated yeast populations collapse after crossing a tipping point. The distribution of population density around equilibrium is shown in spread points; the red square denotes the mean. Insets are traces of replicate populations at dilution factor 1000 (stable) and 1700 (collapsed), y-axis unit: cells/µl. b, Yeast populations are spatially connected by controlled daily dispersal. Each circle corresponds to a habitat patch where a local population grows. A fraction of the local population is transferred to each of its two nearest neighbors, and the rest to itself.

We then connected local yeast populations spatially through controlled dispersal between nearest neighbors on a one dimensional array (Fig. 1b). Spatial coupling between local populations was introduced by adding a dispersal step during the daily dilution. In the dispersal step, 25% (corresponding to a dispersal rate D=2×25%=0.5) of a local population was transferred to each of its nearest neighbors; the rest of the population remained in the patch. For each dilution factor, there were 4 replicate arrays each consisting of 10 patches. A group of isolated populations (D=0) was grown in a similar experimental setting except that there was no mixing between neighbors (Methods). The isolated populations served as a control group and allowed us to investigate the effects of spatial coupling on warning signals. From dilution factor 500 to 1600, both groups of connected and isolated populations survived and reached equilibrium densities in a week; at dilution factor 1700, most of the populations collapsed within the timescale of our experiment (Fig 1a inset).

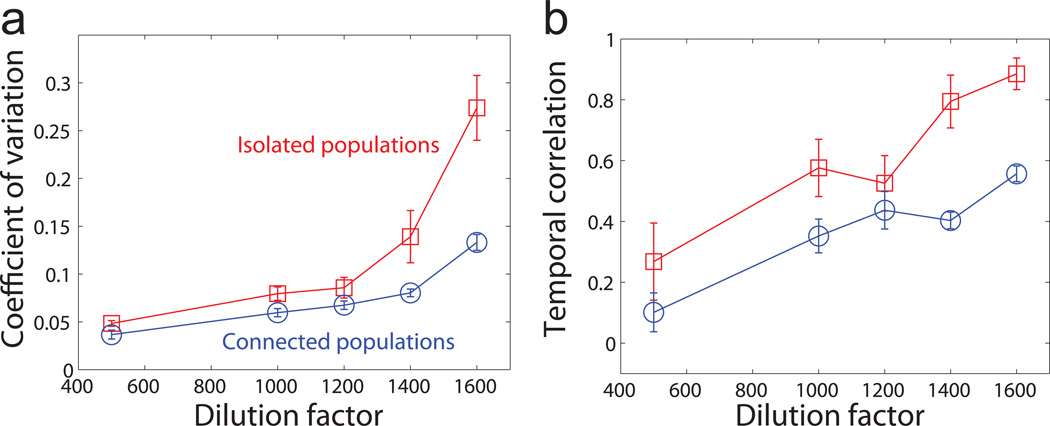
After the populations stabilized, we tracked the fluctuations of population density around equilibrium for at least 5 days to calculate statistical indicators (Methods). Consistent with critical slowing down, we observed a clear increase in the coefficient of variation (CV) of connected populations towards the tipping point (Fig. 2a); however, the magnitude of increase in CV was smaller than in the isolated populations. We then tested lag-1 autocorrelation, a leading indicator for the temporal correlation of fluctuations. As expected, we found that the temporal correlation of connected populations increased gradually to around 0.6 in the vicinity of the tipping point (Fig. 2b). Similar to the observation in CV, the signal in temporal correlation was weaker than in the isolated populations. Although fluctuations of population density in general became larger and more correlated before population collapse, we found that the two warning signals seemed to be suppressed in the presence of dispersal, especially at higher dilution factors.

Figure 2. Early warning signals based on fluctuations show suppressed increase in connected populations.

a, Coefficient of variation (CV). b, Temporal correlation (lag-1 autocorrelation). CV and temporal correlation of both isolated populations (red squares) and connected populations (blue circles) increased before the tipping point. The signals were suppressed in the connected populations, possibly due to the averaging effect of dispersal. Error bars are SEs given by bootstrap for isolated populations and SEMs (n=4) for connected populations.

One explanation for the observed suppression of the two leading indicators in connected populations is that flows between neighbors smooth out the fluctuations across different patches and effectively reduce the autocorrelation in any local population. Reduced size or timescale of fluctuations due to dispersal among populations was predicted in previous theoretical studies of spatially explicit ecological models^8,10,22,27. We note that the smaller warning signals of connected populations in our experiment may be partly due to a minor shift in the tipping point (Supplementary Fig. 2). The averaging effect of dispersal was also found in an independent group of populations subject to “100% dispersal treatment”, where we mixed 10 populations completely each day during the dispersal step. In this extreme scenario, the populations showed almost no increase in variation before the tipping point (Supplementary Fig. 3). Moreover, we demonstrated the suppression of CV and lag-1 autocorrelation by dispersal in analytical derivations based on a spatially explicit first-order autoregressive model (Supplementary Note 1) and in stochastic simulations using a phenomenological model of yeast growth⁶ (Supplementary Fig. 4).

Spatial coupling introduces the possibility of another warning indicator based on spatial fluctuations: spatial correlation. Long-range spatial correlation has been known to occur in the vicinity of some phase transitions²⁸; recent theoretical work in spatially explicit ecological models found that increasing spatial correlation could be a warning signal before transitions to an alternative stable state⁸. We tested the two-point correlation between nearest neighbors in the connected populations but failed to observe any increase near the tipping point (Supplementary Fig. 5). Simulation results with varying sample size showed that no statistically significant increase in spatial correlation should be discerned with the limited samples in our experiment. Thus, our results suggest that to observe the increase in spatial correlation may require more data than other indicators.

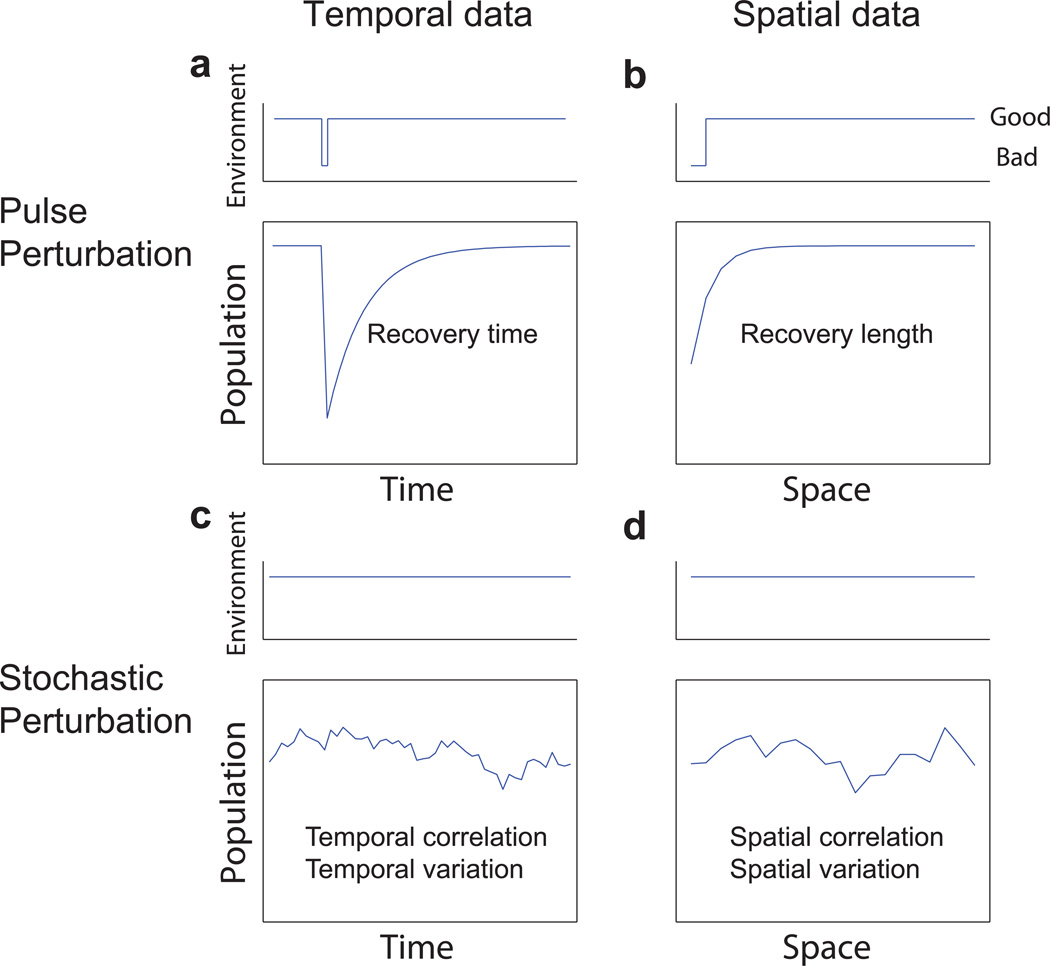
Facing the potential difficulty to observe a strong warning signal based on fluctuations in spatially connected populations, we set out to look for possible new indicators. The existing warning signals can be classified into different categories, based on the nature of the perturbations and measurements (see Fig. 3). Measuring the recovery time after a pulse perturbation (Fig. 3a) can provide a robust indicator of the distance to a tipping point^5,14. In large complex systems, however, it is often impractical to perform such temporal perturbations repeatedly and measure recovery time. Still, due to stochastic perturbations such as demographic noise, population density constantly fluctuates around the equilibrium. Changes of fluctuation patterns such as an increase in variation and correlation (Fig. 3c, d), measured either in time or in space, are also signatures of critical slowing down and consist of another two categories of leading warning signals^{3,4,6–10,21}. Surprisingly, there is one remaining category that has not been proposed: find or create a “pulse perturbation in space” (Fig. 3b) and measure the spatial counterpart of recovery time¹⁴. Adjacent to a region of poor quality, the neighboring good patches will not immediately have reached their carrying capacity; instead the carrying capacity will be reached only further from the bad region (Supplementary Fig. 6). Rather than an increase in the timescale to recover, critical slowing down here manifests itself as an increase in the spatial scale to recover (Supplementary Note 2) , i.e. “recovery length” as compared to “recovery time”.

Figure 3. Early warning signals can be classified into four categories by the nature of perturbations and measurements.

a, Recovery time; b, Recovery length; c, Statistical indicators based on temporal fluctuations; d, Statistical indicators based on spatial fluctuations. The unexplored category of early warning signals is the spatial counterpart of recovery time: “recovery length”. The recovery length characterizes the spatial scale over which population density recovers from a pulse perturbation in space, such as at a boundary with a region of lower quality (b). The recovery length increases towards the tipping point (Supplementary Note 2) and provides a novel indicator of critical slowing down in spatial data.

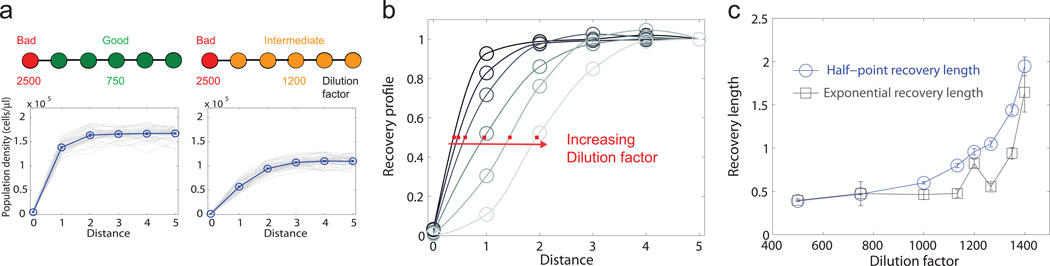
To test our “recovery length” hypothesis, we performed another set of experiment with spatially connected yeast populations (dispersal rate D=0.5), now with two different regions: a relatively good (lower dilution factor) region of 5 patches and a bad (high dilution factor) region of 1 patch (Fig. 4a). Given this sharp boundary between two regions of different quality, population density in the good region recovered gradually in space to the equilibrium value. As the condition of the good region deteriorates, we expect an increase in the spatial scale over which the populations recover. Indeed, we observed a clear change in the steady-state recovery profile of populations with increasing dilution factor of the good region (Fig. 4b). In agreement with our hypothesis, the spatial recovery spanned a much longer distance closer to the tipping point.

Figure 4. Recovery length provides a direct measure of critical slowing down in space.

a, Connected populations in a relatively good region of dilution factor 750 (left) and 1200 (right) recover gradually in space to the equilibrium density. Blue circles denote the steady-state profile of population density after averaging over replicates (shown in gray). b, Recovery profiles at dilution factor 500, 750, 1000, 1200, 1350 and 1400 show an increasing spatial scale of recovery. The profile is normalized by the population density of the patch furthest from the bad region. Lines are shape-preserving interpolations; the position of half recovery is marked by a red square. c, Two different measures of recovery length increase substantially with dilution factor. Error bars are SEs given by bootstrap.

We quantified this spatial scale using two different indicators (Fig. 4c). The first indicator, “half-point recovery length”, measures the distance between the bad region and the location of half recovery (Methods). The half-point recovery length increased gradually with dilution factor from less than 0.5 to around 2. The second indicator, “exponential recovery length”, is obtained by fitting the recovery profile with an exponential function (Methods). Similar to the first indicator, the exponential recovery length increased more than 3-fold as the tipping point was approached. Thus, both measures suggest that the recovery length provides a strong warning signal before population collapse in our system. We also observed an increase in both indicators as we slowly deteriorated the good region and induced the collapse of connected populations in real time (Supplementary Fig. 7).

Recovery length completes the four categories of early warning signals and can help improve our assessment of spatially extended systems. Our results suggest that stronger spatial coupling (higher dispersal rate) suppresses early warning signals in CV and temporal correlation (Supplementary Fig. 4). In contrast, the magnitude of recovery length increases with the level of spatial coupling (Supplementary Note 2). These two categories of early warning signals are therefore complementary: when one signal is weak the other is strong. Also, although our experiment was conducted on a linear array, the use of recovery length can be readily generalized to two-dimensional systems by mapping the profile perpendicular to contours of population density. Unlike the specific spatial patterns found in two-dimensional vegetation systems^24,25, recovery length may provide a generic measure given that the spatially coupled units by themselves would recover more slowly near the tipping point. Finally, from a practical perspective, boundaries between regions of different quality are ubiquitous in nature, thus providing many opportunities to measure the recovery length in populations of interest. One specific example of recovery length would be the “distance of edge influence” in landscape ecology²⁹: it quantifies the spatial scale of edge influence on biota in fragmented landscapes. Data of edge influence for forests at different sites suggest longer recovery length of the Australian tropical forests³⁰, which coincides with the recent forest collapses in Western Australia. In principle, the recovery length can also be measured when spatially extended populations “recover” from a region of higher quality (Supplementary Figs. 6 and 8), suggesting that boundaries may be introduced by conservation efforts (e.g. setting up marine reserves).

Our experiments were performed in the simplest spatial setting possible: homogeneous environments and dispersal rates, a large population size and a safe distance away from the tipping point. In the presence of environmental heterogeneity, measurement of recovery length may fail if the desired sharp boundary between regions of different quality is blurred. However, in this case we expect enhanced signals in spatial correlation⁸ and spatial variation before population collapse (Supplementary Fig. 9). Our experiments have also not explored the effects of spatial coupling on the global stability of a meta-population. On the one hand, spatial coupling may reduce fluctuations and the probability that a random shock will trigger a state shift²²; on the other hand, stochastic local extinctions or the introduction of a bad region can possibly drive the connected populations to collapse before the tipping point of a local population (Supplementary Note 3).

Our work illustrates the important role of spatial coupling, such as the dispersal of populations, in understanding how to apply the current toolbox of warning indicators to natural populations. More empirical studies are required to confirm the generality and applicability of different indicators; nevertheless, being able to observe warning signals in connected populations gives us hope to develop quantitative metrics for assessing the fragility of spatially extended complex systems.

Methods

Experimental protocols

We grew the budding yeast Saccharomyces cerevisiae in 200 μl batch culture on BD Falcon 96-well Microtest plates at 30.7 °C (±0.2°C, standard deviation) using synthetic media (Yeast Nitrogen Bases + Nitrogen, Complete Supplement Mixture) supplemented with 2% sucrose⁶. Cultures were maintained in a well-mixed condition by growing on a shaker at 825 r.p.m. Serial dilutions were performed daily (23 hours of growth) with variable dilution factors. Population densities were recorded each day before the serial dilution by measuring optical density at 600nm using a Thermo Scientific Varioskan Flash Multimode Reader. The calibration between optical density and cell density was based on the previous characterization of this system⁶.

In the group of connected populations, for each dilution factor there were 4 replicate arrays each consisting of 10 patches. Populations were connected by controlled dispersal between nearest neighbors (dispersal rate D=0.5, which is defined as the fraction of population going out of a patch). Reflecting boundary conditions were adopted, meaning that a population on the edge would have 75% of its cells remaining in the patch during the dispersal step. In the group of isolated populations, the experiment was performed in a similar spatial setting except that there was no dispersal (D=0); for each dilution factor there were 4 arrays each consisting of 5 patches, thus a total of 20 replicate populations isolated from each other. The dilution factors for the data presented in Fig. 2 are 500, 1000, 1200, 1400 and 1600. In the experiment to measure recovery length, populations were connected by nearest-neighbor dispersal (D=0.5, reflecting boundary conditions). The dilution factor for the bad region (1 patch) was 2500; the dilution factor for the good region (5 patches) was varied as the environmental driver. The dilution factors for the data presented in Fig. 4 are 500, 750, 1000, 1133, 1200, 1266, 1350 and 1400.

Calculation of statistical indicators

Statistical indicators for the connected populations were calculated among 10 populations in one array on each day and averaged over a span of at least 5 days, after the populations stabilized. The mean value of 4 replicate arrays and SEM (n=4) are shown in Figure 2. For the isolated populations, statistical indicators were calculated on each day among 20 populations over 5 days. We used bootstrap to compute SEs of the indicators by resampling 1000 times the ensemble of replicate populations (for the coefficient of variation and the temporal correlation) or arrays (for the spatial correlation).

The coefficient of variation (CV) was calculated as the sample standard deviation (Supplementary Fig. 3b) divided by the sample mean. Because the local populations in our experiment were grown in a homogeneous environment, in principle they could all be treated as replicates. Assuming the system is ergodic, the CV calculated over an ensemble of replicates can be interpreted either as spatial CV of many populations at one time point or temporal CV of a single population over many time points. The temporal correlation, defined as the lag-1 autocorrelation, was estimated by the Pearson’s correlation coefficient between the population densities at subsequent days. To correct for negative bias in small samples, we used a modified estimator with an additional term $\frac{1}{N}$ for lag-1 autocorrelation³¹. The sample size N=10 for connected populations; N=20 for isolated populations. N is a fixed number for different dilution factors, so using the modified estimators would not affect the trend of indicators. The spatial correlation, defined as the two-point correlation between all neighboring pairs, was estimated by the Moran’s coefficient^8,32. The expectation of Moran’s coefficient is $-\frac{1}{N-1}$ in the absence of spatial correlation³³; we used a modified estimator with an additional term $\frac{1}{N-1}$ so that the expectation is 0. In this case, the sample size N is the number of patches in an array: N=10 for connected populations; N=5 for isolated populations. For detailed formula of the statistical indicators, see Supplementary Note 4.

In the analysis we ensured environmental homogeneity by removing a linear gradient of population density observed in connected populations. The small gradient is presumably caused by some heterogeneity in experimental conditions (temperature, dilution errors, etc.) across the plate. Removing gradient-type spatial heterogeneity before statistical analysis is similar to the detrending procedure commonly used in time-series analysis; it prevents spurious signals such as positive spatial correlation (Supplementary Fig. 10).

Recovery length

After the recovery profile stabilized, we tracked the population density profiles of at least 6 replicates over several days. The half-point recovery length L^half was estimated by performing a shape-preserving interpolation (Matlab function PCHIP, piecewise cubic Hermite interpolating polynomial) to the recovery profile and then locating the position of half recovery at which $n(x=L^{\mathit{\text{half}}})=\frac{1}{2}n(x=5)$. The population density of the bad region (dilution factor 2500) in our experiment was close to 0 (Fig. 4 and Supplementary Fig. 7). In the more general scenario with a sharp boundary between two regions of different quality (Supplementary Fig. 6 and 8), the position of half recovery can be defined as the midpoint between the equilibrium population density of the region of interest and the population density at the boundary. The exponential recovery length was estimated by fitting an exponential function with three parameters c₁ exp(−x/L^exp) + c₂ to the recovery profile n(x). The data points used for exponential fitting are from position 1 to 5 (except for dilution factor 500, the data for fitting are from position 0 to 5). We note that our definition of exponential recovery length is phenomenological, because: 1) the deviation is expected to be exponential only close enough to the equilibrium; 2) at higher dilution factors the profile can deviate from an exponential form (Supplementary Fig. 11). The “kink” in the fitted exponential recovery length (Fig. 4c) may be due to the limited data points used in fitting or experimental errors. For both the half-point recovery length and the exponential recovery length, we used bootstrap to compute SEs for the indicators by resampling the ensemble of steady-state profiles 100 times and fitting the average recovery profile.