Two-dimensional spatial manipulation of microparticles in continuous flows in acoustofluidic systems

Abstract

We report a modeling and experimental study of techniques to acoustically focus particles flowing through a microfluidic channel. Our theoretical model differs from prior works in that we solve an approximate 2-D wave transmission model that accounts for wave propagation in both the solid and fluid phases. Our simulations indicate that particles can be effectively focused at driving frequencies as high as 10% off of the resonant condition. This conclusion is supported by experiments on the acoustic focusing of particles in nearly square microchannels, which are studied for different flow rates, driving frequencies and placements of the lead zirconate titanate transducer, either underneath the microchannel or underneath a parallel trough. The relative acoustic potential energy and the resultant velocity fields for particles with positive acoustic contrast coefficients are estimated in the 2-D limit. Confocal microscopy was used to observe the spatial distribution of the flowing microparticles in three dimensions. Through these studies, we show that a single driving frequency from a single piezoelectric actuator can induce the 2-D concentration of particles in a microchannel with a nearly square cross section, and we correlate these behaviors with theoretical predictions. We also show that it is possible to control the extent of focusing of the microparticles, and that it is possible to decouple the focusing of microparticles in the vertical direction from the lateral direction in rectangular channels with anisotropic cross sections. This study provides guidelines to design and operate microchip-based acoustofluidic devices for precise control over the spatial arrangement of microparticles for applications such as flow cytometry and cellular sorting.

I. INTRODUCTION

Standing acoustic waves are routinely used to dynamically control the positions of microscopic entities (e.g., cells and particles) within quiescent fluids and laminar flow streams¹ for the purposes of separating and isolating specific particle types based on their physical properties (e.g., by size, density, and compressibility),^2–5 transporting and trapping particles and cells,^6–11 aligning particles for efficient enumeration or imaging,^12–14 and assembling particles into higher ordered structures.^15–18 Ultrasonic standing waves can be generated within microfluidic channels (herein referred to simply as microchannels) by exciting them with piezoelectric actuators (e.g., lead zirconate titanate, PZT), which expand and contract with an applied sinusoidal voltage, thereby inducing periodic mechanical perturbations in the form of elastic waves that propagate through the microfluidic device.^19,20 By matching the driving frequency to a resonant mode of the microchannel, an ultrasonic standing wave can be induced in the fluid with a discrete number of pressure nodes, depending on the ratio of the acoustic wavelength to the device geometry. Suspended particles respond to these standing waves by migrating to either its pressure node (where the pressure is approximately constant) or its pressure antinode (where the pressure swings between extremes). The preferred location for the particles depends on its relative density and elastic properties with respect to the fluid medium, which are described by the acoustic contrast coefficient.^21,22 When this coefficient is positive, particles migrate toward the pressure node(s); when this coefficient is negative, particles migrate toward the pressure antinodes.²³

Ultrasound propagation through acoustofluidic devices consists of a complex set of pressure waves produced by the vibrations emitted by the acoustic transducer that scatter at various interfaces (e.g., glass/fluid, silicon/fluid, glass/silicon, silicon/air, or glass/air). An exact solution of the corresponding wave equations presents a difficult computational problem that generally requires numerical methods for accurate description of the pressure distribution within the entire system. Moreover, the boundary conditions are usually not experimentally well characterized, which has hampered the proper quantitative treatment of acoustic particle focusing. The most basic analytical model for wave propagation considers the fluid domain alone and treats internal (fluid-side) boundaries as infinitely rigid walls that perfectly reflect incident waves back toward the interior of the microchannel, an assumption that is widely accepted in classical models to describe a hard surface.²⁴ This simple acoustofluidic model captures the essential features of the pressure distribution, including the locations of the pressure nodes and antinodes as well as the overall wave shape. However, such models also lead to physically unrealistic conclusions, including the prediction of near-infinite pressures within the cavity when the resonance condition is satisfied (i.e., when the wavelength is a half integer multiple of a dimension of the cavity). To avoid this singularity, amendments to this model have considered energy losses due to wave attenuation in the fluid domain through the inclusion of an imaginary component in the wave vector, i.e., k = k′ + ik″.²⁵ While the imaginary component indeed produces losses in the pressure wave that help to avoid singularity, these models do not accurately characterize off-resonance conditions. For example, these attenuation approaches predict greatly deteriorated particle focusing capabilities when the acoustic transducer is only slightly off-resonance (e.g., by less than 1% from the resonant frequency), which contradicts both experimental findings and multi-domain models.^26,27 Several authors have noted that non-perfect wave reflection at the boundaries is another important source of energy loss,^{16,25,28–31} which results from wave transmission through the boundaries (i.e., the lossy-wall boundary condition).^25,31 In the experiments presented herein, we observe that substantial particle focusing (i.e., concentration of suspended particles within the standing wave) can be achieved when the driving frequency deviates from the resonant frequency by as much as 10%.

In order to better understand the focusing capabilities, in particular, the off resonance condition, here we have developed a quasi-2-D model for acoustic propagation that includes both the fluid and solid domains. Within this 2-D limit, we provide approximate analytical solutions of the wave equation, boundary impedances, and acoustic radiation forces and also discuss the influence of the resonance conditions. The model provides a general treatment of resonant conditions in which the microchannel dimensions are either integer or half-integer multiples of the wavelength of the acoustic radiation (which are referred to as the even or odd modes, respectively).

Our study also expands the understanding of acoustic manipulation of particles flowing within microchannels, in comparison with previous studies, which primarily focused on quiescent media³² and demonstrated various self-assembled particle patterns (e.g., lines, arrays, and lattices),^7,15–17 manipulation of single particles (e.g., a cell),^9,10 or size dependent characteristics of the particle motion resulting from the combination of acoustic radiation forces and streaming.^32,33 Studies that have shown such phenomena often rely on the use of at least two acoustic transducers, each of which is activated at a frequency resonant with either the width or depth of a microchannel of rectangular cross section.^34–36 Other more recent studies have demonstrated the usefulness of 2-D acoustic focusing;^37–39 however, none of these studies have investigated particle distributions for off-resonance conditions, which will be encountered whenever 2-D focusing is encountered in an etched channel that is not perfectly square. We are particularly interested in cases where the microchannel aspect ratio deviates from 1.0 (e.g., 0.9–1.1), as is often the case when uncertainties in the fabrication process lead to less than perfectly square cross sections.

We use the wave transmission model to interpret our experimental results on the manipulation (i.e., concentration or focusing) of particles flowing through a slightly off-square cross section microchannel. As we show in Sec. IV, we can tune the control parameters such as driving frequency, flow rate, and the placement of the PZT transducer to achieve either 1-D (in the transverse direction) confinement or 2-D confinement of the suspended particles within a continuous flow. To inspect the 3-D distribution of particles within the microchannel at different driving frequencies and flow rates, we used confocal fluorescence microscopy to observe both suspended particles and the carrier fluid. Furthermore, by measuring the time for convergence (or focusing) of particles upon imposition of an acoustic standing wave, our analytical solution allowed us to obtain a rough estimate the pressure amplitudes generated in our device. These considerations for device design and operation are critical for the optimization of the performance of these devices, potentially leading to new designs tailored for applications in bioassays,^4,6,7 cytometry,^12,13 cell separations,^11,27 and colloidal assembly.¹⁵

II. MODEL

In our theoretical model, we restrict our attention to a nearly square microchannel that is effectively infinite in length, i.e., the channel is so long that it does not support any acoustic modes along its axial dimension. We also consider only the longitudinal pressure waves and ignore all the other structural acoustic waves such as bending waves and shear waves, which is reasonable because none of these waves effectively propagate in the fluidic domain. Since the mean diameter of the particles is larger than 1 μm,⁴⁰ and flow rates of interest are high enough that the residence times of particles in the acoustofluidic channel are short,³² streaming does not significantly change the particle dynamics and therefore is neglected in our analysis. Finally, we approximate the 2-D pressure distribution as the superposition of two 1-D pressure distributions along the width and height of the microchannel. While this model omits several aspects of our experimental design (e.g., how the PZT transducer is physically coupled to the substrate and the efficiency of vibration transmission between the transducer and silicon substrate), it is sufficient for predicting: (i) how the driving frequency influences the shape of the acoustic potential energy distribution and the resultant particle distribution in the 2-D limit; (ii) particle concentration at off-resonant conditions; and (iii) the orders of magnitude for the relevant pressure amplitudes.

Consider a 1-D pressure wave traveling along the positive x-direction (see Fig. 1(d) for the definition of the coordinate system) inside a medium that reaches a fluidic cavity represented by the spatial domain, 0 ≤ x ≤ W, where W is the width of the microchannel. The incoming wave is transmitted and reflected at both boundaries, leading to the general forms for the pressure and acoustic particle velocity^28,30,31,41

$$\begin{array}{c}{p}_1(x<0,t)=(P_0{e}^{-i{k}_{\mathrm{s}}x}+B_1{e}^{+i{k}_{\mathrm{s}}x})e^{i\omega t},\\ p_2(0<x<W,t)=(A_2{e}^{-i{k}_{\mathrm{w}}x}+B_2{e}^{+i{k}_{\mathrm{w}}x})e^{i\omega t},\\ p_3(x>W,t)=A_3{e}^{i(\omega t-k_{\mathrm{s}}x)},\end{array}$$ (1)

$$\begin{array}{c}{v}_1(x<0,t)=(P_0{e}^{-i{k}_{\mathrm{s}}x}-B_1{e}^{+i{k}_{\mathrm{s}}x})e^{i\omega t}/Z_{\mathrm{s}},\\ v_2(0<x<W,t)=(A_2{e}^{-i{k}_{\mathrm{w}}x}-B_2{e}^{+i{k}_{\mathrm{w}}x})e^{i\omega t}/Z_{\mathrm{w}},\\ v_3(x>W,t)=A_3{e}^{i(\omega t-k_{\mathrm{s}}x)}/Z_{\mathrm{s}},\end{array}$$ (2)

where the unknowns, A_i and B_i are coefficients for the forward and backward propagating waves, respectively, in each of the domains x < 0, 0 < x < W, and W < x. These coefficients are determined by matching the boundary conditions, which requires that both the pressure and the normal component of the velocity are continuous across the interface, leading to the solutions^27,28,31

$$\begin{array}{c}{B}_1=i{P}_0(Z_{\mathrm{w}}^2-Z_{\mathrm{s}}^2)\hspace{0.17em}\text{sin}\hspace{0.17em}(k_{\mathrm{w}}W)/G(k_{\mathrm{w}}W),\\ A_2=P_0{Z}_{\mathrm{w}}(Z_{\mathrm{s}}+Z_{\mathrm{w}})e^{+i{k}_{\mathrm{w}}W}/G(k_{\mathrm{w}}W),\\ B_2=P_0{Z}_{\mathrm{w}}(Z_{\mathrm{s}}-Z_{\mathrm{w}})e^{-i{k}_{\mathrm{w}}W}/G(k_{\mathrm{w}}W),\\ A_3=2P_0{Z}_{\mathrm{s}}{Z}_{\mathrm{w}}{e}^{+i{k}_{\mathrm{s}}W}/G(k_{\mathrm{w}}W).\end{array}$$ (3)

These expressions describe the general phenomena of wave propagation in a 1-D layered composite. The characteristic impedance for the i^th medium, given by Z_i = ρ_iC_i, is commonly used to simplify the modeling of multilayer systems.^28–31,41 The factor appearing in all coefficients, 1/G(k_wW) = 1/[2Z_sZ_w cos(k_wW) + i(Z_s²+Z_w²) sin (k_wW)], acts as a amplification factor, which is maximized at resonance (i.e., k_wW = nπ and n = 1, 2, 3,…). This amplification factor provides a convenient way to understand the different types of resonance, such as the odd and even resonant modes that correspond to different types of in phase or out of phase motion of the channels walls, and it is also useful in understanding the magnitude of the acoustic potential energy fields for interpretation of experimental data. Resonance corresponds to maximal coupling of the wave into the microchannel (i.e., no back reflection at the first interface, since B₁ = 0), when the pressure and acoustic velocity are given by p₂ = P₀[cos(k_wx) − iZ_w sin(k_wx)/Z_s]e^iωt and v₂ = P₀[cos(k_wx)/Z_s − isin(k_wx)/Z_w]e^iωt. Conversely, at conditions far from resonance, when k_wW = (n − 1/2)π, the real part of the pressure is reduced by a factor of 2Z_sZ_w/(Z_s² + Z_w²), which corresponds to minimal coupling of the wave into the microchannel and a large back reflection.

FIG. 1.

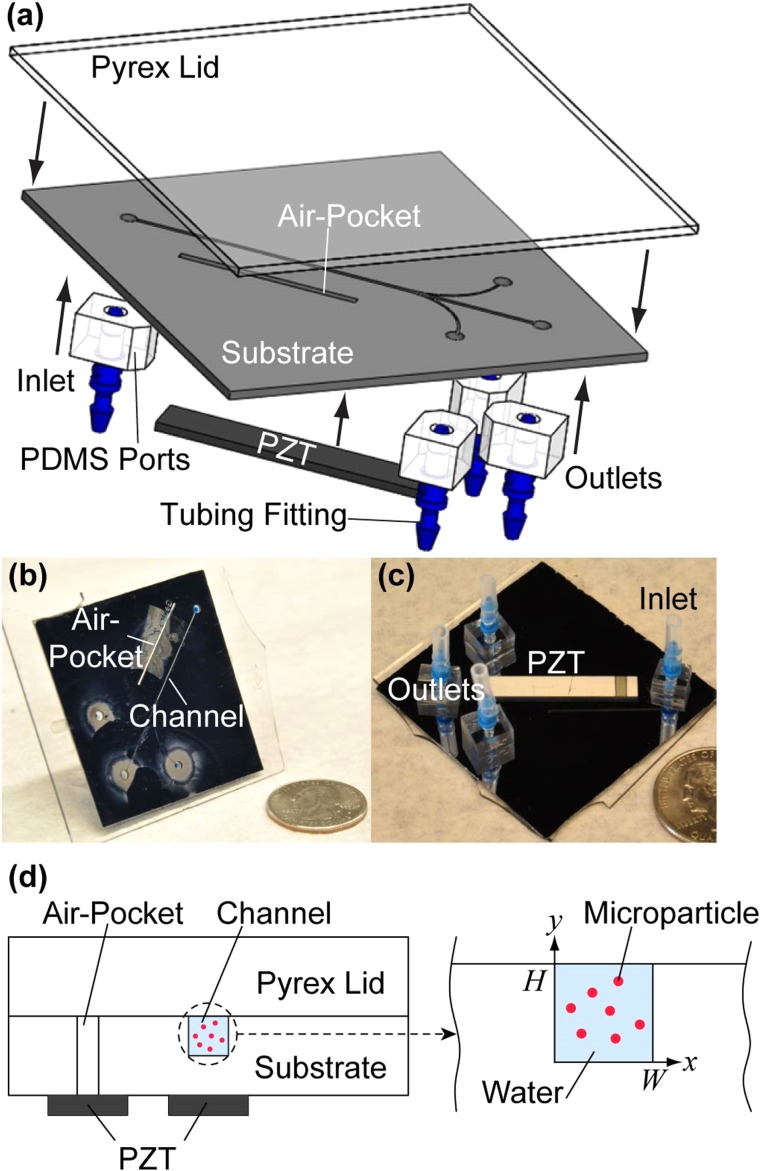
Experimental setup. (a) An illustration of the acoustofluidic chip components. (b) Top side and (c) bottom side of the microfluidic device show the positions of the air pocket, inlets, and outlets as well as the placement of the PZT transducer. (d) An illustration of the two locations where the PZT transducers were placed in our experiments relative to the microchannel. These two PZT transducers are referred to as “air pocket PZT” transducer and “channel PZT” transducer in the text. We note that only one PZT transducer was bonded to the microchannel for each experiment.

III. EXPERIMENTAL METHODS

Figure 1(a) shows a schematic depiction of the components for the acoustofluidic device, and Figures 1(b) and 1(c) are photographic images of a device. Conventional photolithography and deep reactive-ion etching were employed to fabricate patterns in silicon wafers (〈100〉 orientation, Addison Engineering, Inc.). The width and depth of the microchannel were 252 μm and 284 μm, respectively, as measured by an optical profiler (NewView 5000, Zygo Corp.). Borosilicate glass (Borofloat^® 33, Glass B, Schott AG) lids were anodically bonded to the substrates to form the enclosed microchannels.¹³ As shown in Figures 1(c) and 1(d), PZT transducers (841, APC International; d₃₁ = 0.109 nm/V)⁴² were bonded via cyanoacrylate glue (Loctite^® 495, Loctite Corp.) at one of two specific locations (i.e., underneath the microchannel or underneath an air pocket that is etched parallel to the microchannel).

We investigated two distinct methods of introducing acoustic waves into the microchannel, by bonding the actuator either directly underneath the microchannel, or directly underneath a trench (1 mm in width and 23 mm in length) etched all the way through the silicon, parallel to the microchannel (see Fig. 1). Bonding piezoelectric transducers underneath a microfabricated air pocket has been used in spatial manipulation of microparticles in a previous study.³⁴ As we show in Sec. IV, a PZT transducer placed underneath this air pocket (here referred to as the “air pocket PZT” transducer) can decouple acoustic focusing in the x- and y-directions under different driving frequencies compared to the fixed coupled focusing provided by a PZT transducer placed directly underneath the microchannel (herein referred to as the “channel PZT” transducer). The placement of the inlet and outlet ports on the backside of the device allows microscopic observation of the entire microchannel (including the trifurcation point). Polydimethylsiloxane (PDMS, Sylgard^® 184, Dow Corning) was used in the construction of the inlet and outlet ports, which were bonded to the substrate after oxygen-plasma treatment, as shown in Figure 1(a).¹³

A signal generator (DG1022, Rigol Technologies, Inc.) was used to create sinusoidal signals with specified frequencies and peak-to-peak voltages of 5.0 V. A power amplifier (25A250AM6, Amplifier Research, Corp.) connected to the two electric leads (soldered at the two ends of the PZT transducer) was used to raise the voltage applied to the PZT transducers to ≈30 V, as measured by an oscilloscope (TDS2004C, Tektronix, Inc.). We selected this voltage as it is commensurate with the voltages used in our previous studies on microparticle and cell separation.^11,43 The static deformation of the width of the PZT transducer under this voltage is ≈17 nm,⁴² but when responding to an alternating signal, the deformation is a decreasing function of frequency. The typical deformation for a PZT transducer that is excited with a frequency in the megahertz range varies from only 0.1 nm to a few nanometers depending on the amplitude of the driving voltage.^25,26 The temperature of the acoustofluidic device was measured using bonded thermocouples (5SC-TT-K-36–36, Omega Engineering, Inc.) associated with a data acquisition card (cDAQ-9174, National Instruments, Corp.). Under all experimental conditions, the temperature rise of the silicon substrate and borosilicate lid was no more than 13 °C above ambient. We estimate that this maximum variation of temperature should cause a change in the resonant frequency of the fluidic domain by ≈1%.⁴⁴ We note that since the residence time of the fluid inside the microchannel is brief, the temperature of the fluid is not necessarily equilibrated with the temperature of the silicon substrate and borosilicate lid. Therefore, we assume the impact of the temperature rise is negligible in this study (see the supplementary material for more details of the temperature measurements).⁴⁵

Effective use of ultrasonic standing waves for the precise manipulation of particles requires that the acoustic wavelength be much larger than the particle diameter, such that the particle can reduce its potential energy by moving to a nearby acoustic potential energy minimum.² The acoustic force also needs to be sufficiently strong to dominate competing forces such as friction, surface adhesion, inertia, Brownian motion, and gravity and therefore confine particles to well-defined positions or streamlines within the microchannel. Nile red polystyrene particles (5 × 10⁶ particles/mL, mean diameter = 10.4 μm, Spherotech, Inc.), which exhibit positive acoustic contrast coefficients in water (similar to cells), were suspended in an aqueous solution containing 250 μM fluorescein (Sigma-Aldrich, Co.). The fluorescein dye permitted the entire fluidic channel to be visualized in both conventional and confocal microscopes. The particle suspension was injected at a constant flow rate by a syringe pump (NE-300, New Era Pump Systems, Inc.). An upright laser scanning confocal microscope (LSM 780, Carl Zeiss, AG) was used to assess the distribution of particles within the microchannel. To set the limits of the z-stack scanning, the particles were permitted to settle to the microchannel floor in the absence of flow and this position was marked as z = 0. To measure the time required for flowing fluorescent particles to converge into a focused stream upon application of an acoustic standing wave, we used an inverted fluorescent microscope (Axio Observer, Carl Zeiss, AG) equipped with a digital camera operating at 15 frames/s. We also used a high speed camera with a frame rate of 200 frames/s to verify the time necessary for acoustic focusing. For the acquisition of all images, the objective of microscope was placed at precisely the halfway point between the inlet and the location where the microchannel splits three ways toward the outlets.

IV. RESULTS AND DISCUSSION

A. Acoustofluidic wave propagation model

Our solution, similar to 1-D wave transmission models used in previous studies,^{4,12,13,32,40} suggests that two parallel boundaries are moving anti-phase (boundary velocities have opposite signs) for odd resonant modes and in-phase (boundary velocities have the same sign) for even resonant modes. For a more intuitive presentation of these predictions, we numerically simulated the wave propagation and acoustic particle velocity in the x-direction for the first, odd resonant mode (k_wW = π) and the first, even resonant mode (k_wW = 2π), and the results are provided as two animations in the supplementary material as Videos 1 and 2, respectively.⁴⁵ In our device, both the width and depth of the microchannel are near resonance (see below), resulting in substantial acoustic radiation forces in two dimensions. We thus consider wave propagation in the vertical direction by following the same procedure, and while the matching layer (i.e., the material between the PZT transducer and the cavity) is always silicon, the reflector can be either silicon or borosilicate glass in the y-direction. For simplicity, we did not consider the reflection/transmission at solid/air interfaces at the extremities of the acoustofluidic device.

It is useful to obtain relationships for the acoustic impedance at the microchannel boundaries from the wave transmission model. For example, in the x-direction, the impedances can be evaluated at each boundary,³⁰ Z_b = p/v|_x = 0,W, such that

$$Z_{\mathrm{b}}\left(x=0\right)=-i\frac{Z_{\mathrm{s}}{Z}_{\mathrm{w}}\hspace{0.17em}\text{cos}\left(k_{\mathrm{w}}W\right)+i{Z}_{\mathrm{w}}^2\hspace{0.17em}\text{sin}\left(k_{\mathrm{w}}W\right)}{Z_{\mathrm{s}}\hspace{0.17em}\text{sin}\left(\left(k_{\mathrm{w}}W\right)\right)-i{Z}_{\mathrm{w}}\hspace{0.17em}\text{cos}\left(k_{\mathrm{w}}W\right)},$$

$$Z_{\mathrm{b}}(x=W)=Z_{\mathrm{s}}.$$ (4)

For the half-wavelength resonant condition of k_wW = π, the impedances at each boundary are equal, i.e., Z_b(x = W) = Z_b(x = 0) = Z_s. The amplitude of Z_b(x = 0) reaches a maximum at resonance, which corresponds to minimum leakage of the wave from the fluidic domain. Away from resonance, on the other hand, the impedances at the boundaries are unequal, their phase difference increases, and the amplitude of Z_b(x = 0) decreases, resulting in less of the incoming wave entering the fluidic domain from the silicon wall.

To illustrate the influence of the boundary impedance, we present theoretical results of the 1-D wave propagation in the x-direction through the silicon and fluidic domains for microchannels for on-resonance (i.e., k_wW = π and 2π, shown in Videos 1 and 2 in the supplementary material, respectively) and off-resonance conditions (i.e., k_wW = 0.9π and 1.1π, shown in Videos 3 and 4, respectively).⁴⁵ Snapshots of the simulated, normalized velocity waves (v/v₀) at eight time points in a single period (i.e., t = 0, T/8, T/4, 3 T/8, T/2, 5 T/8, 3 T/4, and 7 T/8) are shown in Figures 2(a)–2(c). This simulation reveals two important trends. First, the magnitude of the normalized particle velocity in the fluidic domain is greatest when the channel is in resonance. In the two off-resonance cases, the amplitude of the acoustic pressure inside the fluidic domain is ≈44% compared to the on-resonant case. Snapshots of the corresponding normalized pressure waves (p/P₀) are shown in Figures 2(d)–2(f). Second, we observe for the off-resonant conditions that the location of the velocity maximum oscillates slightly about the channel center. This result indicates that the pressure distribution is no longer a standing wave, using the strictest definition; however, the wave translational motion is so small that it behaves practically like a standing wave and attracts particles to the time-averaged potential energy minimum in the center of the microchannel. The combination of these two effects leads to a broadening of shape of the potential energy minimum, and an overall reduction in the energy depth, which we believe is responsible for the reduced, but non-negligent, acoustic focusing in the slightly off-resonant conditions.

FIG. 2.

Numerical simulations of wave propagation through the acoustofluidic device. Plots of the normalized velocity waves (v/v₀) are shown for (a) k_wW = π, (b) k_wW = 0.9π, and (c) k_wW = 1.1π. Plots of the normalized pressure waves (p/P₀) are shown for (d) k_wW = π, (e) k_wW = 0.9π, and (f) k_wW = 1.1π. The grey regions of the waves indicate calculated values in the silicon domains, the blue regions of the waves indicate calculated values in the fluidic domain, and the dashed lines represent the boundaries between domains. Note: the incoming wave enters from the left-hand side and travels to the right in this simulation.

The motion of small spherical particles (much smaller than the wavelength) suspended inside fluidic cavities excited by an acoustic actuator has been studied in detail over the last few decades.^{21,22,32,40,46} For any given pressure distribution at an arbitrary frequency, the time-averaged acoustic radiation potential energy, U, of a small spherical particle, which was initially derived by Gor'kov²¹ and later by Bruus^22,46 is

$$U=V_{\mathrm{p}}\left[\frac{f_1}{2{\rho }_{\mathrm{w}}{C}_{\mathrm{w}}^2}⟨p_2^2⟩-\frac{3{\rho }_{\mathrm{w}}{f}_2}{4}⟨v_2^2⟩\right],$$ (5)

where f₁ = 1 − β_p/β_w and f₂ = 2(ρ_p − ρ_w)/(2ρ_p + ρ_w), and the angular brackets denote the time average operator of a complex function (β denotes compressibility). The acoustic radiation force on a particle is given by the negative gradient of the potential energy

$${\overrightarrow{F}}_{\mathrm{A}}=-\nabla U.$$ (6)

In the x-direction, the force is given by inserting Eqs. (1)–(3) into (5) and then (6), which leads to

$$F_x(x)=–{F_x}_0(k_{\mathrm{w}}W)\hspace{0.17em}\text{sin}\hspace{0.17em}(2k_{\mathrm{w}}(W–x)),$$ (7)

where F_x0(k_wW) = 2πV_pβ_wP₀² φ[Z_w²(Z_s + Z_w)(Z_s − Z_w)]/λ||G(k_wW)||². In this equation, the overall acoustic contrast coefficient is defined as φ = (f₁ + 3f₂/2), and its sign (positive or negative)² determines the stability of the particle at fixed points.⁴⁷ Particles with positive or negative contrast coefficients both migrate towards the potential energy minima; however, these minima appear at different locations depending on the properties of the particle and the carrier fluid. Specifically, particles with a positive contrast coefficient (as is the case with most particles and cells) have stable, fixed points at the spatial locations of odd multiples of quarter wavelengths in the microchannel, e.g., the location of x = λ/4 (or W/2 as described below). On the contrary, particles with a negative contrast coefficient (as is the case with lipids,² hollow glass,⁴⁸ and silicone particles and gels^4,11,23,43) have stable, fixed points at the locations of even multiples of quarter wavelengths, i.e., the locations include x = 0 or x = λ/2 (i.e., at the walls of the microchannel). Below, the radiation force components thus obtained in the x- and y-directions are used to calculate velocity fields for particles with positive contrast coefficients. For the numerical computations, we assumed room temperature and the following parameters for density and speed of sound in each medium: ρ_s = 2331 kg/m³, C_s = 8490 m/s, ρ_w = 998 kg/m³, C_w = 1481 m/s, ρ_g = 2300 kg/m³, C_g = 5647 m/s, ρ_p = 1050 kg/m³, and C_p = 2350 m/s.^27,29

B. Effect of resonance and amplitude on 2-D particle manipulation

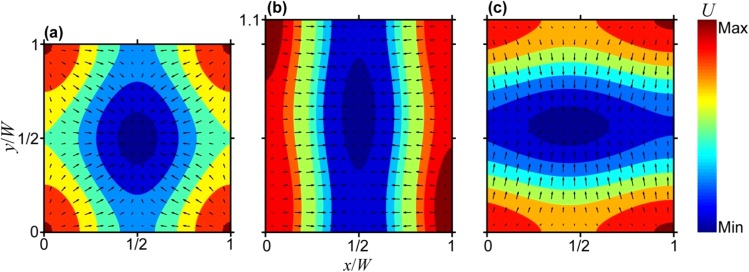
An approximate acoustic energy potential in a cross section of the microchannel can be obtained by the superposition of two independent, 1-D energy distributions in the x- and y-directions. Although the actual energy distribution across the microchannel is more complex, this linear superposition model is sufficient to interpret the distribution of suspended particles, depending on the input frequency and the dimensions of the fluidic cavity. Based on our wave propagation model, Figure 3(a) depicts the acoustic potential energy within a 2-D cross section of a perfectly square microfluidic channel that is excited by two orthogonal waves, each having the same magnitude of P₀. The energy minimum is symmetric in the x-dimension around x = W/2 and in the y-dimension around y = H/2, but the shape of the energy minima in the y-direction is wider than it is in the x-direction. This is because, in the y-direction, the top boundary is borosilicate, which has lower acoustic impedance than silicon, and consequently results in less acoustic energy for focusing in the y-direction. (It is important to note that the potential energy distributions presented in Figure 3 assume that the amplitudes of the waves in the x- and y-directions are equivalent, which is unlikely in real situations.) The negative gradient of the acoustic potential energy yields the acoustic radiation force applied on the suspended particles, which in the over-damped limit is directly proportional to the velocity field of the immersed particles,^27,32 also shown in Figure 3. Particles exhibiting positive acoustic coefficients tend to move towards the low energy regions located near the center of the cross section of the microchannel, and these energy maps are therefore useful in predicting the steady-state distribution of suspended particles in a continuous laminar flow along the length of the microchannel.

FIG. 3.

Two-dimensional energy maps and velocity fields. Contour plots of the relative acoustic potential energy (U) distribution. The arrows represent the velocity field of suspended particles and depict their trajectory towards the energy minimum (shown in dark blue). Calculated for (a) a microchannel with square cross section (W = H) driven at the common resonant frequency, and (b) and (c) a microchannel with rectangular cross section having an aspect ratio of 1.1 that is driven at a frequency of (b) 2.93 MHz (corresponding to resonance in the x-direction, k_wW = π), or (c) 2.62 MHz (corresponding to resonance in the y-direction, k_wH = π).

For the acoustofluidic devices investigated in this article, the aspect ratio of the cross section of the microchannel is approximately 1.1. We operated the device using the calculated resonant frequencies, which we expected would result in the narrowest acoustic focusing bandwidth experimentally (see Fig. 4 below). The length scales for the widths and depths correspond to two resonant frequencies occurring at 2.93 MHz and 2.62 MHz, respectively, which differ by ≈11%. This slightly rectangular microchannel allowed us (i) to test the sensitivity of particle focusing for slightly off-resonance conditions and (ii) to probe the range of conditions in which 1-D and 2-D focusing can be obtained as a function of the driving frequency in a single microfluidic device.

FIG. 4.

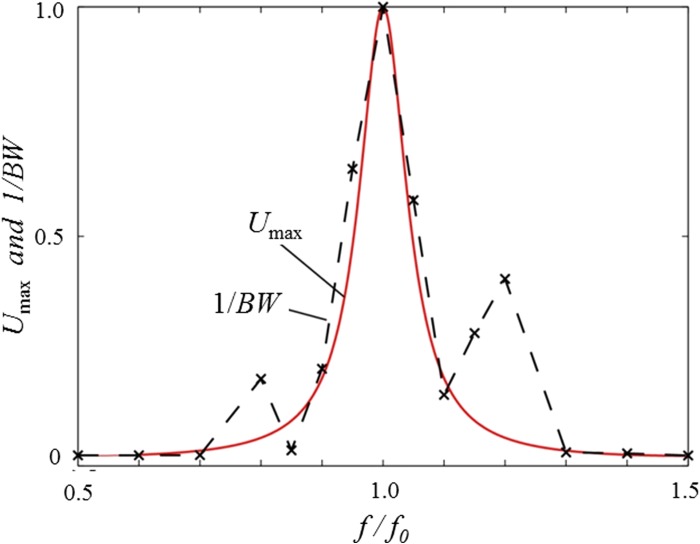
Maximum acoustic potential energy and bandwidth of the microparticles in the x-direction under different driving frequencies. The solid line represents the calculated relative amplitude of the acoustic potential energy (U_max), and the symbols connected by the dashed line (×) represent the experimentally measured reciprocal of the bandwidth (1/BW) of the microparticles across the width of the microchannel at different frequencies at a flow rate of 100 μl/min.

As shown in Figures 3(b) and 3(c), assuming equal power is transmitted to the microchannel along the x- and y-directions, the acoustic potential energy minimum (and thus the velocity field of suspended particles) will be elongated along W/2 in the y-direction when the driving frequency is 2.93 MHz, and along H/2 in the x-direction when the driving frequency is 2.62 MHz. The same effect could, in principle, be achieved in a square microchannel by controlling the relative power transmitted along the x- and y-directions. In Figures 3(b) and 3(c), the energy minimum is shifted slightly off center along the direction that is off-resonance since this dimension is not an integer multiple of the half wavelength. This is because we assume that the acoustic source is located on one side of the microchannel. Despite these approximations, our model predicts salient features of the particle distributions observed in acoustofluidic experiments, as shown later in Figures 5 and 6, which present confocal microscopy images of distributions of particles flowing through the microchannel as a function of the driving frequency, placement of piezoelectric element, and fluid flow rate. Both the cross-sectional view and the top view (i.e., x-y plane and x-z plane, respectively) are presented for these different conditions. In the supplementary material, we provide further details on our experimental results and their analyses including image processing methods, the result of control tests for which the acoustic field was absent, and fluorescence intensity profiles reflecting the particle distributions.⁴⁵ (N.B., throughout the article, we use the terms “focused” and “focusing” in a semi-quantitative sense to describe the degree to which particles are concentrated upon application of an acoustic field.)

FIG. 5.

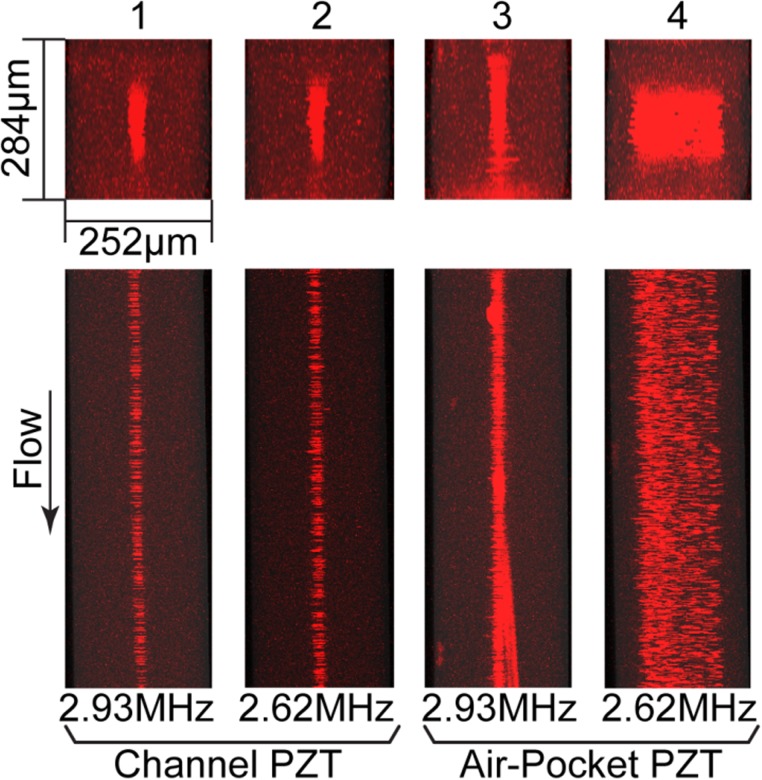
Stacked confocal fluorescence images of x-y planes (top) and x-z planes (bottom) of microchannels (W = 252 μm; H = 284 μm) at low flow rate. Cases 1–4 show image stacks obtained when Q = 20 μl/min. In Cases 1 and 2, the PZT transducer underneath the microchannel was activated at a driving frequency matching the resonant frequency either for width (Case 1) or for depth (Case 2) of the microchannel. Cases 3 and 4 are arranged in the same order as Cases 1 and 2 with regard to resonant conditions, but they were driven by a PZT transducer bonded underneath the air pocket.

FIG. 6.

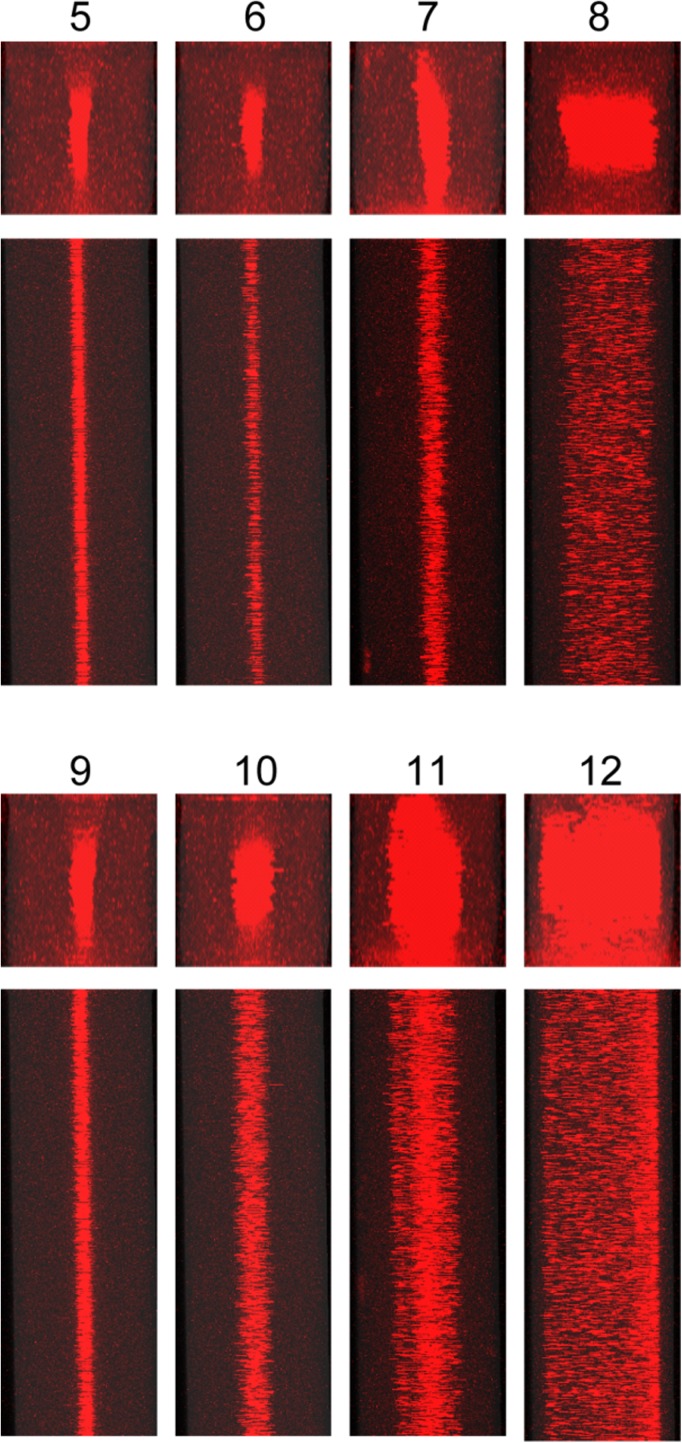
Stacked confocal fluorescent images of microchannels at medium and high flow rate. Cases 5–8 were observed at Q = 100 μl/min. Cases 9–12 were observed at Q = 200 μl/min. The driving frequency and PZT transducer placement corresponding to each image and scale of images is analogous to that in Fig. 5 (i.e., Cases 5, 6, 9, 10: “channel PZT” transducer; Cases 7, 8, 11, 12: “air pocket PZT” transducer; Cases 5, 7, 9 11: 2.93 MHz; and Cases 6, 8, 10, 12: 2.62 MHz).

To examine the dependence of the degree of particle focusing on acoustic frequency, in Figure 4, we show the relative amplitude of the acoustic potential energy, U_max, and the reciprocal of the bandwidth of the microparticles in the microchannel, 1/BW, under different driving frequencies at a flow rate of 100 μl/min. The values for U_max were obtained from Eq. (5) and 1/BW was obtained experimentally. We note that both quantities are normalized from 0 to 1 and that f₀ refers to the half-wavelength resonant frequency. When f = f₀, the amplitude of the acoustic potential energy reaches its maximum value, resulting in the maximum acoustic radiation force. As expected, the highest peak of 1/BW also occurs at this frequency, suggesting that the calculated resonant frequency is indeed very close to the actual resonant frequency. The correlation between U_max and 1/BW also reveals that some focusing is achieved as much as 10% off-resonance, which is consistent with our wave/boundary model. We note that, while there are some differences in the trends of potential energy and bandwidth signal around 0.8f₀ and 1.2f₀, these two curves match each other well in the range of 0.9f₀ to 1.1f₀. The increase in 1/BW at 0.8f₀ and 1.2f₀ was consistently observed in all trials and may be due to an artifact in the microchannel or experiment.²⁷ The emergence of resonance modes along the channel length can generate additional forces that were not accounted for in our model; however, these may be viewed as correction terms and were not required to explain the broadening of the experimental data in the frequency range of 0.9f₀ to 1.1f₀. For the sake of experimental simplicity, we constrained this bandwidth study to the x-direction; however, the same in principles apply in the y-direction.

Figure 5 shows confocal images of particles and fluid flowing in the microchannel at a low flow rate (i.e., Q = 20 μl/min). The average residence time in the section between the inlet and trifurcating point of the microchannel (25 mm in length) is 5.4 s. When the “channel PZT” transducer was activated, as shown as Cases 1 and 2, the acoustic radiation force applied on the particles in both x- and y-directions was substantial not only were the particles well focused at x = W/2 but also toward y = H/2. Interestingly, when the “air pocket PZT” transducer was activated, we only observed substantial acoustic focusing in the dimension at resonance, as shown as Case 3 (resonant in the x-direction) and Case 4 (resonant in the y-direction). That is, the focusing for Case 3 in its resonant dimension, i.e., x-direction, is similar to that observed in Cases 1 and 2, but the focusing in y-direction is poor, and vice versa for Case 4. Figure S4 in the supplementary material provides intensity profiles for the transverse and vertical directions for Cases 1–4.⁴⁵ We note that acoustic streaming, which can be interpreted as second order perturbations on pressure and velocity,^32,33,40 is not considered to have a substantial impact in determining the dynamics of the immersed particles in these experiments. As previously reported, acoustic streaming tends to transport small particles (i.e., smaller than ≈1 μm) towards either the top or the bottom of the microchannel in quiescent fluids or in laminar flow if the residence time is sufficiently long.³² However, as shown in Figures 5 and 6, we did not observe such phenomena, likely due to the imposed fluid flow. For convenience, we provide a brief description of each case tested under the confocal microscope in Table I.

TABLE I.

Case descriptions of acoustic focusing experiments shown in Figures 5 and 6.

	Case	Description
	1	“Channel PZT” transducer driven at f = 2.93 MHz; Q = 20 μl/min
	2	“Channel PZT” transducer driven at f = 2.62 MHz; Q = 20 μl/min
	3	“Air pocket PZT” transducer driven at f = 2.93 MHz; Q = 20 μl/min
	4	“Air pocket PZT” transducer driven at f = 2.62 MHz; Q = 20 μl/min
	5	“Channel PZT” transducer driven at f = 2.93 MHz; Q = 100 μ/min
	6	“Channel PZT” transducer driven at f = 2.62 MHz; Q = 100 μl/min
	7	“Air pocket PZT” transducer driven at f = 2.93 MHz; Q = 100 μl/min
	8	“Air pocket PZT” transducer driven at f = 2.62 MHz; Q = 100 μl/min
	9	“Channel PZT” transducer driven at f = 2.93 MHz; Q = 200 μl/min
	10	“Channel PZT” transducer driven at f = 2.62 MHz; Q = 200 μl/min
	11	“Air pocket PZT” transducer driven at f = 2.93 MHz; Q = 200 μl/min
	12	“Air pocket PZT” transducer driven at f = 2.62 MHz; Q = 200 μl/min

As shown in Figure 6, when the flow rate was increased to an intermediate value (i.e., Q = 100 μl/min), 2-D focusing was less prominent in Cases 5 and 6, wherein the “channel PZT” transducer was activated, as compared to the slower flow rate shown in Cases 1 and 2. For the cases of activation of the “air pocket PZT” transducer (Cases 7 and 8), some focusing was observed in the resonant direction, but in all cases, focusing was poorer than in Cases 5 and 6. While the degrees of focusing in Cases 5–8 are slightly lower than in the corresponding Cases 1–4, the general effects of the placement of the PZT transducer and resonance direction are similar for these two sets of data (see Figure S5 in the supplementary material for the intensity profiles for the transverse and vertical directions for Cases 5–8).⁴⁵ These qualitative differences in the acoustic focusing behaviors observed in Cases 5–8 compared to Cases 1–4 underscore the degree of sensitivity of acoustic focusing as a function of flow rate due to competing inertial effects.⁴⁹

As the flow rate was increased to a high value (i.e., Q = 200 μl/min), the residence time for the particles within the acoustic standing wave was reduced to 0.54 s. As shown in Cases 9 and 10 in Figure 6, when the PZT transducer is activated directly beneath the microchannel, the quality of focusing in the resonant direction is poorer than observed at lower flow rates; moreover, the sensitivity of focusing in the x-direction to the applied frequency was notably more pronounced. Cases 11 and 12 suggest that for such high flow rates, the residence time of the particles in the microchannel is so short that when the “air pocket PZT” transducer was activated, the acoustic field only has a weak effect on the particles. Furthermore, comparing Cases 9 and 11 at this high flow rate, it is clear that imposition of acoustic radiation forces to particles in resonant direction (i.e., the x-direction) is less effective for the placement of the “air pocket PZT” transducer compared to the placement of the “channel PZT” transducer. Similar findings are evident by comparison of Cases 10 and 12. Figure S6 in the supplementary material provides intensity profiles for the transverse and vertical directions for Cases 9–12.⁴⁵

For the acoustofluidic device used in this investigation, we observed better acoustic focusing in both x- and y-directions in the cases driven by the “channel PZT” transducer than in the cases driven by the “air pocket PZT” transducer, but other differences are apparent as well, specifically in relation to interpretation of focusing in view of the potential energy maps and velocity fields presented in in Figure 3. While the data in Cases 1 and 5 are consistent with Figure 3(b), for example, those in Cases 2 and 6 are not consistent with Figure 3(c); both the data in Cases 3 and 7 and those in Cases 4 and 8 are consistent with Figures 3(b) and 3(c), respectively. The differences are likely because the images in Figure 3 assume that the acoustic power is applied equally along both directions, while this is unlikely to occur under the conditions in which the experimental data were generated. Furthermore, for cases using the “channel PZT” transducer, since the pressure amplitude coupled to the microchannel is relatively high in x-direction, the quality of focusing may also become less sensitive to the resonant conditions. Another observation is that there is not much difference in the degree of focusing in the y-direction for most of the on-resonance conditions (e.g., Cases 2, 4, 6, 8 and 10) and in general the highest degree of focusing observed in this direction is significantly less than the maximum degree of focusing observed in the x-direction. This may be due to the magnitude of the potential energy well in the y-direction being lower than it is in the x-direction.

These results and analyses suggest: (1) the extent of acoustic coupling (i.e., focusing in the x- and y-directions in tandem) for a microchannel with an aspect ratio of ≈1 is strongest when the “channel PZT” transducer is activated; and (2) the extent of acoustic coupling is weakest, and therefore more sensitive to the mismatch between the width and depth of the microchannel, when the “air pocket PZT” transducer is activated. By exploiting these differences, perturbations from the “air pocket PZT” transducer may provide a means to independently manipulate particles in a predefined dimension (i.e., to enable 1-D or 2-D acoustic focusing). Such dynamic control the type of acoustic focusing may be useful for a variety of applications in acoustofluidics. For example, 1-D acoustic focusing may be more desired for high throughput cell sorting;¹¹ whereas, 2-D acoustic focusing may be more desired for the precise ordering of particles or cells for applications in sizing³⁸ and flow cytometry.¹²

C. Evaluation of pressure amplitudes, potential energy, and maximum velocities of particles

Based on the calculations in other previous studies,^50,51 one report suggests that if pressure waves within the aqueous solution have magnitudes in the range of 0.1–1.0 MPa, then the characteristic focusing timescale will be in the range of 7–700 ms.²⁷ One of the potential outcomes of the wave transmission model is that the inclusion of energy losses through the boundaries of the microchannel may lead to more accurate predictions of focusing timescales. Assuming that the particle motion is overdamped (low Reynolds number), its trajectory can be modeled by first order dynamics through integration of the velocity^{16,27,52–54}

$$\dot{x}=F_x(x)/6\pi \eta a.$$ (8)

A representative timescale required for a colloidal particle to migrate in the x-direction to the center of the flow stream from an initial position at a lateral wall of the fluid cavity is given by^16,27

$$T_{\text{max}}=\frac{6\pi \eta a}{F_{x0}(\pi )}\underset{a}{\overset{W/2-a}{\int }}\csc \left(2k_{\mathrm{w}}x\right)dx=\frac{6\pi \eta a\cdot \text{ln}\left|{\text{cot}}^2\left(k_{\mathrm{w}}a\right)\right|}{2k_{\mathrm{w}}{F}_{x0}(\pi )}.$$ (9)

We use W/2−a as the upper limit of the integral for computational convenience; using the limit of W/2 leads to an infinite T_max due to a singularly in the integral of Eq. (9) that occurs as a particle approaches a minimum in potential energy in an inertia-free environment.

T_max can be estimated by experimentally measuring the time required for particles distributed across the entire width of a microchannel to focus into a tight band after imposition of a resonant acoustic field. (T_max is comparable to the transverse focus time defined by Augustsson et al. in their study of focusing efficiency during flow.⁴⁴) To demonstrate this approach, Figure 7 presents data from video microscopy that can be used to obtain of an approximation of T_max. We made rough estimates by assuming that Figures 7(a) and 7(e) represent t = 0 and the time at which Figures 7(d) and 7(h) were collected represent T_max. Based on these assumptions, analysis of 10 sets of focusing images (e.g., such as those shown in Figure 7) revealed T_max ≈ 200 ms for the “channel PZT” transducer and T_max ≈ 300 ms for the “air pocket PZT” transducer. We note that this measurement can be easily accomplished with a simple fluorescent microscope with a CCD camera. In Figure S7, we provide a secondary measurement to verify these estimates through the use of a high speed camera, which yields T_max = 140 ms and 280 ms for the two driving methods, which are close to the estimates obtained from the video rate microscopy.⁴⁵ After evaluating Eq. (9), these two timescales lead to pressure amplitudes for the lateral standing waves of ≈0.55 MPa and ≈0.39 MPa, respectively, which are of same order as those obtained for similar experiments in published reports.³⁹ For the excitation conditions of the PZT transducers employed here, the maximum flow rates that provide a residence time to match the lateral convergence time are thus ≈500 μl/min for the “channel PZT” transducer and ≈300 μl/min for the “air pocket PZT” transducer. In practice, however, due to thermal perturbations, mechanical noise and defects in the system, complete focusing at these flow rates may not be achieved. We emphasize that a more precise measure of the pressure amplitude would require techniques such as microparticle image velocimetry or trajectory curve fitting.^27,33,44

FIG. 7.

Time evolution of particle distributions after imposition of a resonant acoustic field. (a)–(d) The particle distribution in the x-direction as a function of time upon excitation with a “channel PZT” transducer. (a) The initial particle distribution (i.e., uniformly distributed across the microchannel). The PZT transducer was actuated at a certain moment between frame (a) and its following frame (b), which is the first frame showing the particles beginning to converge toward the center of the microchannel. (c) The particles substantially concentrated at the center of the microchannel. (d) The particles acoustically focused to their final distribution. (e)–(h) Provide similar images obtained when using the “air pocket PZT” transducer to induce the resonant acoustic field. In all images, the flow rate is 100 μl/min and the PZT transducer is excited to 2.93 MHz. Complete videos of particle focusing (and defocusing) are provided as Videos 5 and 6 in the supplementary material for the cases of the “channel PZT” and “air pocket PZT” transducers, respectively.⁴⁵

With the pressure amplitudes for the lateral standing waves obtained, we provide estimates for the depth of the acoustic potential energy well in the x-direction at resonance from Eq. (5), along with the maximum velocity of an immersed particle in the same direction from Eq. (8). For the “channel PZT” transducer, the depth of the potential energy well is 12.0 fJ, leading to a maximum velocity of ≈1600 μm/s. For the “air pocket PZT” transducer, the depth of the potential energy well in the x-direction at resonance is 6.1 fJ, leading to a maximum velocity of 800 μm/s. These estimates are comparable with those reported in a previous study in which the pressure amplitude in the range of 0.08–0.66 MPa was associated with a potential energy well in the range of 0.34–26 fJ.²⁷ The results presented in Figures 5 and 6 indicate that the amplitude of the pressure and depth of the potential energy well for the vertical standing waves in the microchannel are smaller than those for the lateral standing waves. Using the estimates above for the pressure and potential energy and assuming that the focusing bandwidth in each direction is inversely proportional to its potential energy magnitude, we estimate that, for the “channel PZT” transducer, the depth of the potential energy well in the y-direction at resonance is ≈1 fJ, and corresponding amplitude of the pressure is ≈0.2 MPa. Likewise, for the “air pocket PZT” transducer, the depth of the potential energy well in the y-direction at resonance is ≈1 fJ, and corresponding amplitude of the pressure is ≈0.2 MPa.

V. CONCLUSIONS

We have studied the flow of microparticles in acoustofluidic channels of a nearly square cross section in which acoustic waves were excited by a single PZT transducer bonded in two configurations, either directly underneath the microchannel or under an air pocket trench that runs parallel to the microchannel. We observe that the particles flowing in these microchannels can be concentrated toward the central streamlines (i.e., focused) in both the horizontal (along the width) and vertical (along the depth) directions. We show that the degree of focusing depends on the acoustic frequency (in relation to resonant conditions and slight deviations thereof), flow rate, and placement position of the PZT transducer. While 2-D acoustic focusing has been previously shown using multiple acoustic actuators,^34–36 we use a single PZT transducer driven at a single frequency to fulfill the same task. An advantage of such a configuration is that the power consumption and control circuit of the acoustofluidic system can be proportionally reduced. Since point-of-care applications are among the leading motivations for lab-on-a-chip systems, such a simpler and versatile system may be desirable.

We have developed an approximate model for a 2-D wave propagation that provides a simple means to investigate the distribution of acoustic potential energy in both resonant and non-resonant conditions to predict particle distributions within the microchannel cross-section. This is particularly useful as the microchannel design and the tolerance of the microfabrication process of acoustofluidic devices will affect their performance in practice.

Taking the first odd resonant modes for both the width and depth of the microchannel as examples, we performed numerical calculations to obtain the distributions of the acoustic potential energy and the resultant velocity field of particles across the cross section of microchannels that are either perfectly square or slightly off-square (as in our experimental system). In the latter case, the width and depth of the microchannel have individual resonant conditions that deviated by ≈11%. Comparison of the experimental results to these calculations provides a means to assess the relative pressure amplitude transmitted to the channel in the vertical and horizontal directions by the PZT transducer placed on the device either beneath the pocket or at the air pocket trench. We also demonstrate that simple video microscopy measurements can be used in conjunction with the model to get order of magnitude estimates of the amplitude of the acoustic pressure leading to particle focusing.

These findings provide understanding of acoustic manipulation of particles that can have potential benefit to the design of a variety of acoustofluidic devices, including those used in bioassays,^4,6,7 cytometry,^12,13 cell separations,^4,12 and colloidal assembly.¹⁵ For example, for non-serial acoustic cellular sorting,¹¹ an off-square microchannel actuated by a single piezoelectric transducer placed underneath an air trench parallel to the microchannel may allow tight acoustic focusing laterally, but minimal focusing along the vertical dimension to maximize throughput. In laser-induced fluorescence-based flow cytometry, a square microchannel actuated by a single piezoelectric transducer placed underneath the microchannel may be desirable such that the width and depth are simultaneously at resonance under one frequency, whereby all particles have approximately the same flow velocity within a tightly focused streamline. Alternatively, an off-square acoustofluidic channel that is on-resonance in its depth, but off-resonance in its width might be preferable for implementation in an optical imaging based cytometry system in which cells can be constrained in a single focal plane at the half depth of the microchannel.

NOMENCLATURE

a and V_p

radius and volume of an immersed particle

C_i

speed of sound in i^th medium

f and ω

driving frequency and angular driving frequency

f₁ and f₂

acoustic contrast coefficients

F_x0

amplitude of the acoustic radiation force

p_i

first-order acoustic pressure in i^th medium

P₀

amplitude (base-to-peak) of the incoming wave

Q

convective flow rate through the microchannel

U

acoustic radiation potential energy

v_i

first-order acoustic particle velocity in i^th medium

v₀

amplitude of the acoustic particle velocity of the incoming wave

W and H

width and the depth of the microchannel

x and $\dot{x}$

position and the acoustophoretic velocity of a particle inside the microchannel

Z_i

acoustic impedance of i^th medium

1/G

amplification factor of the pressure amplitude

γ and η

kinematic and dynamic viscosity of the solution

δ

thickness of the acoustic boundary layer

λ_i and k_i

wavelength and wave number in the i^th medium

〈$v$〉

average velocity of the fluid

ρ_i

density of i^th medium

Subscripts

b

boundary

g

borosilicate glass

p

particle

s

silicon

w

water (Room temperature is assumed for estimation of materials properties.)