Abstract
We propose and mathematically examine a theory of calcium profile formation in unwounded mammalian epidermis based on: changes in keratinocyte proliferation, fluid and calcium exchange with the extracellular fluid during these cells’ passage through the epidermal sublayers, and the barrier functions of both the stratum corneum and tight junctions localised in the stratum granulosum. Using this theory, we develop a mathematical model that predicts epidermal sublayer transit times, partitioning of the epidermal calcium gradient between intracellular and extracellular domains, and the permeability of the tight junction barrier to calcium ions. Comparison of our model’s predictions of epidermal transit times with experimental data indicates that keratinocytes lose at least 87% of their volume during their disintegration to become corneocytes. Intracellular calcium is suggested as the main contributor to the epidermal calcium gradient, with its distribution actively regulated by a phenotypic switch in calcium exchange between keratinocytes and extracellular fluid present at the boundary between the stratum spinosum and the stratum granulosum. Formation of the extracellular calcium distribution, which rises in concentration through the stratum granulosum towards the skin surface, is attributed to a tight junction barrier in this sublayer possessing permeability to calcium ions that is less than 15 nm s−1 in human epidermis and less than 37 nm s−1 in murine epidermis. Future experimental work may refine the presented theory and reduce the mathematical uncertainty present in the model predictions.
Introduction
The calcium distribution within the mammalian epidermis is both an indicator of the skin barrier function [1] and a regulator of epidermal structure [2]. Here, using a mathematical model, we propose and examine a theory of the key mechanisms that control the calcium profile in unwounded epidermis.
The epidermis and its calcium profile
The epidermis consists predominantly of keratinocytes [3]. These cells are continuously being produced at the bottom of the epidermis, driven to passively migrate towards the skin surface, and are sloughed away during everyday activity [4]. During this life cycle, keratinocytes express distinct phenotypic changes which characterise the boundaries of four sublayers of the epidermis:
The stratum basale (SB): Keratinocytes proliferate. The exact pattern of proliferation is still a matter of debate [5], and is suggested to involve either one [6, 7] or two cell types [8]. The single progenitor theory posits that a single population of slowly-cycling cells maintains epidermal homeostasis, whilst the more traditional two progenitor theory proposes that the SB consists of two keratinocyte subpopulations: (1) stem cells, which proliferate slowly and indefinitely, each time producing one stem cell and one transit amplifying (TA) cell, and (2) TA cells, which divide symmetrically 3–5 times before leaving the SB [9, 10].
The stratum spinosum (SS): Keratinocytes increase in volume [11] and passively migrate towards the skin surface, displaced from the SB by proliferation there.
The stratum granulosum (SG): Keratinocytes become flattened and disintegrate, reducing their volume [12] and expelling lamellar bodies [13].
The stratum corneum (SC): Denucleated and highly flattened keratinocytes, called corneocytes, combine with lipids from the lamellar bodies exocytosed in the SG, in a “bricks and mortar” architecture [14] that forms the primary skin barrier [4]. Transepidermal water loss (TEWL) experiments, which involve progressive tape-stripping of the SC to identify the thickness that must be removed to cause fluid flow to significantly increase across this sublayer, suggest that this barrier is only strongly impermeable in the top 4–8 μm of the SC [15–17]. Hence we subdivide this epidermal sublayer into the lower SC (progressive barrier) and upper SC (impermeable barrier). At the top of the upper SC, intercorneocyte linking structures degrade and corneocytes are shed from the skin surface [18].
Epidermal calcium is present in three different localisations: the extracellular fluid (ECF), intracellular cytosol and intracellular organelles [19]. Calcium concentrations in the ECF and organelles are significantly higher than in the cytosol [20, 21]. These concentration differences are maintained by calcium pumps present on the membranes of keratinocytes and their intracellular structures, which actively remove calcium from the cytosol [22]. If we consider calcium in the ECF as “extracellular”, and calcium in cytosol and organelles together as “intracellular”, then it is the action of the calcium pumps on the keratinocyte membrane that is crucial for controlling intracellular and extracellular calcium levels [23].
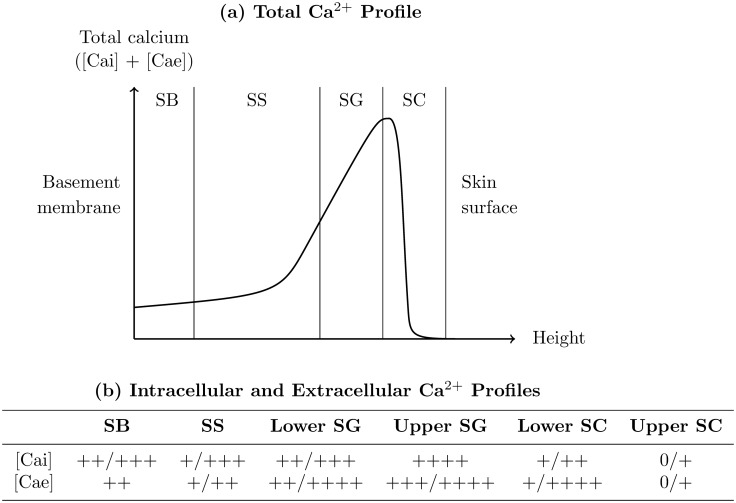
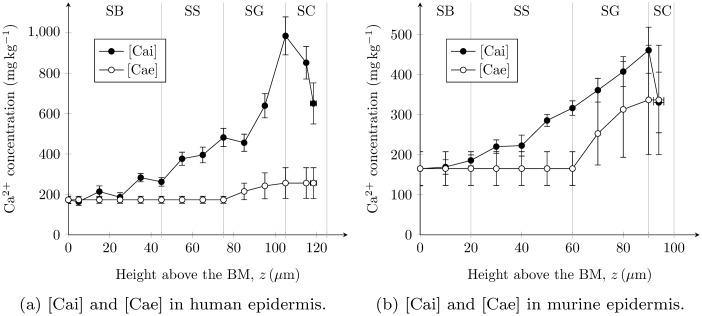
The total epidermal calcium profile, which is a summation of calcium from intracellular and extracellular localisations, has been quantitatively measured using proton-induced X-ray emission (PIXE) [24–28], and in unwounded skin these measurements typically adhere to the profile shown in Fig. 1a. The total calcium concentration is low in the SB, rises gradually to a peak in the SG (the so-called “epidermal calcium gradient”), and drops to near-negligible levels in the SC. Because the PIXE technique has a resolution of ∼ 10 μm [29], it is unclear whether the calcium drop towards the skin surface occurs at the SG-SC interface or further into the SC: the latter interpretation is quite feasible since the skin’s primary barrier might only be fully formed in the upper SC, based on the previously discussed TEWL experiments. PIXE cannot distinguish between the intracellular and extracellular contributions to the epidermal calcium profile.
Figure 1. The epidermal calcium distribution.
(a) Typical shape of the total profile found quantitatively using PIXE (for examples in the experimental literature, see [26, 28]). (b) Typical shape of the semi-quantitative intracellular ([Cai]) and extracellular ([Cae]) profiles measured using ion capture cytochemistry (for examples in the experimental literature, see [32–34]).
On the other hand, the intracellular and extracellular epidermal calcium profiles have been measured separately using ion capture cytochemistry [30, 31], but only semi-quantitatively [32–34]. As indicated in Fig. 1b, both intracellular and extracellular profiles qualitatively agree with the total profiles obtained from PIXE, but it is difficult to make additional interpretations from this semi-quantitative data.
For the past decade, the presence of the epidermal calcium profile has been attributed solely to the presence of the SC barrier [35], which is thought to act as a sieve, selectively allowing water but not calcium to leave the viable epidermis [36]. When the epidermis is wounded, its calcium profile disappears rapidly then reappears gradually with restoration of the skin’s barrier function [1, 37, 38]. This observation fits easily within the conventional sieve view of epidermal calcium profile formation, as the removal of the SC simply removes the impetus for the calcium gradient to form.
However, recent measurements of the epidermal calcium distribution using fluorescent lifetime imaging [36, 39] have brought this view into question. These measurements demonstrated that the bulk of free calcium is present in intracellular organelles [36], and that epidermal barrier disruption triggers a mobilization of high amounts of calcium from these stores [39]. This prompted the questioning of this conventional view that the epidermal calcium profile is regulated only passively by the SC. In previous work, using a mathematical model, we found that this profile is largely intracellular and regulated by sublayer-specific changes in the action of keratinocyte membrane pumps [23]. In the current paper, we extend this analysis further, to propose that there are three key mechanisms that control epidermal calcium profile formation in unwounded skin: the passive impermeable barrier of the SC, tight junction-limited calcium diffusion in the SG, and a phenotypic switch in calcium exchange between keratinocytes and extracellular fluid at the SS-SG boundary. We also investigate the contribution of the stem and TA cell subpopulations of the SB, volume changes of keratinocytes in the SS, and calcium located in the lower SC, to the formation of the calcium profile of unwounded epidermis.
Proposed key mechanisms regulating the calcium profile
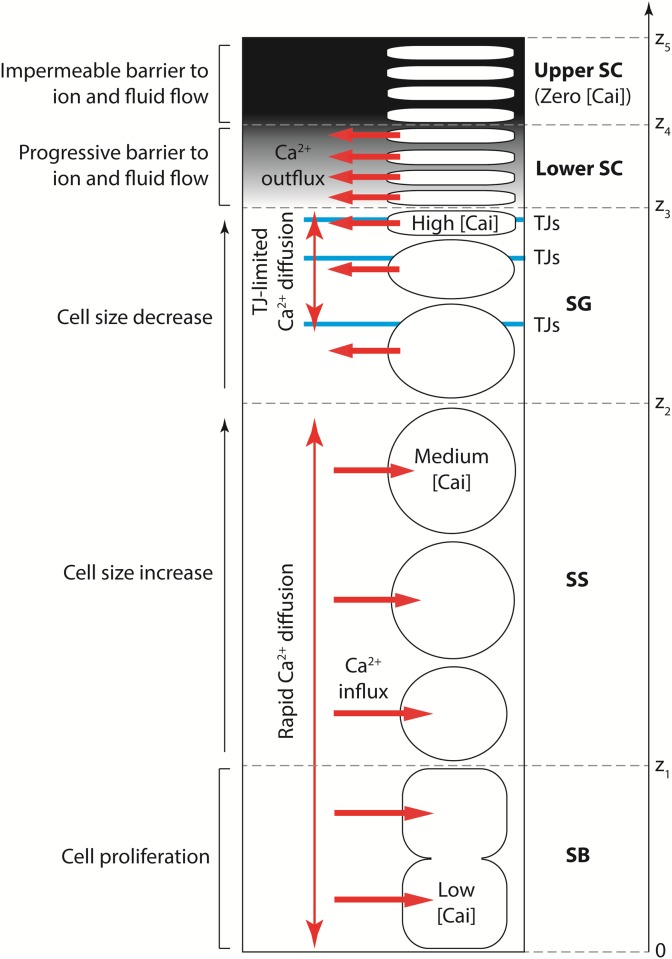
Our proposed theory is presented schematically in Fig. 2. We treat the calcium present in the cytosol and organelles within keratinocytes together as intracellular calcium, with the majority of this calcium likely to be confined to the keratinocyte organelles [21]. Most epidermal calcium is present in this intracellular calcium [36], which possesses a distinct spatial profile that forms as follows. Membrane pumps on keratinocytes act to accumulate calcium intracellularly from the ECF in the SB and SS, and in the SG this behaviour reverses to calcium expulsion into the ECF [23], emptying the intracellular stores [39] so that corneocytes in the upper SC contain negligible levels of intracellular calcium. These mechanisms yield an intracellular calcium profile that is low in the SB, rises gradually towards a peak in the SG, and drops rapidly in the SC, in agreement with the experimental observations for both the total and intracellular profiles (see Figs. 1a and 1b).
Figure 2. Proposed conceptual model of epidermal calcium profile formation in unwounded skin.
The mathematical model presented in this paper simplifies the progressive barrier in the lower SC to a distinct barrier at the lower-upper SC boundary.
The extracellular calcium profile, which possesses far less calcium due to the small volume of the epidermis occupied by the ECF [36, 40], forms as follows. The ECF is essentially water [41], and hence extracellular calcium in the SB and SS diffuses rapidly to near-constant levels throughout these sublayers [23]. In the SG, cell-cell adhesions known as tight junctions (TJs) are located apically between the lateral membranes of neighbouring keratinocytes [42, 43], and form a permeability barrier to calcium ions [44, 45] that reduces the rate of extracellular calcium diffusion there. Because calcium is continuously being expelled by keratinocytes near the skin surface, this TJ-limited calcium diffusion in the SG causes the extracellular calcium concentration to be slightly elevated there, negligibly affecting the calcium levels in the underlying SB and SS [46]. Lipids cannot be responsible for this elevated extracellular calcium concentration in the SG because they are localised only at the SG-SC boundary prior to their contribution as the “mortar” of the SC barrier. Extracellular calcium cannot enter the upper SC due to its barrier function, in agreement with the TEWL experiments [15–17]. These mechanisms together yield an extracellular calcium profile which is nearly constant in the SB and SS, rises in the SG, and drops rapidly in the SC, in agreement with experimental observations of the extracellular profile (see Fig. 1b).
Materials and Methods
Main equations
We mathematically model the epidermis as a saturated porous medium [47]. This modelling strategy has been used previously to consider avascular tumour growth [48–50] and cell behaviour within an artificial scafffold [51], justified for the viable sublayers of the epidermis in our previous paper [23], and proposed for modelling the SC of the epidermis by Kitson and Thewalt [52].
As a porous medium, we assume that the keratinocytes behave uniformly and are analogous to soil particles, and the surrounding ECF is analogous to the water that saturates the soil system. We assume that keratinocytes and ECF are comprised of an identical, incompressible fluid. Calcium is always dissolved in the cells or ECF. Calcium contained in the cytosol and intracellular organelles of cells are considered together simply as intracellular calcium. This simplification means that we do not specifically consider the intracellular dynamics of calcium exchange between the cytosol and organelles. We cannot discount the possibility that the intracellular calcium dynamics may play an important role in the partitioning of calcium between intracellular and extracellular domains, although investigating this is beyond the scope of the present work. As we are only interested here in identifying the extracellular and intracellular contributions to the epidermal calcium profile, consideration of cytosolic and organelle calcium separately is not necessary to investigate our proposed theory. Experimentally, intracellular calcium waves are known to propagate between adjacent keratinocytes [53], but these waves negligibly affect the epidermal calcium profile. Hence, in our model calcium cannot travel directly between keratinocytes, but rather can only be exchanged between cells and the surrounding ECF.
We assume that both the structure and calcium profile of the epidermis have reached a distribution that is stable and unchanging with time. Because of this we consider only one spatial direction z perpendicular to the skin surface. For this simplification, we ensured that any model parameters recorded for the three-dimensional case are also appropriate for the one-dimensional case. The main equations of our model, derived from mass conservation equations for the fluid and calcium present both in cells and ECF, are identical to those from our previous paper [23], but with one important exception. We do not specify the ECF velocity, because it will be unpredictably modified by TJs [54] and aquaporins [55, 56], neither of which were considered in [23]. With all these considerations in mind, the main equations of our model are
| (1a) |
| (1b) |
| (1c) |
where φ is the cell volume fraction, ρ ci and ρ ce are the superficial intracellular and extracellular calcium concentrations respectively, u i and u ce are the physical velocities of the cells and extracellular calcium respectively, f is the rate of change of cell volume fraction due to fluid exchange between ECF and cells, and g is the rate of change of superficial intracellular calcium concentration due to calcium exchange between ECF and cells. Functions f and g are positive when fluid and calcium respectively are being transferred from ECF to cells, and negative when fluid and calcium respectively are being transferred from cells to ECF. We next use equations (1a)–(1c), together with defined boundary conditions, to derive equations for calculating: keratinocyte velocity profiles u i(z) and transit times through the epidermis, the intracellular calcium profile ρ ci(z) and pattern of calcium exchange between keratinocytes and the ECF g(z), and the dependence of the extracellular calcium profile ρ ce(z) on the permeability of the TJ barrier to calcium ions.
Model domain and boundary conditions
In this section, we define the model domain and provide two boundary conditions each for u i(z), ρ ci(z) and ρ ce(z) as part of our proposed theory, although not all of these conditions will be necessary for our subsequent analysis. The epidermal sublayers shown in Fig. 2 are defined as follows: the SB in 0 ≤ z ≤ z 1, the SS in z 1 < z ≤ z 2, the SG in z 2 < z ≤ z 3, the lower SC in z 3 < z ≤ z 4 and the upper SC in z 4 < z ≤ z 5. We assume that the two progenitor theory holds for human and murine epidermis [8]. In the two progenitor theory, the SB consists of stem cell and TA cell subpopulations which are suggested to form two spatially separate compartments [57, 58]. Hence we subdivide the SB into compartments consisting of stem cells, 0 ≤ z ≤ θz 1, and TA cells, θz 1 < z ≤ z 1, where θ is the volume fraction of the SB occupied by stem cells.
In our model, equation (1a) defines the dynamics of epidermal cells, whilst equations (1b) and (1c) define the dynamics of epidermal calcium. Because keratinocytes occupy all sublayers of the epidermis, the model domain for equation (1a) is 0 ≤ z ≤ z 5. Keratinocytes cannot pass through the BM (z = 0) but are continuously expelled at the skin surface (z = z 5), sloughed away during everyday activity [4]. Hence the boundary conditions for equation (1a) are
| (2a) |
| (2b) |
Our description of epidermal calcium profile formation treats the lower SC as a progressive barrier and the upper SC as an impermeable barrier to fluid and ion flow, based on TEWL experiments [15–17] and the observation of non-negligible calcium levels in the lower SC [33]. In our model we simplify this to treat the boundary between the lower and upper SC, denoted z 4, as the impermeable barrier to transport of fluid and ions. Hence the model domain for equations (1b) and (1c) is 0 ≤ z ≤ z 4.
Intracellular calcium cannot travel across the BM because it is contained within keratinocytes, and is completely absent in the corneocytes of the upper SC [34, 37]. Hence the boundary conditions for equation (1b) are
| (2c) |
| (2d) |
The calcium present in the epidermis originates from movement of fluids and calcium across the BM [59], which at steady state must therefore act as a source of extracellular calcium with constant and positive concentration. Extracellular calcium is prevented from entering the upper SC by the impermeable barrier acting at z 4. Hence the boundary conditions for equation (1c) are
| (2e) |
| (2f) |
For the analysis performed in this paper, we will only explicitly require two of the six boundary conditions listed here, equations (2a) and (2f).
Calculating keratinocyte velocity profiles and transit times
Using equation (1a), the keratinocyte velocity profile u i(z) is estimated from profiles that we now define for the cell volume fraction, φ(z), and volume exchange between cells and ECF, f(z). We specify f(z) as
| (3) |
This form expresses the different proliferation rates s 0 and s 1 of stem and TA cells in the SB [60], the rate of volume increase s 2 for keratinocytes migrating through the SS [11], the rate of volume decrease s 3 for keratinocytes migrating through the SG [12], and the relative structural inertness of corneocytes in the SC [61].
The cell volume fraction φ is assumed to be constant and equal to φ v throughout both the viable sublayers (SB, SS and SG) and the lower SC [62]. The “bricks and mortar” architecture of the upper SC [14] constitutes a slow-moving relatively impenetrable barrier to fluid transport [63], equivalent to a sublayer consisting solely of keratinocyte-derived contents (φ = 1). Hence the cell volume fraction profile φ(z) is specified as
| (4) |
The superficial keratinocyte velocity φu i is assumed to be continuous at each of the sublayer boundaries, to ensure that cell mass flow is continuous throughout the epidermis. This consideration, together with equations (1a), (2a), (3) and (4), yield the keratinocyte velocity profile u i(z) as
| (5) |
Rates s 2 and s 3 are obtained from empirical observations of the ratio of keratinocyte volumes between the upper and lower boundaries of the SS, V 1 > 1 (net volume increase from lower to upper boundary), and the SG, V 2 < 1 (net volume decrease from lower to upper boundary), respectively, by use of the equations
| (6a) |
| (6b) |
Equations (6a) and (6b) can be obtained using mathematical procedures similar to the derivation of s 2(R) provided in Appendix B of [23].
Using the cell velocity profiles u i(z) defined by equations (5), (6a) and (6b), transit times through the various epidermal sublayers are calculated via
| (7) |
where τ(z a,z b) is the average time taken for a keratinocyte to move from height above the BM z a to height z b. We assume that the transit through the SB can be approximated by the transit through the TA cell compartment, because the volume of SB occupied by stem cells is negligible compared to TA cells [64], and stem cells possess theoretically infinite transit time because they may never leave the SB. Hence, from equations (5) and (7) the epidermal transit times are given by
| (8a) |
| (8b) |
| (8c) |
| (8d) |
Calculating profiles of intracellular calcium and calcium exchange
In this section we show how the intracellular calcium profile ρ ci(z) and calcium exchange between keratinocytes and ECF g(z), can be estimated from the total epidermal calcium profile ρ(z).
The total calcium profile is a summation of intracellular and extracellular calcium profiles,
| (9) |
but extracellular calcium provides only a small contribution (2–10 mg/kg) to the total calcium profile in the epidermis (100–1100 mg/kg) [23, 36]. Hence, to estimate the intracellular calcium profile ρ ci(z) from the total calcium profile ρ(z) using equation (9), at the scale of ρ(z) we approximate the extracellular calcium distribution by a constant equal to its mean value throughout the epidermis,
| (10) |
Here, r is a nondimensional factor equal to the ratio of the mean extracellular calcium concentration of all sublayers enclosed by [0, z 4] to its concentration at the BM, and whose uncertainty bounds express the variation of the extracellular calcium concentration throughout these sublayers. The BM levels of total and extracellular calcium are related by
| (11) |
an equation that was derived in Appendix C of [23] under two assumptions: (1) the motion of calcium across the BM only involves transfer between the free dermal and extracellular epidermal calcium, and (2) the BM provides no barrier for this transfer.
Combining equations (9)–(11), the intracellular calcium profile can be estimated from the total calcium profile via
| (12) |
Equations (5) and (12) can be used to estimate the keratinocyte velocity profile u i(z) and intracellular calcium profile ρ ci(z). The pattern of calcium exchange g(z) between cells and ECF can then be calculated from these two profiles using equation (1b) [23],
In the following, we derive equations that link the extracellular calcium distribution to the permeability of the TJ barrier.
The effect of tight junctions on extracellular calcium diffusion
TJs regulate the extracellular flow of calcium ions in the SG [44, 45], and we model this as a reduction in the rate of extracellular calcium diffusion there. This effect is introduced through the term representing extracellular calcium flux, ρ ce u ce, that appears in equation (1c). The extracellular calcium flux ρ ce u ce may consist of contributions from both diffusion and advection, the latter of which we expect to be negligible in epidermal sublayers where TJs are not present [23]. However, in epidermal sublayers where TJs are present, for advection to be negligible compared to diffusion we must ensure explicitly that the Péclet number, Pe, satisfies
| (13) |
where is the characteristic length scale over which the effects of diffusion and advection are being compared, ∣u e∣ is the ECF velocity that characterises the advective contribution, and D is the Fickian diffusion coefficient that characterises the diffusive contribution. In this paper we limit our analysis to cases for which inequality (13) is satisfied. We specify the extracellular calcium diffusion coefficient as
| (14) |
where D Ca is the physical diffusion coefficient of calcium in the ECF in the absence of TJs, and ε Ca represents the factor reduction in diffusion coefficient D Ca induced by the presence of TJs.
In equation (14) we have assumed that TJs are evenly spread throughout the SG, which represents a simplification to the dynamic model we proposed for skin equivalent construct growth [46, 65], and that they are mostly absent in other sublayers. Whilst structures similar to the disassembly of TJs have been observed at the SG-SC interface [66] and TJ-like structures have been observed in the SC [67], for simplicity we assume that these structures provide no restriction on extracellular calcium ion flow there.
The permeability of a barrier can be written as a ratio of the diffusion coefficient of the substance within the barrier to the barrier’s width [68]. Hence the permeability of the TJ barrier to calcium, P Ca, which spans the SG z 2 to z 3, and has local diffusion coefficient there of ε Ca D Ca according to equation (14), is
| (15) |
Combining equations (13)–(15), we find that the inequality
| (16) |
is identical to the requirement given by inequality (13). Inequality (16) demonstrates that the permeability of the TJ barrier must be significantly larger than the local ECF velocity in order to disregard the contribution of advection to extracellular calcium dynamics. From [23] we expect that max{∣u e∣} is in the absence of TJs and aquaporins and hence we require
| (17) |
which effectively places a lower limit on the possible values of P Ca that we investigate here. In summary, we include the effect of tight junctions on extracellular calcium dynamics in our model by assuming that the extracellular calcium flux ρ ce u ce in equation (1c) is dominated by Fickian diffusion with coefficient D defined by equation (14), and this approach is valid if the permeability of the TJ barrier in the SG satisfies inequality (17).
Calculating the extracellular calcium profile
To derive an expression for the extracellular calcium profile ρ ce(z), we first equate (1b) and (1c) through the common term g, and assume that Fickian diffusion is the dominant contribution to the extracellular calcium flux, ρ ce u ce = −D dρ ce/dz, to obtain
| (18) |
Both sides of equation (18) are then integrated with limits z and z 4. We thereafter substitute boundary condition (2f), which yields
| (19) |
In epidermal sublayers where TJs are not present (i.e. everywhere except the SG), extracellular calcium kinetics are sufficiently dominated by diffusion that ρ ce is constant [23]. Hence, replacing z by z ′ in equation (19), integrating this equation with limits 0 and z, and substituting equations (14) and (15), yields
| (20) |
In this equation, ρ ci(z) can be calculated from ρ(z) using equation (12). Hence, equation (20) expresses the extracellular calcium profile ρ ce(z) in terms of ρ(z), u i(z) and P Ca, if inequality (17) is satisfied.
Relationship between tight junctions and the extracellular calcium profile
Finally, to clearly demonstrate the effect of the TJ barrier on the extracellular calcium profile, we define R ce as the rise in extracellular calcium through the SG,
| (21) |
From equations (20) and (21), the relationship between the rise in extracellular calcium concentration through the TJ barrier in the SG, R ce, and the permeability of this barrier, P Ca, can be written in the elegant form
| (22) |
where P 0 is a constant that depends on the epidermal keratinocyte velocity and calcium profiles,
| (23) |
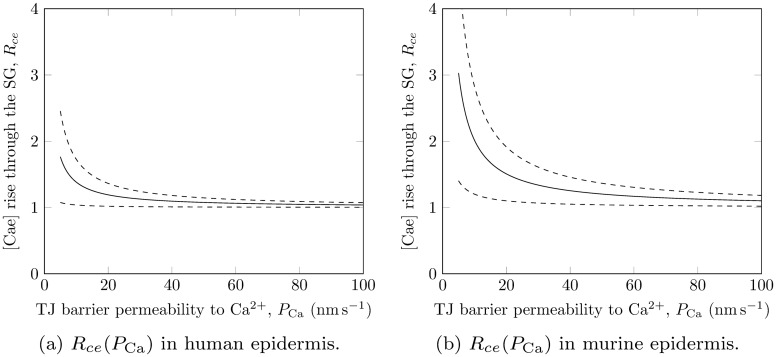
Using equations (22) and (23), the effects of a range of values for the permeability of the TJ barrier to calcium P Ca on the defining feature of the extracellular calcium profile (its rise through the SG, R ce) can be easily investigated, once the value of P 0 is known.
Results
The key predictions of our model are presented here. All mathematical equations were stated and derived in Materials and Methods. All parameters were obtained from experimental literature (see S1 Text) and are stated in Table 1. In our calculations we also used the total calcium profiles ρ(z) for human and murine epidermis reported in [28] and [26] respectively. All uncertainty bounds were calculated using error propagation formulae from [69, 70] under the assumption that the error distributions of all parameters were independent (i.e. zero covariance).
Table 1. Model Parameters.
| Parameter | Value and Reference | |
| Human | Murine | |
| Stem cell volume fraction of the SB, θ | 0.055±0.045 [64] | 0.055±0.045 [64] |
| Height of the SB-SS boundary above the BM, z 1 | 45 μm [95] | 20 μm [26] |
| Height of the SS-SG boundary above the BM, z 2 | 75 μm [95] | 60 μm [26] |
| Height of the SG-SC boundary above the BM, z 3 | 105 μm [95] | 90 μm [26] |
| Height of the inner SC-outer SC boundary above the BM, z 4 | 118.5±1.5 μm [15–16, 28] | 94±2 μm [17, 26] |
| Thickness of the epidermis, z 5 | 125 μm [28] | 100 μm [26] |
| Ratio of keratinocyte volumes SG:SB, V 1 | 1.9±0.5 [96] | 2.8±1.4 [97, 98] |
| Ratio of keratinocyte volumes SC:SG, V 2 | 0.54±0.10 (original) [12] 0.100±0.026 (modified) [96, 99] |
0.068±0.03 [97–99] |
| Proliferation rate of stem cells in the SB, s 0 | 5.6×10−7 s−1 [60] | 1.4×10−6 s−1 [60] |
| Proliferation rate of TA cells in the SB, s 1 | (1.7±1.1)×10−6 s−1 [88, 100] | (2.8±1.3)×10−6 s−1 [101] |
| Physical diffusion coefficient of calcium in the ECF, D Ca | 1×10−9 m2 s−1 [102–104] | 1×10−9 m2 s−1 [102–104] |
| Cell volume fraction in viable epidermis and lower SC, φ v | 0.955±0.025 [36] | 0.9925±0.0025 [40] |
| Ratio of the extracellular calcium distribution to its BM value, r | 1.1±0.6 [33, 34] | 1.25±0.75 [32] |
Parameters used for the numerical solutions in this paper. Justification is provided in S1 Text.
Epidermal transit times and keratinocyte velocities
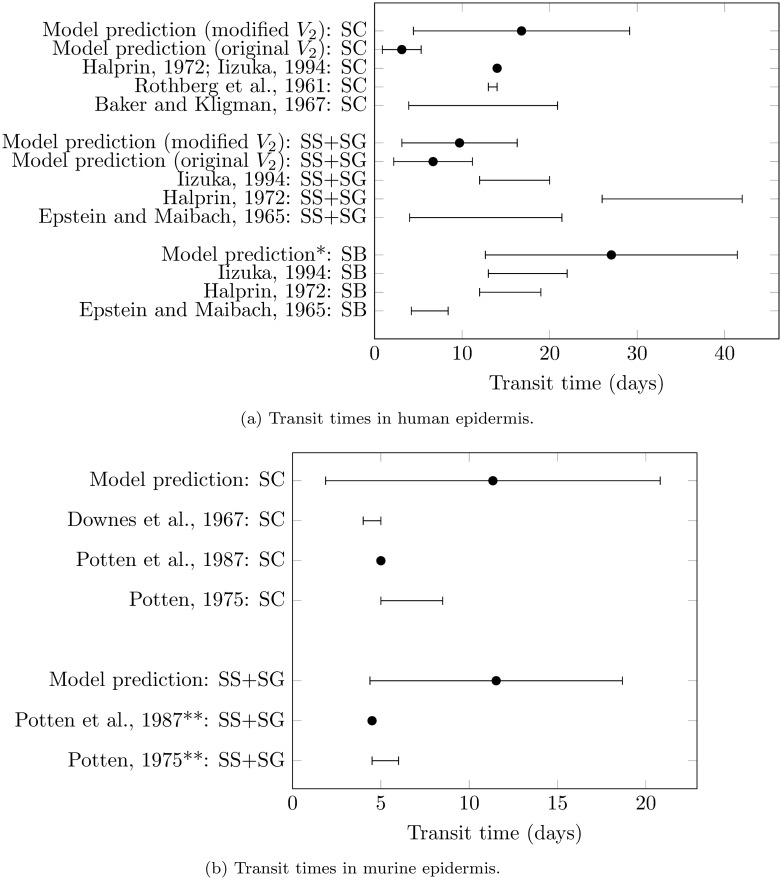
Using equations (5)–(8) of our model, transit times through individual sublayers of human and murine epidermis were calculated. Our model’s predictions of transit times mostly compared favourably with the literature values, as shown in Fig. 3, although it is difficult to quantitatively compare these values due to the large uncertainty present in the transit times both from the literature and predicted by our model. The uncertainty in our model predictions of transit time is due to the uncertainty present in model parameters (Table 1), all of which were obtained from the experimental literature. Hence, a better quantitative comparison of transit times from the literature and model requires experimental data possessing reduced uncertainty. We could not find literature values of transit time through murine SB so did not include comparisons for these.
Figure 3. Comparison of epidermal sublayer transit times predicted by our model with experimental literature values.
(a) Human literature values from [87–91]. (b) Murine literature values from [92–94]. *Model prediction in the SB was independent of the value of V 2. **Value may include some residence time in the SB.
The model prediction of transit time through human SC was much smaller than two of the three corresponding literature estimates. We attributed this discrepancy to our parameter estimate for human V 2 = 0.54±0.10, which was much larger than the estimate for murine V 2 = 0.068±0.034, the latter of which led to reasonable predictions of murine transit times. Hence, we modified our estimate of human V 2 to 0.100±0.026, a value which was calculated from division of literature values for murine V 1×V 2 by human V 1 (see S1 Text). The resulting predicted transit time for human SC agreed far better with the literature values for this transit time (Fig. 3a). Because this modification of V 2 created agreement between estimates of keratinocyte volume size changes and transit times through our model, our analysis suggests that keratinocytes lose at least 87% of their volume during their disintegration in the SG, in both human and murine epidermis.
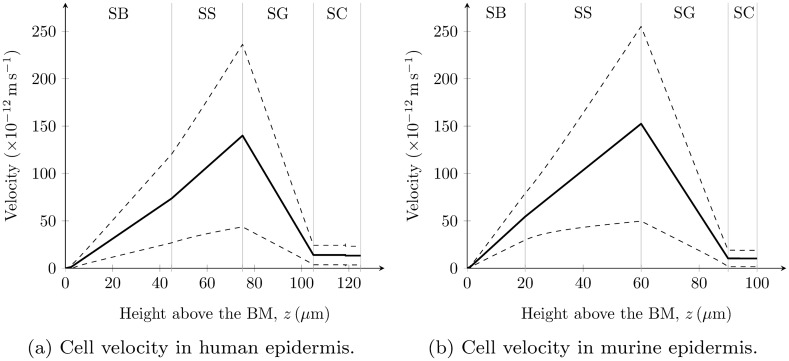
Keratinocyte velocity profiles u i(z) calculated using equations (5), (6a) and (6b) are shown in Fig. 4. For the calculation of the human u i(z) profile, the modified V 2 was used. Regardless of the value of human V 2, in our model results there was little difference between the keratinocyte velocity distributions in the lower sublayers of human and murine epidermis. This conclusion extends to the upper sublayers if the keratinocyte volume decrease through human SG agrees with our modified value for V 2 (i.e. 90.0±2.6% volume reduction).
Figure 4. Keratinocyte velocity profiles predicted by our model.
For (a) the human keratinocyte velocity profile, the modified V 2 = 0.100±0.026 was used in its calculation. The solid and dashed lines represent the mean values and uncertainty bounds (± SD) respectively.
The extracellular calcium rise mediated by tight junctions
Figs. 5a and 5b show the relationships between the rise in extracellular calcium through the SG and the permeability of the TJ barrier there, for human and murine epidermis respectively, that were predicted by our model using equations (22) and (23). Results are only shown for P Ca ≥ 5 nm s−1 in order to satisfy applicability condition (17). As indicated by equation (22), each of these plots is characterised by one parameter P 0 which depends on the epidermal keratinocyte velocity and calcium profiles; to construct Figs. 5a and 5b we obtained P 0 = 3.8±3.2 nm s−1 and P 0 = 10±8 nm s−1 for human and murine epidermis respectively. From these values, we calculated the permeability of the TJ barrier by assuming that the extracellular calcium concentration rises by at least 50% across the SG (i.e. R ce = 1.5), based on experimental data for extracellular calcium distributions (see S1 Table). This calculation yielded TJ barrier permeabilities to calcium ions of P Ca < 15 nm s−1 for human epidermis and P Ca < 37 nm s−1 for murine epidermis.
Figure 5. Extracellular calcium rise through the SG vs TJ permeability to calcium predicted by our model.
The solid and dashed lines represent the mean values and uncertainty bounds (± SD) respectively.
Extracellular and intracellular calcium profiles
Extracellular and intracellular epidermal calcium profiles, predicted from total calcium profiles ρ(z) and keratinocyte velocity profiles u i(z) using the equations of our model, are shown in Figs. 6a and 6b for human and murine epidermis respectively. The intracellular calcium profiles ρ ci(z) were nearly identical to the experimental total calcium profiles [26, 28] from which they were calculated. The extracellular calcium profiles ρ ce(z), calculated using equation (20), possessed constant concentration in the SB and SS due to rapid diffusion of this calcium throughout the ECF, and a rise through the SG due to the presence of TJs (see Fig. 2). In Figs. 6a and 6b we chose the permeability of the TJ barrier to calcium as P Ca = 8 nm s−1 and P Ca = 20 nm s−1 for human and murine epidermis respectively, as these values yielded a calcium rise through the SG of R ce ≈ 1.5 in qualitative agreement with the experimental data (S1 Table). These values of TJ permeability barrier (8 nm s−1 for human epidermis and 20 nm s−1 for murine epidermis) also clearly satisfy the previously stated inequalities of P Ca < 15 nm s−1 for human epidermis and P Ca < 37 nm s−1 for murine epidermis.
Figure 6. Physical intracellular ([Cai]) and extracellular ([Cae]) epidermal calcium profiles predicted by our model.
These profiles are calculated from experimental total calcium profiles reported in [26, 28]. [Cae] profiles are shown for TJ barriers that yield a calcium rise through the SG of R ce ≈ 1.5: (a) P Ca = 8 nm s−1 for human epidermis and (b) P Ca = 20 nm s−1 for murine epidermis.
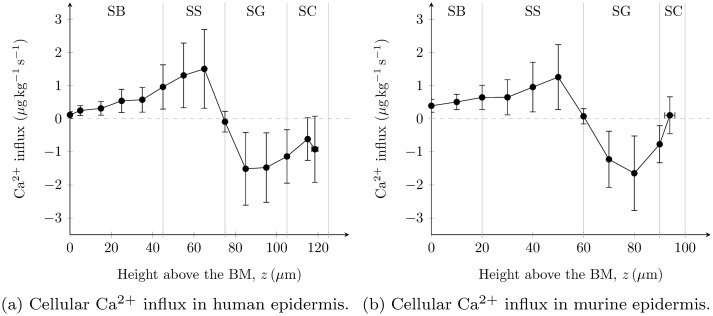
Patterns of calcium exchange g(z) between keratinocytes and the ECF, predicted using equation (1b), are shown in Figs. 7a and 7b for human and murine epidermis respectively. In both plots, a distinct switch in calcium exchange from cellular influx (positive) to outflux (negative) was predicted at the SS-SG boundary, in agreement with our theory (Fig. 2).
Figure 7. Keratinocyte calcium influx profiles g(z) in the epidermis predicted by our model.
These profiles are calculated from experimental total calcium profiles reported in [26, 28].
Discussion
In this paper we investigated the hypothesis that the intracellular and extracellular epidermal calcium profiles in unwounded skin are attributed to three key mechanisms: (1) the primary SC barrier which selectively allows water but not calcium to leave the epidermis [35], (2) progressive intracellular calcium accumulation through the lower epidermal sublayers [36] followed by a phenotypic switch at the SS-SG boundary to expulsion of intracellular calcium to the ECF above this boundary [23], and (3) reduced diffusion of extracellular calcium ions in the SG due to the secondary TJ barrier [43] which together with the aforementioned expulsion of calcium from intracellular stores causes the extracellular calcium concentration to become elevated towards the skin surface [44, 46]. This hypothesis was formulated in a mathematical model (described in Materials and Methods) that predicts intracellular and extracellular calcium profiles in human and murine epidermis (Fig. 6) which agree well with semi-quantitative experimental data available for these profiles [32–34].
We first parameterised the keratinocyte velocity profiles in human and murine epidermis, which is a requirement for the proper investigation of intracellular calcium dynamics. The calculation of these velocity profiles improves over our previous model [23] by including consideration of the slower cycling stem cell subpopulation of the SB [60] and the keratinocyte volume changes through the SS [11], and validating the velocity profiles against several sources of experimental data for keratinocyte transit times in the SB (human only) and the three suprabasal sublayers (SS, SG and SC).
The presence of stem cells in interfollicular epidermis is currently a hotly debated topic [6, 8]. Stem cells have little effect on the keratinocyte velocity profiles and subsequent calculations due to their small potential occupancy of the SB (1–10%, [64]), but their inclusion in the present model is advantageous as it allows validation of these profiles against transit times in the SB. Although our model assumed that the traditional two progenitor theory holds, it can be reduced to the single progenitor theory by setting θ = 0, in which case s 1 is the proliferation rate of these progenitors.
The validation of keratinocyte velocity profiles against epidermal transit time data (Fig. 3) was made somewhat difficult by the uncertainty in both our predicted velocity profiles and the data. Despite this, the validation clearly supported the modification of one of our parameters, the volume change in keratinocytes through the SG for human epidermis (V 2), from its value used in our previous model of unwounded epidermis (R = 1−V 2, [23]). Our results suggested that keratinocytes in human epidermis may reduce their volume by approximately 10-fold during terminal differentiation and that this reduction may be even larger in murine epidermis.
We next investigated the effect of the permeability of the TJ barrier to calcium ions, P Ca, on the extracellular calcium distribution. Our model predictions of P Ca carry large uncertainty due to the cumulative uncertainty in all parameters used to calculate them, and are only applicable if P Ca is significantly greater than (1 nm s−1). Despite these limitations, we found that a value of P Ca that is less than 15 nm s−1 for human epidermis and less than 37 nm s−1 for murine epidermis is sufficient to cause the extracellular calcium distribution to rise by at least 50% across the SG, which is a typical pattern seen in the experimental semi-quantitative calcium profiles measured using ion capture cytochemistry [32–34]. Kirschner et al. [45] recently reported that the permeability of the TJ barrier to calcium ions in cultured primary human keratinocytes was 40–80 nm s−1 within 1–4 days after a switch to high calcium medium (this switch is the key step in triggering keratinocytes to stratify in vitro[2]). These larger experimentally-found values of P Ca, which indicate a reduced TJ barrier to calcium ions, may be attributable to the impaired barrier formation demonstrated by cultured keratinocytes compared to native skin [33].
To further elucidate this point, the transepithelial resistance (TER) of the TJ barrier in the submerged human keratinocytes reported by Kirschner et al.[45] reached a steady-state value of ∼ 150 Ω cm2 after 4 days. In contrast, Sun et al. [71] and Petrova et al. [72] reported that the TER of the TJ barrier in human epidermal equivalents grown at an air-liquid interface (which yields a better representation of native epidermis than submerged keratinocytes [73]) rose to over 1000 Ω cm2 prior to formation of the lipid barrier. TER is the most common experimental measure of TJ barrier permeability [74], and is inversely related to it [75]. These considerations together suggest that the permeability of the TJ barrier should be less in native epidermis than in submerged keratinocytes grown in vitro. This agrees with our model prediction of a TJ barrier permeability to calcium ions in human epidermis that is less than the TJ barrier permeability to calcium ions experimentally observed in cultured human keratinocytes [45].
Finally, we calculated profiles of intracellular calcium, extracellular calcium and the exchange between these two (Figs. 6 and 7), from experimentally-reported total calcium profiles for human epidermis [28] and murine epidermis [26]. For the calculation of extracellular calcium profiles, we set the value of the calcium permeability of the epidermal TJ barrier so that it approximates an extracellular calcium concentration rise of 50% through the SG. The resulting profiles (Fig. 6) indicate that the physical intracellular calcium concentration is typically greater than the physical extracellular calcium concentration. Bearing in mind that intracellular and extracellular calcium are present in cells and ECF which occupy ≥ 93% and ≤ 7% of the epidermal volume respectively [36, 40], our model clearly predicts that intracellular calcium is the main source of the epidermal calcium profile [23].
The predicted pattern of calcium exchange between keratinocytes and the ECF (Figs. 6a and 6b) is significantly modified from our previous calculations of this pattern (Figs. 4c and 4d in [23]), due to the improved parameterisations used here for the keratinocyte volume changes through the SS and the SG, the former of which was assumed to be negligible in our previous models [23, 46]. The updated predictions cast doubt over the assertions in [23] that calcium influx is constant in the SB and SS and that there is a calcium influx peak in the lower SG potentially due to loss of plasma membrane Ca2+-ATPase [76]. However, the improved parameterisations confirmed the key finding of [23] that a change in calcium exchange from cellular influx to outflux actively regulates the epidermal calcium profile. The present theoretical work provides stronger evidence that this active regulation is caused by a phenotypic switch located at the SS-SG boundary (Fig. 7). The origin of this distinct switch in calcium exchange is currently being investigated with time-dependent continuum models developed by members of our research group [77].
Whilst our quantitative theory is able to predict the key features of intracellular and extracellular calcium profiles in unwounded epidermis, it has some potential weaknesses. We have assumed that the SC and TJ barriers are inert entities which regulate the epidermal calcium profile without any existing feedback processes, which is reasonable for considering unwounded epidermis as it represents a steady state condition. However, the formation of these barriers is likely to be dependent both on each other [78] and on the presence of the local calcium concentration [79, 80]. Hence this model cannot be immediately extended to consider temporal dynamics of wounded skin without specifying additional assumptions about the effects of epidermal calcium on the TJ and SC barriers. This is especially important since the rapid secretion by keratinocytes of lamellar bodies (the precursor to lipids that form the “mortar” component of the SC barrier) following barrier disruption is primarily controlled by calcium ions in the SG [13]. Whilst our conceptual model provides a feasible explanation for the formation of the calcium profile, especially as model parameters were obtained from experimental data, we cannot rule out the possibility of the contribution to this profile from other factors, such as the lipid barrier [78], electrophoresis [81], or binding of calcium to molecules such as profilaggrin [82]. In addition, if the factors that contribute substantially to the epidermal calcium profile occur on length scales of cells or smaller, our mathematical treatment of the epidermis as a porous medium may not be appropriate, and individual cell-based models (e.g. [83, 84]) are more suitable.
Our estimates of the TJ barrier permeability to calcium may require revision if the width of this barrier is larger or smaller than the SG. The effective TJ barrier may be larger than the SG if the TJ-like structures observed in the SC [67] reduce the extracellular calcium diffusion rate sufficiently there to yield protrusion of the extracellular calcium rise into the lower SC. On the other hand, the width of the TJ barrier may be smaller than the thickness of the SG, as recent experiments in mouse ear epidermis have suggested that only the TJs forming apically between the second of three cell monolayers of the SG are primarily responsible for its barrier [85]. Future experimental work may resolve this question about the localisation of TJ barrier function.
The investigations of the TJ barrier with our model were also limited to values for its permeability to calcium that satisfy inequality (17), which mathematically states the assumption that the TJ barrier permeability is significantly larger than the local ECF velocity in the absence of TJs. ECF flow is likely to be important for maintaining healthy unwounded epidermis, as occlusion of wounded skin by a vapour-permeable dressing (which permits low rates of transcutaneous water movement) is an adequate substitute for the SC whilst a vapour-impermeable dressing is not [35]. Future direct measurements of the TJ barrier permeability to calcium ions in native epidermis will hopefully confirm the applicability of inequality (17) and our subsequent mathematical theory relating the TJ barrier permeability to the extracellular calcium profile.
In conclusion, we have proposed and mathematically investigated a theory of calcium profile formation in unwounded mammalian epidermis governed by: the impermeable barrier of the SC, TJ-limited calcium diffusion in the SG, and a phenotypic switch in calcium exchange between keratinocytes and ECF at the SS-SG boundary. Future experimental results gained from improved measurement techniques [39, 86] may refine the presented theory and reduce the uncertainty in our model predictions. There are many possibilities for future theoretical work, including the investigation of temporally changing epidermal states for which calcium plays a major role (e.g. wound healing [35], psoriasis [34], and stratification of keratinocyte cultures [2]), and the consideration of our proposed calcium kinetics in individual cell-based models of epidermal homeostasis [83]. We intend that this paper provides a conceptual and quantitative model for future experimental and theoretical research to examine, modify and update, as our understanding of epidermal calcium profile formation becomes increasingly advanced.
Supporting Information
(PDF)
(PDF)
Acknowledgments
The authors wish to thank A. Celli and T. M. Mauro from the School of Medicine, University of California, San Francisco, for the provision of their data for human epidermal sublayer heights.
Data Availability
All data used in this work is either provided in Table 1 or extracted from figures published in references 26 and 28 (Mauro et al. 1998; Behne et al. 2003) using the program xyExtract.
Funding Statement
Matthew P. Adams received a scholarship from the Mathematical Sciences School, Queensland University of Technology, to support this work. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Menon G, Elias P, Lee S, Feingold K (1992) Localization of calcium in murine epidermis following disruption and repair of the permeability barrier. Cell Tissue Res 270: 503–512. 10.1007/BF00645052 [DOI] [PubMed] [Google Scholar]
- 2. Hennings H, Michael D, Cheng C, Steinert P, Holbrook K, et al. (1980) Calcium regulation of growth and differentiation of mouse epidermal cells in culture. Cell 19: 245–254. 10.1016/0092-8674(80)90406-7 [DOI] [PubMed] [Google Scholar]
- 3. Houben E, Paepe KD, Rogiers V (2007) A keratinocyte’s course of life. Skin Pharmacol Physiol 20: 122–132. 10.1159/000098163 [DOI] [PubMed] [Google Scholar]
- 4. Elias P, Feingold K, editors (2006) Skin barrier. Taylor and Francis, New York. [Google Scholar]
- 5. Simons BD, Clevers H (2011) Strategies for homeostatic stem cell self-renewal in adult tissues. Cell 145: 851–862. 10.1016/j.cell.2011.05.033 [DOI] [PubMed] [Google Scholar]
- 6. Clayton E, Doupé DP, Klein AM, Winton DJ, Simons BD, et al. (2007) A single type of progenitor cell maintains normal epidermis. Nature 446: 185–189. 10.1038/nature05574 [DOI] [PubMed] [Google Scholar]
- 7. Doupé DP, Klein AM, Simons BD, Jones PH (2010) The ordered architecture of murine ear epidermis is maintained by progenitor cells with random fate. Dev Cell 18: 317–323. 10.1016/j.devcel.2009.12.016 [DOI] [PubMed] [Google Scholar]
- 8. Mascré G, Dekoninck S, Drogat B, Youssef KK, Broh’ee S, et al. (2012) Distinct contribution of stem and progenitor cells to epidermal maintenance. Nature 489: 257–262. 10.1038/nature11393 [DOI] [PubMed] [Google Scholar]
- 9. Watt F (2001) Stem cell fate and patterning in mammalian epidermis. Curr Opin Genet Dev 11: 410–417. 10.1016/S0959-437X(00)00211-2 [DOI] [PubMed] [Google Scholar]
- 10. Fuchs E (2008) Skin stem cells: rising to the surface. J Cell Biol 180: 273–284. 10.1083/jcb.200708185 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Corcuff P, Bertrand C, Leveque J (1993) Morphometry of human epidermis in vivo by real-time confocal microscopy. Arch Dermatol Res 285: 475–481. 10.1007/BF00376820 [DOI] [PubMed] [Google Scholar]
- 12. Norlén L, Al-Amoudi A (2004) Stratum corneum keratin structure, function, and formation: the cubic rod-packing and membrane templating model. J Invest Dermatol 123: 715–732. 10.1111/j.0022-202X.2004.23213.x [DOI] [PubMed] [Google Scholar]
- 13. Feingold K (2007) The role of epidermal lipids in cutaneous permeability barrier homeostasis. J Lipid Res 48: 2531–2546. 10.1194/jlr.R700013-JLR200 [DOI] [PubMed] [Google Scholar]
- 14. Nemes Z, Steinert PM (1999) Bricks and mortar of the epidermal barrier. Exp Mol Med 31: 5–19. 10.1038/emm.1999.2 [DOI] [PubMed] [Google Scholar]
- 15. Kalia YN, Alberti I, Sekkat N, Curdy C, Naik A, et al. (2000) Normalization of stratum corneum barrier function and transepidermal water loss in vivo . Pharm Res 17: 1148–1150. 10.1023/A:1026474200575 [DOI] [PubMed] [Google Scholar]
- 16. Bashir SJ, Chew AL, Anigbogu A, Dreher F, Maibach HI (2001) Physical and physiological effects of stratum corneum tape stripping. Skin Res Technol 7: 40–48. 10.1034/j.1600-0846.2001.007001040.x [DOI] [PubMed] [Google Scholar]
- 17. Yow HN, Wu X, Routh AF, Guy RH (2009) Dye diffusion from microcapsules with different shell thickness into mammalian skin. Eur J Pharm Biopharm 72: 62–68. 10.1016/j.ejpb.2008.11.004 [DOI] [PubMed] [Google Scholar]
- 18. Pierard GE, Goffin V, Hermanns-Le T, Pierard-Franchimont C (2000) Corneocyte desquamation. Int J Mol Med 6: 217–238. [DOI] [PubMed] [Google Scholar]
- 19. Berridge M, Bootman M, Roderick H (2003) Calcium signalling: dynamics, homeostasis and remodelling. Nat Rev Mol Cell Biol 4: 517–529. 10.1038/nrm1155 [DOI] [PubMed] [Google Scholar]
- 20. Clapham D (2007) Calcium signaling. Cell 131: 1047–1058. 10.1016/j.cell.2007.11.028 [DOI] [PubMed] [Google Scholar]
- 21. Meldolesi J, Grohovaz F (2001) Total calcium ultrastructure: advances in excitable cells. Cell Calcium 30: 1–8. 10.1054/ceca.2001.0216 [DOI] [PubMed] [Google Scholar]
- 22. Brini M, Carafoli E (2009) Calcium pumps in health and disease. Physiol Rev 89: 1341–1378. 10.1152/physrev.00032.2008 [DOI] [PubMed] [Google Scholar]
- 23. Adams MP, Mallet DG, Pettet GJ (2012) Active regulation of the epidermal calcium profile. J Theor Biol 301: 112–121. 10.1016/j.jtbi.2012.02.017 [DOI] [PubMed] [Google Scholar]
- 24. Malmqvist KG, Carlsson LE, Forslind B, Roomans GM, Akselsson KR (1984) Proton and electron microprobe analysis of human skin. Nucl Instrum Meth B 3: 611–617. 10.1016/0168-583X(84)90447-6 [DOI] [Google Scholar]
- 25. Pallon J, Malmqvist KG, Werner-Linde Y, Forslind B (1996) PIXE analysis of pathological skin with special reference to psoriasis and atopic dry skin. Cell Mol Biol 42: 111–118. [PubMed] [Google Scholar]
- 26. Mauro T, Bench G, Sidderas-Haddad E, Feingold K, Elias P, et al. (1998) Acute barrier perturbation abolishes the Ca2+ and K+ gradients in murine epidermis: quantitative measurement using PIXE. J Invest Dermatol 111: 1198–1201. 10.1046/j.1523-1747.1998.00421.x [DOI] [PubMed] [Google Scholar]
- 27. Elias PM, Nau P, Hanley K, Cullander C, Crumrine D, et al. (1998) Formation of the epidermal calcium gradient coincides with key milestones of barrier ontogenesis in the rodent. J Invest Dermatol 110: 399–404. 10.1046/j.1523-1747.1998.00151.x [DOI] [PubMed] [Google Scholar]
- 28. Behne M, Tu CL, Aronchik I, Epstein E, Bench G, et al. (2003) Human keratinocyte ATP2C1 localizes to the Golgi Ca2+ stores. J Invest Dermatol 121: 688–694. 10.1046/j.1523-1747.2003.12528.x [DOI] [PubMed] [Google Scholar]
- 29. Forslind B, Roomans G, Carlsson LE, Malmqvist K, Akselsson K (1984) Elemental analysis on freeze-dried sections of human skin: studies by electron microprobe and particle induced X-ray emission analysis. Scan Electron Microsc Pt 2: 755–759. [PubMed] [Google Scholar]
- 30. Borgers M, Thoné F, Nueten JMv (1981) The subcellular distribution of calcium and the effects of calcium-antagonists as evaluated with a combined oxalate-pyroantimonate technique. Acta Histochem Suppl 24: S327–S332. [PubMed] [Google Scholar]
- 31. Reempts Jv, Borgers M, Offner F (1982) Ultrastructural localization of calcium in the rat retina with a combined oxalate-pyroantimonate technique. Histochem J 14: 517–522. 10.1007/BF01011861 [DOI] [PubMed] [Google Scholar]
- 32. Menon G, Grayson S, Elias P (1985) Ionic calcium reservoirs in mammalian epidermis: Ultrastructural localization by ion-capture cytochemistry. J Invest Dermatol 84: 508–512. 10.1111/1523-1747.ep12273485 [DOI] [PubMed] [Google Scholar]
- 33. Vičanová J, Boelsma E, Mommaas A, Kempenaar J, Forslind B, et al. (1998) Normalization of epidermal calcium distribution profile in reconstructed human epidermis is related to improvement of terminal differentiation and stratum corneum barrier formation. J Invest Dermatol 111: 97–106. 10.1046/j.1523-1747.1998.00251.x [DOI] [PubMed] [Google Scholar]
- 34. Menon G, Elias P (1991) Ultrastructural localization of calcium in psoriatic and normal human epidermis. Arch Dermatol 127: 57–63. 10.1001/archderm.1991.01680010067010 [DOI] [PubMed] [Google Scholar]
- 35. Elias P, Ahn S, Brown B, Crumrine D, Feingold K (2002) Origin of the epidermal calcium gradient: regulation by barrier status and role of active vs passive mechanisms. J Invest Dermatol 119: 1269–1274. 10.1046/j.1523-1747.2002.19622.x [DOI] [PubMed] [Google Scholar]
- 36. Celli A, Sanchez S, Behne M, Hazlett T, Gratton E, et al. (2010) The epidermal Ca2+ gradient: measurement using the phasor representation of fluorescent lifetime imaging. Biophys J 98: 911–921. 10.1016/j.bpj.2009.10.055 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Ahn SK, Hwang SM, Jiang SJ, Choi EH, Lee SH (1999) The changes of epidermal calcium gradient and transitional cells after prolonged occlusion following tape stripping in the murine epidermis. J Invest Dermatol 113: 189–195. 10.1046/j.1523-1747.1999.00650.x [DOI] [PubMed] [Google Scholar]
- 38. Denda M, Hosoi J, Asida Y (2000) Visual imaging of ion distribution in human epidermis. Biochem Biophys Res Commun 272: 134–137. 10.1006/bbrc.2000.2739 [DOI] [PubMed] [Google Scholar]
- 39. Behne MJ, Sanchez S, Barry NP, Kirschner N, Meyer W, et al. (2011) Major translocation of calcium upon epidermal barrier insult: imaging and quantification via FLIM/Fourier vector analysis. Arch Dermatol Res 303: 103–115. 10.1007/s00403-010-1113-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Elias P, Leventhal M (1979) Intercellular volume changes and cell surface expansion during cornification. Clin Res 27: 525A. [Google Scholar]
- 41. Halprin K, Ohkawara A (1967) Glucose entry into the human epidermis: II. The penetration of glucose into the human epidermis in vitro. J Invest Dermatol 49: 561–568. [DOI] [PubMed] [Google Scholar]
- 42. Brandner JM, Kief S, Grund C, Rendl M, Houdek P, et al. (2002) Organization and formation of the tight junction system in human epidermis and cultured keratinocytes. Eur J Cell Biol 81: 253–263. 10.1078/0171-9335-00244 [DOI] [PubMed] [Google Scholar]
- 43. Kirschner N, Houdek P, Fromm M, Moll I, Brandner JM (2010) Tight junctions form a barrier in human epidermis. Eur J Cell Biol 89: 839–842. 10.1016/j.ejcb.2010.07.010 [DOI] [PubMed] [Google Scholar]
- 44. Kurasawa M, Maeda T, Oba A, Yamamoto T, Sasaki H (2011) Tight junction regulates epidermal calcium ion gradient and differentiation. Biochem Biophys Res Commun 406: 506–511. 10.1016/j.bbrc.2011.02.057 [DOI] [PubMed] [Google Scholar]
- 45. Kirschner N, Rosenthal R, Furuse M, Moll I, Fromm M, et al. (2013) Contribution of tight junction proteins to ion, macromolecule, and water barrier in keratinocytes. J Invest Dermatol 133: 1161–1169. 10.1038/jid.2012.507 [DOI] [PubMed] [Google Scholar]
- 46. Adams MP, Mallet DG, Pettet GJ (2012) A continuum model of the growth of engineered epidermal skin substitutes. ANZIAM J (EMAC 2011) 53: C90–C109. [Google Scholar]
- 47. Lemon G, King JR, Byrne HM, Jensen OE, Shakesheff KM (2006) Mathematical modelling of engineered tissue growth using a multiphase porous flow mixture theory. Journal of Mathematical Biology 52: 571–594. 10.1007/s00285-005-0363-1 [DOI] [PubMed] [Google Scholar]
- 48. Please C, Pettet G, McElwain D (1998) A new approach to modelling the formation of necrotic regions in tumours. Appl Math Lett 11: 89–94. 10.1016/S0893-9659(98)00038-X [DOI] [Google Scholar]
- 49. Please C, Pettet G, McElwain D (1999) Avascular tumour dynamics and necrosis. Math Mod Meth Appl S 9: 569–579. 10.1142/S0218202599000294 [DOI] [Google Scholar]
- 50. Landman K, Please C (2001) Tumour dynamics and necrosis: surface tension and stability. IMA J Math Appl Med 18: 131–158. 10.1093/imammb/18.2.131 [DOI] [PubMed] [Google Scholar]
- 51. Lemon G, King J (2007) Multiphase modelling of cell behaviour on artificial scaffolds: effects of nutrient depletion and spatially nonuniform porosity. Math Med Biol 24: 57–83. 10.1093/imammb/dql020 [DOI] [PubMed] [Google Scholar]
- 52. Kitson N, Thewalt JL (2000) Hypothesis: the epidermal permeability barrier is a porous medium. Acta Dermato-Venereologica Supp 208: 12–15. 10.1080/000155500750042808 [DOI] [PubMed] [Google Scholar]
- 53. Tsutsumi M, Inoue K, Denda S, Ikeyama K, Goto M, et al. (2009) Mechanical-stimulation-evoked calcium waves in proliferating and differentiated human keratinocytes. Cell Tissue Res 338: 99–106. 10.1007/s00441-009-0848-0 [DOI] [PubMed] [Google Scholar]
- 54. Furuse M, Hata M, Furuse K, Yoshida Y, Haratake A, et al. (2002) Claudin-based tight junctions are crucial for the mammalian epidermal barrier: a lesson from claudin-1-deficient mice. The Journal of Cell Biology 156: 1099–1111. 10.1083/jcb.200110122 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Ågren J, Zelenin S, HÅkansson M, Elköf AC, Aperia A, et al. (2003) Transepidermal water loss in developing rats: role of aquaporins in the immature skin. Pediatric Research 53: 558–565. 10.1203/01.PDR.0000055777.25933.98 [DOI] [PubMed] [Google Scholar]
- 56. Sougrat R, Morand M, Gondran C, Barré P, Gobin R, et al. (2002) Functional expression of AQP3 in human skin epidermis and reconstructed epidermis. The Journal of Investigative Dermatology 118: 678–685. 10.1046/j.1523-1747.2002.01710.x [DOI] [PubMed] [Google Scholar]
- 57. Jensen UB, Lowell S, Watt FM (1999) The spatial relationship between stem cells and their progeny in the basal layer of human epidermis: a new view based on whole-mount labelling and lineage analysis. Development 126: 2409–2418. [DOI] [PubMed] [Google Scholar]
- 58. Ghazizadeh S, Taichman LB (2005) Organization of stem cells and their progeny in human epidermis. The Journal of Investigative Dermatology 124: 367–372. 10.1111/j.0022-202X.2004.23599.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Menon G, Elias P, Feingold K (1994) Integrity of the permeability barrier is crucial for maintenance of the epidermal calcium gradient. Br J Dermatol 130: 139–147. 10.1111/j.1365-2133.1994.tb02892.x [DOI] [PubMed] [Google Scholar]
- 60. Potten C, Booth C (2002) Keratinocyte stem cells: a commentary. J Invest Dermatol 119: 888–899. 10.1046/j.1523-1747.2002.00020.x [DOI] [PubMed] [Google Scholar]
- 61. Forslind B, Lindberg M, editors (2004) Skin, hair, and nails: structure and function. Marcel Dekker, New York. [Google Scholar]
- 62. Gandolfi A, Iannelli M, Marinoschi G (2011) An age-structured model of epidermis growth. J Math Biol 62: 111–141. 10.1007/s00285-010-0330-3 [DOI] [PubMed] [Google Scholar]
- 63. Blank I, III JM, Emslie A, Simon I, Apt C (1984) The diffusion of water across the stratum corneum as a function of its water content. J Invest Dermatol 82: 188–194. 10.1111/1523-1747.ep12259835 [DOI] [PubMed] [Google Scholar]
- 64. Li A, Simmons P, Kaur P (1998) Identification and isolation of candidate human keratinocyte stem cells based on cell surface phenotype. P Natl Acad Sci USA 85: 3902–3907. 10.1073/pnas.95.7.3902 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Adams MP, Mallet DG, Pettet GJ (2012) Solution methods for advection-diffusion-reaction equations on growing domains and subdomains, with application to modelling skin substitutes. Proceedings of the 4th International Conference on Computational Methods (ICCM2012), Gold Coast, Australia, Paper 230. [Google Scholar]
- 66. Schlüter H, Wepf R, Moll I, Franke WW (2004) Sealing the live part of the skin: the integrated meshwork of desmosomes, tight junctions and curvilinear ridge structures in the cells of the uppermost granular layer of the human epidermis. European Journal of Cell Biology 83: 655–665. 10.1078/0171-9335-00434 [DOI] [PubMed] [Google Scholar]
- 67. Haftek M, Callejon S, Sandjeu Y, Padois K, Falson F, et al. (2011) Compartmentalization of the human stratum corneum by persistent tight junction-like structures. Experimental Dermatology 20: 617–621. 10.1111/j.1600-0625.2011.01315.x [DOI] [PubMed] [Google Scholar]
- 68. Potts RO, Guy RH (1992) Predicting skin permeability. Pharmaceutical Research 9: 663–669. 10.1023/A:1015810312465 [DOI] [PubMed] [Google Scholar]
- 69. Mandel J (1964) The statistical analysis of experimental data. John Wiley & Sons, Inc. [Google Scholar]
- 70. Ku HH (1966) Notes on the use of propagation of error formulas. Journal of Research of the National Bureau of Standards Section C: Engineering and Instrumentation 70C: 263–273. [Google Scholar]
- 71. Sun R, Celli A, Crumrine D, Hupe M, Adame L, et al. (2014) Lowered humidity produces human epidermal equivalents with enhanced barrier properties. Tissue Eng Pt C-Meth Jun 16 [Epub ahead of print] 10.1089/ten.tec.2014.0065 [DOI] [PMC free article] [PubMed]
- 72. Petrova A, Celli A, Jacquet L, Dafou D, Crumrine D, et al. (2014) 3D in vitro model of a functional epidermal permeability barrier from human embryonic stem cells and induced pluripotent stem cells. Stem Cell Rep 2: 675–689. 10.1016/j.stemcr.2014.03.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73. Bernstam L, Vaughan F, Bernstein I (1986) Keratinocytes grown at the air-liquid interface. In Vitro Cellular and Developmental Biology 22: 695–705. 10.1007/BF02621086 [DOI] [PubMed] [Google Scholar]
- 74. Günzel D, Krug S, Rosenthal R, Fromm M (2010) Biophysical methods to study tight junction permeability. Current Topics in Membranes 65: 39–78. 10.1016/S1063-5823(10)65003-X [DOI] [Google Scholar]
- 75. Madara J (1998) Regulation of the movement of solutes across tight junctions. Annual Review of Physiology 60: 143–159. 10.1146/annurev.physiol.60.1.143 [DOI] [PubMed] [Google Scholar]
- 76. Cho JK, Bikle D (1997) Decrease of Ca2+-ATPase activity in human keratinocytes during calcium-induced differentiation. J Cell Physiol 172: 146–154. [DOI] [PubMed] [Google Scholar]
- 77. Personal communications with G. J. Pettet (2014).
- 78. Celli A, Zhai Y, Jiang Y, Crumrine D, Elias P, et al. (2012) Tight junction properties change during epidermis development. Experimental Dermatology 21: 783–801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79. Bleich M, Shan Q, Himmerkus N (2012) Calcium regulation of tight junction permeability. Annals of the New York Academy of Sciences 1258: 93–99. 10.1111/j.1749-6632.2012.06539.x [DOI] [PubMed] [Google Scholar]
- 80. Baek JH, Lee SE, Choi KJ, Choi EH, Lee SH (2013) Acute modulations in stratum corneum permeability barrier function affect claudin expression and epidermal tight junction function via changes of epidermal calcium gradient. Yonsei Medical Journal 54: 523–528. 10.3349/ymj.2013.54.2.523 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81. Cornelissen L, Oomens C, Huyghe J, Baaijens F (2007) Mechanisms that play a role in the maintenance of the calcium gradient in the epidermis. Skin Res Technol 13: 369–376. 10.1111/j.1600-0846.2007.00239.x [DOI] [PubMed] [Google Scholar]
- 82. Markova N, Marekov L, Chipev C, Gan S, Idler W, et al. (1993) Profilaggrin is a major epidermal calcium-binding protein. Mol Cell Biol 13: 613–625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83. Grabe N, Neuber K (2005) A multicellular systems biology model predicts epidermal morphology, kinetics and Ca2+ flow. Bioinformatics 21: 3541–3547. 10.1093/bioinformatics/bti585 [DOI] [PubMed] [Google Scholar]
- 84. Sun T, Adra S, Smallwood R, Holcombe M, MacNeil S (2009) Exploring hypotheses of the actions of TGF-β1 in epidermal wound healing using a 3D computational multiscale model of the human epidermis. PLoS One 4: e8515 10.1371/journal.pone.0008515 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85. Kubo A, Nagao K, Yokouchi M, Sasaki H, Amagai M (2009) External antigen uptake by langer-hans cells with reorganization of epidermal tight junction barriers. The Journal of Experimental Medicine 206: 2937–2946. 10.1084/jem.20091527 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86. Bloksgaard M, Brewer K, Bagatolli LA (2013) Structural and dynamical aspects of skin studied by multiphoton excitation fluorescence microscopy-based methods. European Journal of Pharmaceutical Sciences 50: 5865–94. 10.1016/j.ejps.2013.04.010 [DOI] [PubMed] [Google Scholar]
- 87. Halprin K (1972) Epidermal “turnover time”—a re-examination. Br J Dermatol 86: 14–19. 10.1111/j.1365-2133.1972.tb01886.x [DOI] [PubMed] [Google Scholar]
- 88. Iizuka H (1994) Epidermal turnover time. J Dermatol Sci 8: 215–217. 10.1016/0923-1811(94)90057-4 [DOI] [PubMed] [Google Scholar]
- 89. Rothberg S, Crounse RG, Lee JL (1961) Glycine-C14 incorporation into the proteins of normal stratum corneum and the abnormal stratum corneum of psoriasis. J Invest Dermatol 37: 497–505. 10.1038/jid.1961.150 [DOI] [PubMed] [Google Scholar]
- 90. Baker H, Kligman AM (1967) Technique for estimating turnover time of human stratum corneum. Archives of Dermatology 95: 408–411. 10.1001/archderm.1967.01600340068016 [DOI] [PubMed] [Google Scholar]
- 91. Epstein W, Maibach H (1965) Cell renewal in human epidermis. Arch Dermatol 92: 462–468. 10.1001/archderm.92.4.462 [DOI] [PubMed] [Google Scholar]
- 92. Downes AM, Matoltsy AG, Sweeney TM (1967) Rate of turnover of the stratum corneum in hairless mice. J Invest Dermatol 49: 400–405. 10.1038/jid.1967.156 [DOI] [PubMed] [Google Scholar]
- 93. Potten CS, Saffhill R, Maibach HI (1987) Measurement of the transit time for cells through the epidermis and stratum corneum of the mouse and guinea-pig. Cell Tissue Kinet 20: 461–472. [DOI] [PubMed] [Google Scholar]
- 94. Potten C (1975) Epidermal transit times. Br J Dermatol 93: 649–658. 10.1111/j.1365-2133.1975.tb05115.x [DOI] [PubMed] [Google Scholar]
- 95. Personal communications with T. M. Mauro and A. Celli (2013).
- 96. Bergstresser PR, Pariser RJ, Taylor JR (1978) Counting and sizing of epidermal cells in normal human skin. J Invest Dermatol 70: 280–284. 10.1111/1523-1747.ep12541516 [DOI] [PubMed] [Google Scholar]
- 97. Rowden G (1975) Ultrastructural studies of keratinized epithelia of the mouse. III. Determination of the volumes of nuclei and cytoplasm of cells in murine epidermis. J Invest Dermatol 64: 1–3. 10.1111/1523-1747.ep12540840 [DOI] [PubMed] [Google Scholar]
- 98. Rodrigues LHT, Maia Campos PMBG (2002) Comparative study of the effects of cosmetic formulations with or without hydroxy acids on hairless mouse epidermis by histopathologic, morphometric, and stereologic evaluation. J Cosmet Sci 53: 269–282. [PubMed] [Google Scholar]
- 99. Allen T, Potten C (1976) Ultrastructural site variations in mouse epidermal organization. J Cell Sci 21: 341–359. [DOI] [PubMed] [Google Scholar]
- 100. Castelijns F, Ezendam J, Latijnhouwers M, Vlijmen-Willems IV, Zeeuwen P, et al. (1998) Epidermal cell kinetics by combining in situ hybridization and immunohistochemistry. Histochem J 30: 869–877. 10.1023/A:1003457709690 [DOI] [PubMed] [Google Scholar]
- 101. Potten C (1975) Epidermal cell production rates. J Invest Dermatol 65: 488–500. 10.1111/1523-1747.ep12610194 [DOI] [PubMed] [Google Scholar]
- 102. Kampmeyer P (1952) The temperature dependence of viscosity for water and mercury. J Appl Phys 23: 99–102. 10.1063/1.1701986 [DOI] [Google Scholar]
- 103. Li YH, Gregory S (1974) Diffusion of ions in sea water and in deep-sea sediments. Geochim Cosmochim Ac 38: 703–714. 10.1016/0016-7037(74)90145-8 [DOI] [Google Scholar]
- 104. Williams E, Heusch A, McCarthy P (2008) Thermal screening of facial skin arterial hot spots using non-contact infrared radiometry. Physiol Meas 29: 341–348. 10.1088/0967-3334/29/3/005 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(PDF)
(PDF)
Data Availability Statement
All data used in this work is either provided in Table 1 or extracted from figures published in references 26 and 28 (Mauro et al. 1998; Behne et al. 2003) using the program xyExtract.