Abstract
Intratumoral heterogeneity has been found to be a major cause of drug resistance. Cell-to-cell variation increases as a result of cancer-related alterations, which are acquired by stochastic events and further induced by environmental signals. However, most cellular mechanisms include natural fluctuations that are closely regulated, and thus lead to asynchronization of the cells, which causes intrinsic heterogeneity in a given population. Here, we derive two novel mathematical models, a stochastic agent-based model and an integro-differential equation model, each of which describes the growth of cancer cells as a dynamic transition between proliferative and quiescent states. These models are designed to predict variations in growth as a function of the intrinsic heterogeneity emerging from the durations of the cell-cycle and apoptosis, and also include cellular density dependencies. By examining the role all parameters play in the evolution of intrinsic tumor heterogeneity, and the sensitivity of the population growth to parameter values, we show that the cell-cycle length has the most significant effect on the growth dynamics. In addition, we demonstrate that the agent-based model can be approximated well by the more computationally efficient integro-differential equations when the number of cells is large. This essential step in cancer growth modeling will allow us to revisit the mechanisms of multi-drug resistance by examining spatiotemporal differences of cell growth while administering a drug among the different sub-populations in a single tumor, as well as the evolution of those mechanisms as a function of the resistance level.
Keywords: Agent-based model, integro-differential equations, delay-differential equations, intrinsic heterogeneity, cell density
1. Introduction
1.1. Induced Heterogeneity
The development of a tumor is a complex evolutionary process that involves perturbations in many essential cellular mechanisms. Spatiotemporal cellular dynamics include various types of hallmark alterations that may be acquired through stochastic processes and induced by environmental signals, such as metabolic stress, inflammatory microenvironments, immune responses, and/or therapy. Combinations of these signals produce intratumoral heterogeneity. Many primary human tumors have been discovered to contain genetically and phenotypically distinct cellular subpopulations with different growth rates. This intratumoral heterogeneity has further been found to be a major contributor of drug resistance [17]. Resistance to chemotherapy is a major impediment to successful cancer treatment. Several central mechanisms have been identified as contributing to resistance; however, these do not necessarily account for tumor dynamics [7]. It is known that most patients that are diagnosed with cancer have already developed some level of drug resistance while the tumor is forming. Thus after therapy, they experience a relapse, where the disease could become intractable or even possibly untreatable. Various theoretical and empirical studies aim to predict the development of a tumor, mainly by assuming the existence of abnormal events that cause cancer-related alterations [10]. Understanding the course of malignancy and estimating cancer growth based on tumor cell responses to microenvironmental changes as an induced dynamic process may serve to identify new targets for therapy or methods of prevention.
1.2. Intrinsic Heterogeneity
However, there is another side to this ‘equation’; one that does not necessarily account for tumor heterogeneity that results exclusively from cancer-related irreversible processes. Instead, heterogeneity can arise via typical reversible biological processes that are stochastic, yet nevertheless tightly regulated, in nature. These natural intrinsic mechanisms add another layer of complexity to a cell’s capacity to integrate information, particularly in cancer cells. One such cellular process is the cell-cycle. The cell-cycle is one of the most studied biological processes, and has obvious effects on cancer development, growth, and therapeutic resistance. Eukaryotic intracellular dynamics are mediated by many different molecular components (e.g. transcription factors, proteins, metabolites, RNA, etc.). Each such component operates at a different rate, often under different conditions, and responds to many dynamic inter- and intra-cellular signals, such as pH, temperature, and cellular density in the local environment. In order to maintain an ordered cell-cycle mechanism that would function consistently, despite a routinely noisy microenvironment, variations in gene expression [15], cell-cycle period [22], cell size and age [21], and cellular death period [12, 19] of cells from the same clone must exist. Advances in methods to both study naturally intrinsic significant variations in tumor growth and characterize intratumoral heterogeneity would aid in determining natural fluctuations in cell growth, understanding how tumor development is affected by these natural fluctuations, detecting these types of tumors after treatment, and understanding how induced and intrinsic mechanisms can be found.
1.3. Self-Organized Dynamics
Two frameworks that are commonly used to design mathematical cancer models which predict cellular behavior are individual-based models and continuous deterministic models. Several different individual-based models of tumor growth have been developed recently (see review [1]). Among them are agent-based models (ABMs). The ABM framework is a powerful simulation method that has seen a variety of applications, including bio-medical research [14, 20, 23] and socio-economic modeling [4]. ABMs describe dynamic systems as collections of autonomous decision-making individuals called agents. Each agent assesses its state and makes decisions on the basis of a set of rules. Agents may execute various behaviors appropriate for the system they represent. ABMs are generally more flexible than deterministic models and may take into account virtually any biological phenomenon. Here, we present two mathematical approaches, the ABM and a corresponding integro-differential (IDE) model, to predict the growth of a single ovarian cell line, OVCAR-8, where the cells can be proliferating, dying, or in quiescence. The novelty of our methods lie in the description of cellular decision-making as a function of the global dynamic cell density, with intrinsic variations of the cell-cycle and death process lengths. Decisions concerning actions are based on how the cell senses its environment, in a probabilistic fashion. We study the robustness of cell growth despite noise in division and natural death rates. The entire system dynamic results from the decisions of individual entities that can cause transient or permanent heterogeneity, generate network effects, and potentially lead to significant deviations from stochastic to deterministic predictions. We demonstrate the existence of fluctuations in cell growth using data of proliferation rates as a function of cellular density. This fundamental framework of cellular growth dynamics is a necessary first step that will allow us to work on more complex co-cultured systems based on geometry, which includes a spatial mechanism of drug resistance that could shed light on the spatiotemporal evolution of intratumoral heterogeneity.
2. Agent-Based Model
The first model we introduce is an ABM, where each cell is distinguished with its own state and behavior. This framework permits a simple way to introduce an age structure into the model, which is a main focus of this work.
2.1. Model Construction
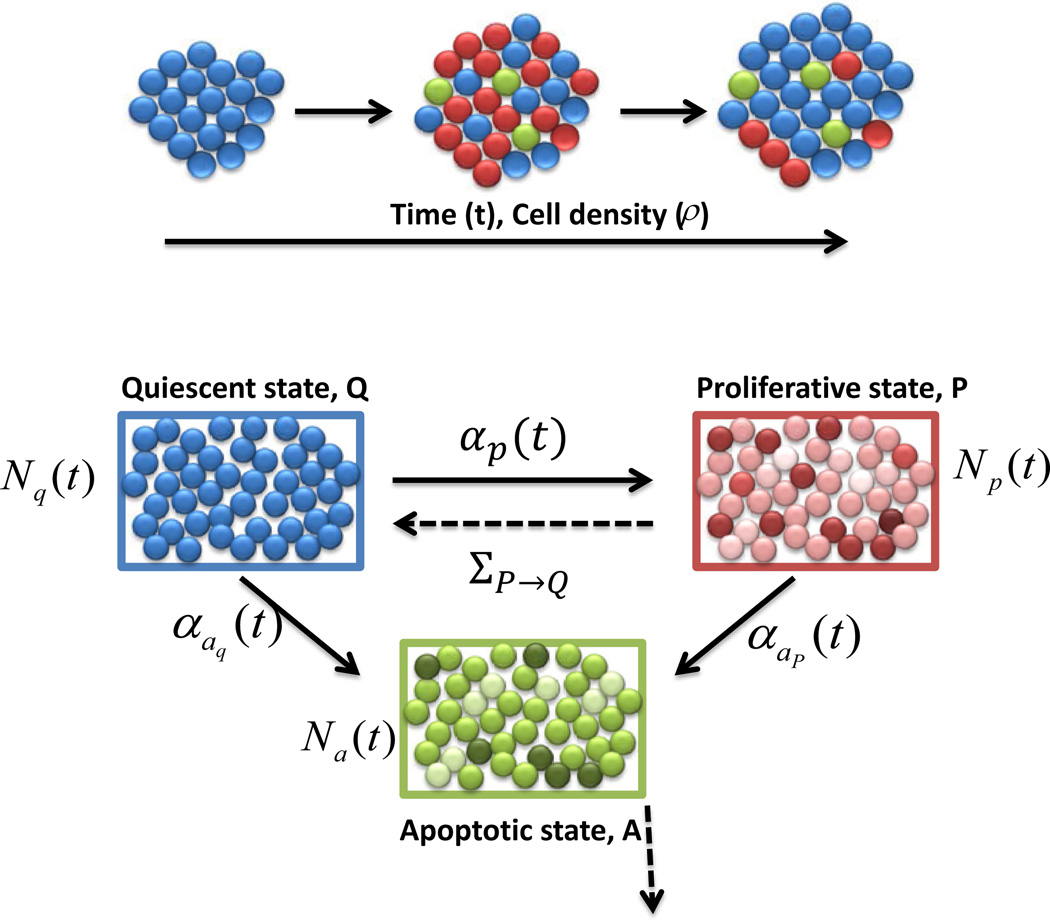
The ABM consists of three compartments of cells: proliferative (P), apoptotic (A), and quiescent (Q). See Figure 1 for an outline of the transitions between compartments. Q consists of cells that are neither dividing nor dying, and acts mainly as a reservoir for the other two compartments. P consists of cells that are currently in any stage of the cell-cycle. When a cell makes a transition from Q into P, a cell-cycle length, LP, is chosen. LP was assumed to be a random variable with normal distribution:
| (1) |
where μ is the mean length of the cell-cycle, and σ is the standard deviation [22]. The value of μ is taken as the doubling time of OVCAR-8 cells, which is estimated to be 24.4416 hours (see Section 4.1). Once a cell is in P, it progresses through the cell-cycle for LP hours, unless a transition occurs to the apoptotic compartment A. Both mother and daughter cells subsequently leave the division stage and become quiescent (Q). The last compartment, A, consists of cells currently in the apoptotic process. Cells in A remain for a random length of time LA, after which the cell transitions out of the apoptotic compartment to complete cell death. Based on the experimental data of Messam and Pittman [12], we approximate LA as a gamma-distributed random variable:
| (2) |
where ω and λ denote the shape and rate parameters, respectively. See Section 4.1 for details.
Figure 1.
Model dynamics. Diagram of transitions between the three cellular compartments in the ABM. Q denotes the quiescent compartment with Nq(t) cells at time t, P denotes the proliferation compartment with Np(t) cells at time t, and A denotes the apoptosis compartment with Na(t) cells at time t. Note that Nq(t),Np(t), and Na(t) are all stochastic processes. The explicit transition rates between the compartments are shown in solid lines, and are labeled as αp(t), αap(t), and αaq(t). The implicit transition rates, due to the completion of cellular cycles, are shown in dotted lines, and have no closed-form expression. For example, ΣP→Q corresponds to the rate of cell-cycle completion. The line originating from compartment A indicates cells that are removed from the simulation.
Lastly, we assumed that transitions between the three compartments are governed both by the global cellular density, labeled ρ, and the random amount of time spent in P or A (LP, LA, respectively). We formulated these transitions in terms of rate parameters. Consider, for example, the transition from Q to P, that is, the probability of a cell entering the cell-cycle from quiescence. We model this using a rate, αp(t), with the interpretation that for a small amount of time Δt, αp(t)Δt is essentially the probability of one cell making a transition from Q into P at some point in the time interval [t, t + Δt]. More precisely, we are assuming a first-order dependence in the time step for transition probabilities, and thus the process can be thought of as Poisson, with non-homogeneous intensity αp(t). Of course, all of this holds only in the limit as Δt → 0+, as theoretically this is a continuous time Markov chain. In practice however, we simulate using small discrete time steps Δt, and take αp(t)Δt as the exact transition probability per cell. All other explicit transition rates (dark lines in Figure 1) have this same interpretation.
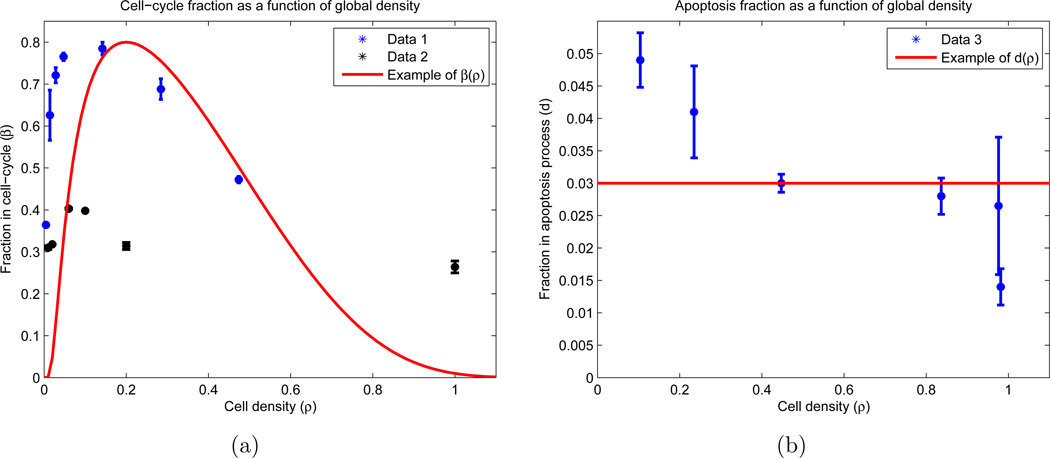
The transition rates are functions of β and d (see AppendixB). One of our fundamental assumptions is that the measurements of β and d did not occur at equilibrium, since the two division fraction data sets do not agree in value (see Figure 2(a)). However, the two curves do agree qualitatively in their general trend, as both contain relative maxima βm ∈ [0.3, 0.8] occurring at some density ρm ∈ (0, 1). Using this observation, we postulated equilibrium distributions β(ρ) and d(ρ) with the same basic structure:
| (3) |
| (4) |
where
| (5) |
There are a total of 4 free parameters in (3)–(4): βm, ρm, ε, and d. See Table A1 for calculated values and explanations, and Figures 2(a) and 2(b) (red curves) for a sample plot of β(ρ) and d(ρ) at an arbitrary parameter set.
Figure 2.
Experimental results with functional forms for cell-cycle and apoptosis fractions. Experimentally (blue and black), OVCAR-8 cells are allowed to attach to the plate for twenty-four hours, and then are incubated for a subsequent twenty-four hours. After this incubation, the cells were stained to determine which percentage of cells reside in the proliferation and apoptosis stages. The experiment was performed using two different techniques for cell synchronization: Data 1 and Data 2 (see AppendixB.1.1 for details). The functional forms (red) correspond to equations (4) and (3), with free parameters taking values βm = 0.75, ρm = 0.15, ε = 1, and d = 0.03. (a) Fraction of cells in division stage (P) as a function of the population density on the plate; (b) Fraction of cells in apoptosis stage (A) as a function of the population density on the plate. Note that we allow ρ > 1.
d(ρ) is chosen as a constant d since its observed range of values is small (0.01 ≤ d ≤ 0.05), and relative to β, appears essentially constant (see Figure 2(b)). However, we do use these values as the lower and upper bound on parameter searches (see Section 4.4). One can also check that β(ρ) in (4) has absolute/relative maximum βm at ρ = ρm, which is the aforementioned desired constraint. ε is a constant which dictates how rapidly β(ρ) decreases for large cellular densities. Condition (5) guarantees that β(1) = d, and furthermore, β(ρ) < d for ρ > 1. Lastly, β(ρ) = 0 for ρ > 1 + ε. The reason for these choices is as follows: we allow the possibility that ε > 1, since it was observed that OVCAR-8 cells may deform their cell membranes and/or grow upon one another in a two-dimensional culture to complete mitosis. Hence, we allow divisions when ρ > 1, but we ensure that death is more likely in this regime. Thus, when ρ > 1, a net increase in cells should only occur from cells that previously entered compartment P and successfully completed cell division; no net flow between compartments P and A exists. Furthermore, when the plate becomes dense enough (i.e. ρ > 1 + ε), no cells can enter P.
The rates that describe the transitions between the cellular compartments are given below:
| (6) |
| (7) |
| (8) |
where
| (9) |
| (10) |
Nq(t), Np(t), and Na(t) are the cell counts in compartments Q, P, and A, respectively, at time t, and K represents a constant that defines ρ = 1, which should be interpreted as the number of cells which occupy a single layer of the culture. Throughout this work, K was scaled to be 40401, for a 201 cell by 201 cell square environment. c > 0 is a per time constant which represents a cellular reaction rate, and γ ∈ [0, 1] is a unitless proportion corresponding to the difference in arrivals to compartment A via compartments P and Q. Note that all quantities are dynamic and stochastic.
2.2. Rate Derivations
In this section, we provide motivation for the forms employed in equations (6)–(8). Consider transitions from quiescence to division (Q to P). Our fundamental assumption is that there exists a theoretical β(ρ) (represented by (4) with sample visualization appearing as the red curve in Figure 2(a)) which yield the fraction of cells that are in compartment P at equilibrium. Hence, all cells on the culture calibrate towards the fraction in this figure. Converting fractions to cell numbers, one can mathematically describe the desired number of proliferative cells as
| (11) |
in general, Np,desired(t) and Np(t) are not equal, and thus cells transfer compartments. By the interpretation of Poisson rates, the number of cells transferring from Q to P in the time interval [t, t + Δt] is approximately αp(t)Q(t)Δt, for small Δt. On the other hand, it is natural to assume that the number of transitioning cells should be proportional to the difference of the desired and current states:
| (12) |
by equation (11). The positive part is there to ensure that we do not take a negative number of cells, i.e., that once a cell is dividing, it cannot return to quiescence without successfully completing mitosis. Assuming all cells react to the disparity between Np,desired(t) and Np(t) at the same constant rate c, (12) can be written as
| (13) |
or equivalently, equation (6), which is the desired expression for αp(t), and will be the transfer rate of one cell from compartment Q to compartment P during [t, t + Δt]. If the population becomes so small that Nq(t) = 0 for some time t, then no cells can transfer, and hence we must augment the expression for αp(t) as
| (14) |
It will be understood that all other rates (αap(t) and αaq (t) in (7) and (8), respectively) have similar piecewise definitions, which we omit stating explicitly because we believe it will cause no confusion to the reader. We also note that in the simulations for this work, the fraction of dying cells is small enough (≤ 5%) to prevent any cell compartment from becoming extinct. This is described in Section 4.
In an analogous way we defined the rates from P to A and from Q to A, which are denoted by αap(t) and αaq (t), respectively. However, Figure 2(b) represents the total number of cells entering A, from both compartments P and Q. To separate the transitions between these compartments, we assumed that the relative number of cells transferring between P and Q differs by a constant. Hence, assuming cells respond with the same rate c as above, the death rates can be written as (7) and (8), where 0 ≤ γ ≤ 1 represents the arrival difference factor. Furthermore, we assume that dividing cells are more prone to cell death than quiescent cells [13], i.e. . Note that (7) and (8) are indeed the correct expressions in our framework, since in a small time Δt, the total number of cells transitioning into compartment A is given approximately by
| (15) |
which is the desired total number of cells.
2.3. ABM Algorithm
We include a brief outline of the steps involved in the algorithm. Suppose at time t we have N(t) cells, each residing in one of the three compartments Q, P, or A, with total cell counts Nq(t), Np(t), and Na(t), respectively. We update the system to time t + Δt by the following steps:
Choose a uniformly random order 𝒪 of the cells.
- Update each cell according to 𝒪:
- If the cell is in compartment Q, do one of the following:
- Enter P with probability αp(t)Δt and choose LP via equation (1).
- Enter A with probability αaq (t)Δt and choose LA via equations (49) and (50).
- Remain in Q with probability 1 − αp(t)Δt − αaq (t)Δt.
- If the cell is in compartment P, do one of the following:
- Enter A with probability αap(t)Δt and choose LA via equations (49) and (50).
- If the elapsed time of the cell-cycle is LP, then with probability 1 − αap(t)Δt, the cell and its daughter move to compartment Q.
- If the elapsed time of the cell-cycle is less than LP, then with probability 1 − αap(t)Δt, the cell-cycle age increases by Δt.
- If the cell is in compartment A, do one of the following:
- If the elapsed time of the apoptosis-cycle is LA, then the cell is removed from the simulation.
- If the elapsed time of the apoptosis-cycle is less than LA, then the apoptosis-cycle age increases by Δt.
Update all cell counts to Np(t + Δt),Na(t + Δt),Nq(t + Δt), and N(t + Δt).
3. Integro-Differential Equation Model
In this work, we study the dynamic mechanisms of cell growth, assuming variations in the cell-cycle and apoptotic periods. The entire system dynamic results from the interactions and decisions of individual cells, which could potentially lead to significant deviations from mean values. However, it is well-known that despite the presence of intrinsic fluctuations, the dynamics of a system with a size that is sufficiently large may be captured by deterministic equations that reflect mean field limits [6, 16, 18]. Thus, we approximate the ABM with a system of integro-differential equations (IDEs) that approximate the expected values of the cellular compartment sizes in time. Details on the derivation and validity of the following system can be found in Section 3.2.
3.1. Approximation of Expected Values
We make the notational convention for mean values: 𝔼[·] ≔ 〈·〉. Following the above discussion, a set of IDEs which approximate the expected value of the ABM random variables is formulated, with corresponding rates evaluated at expected values:
| (16) |
| (17) |
for example. Note that , in general. The IDE system which approximates the mean fields of the three compartment cellular ABM is given below:
| (18) |
| (19) |
| (20) |
Here fp(·; μ, σ) and fa(·) denote the probability density functions (PDFs) for the cell-cycle and apoptotic process length random variables, LP and LA, respectively. Recalling equations (1) and (2), fp(·; μ, σ) and fa(·) are
| (21) |
| (22) |
where Γ(·) is the gamma function.
Equations (18)–(20) represent a system of delay differential equations (DDEs), where the delay is captured by integrals over time. However, instead of possessing a fixed value, we see that the delays are distributed, with relative contributions to the flow determined by the densities fp(·; μ, σ) and fa(·).
3.2. The Derivation of the IDE
Consider the ABM introduced in Section 2. Fix a small time-step Δt > 0 and a time t ≥ 0. Consider the system update from t to t + Δt in the, say, cell-cycle compartment P. We can decompose the random variable Np as follows:
| (23) |
where ap(t,Δt) is the number of cells entering P from Q in the time interval [t, t+Δt], aap(t,Δt) is the number of cells exiting P and entering A in [t, t+Δt], and x(t,Δt) is the number of cells exiting P and entering Q in [t, t + Δt] through successful divisions. Taking the expectation of (23) and using linearity we obtain
| (24) |
We continue by finding expressions for the terms on the right-hand side (RHS) of (24).
Consider 〈ap〉(t,Δt). Using the Poisson interpretation of the ABM, the number of cells transitioning from Q to P in [t, t + Δt] is given by the product of the expected probability of transition of one cell and the expected number of cells currently residing in compartment Q:
| (25) |
Our goal is to simplify the above expression, so as to obtain a closed system of equations; otherwise we must perform Monte-Carlo simulations to compute the above expectations, which would render the deterministic model ineffective. A natural step would then be to reverse the order of the nonlinearity and expectation, while incurring an error, as 〈f(X)〉 ≠ f(〈X〉) for a nonlinear f and a random vector X, in general. However, we recall from Figures 6(c) and 6(d) that the variances in the ABM are small, and hence we expect the error of approximating X with its mean to also be small, even through the function f. Indeed, we can expand a general f(X) in a Taylor series about the mean value of X as
| (26) |
where D2f denotes the Hessian of f. Upon taking expectations and retaining only these first three terms, we obtain
| (27) |
Figure 6.
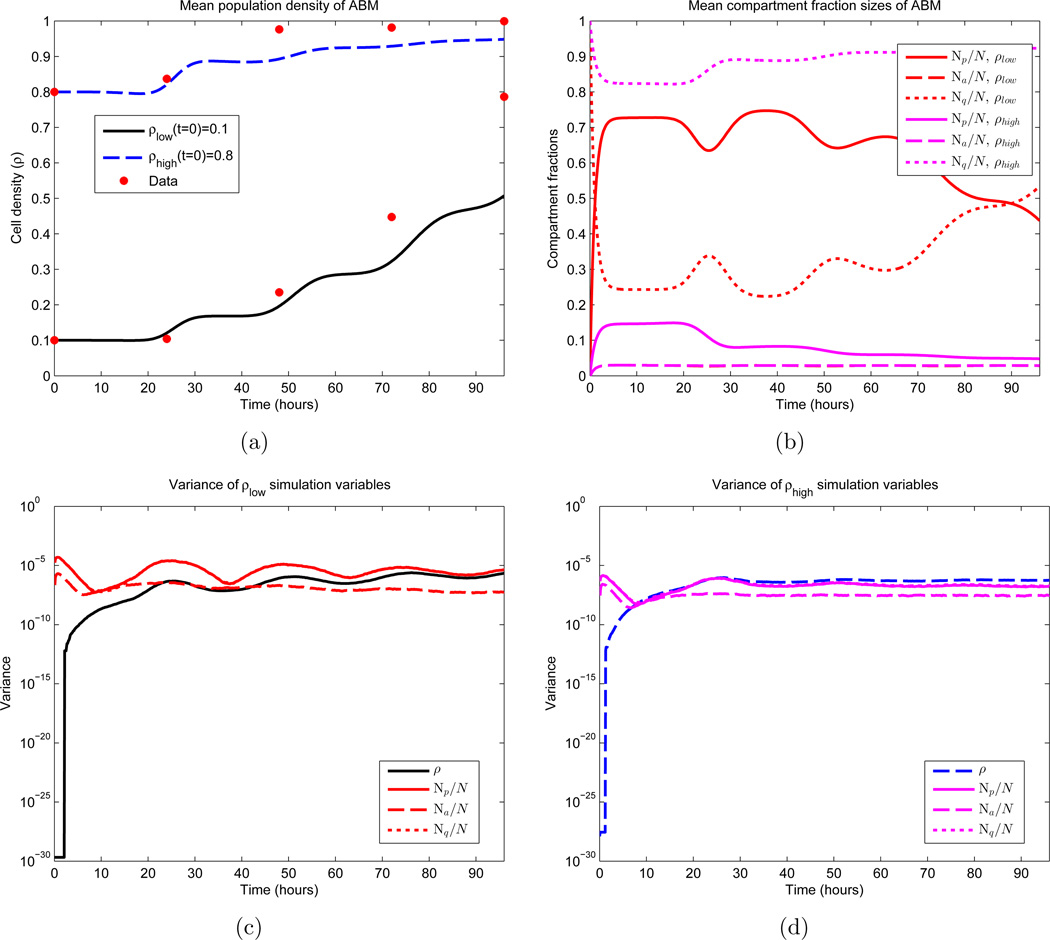
First and second moments of the ABM. Shown are the temporal dynamics of the mean and variance of 1000 Monte Carlo simulations. β and d appear as the red curves in Figures 2(a) and 2(b) respectively, and σ = 3 hours, c = 1 cell per hour, γ= 0.70. Note that these parameters do not yield an optimal fit. See equations (51) and (52) for the two sets of initial conditions. In (b), the values of Na for both sets of initial conditions essentially overlap, making them difficult to distinguish. The same is true for the variances of Np and Nq in (c) and (d). (a) Sample means for the population density; (b) Sample means for the three cellular compartments; (c) Variances for simulations that satisfy ρ(0) = 0.1; (d) Variances for simulations that satisfy ρ(0) = 0.8.
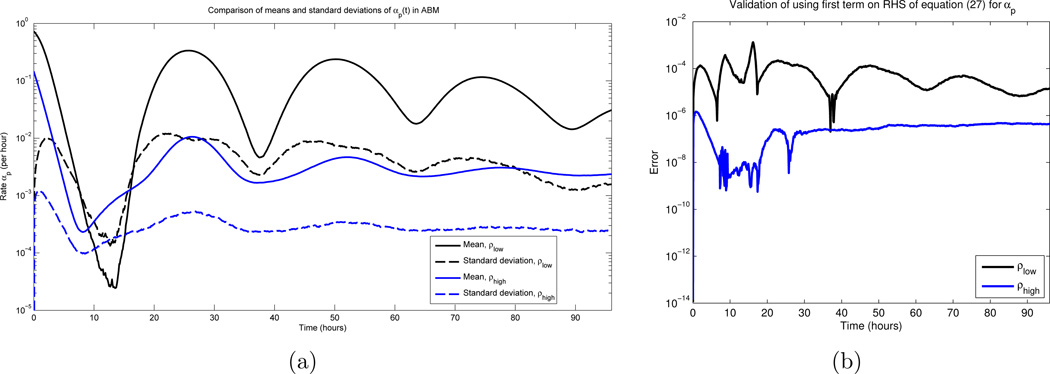
Recall that Df(〈X〉), D2f(〈X〉) are constants with respect to the expectation operator. Furthermore, the last term in (27) is obtained from the quadratic form appearing in (26) (see [11]). Hence, assuming f is sufficiently smooth, our previous variance calculations imply that 〈f(X)〉 ≈ f(〈X〉) [2]. To justify the smoothness condition, note that here, f = αp, where αp is given by equation (6). The Q = 0 case is not an issue since, as discussed in Section 2.2, cell fractions do not become extinct. The only other points where αp could violate smoothness are times such that αp(t) = 0, since the positive part function is non-differentiable here. Hence, it is sufficient to verify that αp(t) is bounded away from 0 for all times t. Thus, we ran 1000 Monte Carlo simulations of the ABM, and calculated the mean and standard deviation of αp(t) at each time point; see Figure 3 (a). All parameters values were as in Section 4.2 below. Note that for each initial condition (ρ(0) = 0.1 and ρ(0) = 0.8), the standard deviation is approximately one order of magnitude smaller than that of the mean. As the mean is bounded away from zero, the law of large numbers implies that αp(t) = 0 is statistically improbable, for most times t. The same conclusions can be verified for the other rates αap(t) and αaq (t). Our statement is about “most times” due to the observation that there is a region in Figure 3 where the the standard deviation is larger than the mean, and hence αp(t) can be 0 with non-zero probability. Indeed, this is observed in realizations. However, this timescale is short and transient, which implies that switching the order of the expectation and the nonlinearity is a valid approximation. We also compare the approximation directly in Figure 3(b), and note that for all times, the error is smaller than 10−3. Furthermore, comparing the stochastic ABM to the obtained continuous DEs is another form of validation (see Section 4.3).
Figure 3.
(a) The mean and standard deviation of αp(t) over all times t ∈ [0, 96] hours, for 1000 Monte Carlo simulations. β and d appear as the red curves in Figures 2(a) and 2(b) respectively, and σ = 3 hours, c = 1 cell per hour. See equations (51) and (52) for the two sets of initial conditions. Note that the standard deviations are roughly an order of magnitude smaller than the mean values, for most times. (b) Error obtained in using the first term on the RHS in equation (27) as an approximation for αp(t)
Using equation (25), the previous justification allows us to approximate 〈ap〉 (t,Δt) as
| (28) |
where is defined as αp evaluated at the expected values of the compartment populations. In the same way, we obtain an approximation for 〈aap〉(t,Δt):
| (29) |
Here is defined analogously to . From this point forward, we drop both the expectation brackets and bars so that, for example, Np(t) denotes the expected population of the dividing cells at time t, and αp(t) denotes the transition rate of a cell to compartment P from compartment Q at time t, where the compartment populations are given by their means. This should cause no confusion with realizations of the ABM, and when comparisons are made, it should be understood that the deterministic results represent expectations. Using this notation and the approximations in (28) and (29) as equalities, equation (24) becomes
| (30) |
To determine 〈x〉(t,Δt), the expected number of cells that complete cell division in the time interval [t, t + Δt], we note the following conditions that must hold for such a cell:
It must enter P at some time t* ≤ t + Δt.
Its length of division ℓ must satisfy t ≤ t* + ℓ ≤ t + Δt, or equivalently, t − t* ≤ ℓ ≤ t − t* + Δt.
It must not enter the apoptotic cycle A at any time in the interval [t*, t + Δt].
In our model formulation, all three of the above events are independent. Thus, to determine 〈x〉(t,Δt), we must add up (i.e. integrate over) all times t*, where 0 ≤ t* ≤ t+Δt, the product of the expected number of cells that enter P at t* and the probability of a cell choosing the correct division length ℓ while not entering A during [t*, t + Δt]. We recall that the division length is distributed according to (1), with corresponding Gaussian probability density function (PDF) fp(·; μ, σ). The expected number of cells that enter P from Q between times t* and t* +Δt* for small Δt* is given approximately by αp(t*)Nq(t*)Δt*, and hence the expected number yielding the correct division length is approximately
| (31) |
However, we must take only the fraction of these cells that remain in P during [t*, t + Δt], which we obtain by multiplying (31) by the probability 𝒫 of a cell not entering A throughout [t*, t + Δt]. Again, an independence assumption between cell-cycle length and the event of entering the apoptosis cycle is used. To calculate 𝒫, we note that
| (32) |
where 𝒫′ is the probability of entering A at some point during [t*, t+Δt]. Dividing [t*, t+Δt] into non-overlapping subintervals via small , the event corresponding to 𝒫′ can be realized as the disjoint union of sub-events, where each sub-event corresponds to entering A in a subinterval with corresponding probability . Mutual exclusivity and the fact that these sub-events cover the event corresponding to 𝒫′ implies that
| (33) |
where in the limit , the expression becomes exact. Here n ∈ ℤ is such that t* + (n − 1)Δt*. Combining (31), (32), and (33) yields an approximation for the number of cells that enter at a fixed t* and carry out a division in [t, t + Δt]:
| (34) |
Adding contributions from every 0 ≤ t* ≤ t+Δt produces 〈x〉(t,Δt). In the limit as Δt* → 0+, the summation becomes an integral, and we obtain
| (35) |
Note that in this limit, (35) is exact. Substituting this expression into (30) yields, upon rearrangement and division by Δt,
| (36) |
Taking the limit of (36) as Δt → 0+, we have, via the Fundamental Theorem of Calculus,
| (37) |
Equation (37) is an integro-differential equation (IDE), where a delay is represented by the integral terms. Indeed, if cells divided after a fixed length of time ℓ, instead of randomly, then fp takes the form of a δ-function, and (37) reduces to a delay-differential equation (DDE):
| (38) |
Hence, (37) represents the expected value of system of DDEs with distributed time delays.
We can similarly derive equations for the expected value of Na(t) and Nq(t):
| (39) |
and
| (40) |
where fa(·) is a gamma PDF for the apoptotic process length (see Section 4.1 and Figure 5(d)). Note that there is no inner integral in (39) since we assumed that once cells enter apoptosis, they cannot escape eventual cell death. Also, a factor of two appears in (40), since the original cell and its daughter both re-enter state Q from P. We can also write an equation for the expected number of the total number of cells, N(t), by summing all of (37), (39), and (40):
| (41) |
Equations (37), (39), and (40) correspond to the system of equations presented in Section 3.1. Standard theory implies existence and uniqueness of these equations [9].
Figure 5.
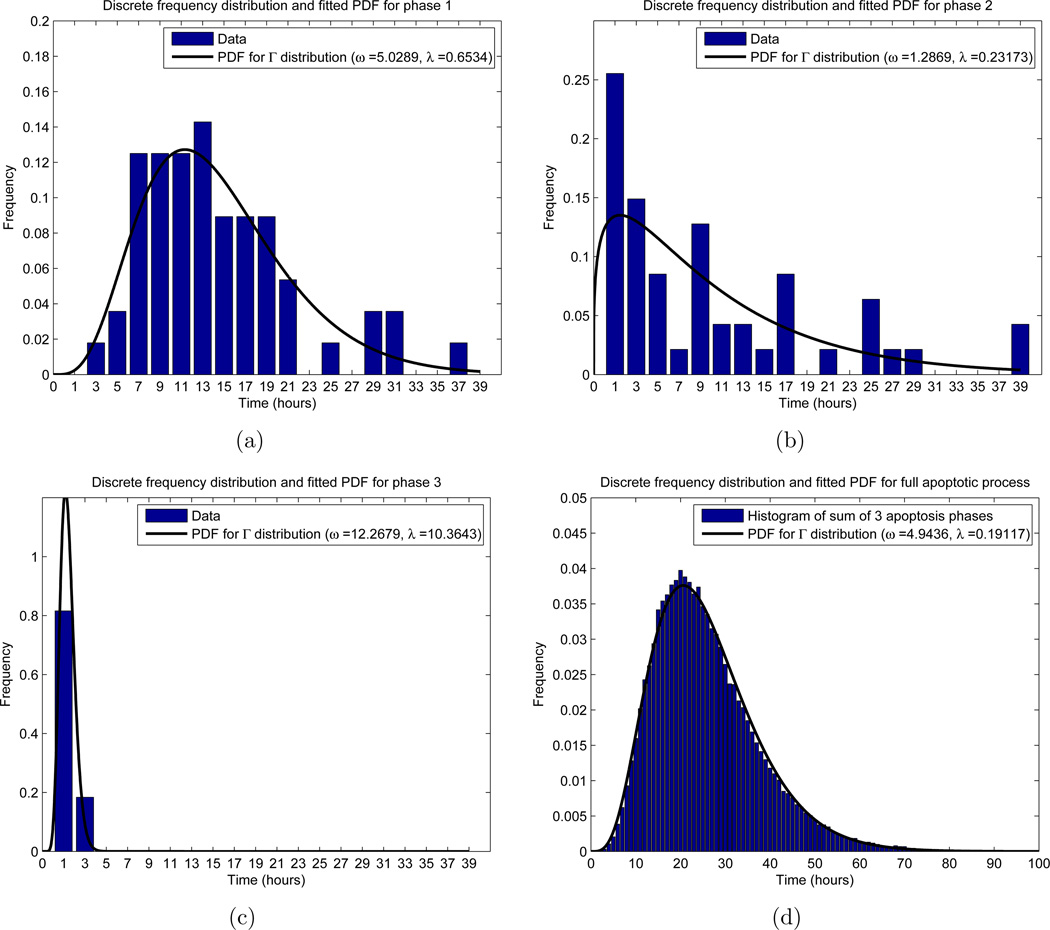
Frequency distributions for the apoptosis process. The x-axis represents the time in the respective phase, while the y-axis labels a fraction of cells. For the experimental results (histogram in (a)–(c)), the x value indicates a range of times, so that for x = i hours, the corresponding y-value (height of the bar) counts the relative frequency of cells with phase length between i − 1 and i+1 hours. For the theoretical distribution (black curve), we allowed the phase length to be a continuous random variable, and fitted a gamma distribution with probability density function (PDF) using MATLAB’s “fitdist.m” function. In (d), we used the PDFs obtained in (a)–(c) to obtain a single gamma distribution for the entire apoptotic process. (a) Phase 1, with n = 56 total cells measured; (b) Phase 2, with n = 47 total cells measured; (c) Phase 3, with n = 49 total cells measured; (d) Total length of time spent in apoptosis, using n = 105 simulations of (50).
3.3. Numerical Methods
We provide a brief outline of the numerical algorithm used in solving (18)–(20). The scheme used was the four-step explicit Adams-Bashforth method [3], which for a general system
| (42) |
discretizes via interpolation of f through four previous points, and hence generates a fourth order accurate method. For an explicit, uniform time-step Δt, the method takes the form
| (43) |
where tn ≔ nΔt, yn ≔ y(tn), and fn ≔ f(tn, yn). For the first 3 steps, (43) is augmented with standard initializations of lower degree Adams-Bashforth methods.
Regarding the calculation of the integrals appearing in (18)–(20), we consider integrals of the form
| (44) |
for arbitrary functions h1 and h2 and time t. These integrals are discretized with the same step-size Δt used in the numerical algorithm described previously. Denoting the inner integral in (44) by I(t, t*), I(t + Δt, t*) is related to I(t, t*) via the approximation
| (45) |
Using (45) to calculate the inner integral requires only one function evaluation and no quadrature, and hence is more numerically efficient than re-integration. Note that we must store values of I(t, ·) at all time points in the discretization. To calculate the complete integral (44), the composite trapezoidal rule with uniform grid spacing Δt was used:
| (46) |
where tk is the kth point, and N is the size of, the discretization. Updating the expression from t → t+Δt requires this calculation at each step, because here, unlike h2, h1 depends explicitly on t, and thus prevents an approximation analogous to (45). Equations (45) and (46) give a complete characterization of the calculation of all integrals appearing in this work.
4. Results
Cell survival is determined by many factors, including the ability of the cell to transition between the cell-cycle and quiescence, and vice versa. These dynamics can be described mathematically, as both an ABM and a system of IDEs, as discussed previously. Using the OVCAR-8 cell line as a model, we performed three fundamental biological experiments, and estimated the following: 1) cell growth and density over 4 days (i.e. ρ(t)), 2) cell proliferation fraction as a function of cell density after 24 hours (i.e. β(ρ)), and 3) cell death fraction as a function of cell density after 24 hours (i.e. d(ρ)). See AppendixB for details and the experimental results.
To describe the biological results, we introduce two mathematical models: an ABM and a set of IDEs. Detailed descriptions of our methods can be found in Sections 2 and 3. The ABM is specified on the level of the cell, which can reside in one of three compartments: proliferative (P), apoptotic (A), and quiescent (Q), with corresponding populations Np,Na, and Nq (see Figure 1). Transitions between the compartments are dictated by both the rates αp, αap, and αaq, and the amount of time spent in the the cell-cycle and the apoptotic process. The rate functions depend on the total cellular density ρ and the equilibrium distributions α(ρ) and d(ρ), while the time spent in P is assumed to be a normal random variable with mean length μ hours, and standard deviation σ hours. Similarly, the amount of time spent in A is modeled with a gamma distribution, with shape parameter ω and rate parameter λ per hour. The IDE system is a set of three equations governing the dynamics of approximations to the expected values of the compartment populations.
4.1. Distribution of Cell-Cycle and Apoptotic Lengths
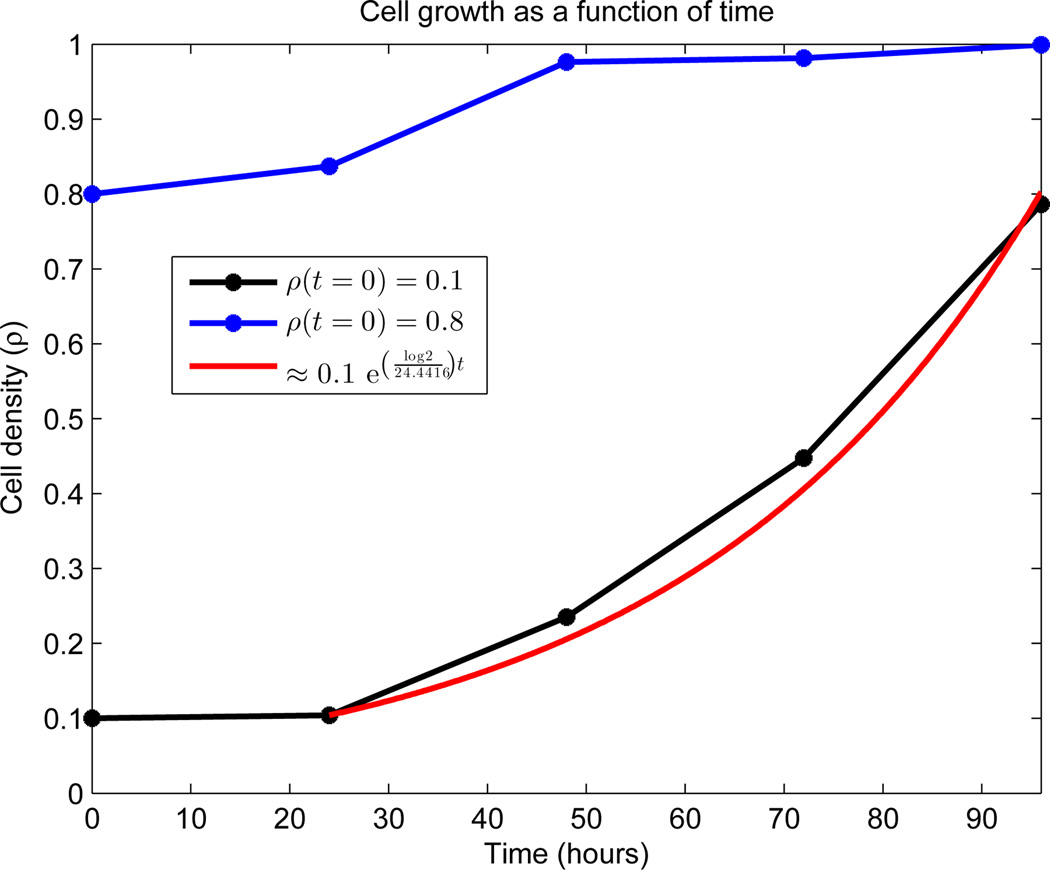
To calculate the mean length of the cell-cycle μ, we used the experimental data appearing in Figure 4. See AppendixB.1.2 for details. We observed essentially exponential growth from day 2 to day 4 in the low density seeding (denoted ρlow). Standard least-squares techniques fit
| (47) |
to the data in this region, and k was related to the mean length of the cell-cycle via the doubling time:
| (48) |
See the red curve in Figure 4 for the results of the calculation, which include μ = 24.4416 hours.
Figure 4.
Growth dynamics of OVCAR-8 human ovarian carcinoma cell line. Global density is measured on the vertical axis as a function of time. Both initial densities (ρ(0) = 0.1 and ρ(0) = 0.8) were generated by random seeding on a 24-well plate and cultured 24 hours prior to the first image. Data was collected every 24 hours, as indicated by stars. No data exists between the points, and the connecting line segments are added merely for viewing elucidation. The estimated density percentage is based on the average of two complete wells. The red curve represents a least-squares fit to the region of exponential growth, with doubling time μ = 24.4416 hours.
The calculation of the distribution of LA was based on the results of [12]. In their work, Messam and Pittman observed that apoptosis could be characterized by three morphological phases. In particular, once apoptosis is triggered, cells begin by exhibiting normal morhphology (phase 1), then plasma membrane bubbling (phase 2), and finally whole cell body blebbing and apoptosis execution (phase 3). Furthermore, the authors obtained experimental results, in the form of frequency distributions, for how long cells remain in each of these three phases. Using their frequency distributions, we fit gamma distributions to each phase, and then independently sum the distributions to obtain the overall apoptosis process length LA as a random variable. Denoting the length of phase i (i = 1, 2, 3) by LAi, this becomes
| (49) |
| (50) |
Here ωi and λi are the shape and rate parameters of phase i, respectively. To find the distributions of each phase, we used the MATLAB function “fitdist.m,” which uses standard maximum likelihood estimation, to find the parameters characterizing the distribution. Moreover, we restricted the search domain to gamma distributions. The results of this, along with the experimental results appearing in [12], can be found in Figure 5. With these computations, we find a probability density function (PDF) for each LAi, and via equations (49) and (50), are able to realize a value for LA for each cell entering A. We are further able to fit a gamma distribution to 105 realizations of (50), which yields (2) with ω = 4.9436 and λ = 0.19117 (Figure 5(d)).
4.2. ABM Simulation
We provide a sample experiment of the ABM, which demonstrates the behavior of the model. We used β(ρ) and d appearing as the red curves in Figures 2(a) and 2(b) respectively, σ = 3 hours, c = 1 cell per hour, and γ = 0.70. We emphasize that these parameters are not a fit to the experimental data appearing in Figure 4. Before computing, we specify the initial conditions, which are used in the models throughout this work, unless explicitly stated otherwise. Experimentally, all cells are initially synchronized as quiescent, so we define
| (51) |
Using the data from Figure 4 as motivation, we simulate two sets of initial conditions, ρlow(0) = 0.1 and ρhigh(0) = 0.8. Equations (10) and (51) imply that
| (52) |
One thousand Monte Carlo simulations were then performed, the results of whose mean and variance calculations appear in Figure 6. The main aspect to note is the expected density dynamics in Figure 6(a), with faster growth for smaller population values coupled with a flattening as ρ approaches 1. In the same figure, we also observe periodic prominences of density increase located approximately 24 hours apart, which coincide with the mean division time μ. In Figure 6(b) we see periodic population fluctuations between the compartments Q and P, as cells complete division and reenter quiescence. A larger fraction of cells migrate to compartment P initially in the simulation satisfying ρlow(0) = 0.1, as β is larger here at time t = 0. We also do not observe much fluctuation in compartment A, which is due to the fact that d(ρ) is taken as a constant. Figures 6(c) and 6(d) are included mainly to quantify the stochasticity in the model (on the order of 10−6). We note that the small variation between realizations is due to the large number of cells in the computation (𝒪(105)). Note also that at time t = 0 the variances evaluate to machine 0, as the initial conditions are identical in every realization.
4.3. Stochastic and Deterministic Comparison
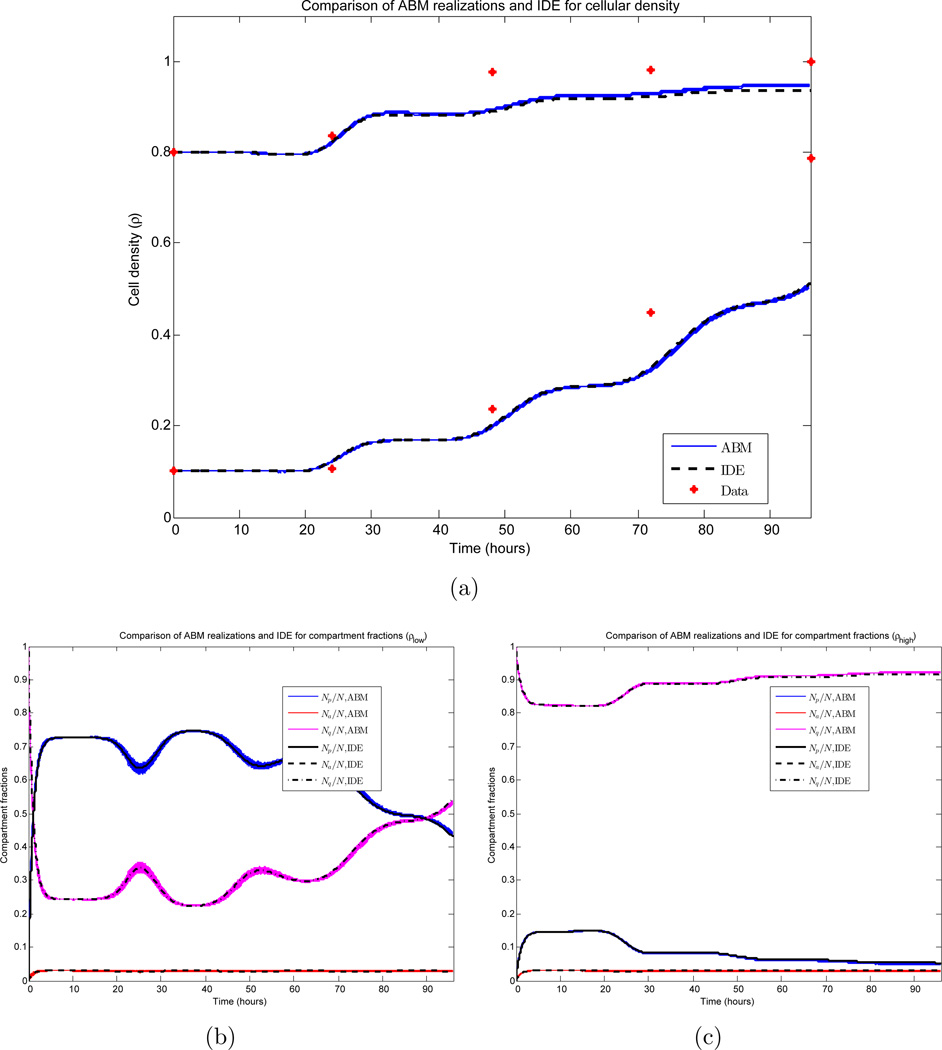
We investigate the relationship between realizations of the ABM and the IDE. Due to the large number of cells in the simulation, the small variances observed in Figures 6(c) and 6(d) imply that individual ABM simulations can be approximated well by their mean value, and the derivation in Section 3.2 (together with Figure 3) further implies that the mean value can be approximated by the solution of the system of IDEs appearing in Section 3. Here, we quantify these approximations. Data from the ABM simulations appearing in Section 4.2 is compared to the numerical solution of the IDE system (18)–(20) with corresponding parameter values and initial conditions. The results appear in Figure 7. The system of IDEs is solved using a four-step explicit Adams-Bashforth method. For more details, see Section 3.3.
Figure 7.
Comparison of ABM and IDE simulations. 1000 Monte Carlo realizations are plotted together with the corresponding IDE. β and d appear as the red curves in Figures 2(a) and 2(b) respectively, and σ = 3 hours, c = 1 cell per hour, γ= 0.70. (a) Cellular density for both sets of initial conditions (ρ(0) = 0.1 and ρ(0) = 0.8); (b) Compartment fractions for ρ(0) = 0.1; (c) Compartment fractions for ρ(0) = 0.8.
Figure 7(a) demonstrates the growth of the global cell density ρ for both the low and high density seedings. All 1000 ABM realizations are plotted (blue), together with the IDE solution (black). Here, we observe both the small variance in the ABM simulations and the accuracy of the IDE approximation. Measuring the error ℰIDE,mean of the IDE to the ABM mean via the maximum of the distances induced by the supremum norm ‖ · ‖∞ for each initial condition, we obtain
| (53) |
As observed in Figures 6(c) and 6(d), ρ has a variance on the order of 10−6, and hence a standard deviation on the order of 10−3. By Chebyshev’s inequality [8], 93.75% of the realizations lie within four standard deviations of the mean; thus the incurred error between the IDE and such a realization can be bounded by
| (54) |
Furthermore, this is a conservative estimate, as the sample expectation of the LHS of (54) at any time t is computed to be 0.003. Similar conclusions are drawn in regards to the compartment populations appearing in Figures 7(b)–7(c). These calculations justify using the deterministic IDE system in the remainder of the work when performing numerical experiments and determining parameter values. We lastly note that for simulations involving small populations, a much higher variance is observed, and the IDE is no longer a valid approximation to ABM realizations. This was investigated by varying the plate size K in both the ABM and IDE simulations. We found that a small number of cells (e.g. K ≈ 100) ensures a small error between the IDE and the expected value of the ABM. More precisely, we observe the L∞ norm (with respect to time) of the error to be bounded above by 0.0216. However, to guarantee that the expected value accurately approximates individual realizations of a stochastic experiment, a larger number of cells is required. For simulations with K = 100, we calculated a relative standard deviation of the ABM simulations to be on the order of 0.14, while for K = 1000, this value decreases to 0.035. Thus we conclude that this system requires K to be on the order of 1000 cells for the IDE to accurately approximate individual ABM realizations.
4.4. Parameter Estimation and Variation
To calculate parameter values that model the measured cellular growth dynamics (Figure 4), we minimized the distance between the experimental data and the deterministic IDE. Denoting the vector of parameters p ≔ (c, γ, d, βm, ρm, ε, σ) and defining
| (55) |
we used MATLAB’s nonlinear least-squares solver “lsqnonlin.m” to minimize the ℓ2 norm of (55) at all measured times:
| (56) |
Here t is measured in hours. The minimization of (56) is performed over the parameter set p, using a constrained trust region algorithm. The constraints were generated both from biological interpretations and also experimental data; they appear below in Table 1, together with their justification. As the routine locates only local minima, 100 random initial parameter sets were used to seed the algorithm, yielding 100 (non-unique) local minimizing parameter sets. The results of this computation appear partially in Figure 8(a)–8(b).
Table 1.
List of minimization parameters and ranges
| Parameter | Min. Value | Max. Value | Comments |
|---|---|---|---|
| c | 0 | ∞ | Rate of transition is always non-negative |
| γ | 0.5 | 1 | See Section 2.2 |
| d | 0.01 | 0.05 | See Section 2.1 |
| βm | 0.3 | 0.8 | See Figure 2(a) |
| ρm | 0.05 | 0.2 | See Figure 2(a) |
| ε | 0 | ∞ | Ensures β(ρ) has a relative maximum |
| σ | 0 | 10 | Lower bound: standard deviation is non-negative Upper bound: essentially excludes possibility of negative cell-cycle length |
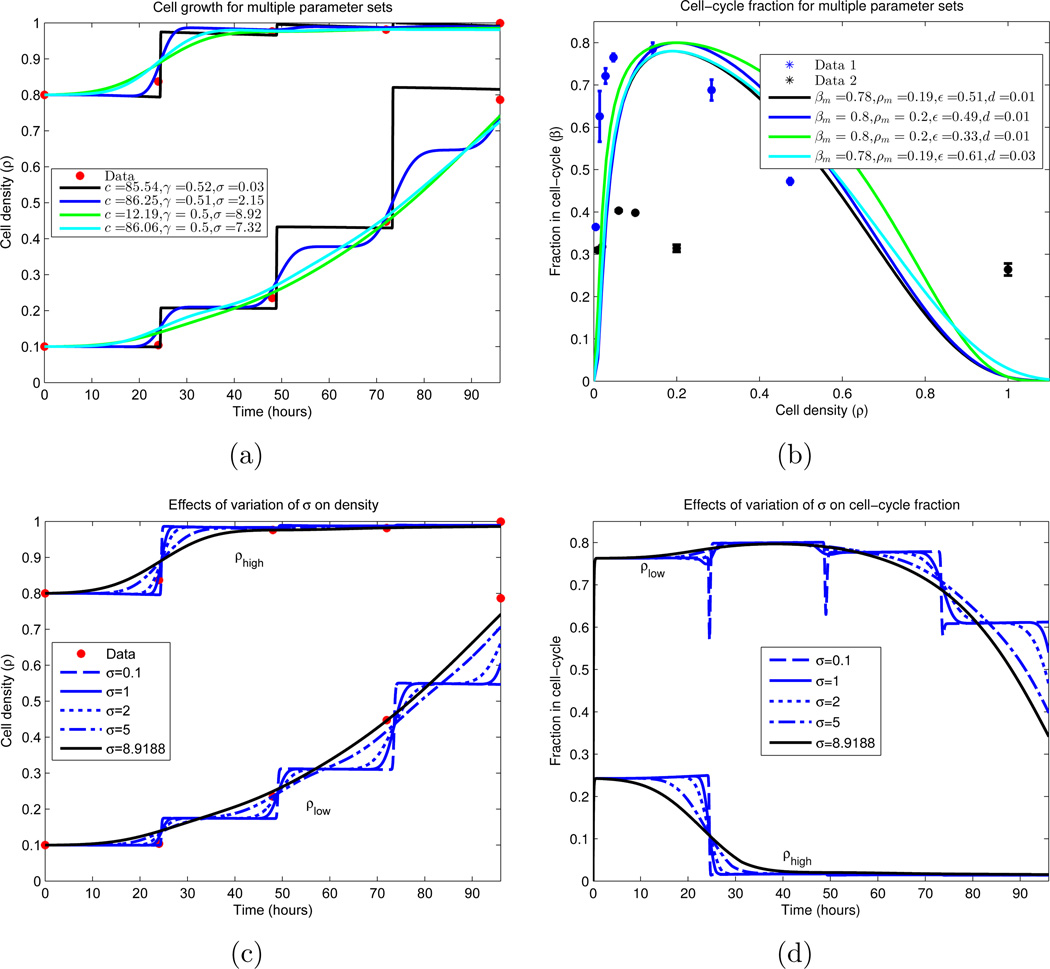
Figure 8.
Cellular growth dynamics for varying parameter sets. (a) A nonlinear least-squares algorithm was used to locate parameter values which minimize the difference between the experimental data and the IDE (equations (18)–(20), together with (9)–(10)). Due to the sparsity of the data (red), multiple local minimums were found. We note that all curves plotted have residuals with ℓ2 norm ∈ [0.0583, 0.0980], and are displayed in descending order by this measure. Similar plot styles in (a) and (b) correspond to the same parameter set. (a) Growth of cellular density in time; (b) Division (β) and death fractions (d = β(1)) for the fitted parameter sets.
(c)–(d) Dependence of IDE solutions on cell-cycle standard deviation σ. σ is varied, while all other parameters are fixed from a local minimizing set located in (a) and (b). We plot the global density growth and cell-cycle fraction for each case. (c) Cellular density ρ for σ variation; (d) Proliferative compartment for σ variation.
Figure 8(a) displays the low and high density cultures, together with the IDE simulations corresponding to four local minimizing parameter sets calculated in the numerical experiment; Figure 8(b) plots the corresponding equilibrium division fraction distributions β(ρ). The four sets are selected as minima of the local minima which display qualitatively different behavior while producing an ℓ2 norm of (56) in [0.0583, 0.0980]. Hence we conclude that no global minimum can be determined, as disparate parameter sets produce equally valid solutions. Indeed, as there are only 8 true data points (initial conditions are constrained) and 7 parameters, uniqueness should not be expected.
Nevertheless, we can still draw biological and experimental conclusions from the results. We observe that the most important parameter which dictates the qualitative structure of the population growth dynamics is the standard deviation of the cell-cycle length σ. For σ = 0.03 hours, the dynamics are essentially piecewise-constant, with steps of growth occurring at multiples of the mean cycle length μ = 24.4416 hours. As σ increases, these steps become smoother, with σ = 8.92 hours showing no visible step structure. See Figures 8(c)–8(d) for further elucidation of the σ dependence. Biologically this dependence on σ is intuitive, since as the population becomes more homogeneous (σ decreases), the overall structure should increase, resulting in more regular growth patterns. Lastly, we note that σ = 0.03 hours seems biologically improbable, as the density curve exhibits a large sensitivity to the measurement time. Indeed, for cells governed by such a σ, differing the measurement time by less than half an hour could yield an approximate 100% change in the measurement value, which is an unrealistic observation.
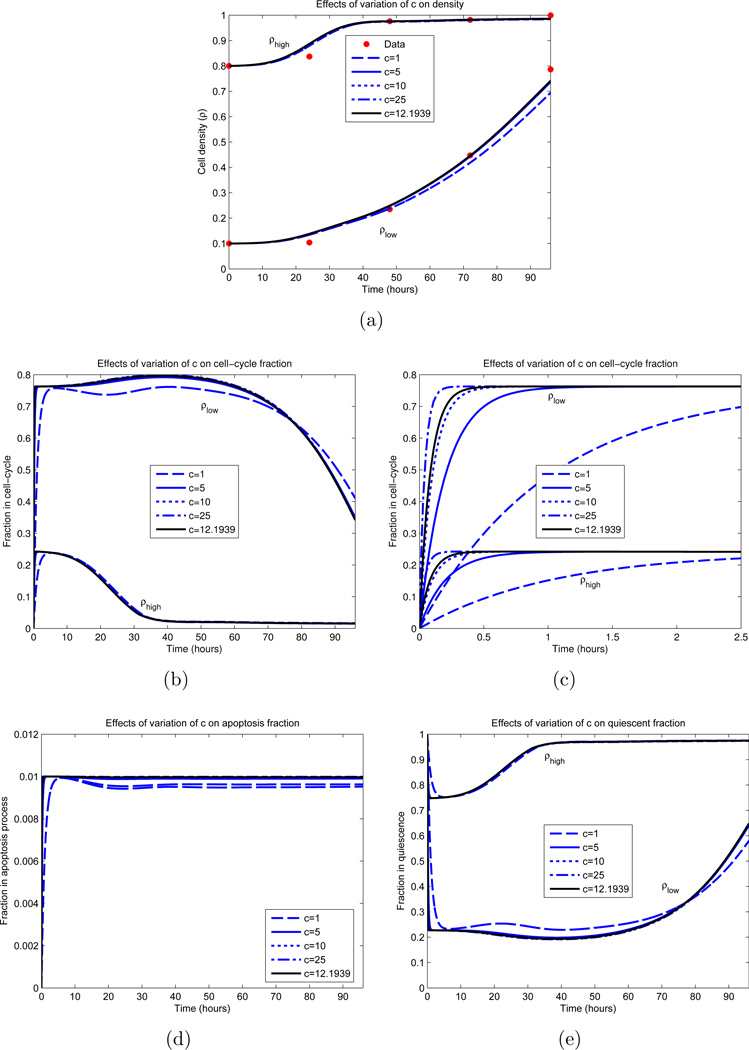
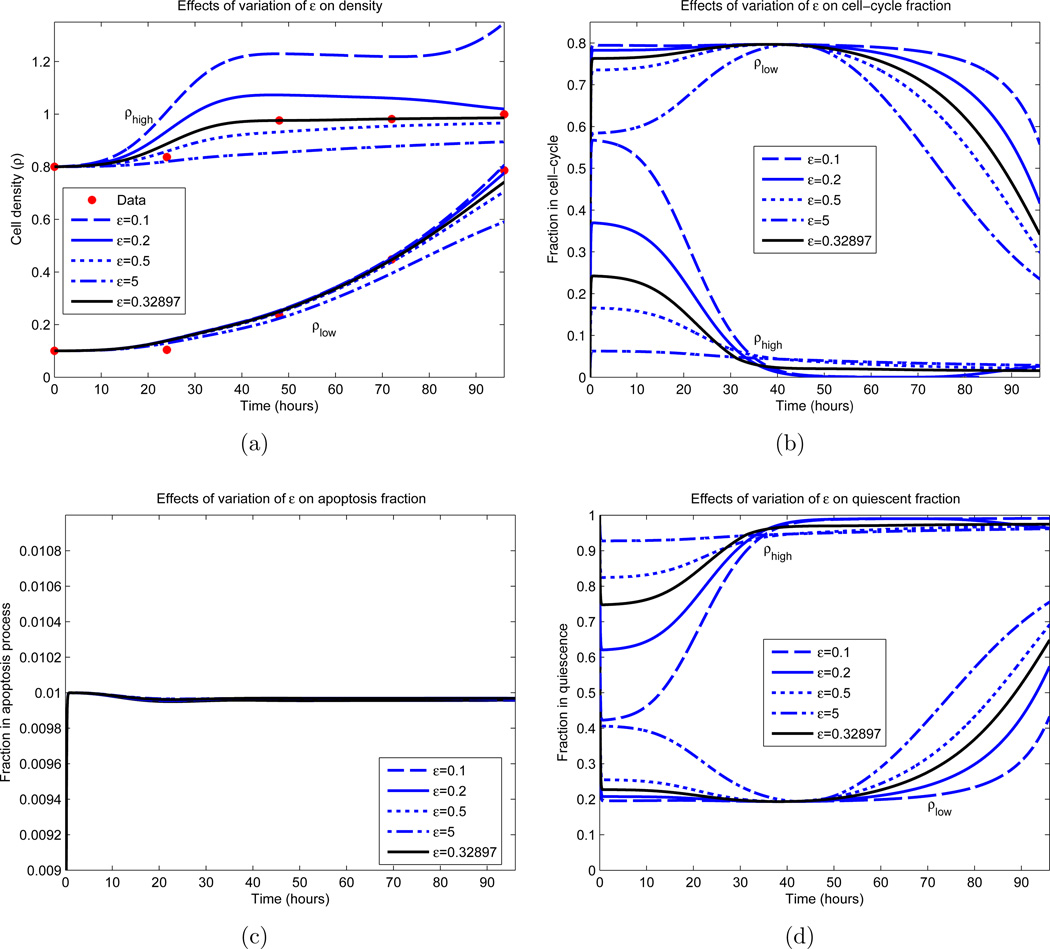
Other parameter values were determined with more certainty. Examining Figure 8(b), we observe that the optimal parameter sets yield a maximal dividing fraction of βm ∈ [0.78, 0.80] at a density of ρm ∈ [0.19, 0.20], both lying in small upper regions of their constraints (see Table 1). γ ∈ [0.50, 0.52] and d ∈ [0.01, 0.03] consistently, with d ≈ 0.01 in most cases. The rate of cellular transfer c and the division fraction parameter ε are more varied, and we investigated the dependence of the model on these parameters; the results appear partially in Figures 9 and 10. Here we vary only the parameter of interest, while leaving the others fixed. In Figure 9(a), we see minimal variation in the cellular growth as c varies over a large range. In particular, we observe that as long as c is not sufficiently small (c > 1 cell per hour), the overall growth dynamics do not vary substantially, and that c’s principal effect is on the rate which cells migrate into the division compartment P (Figure 9(c)). Note that for larger c, the earlier transitions into P occur; however after this initial variation, all parameterizations are relatively synchronized. Contrast this with Figure 10, where the ε dependence is examined. We observe a large variation in the dynamics for small variations in ε, especially in regards to high density growth.
Figure 9.
Dependence of IDE solution on c. All parameters, excluding c, are fixed and obtained from an optimization appearing in Figure 8 (green curves). The parameter values are βm = 0.8, ρm = 0.2, ε = 0.33, d = 0.01, γ = 0.5 and σ = 8.92 hours. The black curve represents the local minimizer. (a) Cellular density ρ; (b) Proliferative compartment; (c) Magnification of t = 0 dynamics of proliferative compartment; (d) Apoptotic compartment; (e) Quiescent compartment.
Figure 10.
Dependence of IDE solution on ε. All parameters, excluding ε, are fixed and obtained from an optimization appearing in Figure 8 (green curves). The parameter values are c = 12.19 cells per hour, βm = 0.8, ρm = 0.2, d = 0.01, γ = 0.5 and σ = 8.92 hours. The black curve represents the local minimizer. (a) Cellular density ρ; (b) Proliferative compartment; (c) Apoptotic compartment; (d) Quiescent compartment.
5. Conclusion
Understanding the mechanisms of cellular growth is an essential step in studying cancer progression and the evolution of drug resistance; thus, it is the subject of the current work. Our main hypothesis is that variations in both the cell-cycle and the apoptotic lengths are central contributing factors to the overall dynamics. We postulate that intrinsic heterogeneity, in the form of distributed cell-cycle and apoptotic process lengths, are fundamental aspects of cell growth, and cannot be ignored. Here, we introduced an ABM, and demonstrated the best approximation of the model to the data. An ABM permits a straightforward procedure for introducing an age-structure on a population, while simultaneously avoiding the technical details of macroscopic limits and population sizes, and hence continuum, age-structured models. Furthermore, our understanding of the biology is cell-driven, so it is natural to specify behavior on the cellular level, as opposed to the population as a whole. Such models are also quite exible and can take into account complex cell-cell and cell-environment interactions in a straightforward manner, which will be the subject of future work.
Formulating an ABM requires information of a cell behavior as a function of the environment. In our model it requires specific transition rates based on a given environmental condition. Our experimental results yield information on the distribution of cells in the cell-cycle and apoptosis process at various global densities, but do not include explicit information on the desired rates. A novel feature of this work is the manner in which the experimental results were incorporated into the ABM, translating the experimental distributions into probabilistic transitions on the cellular level.
It is a difficult task to fit a stochastic model, such as an ABM, to biological data, as different realizations produce different results. However, since the population size is relatively high, we observed that the overall variance of all random variables is small. Thus, the model can be viewed as essentially deterministic, with realized values that are given by their corresponding means. Hence, a system of IDEs which describe the expected values of the dynamic compartment populations was derived. Using this IDE system, we performed standard optimization on these deterministic variables to calculate the model parameters in the least-squared sense. Our results suggest that the IDE accurately describes the dynamics of the ABM, and both models emulate the experimental data for a large range of parameters.
The application of our framework to cancer research is expected to lead to the development of systematic methods for determining treatment strategies, where cellular behavior is governed by random, as opposed to deterministic, events. Furthermore, an expanded model that includes drug effects will allow us to revisit the mechanism of multi-drug resistance by studying the spatiotemporal mechanisms of intratumoral heterogeneity. Intratumoral heterogeneity includes many tumor sub-populations with different cellular dynamic characteristics, such as proliferation rates. Each sub-population may include intrinsic and/or induced heterogeneity mechanisms. Our work may be expanded to incorporate and study the differences between induced vs. intrinsic heterogeneity, and their effects on the resistance level, so that a global understanding and estimation of the total tumor evolution may be achieved.
Acknowledgements
We would like to thank George Leiman, Carol Cardarelli, and all members of the Gottesman lab, Subhadra Banerjee and Karen Wolcott from the NCI FACS Core Facility, for their helpful assistance and discussions. This work was supported by the Intramural Research Program of the National Institutes of Health, Center for Cancer Research, National Cancer Institute and was supported in part by a seed grant from the UMD-NCI Partnership for Cancer Technology. The work of DL was supported in part by the joint NSF/NIGMS program under Grant Number DMS-0758374, and by the John Simon Guggenheim Memorial Foundation.
AppendixA
Table A1.
List of parameters and variables
| Variable/ Parameter |
Range (units) | Interpretation |
|---|---|---|
| t | [0, 96] (hours) | Time |
| Δt | 0.1 (hours) | Time step used in ABM simulations |
| Nq(t) | [0, ∞) | Number of cells in quiescence at time t |
| Np(t) | [0, ∞) | Number of cells in cell-cycle at time t |
| Na(t) | [0, ∞) | Number of cells in apoptosis at time t |
| N(t) | [0, ∞) | Total number of cells at time t |
| μ | 24.4416 (hours) | Mean length of cell-cycle |
| σ | [0, 10] (hours) | Standard deviation of cell-cycle |
| ω1 | 5.0289 | Shape parameter of apoptosis phase 1 |
| λ1 | 0.6534 (per hour) | Rate parameter of apoptosis phase 1 |
| ω2 | 1.2869 | Shape parameter of apoptosis phase 2 |
| λ2 | 0.23173 (per hour) | Rate parameter of apoptosis phase 2 |
| ω3 | 12.2679 | Shape parameter of apoptosis phase 3 |
| λ3 | 10.3643 (per hour) | Rate parameter of apoptosis phase 3 |
| ω | 4.9436 | Shape parameter of entire apoptosis process |
| λ | 0.19117 (per hour) | Rate parameter of entire apoptosis process |
| ρ(t) | [0, ∞) | Density of cells at time t |
| K | 40401 | Number of cells defining full plate (ρ = 1) |
| d(ρ), d | [0.01, 0.05] | Fraction of cells in apoptosis as a function of plate density |
| β(ρ) | [0, 1] | Fraction of cells in cell-cycle as a function of plate density |
| βm | [0, 1] | Relaitve/absolute maximum of β(ρ) |
| ρm | [0, 1] | Maximizing density of β(ρ) |
| ε | (0, ∞) | Parameter governing shape of β(ρ) |
| αp(t) | [0, ∞) | Rate of transition from Q to P |
| αap(t) | [0, ∞) | Rate of transition from P to A |
| αaq (t) | [0, ∞) | Rate of transition from Q to A |
| c | [0, ∞) (per hour) | Cellular reaction rate |
| γ | [0, 1] | Rate difference between αap and αaq |
| fp(·; μ, σ) | [0, ∞) | PDF of 𝒩(μ, σ2) cell-cycle length |
| fa(·) | [0, ∞) | PDF of Γ distributed apoptosis process length |
| Eρ | (−∞, ∞) | Error vector between IDE and experimental data |
AppendixB
AppendixB.1. Experimental Design
This work is aimed at studying the heterogeneity arising from the variation in the cell-cycle and apoptosis length. With this in mind, three sets of experiments were performed: a study of cell growth and density, an analysis of cell proliferative percentage, and an analysis of cell apoptotic percentage. The results of these experiments appear in Figure 2.
AppendixB.1.1. Analysis of Proliferation Percentage
One goal is to understand the role of global density on cellular division. The results appear as means and standard deviations in Figure 2(a). We assume that, for a given cell density, there exists an equilibrium distribution of cells in the cell-cycle, which we define as β(ρ). To determine β(ρ), two series of cell-cycle arrest experiments were performed, each followed by KI-67 measurements.
Cell-Cycle Arrest
OVCAR-8 cells were seeded in different cell densities (see Figure 2(a)) on a 6-well plate with culture medium (RPMI-1640 medium + 10%FBS + 100U/ml Penicillin-Streptomycin + 2 mM Glutamine) for 24 hours prior to cell cycle arrest. To arrest the cells, 2 experiments were performed by changing the starvation medium and the starvation duration. In both experiments, cells were washed 3 times with 1× PBS and replenished with starvation medium. Experiment 1) The medium of RPMI-1640 without Penicillin-Streptomycin, and Glutamine was used for cell cultured in 37°C + 5% CO2 for 24 hours. The data set from this experiment was referred in the text and figures as “Data 1”. Experiment 2) The medium of RPMI-1640 without Glucose, Penicillin-Streptomycin, and Glutamine was used for cell cultured in 37°C + 5% CO2 for 48 hours. The data set from this experiment was referred in the text and figures as “Data 2”. Arrested cells from both experiments were allowed to re-enter cell cycle by washing the cells with PBS 3 times and then replenished with culture medium for 16 hours. The materials: Roswell Park Memorial Institute (RPMI)-1640 medium, Fetal Bovine Serum, Penicillin-Streptomycin, and Glutamine, were purchased from Life Technologies (Grand Island, NY).
Cell-Cycle Analysis by Ki-67 Immunolabeling
OVCAR-8 cells were seeded on 6-well plate with culture medium. Cells were harvested by trypsinization and re-suspended with PBS. Diameter of individual cells was measured by Nexcelom Cellometer (Lawrence, MA). To permeabilize cells, 106 cells were washed with 1× PBS and incubated with −20°C ethanol overnight. For Ki-67 labeling, cells were centrifuged and re-suspended with warm 1× PBS for 15 minutes. Then, cells were incubated with IMDM medium supplemented with 5% FBS and IgG2a-FITC (0.06 µg) or Ki-67-FITC (0.06 µg) at 37°C for 30 minutes. The fluorescence intensity of labeled cells was analyzed by Flow cytometry (BD Biosciences, San Jose, CA). Results were analyzed by FlowJo version 7.6.4 (Ashland OR). IgG2a-FITC and Ki67-FITC were purchased from eBioscience (San Diego, CA), and Iscove’s Modified Dulbecco’s Medium (IMDM) was purchased from Life Technologies (Grand Island, NY).
AppendixB.1.2. Evaluation of Cell Growth and Density
A second goal is to understand the individual cellular mechanics that govern the macroscopic dynamics in cancer cells. Thus, time series data is needed. Experiments were performed which measure the global cellular density over a period of 96 hours in two different seedings: low and high density. See Figure 4 for the results. All experiments were performed using the parental OVCAR-8 and the OVCAR-8-DsRed2 human ovarian carcinoma cell lines [5]. In this study, all of our applicable cell-based assays utilize timelines of 96 hours or less. The cell density curves were generated by randomly seeding 104 and 105 cells per well on 24-well plates and culturing 24 hours prior to the first imaging. The plates were imaged on a Zeiss 710 Confocal microscope on both green and red fluorescent channels, and images were captured every 24 hours for 96 hours. The estimated density percentage is based on the average of two complete wells.
AppendixB.1.3. Analysis of Apoptosis Percentage
As in AppendixB.1.1, we hypothesize that an equilibrium distribution d(ρ) exists for the fraction of cells in the apoptosis process. An analogous experiment was conducted in the aid of determining d(ρ). Percentage of apoptosis-mediated cell death as a function of cell density was measured by a double staining method using the Dead Cell Apoptosis Kit with Annexin V Alexa Fluor® 488 & PI (Invitrogen) according to the manufacturer’s instructions. 104 and 105 parental OVCAR-8 cells were randomly seeded on 24-well plates in drug-free medium and incubated at 37°C for 24 hours to allow cells to attach. The percentages of apoptosis and necrosis were then evaluated by FACS (LSR II). Data from 20, 000 gated events per sample were collected. Cells in early stages of apoptosis were positively stained with Annexin V, whereas cells in late apoptosis and necrosis were positively stained with both Annexin V and PI. The number of cells positively stained with Annexin V was used to estimate the death rate. Experiments were repeated three times; see Figure 2(b) for the results.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Author Contributions
Conceived and designed the methods: JMG, OL, DL, MMG. Performed the experiments: KLF, PS, OL. Modeled and analyzed the data: JMG, OL, DL. Wrote the paper: JMG, OL, DL.
References
- 1.Anderson AR, Quaranta V. Integrative mathematical oncology. Nature Reviews Cancer. 2008;8(3):227–234. doi: 10.1038/nrc2329. [DOI] [PubMed] [Google Scholar]
- 2.Ang AH-S, Tang WH. Probability Concepts in Engineering: Emphasis on Applications to Civil and Environmental Engineering (v. 1) 2nd edition. Wiley; 2006. [Google Scholar]
- 3.Ascher UM. Numerical Methods for Evolutionary Differential Equations (Computational Science and Engineering) 1st edition. Society for Industrial Applied Mathematics; 2008. [Google Scholar]
- 4.Bonabeau E. Agent-based modeling: Methods and techniques for simulating human systems. Proceedings of the National Academy of Sciences of the United States of America. 2002;99(Suppl 3):7280–7287. doi: 10.1073/pnas.082080899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Brimacombe KR, Hall MD, Auld DS, Inglese J, Austin CP, Gottesman MM, Fung K-L. A dual-fluorescence high-throughput cell line system for probing multidrug resistance. Assay and drug development technologies. 2009;7(3):233–249. doi: 10.1089/adt.2008.165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Gardiner C. Stochastic Methods: A Handbook for the Natural and Social Sciences (Springer Series in Synergetics) 4th edition. Springer; 2009. [Google Scholar]
- 7.Gillet J, Gottesman M. Mechanisms of multidrug resistance in cancer. Methods in molecular biology (Clifton, NJ) 2010;596:47. doi: 10.1007/978-1-60761-416-6_4. [DOI] [PubMed] [Google Scholar]
- 8.Grimmett GR, Stirzaker DR. Probability and Random Processes. 3rd edition. Oxford University Press; 2001. [Google Scholar]
- 9.Lakshmikantham V, Rao M. Theory of Integro-Differential Equations (Stability and Control) 1st edition. CRC Press; 1995. [Google Scholar]
- 10.Lavi O, Gottesman MM, Levy D. The dynamics of drug resistance: a mathematical perspective. Drug Resistance Updates. 2012;15(1):90–97. doi: 10.1016/j.drup.2012.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mathai A, Provost SB. Quadratic Forms in Random Variables (Statistics: A Series of Textbooks and Monographs) 1st edition. CRC Press; 1992. [Google Scholar]
- 12.Messam CA, Pittman RN. Asynchrony and commitment to die during apoptosis. Experimental cell research. 1998;238(2):389–398. doi: 10.1006/excr.1997.3845. [DOI] [PubMed] [Google Scholar]
- 13.Panetta J, Evans W, Cheok M. Mechanistic mathematical modelling of mercaptopurine effects on cell cycle of human acute lymphoblastic leukaemia cells. British journal of cancer. 2005;94(1):93–100. doi: 10.1038/sj.bjc.6602893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Piotrowska MJ, Angus SD. A quantitative cellular automaton model of in vitro multicellular spheroid tumour growth. Journal of theoretical biology. 2009;258(2):165–178. doi: 10.1016/j.jtbi.2009.02.008. [DOI] [PubMed] [Google Scholar]
- 15.Pisco AO, Brock A, Zhou J, Moor A, Mojtahedi M, Jackson D, Huang S. Non-darwinian dynamics in therapy-induced cancer drug resistance. Nature communications. 2013;4 doi: 10.1038/ncomms3467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Pitaevskii LP, Lifshitz E. Physical Kinetics: Volume 10 (Course of Theoretical Physics S) 1st edition. Butterworth-Heinemann; 1981. [Google Scholar]
- 17.Saunders NA, Simpson F, Thompson EW, Hill MM, Endo-Munoz L, Leggatt G, Minchin RF, Guminski A. Role of intratumoural heterogeneity in cancer drug resistance: molecular and clinical perspectives. EMBO molecular medicine. 2012;4(8):675–684. doi: 10.1002/emmm.201101131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Shwartz A, Weiss A. Large Deviations for Performance Analysis: QUEUES, Communication and Computing (Stochastic Modeling Series) 1st edition. Chapman and Hall/CRC; 1995. [Google Scholar]
- 19.Spencer SL, Gaudet S, Albeck JG, Burke JM, Sorger PK. Non-genetic origins of cell-to-cell variability in trail-induced apoptosis. Nature. 2009;459(7245):428–432. doi: 10.1038/nature08012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Thorne BC, Bailey AM, Peirce SM. Combining experiments with multi-cell agent-based modeling to study biological tissue patterning. Briefings in bioinformatics. 2007;8(4):245–257. doi: 10.1093/bib/bbm024. [DOI] [PubMed] [Google Scholar]
- 21.Tzur A, Kafri R, LeBleu VS, Lahav G, Kirschner MW. Cell growth and size homeostasis in proliferating animal cells. Science. 2009;325(5937):167–171. doi: 10.1126/science.1174294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wang P, Robert L, Pelletier J, Dang WL, Taddei F, Wright A, Jun S. Robust growth of escherichia coli. Current biology. 2010;20(12):1099–1103. doi: 10.1016/j.cub.2010.04.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zhang L, Wang Z, Sagotsky JA, Deisboeck TS. Multiscale agent-based cancer modeling. Journal of mathematical biology. 2009;58(4–5):545–559. doi: 10.1007/s00285-008-0211-1. [DOI] [PubMed] [Google Scholar]