Trigger loop folding determines transcription rate of Escherichia coli’s RNA polymerase

Significance

RNA polymerase is a vital enzyme responsible for the first step in gene expression. Despite extensive studies, fundamental questions about its kinetic and mechanistic properties still remain unanswered. The trigger loop is a conserved domain within RNA polymerase that has been linked to the enzyme’s average elongation velocity and pausing behavior. In this study, we use optical tweezers, a single molecule technique, to analyze the behavior of two mutant polymerases with a single point mutation in their trigger loop domain and compare it to the WT. By looking at individual enzymes we are able to separate continuous elongation from pausing and create a kinetic and mechanistic model in which trigger loop folding-unfolding dynamics controls transcription elongation.

Abstract

Two components of the RNA polymerase (RNAP) catalytic center, the bridge helix and the trigger loop (TL), have been linked with changes in elongation rate and pausing. Here, single molecule experiments with the WT and two TL-tip mutants of the Escherichia coli enzyme reveal that tip mutations modulate RNAP’s pause-free velocity, identifying TL conformational changes as one of two rate-determining steps in elongation. Consistent with this observation, we find a direct correlation between helix propensity of the modified amino acid and pause-free velocity. Moreover, nucleotide analogs affect transcription rate, suggesting that their binding energy also influences TL folding. A kinetic model in which elongation occurs in two steps, TL folding on nucleoside triphosphate (NTP) binding followed by NTP incorporation/pyrophosphate release, quantitatively accounts for these results. The TL plays no role in pause recovery remaining unfolded during a pause. This model suggests a finely tuned mechanism that balances transcription speed and fidelity.

RNA polymerase (RNAP) has been the subject of study for almost five decades by means of a large array of techniques. In the last decade, crystallographic structures of the bacterial and eukaryotic polymerase have allowed researchers to obtain snapshots of the conformational changes that occur deep inside the enzyme, near its catalytic center. Based on these structures, an element, the F-bridge or bridge helix (BH), was first hypothesized to be the essential component in the translocation mechanism of RNAP (1–4). Later, crystal structures of the full elongation complex [RNA, DNA, and nucleoside triphosphate (NTP) bound] identified another structure in close proximity to the BH, termed the trigger loop (TL) (5–7), as another important element in the translocation mechanism. This structure was seen to adopt distinct conformations during the catalytic process, suggesting its role in the kinetic cycle of RNAP. In particular, the TL was seen to contain a dynamic domain that undergoes an unfolding transition during transcription (here termed the TL-tip) and another which remains helical throughout the cycle known as the TL base helices. These observations prompted further biochemical characterization of these two structures in their WT form and in variety of point mutants of the BH and TL elements (4, 8–12).

The high-resolution structure of an elongation complex of the Thermus thermophilus polymerase (13) shows the TL in a fully folded helix-turn-helix structure and in close contact with the BH (Fig. S1 A–C). This conformation, in which the TL blocks the secondary channel and correctly positions the incoming NTP for incorporation to occur, has been termed “closed” (10, 14). Based on these structures and other biochemical studies (4, 7, 8, 15–18) it has been proposed that NTP binding and the resulting folding of the TL (with its corresponding interactions with the BH) serves as the pawl that rectifies the polymerase's Brownian oscillations on the template by not allowing backward movement of the enzyme. After the incorporation reaction is complete, the resulting pyrophosphate (PPi) is released, prompting the TL to unfold and the polymerase to adopt the open conformation (Fig. S1C). Finally, Brueckner et al. (14, 16, 19) proposed that to reset the cycle, translocation from one base to the next involves the transition from pre- to posttranslocated state and occurs from an unfolded wedged TL conformation, as seen in structures in the presence of α-amanitin. Two other studies (20, 21) have also proposed other translocation intermediates with an unfolded TL. In these conformations, during translocation, it is the BH that is seen to play a more prominent role [as it was originally proposed by Bar-Nahum et al. (4)] and the TL, although unfolded in both cases, is thought to assist the BH in translocation. As a whole, structural studies indicate that transcription elongation most likely involves a concerted motion of the “BH/TL unit” (9, 14, 16, 19–22).

In addition, several bulk studies revealed that most TL mutations that alter RNAP's elongation rate affect its pausing behavior too (4, 8, 10), suggesting that the TL is also involved in polymerase pause regulation. Furthermore, Toulokhonov et al. (8) have shown that in paused complexes the TL adopts a conformation that inhibits nucleotide addition, but which also blocks binding of the transcription inhibitor streptolydigin (known to bind the unfolded TL). This result suggests that during a pause the TL adopts a partially folded conformation, a prediction that is supported by the structure of a backtracked elongation complex (23).

Crystallographic and biochemical studies, as described above, have identified the essential elements involved in the elongation cycle of the enzyme. However, these methods provide only static snap shots and average kinetic parameters of the transcribing enzyme. Thus, methods to follow the enzyme as it transcribes its template in real time can yield complementary dynamical information about transcription elongation. Moreover, because the TL element appears to participate in both active elongation and pausing, it is desirable to separate these two processes. Such separation is very difficult for bulk studies. Here, we rely on the power of single molecule assays to effect this separation and to further clarify the role of the TL element in transcription.

Results

TL Folding Determines the Enzyme’s Pause-Free Velocity.

Two Escherichia coli TL mutants, G1136S and I1134V, containing single point substitutions in the TL-tip have been shown, in bulk experiments, to alter significantly the enzyme's average elongation rate, pausing behavior, and fidelity (4). However, these experiments cannot identify whether the apparent change in elongation rate is due to a change in the frequency of pauses, a change in the rate of recovery from these pauses, or a change in the actual elongation rate, i.e., in the pause-corrected or pause-free velocity of the mutants.

To distinguish between the enzyme’s pausing behavior and elongation rate and between pause frequency (number of pauses per base pair transcribed) and pause duration, we followed in real time the elongation dynamics of individual WT and TL mutants of RNAP using a double trap optical tweezers instrument. Two polystyrene beads were held in separate optical traps inside of a glass chamber (24). An RNAP elongation complex was bound to one of the beads, whereas the downstream end of the DNA was attached to the other bead (Fig. 1, Inset). As the polymerase reinitiated transcription in the presence of saturating 1 mM NTPs concentration, the DNA between the beads shortened, pulling the beads out of the static traps and increasing the force load on the enzyme. The force change and the end-to-end distance were then converted into number of transcribed nucleotides (25). Fig. 1A shows representative traces of individual transcription events for the WT and both mutant enzymes that display the start-and-pause behavior previously described for this enzyme (24, 26–28) and the heterogeneity among individual polymerases. The raw data were filtered, and pauses were identified and removed using a custom-made algorithm so that the enzyme's pause-free velocity and pausing behavior could be independently addressed.

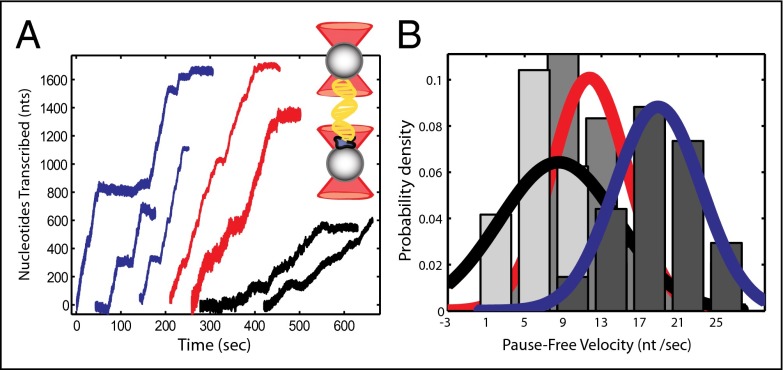
Fig. 1.

Single molecule transcription by E. coli RNA polymerase WT and TL mutants. (A) Individual transcriptional events from passive mode experiments for the WT (red) and the fast and slow mutants (blue and black, respectively). Unfiltered traces were processed to remove pauses and generate histograms of the pause-free velocity. Inset: The double trap geometry, in which stalled RNAP (in blue) is attached to one of the beads, whereas the downstream end of the DNA is attached to the other bead. (B) Histograms of the pause-free velocity for the slow (light gray bars, black fit, n = 12) and fast mutant (dark gray bars, blue fit, n = 17). Velocities for the WT polymerase (gray bars, red fit, n = 18) are also shown for comparison.

Histograms of pause-free velocities for the WT and mutant enzymes reveal that these single point mutations in the TL-tip result in significant changes in the enzyme's pause-free velocities (Fig. 1B). The mean pause-free elongation rates in nucleotides per second under saturating nucleotide concentrations were 18.9 ± 1.0 nt/s (mean ± SEM) for G1136S (fast mutant), 8.5 ± 1.8 nt/s for I1134V (slow mutant), and 11.7 ± 0.9 nt/s for the WT. Transcription rates are Gaussian distributed, with large SDs as reported previously (29–31). The source of the considerable spread in velocity has been studied but remains elusive (32).

TL in Pause Entry and Fidelity.

It is difficult to distinguish between pause frequency and pause duration using ensemble techniques. Analysis of the data obtained here shows that the slow mutant has a pause frequency of 0.053 ± 0.008 pauses per nucleotide (nt⁻¹), five times larger than the fast mutant (0.011 ± 0.002 nt⁻¹) and almost double that of the WT enzyme (0.030 ± 0.003 nt⁻¹; Fig. 2A, open circles). This correlation between velocity and pause frequency has been observed in different contexts (24, 26–28) and reflects the kinetic competition between elongation and the off-pathway paused states.

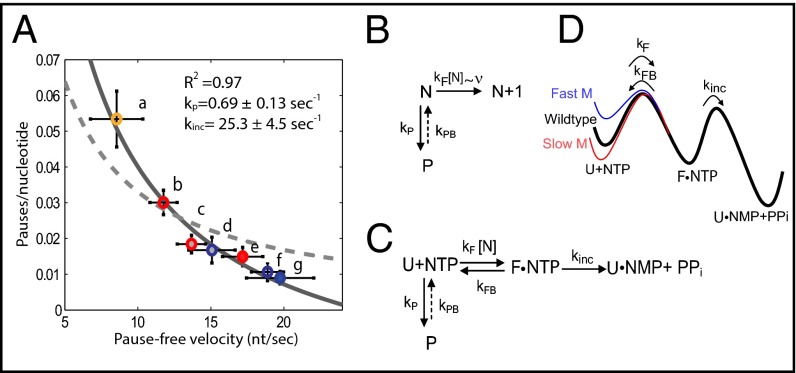
Fig. 2.

Analysis of pause entry as a function of velocity and proposed kinetic schemes. (A) Pause frequency in number of pauses per nucleotide as a function of pause-free velocity (nucleotides per second) for mutants and WT RNAP as follows (a) slow mutant (yellow open circles, n = 12), (b) WT (red open circles, n = 18), and (f) fast mutant (blue open circles, n = 17). In the presence of nucleotide analogs these values become (c) WT ITP (red circles, gray fill, n = 13), (d) fast mutant ITP (blue circles, gray fill, n = 7), (e) WT BrUTP (red circles, light red fill, n = 8), and (g) fast mutant BrUTP (blue circles, light blue fill, n = 7). Error bars shown are SEM. (B) Simplest kinetic scheme in which pausing and elongation compete. This model is not able to reproduce the measured pause frequency vs. velocity plot shown in A (dashed line). (C) Simple kinetic scheme with a two-step elongation process. This model fits the data (solid line, R² = 0.97) and gives values of k_p = 0.69 ± 0.13 s⁻¹ and k_inc = 25.3 ± 4.5 s⁻¹. (D) Effect of point mutations on the transcription energy landscape based on the kinetic scheme shown in C. k_F is faster for the fast mutant and slower for the slow mutant compared with the WT enzyme.

Crystal structures, obtained in the presence of correct and incorrect nucleotides, nucleotide analogs, and inhibitors, have shown the TL in different states of folding (6, 7, 13, 16, 19, 20, 33, 34). Thus, to determine the effect of nucleotide analogs on the TL and hence on the enzyme’s pause frequency and pause-free velocity, we conducted experiments for the fast and the WT enzyme in the presence of 1 mM NTPs as above, but including 200 μM of either inosine triphosphate (ITP) or bromouridine triphosphate (BrUTP). Similar experiments with the slow mutant were not possible due to the low levels of misincorporation by this mutant (4). Prior studies have shown that RNAP's pause frequency can be modified by substituting one of the ribo-nucleotides with an analog (35, 36) or even just by including such an analog at low concentration along with the full complement of the four ribo-nucleotides (37). ITP, a GTP analog, is thought to have a destabilizing effect on the RNA:DNA hybrid because it forms only two hydrogen bonds. By contrast, BrUTP's bromine makes a stronger base-pairing interaction with the template strand than its cognate nucleotide and should have a stabilizing effect on the hybrid (35). This stabilization should help keep the 3′ end of the RNA in register with the catalytic site and thus reduce the number of backtracked pauses (38).

These analogs had a clear impact on the enzymes’ pausing behavior (Fig. 2A, filled circles). Surprisingly, the effect was also seen on their pause-free velocity. For the fast mutant, BrUTP decreased the pause frequency and slightly increased the pause-free velocity, whereas ITP increased the fast mutant's pause frequency and decreased its pause-free velocity. For the WT enzyme, although addition of BrUTP does have the same effect as in the fast mutant, decreasing its pause frequency and increasing its velocity, ITP does not increase its pause frequency or slows it down. This behavior may be explained by the observed tendency of the WT enzyme to enter long backtracks and arrest on misincorporation of ITP (37); accordingly, in the presence of ITP, only the faster WT molecules are measured, resulting in a biasing of the velocity/pause-frequency values.

Once again, the slowing down of the enzyme with ITP is perhaps not surprising, whereas the increase in the pause-free velocity of the enzyme with BrUTP is somewhat unexpected. However, in view of our previous results, these observations can be rationalized if the analogs modulate the rate of elongation in a manner directly proportional to the stability conferred by these nucleotides to the hybrid through contacts that favor the folding of the TL (39). Indeed, in support of this interpretation, all values of velocity and pause frequency, in the presence and absence of analogs and for the mutant and WT enzymes, form a well-defined trend, suggesting that both conditions affect the same kinetic rate (Fig. 2A).

Development of a Kinetic Model.

Accordingly, it should be possible to construct a global kinetic model for elongation that identifies this rate and encompasses all of the data gathered for both the point mutations and the nucleotide analogs experiments. The simplest kinetic scheme in which elongation and pausing compete (24, 27, 28) is shown in Fig. 2B. In this case, the probability of entering a pause is given by $P_p=k_p/\left(k_p+v\right)$, where k_p is the pause entry rate, and v is the pause-free elongation velocity. If the mutations affect the NTP binding/TL folding rate k_F, and k_F completely determines transcription velocity so that v∼k_F, then this simple model should be able to fit the experimental data. However, we find that this model cannot reproduce the velocity dependence of the pause frequency (dashed line in Fig. 2A), suggesting that elongation velocity is not determined by k_F alone.

A second kinetic scheme is one in which the elongation pathway is now divided in two rate-limiting steps: NTP binding/TL folding followed by NTP incorporation/PPi release, is shown in Fig. 2C. The folding of the TL is prompted by the binding of the next NTP and is therefore characterized by the second-order rate coefficient k_F (in μM⁻¹⋅s⁻¹). According to this model, the TL mutations tested here affect the folding stability of this element by modifying k_F. This step is also assumed to be reversible with a reverse rate k_FB. Once in the folded state (F), the irreversible incorporation of the nucleotide and release of PPi occurs with rate k_inc. Finally, because it is known that pauses (P) are states off the main elongation pathway and that the number of pauses decreases with increasing NTP concentration (27), it follows that the pause states can only stem from a state before NTP binding occurs, that is, from the unfolded TL state (U) in Fig. 2C [if pausing where to stem from the folded state (F), higher NTP concentrations would increase the number of pauses, contrary to experimental observation]. Based on the kinetic scheme of Fig. 2C and using the methods derived by Cleland (40), the pausing probability as a function of the pause-free velocity (effective forward rate, v) is given by (see SI Text for a detailed derivation)

$$P_p=\frac{k_p}{k_p+\left(\frac{v{k}_{inc}}{-v+k_{inc}}\right)}.$$

As shown in Fig. 2A (solid line), this model reproduces the experimental data very well (R² = 0.97) with only two fitting parameters, yielding k_p = 0.69 ± 0.13 s⁻¹ and k_inc = 25.3 ± 4.5 s⁻¹, values in good agreement with previously obtained results (24, 41, 42). Expressions obtained for the case in which either k_inc or k_FB are allowed to change while keeping k_F constant were inconsistent with the experimental data (SI Text, Fig. S2, and Table S1).

The changes in free energy between the folded and unfolded states of the TL for the mutant enzymes (x = fast or slow) relative to the WT (wt) can be written as (SI Text) $\mathrm{\Delta }\mathrm{\Delta }{G}_{x-wt}=-k_{B}T\ln \left\{\left[v_x\left(k_{inc}-v_{wt}\right)\right]/\left[v_{wt}\left(k_{inc}-v_x\right)\right]\right\}$. Using this expression, we obtain $\mathrm{\Delta }\mathrm{\Delta }{G}_{SlowM-wt}=+2.2\hspace{0.5em}\text{pNnm}=+0.31\hspace{0.5em}\text{kcal/mol}$ and $\mathrm{\Delta }\mathrm{\Delta }{G}_{FastM-wt}=-5.1\hspace{0.5em}\text{pNnm}=-0.73\hspace{0.5em}\text{kcal/mol}$. The diagram in Fig. 2D summarizes the changes to the transcription energy landscape caused by the TL mutations based on the kinetic model constructed here (see SI Text and Fig. S3 for further discussion).

To estimate k_F for the WT enzyme, we normalize the free energies with respect to the slow mutant by imposing the condition $\mathrm{\Delta }{G}_{slow}\mathrm{=}0$ so that $\mathrm{\Delta }\mathrm{\Delta }{G}_{slow-x}=-k_{B}T\ln \left(k_{FB}/k_{Fx}\right)$ , where x can represent the rate for the WT or the fast enzyme. We can write $k_{FB}/k_{Fx}=e^{-\mathrm{\Delta }\mathrm{\Delta }{G}_{slow-x}/K_{B}T}=\left[v_{slow}\left(k_{inc}-v_x\right)\right]/\left[v_x\left(k_{inc}-v_{slow}\right)\right]$ and because velocity $v=k_{inc}/\left\{1+\left(1/N\right)\left[\left(k_{inc}/k_{Fx}\right)+\left(k_{FB}/k_{Fx}\right)\right]\right\}$, then transcription velocity as a function of nucleotide concentration can be expressed as (SI Text)

$$v=\frac{k_{inc}}{1+\frac{1}{N}\left[\frac{k_{inc}}{k_{Fx}}+\frac{v_{slow}\left(k_{inc}-v_x\right)}{v_x\left(k_{inc}-v_{slow}\right)}\right]}.$$

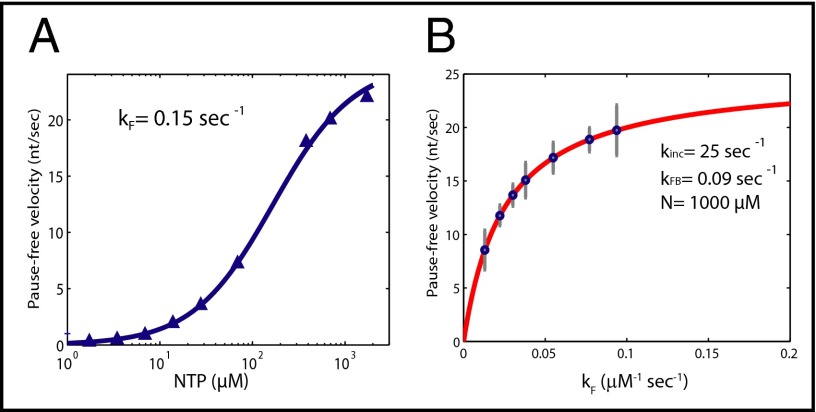
Here N is the nucleotide concentration, and v_x is the measured WT pause-free velocity at saturating nucleotide concentration. Using this equation, we fit some of the published data on the nucleotide dependence of pause-free velocity (26, 27, 41) (SI Text and Fig. S4). As shown in Fig. 3A, the experimental data can be fit well by the derived expression and renders a value of k_F for the WT RNAP (k_Fwt) of 0.15 μM⁻¹⋅s⁻¹ (using data from ref. 41) and, consequently, k_FB = 0.09 s⁻¹ for all three enzymes (see Table S2 for a complete list of values for k_F). It should also be noted that this fit does not require the existence of two NTP binding sites as has been proposed (29).

Fig. 3.

Fitting of nucleotide-dependent data with proposed kinetic scheme and rate-limiting steps of transcription. (A) Elongation velocity as a function of nucleotide concentration for the WT enzyme from Abbondanzieri et al. (41) (blue triangles). The data can be fit by the model in Fig. 2C with values for k_Fwt of 0.15 μM⁻¹⋅s⁻¹ (blue curve). (B) Pause-free velocity as a function of k_F according to $v=\left(k_{F}N{k}_{inc}\right)/\left(k_{F}N+k_{inc}+k_{FB}\right)$ for k_inc = 25 s⁻¹, k_FB = 0.09 s⁻¹, and N = 1,000 μM (solid red line). The blue circles represent the experimentally determined pause-free velocities and their corresponding k_F calculated using $k_F=\left[v\left(k_{inc}+k_{FB}\right)\right]/\left[N\left(k_{inc}-v\right)\right]$. Our model predicts that the TL folding rate k_F and the rate of catalysis/PPi release k_inc are of comparable magnitude, indicating that elongation velocity involves two rate-limiting steps.

It is interesting to note that under saturating nucleotide concentrations (n = 1,000 μM), k_FN is of the same order of magnitude as k_inc; thus, under these conditions, two rate-limiting steps determine the transcription velocity: the TL folding rate on NTP binding (k_FN) and nucleotide incorporation/PPi release (k_inc). Modifying either of them will result in a modification of the pause-free velocity. Fig. 3B shows the relationship between pause-free velocity and k_F both for our experimental data and the model developed here (see figure legend for details). Note that even for a constant k_inc and nucleotide concentration, changes to k_F caused by the mutations or the nucleotide analogs will have an effect on the pause-free transcription velocity. This model also accurately predicts the velocity saturation for high values of k_F as seen in the data, wherein k_inc then becomes the rate-limiting step.

Backtracking and Pause Escape.

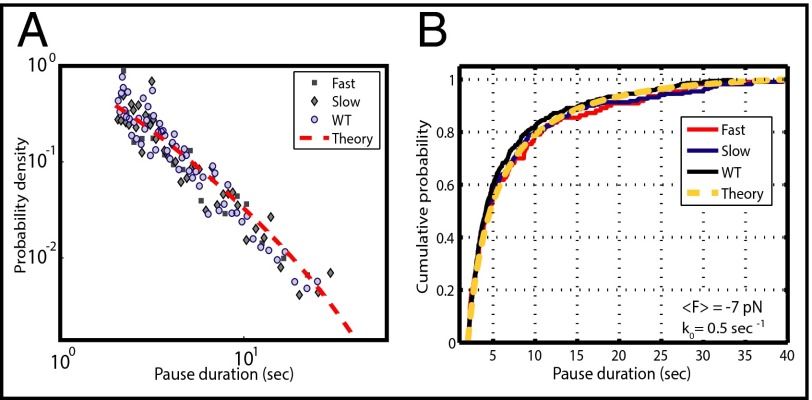
Our model assumes that both mutations and nucleotide analogs affect the elongation pathway only through the modification of the rate k_F. Thus, the distributions of pause durations should remain unaltered and still correspond to the diffusive backtracking mechanism described for both prokaryotic and eukaryotic polymerases (24, 30, 43). As seen in Fig. 4A, a double logarithmic plot of all pauses longer than 2 s does in fact show that pause durations for the fast and slow mutants maintain the expected t^−3/2 dependence of the WT enzyme and are in excellent agreement with the theoretical expression for backtracking developed by Depken et al. (43) (Fig. 4A, dotted line; see fit parameters in legend). As an additional comparison, we plotted the cumulative probability for pauses between 2 and 40 s within a force range of 4–10 pN for both mutants and the WT. As shown in Fig. 4B, the cumulative probability distributions for all three datasets appear indistinguishable from each other and are well predicted by the theoretical expression of the backtracking model (44) (Fig. 4B, dotted line). A two-sample Kolmogorov–Smirnov test (44) confirmed that there is no statistically significant difference between the three distributions (P_Fast,Slow = 0.92; P_{Fast,Wildtype} = 0.4611; P_{Slow,Wildtype} = 0.82; for these distributions to be statistically different at a 95% confidence level, a P value smaller than 0.05 is required). Thus, for these mutants, the TL plays no role in pause exit, in accordance with structural evidence of an intermediate partially unfolded TL conformation during backtracking (8, 23, 45). In addition, this result confirms that the additional pauses observed for the slow mutant involve the same backtracking mechanism described for the WT enzyme.

Fig. 4.

Analysis of pause exit. (A) A double logarithmic plot of pause durations verifies that these distributions are well described by the t^−3/2 power law, as has been previously observed (24, 30, 43). Each point in this histogram corresponds to five independent pauses. The red dotted line is the theoretical prediction according to the model developed by Depken et al. (43) using k₀ = 0.5 s⁻¹ and F = −7 pN (opposing force). (B) A cumulative probability plot of pause durations (44) for the WT and the fast and slow mutants shows indistinguishable distributions, indicating that the TL has no role in the escape from the paused state. The yellow dotted line is the theoretical curve of the Depken model. A two-sample Kolmogorov–Smirnov statistical test further verifies that the difference between these distributions is not statistically significant. Pauses represented in both plots are between 2 and 40 s and span an opposing force range from 4 to 10 pN (average force = −7 pN).

Discussion

A TL mutation that disrupts transcription and renders the polymerase slow is perhaps not unexpected. In contrast, a point mutation that is able to increase the pause-free velocity of an enzyme is much more unusual. Nonetheless, a number of fast polymerases with mutations in the TL have been identified, highlighting the importance that the TL has in rate determination (9–11). As described above, according to the current elongation model (13, 14, 16, 17, 19, 46), the TL-tip folds into a helix when nucleotide binding occurs at each catalytic cycle. Thus, because both of the mutations studied here are located on the TL-tip (Fig. S1), it should be possible to explain the phenotypes observed for the fast and slow mutant polymerases if we assume that either the rate of helix formation or the rate of coil formation of the TL are rate limiting for the cycle and affected by the mutations. The former scenario predicts a positive correlation between the pause-free rate of transcription and the helix propensity of the amino acid substitutions, whereas the latter predicts a negative correlation.

To determine if such a correlation exists and its sign, we look at amino acid helix propensity scales. Despite some variability among them (47, 48), the scales all rate glycine as an amino acid with one of the lowest helix potentials. As seen in Fig. S5, the glycine-to-serine substitution in the fast mutant is associated with increased helix propensity of the TL, making it more favorable to fold. Conversely, the isoleucine-to-valine substitution in the slow mutant is predicted to decrease the helix propensity of the TL, making it less favorable to fold. Thus, a positive correlation between the pause-free rate of transcription and the change in helix propensity of the amino acid substitution is observed. These results can be rationalized if the rate of helix formation is rate limiting for transcription; under these conditions, the faster and slower phenotypes should correlate with the higher and lower helical stability of the TL, respectively, if the rate of coil formation remains invariant. Interestingly, calculated values of the free energy difference between the mutants and the WT enzyme based on helix propensity arguments ($\mathrm{\Delta \Delta }{G}_{SlowM\mathrm{-}wt}\mathrm{=+}0.2\hspace{0.5em}\text{kcal}/\text{mol}$; $\mathrm{\Delta \Delta }{G}_{FastM\mathrm{-}wt}\mathrm{=-}0.5\hspace{0.5em}\text{kcal}/\text{mol}$) are in excellent agreement with values predicted by the proposed kinetic model using our experimental data (see above).

It is true, however, that not only the identity of the amino acid is relevant, but also the position of such substitution within the overall structure of the enzyme. Kireeva et al. (10) studied amino acid substitutions to the TL base helices (Fig. S1B) that would result in helix destabilization and hence could presumably slow down the enzyme, but instead those mutations were seen to increase the catalytic rate. However, because the base helices do not unfold during the transcription reaction, the helical propensity of those amino acids is most likely not relevant. In fact, as is also the case for the mutant polymerases studied by Tan et al. (9), the majority of amino acid substitutions introduced into the TL base helices disrupt interactions with the BH, make the TL more mobile, and therefore cause the polymerase to become hyperactive (49). Moreover, it is unclear if such substitutions also result in changes to the geometry of the domain or break important interactions with other amino acids that could result in modified conformational changes and, therefore, in altered reaction mechanisms.

As a further check of the structural modifications caused by the amino acid substitutions studied here, we carried out computer modeling of the mutant enzymes using the algorithm developed by Benedix et al. [Concoord/Poisson-Boltzmann surface area (CC/PBSA)] (50). These models showed that the structures of the mutants' folded TLs overlay with each other and with the WT structure (Fig. S6). Therefore, we verify that these mutations do not introduce any obvious geometric alterations of the catalytic center nor changes in the position of the residues that make significant contacts to any other part of the enzyme. These facts indicate that the observed phenotypes are not likely due to structural modifications of the folded TL or to significant alterations of the network of contacts within the catalytic center of the enzyme.

Two single molecule studies (51, 52) have compared the kinetics of the WT eukaryotic RNA polymerase II with the single point mutant polymerase E1103G, previously studied by Kireeva et al. (10). This mutation is located on the TL base helices in a region distal from the enzyme’s active site and that does not undergo any folding dynamics. The hyperactivity of this mutant is thought to stem from the loss of contacts of the TL’s open conformation, which indirectly biases the TL closed state (11, 49). Larson et al. also investigated the double E1103G/H1085A substitutions at the single molecule level. His1085 is a conserved residue that is directly involved in NTP catalysis by protonation of PPi before nucleophilic attack (12, 53) and in PPi release/TL unfolding by helping the PPi escape the active site and guiding the TL toward the unfolded state (54). Therefore, a mutant of this residue is likely to lead to altered reaction mechanisms for NTP addition and TL unfolding/PPi release, and not only to modified rates of the WT mechanism. In contrast, the mutants analyzed in the present study are, in essence, true kinetic mutants because their substitutions do not result in modifications to the geometry of the active site or to interresidue interactions, as mentioned above. Hence, elongation by the mutants chosen here is expected to follow the WT reaction pathway but with a faster/slower kinetic rate, thereby directly probing the intrinsic kinetics of transcription.

Furthermore, in contrast to the E1103G mutation, the mutants of this study do not present any differences in their force-velocity curves (Fig. S7). Previous single molecule studies of RNAP have also found a weak or negligible force dependence of velocity for opposing loads (24, 27, 30, 55). A force-independent velocity indicates that the translocation step of the enzyme (a force-dependent process by definition) does not coincide with the rate-limiting step of the cycle under these conditions. Thus, we expect that changes in elongation velocity of both TL-tip mutants are not related to variations in the translocation step but must stem from changes in processes encompassed between NTP binding and PPi release. In fact, we established TL folding on NTP binding followed by NTP incorporation/PPi release as the two rate-limiting processes. This finding is consistent with the measured force-velocity curves because there is no reason to believe that either of these two rate-limiting steps should be force sensitive.

Finally, as predicted by the kinetic model developed here, the presence of the two rate-determining steps—given by k_FN and k_inc—should be more evident at low NTP concentrations, for which k_FN is slower. This biphasic characteristic (kinetics of elongation are better represented by a double rather than a single exponential fit) has in fact already been observed using rapid kinetic methods for the bacterial polymerase (56, 57), as well as for the eukaryotic enzyme (10, 58) for NTP concentrations of 100 μM and lower.

The data presented here also suggest that nucleotide analogs have an effect on transcription rate through the influence of their binding energy on k_F (Fig. 2A) and therefore on the ability of the TL to fold. Different nucleotides affect TL folding by modulating the stability of the folded relative to the unfolded state (Fig. 2D). This observation highlights the importance of the network of contacts that exist in the closed conformation of the enzyme between the incoming NTP and the TL/BH unit and how these interactions can either assist or hinder the folding of the TL necessary for elongation. This mechanism also suggests a role of the TL in fidelity control as has been proposed (4, 7, 10, 34, 46, 59).

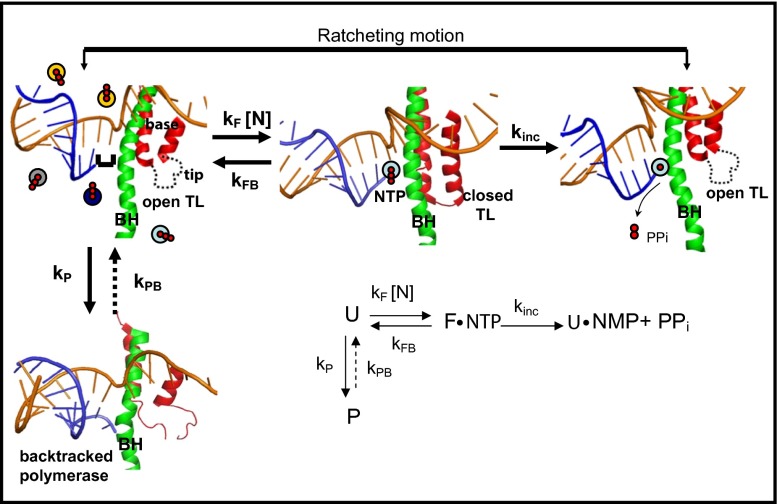
Fig. 5 summarizes our proposed kinetic and mechanistic model of elongation. As a whole, this model suggests that through the tuning of the intracellular NTP concentration, the enzyme can switch between rate-determining steps, providing an extra level of regulation: because TL folding is sensitive to the identity of the incoming nucleotide, the polymerase should be more responsive to specific regulatory sequences if the intracellular NTP concentrations are low, conditions under which k_FN is slower. In contrast, higher nucleotide concentrations could maintain a constant transcription speed, independent of sequence, and be mainly determined by the NTP incorporation/PPi release rate k_inc. Thus, at the cellular level, the TL and its interactions with the BH may be an ingenious solution to the enzyme’s balance of transcription speed, fidelity, and regulation.

Fig. 5.

Diagram of structural changes that occur during elongation. Template DNA is shown in gold, RNA in blue; the TL structure is shown in red and the BH in green. (From Left to Right) The complex is in a posttranslocated position in which the NTP binding site is available for the next NTP to bind, and the polymerase is in an open conformation with an unfolded TL. Here the colored circles represent the four types of NTPs in solution. Next, once NTP binds, the TL folds into its double helical structure putting the polymerase in a closed conformation, which blocks the secondary channel and correctly positions the incoming NTP so incorporation can occur. After NTP incorporation is complete, the resulting PPi is released, the TL unfolds and the polymerase again adopts an open conformation. After nucleotide incorporation, the polymerase is in a pretranslocated state, and movements of the BH and the unfolded TL then take the polymerase to the posttranslocated state for the start of another cycle. The diagram also shows the pausing pathway, in which the TL is partially unfolded and the 3′ end of the RNA is displaced from the catalytic site of the enzyme. The structures used are based on the T. Thermopilus crystal structures in the absence [Protein Data Bank (PDB) ID code 2O5I] and presence (PDB ID code 2O5J) of NTP, and the paused state is based on the Pol II backtracked structure (PDB ID code 3GTJ). (Inset) Simplified kinetic scheme.

Materials and Methods

The two mutant and WT RNA polymerases used, identified, and purified by the Nudler Laboratory at New York University (60) were initiated and stalled on the template DNA by means of a λ_PR promoter and a sequence that lacked GMP. The downstream end of the DNA used in this experiment is ligated to a digoxigenin handle. The stalled elongation complexes are then bound to anti-dig polystyrene beads (Spherotech) with a radius of 2.1 μm. These beads are suspended in transcription buffer containing 20 mM Tris, pH 7.9, 20 mM NaCl, 10 mM MgCl₂, and 20 mM DTT and adjusted to a pH of 7.9. Once in the chamber, a tether is made between one of the anti-dig beads containing the complexes and another 2.1-μm streptavidin bead (Spherotech). The starting force on the tether was 3–4 pN. A buffer containing transcription buffer and a full set of nucleotide triphosphates at a saturating concentration of 1 mM (Fermentas) and 1 μM PPi (Fluka Biochemica) was used to reinitate transcription. For experiments with nucleotide analogs, this same buffer was supplemented with 200 mM of either inosine 5′-triphosphate trisodium salt (ITP; Sigma-Aldrich) or 5-bromouridine 5′-triphosphate sodium salt (BrUTP; Sigma-Aldrich). In this passive mode experiment, the distance between the traps is kept constant so that when transcription restarts and the DNA between the beads shortens, the force on the polymerase increases.

Force data were converted into number of nucleotides transcribed using the extensible Worm-Like-Chain model of DNA elasticity (25). Data were filtered, and the velocity was obtained by differentiating the number of bases transcribed. Pauses longer than 2 s were removed by setting a threshold 2–3 SDs from the average velocity and average dwell time. Both methods provided equivalent results. Further details about sample preparation and data analysis are provided in the SI Materials and Methods.