Inference for dynamic and latent variable models via iterated, perturbed Bayes maps

Significance

Many scientific challenges involve the study of stochastic dynamic systems for which only noisy or incomplete measurements are available. Inference for partially observed Markov process models provides a framework for formulating and answering questions about these systems. Except when the system is small, or approximately linear and Gaussian, state-of-the-art statistical methods are required to make efficient use of available data. Evaluation of the likelihood for a partially observed Markov process model can be formulated as a filtering problem. Iterated filtering algorithms carry out repeated Monte Carlo filtering operations to maximize the likelihood. We develop a new theoretical framework for iterated filtering and construct a new algorithm that dramatically outperforms previous approaches on a challenging inference problem in disease ecology.

Abstract

Iterated filtering algorithms are stochastic optimization procedures for latent variable models that recursively combine parameter perturbations with latent variable reconstruction. Previously, theoretical support for these algorithms has been based on the use of conditional moments of perturbed parameters to approximate derivatives of the log likelihood function. Here, a theoretical approach is introduced based on the convergence of an iterated Bayes map. An algorithm supported by this theory displays substantial numerical improvement on the computational challenge of inferring parameters of a partially observed Markov process.

An iterated filtering algorithm was originally proposed for maximum likelihood inference on partially observed Markov process (POMP) models by Ionides et al. (1). Variations on the original algorithm have been proposed to extend it to general latent variable models (2) and to improve numerical performance (3, 4). In this paper, we study an iterated filtering algorithm that generalizes the data cloning method (5, 6) and is therefore also related to other Monte Carlo methods for likelihood-based inference (7–9). Data cloning methodology is based on the observation that iterating a Bayes map converges to a point mass at the maximum likelihood estimate. Combining such iterations with perturbations of model parameters improves the numerical stability of data cloning and provides a foundation for stable algorithms in which the Bayes map is numerically approximated by sequential Monte Carlo computations.

We investigate convergence of a sequential Monte Carlo implementation of an iterated filtering algorithm that combines data cloning, in the sense of Lele et al. (5), with the stochastic parameter perturbations used by the iterated filtering algorithm of (1). Lindström et al. (4) proposed a similar algorithm, termed fast iterated filtering, but the theoretical support for that algorithm involved unproved conjectures. We present convergence results for our algorithm, which we call IF2. Empirically, it can dramatically outperform the previous iterated filtering algorithm of ref. 1, which we refer to as IF1. Although IF1 and IF2 both involve recursively filtering through the data, the theoretical justification and practical implementations of these algorithms are fundamentally different. IF1 approximates the Fisher score function, whereas IF2 implements an iterated Bayes map. IF1 has been used in applications for which no other computationally feasible algorithm for statistically efficient, likelihood-based inference was known (10–15). The extra capabilities offered by IF2 open up further possibilities for drawing inferences about nonlinear partially observed stochastic dynamic models from time series data.

Iterated filtering algorithms implemented using basic sequential Monte Carlo techniques have the property that they do not need to evaluate the transition density of the latent Markov process. Algorithms with this property have been called plug-and-play (12, 16). Various other plug-and-play methods for POMP models have been recently proposed (17–20), due largely to the convenience of this property in scientific applications.

An Algorithm and Related Questions

A general POMP model consists of an unobserved stochastic process $\left\{X\left(t\right),t\ge t_0\right\}$ with observations $Y_1,\dots ,Y_N$ made at times $t_1,\dots ,t_N$. We suppose that $X\left(t\right)$ takes values in $\mathbb{X}\subset {\mathrm{ℝ}}^{\text{dim}\left(\mathbb{X}\right)}$, $Y_n$ takes values in $\mathbb{Y}\subset {\mathrm{ℝ}}^{\text{dim}\left(\mathbb{Y}\right)}$, and there is an unknown parameter θ taking values in $\mathrm{\Theta }\subset {\mathrm{ℝ}}^{\text{dim}\left(\mathrm{\Theta }\right)}$. We adopt notation $y_{m:n}=y_m,y_{m+1},\dots ,y_n$ for integers $m\le n$, so we write the collection of observations as $Y_{1:N}$. Writing $X_n=X\left(t_n\right)$, the joint density of $X_{0:N}$ and $Y_{1:N}$ is assumed to exist, and the Markovian property of $X_{0:N}$ together with the conditional independence of the observation process means that this joint density can be written as

$$\begin{array}{l}{f}_{X_{0:N},Y_{1:N}}\left(x_{0:N},y_{1:N}\hspace{0.17em};\theta \right)\hfill \\ =f_{X_0}\left(x_0\hspace{0.17em};\theta \right){\displaystyle \prod _{n=1}^N{f}_{X_n|X_{n-1}}\left(x_n|x_{n-1}\hspace{0.17em};\theta \right)f_{Y_n|X_n}\left(y_n|x_n\hspace{0.17em};\theta \right)}.\hfill \end{array}$$

The data consist of a sequence of observations, $y_{1:N}*$. We write $f_{Y_{1:N}}\left(y_{1:N}\hspace{0.17em};\theta \right)$ for the marginal density of $Y_{1:N}$, and the likelihood function is defined to be $\ell \left(\theta \right)=f_{Y_{1:N}}\left(y_{1:N}*\hspace{0.17em};\theta \right)$. We look for a maximum likelihood estimate (MLE), i.e., a value $\widehat{\theta }$ maximizing $\ell \left(\theta \right)$. The IF2 algorithm defined above provides a plug-and-play Monte Carlo approach to obtaining $\widehat{\theta }$. A simplification of IF2 arises when $N=1$, in which case, iterated filtering is called iterated importance sampling (2) (SI Text, Iterated Importance Sampling). Algorithms similar to IF2 with a single iteration $\left(M=1\right)$ have been proposed in the context of Bayesian inference (21, 22) (SI Text, Applying Liu and West’s Method to the Toy Example and Fig. S1). When $M=1$ and $h_n\left(\theta |\phi \hspace{0.17em};\sigma \right)$ degenerates to a point mass at φ, the IF2 algorithm becomes a standard particle filter (23, 24). In the IF2 algorithm description, ${\mathrm{\Theta }}_{n,j}^{F,m}$ and $X_{n,j}^{F,m}$ are the jth particles at time n in the Monte Carlo representation of the mth iteration of a filtering recursion. The filtering recursion is coupled with a prediction recursion, represented by ${\mathrm{\Theta }}_{n,j}^{P,m}$ and $X_{n,j}^{P,m}$. The resampling indices $k_{1:J}$ in IF2 are taken to be a multinomial draw for our theoretical analysis, but systematic resampling is preferable in practice (23). A natural choice of $h_n\left(\theta |\phi \hspace{0.17em};\sigma \right)$ is a multivariate normal density with mean φ and variance ${\sigma }^2\mathrm{\Sigma }$ for some covariance matrix $\mathrm{\Sigma }$, but in general, $h_n$ could be any conditional density parameterized by σ. Combining the perturbations over all of the time points, we define

$$h\left({\theta }_{0:N}|\phi \hspace{0.17em};\sigma \right)=h_0\left({\theta }_0|\phi ;\sigma \right){\displaystyle \prod _{n=1}^N{h}_n\left({\theta }_n|{\theta }_{n-1}\hspace{0.17em};\sigma \right)}.$$

We define an extended likelihood function on ${\mathrm{\Theta }}^{N+1}$ by

$$\begin{array}{l}\stackrel{⌣}{\ell }\left({\theta }_{0:N}\right)={\displaystyle \int \dots }{\displaystyle \int d{x}_0\dots d{x}_N\{f_{X_0}\left(x_o\hspace{0.17em};{\theta }_0\right)}\\ \times {\displaystyle \prod _{n=1}^N{f}_{X_n|X_{n-1}}\left(x_n|x_{n-1}\hspace{0.17em};{\theta }_n\right)f_{Y_n|X_n}\left(y_n^{*}|x_n\hspace{0.17em};{\theta }_n\right)}\}.\end{array}$$

Each iteration of IF2 is a Monte Carlo approximation to a map

$$T_{\sigma }f\left({\theta }_N\right)=\frac{{\displaystyle \int \stackrel{⌣}{\ell }\left({\theta }_{0:N}\right)h\left({\theta }_{0:N}|\phi \hspace{0.17em};\sigma \right)f\left(\phi \right)d\phi \hspace{0.17em}d{\theta }_{0:N-1}}}{{\displaystyle \int \stackrel{⌣}{\ell }\left({\theta }_{0:N}\right)h\left({\theta }_{0:N}|\phi \hspace{0.17em};\sigma \right)f\left(\phi \right)d\phi \hspace{0.17em}d{\theta }_{0:N}}},$$ [1]

with f and $T_{\sigma }f$ approximating the initial and final density of the parameter swarm. For our theoretical analysis, we consider the case when the SD of the parameter perturbations is held fixed at ${\sigma }_m=\sigma >0$ for $m=1,\dots ,M$. In this case, IF2 is a Monte Carlo approximation to $T_{\sigma }^{M}f\left(\theta \right)$. We call the fixed σ version of IF2 “homogeneous” iterated filtering since each iteration implements the same map. For any fixed σ, one cannot expect a procedure such as IF2 to converge to a point mass at the MLE. However, for fixed but small σ, we show that IF2 does approximately maximize the likelihood, with an error that shrinks to zero in a limit as $\sigma \to 0$ and $M\to \infty$. An immediate motivation for studying the homogeneous case is simplicity; it turns out that even with this simplifying assumption, the theoretical analysis is not entirely straightforward. Moreover, the homogeneous analysis gives at least as much insight as an asymptotic analysis into the practical properties of IF2, when ${\sigma }_m$ decreases down to some positive level $\sigma >0$ but never completes the asymptotic limit ${\sigma }_m\to 0$. Iterated filtering algorithms have been primarily developed in the context of making progress on complex models for which successfully achieving and validating global likelihood optimization is challenging. In such situations, it is advisable to run multiple searches and continue each search up to the limits of available computation (25). If no single search can reliably locate the global maximum, a theory assuring convergence to a neighborhood of the maximum is as relevant as a theory assuring convergence to the maximum itself in a practically unattainable limit.

Algorithm IF2. Iterated filtering
input:
Simulator for $f_{X_0}\left(x_0\hspace{0.17em};\theta \right)$
Simulator for $f_{X_n|X_{n-1}}\left(x_n|x_{n-1}\hspace{0.17em};\theta \right)$, n in $1:N$
Evaluator for $f_{Y_n|X_n}\left(y_n|x_n\hspace{0.17em};\theta \right)$, n in $1:N$
Data, $y_{1:N}*$
Number of iterations, M
Number of particles, J
Initial parameter swarm, $\left\{{\mathrm{\Theta }}_j^0,j\hspace{0.5em}\text{in}\hspace{0.17em}1:J\right\}$
Perturbation density, $h_n\left(\theta |\phi \hspace{0.17em};\sigma \right)$, n in $1:N$
Perturbation sequence, ${\sigma }_{1:M}$
output: Final parameter swarm, $\left\{{\mathrm{\Theta }}_j^M,j\hspace{0.5em}\text{in}\hspace{0.17em}1:J\right\}$
For m in $1:M$
${\mathrm{\Theta }}_{0,j}^{F,m}\sim h_0\left(\theta |{\mathrm{\Theta }}_j^{m-1}\hspace{0.17em};{\sigma }_m\right)$ for j in $1:J$
$X_{0,j}^{F,m}\sim f_{X_0}\left(x_0;{\mathrm{\Theta }}_{0,j}^{F,m}\right)$ for j in $1:J$
For n in $1:N$
${\mathrm{\Theta }}_{n,j}^{P,m}\sim h_n\left(\theta |{\mathrm{\Theta }}_{n-1,j}^{F,m},{\sigma }_m\right)$ for j in $1:J$
$X_{n,j}^{P,m}\sim f_{X_n|X_{n-1}}\left(x_n|X_{n-1,j}^{F,m};{\mathrm{\Theta }}_j^{P,m}\right)$ for j in $1:J$
$w_{n,j}^m=f_{Y_n|X_n}\left(y_n^{*}|X_{n,j}^{P,m};{\mathrm{\Theta }}_{n,j}^{P,m}\right)$ for j in $1:J$
Draw $k_{1:J}$ with $\mathrm{\mathbb{P}}\left(k_j=i\right)=w_{n,i}^m/{\displaystyle {\sum }_{u=1}^J{w}_{n,u}^m}$
${\mathrm{\Theta }}_{n,j}^{F,m}={\mathrm{\Theta }}_{n,k_j}^{P,m}$ and $X_{n,j}^{F,m}=X_{n,k_j}^{P,m}$ for j in $1:J$
End For
Set ${\mathrm{\Theta }}_j^m={\mathrm{\Theta }}_{N,j}^{F,m}$ for j in $1:J$
End For

The map $T_{\sigma }$ can be expressed as a composition of a parameter perturbation with a Bayes map that multiplies by the likelihood and renormalizes. Iteration of the Bayes map alone has a central limit theorem (CLT) (5) that forms the theoretical basis for the data cloning methodology of refs. 5 and 6. Repetitions of the parameter perturbation may also be expected to follow a CLT. One might therefore imagine that the composition of these two operations also has a Gaussian limit. This is not generally true, since the rescaling involved in the perturbation CLT prevents the Bayes map CLT from applying (SI Text, A Class of Exact Non-Gaussian Limits for Iterated Importance Sampling). Our agenda is to seek conditions guaranteeing the following:

• (A1)For every fixed $\sigma >0$, ${\lim }_{m\to \infty }{T}_{\sigma }^{m}f=f_{\sigma }$ exists.
• (A2)When J and M become large, IF2 numerically approximates $f_{\sigma }$.
• (A3)As the noise intensity becomes small, ${\lim }_{\sigma \to 0}{f}_{\sigma }$ approaches a point mass at the MLE, if it exists.

Stability of filtering problems and uniform convergence of sequential Monte Carlo numerical approximations are closely related, and so A1 and A2 are studied together in Theorem 1. Each iteration of IF2 involves standard sequential Monte Carlo filtering techniques applied to an extended model where latent variable space is augmented to include a time-varying parameter. Indeed, all M iterations together can be represented as a filtering problem for this extended POMP model on M replications of the data. The proof of Theorem 1 therefore leans on existing results. The novel issue of A3 is then addressed in Theorem 2.

Convergence of IF2

First, we set up some notation. Let $\left\{{\stackrel{⌣}{\mathrm{\Theta }}}_{0:N}^m,m=\mathrm{1,2},\dots \right\}$ be a Markov chain taking values in ${\mathrm{\Theta }}^{N+1}$ such that ${\stackrel{⌣}{\mathrm{\Theta }}}_{0:N}^1$ has density ${\displaystyle \int h\left({\theta }_{0:N}|\phi \hspace{0.17em};\sigma \right)f\left(\phi \right)d\phi }$, and ${\stackrel{⌣}{\mathrm{\Theta }}}_{0:N}^m$ has conditional density $h\left({\theta }_{0:N}|{\phi }_N\hspace{0.17em};\sigma \right)$ given ${\stackrel{⌣}{\mathrm{\Theta }}}_{0:N}^{m-1}={\phi }_{0:N}$ for $m\ge 2$. Suppose that $\left\{{\stackrel{⌣}{\mathrm{\Theta }}}_{0:N}^m,m\ge 1\right\}$ is constructed on the canonical probability space $\mathrm{\Omega }=\left\{\left({\theta }_{0:N}^1,{\theta }_{0:N}^2,\dots \right)\right\}$ with ${\theta }_{0:N}^m={\stackrel{⌣}{\mathrm{\Theta }}}_{0:N}^m\left(\vartheta \right)$ for $\vartheta =\left({\theta }_{0:N}^1,{\theta }_{0:N}^2,\dots \right)\in \mathrm{\Omega }$. Let $\left\{{\mathrm{ℱ}}_m\right\}$ be the corresponding Borel filtration. To consider a time-rescaled limit of $\left\{{\stackrel{⌣}{\mathrm{\Theta }}}_{0:N}^m,m=\mathrm{1,2},\dots \right\}$ as $\sigma \to 0$, let $\left\{W_{\sigma }\left(t\right),t\ge 0\right\}$ be a continuous-time, right-continuous, piecewise constant process defined at its points of discontinuity by $W_{\sigma }\left(k{\sigma }^2\right)={\stackrel{⌣}{\mathrm{\Theta }}}_N^{k+1}$ when k is a nonnegative integer. Let $\left\{{\stackrel{⌣}{Z}}_{0:N}^m,m=\mathrm{1,2},\dots \right\}$ be the filtered process defined such that, for any event $E\in {\mathrm{ℱ}}_M$,

$${\mathrm{\mathbb{P}}}_{\stackrel{⌣}{Z}}\left(E\right)=\frac{{\mathbb{E}}_{\stackrel{⌣}{\mathrm{\Theta }}}\left[{\stackrel{⌣}{\ell }}_{1:M}{I}_E\right]}{{\mathbb{E}}_{\stackrel{⌣}{\mathrm{\Theta }}}\left[{\stackrel{⌣}{\ell }}_{1:M}\right]},$$ [2]

where $I_E$ is the indicator function for event E and

$${\stackrel{⌣}{\ell }}_{1:M}\left(\vartheta \right)={\displaystyle \prod _{m=1}^M\stackrel{⌣}{\ell }\left({\theta }_{0:N}^m\right)}.$$

In Eq. 2 , ${\mathrm{\mathbb{P}}}_{\stackrel{⌣}{Z}}\left(E\right)$ denotes probability under the law of $\left\{{\stackrel{⌣}{Z}}_n^m\right\}$, and ${\mathbb{E}}_{\stackrel{⌣}{\mathrm{\Theta }}}$ denotes expectation under the law of $\left\{{\stackrel{⌣}{\mathrm{\Theta }}}_n^m\right\}$. The process $\left\{{\stackrel{⌣}{Z}}_n^m\right\}$ is constructed so that ${\stackrel{⌣}{Z}}_N^m$ has density $T^{m}f$. We make the following assumptions.

• (B1)$\left\{W_{\sigma }\left(t\right),0\le t\le 1\right\}$ converges weakly as $\sigma \to 0$ to a diffusion $\left\{W\left(t\right),0\le t\le 1\right\}$, in the space of right-continuous functions with left limits equipped with the uniform convergence topology. For any open set $A\subset \mathrm{\Theta }$ with positive Lebesgue measure and $\mathit{ϵ}>0$, there is a $\delta \left(A,\mathit{ϵ}\right)>0$ such that $\mathrm{\mathbb{P}}\left[W\left(t\right)\in A\hspace{0.5em}\mathrm{for}\mathrm{all}\hspace{0.5em}\mathit{ϵ}\le t\le 1|W\left(0\right)\right]>\delta$.
• (B2)For some $t_0\left(\sigma \right)$ and ${\sigma }_0>0$, $W_{\sigma }\left(t\right)$ has a positive density on $\mathrm{\Theta }$, uniformly over the distribution of $W\left(0\right)$ for all $t>t_0$ and $\sigma <{\sigma }_0$.
• (B3)$\ell \left(\theta \right)$ is continuous in a neighborhood $\left\{\theta :\ell \left(\theta \right)>{\lambda }_1\right\}$ for some ${\lambda }_1<{\text{sup}}_{\phi }\ell \left(\phi \right)$.
• (B4)There is an $\mathit{ϵ}>0$ with ${\mathit{ϵ}}^{-1}>f_{Y_n|X_n}\left(y_n*|x_n,\theta \right)>\mathit{ϵ}$ for all $1\le n\le N$, $x_n\in \mathbb{X}$ and $\theta \in \mathrm{\Theta }$.
• (B5)There is a $C_1$ such that $h_n\left(\theta |\hspace{0.17em}\phi \hspace{0.17em};\sigma \right)=0$ when $\left|\theta -\phi \right|>C_1\sigma$, for all σ.
• (B6)There is a $C_2$ such that ${\text{sup}}_{1\le n\le N}\left|{\theta }_n-{\theta }_{n-1}\right|<C_1\hspace{0.17em}\sigma$ implies $\left|\stackrel{⌣}{\ell }\left({\theta }_{0:N}\right)-\ell \left({\theta }_N\right)\right|<C_2\hspace{0.17em}\sigma$, for all σ and all n.

Conditions B1 and B2 hold when $h_n\left(\theta |\phi \hspace{0.17em};\sigma \right)$ corresponds to a reflected Gaussian random walk and $\left\{W\left(t\right)\right\}$ is a reflected Brownian motion (SI Text, Checking Conditions B1 and B2). More generally, when $h_n\left(\theta |\phi \hspace{0.17em};\sigma \right)$ is a location-scale family with mean φ away from a boundary, then $\left\{W\left(t\right)\right\}$ will behave like Brownian motion in the interior of $\mathrm{\Theta }$. B4 follows if $\mathbb{X}$ is compact and $f_{Y_n|X_n}\left(y_n*|x_n\hspace{0.17em};\theta \right)$ is positive and continuous as a function of θ and $x_n$. B5 can be guaranteed by construction. B3 and B6 are undemanding regularity conditions on the likelihood and extended likelihood. A formalization of A1 and A2 can now be stated as follows.

Theorem 1. Let $T_{\sigma }$ be the map of Eq. 1 and suppose B2 and B4. There is a unique probability density $f_{\sigma }$ such that for any probability density f on $\mathrm{\Theta }$,

$$\underset{m\to \infty }{\text{lim}}{\left|\left|T_{\sigma }^{m}f-f_{\sigma }\right|\right|}_1=0,$$ [3]

where ${\left|\left|f\right|\right|}_1$ is the $L^1$ norm of f. Let $\left\{{\mathrm{\Theta }}_j^M,\hspace{0.17em}j=1,\dots ,J\right\}$ be the output of IF2, with ${\sigma }_m=\sigma >0$. There is a finite constant $C>0$ such that, for any function $\varphi :\mathrm{\Theta }\to \mathrm{ℝ}$ and all M,

$$\mathbb{E}\left\{\left|\frac{1}{J}{\displaystyle \sum _{j=1}^J\varphi \left({\mathrm{\Theta }}_j^M\right)}-{\displaystyle \int \varphi \left(\theta \right)f_{\sigma }\left(\theta \right)d\theta }\right|\right\}\le \frac{C\hspace{0.17em}{\text{sup}}_{\theta }\left|\varphi \left(\theta \right)\right|}{\sqrt{J}}.$$ [4]

Proof. B2 and B4 imply that $T_{\sigma }^k$ is mixing, in the sense of ref. 26, for all sufficiently large k. The results of ref. 26 are based on the contractive properties of mixing maps in the Hilbert projective metric. Although ref. 26 stated their results in the case where T itself is mixing, the required geometric contraction in the Hilbert metric holds as long as $T^k$ is mixing for all $K\le k\le 2K-1$ for some $K\ge 1$ (ref. 27, theorem 2.5.1). Corollary 4.2 of ref. 26 implies Eq. 3, noting the equivalence of the Hilbert projective metric and the total variation norm shown in their lemma 3.4. Then, corollary 5.12 of ref. 26 implies Eq. 4, completing the proof of Theorem 1. A longer version of this proof is given in SI Text, Additional Details for the Proof of Theorem 1.

Results similar to Theorem 1 can be obtained using Dobrushin contraction techniques (28). Results appropriate for noncompact spaces can be obtained using drift conditions on a potential function (29). Now we move on to our formalization of A3:

Theorem 2. Assume B1–B6. For ${\lambda }_2<{\text{sup}}_{\phi }\ell \left(\phi \right)$, ${\lim }_{\sigma \to 0}{\displaystyle \int f_{\sigma }\left(\theta \right)1_{\left\{\ell \left(\theta \right)<{\lambda }_2\right\}}\hspace{0.17em}d\theta =0}$.

Proof. Let ${\lambda }_0={\text{sup}}_{\phi }\ell \left(\phi \right)$ and ${\lambda }_3={\text{inf}}_{\phi }\ell \left(\phi \right)$. From B4, $\mathrm{\infty }>{\lambda }_0>{\lambda }_3>0$. For positive constants ${\mathit{ϵ}}_1$, ${\mathit{ϵ}}_2$, ${\eta }_1$, ${\eta }_2$ and ${\lambda }_1<{\lambda }_0$, define

$$e_1=\left(1-{\mathit{ϵ}}_1\right)\log \left({\lambda }_0+{\mathit{ϵ}}_2\right)+{\mathit{ϵ}}_1\log \left({\lambda }_2+{\mathit{ϵ}}_2\right),$$

$$e_2=\left(1-{\eta }_1\right)\log \left({\lambda }_1-{\eta }_2\right)+{\eta }_1\log \left({\lambda }_3-{\eta }_2\right).$$

We can pick ${\mathit{ϵ}}_1$, ${\mathit{ϵ}}_2$, ${\eta }_1$, ${\eta }_2$, and ${\lambda }_1$ so that $e_1<e_2$. Suppose that $\left\{{\stackrel{⌣}{\mathrm{\Theta }}}_n^m\right\}$ is initialized with the stationary distribution $f=f_{\sigma }$ identified in Theorem 1. Now, set M to be the greatest integer less than $1/{\sigma }^2$, and let $F_1$ be the event that $\left\{{\mathrm{\Theta }}_N^m,m=1,\dots ,M\right\}$ spends at least a fraction of time ${\mathit{ϵ}}_1$ in $\left\{\theta :\ell \left(\theta \right)<{\lambda }_2\right\}$. Formally,

$$F_1=\left\{\vartheta \in \mathrm{\Omega }:\frac{1}{M}{\displaystyle \sum _{m=1}^M{1}_{\left\{\ell \left({\theta }_N^m\right)<{\lambda }_2\right\}}>{\mathit{ϵ}}_1}\right\}.$$

We wish to show that ${\mathrm{\mathbb{P}}}_{\stackrel{⌣}{Z}}\left[F_1\right]$ is small for σ small. Let $F_2$ be the set of sample paths that spend at least a fraction of time $\left(1-{\eta }_1\right)$ up to time M in $\left\{\theta :\ell \left(\theta \right)>{\lambda }_1\right\}$, i.e.,

$$F_2=\left\{\vartheta \in \mathrm{\Omega }:\frac{1}{M}{\displaystyle \sum _{m=1}^M{1}_{\left\{\ell \left({\theta }_N^m\right)>{\lambda }_1\right\}}}>\left(1-{\eta }_1\right)\right\}.$$

Then, we calculate

$$\begin{array}{c}{\mathrm{\mathbb{P}}}_{\stackrel{⌣}{Z}}\left[F_1\right]=\frac{{\mathbb{E}}_{\stackrel{⌣}{\mathrm{\Theta }}}\left[{\stackrel{⌣}{\ell }}_{1:M}{1}_{F_1}\right]}{{\mathbb{E}}_{\stackrel{⌣}{\mathrm{\Theta }}}\left[{\stackrel{⌣}{\ell }}_{1:M}\right]}\\ \le \frac{{\mathbb{E}}_{\stackrel{⌣}{\mathrm{\Theta }}}\left[{\stackrel{⌣}{\ell }}_{1:M}{1}_{F_1}\right]}{{\mathbb{E}}_{\stackrel{⌣}{\mathrm{\Theta }}}\left[{\stackrel{⌣}{\ell }}_{1:M}{1}_{F_2}\right]}\\ \le \frac{{\mathbb{E}}_{\stackrel{⌣}{\mathrm{\Theta }}}\left[{\displaystyle {\prod }_{m=1}^M\left\{\ell \left({\theta }_N^m\right)+C_2\sigma \right\}{1}_{F_1}}\right]}{{\mathbb{E}}_{\stackrel{⌣}{\mathrm{\Theta }}}\left[{\displaystyle {\prod }_{m=1}^M\left\{\ell \left({\theta }_N^m\right)-C_2\sigma \right\}{1}_{F_2}}\right]}\end{array}$$ [5]

$$\le \frac{{\mathbb{E}}_{\stackrel{⌣}{\mathrm{\Theta }}}\left[\text{exp}\left\{M{e}_1\right\}{1}_{F_1}\right]}{{\mathbb{E}}_{\stackrel{⌣}{\mathrm{\Theta }}}\left[\text{exp}\left\{M{e}_2\right\}{1}_{F_2}\right]}$$ [6]

$$=\text{exp}\left\{\left(e_1-e_2\right)M\right\}\frac{{\mathrm{\mathbb{P}}}_{\stackrel{⌣}{\mathrm{\Theta }}}\left[F_1\right]}{{\mathrm{\mathbb{P}}}_{\stackrel{⌣}{\mathrm{\Theta }}}\left[F_2\right]}.$$ [7]

We used B5 and B6 to arrive at Eq. 5, then, to get to Eq. 6, we have taken σ small enough that $C_2\sigma <{\mathit{ϵ}}_2$ and $C_2\sigma <{\eta }_2$. From B3, $\left\{\theta :\ell \left(\theta \right)>{\lambda }_1\right\}$ is an open set, and B1 therefore ensures each of the probabilities ${\mathrm{\mathbb{P}}}_{{\mathrm{\Theta }}_{1:M}}\left[F_1\right]$ and ${\mathrm{\mathbb{P}}}_{{\mathrm{\Theta }}_{1:M}}\left[F_2\right]$ in Eq. 7 tends to a positive limit as $\sigma \to 0$ given by the probability under the limiting distribution $\left\{W\left(t\right)\right\}$ (SI Text, Lemma S1). The term $\text{exp}\left\{\left(e_1-e_2\right)M\right\}$ tends to zero as $\sigma \to 0$ since, by construction, $M\to \infty$ and $e_1<e_2$. Setting $L=\left\{\theta :\ell \left(\theta \right)\le {\lambda }_2\right\}$, and noting that $\left\{{\stackrel{⌣}{Z}}_N^m,m=\mathrm{1,2},\dots \right\}$ is constructed to have stationary marginal density $f_{\sigma }$, we have

$$\begin{array}{c}{\displaystyle \underset{L}{\int }{f}_{\sigma }\left(\theta \right)d\theta }=\frac{1}{M}{\displaystyle \sum _{m=1}^M\left\{{\mathrm{\mathbb{P}}}_{\stackrel{⌣}{Z}}\left[{\stackrel{⌣}{Z}}_N^m\in L|F_1\right]{\mathrm{\mathbb{P}}}_{\stackrel{⌣}{Z}}\left[F_1\right]+{\mathrm{\mathbb{P}}}_{\stackrel{⌣}{Z}}\left[{\stackrel{⌣}{Z}}_N^m\in L|F_1^c\right]{\mathrm{\mathbb{P}}}_{\stackrel{⌣}{Z}}\left[F_1^c\right]\right\}},\\ \le {\mathit{ϵ}}_1+{\mathrm{\mathbb{P}}}_{\stackrel{⌣}{Z}}\left[F_1\right],\end{array}$$

which can be made arbitrarily small by picking ${\mathit{ϵ}}_1$ small and σ small, completing the proof.

Demonstration of IF2 with Nonconvex Superlevel Sets

Theorems 1 and 2 do not involve any Taylor series expansions, which are basic in the justification of IF1 (2). This might suggest that IF2 can be effective on likelihood functions without good low-order polynomial approximations. In practice, this can be seen by comparing IF2 with IF1 on a simple 2D toy example $\left(\text{dim}\left(\mathrm{\Theta }\right)=\text{dim}\left(\mathbb{X}\right)=\text{dim}\left(\mathbb{Y}\right)=2\right)$ in which the superlevel sets $\left\{\theta :\ell \left(\theta \right)>\lambda \right\}$ are connected but not convex. We also compare with particle Markov chain Monte Carlo (PMCMC) implemented as the particle marginal Metropolis–Hastings algorithm of ref. 17. The justification of PMCMC also does not depend on Taylor series expansions, but PMCMC is computationally expensive compared with iterated filtering (30). Our toy example has a constant and nonrandom latent process, $X_n=\left(\exp \left\{{\theta }_1\right\},{\theta }_2\exp \left\{{\theta }_1\right\}\right)$ for $n=1,\dots ,N$. The known measurement model is

$$f_{Y_n|X_n}\left(y|x\hspace{0.17em};\theta \right)\sim \text{Normal}\left[x,\left(\begin{array}{cc}100& 0\\ 0& 1\end{array}\right)\right],$$

This example was designed so that a nonlinear combination of the parameters is well identified whereas each parameter is marginally weakly identified. For the truth, we took $\theta =\left(\mathrm{1,1}\right)$. We supposed that ${\theta }_1$ is suspected to fall in the interval $\left[-\mathrm{2,2}\right]$ and ${\theta }_2$ is expected in $\left[\mathrm{0,10}\right]$. We used a uniform distribution on this rectangle to specify the prior for PMCMC and to generate random starting points for all of the algorithms. We set $N=100$ observations, and we used a Monte Carlo sample size of $J=100$ particles. For IF1 and IF2, we used $M=100$ filtering iterations, with initial random walk SD 0.1 decreasing geometrically down to 0.01. For PMCMC, we used ${10}^4$ filtering iterations with random walk SD 0.1, awarding PMCMC 100 times the computational resources offered to IF1 and IF2. Independent, normally distributed parameter perturbations were used for IF1, IF2, and PMCMC. The random walk SD for PMCMC is not immediately comparable to that for IF1 and IF2, since the latter add the noise at each observation time whereas the former adds it only between filtering iterations. All three methods could have their parameters fine-tuned, or be modified in other ways to take advantage of the structure of this particular problem. However, this example demonstrates a feature that makes tuning algorithms tricky: The nonlinear ridge along contours of constant ${\theta }_2\exp \left({\theta }_1\right)$ becomes increasingly steep as ${\theta }_1$ increases, so no single global estimate of the second derivative of the likelihood is appropriate. Reparameterization can linearize the ridge in this toy example, but in practical problems with much larger parameter spaces, one does not always know how to find appropriate reparameterizations, and a single reparameterization may not be appropriate throughout the parameter space.

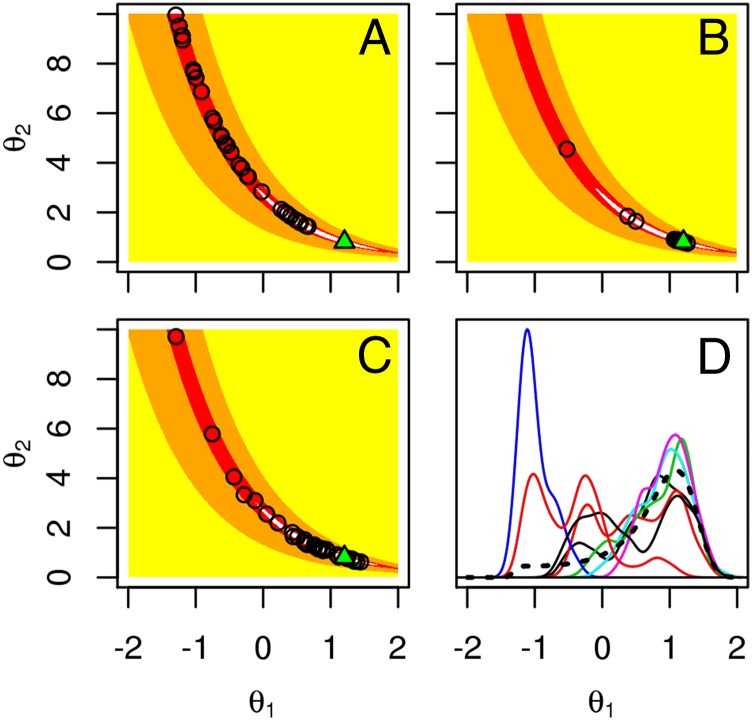
Fig. 1 compares the performance of the three methods, based on 30 Monte Carlo replications. These replications investigate the likelihood and posterior distribution for a single draw from our toy model, since our interest is in the Monte Carlo behavior for a given dataset. For this simulated dataset, the MLE is $\theta =\left(1.20,0.81\right)$, shown as a green triangle in Fig. 1 A−C. In this toy example, the posterior distribution can also be computed directly by numerical integration. In Fig. 1A, we see that IF1 performs poorly on this challenge. None of the 30 replications approach the MLE. The linear combination of perturbed parameters involved in the IF1 update formula can all too easily knock the search off a nonlinear ridge. Fig. 1B shows that IF2 performs well on this test, with almost all of the Monte Carlo replications clustering in the region of highest likelihood. Fig. 1C shows the end points of the PMCMC replications, which are nicely spread around the region of high posterior probability. However, Fig. 1D shows that mixing of the PMCMC Markov chains was problematic.

Fig. 1.

Results for the simulation study of the toy example. (A) IF1 point estimates from 30 replications (circles) and the MLE (green triangle). The region of parameter space with likelihood within 3 log units of the maximum (white), within 10 log units (red), within 100 log units (orange), and lower (yellow). (B) IF2 point estimates from 30 replications (circles) with the same algorithmic settings as IF1. (C) Final parameter value of 30 PMCMC chains (circles). (D) Kernel density estimates of the posterior for ${\theta }_1$ for the first eight of these 30 PMCMC chains (solid lines), with the true posterior distribution (dotted black line).

Application to a Cholera Model

Highly nonlinear, partially observed, stochastic dynamic systems are ubiquitous in the study of biological processes. The physical scale of the systems vary widely from molecular biology (31) to population ecology and epidemiology (32), but POMP models arise naturally at all scales. In the face of biological complexity, it is necessary to determine which scientific aspects of a system are critical for the investigation. Giving consideration to a range of potential mechanisms, and their interactions, may require working with highly parameterized models. Limitations in the available data may result in some combinations of parameters being weakly identifiable. Despite this, other combinations of parameters may be adequately identifiable and give rise to some interesting statistical inferences. To demonstrate the capabilities of IF2 for such analyses, we fit a model for cholera epidemics in historic Bengal developed by King et al. (10). The model, the data, and the implementations of IF1 and IF2 used below are all contained in the open source R package pomp (33). The code generating the results in this article is provided as supplementary data (Datasets S1 and S2).

Cholera is a diarrheal disease caused by the bacterial pathogen Vibrio cholerae. Without appropriate medical treatment, severe infections can rapidly result in death by dehydration. Many questions regarding cholera transmission remain unresolved: What is the epidemiological role of free-living environmental vibrio? How important are mild and asymptomatic infections for the transmission dynamics? How long does protective immunity last following infection? The model we consider splits up the study population of $P\left(t\right)$ individuals into those who are susceptible, $S\left(t\right)$, infected, $I\left(t\right)$, and recovered, $R\left(t\right)$. $P\left(t\right)$ is assumed known from census data. To allow flexibility in representing immunity, $R\left(t\right)$ is subdivided into $R_1\left(t\right),\dots ,R_k\left(t\right)$, where we take $k=3$. Cumulative cholera mortality in each month is tracked with a variable $M\left(t\right)$ that resets to zero at the beginning of each observation period. The state process, $\left\{X\left(t\right)=\left(S\left(t\right),I\left(t\right),R_1\left(t\right),\dots ,R_k\left(t\right),M\left(t\right)\right),t\ge t_0\right\}$, follows a stochastic differential equation,

$$\begin{array}{c}dS=\left\{k\mathit{ϵ}{R}_k+\delta \left(S-H\right)-\lambda \left(t\right)S\right\}dt+dP-\left(\sigma SI/P\right)dB,\\ dI=\left\{\lambda \left(t\right)S-\left(m+\delta +\gamma \right)I\right\}dt+\left(\sigma SI/P\right)dB,\\ d{R}_1=\left\{\gamma I-\left(k\mathit{ϵ}+\delta \right)R_1\right\}dt,\\ ⋮\\ d{R}_k=\left\{k\mathit{ϵ}{R}_{k-1}-\left(k\mathit{ϵ}+\delta \right)R_k\right\}dt,\end{array}$$

driven by a Brownian motion $\left\{B\left(t\right)\right\}$. Nonlinearity arises through the force of infection, $\lambda \left(t\right)$, specified as

$$\begin{array}{c}\lambda \left(t\right)=\overline{\beta }\exp \left\{{\beta }_{\text{trend}}\left(t-t_0\right)+{\displaystyle \sum _{j=1}^{N_s}{\beta }_j{s}_j\left(t\right)}\right\}\left(I/P\right)\\ +\overline{\omega }\exp \left\{{\displaystyle \sum _{j=1}^{N_s}{\omega }_j{s}_j\left(t\right)}\right\},\end{array}$$

where $\left\{s_j\left(t\right),j=1,\dots ,N_s\right\}$ is a periodic cubic B-spline basis; $\left\{{\beta }_j,j=1,\dots ,N_s\right\}$ model seasonality of transmission; $\left\{{\omega }_j,j=1,\dots ,N_s\right\}$ model seasonality of the environmental reservoir; $\overline{\omega }$ and $\overline{\beta }$ are scaling constants set to $\overline{\omega }=\overline{\beta }=1{\hspace{0.17em}\text{y}}^{-1}$, and we set $N_s=6$. The data, consisting of monthly counts of cholera mortality, are modeled via $Y_n\sim \text{Normal}\left(M_n,{\tau }^2{M}_n^2\right)$ for $M_n={\displaystyle {\int }_{t_{n-1}}^{t_n}m\hspace{0.17em}I\left(s\right)ds}$.

The inference goal used to assess IF1 and IF2 is to find high-likelihood parameter values starting from randomly drawn starting values in a large hyperrectangle (Table S1). A single search cannot necessarily be expected to reliably obtain the maximum of the likelihood, due to multimodality, weak identifiability, and considerable Monte Carlo error in evaluating the likelihood. Multiple starts and restarts may be needed both for effective optimization and for assessing the evidence to validate effective optimization. However, optimization progress made on an initial search provides a concrete criterion to compare methodologies. Since IF1 and IF2 have essentially the same computational cost, for a given Monte Carlo sample size and number of iterations, shared fixed values of these algorithmic parameters provide an appropriate comparison.

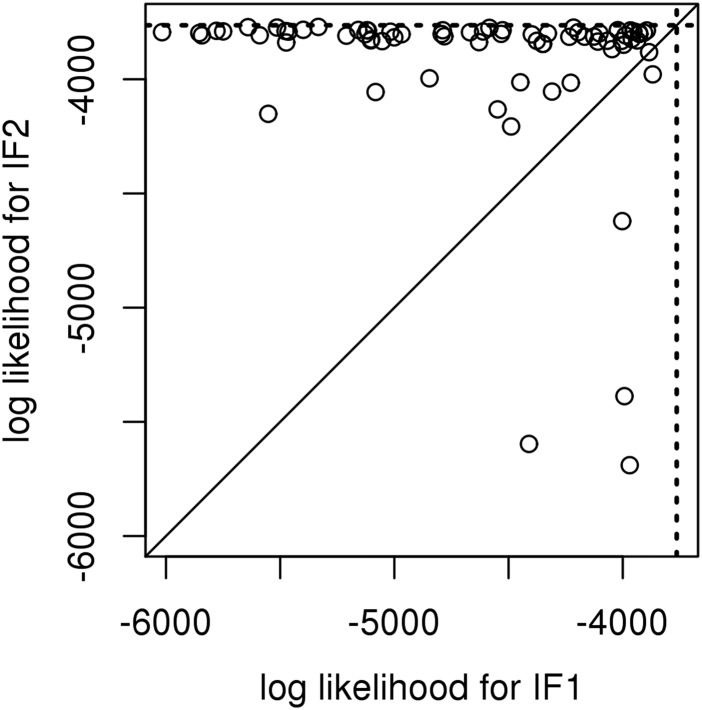
Fig. 2 compares results for 100 searches with $J={10}^4$ particles and $M=100$ iterations of the search. An initial Gaussian random walk SD of 0.1 geometrically decreasing down to a final value of 0.01 was used for all parameters except $S_0$, $I_0$, $R_{\mathrm{1,0}}$, $R_{\mathrm{2,0}}$, and $R_{\mathrm{3,0}}$. For those initial value parameters, the random walk SD decreased geometrically from 0.2 down to 0.02, but these perturbations were applied only at time $t_0$. Since some starting points may lead both IF1 and IF2 to fail to approach the global maximum, Fig. 2 plots the likelihoods of parameter vectors output by IF1 and IF2 for each starting point. Fig. 2 shows that, on this problem, IF2 is considerably more effective than IF1. This maximization was considered challenging for IF1, and (10) required multiple restarts and refinements of the optimization procedure. Our implementation of PMCMC failed to converge on this inference problem (SI Text, Applying PMCMC to the Cholera Model and Fig. S2), and we are not aware of any previous successful PMCMC solution for a comparable situation. For IF2, however, this situation appears routine. Some Monte Carlo replication is needed because searches occasionally fail to approach the global optimum, but replication is always appropriate for Monte Carlo optimization procedures.

Fig. 2.

Comparison of IF1 and IF2 on the cholera model. Points are the log likelihood of the parameter vector output by IF1 and IF2, both started at a uniform draw from a large hyperrectangle (Table S1). Likelihoods were evaluated as the median of 10 particle filter replications (i.e., IF2 applied with $M=1$ and ${\sigma }_1=0$) each with $J=2\times {10}^4$ particles. Seventeen poorly performing searches are off the scale of this plot (15 due to the IF1 estimate, 2 due to the IF2 estimate). Dotted lines show the maximum log likelihood reported by ref. 10.

A fair numerical comparison of methods is difficult. For example, it could hypothetically be the case that the algorithmic settings used here favor IF2. However, the settings used are those that were developed for IF1 by ref. 10 and reflect considerable amounts of trial and error with that method. Likelihood-based inference for general partially observed nonlinear stochastic dynamic models was considered computationally unfeasible before the introduction of IF1, even in situations considerably simpler than the one investigated in this section (19). We have shown that IF2 offers a substantial improvement on IF1, by demonstrating that it functions effectively on a problem at the limit of the capabilities of IF1.

Discussion

Theorems 1 and 2 assert convergence without giving insights into the rate of convergence. In the particular case of a quadratic log likelihood function and additive Gaussian parameter perturbations, ${\lim }_{M\to \infty }{T}_{\sigma }^{M}f$ is Gaussian, and explicit calculations are available (SI Text, Gaussian and Near-Gaussian Analysis of Iterated Importance Sampling). If $\log \ell \left(\theta \right)$ is close to quadratic and the parameter perturbation is close to additive Gaussian noise, then ${\text{lim}}_{M\to \infty }{T}_{\sigma }^{M}f$ exists and is close to the limit for the approximating Gaussian system (SI Text, Gaussian and Near-Gaussian Analysis of Iterated Importance Sampling). These Gaussian and near-Gaussian situations also demonstrate that the compactness conditions for Theorem 2 are not always necessary. In the case $N=1$, IF2 applies to the more general class of latent variable models. The latent variable model, extended to include a parameter vector that varies over iterations, nevertheless has the formal structure of a POMP in the context of the IF2 algorithm. Some simplifications arise when $N=1$ (SI Text, Iterated Importance Sampling, Gaussian and Near-Gaussian Analysis, and A Class of Exact Non-Gaussian Limits) but the proofs of Theorems 1 and 2 do not greatly change.

A variation on iterated filtering, making white noise perturbations to the parameter rather than random walk perturbations, has favorable asymptotic properties (3). However, practical algorithms based on this theoretical insight have not yet been published. Our experience suggests that white noise perturbations can be effective in a neighborhood of the MLE but fail to match the performance of IF2 for global optimization problems in complex models.

The main theoretical innovation of this paper is Theorem 2, which does not depend on the specific sequential Monte Carlo filter used in IF2. One could, for example, modify IF2 to use an ensemble Kalman filter (20, 34) or an unscented Kalman filter (35). Or, one could take advantage of variations of sequential Monte Carlo that may improve the numerical performance (36). However, basic sequential Monte Carlo is a general and widely used nonlinear filtering technique that provides a simple yet theoretically supported foundation for the IF2 algorithm. The numerical stability of sequential Monte Carlo for the extended POMP model constructed by IF2 is comparable, in our cholera example, to the model with fixed parameters (SI Text, Consequences of Perturbing Parameters for the Numerical Stability of SMC and Fig. S3).