Denoising the Speaking Brain: Toward a Robust Technique for Correcting Artifact-Contaminated fMRI Data under Severe Motion

Abstract

A comprehensive set of methods based on spatial independent component analysis (sICA) is presented as a robust technique for artifact removal, applicable to a broad range of functional magnetic resonance imaging (fMRI) experiments that have been plagued by motion-related artifacts. Although the applications of sICA for fMRI denoising have been studied previously, three fundamental elements of this approach have not been established as follows: 1) a mechanistically-based ground truth for component classification; 2) a general framework for evaluating the performance and generalizability of automated classifiers; 3) a reliable method for validating the effectiveness of denoising. Here we perform a thorough investigation of these issues and demonstrate the power of our technique by resolving the problem of severe imaging artifacts associated with continuous overt speech production. As a key methodological feature, a dual-mask sICA method is proposed to isolate a variety of imaging artifacts by directly revealing their extracerebral spatial origins. It also plays an important role for understanding the mechanistic properties of noise components in conjunction with temporal measures of physical or physiological motion. The potentials of a spatially-based machine learning classifier and the general criteria for feature selection have both been examined, in order to maximize the performance and generalizability of automated component classification. The effectiveness of denoising is quantitatively validated by comparing the activation maps of fMRI with those of positron emission tomography acquired under the same task conditions. The general applicability of this technique is further demonstrated by the successful reduction of distance-dependent effect of head motion on resting-state functional connectivity.

Introduction

Extracting valid biological signals in the presence of complex and often overwhelming sources of artifacts (Caparelli, 2005) has always been a vexing problem for functional magnetic resonance imaging (fMRI) – the most popular neuroimaging technique for mapping brain activity. Unfortunately, while a proliferating number of fMRI studies have appeared over the past two decades, the impact of imaging artifacts in cognitive neuroscience research may have been significantly underestimated. Recently, increasing attention has been paid to this issue because neglecting it may have led to spurious results and misleading theories arising from artifacts correlated with experimental manipulations (Deen and Pelphrey, 2012). For example, it was found that a leading theory on the cause of autism (Power et al., 2010) might have been undermined by a systematic difference in the amount of head motion between subject groups (Power et al., 2012). Similar investigations (Mowinckel et al., 2012; Van Dijk et al., 2012) also identified potential confounds in an fMRI study that had proposed a novel mechanism for cognitive decline in normal aging (Andrews-Hanna et al., 2007).

Although vigorous discussions on this issue have now been mostly focused on head motion effects in resting-state connectivity (e.g., Power et al., 2014; Satterthwaite et al., 2012; Yan et al., 2013), it actually has much broader impact on the entire range of fMRI experiments. The confounding effects of stimulus correlated motion have long been recognized (Hajnal et al., 1994) in the analysis of task-based activity. In the most severe cases, e.g., studies of continuous overt speech production, researchers need to rely on other imaging techniques instead of conventional fMRI (Kemeny et al., 2005), due to the heavy distortion of blood oxygenation level dependent (BOLD) signals caused by various movement-related mechanisms (Barch et al., 1999; Birn et al., 1998).

Until now, one of the most commonly used methods for dealing with motion-related artifacts is a technique called scrubbing (Power et al., 2012), also known as frame or volume censoring (Fair et al., 2012; Power et al., 2014), which identifies and rejects noise-contaminated images based on a set of criteria for estimating the degree of motion or amount of artifactual changes in image intensity: e.g., framewise displacement (FD), an empirical sum of the rigid-body motion between consecutive images in all directions; DVARS, a whole-brain measure of the temporal derivative (D) of image intensity computed by taking the root-mean-square variance across voxels (VARS). Although this method is straightforward to understand and easy to apply, it has at least three apparent limitations: 1) statistical power is reduced because of the rejection of images, especially when there is a significant degree of motion present in the data; 2) artifacts with potential detrimental effects, though not meeting the threshold for rejection, still exist in the remaining images; 3) inability to derive continuous time series may jeopardize analytical methods that depend upon on an unbroken temporal sequence of images, e.g., methods utilizing causality, periodicity, phase, and entropy measures.

These significant limitations have created a growing demand for development of a robust technique – whether data-driven or model-based – that can thoroughly remove all major sources of artifacts, and, critically, can preserve the integrity of continuous fMRI time series. Here we present a blind source separation (BSS) technique based on spatial independent component analysis (sICA) that addresses these demands. We believe that it represents an effective solution for the following two reasons.

First, a BSS technique eliminates the need to obtain accurate predictor measurements or to establish quantitative relationships between motion predictors and imaging artifacts, both of which are required in model-based denoising. This feature is particularly important given the complex and nonlinear mechanisms by which the fMRI artifacts are generated (Caparelli, 2005). For example, the use of Volterra expanded rigid-body alignment parameters as nuisance covariates (which is a typical example of a general class of model-based denoising methods called nuisance variable regression; Lund et al., 2006) can reduce certain effects of head motion such as the spin history effect (Friston et al., 1996), but fails to account for other mechanisms of residual head motion such as susceptibility-by-motion interaction (Andersson et al., 2001; Wu et al., 1997), or effects due to non-rigid motion that are present in only a fraction of slices during multislice echo planar imaging (EPI). Another popular denoising method, RETROICOR (Retrospective Image-Based Correction; Glover et al., 2000), removes physiological noise based on predictors computed from auxiliary cardiac and respiratory recordings. But its effectiveness in practical application often suffers from inaccuracies in cardiac/respiratory peak detection caused by measurement noise of these auxiliary recordings.

Second, because sICA optimizes spatial rather than temporal independence, and utilizes higher-order statistics rather than simple correlation (Calhoun and Adali, 2006), it is ideally suited for the removal of task-correlated motion, which inevitably affects many of the interactive tasks requiring either overt motor (Field et al., 2000) or verbal (Barch et al., 1999) responses. These are typical instances in which a regression model fails to give an unbiased estimate due to multicollinearity between artifacts and effects of interest (Johnstone et al., 2006).

However, certain features of the BSS approach have prevented the wide adoption of sICA as the method of choice for fMRI denoising. One major obstacle has been the lack of a common ground truth for identifying “what is signal and what is noise” (McKeown et al., 2003). While the neural mechanisms of signal components may vary experiment by experiment, each type of structured noise should have common characteristics that can be systematically studied according to their physical or physiological mechanisms (e.g., those described in Lund et al., 2006). Such a quantitative and mechanistic classification scheme has yet to be established, although an early publication (McKeown et al., 1998) included some qualitative descriptions of a very limited number of stereotyped components. Another study (Kelly et al., 2010) attempted to characterize sICA components by highly subjective and often ambiguous visual appearances such as the “spottiness” and “peripheralness” of component maps or the frequency spectra and spike distributions of component time courses, without any concrete measures related to their mechanisms of generation. A classification scheme purely based on these visual appearances may yield misleading results even if the inter-rater agreement is high. This is because common errors among raters may be driven by spatial overlaps between focal artifacts and cortical structures or by temporal similarity between task-correlated motion and cerebral activity.

The second, closely related issue is the need to develop a reliable computational method to automate the binary classification of signal and noise components. There have been several published studies aimed at resolving this issue, but their practical utility is generally limited by some common problems. First, due to the lack of a ground truth, the accuracies of these methods were either completely untested (Kochiyama et al., 2005; Kundu et al., 2012; Thomas et al., 2002) or only tested against the subjective classification scores of one or two human experts whose operational criteria or inter-rater reliability were often not reported (Bhaganagarapu et al., 2013; De Martino et al., 2007; Perlbarg et al., 2007; Tohka et al., 2008). Second, the quantitative measures (i.e., features) used for classification, which are usually based on the temporal (Kochiyama et al., 2005; Perlbarg et al., 2007; Rummel et al., 2013), spectral (Thomas et al., 2002), spatial or combined (Bhaganagarapu et al., 2013; De Martino et al., 2007; Tohka et al., 2008) properties of each component (as an exception, see Kundu et al., 2012), either were arbitrarily selected or had limited applicability due to an uncommon experimental setup (Kochiyama et al., 2005; Kundu et al., 2012; Thomas et al., 2002). A systematic method for individual feature selection is still lacking for the binary classification of sICA components. Third, the thresholds of these classification features were determined by arbitrary tuning (Kundu et al., 2012; Perlbarg et al., 2007; Rummel et al., 2013) or supervised learning (De Martino et al., 2007; Tohka et al., 2008) based only on a few pre-labeled datasets, thus the generalizability of these methods may be unreliable due to the variation of ICA components across datasets.

The next unresolved question is: by what means is it possible to effectively validate the results of denoising? This is especially critical for a BSS technique such as sICA because the signal-noise separability of fMRI data after source decomposition is largely untested. Since one of the most problematic issues caused by imaging artifacts is the potential introduction of both false positives and false negatives, the effectiveness of denoising should not be solely evaluated by the increase or decrease of task-based activity or resting-state connectivity in the absence of an absolute reference. This appears to be another common problem in the previous investigations (e.g., Kundu et al., 2012; Tohka et al., 2008).

In brief, previous implementations of sICA as a data-driven denoising approach, while theoretically sound and well intentioned, have essentially remained conceptual. The primary goal of this study is to present a robust technique, as well as a complete and general framework for empirical evaluation of existing and future sICA-based denoising techniques, by thoroughly resolving each of the fundamental issues outlined above.

One of the important methodological advances represented by our technique is based on the novel observation that by expanding the analysis mask of sICA to whole-head coverage, fMRI intensities in extracerebral soft tissues (e.g., muscles, arteries, ocular structures, etc.) or air cavities (e.g., larynx and frontal sinus) where artifacts may originate, can be directly revealed in the same components that contain artifacts within brain tissue (Fig. 1b). These extracerebral noise sources, which are usually obscured by their low intensity in other types of analysis, not only provide salient spatial information for the classification of a variety of noise components, but also help identify their potential mechanisms of generation.

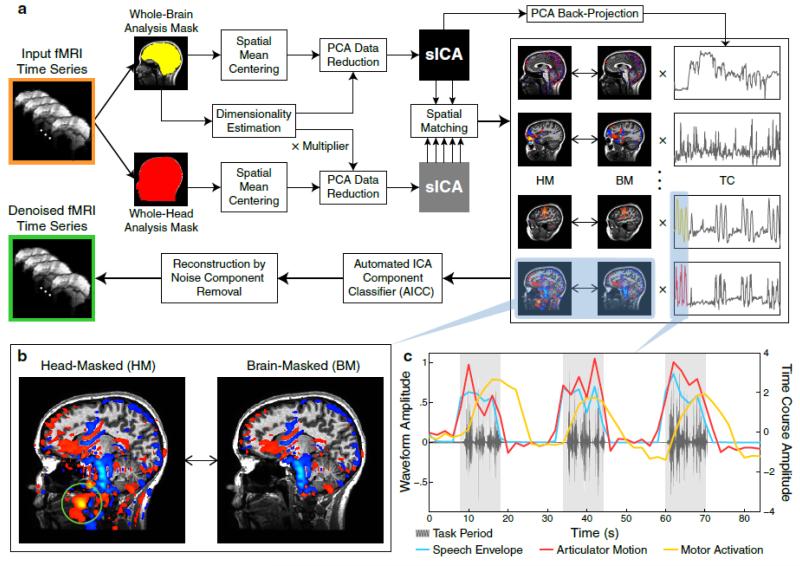
Fig. 1. A Data-Driven Denoising Technique for fMRI.

(a) A schematic workflow depicting the entire denoising procedure. The centerpiece is a dual-mask sICA method that involves separate decompositions within a brain mask (BM) and a head mask (HM) applied to the sagittally acquired fMRI time series of each individual subject. In addition to the voxels belonging to the BM, the HM also includes extracerebral voxels, which contain signals indicating the location where artifacts originate from. The result of dual-mask decompositions is a set of spatially matched HM and BM component maps with the corresponding time courses computed from the BM components. See Materials and Methods for the description of each processing step.

(b) An enlarged display of the HM and BM component maps for a noise component associated with the movement of articulators during an overt speech production task. The green circle indicates its source of origin inside the oral cavity.

(c) A closer look at time course segments of articulator motion (red) and motor activation (yellow) components overlaid on the acoustic waveform (grey) of the recorded speech. Both time courses were correlated with speech production. However, the time course of articulator motion instantaneously fluctuates with the speech envelope (blue), which provides a gross estimate for the degree of articulatory motion; whereas the time course of motor activation has typical characteristics of neural/hemodynamic responses – smoother and delayed peaks, followed by commonly observed undershoots.

Moreover, we are also able to corroborate these mechanisms by examining the temporal correlations between component time courses and existing measurements of physical or physiological motion (Fig. 1c). Although we do not recommend using these auxiliary measurements directly for model-based denoising due to the various reasons mentioned above (measurement or prediction inaccuracy, multicolinearity, etc.), they nevertheless play an important role in identifying the potential source mechanisms after BSS.

Crucially, our technique incorporates a dual-mask method with spatially matched components in both a whole-brain analysis mask and a whole-head analysis mask (Fig. 1a). As a key bridge toward a mechanistic classification of sICA components, this innovative procedure not only overcomes a known trade-off between the analysis mask size and the spatial discriminatory power of ICA (Formisano et al., 2002), but also allows a more accurate estimation of component time courses that represent the intracerebral dynamics of interest.

The mechanistic classification scheme derived from the above methods also provides a methodological basis for designing and validating automated computer algorithms aimed at binary component classification. Furthermore, rather than relying on arbitrarily selected features or algorithms with limited applicability, we present a general framework for guiding the design of automated classifiers, and for evaluating their performance and generalizability. In particular, the two quantitative criteria that we proposed for feature selection – sensitivity index and bimodality coefficient – can be applied to estimating the performance of a wide range of classification features. The machine learning classifier developed with our technique, which is based on a simple set of spatial features and an unsupervised expectation maximization algorithm, achieves a near perfect accuracy and sufficient generalization for fully-automated (i.e., without further needs for human verification) and broad (i.e., in a variety of experimental paradigms) applications.

As a proof of principle, the power of our technique was demonstrated in the context of imaging continuous overt speech production. The reason for selecting speech production for our primary investigation is not only because it represents one of the most egregious examples of experimentally induced artifacts, well documented by a series of studies (Barch et al., 1999; Birn et al., 1998; Kemeny et al., 2005; Mehta et al., 2006), but also due to the availability of a true estimate of task-based activity for evaluating the effectiveness of denoising.

A true estimate of task-based activity cannot be obtained by using BOLD fMRI alone because most of the artifacts are intrinsically associated with the physical aspects of magnetic fields employed by the technique (e.g., field inhomogeneity and magnetic susceptibility; Caparelli, 2005). In this study, positron emission tomography (PET) – the de facto “gold standard” for imaging continuous overt speech production (Kemeny et al., 2005) – was used as a vehicle for cross-modal validation, since these artifacts are clearly absent in PET (although this imaging modality is less commonly used nowadays in cognitive research due to radiation dose limitations and a relatively poor temporal resolution; see Supplementary Appendix A for more details on why and how to use PET as a reference measure for our purposes).

Finally, the general applicability of our technique was investigated using the resting-state data published by Power et al. (2012). Although a true estimate of resting-state connectivity is currently not available, several quantitative measures, such as FD, DVARS, and the distant-dependent effect of head motion, have been systematically investigated in a series of studies (Fair et al., 2012; Power et al., 2012; Power et al., 2014). Hence, they can be utilized as endpoints to compare the performance of the present technique with previous methods in a quantitative way.

Materials and Methods

Subjects and Experimental Paradigm

Eighteen healthy, right-handed, native English speakers (7 males, 11 females; aged 20-32 years) participated in this study. All participants were scanned in an fMRI experiment and 17 of them participated in a subsequent PET experiment. Approval for these experiments was obtained from the institutional review board of the National Institutes of Health.

Prior to the experiments, participants were trained to be familiar with all stimulus materials including narrative stories and pseudowords. Each of the narrative stories was represented by a set of three picture cards. Each of the pseudowords was a non-lexical consonant-vowel string that conformed to the phonotactic rules of English.

The fMRI experiment, including a total of 903 acquired volumes used for data analysis, was split into four runs. The first three runs each contained eight, 30s task blocks interspersed with 18s rest intervals. Each of the four task conditions – production and comprehension of either narratives or pseudowords – was presented in six blocks that were equally distributed across runs and randomly ordered within each run. The last run contained only narrative tasks in 10s block duration, separated by 16s rest intervals. Due to the shortened block duration, the beginning, middle, and end of each story were separated into three consecutive blocks. The stories used for these tasks and the task modality (production and comprehension, each containing four stories distributed in 12 blocks) were both arranged in random orders.

The PET experiment contained 15 scans, which were organized in three cycles (five scans per cycle). Each cycle started with a resting scan followed by scans containing each of the four speech tasks in a random order. Scanning was automatically triggered by the detection of radiotracer in the brain and continued for 60 seconds. During each cycle, the time interval between injection and scan onset was measured in the resting scan to estimate the vein-to-brain time, which was used to calibrate the post-injection time of task onset. As a result, each speech task always began at approximately 8 seconds before the onset of scanning.

Image Acquisition Parameters

T2*-weighted BOLD fMRI images were acquired on a General Electric (GE) Signa HDxt 3.0 Tesla scanner (GE Healthcare, Waukesha, WI, USA) with an 8-channel brain coil. Foam padding was applied inside the coil to minimize head motion. A single-shot gradient-echo EPI sequence was used. The detailed scanning parameters were as follows: repetition time (TR) = 2000 ms, echo time (TE) = 30 ms, flip angle = 90°; matrix size = 64 × 64, field of view (FOV) = 227 mm; ASSET (Array Spatial Sensitivity Encoding Technique) parallel imaging factor = 2. Whole-brain coverage was achieved for all subjects using 40 interleaved sagittal slices with a thickness of 4 mm. Phase encoding was oriented in the anterior-posterior direction. The first four images of each scanning time series were discarded to avoid T1 saturation effects. In addition to the functional data, a T1-weighted high-resolution structural MRI image was acquired sagittally using a 3D MPRAGE (Magnetization Prepared Rapid Acquisition Gradient Echo) sequence.

The benefits of using sagittal image acquisition are three-fold: 1) off-plane motion is minimized because the prominent nodding motion during speech – primarily in the inferior-superior and pitch directions (Barch et al., 1999) – is confined to the sagittal plane; 2) it also facilitates the use of in-plane image registration for correcting non-rigid motion (Huang et al., 2002); 3) it allows the squared in-plane FOV to cover nearly the whole head – including the tongue body and soft tissues surrounding the upper airways, without sacrificing the temporal resolution.

PET images were acquired on a GE Advance scanner. A thermoplastic face mask was molded for each subject and attached to the scanner bed to maintain head position throughout the experiment. An axial FOV of 153 mm was collected, which allowed for whole-brain coverage, and contained 35 slices with a reconstructed resolution of 6.5 mm FWHM (Full Width at Half Maximum) in x-, y- and z-directions. For each scan, 10 mCi of H₂¹⁵O was injected intravenously. Injections were separated by 5 minute intervals.

Measurements of Head Motion, Physiological and Acoustic Data

During the fMRI scans, head motion was monitored in real time by six rigid-body alignment parameters computed with a real-time image registration algorithm (Cox and Jesmanowicz, 1999). A scanning run was repeated if the cumulative movements in any directions exceeded 4 millimeters (translational) or 4 degrees (rotational). Cardiac and respiratory states were monitored respectively by a plethysmographic pulse oximeter installed on the left index finger and a pneumatic belt placed around the abdomen. These physiological data were time-locked to the onset of each fMRI time series and recorded at a sampling rate of 40 Hz. During the entire experiment, overt verbal responses from the production tasks were continuously recorded by a FOMRI-II noise canceling optical microphone (Optoacoustics, Or-Yehuda, Israel) at a sampling rate of 44.1 kHz. TTL (transistor-transistor logic) pulses were utilized to synchronize the timing between fMRI, stimulus presentation, and acoustic recording.

The speech envelope of the acoustic recording, which served as a reference time series for validating articulator motion components, was computed from the root mean square of all the waveform samples within each 2-s TR. Rigid-body alignment parameters were recomputed offline using the same algorithm that was used for online monitoring. Their first-order Volterra series, including 24 predictors, were used as reference time series for validating head motion components. The reference time series for physiological noise components were constructed using the first and second order Fourier series expanded from the cardiac and respiratory phases at the onset of each TR. See Lund et al. (2006) for more information on the mathematical implementation of the head motion and physiological noise predictors. Notably, instead of being used for model-based denoising, these time series were utilized here only for validating the physical or physiological mechanisms of sICA noise components.

Functional and Mask Image Preparation before Denoising

Prior to the denoising procedure, the fMRI images were spatially aligned by both in-plane and rigid-body registration algorithms in AFNI (Cox, 1996). The former was applied before, and the latter after, slice-time correction.

The high resolution structural T1 image acquired in the same scanning session was co-registered to the fMRI images using a mutual-information based algorithm (Maes et al., 1997). The segmentation and normalization of the structural image was then computed in a unified framework based on the tissue probability maps provided by SPM5 (Ashburner and Friston, 2005). Following segmentation, the resulting grey and white matter tissue class images were added up and resampled to the fMRI data space for creating a brain mask (BM) image. In addition, a head mask (HM) image was created from the structural image prior to segmentation via intensity thresholding, spatial clustering and resampling.

Procedure of the Denoising Technique

The denoising procedure includes three essential steps: dual-mask sICA, component classification, and reconstruction of the denoised dataset.

Dual-Mask sICA

The sICA for brain-masked (BM) and head-masked (HM) data were implemented by the Infomax algorithm (Bell and Sejnowski, 1995) in GIFT (Group ICA fMRI Toolbox; Calhoun et al., 2001). Similar results can be obtained using other algorithms such as FastICA (Hyvarinen and Oja, 2000).

The order of source dimensionality for the BM data was first estimated by the minimum description length (MDL) criterion (Li et al., 2007). MDL was not used for the HM data because it was frequently impossible to identify a reliable local minimum. We assume that the relationship between the BM and HM orders is approximately linear under the same experimental settings. The HM order can be determined by applying a fixed multiplier (2.5 for the current study) to the estimated BM order, which was heuristically determined by optimizing the spatial correlation between the BM and HM component maps (see Fig. S1 in Supplementary Data). Given the extra spatial coverage included in the HM, a much higher order is required for achieving a comparable spatial discriminatory power. An underestimation of this order may result in false positives for noise component detection because of the merging of signal and noise into the same components.

Prior to the decompositions, ICA specific preprocessing steps (including spatial mean centering, whitening and dimensionality reduction) were applied to reduce the complexity of the model (Hyvarinen and Oja, 2000). Whitening and dimensionality reduction were achieved with principal component analysis (PCA). Centering is an integral part of PCA that minimizes the mean square error in approximating the data.

After the decompositions, spatial matching between the BM and HM components was confined to voxels within the brain mask and assessed by the absolute value of their Pearson’s correlation coefficient. The matching was non-exhaustive and non-unique. There were extra HM components that were not matched to BM components and were simply discarded. In addition, the same HM component could potentially be matched to multiple BM targets if they completely or partially merged into a single component during the HM decomposition, but this rarely occurred because of the dimensionality multiplier applied to HM data. To improve the stability of source decomposition and the reliability of spatial matching, the sICA for both the BM and HM data were repeated for multiple runs with random initial weights (see Supplementary Appendix B and Fig. S2 for more details).

Component Classification

The mechanistic classification scheme used here is primarily based on the combined use of spatial information provided by the HM component and the correlations between the BM component time course and three types of reference time series (speech envelope, rigid-body alignment parameters, RETRICOR predictors). By this means, a component is labeled as noise only if it possesses the clear characteristics of one of the five following noise categories: articulator motion, head motion, physiological motion, eye motion, and other structured noise; the remaining components are all labeled as signal. As such, a subdivision of noise components is mandatory even though the goal is for binary signal/noise classification. Due to the complexity of spatiotemporal information involved in this subdivision, it was performed by two human experts instead of a complete automated procedure. However, the identification of the objective mechanisms of artifact generation based on their extracerebral origins and reference motion measures fundamentally distinguishes this approach from previous methods that are purely based on subjective visual appearances (Kelly et al., 2010). Afterward, the classification scores of one of the experts were used as the ground truth for validating our binary automated independent component classifier (AICC). The other set of scores were used to evaluate inter-rater agreement.

AICC is based on a set of features that were developed from the spatial characteristics of noise components obtained during the process of mechanistic classification, and designed for simple computational implementations (outlined in Supplementary Appendix C.1). Temporal information is not used in AICC for the following reasons: 1) it ensures a broader application of the technique by eliminating the needs for auxiliary (e.g., cardiac, respiratory, etc.) measurements; 2) it improves the generalizability of the algorithm (see Supplementary Appendix C.1 for an explanation); 3) although temporal information is essential for the accurate subdivision of noise components, it may be redundant for binary signal/noise classification (which will be demonstrated in the Results and Discussion section).

Rather than relying on fine-grained anatomical information, the three primary features of AICC – out-of-brain ratio, scattering degree, and slice-wise variation – measure the relative intensity distributions at different spatial partitions, expressed as the ratios of sum of squared intensities. These features are insensitive to the splitting or merging of components caused by changes in dimensionality. A fourth, complementary feature measures spatial correlations with a set of noise templates created from the boundary of the brain mask or by a secondary sICA applied on the learning datasets (here called “flexible templates”, which are comprised of a few noise components with spatial patterns most consistently observed across datasets).

In addition, the above classification features were further evaluated among a number of existing and newly proposed spatial measures based on the combined use of two feature selection criteria (see Supplementary Appendix C.2 for more details). These selection criteria follow two principles: 1) a feature with high performance should separate the signal and noise components distantly along its distribution range, represented by a high sensitivity index (SI > 2); 2) the ideal probability distribution of a feature should be bimodal, with clearly separable peaks, represented by a good bimodality coefficient (BC >> 0.555; we recommend at least 0.6). Notably, SI is a bias-free and nonparametric measure independent of the threshold as well as the shape of signal/noise distributions. These properties make it a robust and universal criterion for individual feature selection. Furthermore, the practical performance of a feature in machine learning should also depend on a clearly distinguishable boundary between the binary signal/noise classes. Hence, BC, a measure for bimodality, provides very useful information for estimating the ambiguity of learning even without the need for pre-labeling the components.

A component is classified as “noise” if any of the four features outlined above meets the threshold determined by an unsupervised expectation maximization (EM) algorithm. Once the thresholds are determined, the decision rules of the four features, which can be in any order, are applied sequentially in a binary decision tree. The remaining components filtered by the decision tree are classified as “signal”. More details of the EM algorithm, as well as several other popular learning algorithms with which it has been compared (in terms of their performance and generalizability), are summarized in Supplementary Appendix C.3.

Sensitivity and specificity scores of AICC were computed by the percentages of true positives and true negatives identified by AICC among the total numbers of noise and signal components in the ground truth of classification. Detection of noise components by AICC is defined here as “positive”.

Reconstruction by Noise Component Removal

Reconstruction of the denoised dataset was based on the spatial maps and time courses of the BM components according to the classification result of AICC. The denoised fMRI time series (X_R) was computed by subtracting the noise components from the input fMRI time series (X):

$$X_R=X-A_N\cdot S_N,$$

where S_N is the estimated source matrix of the noise components selected by AICC; A_N consists of the time courses of these noise components computed by a PCA back-projection from the estimated ICA mixing matrix (Calhoun et al., 2001).

Importantly, all the processing steps in our denoising procedure were performed at the single-subject, single-session level. There are several notable advantages to this approach: 1) signal-noise separation is maximized by avoiding the blurring caused by spatial interpolations (which take place during spatial normalization and smoothing) within each subject and anatomical variations across subjects, both of which occur in group ICA; 2) since it utilizes only one step of data reduction, considerably more spatial variance can be retained (usually above 99.95%) than is the case in multi-level group data reduction; 3) subsequently, this approach eliminates an often less accurate recomputation of each subject’s components from the group ICA components (Calhoun et al., 2001); 4) if multiple fMRI time series using the same imaging parameters are collected for each subject, they can be temporally concatenated and treated as a single session to improve the accuracy of decomposition.

Post-Denoising fMRI Data Processing

After denoising, both the denoised and uncorrected (processed by head motion and slice-time correction only) fMRI datasets were transformed into a standard brain space by applying the affine plus nonlinear spatial normalization parameters of the structural image. The resulting datasets, with a resampled voxel size of 3×3×3 mm³, were spatially smoothed in AFNI with a stepwise and mask-confined fashion to a target FWHM of 10 mm. Because noise variances were only removed for voxels within the BM during denoising, masked smoothing prevented voxels at the brain boundary from being contaminated by artifacts outside the brain.

PET Image Processing

The preprocessing of PET images included the following steps: 1) spatial alignment of all images within each subject; 2) transformation into a standard brain space by applying the combined parameters between a mutual-information based PET-MRI co-registration and the spatial normalization of the MRI image; 3) spatial smoothing with a fixed 8 mm FWHM Gaussian kernel to achieve a final smoothness of approximately 10 mm ($\approx \sqrt{{6.5}^2+8^2}$) FWHM that matched the final smoothness of the fMRI datasets; 4) masking and proportional scaling to a whole-brain mean of 100; 5) converting image intensities into percent signal change by subtracting a mean image of the three resting scans from all task scans. All of these procedures were implemented in MATLAB (The MathWorks, Inc.) based on functions provided by the SPM8 software.

Statistical Parametric Mapping at the Individual and Group Levels

For each subject, the images within each preprocessed fMRI time series were fitted by a general linear model (Worsley and Friston, 1995). The main predictors in this model were a set of hemodynamic response functions resulting from the convolution of boxcar functions representing task on/off states with a canonical BOLD impulse response. Additionally, the whole-brain mean signal was used as a nuisance covariate to account for CO₂-related global hemodynamic fluctuations (Birn et al., 2006; Macey et al., 2004), which is justifiable by the low signal to global noise level (Chen et al., 2012) of the fMRI data acquired in continuous overt speech production ^{Footnote 1}. It is critical to include this covariate because the sICA method used for denoising is not sensitive to such globally distributed effects. This is likely due to an intrinsic limitation of sICA as well as a direct consequence of spatial mean centering performed prior to sICA.

The above model was computed for both the denoised and uncorrected datasets. The degrees-of-freedom reduction due to noise component removal (overall 7.1% across 18 datasets) at the individual level was not taken into account because we were only interested in the resulting fit coefficients, which were subsequently used as inputs for group analysis.

The group-level SPMs comparing fMRI and PET were generated using standardized signal change (cf. Supplementary Appendix A). This measure makes it possible to perform quantitative comparisons across imaging modalities on the datasets collected from the same cohort of subjects based on the same set of cognitive tasks, minimizing the possible discrepancies caused by task or statistical threshold differences. The analysis first involved a whole-brain voxel-wise ANOVA that compared the standardized signal change between uncorrected fMRI, denoised fMRI and PET datasets, and between the four 30s task conditions within each imaging dataset. Then the analysis was narrowed down to a target region of interest (ROI) selected by its location of noise susceptibility as well as importance in functional roles. Again, this analysis benefited from the use of standardized signal change, since the activation data from fMRI and PET can be entered into the same ANOVA model after variance equalization.

Denoising and Analysis of Resting-State fcMRI Data

The entire image processing procedure applied on the 22 resting-state datasets (for subject information and image acquisition details, see Power et al., 2012) was similar to that applied on our speech datasets. The only differences are described as follows. First, in-plane registration was not applied on the functional images as they were acquired with oblique axial slices that are not optimized for confining head motion into the slice direction; and the rigid-body registration was computed using SPM8 instead of AFNI. Second, MDL dimensionality estimate for the BM data may fail to detect a local minimum in some datasets with severe head motion. In such cases, the order of BM sICA was capped at the 40% of total image number instead of using MDL to avoid a dramatic loss of temporal degrees of freedom (DF). The overall DF reduction after sICA denoising is 32.2% across all the resting-state datasets, which is comparable to an overall 29.1% DF reduction caused by scrubbing in our analysis.

The procedures for scrubbing and ROI-based functional connectivity analysis were similar to those documented in Power et al. (2012) except for the following differences: 1) DVARS was computed prior to global signal removal and filtering on the uncorrected or denoised data after spatial normalization and smoothing; 2) only the whole-brain mean was used for global signal removal via GLM in our analysis whereas ventricular and white-matter means were also used by Power et al. (2012); 3) a low-pass equiripple finite impulse response filter (pass edge: 0.08 Hz; stop edge: 0.12 Hz; attenuation: 60 dB) was applied on the residual time series after global signal removal, which had been high-pass filtered at 128 sec (≈ 0.008 Hz) during the GLM computation in SPM8; 4) twenty-seven out of the 264 spherical ROIs (Power et al., 2012) were excluded during the computation of correlation matrices as they contained voxels outside the brain, likely due to a difference in the spatial normalization procedure.

Results and Discussion

Characterization and Mechanistic Classification of Structured Noise Components

The denoising technique presented here starts with and builds upon the fundamental understanding of the spatiotemporal characteristics of sICA components, which includes three aspects. First, descriptive characteristics for defining each noise category are derived from more than a thousand components across 18 datasets collected during different task states (speech production/comprehension and resting fixation). Second, a set of spatial features are derived from the above characteristics for the purpose of binary signal/noise classification (Fig. 2). These clearly observable features not only facilitate human classification, but can be used to obtain quantitative measures that automate this procedure with machine learning. Third, for the major noise categories, we also provide mechanistic validations based on temporal correlations with reference time series, which are derived from physical or physiological motion measures related to each category.

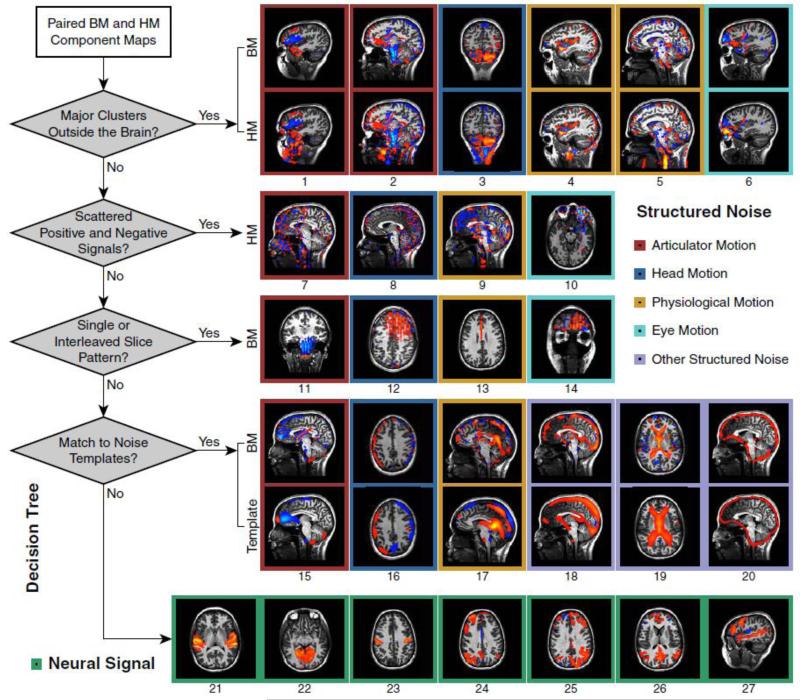
Fig. 2. A Component Classification Scheme Based Only on Spatial Features.

On the left side is a binary (“signal” or “noise”) decision tree diagram containing four spatial features that can be utilized for machine learning. This simple yet effective classification method is capable of identifying all major sources of imaging artifacts. Examples of typical noise and signal components are shown in the image panels on the right. Individual sources of noise components (1-20) are described in the text. General categories are indicated by colors at the perimeter of each box. Note that the mapping between the four spatial features and the five noise categories are multi-to-multi. Labels for commonly observed neural signal components are listed as follows: (21) auditory; (22) medial primary visual; (23) motor; (24) left executive-control network; (25) right executive-control network; (26) default mode network; (27) perisylvian language network. The spatial distributions of these signal components bear a strong similarity to the functional networks documented by previous group ICA studies (e.g., Calhoun et al., 2008).

The typical temporal characteristics of articulator motion components – a special category of artifacts that are uniquely observed in overt speech production – have been illustrated in Fig. 1c. Their spatial properties are described in Supplementary Text S1.

Since our primary goal is to design a comprehensive and general-purpose denoising technique, the classification of noise components should certainly encompass all common categories of fMRI artifacts – in particular, head motion and physiological noise.

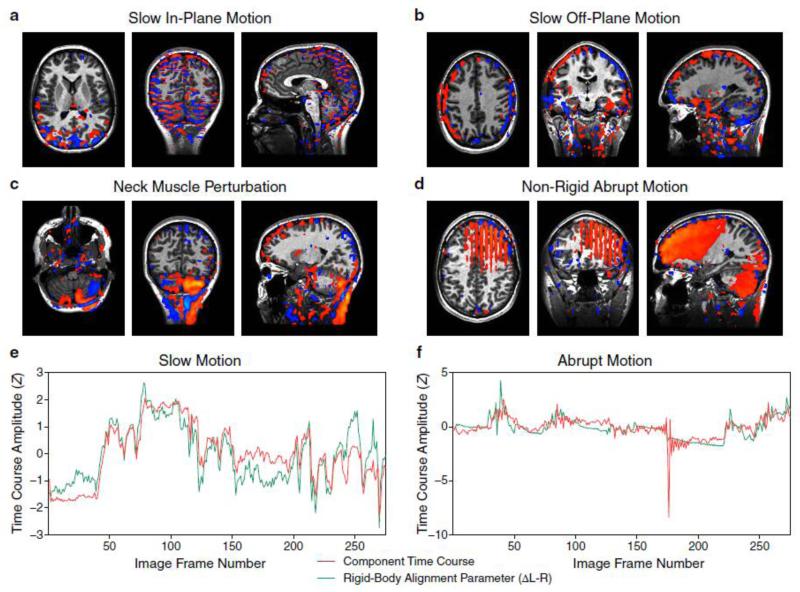
Residual head motion, a ubiquitous source of fMRI artifact known to exist even after perfect spatial realignment (Friston et al., 1996), comprises a majority category of noise components. These can be further subdivided into at least four types (Fig. 3a-d and Fig. S4). The first three types are related to slow head motion, and can be distinguished by both their spatial characteristics and the subsets of temporally correlated rigid-body alignment parameters. The first type – components primarily correlated with in-plane motion, are the most common among all noise components in our data, probably due to the prominent nodding motion during speech production as well as the sagittal image acquisition used in the experimental setup. Their scattered/interspersed spatial characteristics (Fig. 3a and Fig. 2, Panel 8) are distinguishable from the second type – components primarily correlated with off-plane motion (Fig. 3b). The latter may be spatially identified with a predefined template (Fig. 2, Panel 16) or through the use of other spatial features such as out-of-brain ratio and scattering degree as depicted in a decision tree (Fig. 2, left panel). However, further investigation will need to be done to determine the detailed physical mechanisms relevant to these distinct spatial maps, e.g., spin-history effects (Friston et al., 1996). A third, special type of components associated with head motion contains artifacts that appear in the posterior cerebellum (Fig. 3c). This is likely due to a direct perturbation of the static magnetic field (Yetkin et al., 1996) by neck muscle contraction. The time courses of these components are highly correlated with either in-plane or off-plane head motion. It would be hard to spatially differentiate them from real cerebellar activity if head-masked component maps were not provided (Fig. 2, Panel 3). The final type of components in this category, associated with abrupt head motion (Fig. 3f), can be distinguished from slow head motion (Fig. 3e) based on the existence of sharp spikes evident in component time courses, but sometimes not in rigid-body alignment parameters. An interleaved slice pattern may also be observed in their spatial maps (Fig. 3d and Fig. 2, Panel 12). These characteristics are signs of potential non-rigid motion.

Fig. 3. Major Types of Head Motion Components.

(a) Interspersed positive and negative signals associated with slow in-plane motion.

(b) Noise signals associated with slow off-plane motion detected at the edge of brain. For slices collected in the sagittal direction, the signs are inversely related in the left and right hemispheres and between the superior and inferior borders.

(c) Motion artifacts contaminating the fMRI signal from the posterior cerebellum.

(d) An interleaved slice pattern introduced by abrupt in-plane motion. Its unique spatial pattern can be distinguished from other noise categories containing slice-wise variations (e.g., Panel 11, 13, and 14 of Fig. 2) based on large, homogeneous areas of intensity distribution in the affected sagittal slices.

(e) A high degree of correlation between component time courses (red) and rigid-body alignment parameters (green) for slow head motion.

(f) One (or more) sharp spike(s) in the time course showing no correlation with the rigid-body alignment parameters, indicating the likely occurrence of non-rigid abrupt motion.

Another important noise category includes artifacts associated with pulsations of cerebral arteries and cerebrospinal fluid (CSF), which are common types of physiological motion. All the arterial components and a majority of the CSF components are cardiac related, manifesting clear and unique temporal characteristics (Fig. 4a): rapid and quasi-periodic oscillations with near evenly distributed amplitudes over the entire time course. These properties can be quantified by RETROICOR cardiac predictors, i.e., Fourier series constructed from cardiac phases (Fig. 4b). In addition, some CSF components, e.g., those located at the cistern of great cerebral vein (Fig. 2, Panel 17), are weakly correlated with RETROICOR respiratory predictors, reflecting a respiratory influence on CSF pulsations (Friese et al., 2004).

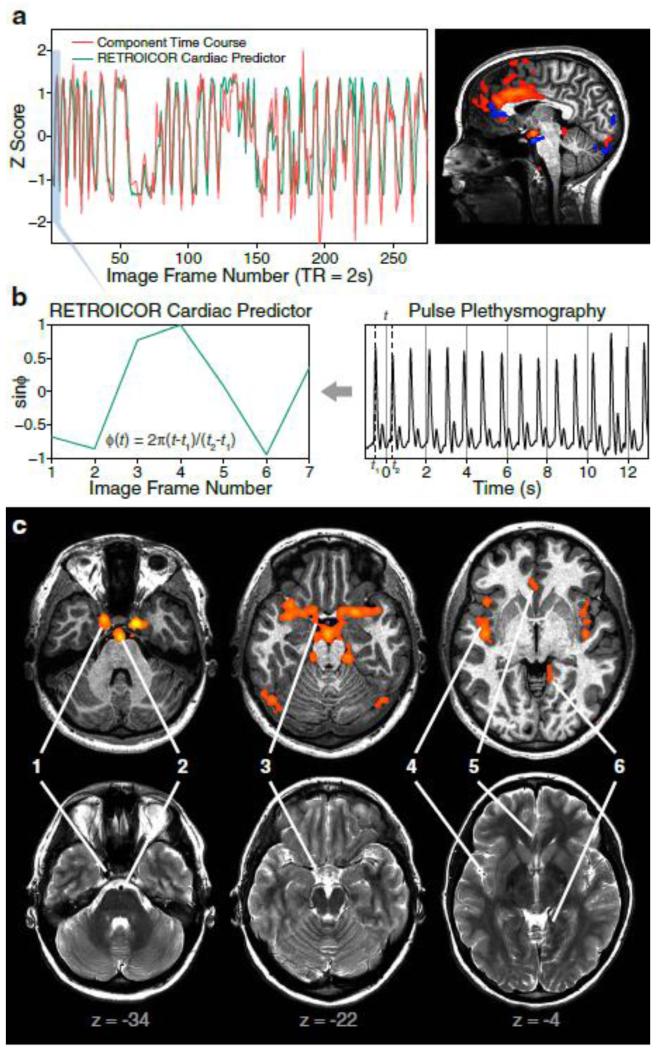
Fig. 4. Noise Components Reflecting Cerebral Artery Pulsations.

(a) Time course and sagittal view of an individual component reflecting the pulsation of the anterior cerebral artery. The component time course (red) faithfully follows the fluctuations of a RETROICOR cardiac predictor (green).

(b) Construction of the RETROICOR cardiac predictor using a first-order Fourier series of the cardiac phase (φ). Note that the constructed time series is less periodic and oscillates at a much lower frequency than the original pulse signals due to an aliasing effect caused by undersampling.

(c) A refined whole-brain representation of cerebral artery pulsations by all such components identified from an individual dataset. Top row: temporal standard deviation map (red-yellow overlay) of fMRI time series reconstructed from cerebral artery pulsation components. Bottom row: the lumens of arteries appear as discrete hypointensities on co-registered fast spin-echo T2 images, which accurately match the locations of fMRI signals in the top row: (1) internal carotid artery; (2) basilar artery; (3) the Circle of Willis; (4) middle cerebral artery; (5) anterior cerebral artery; (6) posterior cerebral artery. Bottom values indicate z-coordinates in MNI (Montreal Neurological Institute) space.

Although slice-time correction is performed prior to sICA, cerebral artery pulsations at different slice locations are usually decomposed into different components. This indicates that the source separation is sensitive to the fine-grained temporal differences in cardiac phases, and also makes it possible to identify the resulting components based on a distinct spatial pattern with intensities distributed only in a single slice (Fig. 2, Panel 13; Fig. 4a, right image panel). In many of the components (Fig. 2, Panel 4), the pulsations of arteries inside the brain (e.g., middle cerebral artery) coexist with extracerebral arteries (e.g., external carotid artery), which can be identified with the dual-mask method. The head-masked components again provide important spatial anchors to avoid the confusion between artifacts caused by artery pulsations and cerebral activity (e.g., due to the spatial overlap between the anterior/middle cerebral arteries and the anterior cingulate or insula). Additionally, cardiac-related CSF pulsations can either be identified by scattered positive or negative clusters within the subarachnoid space and ventricles (Fig. 2, Panel 9), or by the existence of a strong extracerebral cluster in the central canal of the spinal cord (Fig. 2, Panel 5).

The power of sICA for removing cardiac-related effects can also be demonstrated by the marked similarities between the whole-brain distribution reconstructed from arterial components (Fig. 4c) and the spatial map obtained with a model-based RETROICOR method (Dagli et al., 1999). However, there is an apparent advantage to using sICA instead of RETOICOR because the former does not rely on recording pulse plethysmography, which is often noisy in itself due to subjects’ finger or hand movements.

In addition to the three major noise categories defined above, components related to eye motion (Fig. 2, Panel 6, 10, 14) fall into a distinct category. They may originate from physical mechanisms similar to those associated with articulator motion (Beauchamp, 2003). For the convenience of quantitative analysis, the remaining noise components, which only accounts for a small number (Table S1), are combined into a single “other” category. For example, components of dural venous sinuses (Fig. 2, Panel 18) and ventricles (Fig. 2, Panel 19) can be spatially identified by matching to predefined templates although their temporal mechanisms are not clear to us. The boundary of the brain (Fig. 2, Panel 20) also appears as a single component per dataset, which might be related to minor spatial misalignment or interpolation errors (Grootoonk et al., 2000).

There has been a previous discussion on the deterministic and stochastic properties of sICA components (McKeown et al., 2002): specifically, what proportion of components exhibit reproducible spatiotemporal characteristics across datasets? As a noise free ICA model (Hyvarinen and Oja, 2000) is employed in our technique, we hypothesize that the random thermal noise variance may have been taken away primarily by the PCA data reduction step, with a relatively small amount distributed across sICA components in both signal and structured noise categories. In this sense, we claim here that all components are “deterministic” (i.e., mechanistically identifiable, representing either BOLD response or structured noise) so that there are actually no “random” noise components (Thomas et al., 2002) resulting from sICA.

It is this deterministic property that makes it possible for a systematic classification of all components observed in our study. Our results indicate that BOLD response and structured noise are for the most part separated into different components by the dual-mask sICA, and that a majority of the noise components can be clearly assigned to one of the categories defined above in a mechanistic manner. In rare cases where ambiguous components contain significant amounts of both signal and noise, which could result from a significant underestimate of the source dimensionality, they should not be removed for the sake of signal preservation.

The reliability and accuracy of this classification can be proven in the following ways. First, we have been able to evaluate the inter-rater agreement between two human experts who performed the above classification independently. Fleiss’ kappa statistic showed an almost perfect agreement between the two experts in terms of both the binary signal/noise classification (κ = 0.9952, P < 0.0001; disagreed in 2 components out of 1,419) and the subdivision of noise (κ = 0.9648, P < 0.0001; disagreed in 28 components out of 1,164). These data indicate that our taxonomic definitions based on these spatiotemporal characteristics are reliable and consistent across all components in each category.

Second, summary statistics on the temporal correlations between component time courses and reference motion measures were obtained for noise components identified as belonging or not belonging to the three major noise categories as well as for neural signal components (Table 1, right three columns). The components belonging to each noise category showed significantly higher temporal correlations than the other two columns (P < 0.0001 for all two-sample t-tests). These data indicate that the noise categories by our definition are accurately related to distinct physical or physiological mechanisms of artifact generation.

Table 1. Pearson’s Correlation Coefficients between Component Time Courses and Reference Motion Measures.

Means and standard deviations were computed from the maximal absolute correlation values across four runs for each component. Articulator motion and head motion components were pooled across all subjects. Physiological motion components were only pooled across seven subjects in whom cardiac peaks were reliably detected from pulse plethysmography. The right three columns were compared using Student’s t-tests after Fisher’s z’-transformation. Note that some baseline correlations with reference time series were observed for the categories of articulator and head motion. That is. the correlation coefficients of signal components or noise components not belong to those categories are still relatively high. This is because both types of motion can fluctuate with the task on off states in an alternating bos-car design (Fig, 1c).

		Temporal Correlation (Mean±SD)
Target Category	Reference Motion Measures	Noise Components		Signal Components
		Belonging	Not Belonging
Articulator Motion	Speech Envelope	D.546±=0.182	0.309±0.167	0 32±0.133
Head Motion	Vclteira Expanded Rigid- Body Alignment Parameters	0.793±0.115	0.418±0.189	0.458±0.168
Physiological Motion	RETROICOR Predictors	0.497±0.208	0.123±0.042	0.131±0.043

Third, the subdivision of sICA components also gives us an opportunity to measure the amount of temporal variance explained by each signal/noise category (see Inline Supplementary/IS Fig. 1 and Supplementary Text S2). These measures provide quantitative evidence for the validity of classification as well as for the effectiveness of denoising at the individual level. For example, the neural signal components only account for a fairly small percentage of overall temporal variance (IS Fig. 1a). This finding, together with the functional brain networks clearly identified in their component maps (Fig. 2, bottom panels), provides compelling evidence that there is minimal noise remaining in the components identified as signal.

In summary, we provide the first comprehensive mechanistically-based classification scheme that broadly categorizes all major types of noise components (including those specifically related to overt speech production). The associated findings, such as the spatiotemporal characteristics and temporal variance measurements for each category of artifacts, should enhance the understanding of the noise properties of fMRI in general.

Performance and Generalizability of Automated Component Classifiers

Significant drawbacks of the mechanistic classification method performed by human experts are that this approach is time-consuming (typically taking more than an hour for each individual dataset) and requires extensive training of the raters. An accurate and fully automated machine classifier not only dramatically decreases human effort when processing a large number of datasets, but also minimizes potential errors that can be caused by insufficient expertise of the human raters.

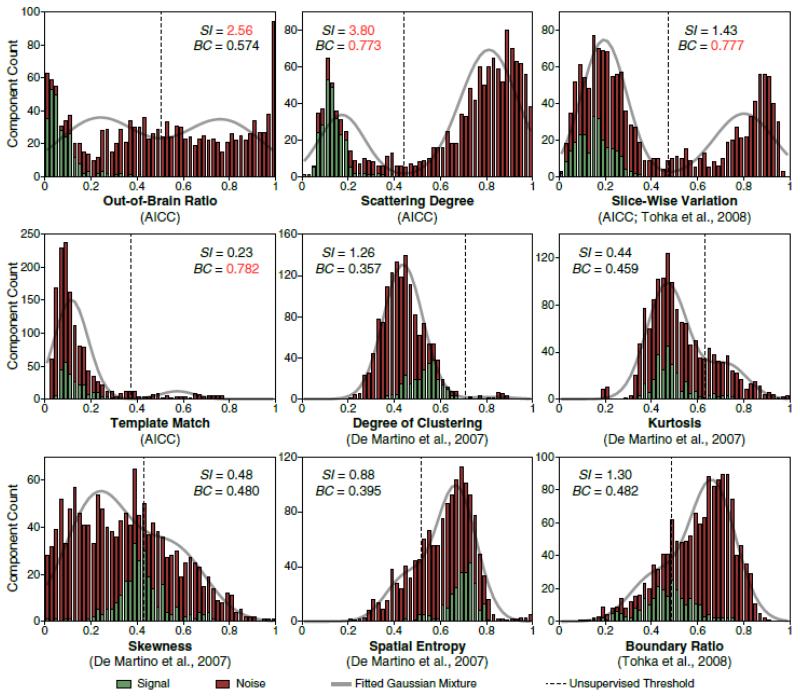
Along with the development of the mechanistic classification scheme, we also derived a simple set of spatial features (Fig. 2, left panel) that can be used to obtain quantitative measures for automating the binary classification of signal and noise components. Although we emphasize the importance of utilizing temporal information for validating the taxonomy of structured noise, there is a significant advantage in the generalizability of a binary component classifier when relying only on spatial features (cf. Supplementary Appendix C.1). The remaining question is whether the use of spatial features alone is sufficient to achieve accurate classification. This issue is addressed by a comparative evaluation of each feature (Fig. 5) based on two performance criteria – sensitivity index (SI) and bimodal coefficient (BC), as well as a direct assessment of the overall sensitivity and specificity of AICC according to the ground truth classification scores established by a human expert.

Fig. 5. Selection of Optimal Classification Features Based on Two Performance Criteria.

Histograms depict the counts of signal and noise components associated with 50 bins that uniformly divide the range of each spatial feature. The values of kurtosis, skewness and spatial entropy were transformed to a range between 0 and 1 by dividing each by its respective maximum. A two-component Gaussian mixture model (solid grey curve) was fitted to the distribution of each feature. The dashed lines indicate the thresholds automatically detected by an unsupervised expectation maximization algorithm. The two performance criteria for feature selection, sensitivity index (SI) and bimodal coefficient (BC), are annotated in each panel. Values in red indicate good performance (SI > 2 or BC > 0.6).

Among all the spatial features that we have compared, the scattering degree, a novel feature of AICC, is the most powerful in terms of providing the best combination of SI and BC. The out-of-brain ratio provides a very good SI but only a moderate BC. The slice-wise variation, which was originally introduced by Tohka et al. (2008), was incorporated into our classifier due to its good BC and moderate SI. The combination of these three features identified 94.6% of all noise components in our speech datasets (Table S1) and 97.8% of all noise components in a set of pediatric resting-state data published by Power et al. (2012), which was used to test the generalizability of AICC (Table S2).

In addition, the values of these two performance criteria appeared to vary under different experimental settings (Fig. 5 and Table S2), likely affected by image acquisition parameters, task paradigms, and subject groups. For example, the value of SI for the out-of-brain ratio is lower in the resting-state data than in our speech data, which may be caused by a smaller extracerebral spatial coverage and significantly less contribution of articulator motion; in contrast, an increase of SI for the scattering degree in the resting-state data may be due to the more severe head motion that occurs in children during data collection, which was most successfully captured by this feature. Thus, the combination of multiple spatial features ensures the high performance and generalizability of AICC. In addition, although it is critical to obtain sufficient extracerebral coverage to be used in the dual-mask sICA method for the establishment a mechanistic classification scheme and for the detection of overt speech artifacts, this is not required by the routine application of our denoising technique to other datasets acquired with different slice orientations.

Besides the three spatial features noted above, which measure relative intensity distributions at different spatial partitions, AICC also includes a fourth feature based on the global match with predefined (but “flexible”) noise templates. Although this feature has a very low SI and accounts for only a small fraction of total noise components (Table S1/S2), it is included as a complementary feature in order to capture noise components consistently missed by the other three features. Among the several flexible templates used in this study, templates for dural venous sinuses and ventricles are most effective (Table S3, unique counts). These templates are highly generalizable (Table S3, detection rates) to data collected with markedly different image acquisition settings (e.g., the different hardware platform, slice orientation and voxel geometry of the resting-state data), which are critical for fully automated applications in novel datasets. Nevertheless, in cases when there were no stereotypic components captured by this feature, AICC could still yield a sufficiently high performance based on the aforementioned sensitivity scores derived from the three primary features.

In contrast to the set of features selected by AICC, most of the spatial features employed in two previous studies (De Martino et al., 2007; Tohka et al., 2008) showed unimodal distributions that failed to separate signal and noise components effectively. These results may explain the suboptimal performance of these automated classifiers in terms of their overall accuracies, when compared with human classification.

Although only spatial features were included for comparisons in Fig. 5, our performance criteria for feature selection are applicable to temporal and spectral features as well. However, based on the ground truth established by our mechanistic classification, we have been able to demonstrate the sufficiency of an optimal set of spatial features by the strikingly high sensitivity (99.1%; 10 false negatives out of 1,166 noise components in our speech data) and specificity (100%; 0 false positives out of 253 signal components) of AICC. Meanwhile, this also indicates that the temporal information provided by component time courses is redundant (and even confounding in some cases; cf. Supplementary Appendix C.1) for binary signal/noise classification. Therefore, the use of temporal and spectral features is not recommended in order to maximize the generalizability of the classifier.

In addition, the two performance criteria should be applicable to all other types of classification features measured on a single dimension, including those derived from the linear echo time (TE) dependence of BOLD susceptibility effects proposed by a recent study (Kundu et al., 2012). Due to the requirement of multi-echo imaging for the use of these features (which greatly limits their general applicability), we were not able to directly compare their performance with our spatial features. Nevertheless, as shown in our speech production data, a significant number of noise components are potentially related to susceptibility distortion artifacts, which should be affected by TE as well. This might cause a difficulty in separating them from BOLD response if based solely on TE dependence.

Finally, the evaluation of automated component classifiers should also include the machine learning algorithms that are employed in each case. A direct comparison on the generalizability of several commonly used supervised and unsupervised learning algorithms is illustrated in Fig. S5. Although all of these algorithms achieved decent results utilizing the spatial features we selected, the unsupervised expectation maximization algorithm appeared to be the most optimal based on its balanced good performance in sensitivity/specificity and the fully automatic nature of its threshold detection (which does not rely on any pre-labeled training data).

Cross-Modal Validation for the Effectiveness of Denoising

Given the dramatic decrease of noise-induced variance, it is expected that within-subject contrast-to-noise ratio will be enhanced after denoising. Two critical questions remain: how will the effect of this individual-level denoising be transferred to group-level activation estimates, and can it help reduce false positives or false negatives in statistical parametric maps that compare different task conditions?

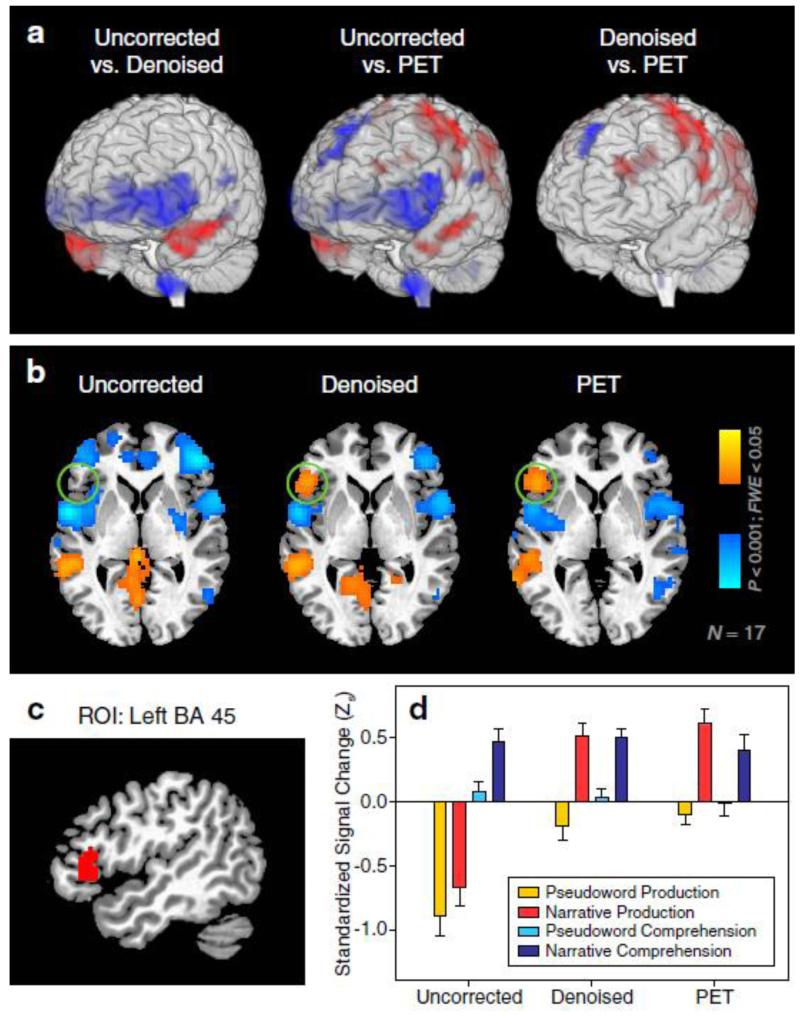
A direct contrast between the uncorrected and denoised fMRI images at the group level revealed the systematic biases in estimating task-related signals during narrative speech production (Fig. 6a, left panel). These include signal attenuations in the inferior frontal lobes bilaterally and the lower brain stem, and bilateral signal enhancements in the anterior temporal lobes (ATLs). The directions of bias and affected locations largely agree with previous reports of artifact-induced static magnetic field changes (Birn et al., 1998) and noise-susceptible regions that appear to be consistent across subjects (Mehta et al., 2006). Signal attenuations and enhancements in the same locations were also found in the contrast between uncorrected fMRI and PET (Fig. 6a, middle panel), but were not seen in the contrast between denoised fMRI and PET (Fig. 6a, right panel), further confirming that signal changes in these basal brain areas are artifact-driven and can be successfully removed by sICA denoising.

Fig. 6. Validating fMRI Denoising with PET.

(a) Direct group-level comparisons of standardized signal changes between uncorrected fMRI, denoised fMRI and PET datasets for the narrative production task. Student’s t-statistics, thresholded at two-tailed P < 0.001 for each voxel and family-wise error rate (FWE) < 0.05 for each cluster (containing minimally 50 voxels), were rendered on a 3-dimensional translucent brain template: red indicates signal increases; blue indicates signal decreases. Differences between denoised fMRI and PET in the dorsal brain regions (e.g., motor cortex) are likely due to differential regional sensitivities between the two imaging modalities.

(b) Group level voxel-wise t-maps showing contrasts between narrative production and pseudoword production. An axial slice at MNI z = 0 is used for illustration. Green circles indicate restoration of left IFG activation after denoising.

(c) A sagittal slice (MNI x = −48) showing the region of interest (ROI) selected for more detailed statistical comparisons. See also Fig. S6 for the definition of this ROI based on PET images.

(d) Standardized signal changes averaged across all voxels within the ROI depicted in (c). Bars represent means and standard errors across 17 subjects.

Crucially, most of the noise affected regions – including left Brodmann Area (BA) 45 (pars triangularis, a portion of Broca’s area), BA 47 (pars orbitalis), and bilateral ATLs – are commonly involved in language tasks, and are activated in PET during narrative speech production and comprehension as compared to low-level pseudoword conditions (Fig. S6). These results are also similar to what has been reported in previous PET studies (Awad et al., 2007; Braun et al., 2001). Among these regions, left BA 45 and 47 are subject to artifactual attenuation and are therefore potential sites of false negatives. Indeed, when comparing narrative to pseudoword production, activations of the left BA45/47 were found in both the denoised fMRI and PET, but not in the uncorrected fMRI (Fig. 6b). It is important to note that both the experimental and control conditions in this comparison utilized overt speech production. Thus, this false negative result failed to support the claim of a previous study (Barch et al., 1999) that the deleterious effects of artifacts can be “cancelled out” when comparing two overt speech conditions at the group level. On the other hand, the activation of the ATLs in a previous BOLD fMRI study of sentence and pseudoword production has been reported as false positives (Kemeny et al., 2005). However, activations of these regions in the narrative vs. pseudoword contrast employed in the current study likely represent true positives, as they were found in the comparable PET contrast as well (Fig. S6).

One may argue that differences observed in the above side-by-side comparisons (Fig. 6b) could result from an arbitrary choice of statistical threshold that lies between the significance levels of different datasets. This can be resolved by using a region of interest (ROI) analysis (Fig. 6c/d) that examines the interaction effects between the datasets and task conditions used for generating these contrasts. The ROI was defined by a cluster of conjoint activation between production and comprehension in PET (Fig. S6).

In the omnibus model, we observed a significant three-way interaction (F_{2, 25} = 3.71, P = 0.0388) between dataset (uncorrected, denoised, PET), task modality (production, comprehension) and stimulus materials (narrative, pseudoword). After breaking down the model by task modality, a significant two-way interaction (F_{2, 25} = 5.44, P = 0.0109) between dataset and stimulus materials was found in production tasks only. Further analysis comparing the task-related signals relative to the implicit baseline indicated significant positive activations for narrative production in the denoised fMRI (t₂₅ = 4.44, P = 0.0002) and PET (t₂₅ = 5.44, P < 0.0001) datasets; whereas pseudoword production showed nonsignificant deactivation in both datasets. The direct contrasts between narrative and pseudoword production were significant after adjusting for multiple comparisons with the Tukey-Kramer method (denoised fMRI: t₂₅ = 5.69, P_adj < 0.0001; PET: t₂₅ = 5.96, P_adj < 0.0001). However, for the uncorrected fMRI data, this effect was masked by what appeared to be strong deactivations in both tasks (narrative: t₂₅ = −5.32, P < 0.0001; pseudoword: t₂₅ = −7.95, P < 0.0001). In contrast, the comprehension tasks showed similar activation patterns across all three datasets. This attests to the specificity of denoising for removing only noise-induced effects without altering task-related signals.

In short, our denoising procedure has proven to be successful in restoring true task-related signals and eliminating false negatives in fMRI data collected during continuous overt speech production.

It is of note that the activation of left BA45/47 has been reported in previous fMRI studies on sentence- or word-level production that utilized sparse image acquisition (Dhanjal et al., 2008) or discarded images during short blocks (Birn et al., 2010), i.e., methods that can circumvent overt speech artifacts but may not be used for studying continuous overt speech production in ecological settings. These results do not contradict our findings that false negatives can occur in these areas, which can be attributed to two important differences: 1) our data were collected during discourse-level production with much longer blocks (30s duration) that introduce a more severe level of artifacts (Birn et al., 2004); 2) we did not apply any methods for circumventing artifacts to the uncorrected data demonstrated above.

Further investigations on these issues are presented in Inline Supplementary Fig. 2 and Supplementary Text S3 by comparing our denoising technique to previous methods for imaging overt speech production. Significantly, we found that although the previous methods can reduce artifacts to some degree, they may still systematically bias the true magnitude of activation due to the faulty assumption that artifacts cease immediately after speech. Moreover, while shortening the block duration can alleviate the artifacts in the uncorrected data, it shows no beneficial effects after denoising. That is, there is practically no duration limit when applying our technique to speech production tasks.

General Applications and Technological Outlook

The denoising technique introduced here opens a new avenue for achieving reliable BOLD fMRI measurements under conditions in which research subjects freely engage in overt speaking. And it can be equally applied to investigating vocal music performance, or other cognitive processes that involve overt verbal responses, e.g., verbal paradigms of memory and attention.

More importantly, because this technique is able to characterize and remove all common types of imaging artifacts, it should be generally applicable to a broad range of fMRI studies including resting-state function connectivity MRI (fcMRI). Here we present a brief demonstration by applying the same denoising procedure and reanalyzing the 3-T children cohort data published by Power et al. (2012). The generalizability of our automated independent component classifier to these foreign datasets has been demonstrated above (Fig. S5 and Table S2). Here we focus on comparing the effectiveness of sICA denoising with scrubbing, based on two metrics derived from the findings of Power et al. (2012). Unlike the speech production experiment, there is no reference measure available to assess the true functional connectivity in a resting-state experiment. However, we were able to establish a hypothetical ground truth for each metric by assuming if the confounding effect of head motion was non-exist.

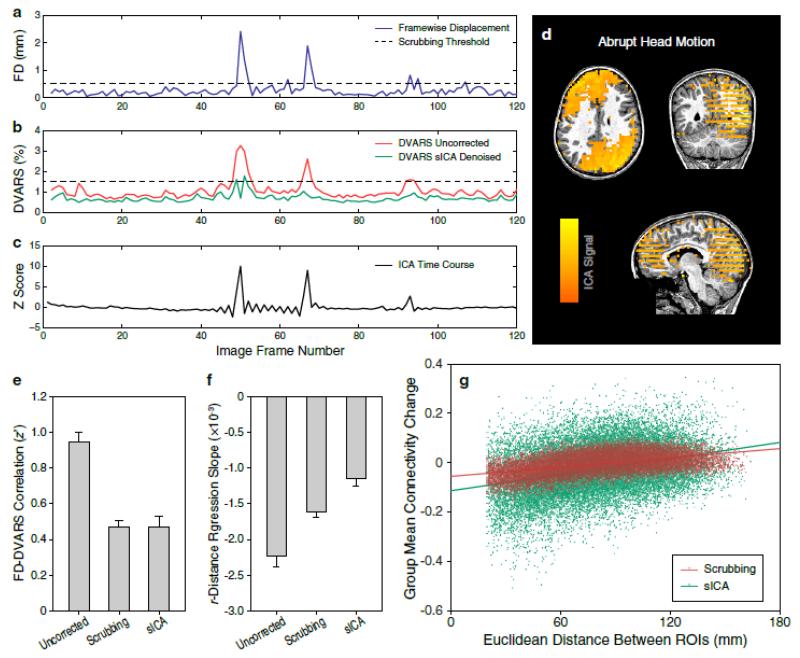
The first metric measures the correlation between FD and DVARS as the abrupt changes of head position (Fig. 7a) usually predict the intensity spikes in the fMRI time series prior to denoising (Fig. 7b, red curve). When examining the sICA results from these datasets, we frequently identified noise components with spatiotemporal characteristics clearly related to abrupt head motion (Fig. 7c/d). The spikes in DVARS time series were successfully attenuated in the reconstructed datasets after sICA denoising (Fig. 7b, green curve). In an ideal situation, if head motion did not contribute to the fluctuation of fMRI intensities, we would expect a near-zero correlation between FD and DVARS. Although not meeting with such an ideal condition, group-level analysis indicated that this correlation metric (Fig. 7e; represented by the Fisher’s z’-transformed correlation coefficient) was significantly reduced by both scrubbing (t₄₁ = −10.74, P_adj < 0.0001) and sICA denoising (t₄₁ = −10.44, P_adj < 0.0001) to a similar level as compared to the uncorrected data.

Fig. 7. Comparing Scrubbing and sICA Denoising on Resting-State Data.

(a) The framewise displacement (FD) of a single fMRI session acquired from a normal child. The dashed line indicates the threshold (0.5 mm) used for scrubbing.

(b) The DVARS time series computed from uncorrected (red) and sICA denoised (green) data from the same fMRI session. The DVARS of uncorrected data largely correlated with the fluctuation of FD in (a), with two significant spikes centered at Frames 50 and 67 respectively. The dashed line indicates the DVARS threshold for scrubbing (1.5% signal change). The spikes are minimally observed in the DVARS time series after sICA denoising.

(c) The time course and (d) spatial map of an ICA component decomposed from the same fMRI dataset, whose variance is removed after denoising. The time course contains spikes at the same locations observed in the FD and DVARS time series. The spatial map shows a large degree of slice-wise variation. Both indicate the existence of abrupt head motion.

(e) Temporal correlation between FD and DVARS in the uncorrected and denoised datasets. Bars represent means and standard errors across 22 subjects.

(f) Within-subject linear regression slope between the measured functional connectivity (r, Pearson’s correlation coefficient) and the Euclidean distance of ROI centers. These ROIs are spherically shaped and sampled across the entire cortical grey matter. Functional connectivity was computed for all pairwise combinations between ROIs.

(g) Scatter plots and regression lines (red for scrubbing; green for sICA denoising) between the group mean functional connectivity change per pair of ROIs (across subjects: $\overline{\Delta r}=\overline{r_{denoised}-r_{uncorrected}}$) and the distance of ROI centers.

The second metric is represented by the slope of linear regression line between the measured functional connectivity and the Euclidean distances of ROI centers. This metric arises from an established theory suggesting that brain development is accompanied by the strengthening of long distance correlations and the weakening of short distance correlations (Power et al., 2010), which appeared to be confounded by the systematic difference in head motion between adults and children during fMRI scans (Power et al., 2012). That is, a negative linear relationship between measured functional connectivity and distance can be driven by the severe head motion that introduces spurious correlations varying across distance (Satterthwaite et al., 2012). This distance-dependent effect of head motion has been predominantly observed in the children group, hence potentially leading to a false conclusion of between-group differences in true functional connectivity. Ideally, if there were no such or any other confounding effects that introduce local correlations (e.g., spatial smoothing, which has been effectively minimized by excluding ROI pairs with less than 20 mm distance), a zero linear regression slope might be treated as a hypothetical ground truth ^{Footnote 2}. Our results (Fig. 7f) indicate that sICA denoising significantly outperforms scrubbing when this metric is used as an endpoint, i.e., the result of sICA denoising more closely approaches to the hypothetical ground truth value than scrubbing (t₃₉ = 4.15, P_adj = 0.0005).

In order to compare with the original findings presented by Power et al. (2012), we also performed a group-level regression analyses using the mean connectivity change across subjects ($\overline{\Delta r}$) for each pair of ROI (Fig. 7g). The regression for scrubbing showed slightly higher slope (6.2×10⁻⁴ Δr/mm) and R² value (0.25) than the results published by Power et al. (2012), probably due to minor differences in the image processing routine. The regression for sICA denoising showed an even higher slope (10.8×10⁻⁴ Δr/mm) but a lower R² value (0.12). The decrease in R² is apparently caused by the larger range of Δr after sICA denoising, which increases the residual error of the model. This is not surprising for two reasons: 1) sICA denoising operates on the entire fMRI time series rather than local image frames; 2) sICA removes other sources of artifacts (e.g., physiological noise, which may not be distance-dependent) beyond head motion. Both of these two aspects may introduce larger non-distance-dependent changes in the correlation between time series, and hence a more scattered range of Δr as indicated by Fig. 7g.

Besides scrubbing, there are other commonly used methods for reducing the distance-dependent effect of head motion, such as nuisance variable regression using Volterra expanded rigid-body alignment parameters at the individual-level (Lund et al., 2006) or using the mean motion estimate of each subject as a covariate during group analysis (Fair et al., 2012). Recent studies (Power et al., 2014; Yan et al., 2013) indicate that these methods are generally not as effective as scrubbing. Therefore, direct comparisons with them were not carried out in the current study. In addition to these retrospective correction (i.e., artifact correction performed on images that have already been collected) methods, see also Supplementary Text S4 for a brief comparison of our technique with prospective motion correction – a class of real-time head motion correction methods based on external tracking mechanisms.

Finally, the routine use of ultra-high field instruments in whole-brain human fMRI research should become increasingly common in the near future. The substantial increase of susceptibility and physiological artifacts with increasing field strength, together with improvements in the spatial separability of signal and noise due to reduced partial volume effects (De Martino et al., 2011), should encourage an expanded role for the methods we present.

Conclusions

In conclusion, our denoising technique can be applied in a variety of experimental paradigms for improving the reliability of fMRI measurements. The entire procedure is fully automated and has minimal impact on other features of conventional data processing. Both the mechanistic component classification scheme that is proposed as a ground truth of denoising, and the general framework for designing/evaluating automated component classifiers, appear to achieve their goals in the current study; and may as well serve as methodological bases for future development.

Furthermore, since there is no perfect signal/noise separation (whether model-based or data-driven) existing in practice (Caparelli, 2005), investigating experimental conditions that are most susceptible to motion effects (e.g., continuous overt speech production and pediatric fMRI data employed by the current study) can provide empirical support for the robustness of denoising. By comparing the experimental results after denoising to the established real or hypothetical ground truth, and by comparing our technique to those commonly adopted in the field, we have been able to demonstrate that the proposed technique appears to be robust in these “catastrophic” situations, and should have the potential to be a general solution for fMRI artifact removal.

Highlights.

• Dual-mask sICA capable of revealing the extracerebral origins of fMRI artifacts

• A mechanistic component classification scheme as a fundamental of sICA denoising

• A general framework for evaluating the performance/generalizability of IC classifiers

• Quantitative validation of the effectiveness of denoising across imaging modalities