Co-ordinated detection of microparticles using tunable resistive pulse sensing and fluorescence spectroscopy

Abstract

Tunable resistive pulse sensing (TRPS) has emerged as a useful tool for particle-by-particle detection and analysis of microparticles and nanoparticles as they pass through a pore in a thin stretchable membrane. We have adapted a TRPS device in order to conduct simultaneous optical measurements of particles passing through the pore. High-resolution fluorescence emission spectra have been recorded for individual 1.9 μm diameter particles at a sampling period of 4.3 ms. These spectra are time-correlated with RPS pulses in a current trace sampled every 20 μs. The flow rate through the pore, controlled by altering the hydrostatic pressure, determines the rate of particle detection. At pressures below 1 kPa, more than 90% of fluorescence and RPS events were matching. At higher pressures, some peaks were missed by the fluorescence technique due to the difference in sampling rates. This technique enhances the particle-by-particle specificity of conventional RPS measurements and could be useful for a range of particle characterization and bioanalysis applications.

I. INTRODUCTION

The idea behind resistive pulse sensing (RPS) is as simple as it is powerful. A membrane containing a micro- to nanoscale pore is placed in an aqueous electrolyte and a constant voltage is applied across the membrane. Particles traversing the pore alter the ionic current and are detected as short-lived pulses in the ionic resistance. The technique is capable of measuring the concentration, size, and charge of the particles, as these properties are linked to the frequency, magnitude, and duration of the current pulses. First applied to the Coulter counter¹ for sizing and counting cells in blood, RPS has developed to be capable of detecting single molecules.² It has been used to investigate many particle types (e.g., synthetic nanoparticles, proteins,³ viruses,⁴ and liposomes⁵) over a wide range of length scales.⁶ Methods, such as track etching,⁷ electron beam lithography,⁸ and ion beam sculpting,⁹ have been used to make pores in materials like silicon, silicon nitride, glass, and polycarbonate¹⁰ down to an opening of a few nanometers. Inspired by the high selectivity of biological nanopores, more specific detection of target molecules can be achieved with chemically functionalised pores.^11,12 Kasianowicz et al.¹³ were the first to use a α-haemolysin pore to detect single DNA strands, with the ultimate aim to sequence DNA, which remains the most active field in RPS science.^14,15 Unlike dynamic light scattering techniques,¹⁶ which measure the average properties of particle distribution, RPS probes each single particle.

Tunable RPS (TRPS) has the advantage over a fixed size pore that by reversibly stretching and relaxing the elastomeric membrane,¹⁷ the pore diameter can be adjusted. In doing so, the signal to noise ratio can be optimised, allowing accurate measurements of polydisperse particle mixtures.¹⁸ Tunable pores are fabricated by puncturing an elastomeric polyurethane “cruciform” membrane with a chemically etched tungsten needle,¹⁹ leading to a typical conical pore shape. TRPS is able to measure the concentration^20,21 as well as the size²² and the ζ-potential^23,24 of particles as small as 50 nm in diameter. The technique has recently been used to study microbeads in a magnetic field²⁵ and to monitor aptamer-protein interactions^26,27 among other applications.

Combining RPS with spectroscopic measurements is useful due to the collection of additional specific information about individual particles. Fluorescence spectroscopy is a broadly used tool in biosensing²⁸ and makes use of the intrinsic fluorescence of biomolecules as well as introduced fluorescent labels to identify the analyte, e.g., to distinguish between cancerous and normal cells.²⁹ By correlating fluorescence with parameters, such as size and electrophoretic mobility, a wide range of information can be gathered on a high-throughput, particle-by-particle basis. Since low Reynolds number flow through a pore is laminar and can be accurately controlled, RPS also provides a good means to guide particles through the optical detection region with a defined pathway and speed, which is an improvement over the stochastic particle motion prevalent in conventional solution-based optical detection methods. Spectral flow cytometry addresses this issue and is now an established tool in the biosciences.³⁰ While this technique provides spectral information of single particles in solution, it is not able to provide additional information, such as size and charge, at the same time. Furthermore, the typical particle size in spectral flow cytometry is several μm, while TRPS covers length scales from tens of micrometers down to less than 100 nm. Although the work is this paper concerns micrometer sized particles, there is potential to extend the co-ordinated sensing methodology to submicron particles including (but not limited to) drug delivery vehicles, extracellular vesicles, viruses, emulsions, and synthetic particles used in assays. In many of these cases, measurement and analysis of the physical and chemical properties present fundamental research question.

Previous attempts to combine RPS with optical measurements in which intensities were measured, but without detailed spectral information, have included the detection of single molecules.^31–36 Heron et al.³³ achieved this using α-haemolysin pores, while Soni et al.³⁴ obtained good signal agreement using DNA-molecules traversing a solid-state nanopore. Song et al.³⁵ showed that simultaneous detection is possible using carbon nanotubes and charged dye molecules. Kurz et al.³⁶ could visualize the translocation of DNA molecules through a silicon-nitride pore using scanning confocal microscopy and correlated the intensity with the current signal. Another group³⁷ made the observation that a laser can be utilized to modulate the surface charge and therefore the translocation dynamics in solid-state nanopores in order to significantly slow down the translocation speed of DNA.

In this paper, we introduce a technique that increases the specificity of co-ordinated resistive pulse and optical data by acquiring high resolution spectra instead of the overall fluorescence intensity. To demonstrate our technique, we use fluorescently labelled 1.9 μm diameter spherical beads, with a view to extending the technique to smaller scales accessible by TRPS in the future. The use of tunable pores also provides some particular advantages, such as the ability to measure polydisperse particle mixtures and the experimental flexibility provided by tuning the pore, which could lead to a new range of experimental possibilities.

II. MATERIAL AND METHODS

A. qNano and modified flow cell

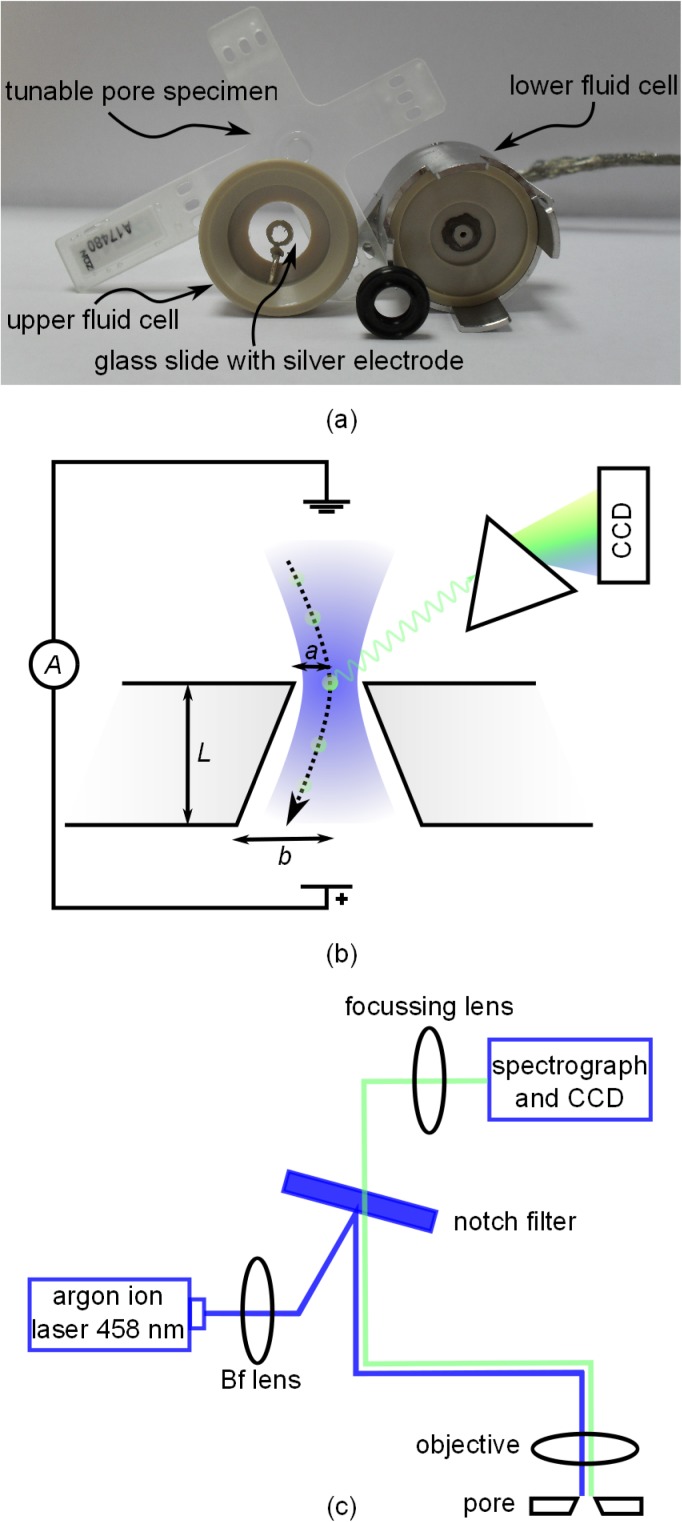
Detailed recent descriptions of TRPS experiments can be found elsewhere.^24,25,27 The commercial TRPS device (qNano, Izon Science Ltd.) uses a cross-shaped polyurethane membrane specimen containing a tunable pore. The center of the specimen, where the pore is located, is sandwiched in the fluid cell of the device (Fig. 1(c)). As a result of the fabrication method, the pores are conically shaped. In experiments, the small-side pore aperture is facing the upper half of the fluid cell. Both halves of the cell are filled with electrolyte solution, with only the top half of the fluid cell also containing the analyte particles. Ag/AgCl electrodes in the fluid cell are used to apply a constant electric potential and to measure the resulting ionic current. The particles are driven through the pore by a combination of hydrodynamic, electroosmotic, and electrophoretic transport.

FIG. 1.

(a) Schematic illustration of the experiment in cross-section with geometrical parameters labelled. The trajectory of a particle through the pore is indicated by the dotted line. The laser beam used for excitation has a Gaussian profile with a width comparable to the pore diameter and is represented by the blue shading. Emitted light is dispersed into spectral components with a diffraction grating and detected with a liquid nitrogen-cooled CCD chip. (b) Illustration of the excitation and collection pathways and the optical components used in the setup. (c) Dismantled fluid cell with tunable pore specimen. Surfaces that face upwards in the experiment are facing the camera. The rubber o-ring is placed in contact with the lower fluid cell, under the specimen.

The commercial flow cell design was adapted to enable simultaneous TRPS and fluorescence experiments (Fig. 1(c)). A round standard cover glass (16 mm diameter and 0.17 mm thickness) with a painted silver electrode (silver chloride paste) was used to provide both optical access to the pore orifice and electrical contact to the upper half of the fluid cell. To control the hydrostatic pressure at the pore, a tube was attached to the lower half of the fluid cell and filled with electrolyte. By simply moving the tube up and down, the pressure can be adjusted in a way that the desired direction and speed of fluid and particles through the pore are achieved.

In experiments presented here, we used a pore specimen rated as most suitable for measurements of 1 μm to 4 μm particles (manufacturer's label NP2000). The stretch between opposite jaws of the qNano was applied mechanically in the horizontal plane. The degree of stretching was set in order to achieve a high enough signal to noise ratio to clearly identify translocation events while keeping the likelihood of a blocking of the pore at a minimum. For the specimen used, the optimised stretch (48 mm between jaws) was not altered. The hydrostatic pressure at the pore orifice was too small (maximum 150 mm of water) to significantly affect the size or shape of the pore. A constant potential of V = 0.1 V was applied and the current was recorded at a sampling rate of 50 kHz using the customised software (Izon Control Suite Version 2.2). Previous work²⁰ has shown that the pores are not perfectly round in cross section. Therefore, the characteristic dimension for the pore radii is chosen to be the hydraulic radius, equal to 2A/p, where A is the cross sectional area and p the perimeter. A and p were measured for both pore apertures using the microscope and the camera feature of the Labram. The radii a and b (see Fig. 1(a)) of the small and large pore openings at 48 mm stretch were deduced to be 4.1 μm and 24.5 μm, with estimated measurement uncertainties of 10% and 5%, respectively. Using the pore-resistance model described in Ref. 38, the particle diameter can be calculated for each event from the observed current peak magnitude Δi as

$$d=\sqrt[3]{\frac{4\pi a^4}{\rho }\left(\frac{V}{i_{\mathit{b}\mathit{g}}-\Delta i}-\frac{V}{i_{\mathit{b}\mathit{g}}}\right)},$$ (1)

where i_bg is the background current when there is no particle in the pore and ρ is the resistivity of the electrolyte (0.86 Ω m for a 0.1M KCl solution, from Ref. 39).

B. Control of particle transport

Compared to the TRPS signals which are recorded at a sampling rate of 50 kHz, the optical detection is much slower with a time resolution of 4.3 ms between two spectra. Particles have to traverse the pore at a speed and frequency sufficiently low so that individual beads are optically distinguishable. Transport of particles in RPS can be understood using the Nernst-Planck approach.⁴⁰ Electroosmotic, electrophoretic, and pressure-driven flow are the relevant transport mechanisms governing the flow of particles through a pore. A recent study made a comparison of transport mechanism for TRPS.²⁵ In our experiments using μm-scale particles, pressure-driven transport is expected to dominate electroosmotic and electrophoretic transport. This makes the applied pressure the crucial variable determining the fluid and therefore particle velocity through the pore. The simple pressure system we use, made of a tube filled with electrolyte solution that is free to move in axial direction, has proven to be capable of controlling the pressure sufficiently. All experiments presented here were conducted at hydrostatic pressures across the membrane between 10 mm and 100 mm of water (1 mm water = 9.81 Pa). Using the pressure-flow model developed in Ref. 24, the fluid flow through the pore and therefore the translocation speed of the particles and their event frequency are linearly dependent on the applied pressure. The flow rate Q ([Q] = m³ s⁻¹) through a conical shaped pore can be evaluated using²⁵

$$Q=\frac{P}{\eta }\left(\frac{a^3{b}^3}{\frac{3}{2}(a^3+b^3)+\frac{8L}{3\pi }(a^2+ab+b^2)}\right),$$ (2)

where P is the hydrostatic pressure across the pore, η is the viscosity of the electrolyte (1.002 mPa s for water at 293 K, Ref. 41), and L is the pore length. L is equivalent to the membrane thickness and is dependent on the applied stretch. It can be measured optically by bringing distinct membrane features into focus under a microscope and measuring the difference in the stage position for the two membrane surfaces. L was measured to be 180 μm for our pore specimen, with an estimated uncertainty of 5%. The particle concentration C ([C] = particles m⁻³) can then be calculated from the particle count J ([J] = particles s⁻¹) and the relation C = J/Q.

C. Optical setup

A Labram Raman system from Horiba Jobin Yvon was adopted to measure the fluorescence spectrum of analyte particles travelling through the tunable pore. Fig. 1(b) shows a schematic illustration of the optical setup. The 458 nm line of a tunable argon-ion laser (Melles-Griot 543-AP-A01) was used for the excitation. Because the TRPS apparatus did not fit directly under the microscope, it was placed on a platform firmly attached to the optical table. Two translation stages mounted underneath the qNano allowed it to be positioned in the lateral direction. The laser was coupled out of the Labram with two mirrors and then focussed onto the pore orifice with a 20 times long working distance objective (Olympus, numerical aperture of 0.35, focal length 9 mm, working distance 21 mm). The total power of the laser at the pore was measured with a power meter (PM100 from Thorlabs) to be 0.4 mW. A micrometer fine translation stage provided exact axial positioning of the objective, which also collected the backscattered light. The axial collection depth of the objective or effective height H_eff as introduced in Ref. 42 was measured to be 250 μm. A band-stop or notch filter (Horiba Jobin Yvon, Type HSPF) was used to block the laser light and light that was elastically scattered in the sample from reaching the detector. The collected light was dispersed by a 300 lines/mm grating onto a nitrogen-cooled 1024 × 256 pixel CCD chip. The electronic gain of the CCD was set so that one count equals two incident photons. Every 4.3 ms, a spectrum was captured and recorded. A silicon sample with its characteristic 520 cm⁻¹line was used to calibrate the spectrometer.

To estimate the laser spot size at the pore orifice, we followed the formalism developed by Self for Gaussian beam optics.⁴³ The beam of the argon-ion laser has a waist of w₀ = 350 μm and a half divergence of θ₀ = 0.5 mrad (Ref. 44) at the laser exit. We used a lens (focal length 1000 mm, labelled “Bf lens” in Fig. 1(b)) to focus the laser beam onto the back focal plane of the objective in order to create a larger, more uniform, and less divergent beam at the front focal point of the objective. With Self's equations, we found the width w of the spot at the objective focus (focal length of 9 mm, the distance from the laser to the back focal plane of the objective was 2500 mm) to be 3.51 μm. Illumination across the pore diameter (8.2 μm diameter) is therefore not uniform but broad enough to detect the traversing particles. A variation in the optical signal depending on the actual trajectory of a particle through the pore is expected as the laser intensity at the width w is 1/e² or about 14% of the intensity at the center. The half divergence and Rayleigh range of the focussed laser spot were calculated to be θ₀ = 53 mrad and 64 μm. The beam diameter is therefore relatively slowly spreading and reaches twice its width at a distance of 111 μm away from the pore.

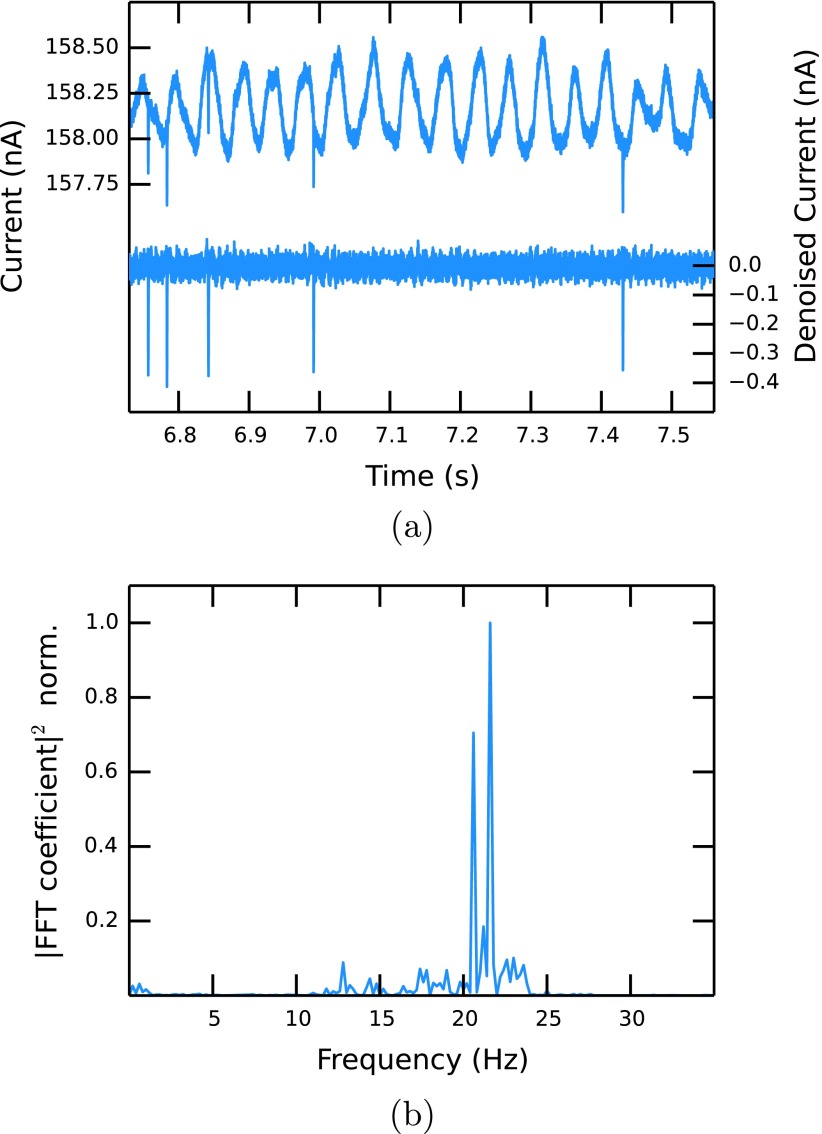
An important point of the experiment is that the laser spot is centred onto the middle of the pore orifice as indicated in Fig. 1(a). Rough alignment can be achieved using the microscope optics, but we found that a laser-induced noise source in the electrical signal can be utilized for a more accurate alignment. When the laser shines on the pore orifice, a sudden increase in the current of up to 10% of the baseline current is observed, which is modulated with a low-frequency signal (Fig. 2(a)). An analysis of the power density spectrum of the noise shows two peaks with frequencies of 20.5 Hz and 21.5 Hz, see Fig. 2(b). The close proximity of the peaks leads to beating, which is observed at the frequency of 1 Hz. Although this effect is mostly undesirable, we observed that the amplitude of this noise is highly dependent on the relative position of the laser focus to the pore and the best alignment is achieved when the noise amplitude is maximised.

FIG. 2.

(a) Examples of unfiltered (upper) and denoised (lower, 75 Hz highpass FIR filter) current traces. (b) Power spectral density of the unfiltered current signal.

The origin of the noise is still unclear and we found no dependencies of its frequency on the laser wavelength, the pore size, the pore stretch, the voltage, or the electrolyte strength. A linear dependency of the noise amplitude on the laser intensity was observed. The noise disappears immediately when the laser is switched off or slightly focussed away from the pore orifice. The latter observation indicates that mechanical coupling of the laser to a natural frequency of the membrane is not likely to be the case for the observed noise. Furthermore, the fundamental mode of a thermoplastic polyurethane membrane (Young modulus of 51.7 MPa, Poisson ratio of 0.49, dimensions as above) is of the order of several kHz, much higher than the observed value. A similar phenomenon has been observed before in solid state nanopores using a high power infra-red laser, in which case it was related to heating of the electrolyte solution and the resulting increase of electrolyte conductivity.⁴⁵ This explanation does not apply to our experiment, since the absorption coefficient of water at 458 nm is three orders of magnitude smaller than in the infra-red and the laser power is also much lower. Also absorption of light by the pore material and a resulting thermal effect is unlikely as polyurethane shows no absorption in the region of the laser wavelength. As the effect is very sensitive to the relative positioning and the resulting illumination of the pore walls, we suspect that a surface modification in form of a charge generation could be the reason for this effect, but further investigation is required.

D. Solutions and particles

Solutions contained 0.1M KCl and 3 mM ethylene diamine tetraacetic acid (EDTA) in deionised water and were buffered with tris(hydroxymethyl) aminomethane. The pH was adjusted to 8 using HCl and KOH. A small amount (0.01%) of Triton X-100 was added to increase pore wetting. The solutions were filtered through a 0.2 μm filter (Millipore) prior to use. The particles used in experiments were carboxylated polystyrene beads with a nominal diameter of 1.9 μm, purchased from Sigma-Aldrich (product number L4530). Due to their surface modification and the pH of the solution, the particles carry a negative effective charge. As discussed earlier, the resulting electrophoretic transport when exposed to an electric field is much smaller than the hydrodynamic transport in our experiments and can therefore be neglected. The as-received particle solution was diluted with electrolyte by a factor of 5000 to a concentration of about 1.33 × 10⁶ particles/ml and sonicated for about 5 min prior to experiments. A fluorescent dye with a maximum excitation at 470 nm is embedded in the polymer matrix. The emission has its maximum at 505 nm. We measured the total fluorescence cross-section of a single bead to be 3.17 × 10⁻⁹ cm² by comparing its signal to the Raman intensity of a reference standard (2-Bromo-2-methylpropane).⁴⁶ Taking a typical cross-section of a fluorescent molecule, we can estimate the number of molecules per bead to be of the order of about 10⁷.

E. Data analysis

Before the information from the electrical and optical measurement can be compared, both traces must be separately post-processed. First, the low frequency noise in the current trace was removed using a Finite Impulse Response (FIR)⁴⁷ highpass filter algorithm with a cutoff frequency of 75 Hz and a Kaiser window of 20 Hz width. Removing the low frequency parts of the signal efficiently not only gets rid of the unwanted oscillations but also causes the baseline current, which is ∼150 nA in the raw signal, to become 0 nA. A typical current trace before and after the filter process is shown in Fig. 2(a). The filtered trace is scanned by software developed in-house to identify resistive pulses using a moving window of 100 data points and a pulse threshold of 0.2 nA, similar to the method described in Ref. 48. Every event is characterised and identified by its start time, end time, the time at the peak, and the peak height. For each experiment, the bead size distribution, the average size, and the bead concentration are calculated using Eqs. (1) and (2).

Although the noise described above is also observable in the optical trace, it is not large enough to necessitate filtering the signal. The first post-processing step for the optical data is to integrate the measured spectra (Fig. 3) to obtain the overall fluorescence intensity as a function of time. Events are then identified and characterised in the same way as with the current data. The algorithm window size is smaller (10 data points) due to the lower sampling rate, while the pulse threshold is 200 counts. The stable background count seen in the optical trace originates in the intrinsic fluorescence of the pore material. Since the optical data are recorded separately from the current data, the two traces have to be aligned to enable synchronisation. This is done by calculating the correlation function of the two time series and shifting them relative to each other so that the correlation peak has its maximum at 0.

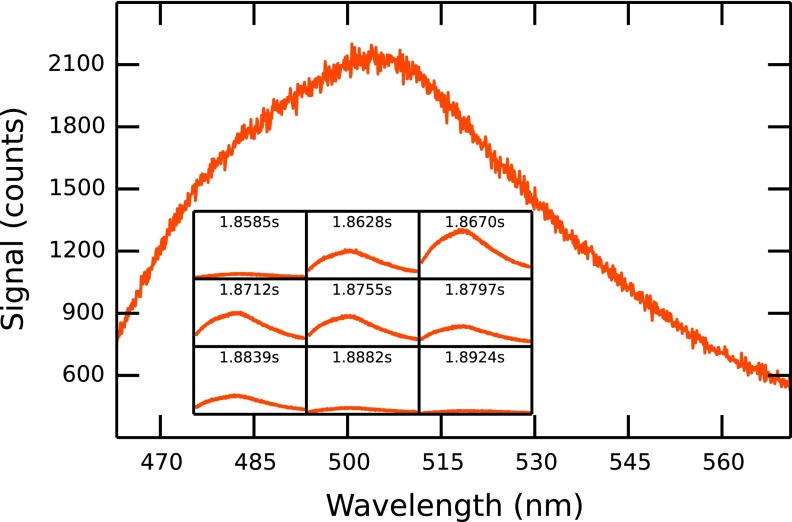
FIG. 3.

Fluorescence spectrum of a particle traversing the pore at low speed (experiment D1). The inset shows the signal intensity and the recorded time for 9 consecutive frames.

III. RESULTS AND DISCUSSION

Table I summarizes five demonstrative experiments which were conducted at different hydrostatic pressures but otherwise exactly the same parameters. Pressure values are known to an uncertainty of ±1 mm water for experiments D1 and D3. Experiment U1 was conducted at a negative pressure in order to drive particles upwards through the pore at a medium speed, and the pressure for D2 was set near the middle of the two known points. The pressure in experiment D4 was chosen to be ∼150 mm water, which resulted in a blocking of the pore and the premature termination of the current recording. The recorded time for each experiment is 9.686 s, determined by the CCD memory capacity, except for D4 (6.512 s).

TABLE I.

Details of five experiments with co-ordinated resistive pulse and optical measurements, including the number of identified events and their matching rate at different applied pressures. Numbers of events which show no corresponding events in the other trace are given in brackets. The Wilson score⁴⁹ is a lower bound for the matching percentage at 97.5% confidence, assuming a binomial distribution.

Experiment	Pressure (mm water)	Number of events				Wilson score (%)
TRPS	Fluorescence	Matching	Double events
D1	10 ± 1	8 (0)	8 (0)	8 (100%)	0	76
U1	∼−30	22 (0)	21 (0)	20 (91%)	1	78
D2	∼70	58 (4)	54 (0)	54 (93%)	0	87
D3	100 ± 1	82 (3)	76 (1)	71 (87%)	4	82
D4	∼150	83 (4)	71 (0)	63 (76%)	8	70

While a resistive pulse in the current trace consists of up to a hundred data points covering a time span of 2 ms, a corresponding event in the optical signal trace is usually about 5 data points (21.5 ms) long. This is due to the difference in time resolution of the two techniques (50 kHz in the electrical and 230 Hz in the optical detection). The longer total time span of an optical event can also be explained by the larger axial detection depth of the objective used compared to the active zone in which the RPS device can detect the particle. While a particle within ∼100 μm on either side from the pore orifice can still be detected optically, the current is indistinguishable from the background value when the bead is just ∼20 μm inside the pore. Fig. 3 shows the spectrum and its time evolution for a particle moving through the pore at low pressure (10 mm water, experiment D1). A rise of the measured intensity to its peak height when the particle is at or close to the pore orifice can be observed. As the particle moves through the pore and out of the laser spot, the signal decreases again towards a constant background level. The spectral shape stays constant in this process and single spectra can be superimposed by multiplication.

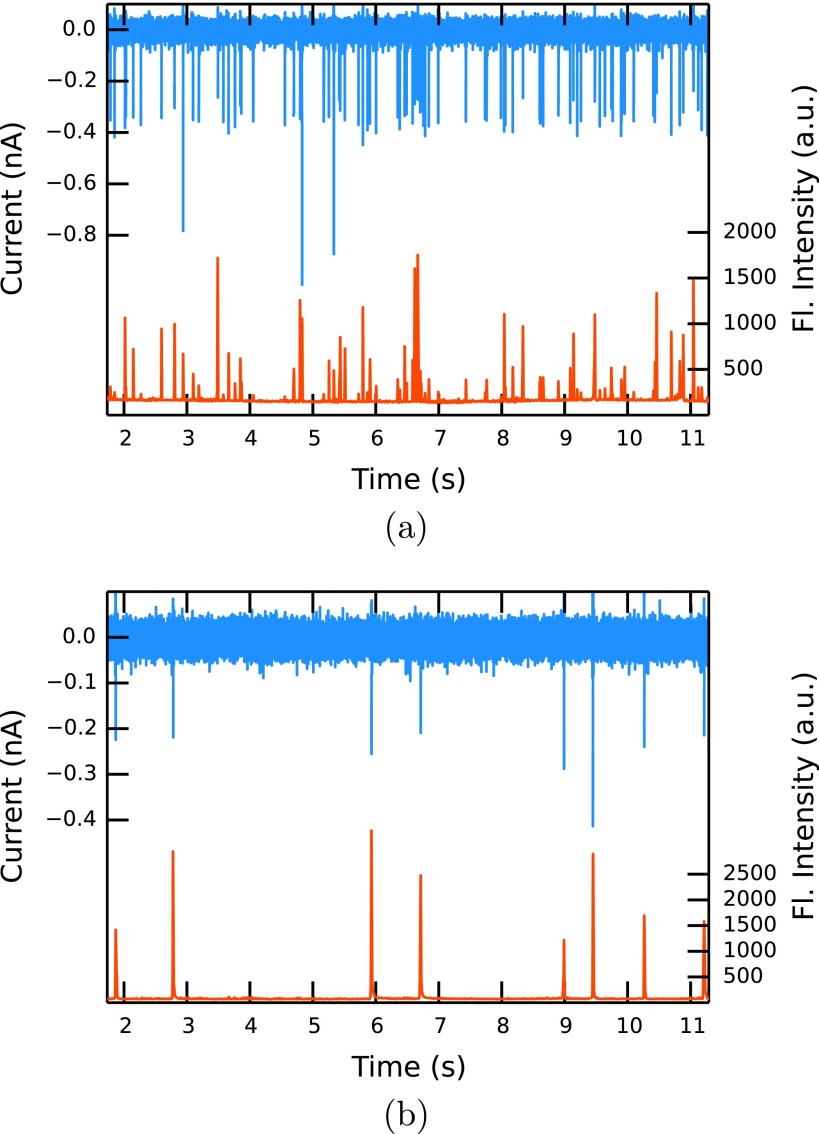
Figures 4(a) and 4(b) show the co-ordinated results obtained from measurements at relatively fast (D3) and slow (D1) fluid velocities, respectively. While 82 translocations can be detected in the current at high pressure (100 mm ± 1 mm water), only 8 events are observed in the same time at low pressure (10 mm ± 1 mm water). This approximate ratio of events (10:1) is expected as the volumetric flow rate should be proportional to the applied pressure (see Eq. (2)). The event rates for experiments U1, D2, and D4 are also consistent with the approximate applied pressures. Compared to a solution based method that relies on diffusion (diffusion constant D of a bead of 0.23 μm²s⁻¹, average concentration of 0.01 particles/detection volume), a much higher throughput of more than 10 particles s⁻¹ can be achieved in our setup.

FIG. 4.

Current (blue, upper) and fluorescence intensity (red, lower) traces at high (100 mm water, experiment D3) (a) and low (10 mm water, experiment D1) (b) hydrostatic pressure.

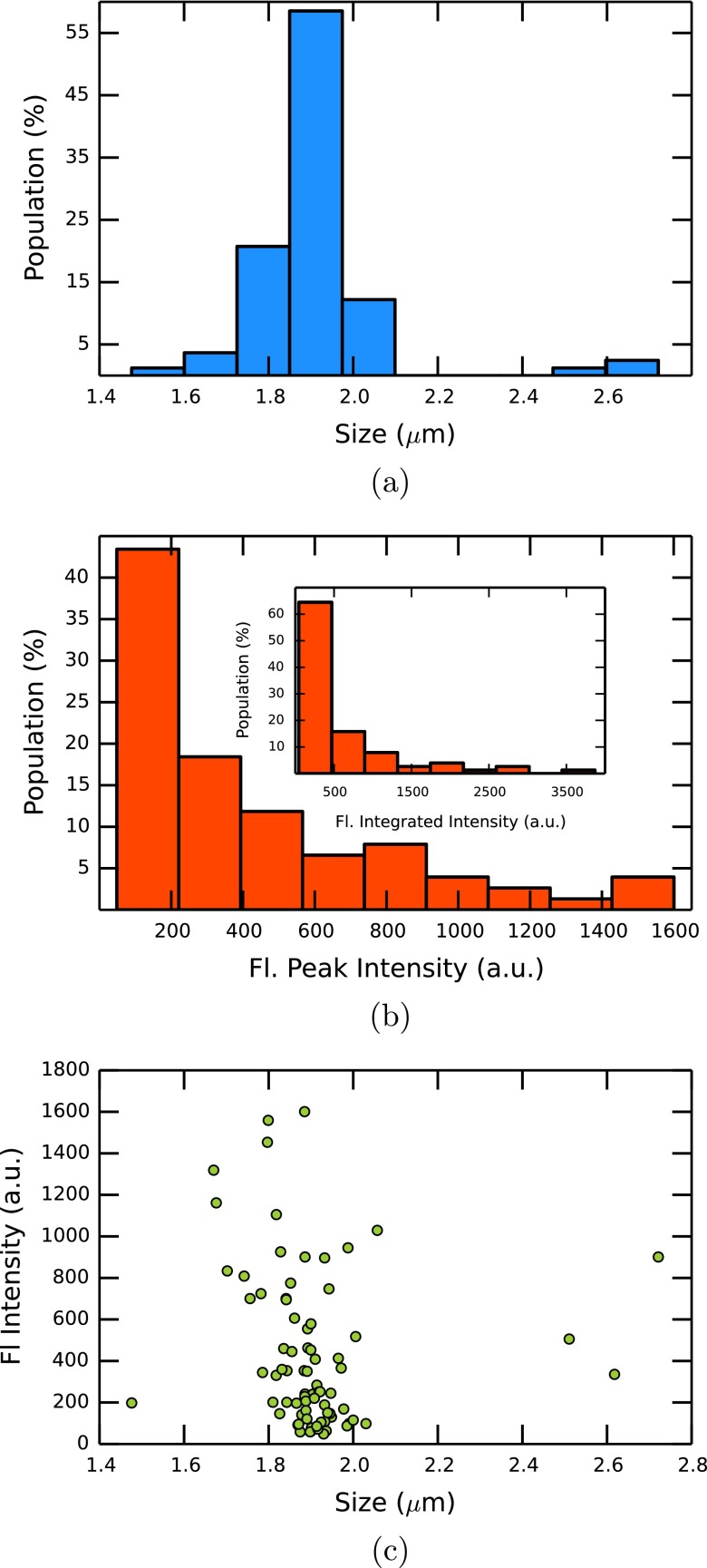
The current peak heights from experiment D3 and therefore the calculated particle sizes using Eq. (1) show a narrow distribution (Fig. 5(a)) around the nominal diameter of 1.9 μm. As the current peak height is proportional to the particle volume,²² the three events in Fig. 4(a) which have about double the typical current peak height and appear to have a diameter of about 2.5 μm are most probably due to agglomeration of two particles. The variation of peak heights in the fluorescence trace is much greater (Fig. 5(b)). The beads show a reasonably uniform fluorescence intensity when immobilized on a glass slide and measured one by one, so the peak height variation cannot simply be explained by variations in the intrinsic fluorescence. The probable reason for the non-uniform fluorescence peak sizes is that the particles can move through the pore on different paths. Some beads travel close to the center where there is high laser intensity, whereas the intensity is smaller for beads travelling close to the pore walls. With the beam width of 3.51 μm, a bead travelling at the very edge of the pore is exposed to a laser intensity of about 20% of the intensity experienced by beads travelling through the middle. This value drops to 6% under the assumption that the laser center is 1 μm off-centre. The distribution shows peak heights from 150 to 1500 counts with the majority at the small end of the distribution, suggesting that most particles travel close to the pore walls. This hypothesis is strengthened by the observation that the intensity distribution becomes even more non-uniform if the back focal plane lens is removed and the spot size of the laser beam at the pore becomes smaller. The variation of fluorescence peaks could be explained by detection of multiple particles. This possibility can be excluded as the fluorescence signal usually falls to the background level between peaks, unless in the case of the double events discussed below. Furthermore, there is only one instance of a measurable optical signal that did not produce a resistive pulse. Many more such events would be expected if two or more particles were detected optically at the same time. In addition, Fig. 5(c) shows no clear correlation between the fluorescence intensity and the number of particles passing through the pore. Another possible explanation for the high variation in fluorescent peak heights could be the low sampling period compared with the relatively high particle velocity of up to 20 mm s⁻¹ at the pore orifice. Undersampling can lead to an underestimation of peak heights as discussed in Ref. 50. In our setup, the acquisition of the optical signal is continuous and each spectrum represents the counts in the sampling window. If undersampling is a factor, the integrated intensity over each fluorescence peak should still be consistent, which is not the case ((Fig. 5(b) inset). The time proportion when the CCD is reading out the signal and is therefore insensitive to detection is only 1% of the sampling window. The maximum distance a particle can travel during this time is too short to explain the variation in peak heights alone. It might play a role in future experiments with smaller detection volumes, i.e., when a pinhole is used.

FIG. 5.

Particle size (a) and fluorescence intensity (b) distribution in experiment D3. (c) Scatter plot of current peak heights and fluorescence intensities of the events for experiment D3.

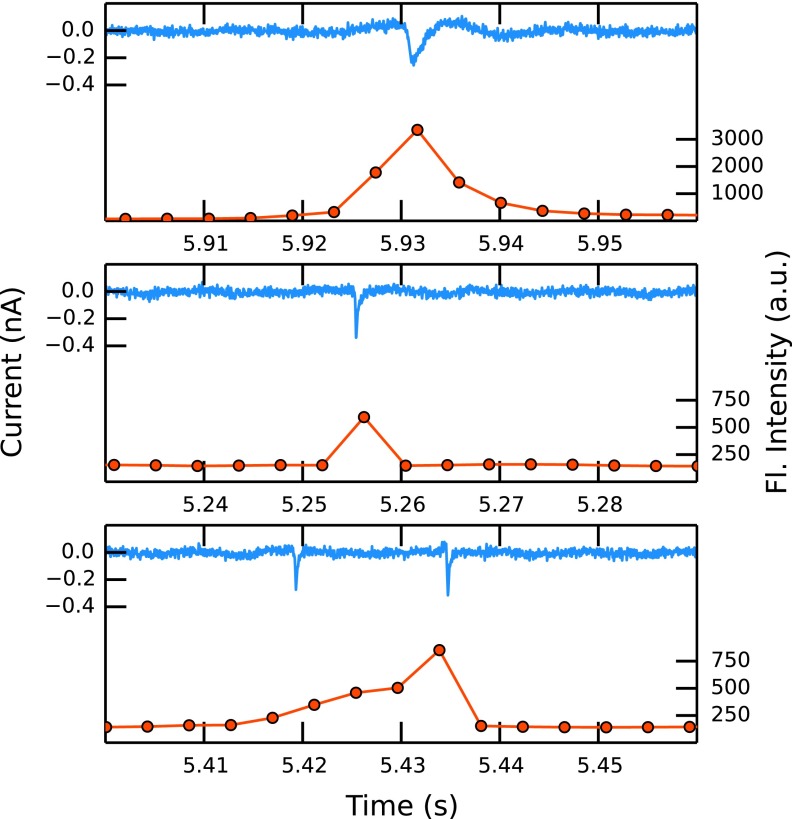
To illustrate the effect of the fluid velocity on the pulse shapes, three events representing slow (top), fast (middle), and double (bottom) events are plotted in Fig. 6. It is clear that the width and therefore the number of data points used to sample each event corresponds to the velocity of the particle translocation. Two particles moving through the pore in close succession cannot be resolved in the fluorescent trace, and this is misinterpreted as one long event. The characteristic asymmetric shape of the resistive pulses is a result of the conical pore shape.

FIG. 6.

Typical events from experiments D1 (low-pressure, top) and D3 (high-pressure, middle), and a “double event” as described in the text (bottom).

Table I summarizes the identified events in the 5 experiments. The number of events observed in the current trace is always larger than in the optical trace, especially at high pressures. This is to some extent due to the effect that particles passing through the pore in close succession cannot be distinguished as different events in the optical trace. Some other events are not picked up by the algorithm because their intensities are too small, but can be seen in the raw trace. There is a clear increase of double events and undetected events and therefore a decrease of the matching rate as the pressure is increased. Depending on the particle concentration, the pressure can be adjusted to optimise the event frequency and therefore the matching rate of the correlated detection in our setup. The rate at which single resistive and fluorescence pulses are matched is recorded in Table I, along with a lower bound at 97.5% confidence, assuming a binomial distribution for matched and unmatched events. Overall, the matching rate is very likely to be better than 83% in all experiments.

There is only one unmatched positive detection in all the fluorescent traces. To get a higher throughput and reduce the number of double events, the detection volume could be reduced using a pinhole in the collection path. This could be especially useful when measuring smaller particles and particles at higher concentrations. We are aware that the fluorescent beads we are using are bright compared to biological samples. To increase the optical signal when smaller or less intense samples are measured, an objective with a higher numerical aperture and/or higher laser powers have to be used. There is also possible improvement in the efficiency of the spectrometer, which was measured to be ∼2%. That means that only one in 50 photons collected by the objective is detected on the CCD. The rest are lost mainly due to imperfect mirrors, the grating, and the quantum efficiency of the CCD.

To achieve a bigger spot size and therefore a more uniform illumination of the pore orifice, either a focussing lens with a shorter or an objective with a longer focal length can be used. Implementation of both is not feasible in our current setup as excitation and collection pathways are partly parallel and a field lens can be used only in the position before the notch filter. Using an objective with longer focal length leads to an increase in the axial detection height and therefore an increase in false positive detection events.

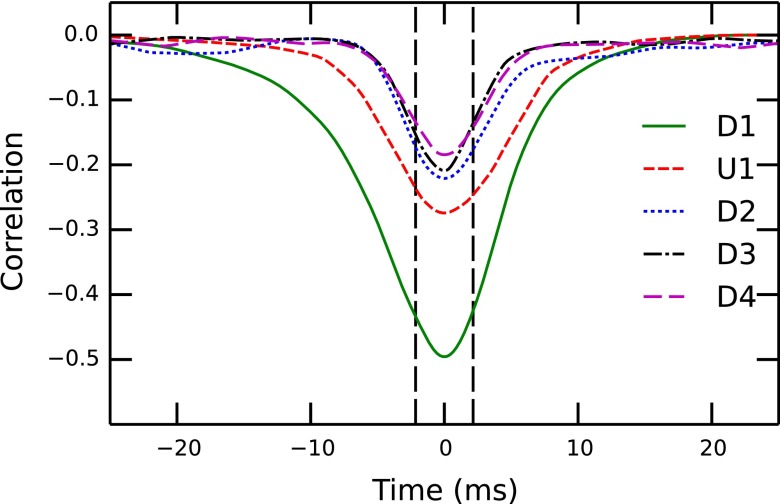
The correlation functions we used to align the traces are shown in Fig. 7. The width of each correlation peak is related to the event width of the optical measurement and is limited by the sampling rate of 4.3 ms. The peak height decreases with increasing pressure, which reflects the smaller matching rate and the fact that an increase in the number of events leads to more closely spaced events.

FIG. 7.

The calculated correlation functions of the experiments in Table I. The sampling rate in the optical measurement of 4.3 ms is indicated with vertical dotted lines.

The calculated average particle sizes and concentrations are summarised in Table II. The values for the particle diameter agree very well with the nominal value of 1.9 μm claimed by the supplier. The nominal concentration deduced from the supplier information and the dilution of 5000 is 1.33 × 10⁶ particles ml⁻¹, slightly higher than the values derived from the particle count. Taking into account uncertainties due to the dilution and the pore dimensions, the values are in reasonable agreement. The dominant uncertainty is that of the small pore diameter (10%) suggesting an absolute uncertainty of at least 13% in size and 30% in concentration measurements. The usual, more accurate method for TRPS measurements is to use calibration beads of known size²² or concentration.²⁰

TABLE II.

Mean diameter and concentration of particles, calculated using Eqs. (1) and (2), respectively. Diameter uncertainties represent a standard error in the mean.

Experiment	Mean diameter (μm)	C (×106 ml−1)
D1	1.85 ± 0.06	1.10
U1	1.88 ± 0.02	1.01
D2	1.93 ± 0.02	1.14
D3	1.91 ± 0.02	1.12
D4	1.86 ± 0.02	1.13

IV. CONCLUSION AND OUTLOOK

In this proof of principle study, we have demonstrated the co-ordinated detection of colloidal microparticles using two complementary techniques. Tunable resistive pulse sensing data were used to measure particle size and particle concentration, while optical measurements add full spectral information on a particle-by-particle basis. The data show close correlation in time and by slowing the fluid and therefore event frequency, a matching rate in excess of 90% can be achieved. Ongoing work will focus on experimental development in order to extend detection to smaller particles. The technique can also be exploited to study particles with different emission spectra but otherwise identical properties, suggesting possible applications in the biosciences. With improved optical detector efficiency, Surface-Enhanced Raman Spectroscopy (SERS) would become another candidate for optical co-ordination with TRPS.