Selecting on Treatment: A Pervasive Form of Bias in Instrumental Variable Analyses

Abstract

Instrumental variable (IV) methods are increasingly being used in comparative effectiveness research. Studies using these methods often compare 2 particular treatments, and the researchers perform their IV analyses conditional on patients' receiving this subset of treatments (while ignoring the third option of “neither treatment”). The ensuing selection bias that occurs due to this restriction has gone relatively unnoticed in interpretations and discussions of these studies' results. In this paper we describe the structure of this selection bias with examples drawn from commonly proposed instruments such as calendar time and preference, illustrate the bias with causal diagrams, and estimate the magnitude and direction of possible bias using simulations. A noncausal association between the proposed instrument and the outcome can occur in analyses restricted to patients receiving a subset of the possible treatments. This results in bias in the numerator for the standard IV estimator; the bias is amplified in the treatment effect estimate. The direction and magnitude of the bias in the treatment effect estimate are functions of the distribution of and relationships between the proposed instrument, treatment values, unmeasured confounders, and outcome. IV methods used to compare a subset of treatment options are prone to substantial biases, even when the proposed instrument appears relatively strong.

Because instrumental variable (IV) methods can identify treatment effects even in the presence of unmeasured confounding, these methods are increasingly being used in comparative safety or effectiveness studies (1). Many such studies have addressed research questions comparing 2 particular treatments and therefore have ignored other possible treatments (including no treatment) (2). While restriction of an analysis to patients who have received the treatments of interest follows naturally from the analytical strategies using non-IV methods, this selection can induce bias in IV methods. Unlike other biases specific to IV methods (1–6), this selection bias has rarely been noticed in applications (7), and its structure and implications have not been thoroughly described.

Here we describe the structure of this selection bias, as well as its magnitude and direction. We first consider a calendar time instrument. We then consider other commonly suggested instruments, including a preference-based instrument proposed for a study of patients initiating 2 classes of statin therapy. We start by briefly describing the IV estimator and the conditions required for its validity.

IV ESTIMATION

Suppose we want to estimate the effect of a dichotomous, time-invariant treatment X on an outcome Y. We will use superscripts to denote counterfactuals; for example, Y^x indicates the counterfactual outcome Y under treatment X = x. A pretreatment variable Z is an “instrument” if 3 conditions hold: 1) Z is associated with X; 2) Z only causes Y through X (i.e., Y^z,x = Y^x for all values x and z); and 3) there is no confounding between Z and Y (i.e., exchangeability; $Z\coprod Y^x$ for all x).

When an instrument Z exists, the standard IV estimator

$$\frac{E[Y|Z=1]-E[Y|Z=0]}{E[X|Z=1]-E[X|Z=0]}$$

identifies the average treatment effect in the population if a fourth condition of effect homogeneity across levels of the instrument holds (8), or it identifies the average treatment effect in a subset of the population (the “compliers”) if a different fourth condition of monotonicity holds (9). We argue below that condition 3 may be violated in studies restricted to a subset of the possible treatments. We begin with an example provided under the overall sharp null hypothesis (i.e., both the instrument and the treatment have no effect on any individual's outcome), which guarantees that conditions 2 and 4 hold.

STRUCTURE OF THE SELECTION BIAS

Consider 2 treatments for the same illness, and suppose that we are interested in estimating the average effect of treatment 2 versus treatment 1 on risk of death for patients with this particular illness. In 2014, treatment 1 is slightly more popular than treatment 2: Of all patients with this illness (i.e., those who have indications for these treatments), 50% are prescribed treatment 1, 40% are prescribed treatment 2, and 10% are prescribed neither treatment (i.e., including different drugs or no pharmacological treatment). In 2014, assume that the decision to treat with treatment 1 versus treatment 2 versus neither is essentially random. In 2015, however, new evidence of harmful side effects of treatment 1 is reported, and the Food and Drug Administration issues a warning: Treatment 1 has been found to increase risk of cardiovascular disease (CVD). There is a sudden shift in prescribing practices: For patients with this illness who have no serious CVD risk factors, 40% are prescribed treatment 1, 45% are prescribed treatment 2, and 15% are prescribed neither; for patients with 1 or more serious CVD risk factors, none (0%) are prescribed treatment 1, 50% receive treatment 2, and 50% receive neither.

Such a large and sudden shift in prescribing practices is a natural experiment that invites the comparison of treatments 1 and 2 via an IV analysis using calendar time as the proposed instrument (assuming no other strong time trends occurred during the study period). Note that the treatment X can take the values 1 (treatment 1), 2 (treatment 2), and 3 (neither). However, the typical IV analysis will use only observations from patients who are prescribed either treatment 1 or treatment 2 (i.e., X = 1 or X = 2).

The crude treatment effect estimate comparing treatment 2 with treatment 1 would be confounded, because patients actually prescribed treatment 1 would have fewer CVD risk factors than patients prescribed treatment 2 (specifically during the second time period). To understand whether the IV analysis would be confounded, we compare patients seen in the prewarning (Z = 0) and postwarning (Z = 1) time periods who were prescribed treatment 1 or 2. Prewarning, the risk of death Y in patients prescribed treatment 1 or 2 would approximately equal the risk of death in all patients (because treatment decisions were essentially random and we have assumed an overall sharp null). Postwarning, the risk of death in patients who were prescribed treatment 1 or 2 would be lower (because the patients actually prescribed treatment 1 would have fewer CVD risk factors). Thus, the measured association between the proposed instrument Z and the risk of death Y (i.e., the numerator for the standard IV estimator) would be different from zero in analyses restricted to patients prescribed treatment 1 or 2 when in fact it should be zero. Consequently, the treatment effect estimated with the IV analysis would also be biased.

The structure of this potential bias is illustrated in a causal diagram in Figure 1. By restricting the analysis to patients prescribed treatment 1 or 2, we are selecting treatment values X = 1 and X = 2. This selection on X, represented by a box around X in the causal diagram, implies that we are conditioning on the collider X in the path Z − X − U − Y; that is, Z and Y will be associated because of collider stratification (10). Calendar time Z meets instrumental condition 3 unconditionally, but not in the analysis that selects on treatment.

Figure 1.

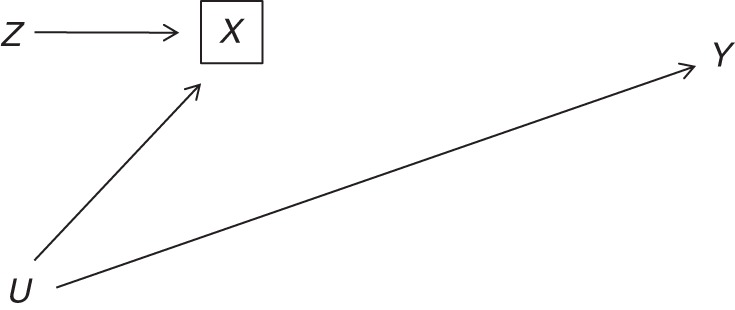
Selection bias in an instrumental variable analysis restricted to patients who were prescribed a subset of the treatment options. Z represents the proposed instrument; X represents the treatment the patient was prescribed (X = 1 if treatment 1, X = 2 if treatment 2, and X = 3 if neither treatment); U is a set of unmeasured confounders; and Y is the outcome. The box around X indicates restriction to patients prescribed X = 1 or X = 2.

MAGNITUDE AND DIRECTION OF SELECTION BIAS

A small bias in the IV numerator can be amplified into a much larger bias for the treatment effect estimate (1). We chose our calendar time instrument example to be of similar apparent strength as proposed instruments in published epidemiologic studies to mirror the magnitude of expected amplification (2). Note that one subtlety in repurposing previous results concerning bias in the IV numerator to understand this particular bias is that the IV denominator is also affected by the selection by treatment, and thus the functional form of the bias is slightly more complicated.

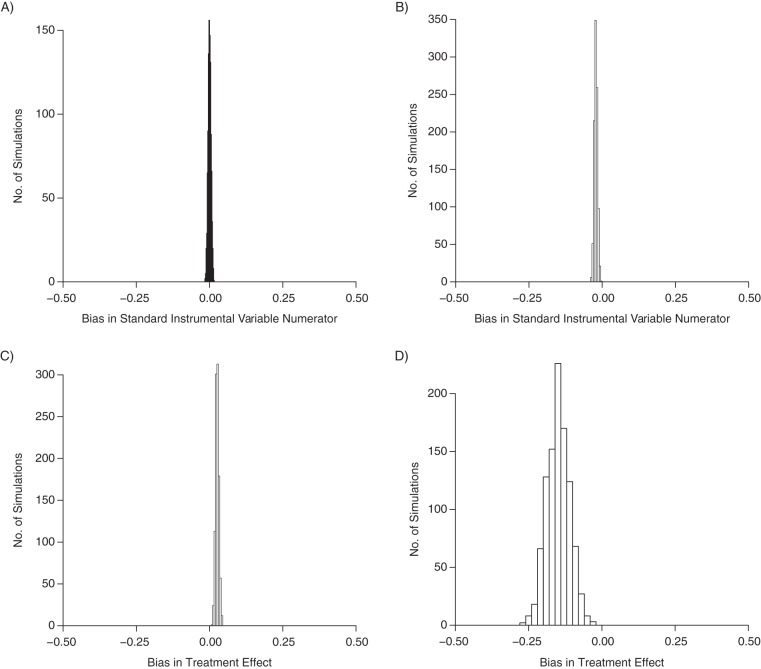
We can explore the magnitude and direction of bias due to selecting on treatment via simulations. For example, we generated data under the scenario described for our calendar-time example (Figure 2). The association between calendar time and outcome is null unconditionally, but a small association arises among persons who received either treatment 1 or treatment 2 (mean risk difference = −2 deaths per 100 patients). Now consider the treatment effect, that is, the causal risk difference comparing treatment 2 with treatment 1, which we know should be null. If we restrict our analysis to persons who received treatment 1 or 2 and estimate the crude association, treatment 2 appears slightly more harmful (mean risk difference = 3 deaths per 100 patients). The restricted analysis follows naturally from the research question, and the bias is due to unmeasured confounding by CVD risk factors. If we use the IV analysis to estimate the treatment effect, the bias in the IV numerator is amplified in the standard IV estimate: Treatment 2 appears strongly protective relative to treatment 1 (mean risk difference = −15 deaths per 100 patients).

Figure 2.

Results from a simulation with a dichotomous instrument Z, a trichotomous treatment X, and a dichotomous outcome Y. We generated 1,000 samples of 20,000 patients such that Z_i ∼ bernoulli(0.5), U_i ∼ bernoulli(0.2), Y_i ∼ bernoulli(0.1 + 0.3U_i), and X_i ∼ multinom(0.5 − 0.1Z_i − 0.4Z_iU_i, 0.4 + 0.05Z_i + 0.05Z_iU_i, 0.1 + 0.05Z_i + 0.35Z_iU_i). Results are shown for the distribution of the bias across the simulations in the standard instrumental variable numerator in the entire population (mean bias = 0) (A) and in analyses restricted to observations with X = 1 or X = 2 (mean bias = −0.02) (B). In estimating the treatment effect on the risk difference scale, the mean bias from our simulations based on a crude treatment effect estimate was 0.03 (C), while the mean bias from the instrumental variable analysis was −0.15 (D).

To understand the bias in the numerator of the IV estimator, we can (to some degree) repurpose results on the magnitude and direction of collider-stratification bias (10). Specifically, the bias in the IV numerator is a function of how strongly the proposed instrument is associated with treatment, how strongly treatment is associated with the outcome through the unmeasured confounders (which is a function of the strengths of the confounder-treatment and confounder-outcome associations), and the distribution of treatment values.

However, much of the collider-stratification literature is based on dichotomous colliders. Because here the collider is trichotomous and represents our treatment of interest, another subtlety arises. To explain, we need to expand the causal diagram in Figure 1 by representing our trichotomous X with 2 dichotomous indicators X′ (1 if X = 1 or X = 2, 0 if X = 3) and X″ (1 if X = 1, 2 if X = 2, and undefined if X = 3). Thus, IV analyses restricted to persons with X = 1 or X = 2 are restricted to persons with X′ = 1, but they include persons with both levels of X″. In our calendar-time example, during the second time period (Z = 1), relative to patients without the confounder, those with the confounder were less likely to receive treatment 1, more likely to receive treatment 2, and more likely to receive neither treatment. This implies that there is an arrow from U to X′ and another arrow from U to X″ (Figure 3A). Suppose instead it were the case that, within each level of calendar period Z, although the probability of receiving neither treatment (X = 3) versus receiving treatment 1 or 2 (X = 1 or X = 2) may depend on the confounder U, the probability of receiving treatment 2 given that a subject received either treatment 1 or treatment 2 did not further depend on U. Then there would be an arrow from U to X′ but no arrow from U to X″ (Figure 3B). Finally, suppose it were the case that, within each level of Z, the probability of receiving neither treatment (X = 3) versus receiving treatment 1 or treatment 2 (X = 1 or X = 2) did not further depend on the confounder U, but the probability of receiving treatment 2 given that a subject received either treatment 1 or treatment 2 could depend on U. Then there would be an arrow from U to X″ but no arrow from U to X′ (Figure 3C).

Figure 3.

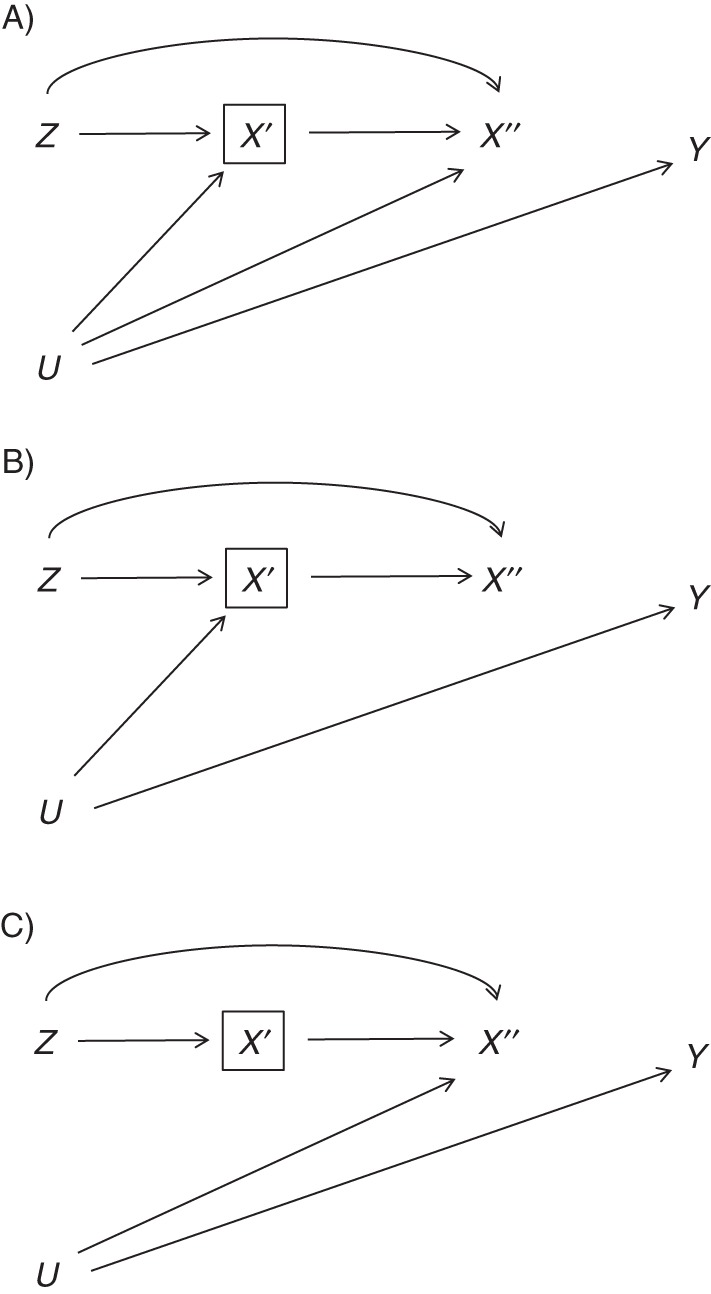
Three possible ways in which an unmeasured confounder may affect treatment decisions: 1) the confounder affects decisions between receiving one of the treatments of interest and other alternatives and also decisions between the 2 treatments of interest (A); 2) the confounder only affects decisions between receiving one of the treatments of interest and alternatives (B); and 3) the confounder only affects decisions between receiving the 2 treatments of interest (C). Z is the proposed instrument; U is an unmeasured confounder; Y is the outcome; X′ is an indicator of being prescribed treatment 1 or 2 versus neither treatment; and X″ is an indicator of being prescribed treatment 1 versus treatment 2 and is undefined otherwise. The box around X′ indicates restriction to patients prescribed X = 1 or X = 2.

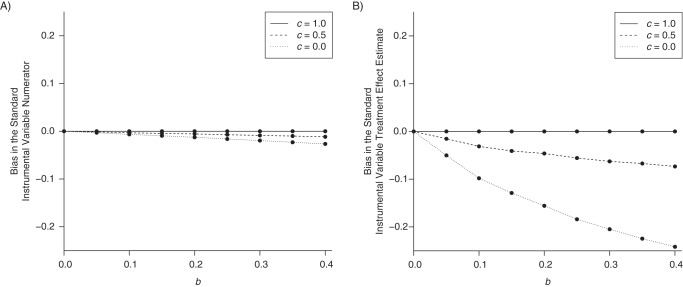
In Web Appendix 1 (available at http://aje.oxfordjournals.org/), we describe appropriate and inappropriate analytical approaches under the 3 scenarios. We show that an IV analysis restricted to subjects who took either treatment 1 or treatment 2 would be inappropriate for data generated under the causal diagrams in parts A and B of Figure 3 but not part C. In fact, we show under the causal diagram in Figure 3C that such an IV analysis remains valid even when we 1) relax the overall sharp null assumption ($Y_i^{x=1}=Y_i^{x=2}=Y_i^{x=3}$ for all subjects i) used in our calendar-time example, 2) allow $Y_i^{x=3}$ to differ from both of the treatment counterfactuals by adding a causal arrow from X′ to Y, and 3) allow $Y_i^{x=1}$ and $Y_i^{x=2}$ to differ by adding a causal arrow from X″ to Y (Web Figures 1 and 2). The causal diagrams in Figure 3 all include an arrow from Z to X′ (i.e., the probability of receiving treatment 1 or 2 versus alternatives depends on the instrument), while if this arrow were absent an IV analysis may be valid (7). In Figure 4, we illustrate the magnitude of bias using data generated under assumptions encoded in each of the 3 causal diagrams in Figure 3. Web Appendices 1 and 2 describe these simulations and the reasons why standard sensitivity analysis formulas for selection bias due to collider stratification are not directly applicable here.

Figure 4.

Summary of bias in the standard instrumental variable numerator (A) and the treatment effect estimated with the standard instrumental variable estimator (B) as a function of the relationship between a binary confounder U and treatment X. We generated 1,000 samples of 20,000 patients such that Z_i ∼ bernoulli(0.5), U_i ∼ bernoulli(0.2), Y_i ∼ bernoulli(0.1 + 0.3U_i), and X_i ∼ multinom(0.5 − 0.1Z_i − bZ_iU_i, 0.4 + c × 0.1 × Z_i + c × b × Z_iU_i, 0.1 + (1 − c) × 0.1 × Z_i + (1 − c) × b × Z_iU_i). We varied b between 0 and 0.4 (x-axis) and varied c to be 0, 0.5, and 1. When c = 0, U does not affect the decision between the treatments of interest (as per the assumptions in Figure 3B); when c = 1, U does not affect the decision between the treatments of interest and the alternatives (as per the assumptions in Figure 3C).

In practice, it will generally be impossible to determine which of the causal diagrams in Figure 3 represents a study. Figure 3A will be a better representation whenever patient characteristics that affect the decision between 2 treatments also affect the decision between those treatments and alternatives. In these settings, confounding by indication is often expected to be less tractable when comparing treatment with no treatment than when comparing 2 active treatments, which implies that investigators may be more successful in blocking the path from U to X″ than in blocking the path from U to X′.

SELECTION BIAS FOR PREFERENCE-BASED INSTRUMENTS

The same form of selection bias can also occur with preference-based instruments whenever there is selection on treatments. However, for calendar-time instruments, the instrument directly causes the treatment (i.e., in Figure 1, there is an arrow directly from Z to X), while we do not directly observe the physician's or facility's preferences and therefore rely on a surrogate instrument for preference (1). For example, some investigators have proposed a proxy of provider preference that is a function of the provider's prescribing decisions for his or her prior patients (11, 12). When comparing a subset of possible treatments with a preference-based proposed instrument, a similar structure of collider-stratification bias is possible, but the magnitude of bias will be a function of how the unobserved preference variable is related to the treatment values and the measured preference proxy. In Web Appendix 2, we propose a framework for simulations mirroring such instruments.

Data from a published observational study on statin therapy and diabetes risk help to illustrate the potential impact of this bias. Using an empirical example has the further benefit of presenting results when the bias is of a more complicated form: In reality, treatment decisions will be driven not by a single dichotomous confounder but rather by a combination of many observed and unobserved patient and physician characteristics. The data come from the Health Improvement Network, a large database of anonymized longitudinal medical records from over 500 primary-care practices in the United Kingdom. The eligibility criteria and the cohort have been described in detail elsewhere (13). In brief, using medical records collected between January 2000 and December 2010, the study included men and women aged 50–84 years who had not been prescribed any statins in the past 2 years, had at least 2 years of continuous recording in the database, and did not have a history of diabetes, cancer, chronic liver or kidney disease, schizophrenia, or antipsychotic medication use. The authors studied the effect of initiating statin therapy on diabetes risk. They found some evidence that lipophilic statin medications, but perhaps not hydrophilic statin medications, may be associated with increased diabetes risk relative to no statin therapy (13).

Suppose the authors had directly compared the effect of hydrophilic statin therapy on the 12-month risk of diabetes with the effect of lipophilic statin therapy via IV estimation using a preference-based instrument. Following previous studies (11, 12), each patient's instrument value could be determined by measuring the class of statin therapy prescribed at the same general practice to the prior patient who met the same eligibility criteria and initiated statin therapy. Necessarily, for each general practice, we would exclude patients who had been seen before the first eligible patient was prescribed a statin.

Of 266,738 patients who met these criteria, 12,663 were prescribed a lipophilic statin, 858 were prescribed a hydrophilic statin, and 253,217 were prescribed neither (including polydrug therapy (n = 30) or no statin (n = 253,187)). The distributions of data on the preference proxy, treatment decision, and risk of diabetes are shown in Table 1. Only 5% of patients were prescribed a statin. Using the analogy of a randomized trial, the overwhelming majority of patients were “noncompliant” in the sense that they did not take treatment; this implies that the “intent-to-treat” effect (IV numerator) will not be informative about the relative effectiveness of treatment 1 versus treatment 2. We consider this example in more detail in Web Appendix 1. In particular, we report treatment effect estimates obtained with IV and non-IV approaches (Web Table 1). Because unmeasured patient characteristics U probably influence decision-making on whether to treat with a statin (U to X′), decision-making on type of statin (U to X″), and diabetes risk (U to Y), and because our data demonstrate that the probability of receiving any statin differs across levels of the instrument (Z to X′), a causal diagram similar to that in Figure 3A is again the most likely data-generating process (under the sharp null), implying that all of our reported estimates will be biased.

Table 1.

Distribution of Proposed Instrument, Treatment, and Outcome for Patients Seen at Primary-Care Practices in the United Kingdom, 2000–2010^a

No. of Patients	Prior Treated Patient's Statin Class	Patient's Statin Class	12-Month Risk of Diabetes
			No. of Cases	%
239,092	Lipophilic	Neither lipophilic nor hydrophilicb	2,780	1.16
12,155	Lipophilic	Lipophilic	213	1.75
456	Lipophilic	Hydrophilic	7	1.54
14,125	Hydrophilic	Neither lipophilic nor hydrophilicb	167	1.18
508	Hydrophilic	Lipophilic	11	2.17
402	Hydrophilic	Hydrophilic	14	3.48

^aStudy population was based on analyses of the Health Improvement Network database presented by Danaei et al. (13).

^bEither no statin (n = 253,187) or polydrug therapy (n = 30).

As this example shows, evaluating the impact of selecting on treatment in IV analyses requires the identification of persons who were eligible for the treatments of interest but did not receive them. For comparability purposes, we applied the same eligibility criteria as those used in a previously published study of the same data (13). In studies that cannot identify eligible patients who did not receive the treatments of interest, the magnitude or even the direction of bias remains unknown, and thus avoidance of IV methods that select on treatment seems desirable. In studies that can identify eligible patients who did not receive the treatments of interest, investigators may consider IV approaches using 3 or more levels of the instrument and the treatment as valid alternatives to the standard IV estimator.

DISCUSSION

We have described the bias in IV analyses of observational studies due to selecting on a subset of available treatments, adding to the list of sources of bias that are unique to IV methods (1–6). Our simulations underscored how bias in the IV numerator is amplified in the treatment effect estimate and how these estimates may be biased in counterintuitive directions. We used calendar time- and preference-based instruments as examples, with simulations described in Web Appendix 2 that could be adapted to understand the magnitude and direction of plausible bias for other instruments.

The structure of this bias is related to known limitations of the intent-to-treat effect and naive per-protocol analyses in head-to-head randomized trials that compare 2 active therapies. When both treatments are superior to no treatment and the proportion of subjects who did not take either treatment differs across the treatment arms, the intent-to-treat effect estimate will be different from zero even if both therapies have exactly the same effect (14, 15). When the only form of noncompliance is refusing (and not switching) treatments, the commonly used naive per-protocol analysis restricted to persons who actually took treatment 1 or 2 can be biased. More generally, when subjects can both switch and refuse treatment, a naive per-protocol analysis can also result in selection bias. This selection bias has the same structure as the one described in this paper for IV analyses that select on treatment (16).

Consider an analytical strategy in which we report the intent-to-treat effect estimate restricted to patients who took treatment 1 or 2 (which would include those who were assigned treatment 1 but took treatment 2, and vice versa). This strategy would not generally be used to analyze a randomized trial, but it is prone to the same selection bias as the naive per-protocol analysis. However, note that this is exactly the strategy used in an IV analysis that selects on treatment: The IV numerator is the intent-to-treat estimate restricted to the subset of patients receiving the treatments of interest. In the randomized trial setting, one can overcome the limitations of the intent-to-treat or naive per-protocol analyses using g-methods under the assumption that one has obtained and appropriately adjusts for data on a set of covariates that make the subjects who took neither active treatment exchangeable with those who took an active treatment conditional on these covariates and treatment arm (14–19). In fact, under such an assumption, one can also perform a valid IV analysis with the goal of estimating the average causal effect of treatment 2 versus treatment 1 (20). (See Web Appendix 1 for further discussion.)

We stress that unless the assumptions encoded in Figure 3C seemed plausible initially, the IV approach (20) is valid only if one can successfully obtain data on a sufficiently large set of covariates to satisfy the above exchangeability assumption. Because the unmeasured patient characteristics that affect the decision between 2 treatments may often affect the decision between those treatments and alternative options, we believe that in many (if not most) epidemiologic studies that have used IV methods, the IV estimates that have been reported are biased because of the same unmeasured covariates that motivated the investigators to use an IV approach; and although this bias can be decreased by measuring additional covariates and then applying g-methods, it generally cannot be eliminated.