Brachytherapy Application with in situ Dose-painting Administered via Gold-nanoparticle Eluters

Abstract

Purpose

Recent studies show promise that administering gold nanoparticles (GNP) to tumor cells during brachytherapy could significantly enhance radiation damage to the tumor. A proposed new strategy for sustained administration of the GNP in prostate tumors is to load them into routinely used brachytherapy spacers for customizable in-situ release after implantation. This in silico study investigates the intra-tumor biodistribution and corresponding dose enhancement over time due to GNP released from such GNP-loaded brachytherapy spacers (GBS).

Method and Materials

An experimentally determined intra-tumoral diffusion coefficient (D) for 10 nm nanoparticles was employed to estimate D for other sizes using the Stoke-Einstein equation. GNP concentration profiles, obtained using D, were then employed to calculate the corresponding dose enhancement factor (DEF) for each tumor voxel using dose-painting by numbers approach, for times relevant to the considered brachytherapy sources' lifetimes. The investigation is carried out as a function of GNP size for clinically applicable low dose rate brachytherapy sources: I-125, Pd-103, Cs-131.

Results

Results showed that dose enhancement to tumor voxels/sub-volumes during brachytherapy can be customized by varying the sizes of GNP released or eluted from the GBS. For example, using 7 mg/g GNP concentration, significant DEF (> 20%) could be achieved 5 mm from a GBS after 5, 12, 25, 46, 72, 120, and 195 days, respectively, for GNPs sizes of 2 nm, 5 nm, 10 nm, 20 nm, 30 nm 50 nm, and 80 nm when treating with I-125.

Conclusions

Analyses show that using Cs-131 provides the highest dose enhancement to tumor voxels. However, given its relatively longer half-life, I-125 presents the most flexibility for customizing the dose enhancement as a function of GNP size. The findings provide a useful reference for further work towards potential development of a new brachytherapy application with in-situ dose-painting administered via gold-nanoparticle eluters, for prostate cancer.

1. Introduction

A number of recent studies have concluded that administering gold nanoparticles (GNP) to cancer cells during brachytherapy could lead to significant dose enhancement to the tumor [1–4]. However, delivery of sufficiently potent concentrations of nanoparticles into solid tumors remains a challenge [5–7]. This is mostly attributed to the physiological barriers imposed by the abnormal tumor vasculature and the dense interstitial matrix, a complex assembly of collagen, glycosaminoglycan, and proteoglycans, which may hinder deep penetration of the nanoparticles [5,7].

In an effort to overcome this challenge, a recent study [8] has proposed a biological in-situ dose painting approach in which inert brachytherapy spacers, routinely used for increasing spatial accuracy during brachytherapy, could be loaded with radiosensitizing drugs to be released or eluted in situ after implantation to enhance therapeutic ratio. The study concluded that drug loading in such implantable devices, as brachytherapy spacers, provides new opportunities for therapy modulation via biological in situ dose painting.

Building on these concepts, this study explores the feasibility of a potential approach where GNP, which are relatively non-toxic [2,8–12], would be loaded in the inert brachytherapy spacers instead of drugs. Such a gold-loaded brachytherapy spacer (GBS) could be produced by coating the inert spacers with polymer films containing GNP similar to procedures for coating fiducials with polymer films loaded with poly(D,L-lactide-co-glycolide) (PLGA) nanoparticles [13]. Alternatively, there is potential for producing GBS by incorporating GNP in PLGA polymer millirods during the gel phase of production [14]. After implantation of the GBS, the polymer coating on the GBS would degrade, releasing the GNP in situ, which then diffuse into the tumor sub-volume. The sustained release of GNP, in-situ, from the GBS, and consequent 3-dimensional intra-tumor biodistribution over time could then be customized by varying GNP size, initial concentration, etc to enhance brachytherapy effect in desired tumor sub-volumes. Since, implantation of inert spacers is already part of routine clinical practice, replacing the inert spacers with GBS would come at virtually no additional inconvenience to patients. The theoretical feasibility of this potential new approach is explored in this work by investigating the intra-tumor biodistribution and corresponding dose enhancement over time for GNP released from the GBS, as a function of nanoparticle size for different low dose rate (LDR) brachytherapy sources I-125, Pd-103, and Cs-131.

2. Materials and methods

An in vivo determined diffusion coefficient, D, of 2.2 × 10⁻⁸ cm²s⁻¹ for 10 nm nanoparticles [15] was employed to estimate D for other nanoparticle sizes (2, 5, 20, 30, 50, and 80 nm) by using the Stokes-Einstein equation (equation 1):

$$D=\frac{K_{B}T}{6\pi \eta r}$$ (1)

Here r is the radius of the nanoparticles, K_B the Boltzmann's constant, T the absolute temperature, and η the viscosity. Assuming a burst release of the GNP from the GBS, the diffusion of the GNP, given by the concentration C (x, t), as a function of distance (x) from the spacer over time (t) can be calculated by applying equation 2:

$$\frac{C(x,t)-C_0}{C_S-C_0}=1-erf\left(\frac{x}{2\sqrt{Dt}}\right)$$ (2)

Equation 2 is a solution of Fick's second law of diffusion for the given boundary conditions that the concentration of GNP in the tumor cells is C₀ (considered zero here) prior to burst release, while the concentration of GNP in the GBS is C_s. For simplicity in this initial study, C_s was assumed to be 7 mg/g since this concentration has been employed in previous in vivo studies on GNP [1,16,17]. erf is the error function employed in modeling one-dimensional diffusion in the previous in vivo experimental work [15]. The concentration profile calculations assumed steady release of GNP, with minimal elimination during treatment, with the main mechanism of GNP motion being via diffusion [7]. The assumption of burst release allows the use of 7 mg/g concentration of GNP present in voxels at the interface between the spacer and the tumor subvolume. The steady state assumption implies that the number of nanoparticles released from the spacer per unit time remains constant so that at the spacer/tumor interface, voxels there always have at least 7 mg/g. The implications of these assumptions and others will be discussed in the discussion section. The concentration C(x, t) was investigated for different size GNP (2, 5, 10, 20, 30, 50 and 80 nm) over times relevant to the brachytherapy source lifetimes. The range of investigated distances considered was informed by previous studies on prostate tumor sizes, with mean tumor radius of about 10 mm[18,19], and possible high-risk (hypoxic) tumor sub-volume sizes which can be up to 50% of the tumor with corresponding radius of up to 8 mm [20].

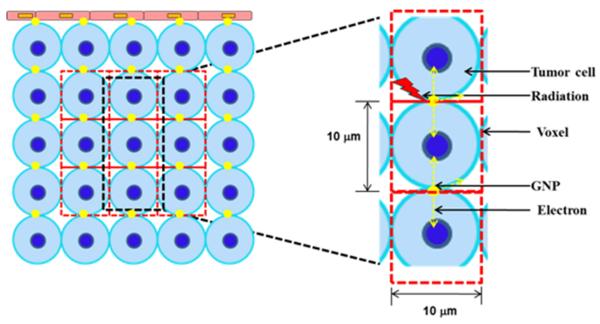
Dose enhancement or radiation boosting of a high-risk tumor sub-volume with functional image voxels obtained via methods such as Magnetic Resonance Imaging (MRI) or Positron Emission Tomography (PET) imaging, is customarily referred to as dose painting. In dose-painting by numbers (DPBN), dose is planned or assigned to each high-risk tumor voxel based on the local distribution of functional imaging parameters derived from the PET or MRI. A similar approach was employed in this study, whereby, dose enhancement factor (DEF), was assigned to each tumor voxel based on the local distribution or concentration of GNP. The DEF represents the ratio of dose to each tumor voxel with and without GNP. Detailed steps for calculating DEF due to radiation-induced photo-/Auger electrons emitted by GNP are described and validated with results using Monte Carlo Simulations in previously published work [17,21–23] involving tumor endothelial cells modeled as a rectangular slab (10 μm × 10 μm × 2 μm). The same steps were used here, except for the use of a slab of size 10 μm × 10 μm × 10 μm representing a tumor voxel or sub-volume containing a tumor cell of diameter 10 μm (Figure 1). In brief, photons from the LDR brachytherapy sources, that would yield a given dose without GNP (e.g. from the treatment planning system), interact with the GNP associated with each tumor voxel via the photoelectric effect to yield photo-/Auger electrons as illustrated in figure 1. An emitted electron loses/deposits its kinetic energy, E, in the tumor voxel as described by the Cole formula [24] (equation 3):

$$\frac{dE}{dR}=3.316{(R+0.007)}^{-0.435}+0.0055R^{0.33}$$ (3)

Here R = R_tot −r, where r is the distance from the photoelectron emission site, and R_tot is the total range of the photoelectron (equation 4).

$$R_{tot}=0.431{(E+0.367)}^{1.77}-0.007$$ (4)

The total energy (dose = energy/tumor mass) deposited in a tumor voxel is then calculated by simple integration of equation 3 for the range of emitted photo-/Auger electron energies. In the DEF calculations, it is considered that the local GNP concentration over immediately neighboring tumor voxels (highlighted in figure 1) is uniform or approximately the same as that of the investigated voxel. Hence, the specific location of the nanoparticle in the voxel does not influence the calculated DEF, with the energy deposited by photo-/Auger electrons in an adjacent voxel ('cross-fire') accounted for. Given that the range of a photo-/Auger electron from GNP for the investigated brachytherapy sources is less than 10 μm, the micrometer-range dose enhancement from the electrons is expected to be more highly localized than brachytherapy radiation. This could allow for planned dose-painting or subvolume radiation boosting without any significant increase in dose to the rectum and other organs at risk not containing GNP. The DEF profiles as a function of time for the different GNP sizes were investigated for three brachytherapy sources: Pd-103 (average photon energy of 21 keV; half life of 17.2 days), I-125 (average photon energy of 27 keV; half life of 59.4 days), and Cs-131 (average photon energy of ca. 30 keV; half life of 9.7 days).

Figure 1.

(Left) Schematic of tumor sub-volume cross-section showing tumor cells with GNP. (Right) Model for calculating DEF to tumor voxels; radiation-induced photoelectrons from GNP deposit their energy in the tumor voxel (Figures not to scale.)

3. Results

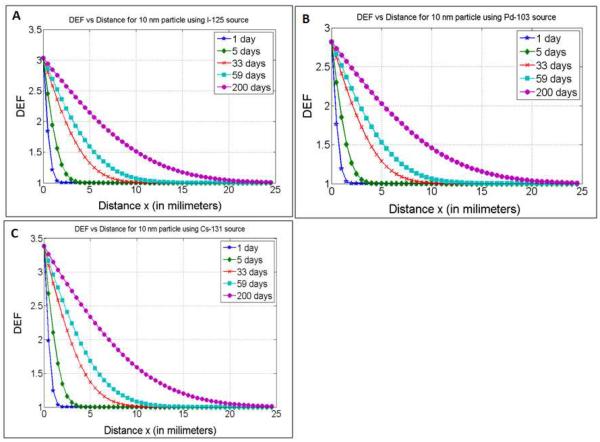
The concentration versus distance profiles for the 10 nm particle with experimentally determined D is shown in figure 2A for different times. The sample times considered were days: 1, 2, 5, 10 (half-life of Cs-131), 17 (half-life of Pd-103), 33 (number of days after which 90% of Cs-131 dose is delivered), 59 (number of days after which 90% of Pd-103 dose is delivered, and approximate half-life of I-125), 200 (number of days after which 90% of I-125 dose is delivered). Figure 2B shows DEF versus concentration plot for the different sources considered. The results highlight monotonic linear increase in DEF with concentration as would be expected. Despite higher average photon energies, which result in relatively fewer numbers of emitted photoelectrons, the DEF for Cs-131 for a given concentration is higher than that of I-125 and Pd-103. A closer analysis indicated that, despite the fewer number of photoelectric interactions by Cs-131 photons, the photoelectrons produced with the L-edge of gold (ca. 13 keV) are more energetic than those produced by I-125 or Pd-103 photons. The higher overall energy deposited by the more energetic albeit fewer electrons resulted in higher DEF compared to the other sources which had relatively higher number of emitted photoelectrons but with overall less energy.

Figure 2.

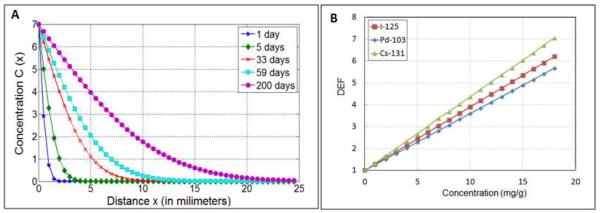
(A) Concentration as a function of distance for 10 nm GNP at different times after release; (B) DEF versus concentration for I-125, Pd-103, Cs-131 LDR brachytherapy sources.

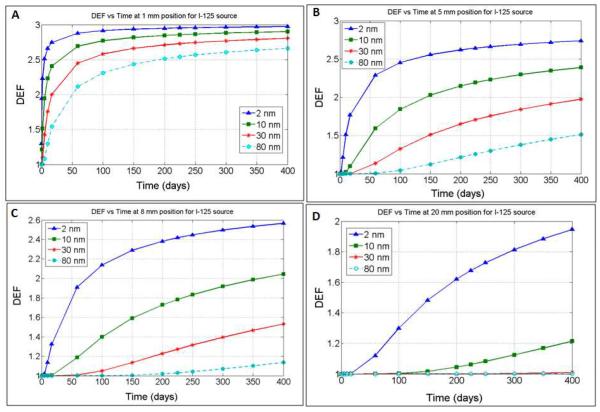
DEF versus distance profiles are shown in figure 3A–C for I-125, Pd-103, and Cs-131, respectively. In general, the results show that for any given position, the DEF increases over time as would be expected due to increased GNP concentration. The time evolution of the DEF is further illustrated in figure 4 for I-125 as a function of different GNP sizes, with D values ranging from 11 × 10⁻⁸ cm²s⁻¹ to 0.275 × 10⁻⁸ cm²s⁻¹. The results are shown for sample distances: 1 mm, 5 mm, 8 mm, and 20 mm, with the generated profiles showing greater DEF over time for smaller GNPs sizes at the distances considered due to faster diffusion. For example, significant DEF (> 20%) could be achieved 5 mm from a spacer after 5, 12, 25, 46, 72, 120, and 195 days, respectively, for GNPs sizes of 2 nm, 5 nm, 10 nm, 20 nm, 30 nm, 50 nm, and 80 nm when treating with I-125. Table 1 highlights these results in comparison to those obtained for Pd-103 and Cs-131 sources. It is observed that for Pd-103, significant DEF could be achieved at 5 mm after 5, 13, 27.5, 50, 77.5, 130, and > 200 days respectively for 2 nm, 5nm, 10 nm, 20 nm, 30 nm 50 nm, and 80 nm size GNPs. For Cs-131 significant DEF could be achieved at the same position after 5, 11, 24, 42.5, 67.5, 110, and 176 days respectively for 2 nm, 10 nm, 20 nm, 30 nm 50 nm, and 80 nm size GNPs.

Figure 3.

DEF as a function of distance when using 10 nm GNP during I-125, Pd-103 and Cs-131 brachytherapy

Figure 4.

DEF as a function of time for different size nanoparticle at a distance of (A) 1 mm (B) 5 mm (C) 8 mm and (D) 20 mm from the GBS when using I-125.

Table 1.

Time in days for achieving significant DEF (> 20%) at selected positions as a function of nanoparticle size for I-125, Pd-103 and Cs-131 sources for GBS with 7 mg/g concentration.

		I-125 source	Pd-103 source	Cs-131 source
Position (mm)	GNP Size (nm)	Time (days)	Time (days)	Time (days)
1	2	0	0	0
1	5	0.5	0.5	0.5
1	10	1	1	0.9
1	20	2	2	1.7
1	30	3	3.1	2.7
1	50	4.9	5.1	4.4
1	80	7.8	8.2	7.1
5	2	5	5	5
5	5	12	13	11
5	10	25	27.5	24
5	20	46	50	42.5
5	30	72	77.5	67.5
5	50	120	130	110
5	80	195	>200	176
8	2	12	13	11.5
8	5	31	34	29
8	10	60	66	56
8	20	120	132	>200
8	30	182	198	>200
8	50	>200	>200	>200
8	80	>200	>200	>200
20	2	72	82	70
20	5	192	>200	177
20	10	>200	>200	>200
20	20	>200	>200	>200
20	30	>200	>200	>200
20	50	>200	>200	>200
20	80	>200	>200	>200

Table 1 results demonstrate the potential for customizing the DEF as a function of GNP size; the results provide preliminary indication of what range of GNP sizes may be appropriate when planning for the different brachytherapy sources at a given distance from a GBS. For example, the data suggests that significant DEF is achievable for any of the brachytherapy sources at very close distances (ca. 1 mm) from the GBS for any of the nanoparticle sizes considered. Meanwhile, employing GNP of greater than 50 nm size to achieve significant dose enhancement at 5 mm distance or greater may not be expedient, particularly during Cs-131 or Pd-103 brachytherapy given their relatively shorter half-life values. Even GNP sizes of greater than 20 nm may not be practical for Cs-131 for achieving significant DEF at distances 5 mm or more, as over 90% of the treatment dose (ca. 104 of typical 115 Gy) would already be delivered by day 34, and hence the DEF (> 20%) would apply to very little remaining dose. Meanwhile, given the higher half-life of about 59 days, the use of I-125 as a source apparently may afford greater flexibility to customize the DEF as a function of GNP size.

4. Discussion

Altogether, the in silico results demonstrate the feasibility for prostate cancer, highlighting the potential to optimize treatment efficacy depending on GNP size for a given brachytherapy source type. The choice of brachytherapy source type for such an approach will ultimately also depend on the GBS polymer degradation rate. A recent study [14] investigating the degradation of PLGA polymer as a function of different polymer weight ratios indicated that many days may be needed for in vivo biodegradation to achieve steady state release of a drug loaded in PLGA. Taking these factors into account, the preliminary results in this work indicate that there would be even less flexibility in the use of brachytherapy sources with short half-life like Cs-131 or Pd-103. Based on the results, such sources would likely have to be used mainly in conjunction with ultrasmall GNP with quick release GBS. The range of nanoparticle sizes available for customization of the dose enhancement would be more limited for such sources with shorter half-life.

The current study determined DEF profiles due to release of GNP from one GBS only. In practice one would be able to use more than one GBS, which would allow for more flexibility or degrees of freedom for customization. Essentially, it may be more practical to load GNP in more spacers than to load just one spacer with a high concentration of GNP. The maximum loading capacity of GBS, in any case, remains to be determined experimentally. Also related to this, the starting concentration of GNP which was chosen to be 7 mg/g based on previous studies may be variable. It may be possible to employ higher concentrations, which could allow for higher DEF values over time for each tumor voxel compared to the results shown in this study. However, this initial study provides a useful reference when planning future more extensive studies with three dimensional diffusion, and with possible superposition of concentrations from neighboring spacers (typically 5 mm apart).

It is worth noting that such three dimensional diffusion would likely not be isotropic [7] and D may depend on tumor type. While the effect of employing the Stokes-Einstein equation with same viscosity coefficient may not be significant for GNP < 10 nm [25], restricted diffusion is expected to be significant for larger sizes, resulting in higher potential for non-isotropic diffusion. Also the Stoke-Einstein formalism does not take into account potential variations in vascularization or higher interstitial pressure. These factors could influence the distribution of the GNP. A recent review [7] highlights possibilities that could minimize the influence of these variables e.g. normalization of the extracellular matrix, using matrix-modifying agents, which could also enable more uniform distribution. Planned studies would investigate optimal combination of these approaches for enhancing brachytherapy using GNP.

The current study did not consider possible elimination of GNP from the tumor during the treatment. This would, in principle, potentially reduce the available GNP for dose enhancement and hence the DEF values. Studies show that any elimination would depend on nanoparticle size, shape and on whether it is functionalized or not. Functionalization to actively bind to tumor cells or facilitate GNP tumor cell uptake would minimize elimination but also reduce GNP diffusion distance [7,15]; hence more work would be needed to find the right balance. In general, an advantage of using nanoparticles in nanomedicine is their enhanced retention in tumors and ability to functionalize the nanoparticle, and so it should be possible to find the optimal balance. Experimental studies providing information on the uptake, retention/elimination rates of nanoparticles in tumors as a function of nanoparticle size and other factors would benefit further work.

While the current study used analytically calculated DEF, in principle, DEF values from other studies as a function of concentration could also be employed including dose enhancement calculated via Monte Carlo simulations. Montenegro, Pradhan, Nahar and other co-workers [26–28] proposed a Resonant Nano-Plasma Theranostics method using Monte Carlo simulations to calculate the dose enhancement from high-Z nanoparticles. Their results also showed significant enhancement by gold nanoparticles for photon sources in the kV energy range. Other authors [1,2,24] have also employed Monte Carlo to calculate dose enhancement values due to GNP for the studied concentration. The analytical approach employed here to calculate the DEF values was validated in comparison with Monte Carlo results in previous publications [17,22–24].

The uncertainties in DEF for the analytical approach are estimated to be within 10% [22]. Despite the small (micrometer range) tumor voxel/subvolume considered (figure 1), the local concentration of GNP may not be homogenous. DEF calculations show that variations in local concentrations of down to 1 mg/g would still achieve a significant dose enhancement of over 20% for all brachytherapy sources considered. Also, the DEF values were calculated, without considering the specific location of the GNP in the voxel or cell. Hence the dose enhancement to the nucleus (damage to DNA) is expected to be higher for GNP closer to the nucleus and lower for GNP further away from the nucleus given the shorter range of Auger electrons. Recent research has indicated that nuclear targeting of GNP in cancer cells is feasible [29]. Such targeting could help localize more GNP near the nucleus, minimizing this uncertainty while maximizing dose enhancement to the nucleus. Beside targeting, other design parameters e.g. GNP size (which also determines uptake into the cell), or spacer location could be considered in minimizing uncertainties or ensuring sufficiently potent GNP concentration in target tumor sub-volume. Ultimately, because of the complex interplay of these different factors, experimental studies are needed to determine the optimal parameters for maximizing the dose enhancement to target tumor sub-volume.

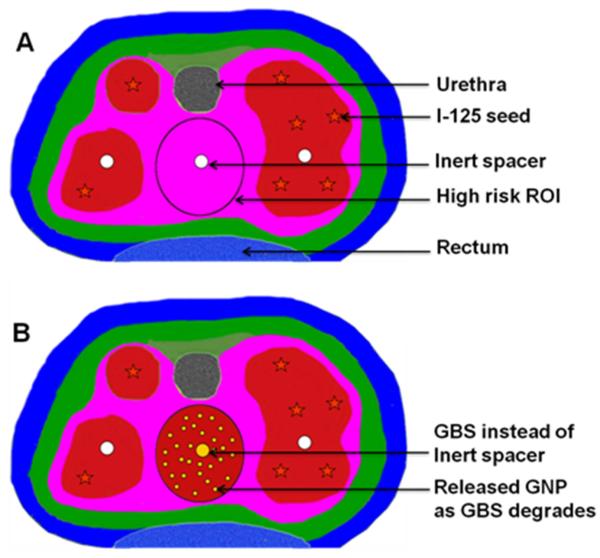
Figure 5 is a schematic to highlight the potential clinical impact, if the GBS approach can be developed. The color wash in figure 5A illustrates the dose distribution prescribed by a physician's treatment plan for a patient using I-125 seed irradiation only. Red color areas have the highest dose followed by pink. The circle (O) is a hypothetical high-risk tumor sub-volume or ROI identified via MRI or PET needing a dose boost, which cannot be achieved without increased dose (toxicity) to the rectum. In comparison figure 5B illustrates potential dose distribution using this approach when the GBS is used instead of usual inert spacer. The I-125 radiation plus additional dose from radiation induced photo-/Auger electrons from the released GNP leads to dose boost (red color) to the high risk ROI without increased toxicity to urethra/rectum. If such an approach can be successfully developed, this could potentially be employed during initial treatment of locoregional prostate cancer for sub-volume radiation boosting to high-risk tumor sub-volumes while minimizing dose to neighboring organs at risk. Kuban et al [30] recently reported that, if dose to normal tissue like the rectum can be minimized, even moderate radiation boosting would significantly decrease prostate cancer recurrence.

Figure 5.

(A) Illustration of hypothetical I-125 radiation-only dose distribution for prostate cancer. (B) Illustration of Dose distribution using the present approach where GBS is used instead of usual inert spacer.

In-situ administration of GNP would potentially be more cost effective compared to intravenous administration. In-situ administration with the GBS also circumvents the central problem in the use of nanoparticles, i.e. directing a substantial amount to the intended treatment site or tumor sub-volume. The findings in this work provide impetus for further work towards development of a potential GNP-aided brachytherapy application, employing GBS for customizable and sustained in-situ administration of the GNP.