Should evolutionary geneticists worry about higher-order epistasis?

Abstract

Natural selection drives evolving populations up the fitness landscape, the projection from nucleotide sequence space to organismal reproductive success. While it has long been appreciated that topographic complexities on fitness landscapes can arise only as a consequence of epistatic interactions between mutations, evolutionary genetics has mainly focused on epistasis between pairs of mutations. Here we propose a generalization to the classical population genetic treatment of pairwise epistasis that yields expressions for epistasis among arbitrary subsets of mutations of all orders (pairwise, three-way, etc.). Our approach reveals substantial higher-order epistasis in almost every published fitness landscape. Furthermore we demonstrate that higher-order epistasis is critically important in two systems we know best. We conclude that higher-order epistasis deserves empirical and theoretical attention from evolutionary geneticists.

Introduction

Epistasis is the geneticist’s term for mutational interaction. Colloquially, epistasis can be regarded as our surprise at the phenotype when mutations are combined, given the constituent mutations’ individual effects. The recognition of epistasis between pairs of mutations in both discrete, Mendelian [1] and continuous [2,3] traits goes back roughly 100 years, but recent experimental advances draw attention to interactions between more than two mutations. For example, how often does pairwise epistasis itself vary with genetic background [4•,5••]? Critically, such higher-order interactions cannot be captured by pairwise epistasis [6,7].

Epistasis is also fundamental to systems biology, because interdependencies are intrinsic to networks, its central object of study. For example, data on pairwise epistasis between gene deletions have provided insight into metabolic networks in yeast [8••,9,10 and E. coli [11]. Epistasis is also of critical importance to the analysis of genome-wide association data [12,13]

For population and evolutionary geneticists, one phenotype is of particular interest: reproductive success (or fitness). Theoretical and experimental results link pairwise epistasis for fitness to speciation [e.g. [14,15]], the evolutionary advantage of recombination [e.g. [16–18]] and opportunities for adaptation [e.g. [19••,20]]. Our own interest in higher-order epistasis began from an appreciation that only epistasis [21,22•] can give rise to topographic complexities on the fitness landscape [23]. To illustrate this point, first consider nucleotide sequence space [24], in which all pairs of genotypes differing by a single point mutation are adjacent to one another. The fitness landscape is then the projection from such a spatially organized sequence space to organismal fitness. Finally, ruggedness in the fitness landscape arises if an only if the sign of the fitness effect of mutations varies with genetic background, elsewhere called sign epistasis [21]. Importantly however, we lack a more complete quantitative understanding of the relationship between landscape topography and higher-order epistasis.

Here we first review recent empirical studies that follow the groundbreaking approach of Malcolm et al. [25] to describe fitness landscapes using reverse genetics. That study characterized the combinatorially complete set of eight alleles of an avian lysozyme defined by all combinations of three missense mutations. Other studies have used traditional genetic crosses or random mutagenesis to describe fitness landscapes. Whatever their method, these recent surveys demonstrate that fitness landscapes are not terribly smooth [19••,25–29,30••].

The next challenge is to characterize the epistasis in these data [31•]. In any system defined by point mutations at L sites, there are $\left(\begin{array}{c}L\\ k\end{array}\right)$ subsets of k mutations which may or may not interact. Consequently there may be this number of epistatic terms of order k. Here we propose a generalization of the classical population genetic framework which allows us to compute epistasis of all orders (see Box 1). Using this approach we find substantial amounts of higher-order epistasis in almost every published dataset. We also show that higher-order epistasis is of evolutionary importance in two systems we know best.

Box 1 - A natural framework for computing epistasis of arbitrary order.

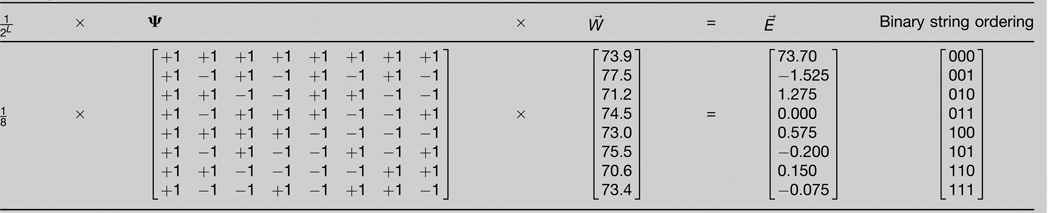
Abstractly, any combinatorially complete fitness landscape is a mapping from all 2^L genotypes defined by L biallelic loci to fitness [21]. This can be represented as a vector W⃑ of 2^L fitness values, ordered by an L bit binary number whose digits 1 and 0, respectively, signal the presenceor absence of the mutation at the corresponding loci [28]. Thus for example, in a system with three mutations there are 2³ = 8 fitness values in W⃑, and the element W₀₁₁ represents the fitness of the genotype carrying mutations at only the second and third loci.

The Walsh Transform is a linear transformation of W⃑ into another vector E⃑, called the Walsh coefficients [57–59]. E⃑ also has 2^L values, again ordered by an L bit binary number, but here digits 1 and 0 represent the presence or absence of a contribution from the mutation at each locus to the corresponding interaction term. For example again assuming three mutations, E₀₁₁ represents the interaction between the second and third loci.

The Walsh transformation yields E⃑ by multiplying W⃑ with an invertible, symmetric 2^L × 2^L transformation matrix ψ together with a constant 2^−L (figure). Because ψ is its own inverse to within a constant, subsequent multiplication of E⃑ by ψ restores W⃑. (Algebraically, 2^−L. ψ·ψ = I, where I is the identity matrix.) In general, there will then be $\left(\begin{array}{c}L\\ k\end{array}\right)$ terms involving exactly k interacting loci in E⃑; we describe these as k^th order terms, and note that the order of each element in E⃑ is the number of 1’s in its subscript.

A critical feature of the Walsh framework is that its basis is orthogonal, since the dot product of any two row vectors in ψ is zero. In other words, each Walsh coefficient is independent of all others, which explains why pairwise interactions cannot capture higher-order terms. This orthogonality also links the Walsh transform to both the discrete Fourier transform [60,61], and 2^k factorial analysis from experimental design [46,62].

We now develop the connection between Walsh coefficients and familiar population genetic parameters.

First order Walsh coefficients (i.e. those with a single 1 in their subscript) are related to classical selection coefficients (s = W_mutant – W_w.t., w.t. denotes wild-type), which represent the fitness effect of single mutations. To see this consider E₀₀₁ (the second line in the 3-locus case illustrated in the figure):

$$\frac{1}{8}[(W_{000}-W_{001})+(W_{010}-W_{011})+(W_{100}-W_{101})+(W_{110}-W_{111})]$$

By grouping terms we have highlighted the fact that E₀₀₁ is proportional to the sum of four quantities: the effect of a mutation at the rightmost locus on the 000, 010, 100, and 110 genetic backgrounds. Thus, E₀₀₁ is exactly half the effect of a mutation at the rightmost locus, averaged over all backgrounds. Following the subscripting convention outlined above for E⃑, we compute the average selection coefficient for the rightmost mutation $\overline{s_{001}}\equiv 2E_{001}$ given the combinatorially complete fitness vector W⃑. We similarly compute average selection coefficients $\overline{s_{010}}\equiv 2E_{010}$ and $\overline{s_{100}}\equiv 2E_{100}$ for mutations at the center and leftmost loci.

Continuing in this manner we see that second order Walsh coefficients (i.e. those with two 1’s in their subscript) are intimately related to pairwise epistatic coefficients. Classically, epistasis between two mutations i and j is represented by e_ij, equal to the difference between a double mutant’s expected and observed fitness. Assuming an additive expectation, this means that for two arbitrary mutations A and B, e_AB = W_AB -[W_w.t. + (W_A - W_w.t.) + (W_B - W_w.t.)] = (W_w.t. - W_A) - (W_B - W_AB). (Note that e_AB is symmetric with respect to mutations A and B: e_AB= e_BA.)

Now compare the rightmost expression for e_AB with a second order Walsh coefficient, for example,

$$E_{011}=\frac{1}{8}\{[(W_{000}-W_{001})-(W_{010}-W_{011})]+[(W_{100}-W_{101})+(W_{110}-W_{111})]\}$$

(the fourth line of the figure). The two terms in square brackets each have the structure of e_AB. Furthermore, these terms are identical except for allelic state at the leftmost locus, that is, except for genetic background. Thus E₀₁₁ is exactly one fourth the epistasis between the rightmost two loci averaged across backgrounds. Again following the subscripting convention above, we compute the average epistasis between these two loci as $\overline{e_{001}}\equiv 4E_{011}$. (And similarly $\overline{e_{101}}\equiv 4E_{101}$ and $\overline{e_{110}}\equiv 4E_{110}$.)

The pattern described for first and second order Walsh coefficients can be generalized up to Lth order interactions on combinatorially complete datasets of L mutations. In particular, every k^th order Walsh coefficient will be proportional to the sum of 2^L-k interaction terms, each of which involves 2^k differences. Hence, we compute the k^th order epistatic coefficient as 2^k times the corresponding Walsh coefficient. We note in passing a close connection between our epistatic coefficients and those in the Taylor expansion of the fitness landscape [61].

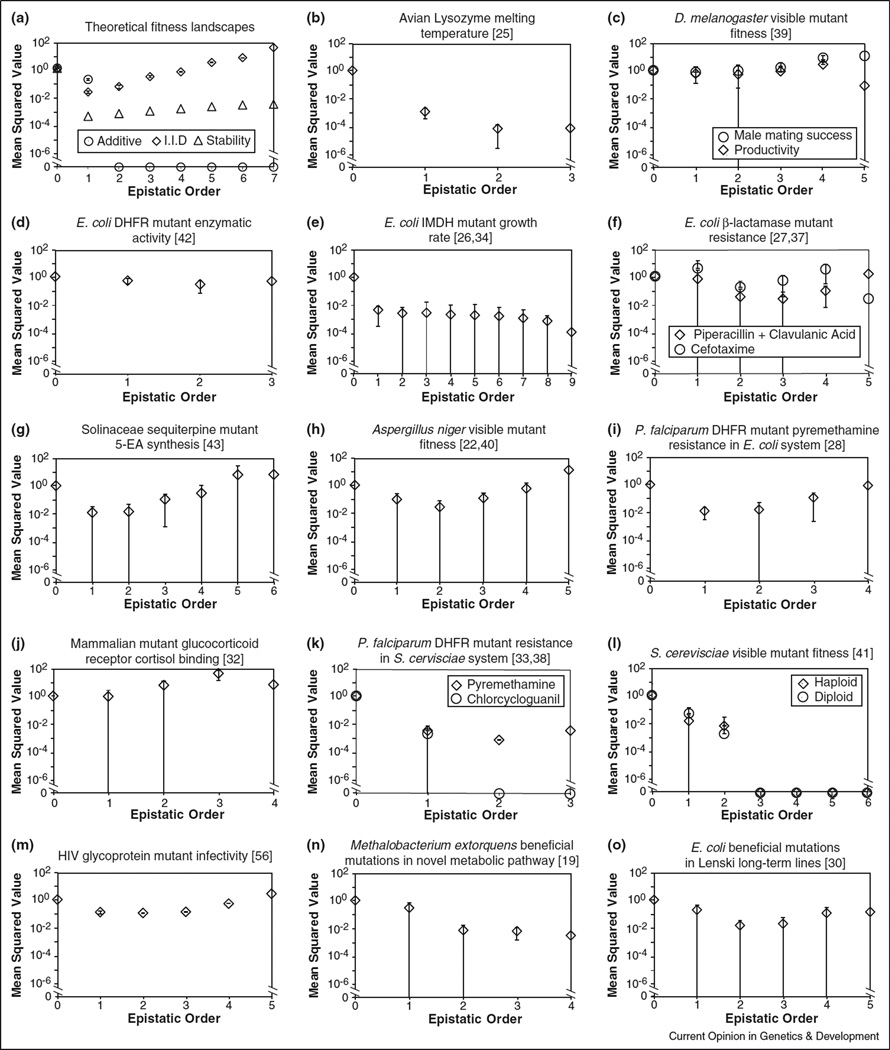
Two points of reference are useful (Figure 1a). On additive (or log-transformed multiplicative) fitness landscapes, all epistatic coefficients of second order and above are numerically equal to zero. And in contrast, on fitness landscapes whose values are independent and identically distributed on any probability density function, mean squared epistatic coefficients increase exponentially with order. We expect biological datasets to lie between these two extremes.

Empirical fitness landscapes

Table 1 lists the 14 systems we know of in which fitness (or a proxy phenotype) for all combinations of some set of point mutations has been reported. Interestingly, while the datasets are formally similar, these studies spring from three distinct intellectual traditions.

Table 1.

Published combinatorially complete fitness landscapes^a

System (assay)	Number of mutations	Number of genes	Largest combinatorially complete subset	Study’s main findings	Figure 1 panel	Citation
Avian lysozyme (melting temperature)	3	1	3	No selectively neutral pathway links the only two extant alleles	b	[25]
D. melanogaster visible mutant (productivity and male mating success)	5	5	5	Epistasis and sexual selection may attenuate genetic load in natural populations. Higher-order epistasis observed.	c	[39]
E. coli dihydrofolate reductase mutants (in vitro enzymatic activity)	5	1	3	Fitness landscape smoother than random; first study to offer quantitative definition of roughness	d	[42]
E. coli isopropyl malate dehydrogenase mutants (growth rate)	7	1	7	Essentially all epistasis for fitness arises in mapping from biochemistry to fitness	e	[26,34]
E. coli β-lactamase mutants (resistance against two antibiotics)	5	1	5	Sign epistasis constrains the number of selectively accessible mutational trajectories to highest-fitness allele; adaptive trajectories are rarely reversed when environment changes	f	[27,37••]
Solinaceae sequiterpine mutants (5-EA synthesis)	9	1	6	Rugged landscape in which alternate catalytic specificities are often mutationally nearby	g	[43]
A. niger visible mutations (growth rate)	8	8	5	Genetic recombination does little to speed adaptation; fitness landscapes have intermediate ruggedness	h	[22•,40]
P. falciparum dihydrofolate reductase mutants in E. coli (resistance against an antimalarial drug)	4	1	4	Clinical data consistent with evolutionary trajectory predicted from in vitro results	i	[28]
Mammalian glucocorticoid receptor mutants (cortisol binding)	4	1	4	Epistasis renders evolutionary trajectories selectively irreversible	j	[32]
P. falciparum dihydrofolate reductase mutants in S. cervisiae (resistance against two antimalarial drugs)	5	1	3	Landscapes not well correlated across environments	k	[33,38]
S. cerevisiae visible mutations (growth rate)	6	6	6	Epistasis is variable and genetic recombination does little to speed adaptation	l	[41]
HIV glycoprotein mutants (in vitro infectivity)	7	1	5	Common, strong epistasis. Higher-order effects noted	m	[56]
Metholobacterium extorquens beneficial mutations in novel metabolic pathway (growth rate)	4	4	4	Negative pairwise epistasis among beneficial mutations	n	[19••]
E. coli beneficial mutations (growth rate)	5	5	5	Negative pairwise epistasis among beneficial mutations	o	[30••]

^aSorted by year of publication.

The original case [25] begins from the observation that in game bird lysozyme, threonine-isoleucine-serine and serine-valine-threonine are the only two amino acid triplets that are ever observed at residues 40, 55 and 99, respectively. The authors reasoned that these two extant forms must be linked phylogenetically by some succession of functionally equivalent alleles defined by other combinations of these three residues. They thus synthesized all six such lysozymes, and characterized the melting temperature of each. Remarkably, all conceivable mutational trajectories between the two extant triplets include at least one mutational intermediate whose melting temperature is outside the physiologically permissible range [25]. Thus this system exhibits sign epistasis [21], since the same mutations increase melting temperature in some genetic contexts while reducing it in others [see Figure 2 in citation [25]]. The authors concluded that some compensatory processes must have been at work during the evolution of bird lysozyme: either other residues influencing melting temperature, or natural selection responding to other enzymatic properties conferred by these mutations.

Figure 2. The Walsh transform of the fitness landscape W⃑ into Walsh coefficients E⃑.

Here we consider the fitness landscape defined by all combinations of L = 3 mutations in the avian lysozyme characterized by Malcolm et al. [[25]; melting temperature is used as a proxy for fitness]. Each row is ordered by a binary string whose bits left-to-right correspond to the T40S, I55V and S91T mutations. (Here, T, S, I and V stand for threonine, serine, isoleucine and valine, respectively, and the number is the mutated residue in the enzyme.) In the case of the fitness landscape vector W⃑, each ‘1’ in the string signals a contribution from that mutation to the corresponding fitness value. In the Walsh coefficients vector W⃑, each ‘1’ in the string signals a contribution from that mutation to the corresponding interaction coefficient. Thus for example we observe that the Walsh coefficient corresponding to the S91T mutation is equal to −1.53°C (second line) and that Walsh coefficient corresponding to the I55V and S91T mutations (fourth line) is equal to zero. ψ can be written for arbitrary L, as for example with the hadamard() function in the software package Matlab (Mathworks, Natick, MA).

Many studies follow the lysozyme tradition, finding that sign epistasis is widespread [26–28,32,33] though not ubiquitous [19••,30••]. This work has further stimulated study of the underlying molecular mechanisms of epistasis [32,34,35,36••] as well as epistasis across environments [37••,38] and epistatic opportunities for evolutionary reversions [32,37••].

Quite a different motivation for developing such datasets stems from an interest in genetic load (the steady-state fitness cost of recurrent deleterious mutations) [reviewed in [39]] and relatedly, the ability of genetic recombination to reduce genetic load [reviewed in [40]]. Perhaps because they derive from older theoretical questions, these studies often used traditional genetic crosses of visible markers [39–41]. Interestingly, although extensive epistasis is observed (including sign epistasis), this work tends not to support the hypothesis that genetic recombination can more effectively purge deleterious mutations [41] or speed adaptation [40]. (But see Conclusions.)

The final class of studies comes from the protein engineering community. This work uses random mutagenesis to search for novel enzymatic variants exhibiting desired catalytic properties in the mutational neighborhood around some starting allele. Thus this work is not principally concerned with abstract properties of the fitness landscape, but of course these properties influence results. As with the other two classes of studies, this work has revealed considerable topographic complexities on fitness landscapes [e.g. [42,43]].

Is higher-order epistasis evolutionarily important?

Thus topographic complexities are widespread on biological fitness landscapes. In order to quantify the underlying epistasis, we computed all epistatic coefficients for all datasets in Table 1 using the approach proposed in Box 1. Figure 1 presents mean squared values as a function of interaction order for each system. In almost every case the mean magnitude of higher-order epistatic coefficients is as large as or larger than the pairwise effects. Although considerable heterogeneity exists among systems, it appears that substantial higher-order epistasis is common in nature.

Figure 1.

Epistatic coefficients as a function of order. Because epistatic coefficients may be positive or negative (Box 1), mean squared values are shown. The zeroth-order epistatic coefficient is the mean fitness across all genotypes (see Box 1); in each case here, fitness values were normalized to make this quantity equal to 1.0. First-order and second-order coefficients are analogous to classical selection coefficients and classical pairwise epistasis terms, respectively (see Box 1). Error bars represent standard deviation among coefficients of given order; those that extend to the x-axis overlap 0. (a) Theoretical fitness landscapes. Additive (circle) genotypic fitness values are the sum of the fitness effects of constituent mutations, which in turn were drawn uniformly on the interval [0, 1]. Here, all pairwise and higher epistatic coefficients are zero. I.I.D. (squares) genotypic fitness values were drawn independently and identically from a uniform distribution over [0, 1]. Here, magnitude of mean squared epistatic coefficient increases exponentially with order. We expect empirical results to lie in between these two extremes. Enzyme folding stability model (triangles) considers the fitness landscape defined by 1/(1 + e^ΔG/k_bT) over 7 missense mutations with identical and additive ΔΔG = 1 kcal/mol [44••]. Here ΔG is the free energy of folding, k_b is Boltzman’s constant and T is temperature. See text for further details. (b–o) Empirical fitness landscapes in Table 1; citations given in square brackets. Growth rate (panels c, e, h, l, n and o) and drug resistance (f, i and k) values were log-transformed before epistatic coefficients were computed. In cases where more than one combinatorially complete subset of mutations was identified (panels d, g, k, m) results for a randomly selected subset is shown.

We next addressed the evolutionary consequences of higher-order epistasis by re-examining two published systems in greater detail. Typical of the work summarized in Table 1, we previously characterized the combinatorially complete fitness landscape defined by five mutations in the β-lactamase gene of E. coli [27]. These mutations jointly increase resistance to the antibiotic cefotaxime ~100,000-fold, and together define 5! = 120 possible mutational trajectories linking the starting and highest-resistance β-lactamase alleles. Importantly, four of these five mutations exhibit sign epistasis, and consequently, resistance increased monotonically on only 18 of the 120 trajectories [27]. In other words, epistasis renders many mutational trajectories selectively inaccessible.

What is the relationship between selective accessibility and epistatic coefficients in these data? To test the hypothesis that higher-order terms might contribute only modestly to the number of selectively accessible mutational trajectories, we took advantage of the fact that one can easily convert from epistatic components back to fitness landscapes (see Box 1). For each order we thus computed the number of selectively accessible trajectories on the premise that all higher-order epistatic coefficients were zero. When only first-order terms are nonzero the landscape is by definition additive (see circles in Figure 1a) and thus drug resistance must increase monotonically along all 120 mutational trajectories. But interestingly, the number of selectively accessible trajectories drops almost linearly (r² = 0.97) as successively higher-order epistatic coefficients are included in the landscape (data not shown). Thus this characteristic of fitness landscapes seems to depend almost equally on all orders of epistasis.

We also computed all epistatic coefficients on the fitness landscape defined by a simple model of protein folding stability [44••] given by 1/(1 + e^ΔG/k_bT). Here ΔG is the free energy of folding, k_b is Boltzman’s constant and T is temperature. Beginning from a wild type protein with typical folding stability ΔG = −8 kcal/mol [44••], assuming that ΔG values are additive [45] and that mutations have ΔΔG = 1 kcal/mol [44••], we find that on this landscape mean squared epistatic coefficients for fitness increase monotonically and almost exponentially with order (triangles in Figure 1a).

Conclusions: evolutionary biologists should worry about higher-order epistasis

While empirical fitness landscapes were first characterized almost 25 years ago [25], the past few years have seen an explosion in this work, and several empirical facts are now beginning to emerge. Here we propose a natural generalization to the classical measure for pairwise epistasis (Box 1) which reveals substantial higher-order epistasis in almost every empirical system examined (Figure 1). We also show that higher-order epistasis is of critical evolutionary importance in the two systems we know best. As outlined in the introduction, these findings have direct implications for many branches of systems biology.

We are aware of two other studies that explore higher-order interactions in experimental data using an approach closely related to ours. One demonstrates several intriguing regularities among higher-order interactions in a meta-analysis of 113 combinatorially complete experiments from the engineering literature [46]. The other shares our specific interests in the statistical properties of fitness landscapes [47].

Our chief novelty has been to propose a generalization to the classical population genetic approach for computing pairwise epistasis, to now address epistatic interactions of all order. Importantly, higher-order epistasis is formally independent of the pairwise effects (see Box 1). While we have not addressed the consequences of experimental measurement error for our approach, the influence of such noise on interaction coefficients computed in a closely related manner was very modest [47] in one dataset [43] examined here. We also note that other approaches for computing epistatic coefficients of arbitrary order are possible and may prove useful in some contexts.

The theoretical implications of higher-order epistasis remain unknown. For example, substantial attention has traditionally been paid to the role of positive and negative pairwise epistasis in the evolutionary persistence of genetic recombination [48], but under what circumstances will recombination be favored in the face of higher-order effects [40,49,50]? Moreover we now have several classification schemes for epistasis, including the distinction between one-dimensional and multidimensional epistasis [50], sign and magnitude epistasis [21] and between pairwise and higher-order effects. These definitions derive from different intellectual motivations, but it may be possible to use the present framework to integrate these traditions into a single conceptual apparatus.

Finally, we acknowledge an important limitation to the approach used here: its dependence on combinatorially complete datasets. This follows from the fact that the fitness landscape and its epistatic coefficients are simple transformations of one another: they both have 2^L degrees of freedom. Thus as L (the number of mutations of interest) increases in any given system, the amount of bench work required to compute all epistatic coefficients increases exponentially [51]. Fortunately our framework can also yield expressions for a subset of epistatic coefficients from combinatorially incomplete datasets of corresponding size [46,52]. Recently published analyses based on alignments of naturally occurring protein-coding sequences demonstrate that a great deal of evolutionary information is already present in pairwise epistasis [53,54•,55]. We now look forward to analogous work that capitalizes on the theoretical opportunities posed here to explore the consequences of epistatic interactions among mutational subsets larger than two but possibly still much smaller than L.