The value of monitoring to control evolving populations

Significance

Evolution of drug resistance, as observed in bacteria, viruses, parasites, and cancer, is a key challenge for global health. We approach the problem using the mathematical concepts of stochastic optimal control to study what is needed to control evolving populations. We focus on the detrimental effect of imperfect information and the loss of control it entails, thus quantifying the intuition that to control, one must monitor. We apply these concepts to cancer therapy to derive protocols where decisions are based on monitoring the response of the tumor, which can outperform established therapy paradigms.

Abstract

Populations can evolve to adapt to external changes. The capacity to evolve and adapt makes successful treatment of infectious diseases and cancer difficult. Indeed, therapy resistance has become a key challenge for global health. Therefore, ideas of how to control evolving populations to overcome this threat are valuable. Here we use the mathematical concepts of stochastic optimal control to study what is needed to control evolving populations. Following established routes to calculate control strategies, we first study how a polymorphism can be maintained in a finite population by adaptively tuning selection. We then introduce a minimal model of drug resistance in a stochastically evolving cancer cell population and compute adaptive therapies. When decisions are in this manner based on monitoring the response of the tumor, this can outperform established therapy paradigms. For both case studies, we demonstrate the importance of high-resolution monitoring of the target population to achieve a given control objective, thus quantifying the intuition that to control, one must monitor.

The progression of cancer is an evolutionary process of cells driven by genetic alterations and selective forces (1). The frequent failure of cancer therapies, despite a host of new targeted cancer drugs, is largely caused by the emergence of drug resistance (2). Cancer therapy faces a real dilemma: the more effective a new treatment is at killing cancerous cells, the more selective pressure it provides for those cells resistant to the drug to take over the cancer population in a process called competitive release (3, 4).

A genetic innovation conferring resistance can either be already present as standing variation or in close evolutionary reach, via de novo mutations. The probability of these events is often proportional to the genetic diversity of the tumor. Therefore, resistance is a problem especially for genetically heterogeneous cancers (5). This diversity can be the result of a variable microenvironment, with different pockets of acidity, blood supply, and geometrical constraints of surrounding tissue (2). Also, late-stage cancers not only carry the cumulative archaeological record of their evolutionary history (6) but can also become genetically unstable and fall victim to chromothripsis (7), kataegis (8), and other disruptive mutational processes (9, 10). Thus, the probability of treatment success is higher in genetically homogeneous and/or early-stage cancers (11). Taken together, these considerations place emphasis on early detection of tumors.

In cases where early detection is not achieved, the pertinent question is how to avoid treatment failure in the presence of genetic heterogeneity, which seems to be the norm for most solid cancers. One obvious attempt is to make treatments more complex and thus put the resistance mechanisms out of reach of the tumor. In combination therapy, the tumor is simultaneously treated with two or more drugs that would require different, possibly mutually exclusive, escape mechanisms for cells to become resistant. This approach has proven to be successful in the treatment of HIV and is discussed as a possible model also for cancer (12). In the context of cancer, this form of personalized therapy is not yet widely realized, mainly because of the much richer repertoire of genetic variation and adaptability of cancer cells and a comparable shortage of drugs targeting distinct biological pathways. For a recent study of the conditions under which combination therapy is expected to be successful in cancer, see ref. 13.

For application of single drugs, there are a number of studies that concentrate on how the therapeutic protocol itself can be optimized. It was realized that all-out maximum tolerated dose chemotherapy is not the only, or necessarily the best, treatment strategy (14). Alternative dosing schedules have been proposed such as drug holidays, metronome therapy (15), and adaptive therapy (16). The realization of Gatenby et al. in ref. 16 is that cancer, as a dynamic evolutionary process, can be better controlled by dynamically changing the therapy, depending on the response of the tumor. Their protocol of reducing the dose while the tumor shrinks and increasing it under tumor growth showed a drastic improvement of life expectancy in mice models of ovarian cancer (16). Furthermore, Gatenby et al. made the important conceptual step of reformulating cancer therapy to be not necessarily about tumor eradication. Instead, dynamic maintenance of a stable tumor size can also be a preferable outcome.

Motivated by this experiment, we conjecture that there are substantial therapy gains in optimal applications of existing drugs, as of yet underexploited. As a first step toward using this potential we would like to formalize the intuition of Gatenby et al. To this extent, we aim to establish a theoretical framework for the adaptive control of evolving populations. In particular, we connect the idea of adaptive therapy to the paradigm of stochastic optimal control, also known as Markov decision problems. For other applications of stochastic control in the context of evolution by natural selection see refs. 17, 18. A stochastic treatment is necessary due to the nature of evolutionary dynamics where fluctuations (so-called genetic drift) matter even in large populations. For instance, the dynamics of a new beneficial mutation is initially dominated by genetic drift before it becomes established (19). Stochastic control is a well-established field of research which provides not only a natural language for framing the task of cancer therapy, but also a set of general purpose techniques to compute an optimal control or therapy regimen for a given dynamical system and a given control objective. Although we demonstrate the main steps in this program, we focus on the detrimental effect of imperfect information and the loss of control it entails, thus quantifying the intuition that to control, one must monitor. The informational value of continued monitoring is a natural concept for controlled stochastic systems, whereas in deterministic models successful control usually does not rely on sustained observations.

We first introduce the concepts of stochastic optimal control using a minimal evolutionary example: how to keep a finite population polymorphic under Wright–Fisher evolution by influencing the selective difference between two alleles. If perfect information about the population is available, the polymorphism can be maintained for a very long time. We will show how imperfect information due to finite monitoring can lead to a quick loss of control and how some of it can be partially reclaimed by informed preemptive control strategies. We then move to our main problem and introduce a minimal stochastic model of drug resistance in cancer that incorporates features such as variable population size, drug-sensitive and -resistant cells, a carrying capacity, mutation, selection, and genetic drift. After computing the optimal control strategies for a few important settings under perfect information, we demonstrate the effect of imperfect monitoring. If only the total tumor size can be monitored, we show how a control strategy emerges that can adaptively infer, and thus exploit, the inner tumor composition of susceptible and resistant cells.

Controlling Evolving Populations

One can think about cancer therapy as the attempt to control an evolving population by means of drug treatment. Typically, the drug changes some of the parameters of the evolutionary process, such as the death rate of drug-sensitive cells. With application of the drug, one can thus actively influence the dynamics of the stochastic process and change its direction. All this happens with a concrete aim, such as to minimize the total tumor burden in the long term. To introduce some of the concepts of stochastic optimal control, we use an example with a nontrivial control task.

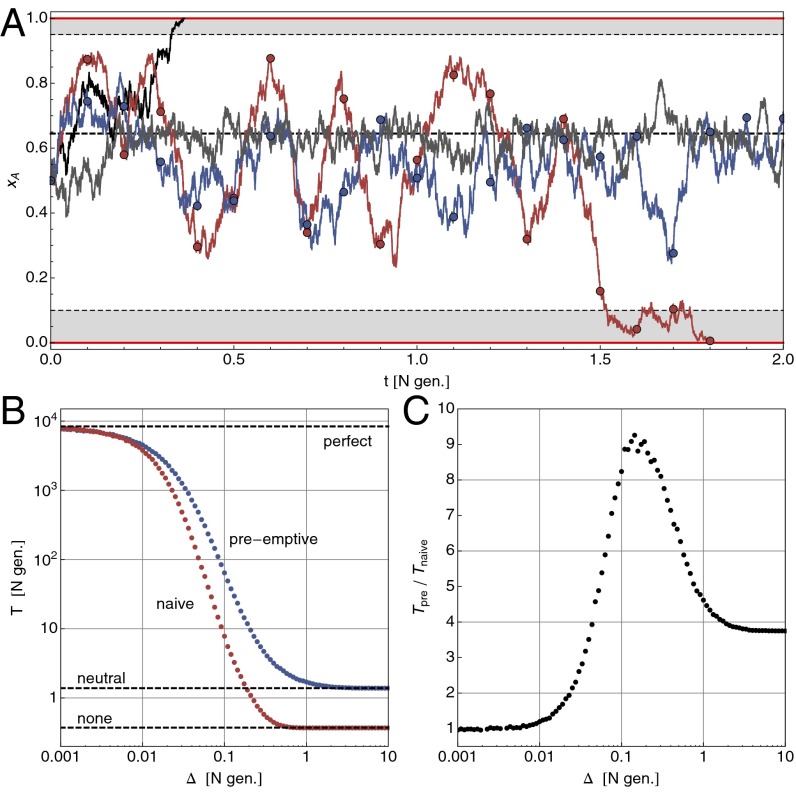
Imagine a biallelic and initially polymorphic population of constant size N under the Wright–Fisher model of evolution (20), i.e. binomial resampling of the population in each generation. The A allele confers a selective advantage of size $\sigma =N\left(f_A-f_B\right)\gg 1$ over the B allele and will, without intervention, eventually take over the entire population (f denotes reproductive rates; see Fig. 1A). Assuming mutation to be negligible, the task at hand is to avoid, or at least delay, such a loss in diversity. Now assume that we can change the selection coefficient externally by a quantity $u\in \left[-u_c,0\right]$ in the form $\sigma \to \sigma +u$. Ideally, we would have $\left|u_c\right|>\sigma$, but this is not a necessary condition. In this setting, the control problem can be stated as follows: for a population with an initial A-allele frequency of $x_0=n_0/N\in \left(\mathrm{0,1}\right)$, what is the optimal control protocol ${\overline{u}}_{0:T}\left(x_0\right)$ that maximizes the probability that the polymorphism is still alive after a time of T generations?

$${\overline{u}}_{0:T}\left(x_0\right)=\underset{u_{0:T}}{\mathrm{argmax}}P\left(x_T\in \left(0,1\right)|x_0\right),$$ [1]

where the maximization is to be done over all possible sequences of controls $u_{0:T}=u_0{u}_1\dots u_T$ $\left(u_t\in \left[-u_c,0\right]\right)$. Note that the stochastic nature of the process makes the control optimal only in the sense of expected outcomes. Individual realizations might well fall short of, or exceed, the implied mean survival time. It is helpful to picture a large ensemble of such populations, all starting off at frequency $x_0$, all being individually nudged by selection according to a (yet to be found) optimal protocol. When a trajectory hits one of the boundaries before the final time T, it is lost. The optimal control can thus also be seen to minimize this cost of extinction. The standard technique to solve problems of this kind is to use a dynamic programming ansatz. Assuming that a partial problem starting from some intermediate point $\left(x_t,t\right)$ $\left(0<t<T\right)$ has already been solved, we define the cost-to-go $J\left(x_t,t\right)$ as the corresponding optimal cost. From this definition follows a backward-recurrence relation for J: the cost-to-go at $\left(x_t,t\right)$ is the expected cost-to-go one step later, where the average depends via the propagator W on the control decision $u_t$ at the current time (21):

$$J\left(x_t,t\right)=\underset{u_t}{\min }\hspace{0.17em}{\displaystyle \sum _{x^{\prime }}J\left(x^{\prime },t+1\right)W\left(x^{\prime }|x_t;u_t\right)}.$$ [2]

The absorbing boundary conditions take the form $J\left(0,t\right)=J\left(1,t\right)=T-t$. The right-hand side of Eq. 2 can also include a term $V\left(x_t,u_t\right)$ that describes the potential cost to be at x and the control cost to apply u. Here, both are assumed zero and cost is paid only at the boundaries. For Wright–Fisher evolution, the transition matrix W can be expressed as the probability under binomial sampling to draw ${n\prime }_A=N\hspace{0.17em}x\prime$ individuals of the A allele. The crucial computational advantage of this relation is that the hard optimization in the space of all control protocols $u_{0:T}$ is exchanged for a simple scalar optimization over $u_t$. In statistical physics, this technique is referred to as the transfer-matrix method. The intuitive interpretation of Eq. 2 is that the decision for a control now relies on future controls to be carried out optimally. In practice, the results of the local optimizations $\left(\overline{u}\left(x_t,t\right)=\underset{u_t}{\mathrm{argmin}}\dots \right)$ constitute the optimal control to be applied when the system is at $x_t$ at time t. In many applications (21), it is also useful to consider a receding time horizon, such that $\overline{u}\left(x,0\right)$ is a stationary control. In general, the solution to Eq. 1 is not guaranteed to be unique. However, even degenerate optimal controls would achieve the same optimal value of the control objective (22).

Fig. 1.

Optimal control of a finite population under Wright–Fisher evolution to maintain a polymorphism. The intrinsic selection coefficient is $\sigma =10$ and control shifts selection to $\sigma +u$. (A) Sample trajectories starting at $x_0=0.5$: without control ($u\equiv 0$, black line) the polymorphism is lost on a time scale of $1/\sigma$. With optimal control under perfect information (gray line, $\sigma +u=\sigma =10$ for $x<x_c\approx 0.64$, else $\sigma +u=\sigma -u_c=-20$), it can be maintained for an average of 8,000 N generations. With finite monitoring ($\mathrm{\Delta }=0.1$, measurements $x_i$ at circles), naive control $\left(u\equiv \overline{u}\left(x_i\right)\right)$, red line, is prone to overshooting, whereas preemptive control (blue line) tries to avoid this by switching to a neutral regime after a short time. (B) Loss of control under finite monitoring: as $\mathrm{\Delta }$ grows, so does the probability that the polymorphism is already lost at the next measurement. Shown is the mean survival time over 5,000 trajectories with $N={10}^4$ on a logarithmic scale. (C) Under preemptive control, some of the loss of control can be regained, especially for intermediate values of $\mathrm{\Delta }$.

Throughout this study, we apply the diffusion approximation ($N\to \infty$, while $\sigma ,u_c$ fixed and $\tau =t/N$), where the infinitesimal form of Eq. 2, the so-called Hamilton–Jacobi–Bellman equation (21, 23), is valid.

$$-{\partial }_{\tau }J\left(x,\tau \right)=\underset{u_{\tau }}{\min }\hspace{0.17em}x\left(1-x\right)\left[\left(\sigma +u_{\tau }\right){\partial }_x+\frac{1}{2}{\partial }_x^2\right]J\left(x,\tau \right).$$ [3]

We propose an ansatz to solve the control problem for the Wright–Fisher example, and confirm it by direct numerical application of Eq. 2 (see also Fig. S1). For a treatment of finite mutation rate, see SI Text and Fig. S2.

Optimal Control of a Wright–Fisher Population with Perfect Monitoring.

The optimal control function $\overline{u}\left(x_t,t\right)$ maximizes the probability that a polymorphism is still present after a time T. In the infinite horizon time limit $T\to \infty$, where the optimal control becomes stationary $\overline{u}\left(x\right)$, we expect it to also maximize the mean first passage time $\langle T_x^{\left(\mathrm{0,1}\right)}\rangle$ out of the interval $\left(0,\hspace{0.17em}1\right)$ (for any fixed starting position x). In Eq. 3, the control variable u appears only linearly. This means that only the two extreme control strengths are ever used to steer the system. This particular type of control is called bang-bang. It follows that the control profile $\overline{u}\left(x\right)$ will have the form of a step function with critical frequency $x_c$,

$$\sigma +\overline{u}=\{\begin{array}{ll}\sigma ,\hfill & x<x_c\hfill \\ \sigma -u_c,\hfill & x\ge x_c\hfill \end{array}.$$ [4]

The only remaining parameter is the critical threshold $x_c\left(\sigma ,u_c\right)$. To find an expression for the objective function $\langle T^{\left(\mathrm{0,1}\right)}\rangle \left(x_c,\sigma ,u_c\right)$, we can consider the optimally controlled system as the simplest example of evolution under frequency-dependent, piecewise constant selection $\sigma +\overline{u}\left(x\right)$. The mean first passage time can then be found analytically using standard methods for stochastic processes (24) (SI Text and Fig. S1). At the correct threshold and with strong selective forces ($\sigma \gg 1$ and $\sigma -u_c\ll -1$), the gains are substantial and the polymorphism can be maintained for very long times.

Loss of Control due to Imperfect Monitoring.

The main assumption made so far was that perfect information is available about the state of the system in the form of continuous (in time), synchronous (without delay), and exact (without error) measurements of x. These requirements are impossible to achieve in practice, when monitoring is always imperfect. As we will see, when the assumption of perfect information is relaxed, not only is control over the system lost, but the control profile $\overline{u}\left(x\right)$ also ceases to be optimal. Rather than turning to the theory of partially observable Markov decision problems (25), we will use numerical analysis to demonstrate the effect of monitoring with finite resolution in time (relaxing the first condition).

Consider the situation where measurements of the frequency x are given only at discrete times $\left\{{\tau }_i\right\}$, whereas no information is available during the intervals of length $\mathrm{\Delta }={\tau }_{i+1}-{\tau }_i$. The immediate question is, given a measurement $x_i$, what control should one apply while waiting for the next measurement? The perfect-information control $\overline{u}\left(x_i\right)$ is correct only initially, and thus only in the limit $\mathrm{\Delta }\to 0$. However, it is intuitively clear that a naive protocol, applying $\overline{u}\left(x_i\right)$ during the entire interval $\mathrm{\Delta }$, cannot be optimal, because it does not anticipate the dynamics of x under this regime (see the decrease in survival time in Fig. 1B). For example, for $0<x_i<x_c$ the initial control is $u=0$, $\sigma +u>0$ and the frequency will, on average, increase and eventually cross the threshold $x_c$. If one could observe the population at that point, the control should be switched to $u=-u_c$ until x crosses $x_c$ from above. The total result of the naive strategy is to amplify fluctuations due to this overshooting.

Playing-To-Win vs. Playing-Not-To-Lose.

Without a continuous flow of observations as input, a preemptive control protocol $u^{\mathrm{\ast }}\left(\tau ,x_i\right)$ during the interval $\mathrm{\Delta }$ must be precomputed and then faithfully carried out. In the discrete-time (Wright–Fisher evolution) setting, there are $N\mathrm{\Delta }$ generation updates until the next measurement and therefore $2^{N\mathrm{\Delta }}$ different bang-bang protocols to choose from. However, the example above suggests to search for a preemptive control in a much smaller space, namely within those protocols that start with either $u^{\mathrm{\ast }}=0$ or $u^{\mathrm{\ast }}=-u_c$ and then switch, at some later time ${\tau }_c\left(x_i,\mathrm{\Delta }\right)$, to a neutral regime with $u^{\mathrm{\ast }}=-\sigma$ (if available). The size of this space is only $2\hspace{0.17em}N\mathrm{\Delta }$ (we note that for finding an optimal control one would need to search protocols in the full space). The effect of such a control scheme is to move the population to a safe place and then try to keep it there. There are two important observations: first, this informed control outperforms the naive protocol significantly, especially for intermediate values of $\mathrm{\Delta }$ (Fig. 1 B and C); second, the safe parking position moves away from the boundary toward $x=0.5$ for larger values of $\mathrm{\Delta }$ (Fig. S3). This shift from an aggressive control strategy under perfect information ($\mathrm{\Delta }=0$, $x_c$ close to a boundary) to a more and more conservative one (aiming for $x=0.5$ and trying to stay there) can be summarized as playing-to-win vs. playing-not-to-lose.

A similar loss of control can be expected for other types of monitoring imperfections and is a general feature of stochastic optimal control. It is important to note that the perfect-information control problem, and its solution $\overline{u}$, is a typical starting point for the analysis. The naive control protocol above is indeed optimal for $\mathrm{\Delta }\to 0$, and still a very good option for $\mathrm{\Delta }\ll 1$ (in units of N generations). In most cases, as we will see in the adaptive cancer therapy model below, finding $\overline{u}$ is challenging in itself and can be a good guidance for finding well-performing control protocols even under imperfect conditions.

Application to Adaptive Cancer Therapy

Here we first introduce a minimal stochastic model of drug resistance in cancer. For different qualitative regimes, we then find the optimal adaptive therapy with perfect information. Finally, we extend these ideas to the case where only the total cell population size can be observed but no readout of the fractions of susceptible and resistant cells is available. In the context of models of the cell cycle, deterministic control theory has previously been applied to find optimal cancer treatment protocols (e.g. refs. 26–28). However, for the key concepts of this study—adaptive therapy and finite monitoring—stochastic control theory is needed and in fact leads to control protocols that exploit fluctuations.

A Minimal Model of Drug Resistance in Cancer.

The desired features of a minimal model of drug resistance in cancer include: (i) a variable tumor cell population size N, (ii) at least two cell types, drug-sensitive and drug-resistant, (iii) a carrying capacity K that describes a (temporary) state of tumor homeostasis, and (iv) the possibility for mutation and selection between cell types. Control over the tumor can be applied via a drug that changes the evolutionary dynamics by increasing, for example, the death rate of sensitive cells. We will assume here, as others have done in the context of cancer (11), a well-mixed cell population where the birth (or rather duplication) rate of cells is regulated by the carrying capacity. The dynamics of the model we have chosen here is encapsulated in the following birth and death rates for sensitive and resistant cells:

$$\begin{array}{l}{B}_i\left(n_s,n_r\right)=\frac{\left(1+g_i\right)n_i}{1+g\frac{N}{K}+a\frac{n_s}{K}}+{\mu }_0\left(n_{\overline{i}}-n_i\right),\\ D_i\left(n_s,n_r\right)=n_i\left(1+F_i\left(u\right)\right),\hspace{1em}i\in \left\{s,r\right\},\hspace{0.17em}\overline{s}=r,\hspace{0.17em}\overline{r}=s,\end{array}$$ [5]

with free growth rates $g_s=g+a$, $g_r=g$, growth advantage $a\ge 0$, and mutation rate ${\mu }_0$ between cell types. $F_i$ encodes the effect of the drug $\left(u=1\right)$ or its absence $\left(u=0\right)$ on cell type i. For $N\ll K$, the absolute growth rates are $g_i-F_i$. A drug effect of the form

$$F_s\left(u\right)=u{f}_s\hspace{1em}\text{and}\hspace{1em}{F}_r\left(u\right)=\left(1-u\right)f_r,$$ [6]

renders the drug effective if $f_s>g+a$. The value $f_r=0$ corresponds to drug resistance as such, but $f_r>g$ implies that resistant cells thrive under the drug and are drug-addicted. Such an effect has been observed in mice with melanoma carrying oncogene BRAF mutation treated with vemurafenib (29). Altogether, sensitive and resistant cells initially grow exponentially until the total population size $N=n_s+n_r\approx K$. For some of the protocols that we derive, it is important that the tumor is close to or can reach carrying capacity during treatment (e.g. patients who are inoperable or whose primary tumors are not resectable). At that stage, competition for resources, space, etc. becomes fierce. If sensitive cells have a differential growth advantage $a>0$ (they might not have to maintain an expensive resistance mechanism), resistant cells will eventually be removed from the tumor or reduced to a small fraction (of size ${\mu }_0/a$). In reality, this scenario might not materialize, as the next mutation could propel the tumor into a new phase of exponential growth.

For the stochastic version of this process we can assume independent and individual birth and death events with the above probabilities per unit time. In analogy to the Wright–Fisher binomial update rule, here we can use a Poisson-like update.

$$n_i\to {n\prime }_i=n_i+\mathrm{\Delta }{n}_i,\hspace{0.17em}\text{with}\hspace{0.17em}\mathrm{\Delta }{n}_i=\mathrm{\Delta }{n}_i^{+}-\mathrm{\Delta }{n}_i^{-}$$ [7]

$$\mathrm{\Delta }{n}_i^{+}\sim \text{Pois}\left(B_i\right),\hspace{0.17em}\mathrm{\Delta }{n}_i^{-}\sim \text{Pois}\left(D_i\right),\hspace{0.17em}\langle \mathrm{\Delta }{n}_i\rangle =B_i-D_i.$$

The total increment $\mathrm{\Delta }{n}_i$ follows a Skellam distribution. When we let $K\to \infty$ while fixing the combinations $\gamma \equiv Kg$, $\alpha \equiv Ka$, $\mu \equiv K{\mu }_0$, and ${\varphi }_i=K{f}_i$ and setting $t=\tau /K$, the system is described by a Fokker–Planck evolution equation (30) for the distribution $P\left(x_s,x_r,t\right)$ with $x_i\equiv n_i/K$ (SI Text). This scaling exercise is mainly important because it allows to relate systems with small K (hundreds to thousands, as required for numerical analysis) to systems with large K ($\mathrm{\gtrsim }{10}^8$, as present in real cancers).

Optimal Cancer Therapy with Perfect Monitoring.

With the minimal model of drug resistance in cancer introduced above, we can start the program of stochastic optimal control to compute adaptive therapy protocols. The first task is to define the goal of such a program: what is the quantity one aims to optimize? One very important objective is to maximize the (expected) time until the cancer proceeds to the next, possibly lethal stage. This could mean the emergence of a new cell type with a much higher carrying capacity, e.g. with metastatic potential. We will denote this critical event simply with a “driver” event or “metastasis.” The rate of metastasis emergence is a combination of tumor size and the rate ${\nu }_0$ (per cell and generation) for the necessary features to appear via mutation.

Earlier, the optimal control for the Wright–Fisher evolution example turned out to be a piecewise constant function of allele frequency. Here, we need to find a control profile $\overline{u}\left(n_s,n_r\right)$. With perfect information, we would know $n_s$ and $n_r$ at all times and would base the control decision adaptively on these measurements. In analogy to Eq. 1, the control objective can be expressed as

$${\overline{u}}_{0:T}\left(n_{s0},n_{r0}\right)=\underset{u_{0:T}}{\mathrm{argmax}}\exp \left(-{\nu }_0{\displaystyle \sum _{t=0}^T\left(n_{st}+n_{rt}\right)}\right),$$ [8]

where the right-hand side is the probability that metastasis has not yet happened after T generations (for ${\nu }_{0}K\ll 1$). Here, the control objective is a nonlinear function of the entire trajectory ${\left(n_s,n_r\right)}_{0:T}$. As such, it is the simplest manifestation of a so-called risk-sensitive control problem (see e.g. ref. 31). The above formulation assumes a finite (receding) horizon time T and also that control itself is cost-free. In cancer therapy, especially chemotherapy, this is certainly not the case: the side effects of treatment incur a considerable cost in terms of life quality and medical care. The difficulty, however, lies in quantifying these control costs in a manner that would make them comparable to the potential costs considered here. A simple extension of the above control objective to include such a control cost is demonstrated in SI Text and Fig. S4. The recurrence equation for the cost-to-go $J\left(n_s,n_r,t\right)$ for the control objective above is given by (31)

$$J\left(n_s,n_r,t\right)=e^{-{\nu }_0\left(n_s+n_r\right)}\underset{u\in \left\{\mathrm{0,1}\right\}}{\max }\langle J\left(t+1;u\right)\rangle ,$$ [9]

$$\langle J\left(t^{\prime };u\right)\rangle \equiv {\displaystyle \sum _{{n\prime }_s,{n\prime }_r}J\left({n\prime }_s,{n\prime }_r,t^{\prime }\right)\hspace{0.17em}W\left({n\prime }_s,{n\prime }_r|n_s,n_r;u\right)},$$ [10]

with boundary condition $J\left(T\right)=1$. The (microscopic) transition matrix W is the product of the two Skellam distributions resulting from Eq. 7 (including boundary conditions). With this equation, we can solve the dynamic programming task numerically for moderate values of K (see Fig. S5). For the numerical analysis, we have to introduce an upper bound $\tilde{N}\gg K+\sqrt{K}$ for the population size. The resulting control profiles for a number of different parameter regimes is shown in Fig. 2.

Fig. 2.

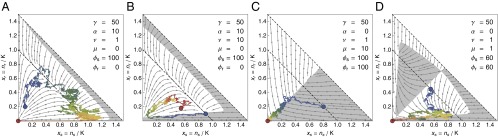
Control of a tumor cell population. (A–D) The optimal control profile under perfect information about $n_s$ and $n_r$ for different parameters of the cancer model. In the white areas, $\overline{u}=0$ (no drug), whereas in the gray areas, $\overline{u}=1$ (with drug). The arrows indicate the deterministic flow. All profiles were calculated via Eq. 9 with $T=K/\nu$ generations and $K=500$ with an absorbing boundary at $N=750$. The sample trajectories were simulated with $K={10}^4$ and controlled according to these profiles. The coloring of the trajectories shows the temporal evolution from blue to red. (A) When selection against resistance is stronger than driver emergence, $\alpha \gg \nu$, the optimal protocol is to wait until resistant cells are cleared from the system before the drug is applied. (B) For higher driver emergence rates, the drug is applied earlier, which can lead to cycles. (C) For drug-sensitive $\left({\varphi }_s\gg \gamma \right)$ and drug-addicted cells $\left({\varphi }_r\gg \gamma \right)$ with high mutation $\left(\mu \gg 1\right)$, the control in the symmetric case $\left({\varphi }_s={\varphi }_r\right)$ is a simple majority rule and very effective. (D) For smaller mutation $\left(\mu =1\right)$, the optimal strategy first homogenizes the tumor before trying to remove it.

In the case of ${\varphi }_r=0$, resistant cells are unaffected by the drug. If maintenance of the resistance mechanism is costly $\left(\alpha >0\right)$, the only way that they can be removed from the population is when selection can act against them. This only happens at $N\sim K$ and with $u=0$ (no drug). If this can take place before the next driver typically appears (if $\alpha =Ka\gg KN{\nu }_0\sim K^2{\nu }_0\equiv \nu$), then the optimal control protocol is to postpone treatment until the resistant cells are sufficiently cleared from the system so that genetic drift has a chance of removing the remaining part (Fig. 2A). However, this parameter regime of very high selection against resistance and/or very low rate of driver mutation, and therefore this therapy option, is not realistic for cancer. For higher values of $\nu /\alpha$, the optimal strategy is to apply the drug earlier (Fig. 2B). This procedure can lead to cycles of tumor size reduction followed by regrowth, with the overall effect of extending the time until metastasis.

If ${\varphi }_r>\gamma$ (and ${\varphi }_s>\gamma +\alpha$), resistant cells are actually drug-addicted and thrive only in its presence. Such a situation would be easy to control with perfect information about $n_s$ and $n_r$. For example, if mutation between cell types is rapid $\left(\mu \gg 1\right)$, a majority rule is optimal (Fig. 2C). For a lower mutation rate, the optimal protocol first tries to amplify one cell type before switching to an environment that is deadly for most cells (Fig. 2D).

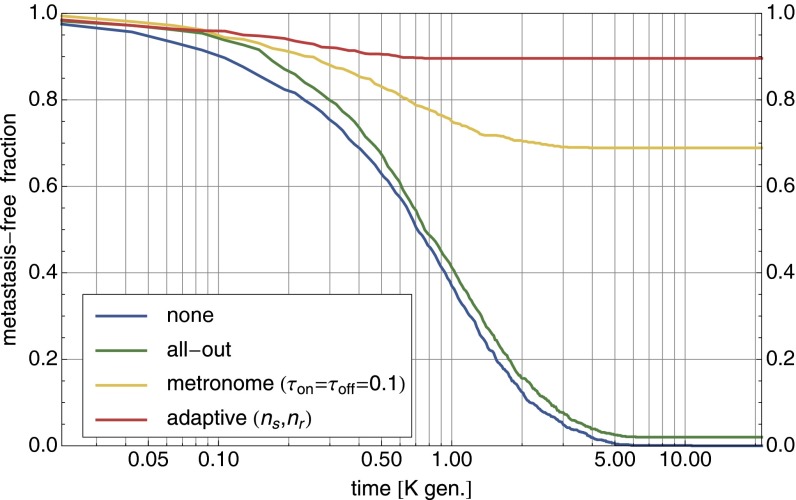
The effectiveness of different therapy protocols is compared in Fig. 3 with 1,000 stochastic forward simulations (with $K={10}^4$) for the parameter setting of Fig. 2D. Whereas no therapy $\left(u=0\right)$ and all-out therapy $\left(u=1\right)$ both ultimately end with the occurrence of metastasis, adaptive therapy can bring the tumor size down to zero in the majority of cases. In metronome therapy, the drug is applied (withheld) for fixed time intervals ${\tau }_{\text{on}}$ $\left({\tau }_{\text{off}}\right)$. With numerically optimized values for the time intervals, metronome therapy is quite competitive compared with adaptive therapy.

Fig. 3.

Comparison of cancer therapies. For the parameter setting of Fig. 2D, different therapies are compared via 1,000 forward simulations with $K={10}^4$. Shown is the fraction of runs that have not yet developed a metastasis mutation as a function of elapsed time. All-out maximum dosage therapy $\left(u\equiv 1\right)$ is only slightly better than no therapy $\left(u\equiv 0\right)$ in avoiding metastasis. Much better is metronome therapy with ${\tau }_{\text{on}}={\tau }_{\text{off}}=0.1\hspace{0.17em}K\hspace{0.17em}\text{generations},$ with almost 70% success rate (values numerically optimized). Adaptive therapy removes the tumor in close to 90% of runs.

All these control strategies require perfect information, not only in the sense of the earlier Wright–Fisher example (continuous, synchronous, and exact), but also in terms of the inner tumor composition $N=n_s+n_r$, which presupposes that sensitive and resistant cells can be distinguished.

Loss of Therapy Efficacy due to Low-Resolution Monitoring.

There are very few cases where the genetic basis for a drug-resistance mechanism is known and can be specifically monitored (29, 32). In most cases the regrowth of the tumor under the drug is observed without understanding the exact biological processes responsible for the resistance. Here we aim to find rational control strategies when only the total tumor cell population size can be monitored. The adaptive therapy protocol that was applied by Gatenby et al. in ref. 16 (coupling the drug concentration to the tumor size) is one example of such a strategy.

Consider the situation where only the total population size $N=n_s+n_r$ can be (perfectly) monitored, whereas the dynamical laws in Eqs. 5–7 and all parameter values are known. Under these circumstances, the perfect-information optimal control profiles from the last section cannot be used directly. However, there is still valuable information available. The response $N_{\tau }\to N_{\tau +\mathrm{\Delta }\tau }$ of the tumor size to a control choice over a time interval $\mathrm{\Delta }\tau$ can give an indication of the inner tumor composition. As we have seen earlier, the length of time interval $\mathrm{\Delta }\tau$ should be shorter than all other intrinsic time scales to enable control. The procedure we follow is to first derive an effective propagator $W_{\text{eff}}\left(N_{\tau +\mathrm{\Delta }\tau }|N_{\tau },N_{\tau -\mathrm{\Delta }\tau },u_{\tau -\mathrm{\Delta }\tau };u_{\tau }\right)$ (SI Text) and then repeat the cost-to-go calculation of Eqs. 9 and 10. This propagator takes into account not only the current size $N_{\tau }$, but also the last measurement $N_{\tau -\mathrm{\Delta }\tau }$ and the last control decision $u_{\tau -\mathrm{\Delta }\tau }$. It follows from the microscopic W used in Eq. 10 by integrating over the internal degrees of freedom $n_s$ and $n_r$ at the three time points. Accordingly, the control profile is now a function of $\left(N_{\tau -\mathrm{\Delta }\tau },u_{\tau -\mathrm{\Delta }\tau },N_{\tau }\right)$. For the parameter values leading to the majority rule in Fig. 2C, the new control profile is shown in Fig. S6. The drug regimen ($u=0$ or $u=1$) is maintained as long as the tumor size decreases sufficiently. At the first sign of possible reversal, the regimen is switched.

Discussion

We used stochastic control theory to quantify optimal control strategies for models of evolving populations. We hope our results will lead to interesting new designs of microbial and cancer cell evolution experiments where feedback plays a central role in achieving a given control task. We further demonstrated how control can be maintained with finite resources, when the monitoring necessary for adaptive control is imperfect. These strategies all depend on our ability to anticipate evolution, i.e. on a knowledge of the relevant equations of motion and their parameter values. For cancer, such detailed knowledge of evolutionary dynamics is certainly not yet available. Sequencing technologies are facing up to the challenge of tumor control with finite information, already accelerating progress in the monitoring of serial biopsies of tumors, circulating tumor cells, or cell-free tumor DNA in the bloodstream (33, 34). Once such time-resolved data become prevalent, we can start to learn and improve dynamical tumor models and compute their optimal control strategies. For instance, genetic heterogeneity within the tumor is now becoming quantifiable from sequencing data via computational inference (35–37). Heterogeneity and subclonal dynamics have been found to have an impact on treatment strategy selection (38). Furthermore, all other available sources of clinical data, such as medical imaging, can provide additional information on cellular phenotypes and should be integrated into personalized and data-driven tumor control (see e.g. ref. 39 for imaging data-based computational modeling of pancreatic cancer growth dynamics to guide treatment choice and ref. 40 for integrative analysis of imaging and genetic data).

Beyond cancer, the need to control evolving populations is a key global health challenge as resistant strains of bacteria, viruses, and parasites are spreading (41, 42). Any long-term success in controlling evolution depends, at the very least, on mastering the following components. Firstly, on a quantitative understanding of the underlying evolutionary dynamics. Progress in the understanding is best demonstrated by predicting evolution; this has so far proven difficult, even in the short term. Nevertheless, new population genetic approaches applied to data are promising––see influenza strain prediction in ref. 43. Secondly, the success of control will depend on the availability of a sufficient arsenal of non–cross-resistant therapeutic agents. These therapeutics should be combined with the ability to decide an appropriate drug regimen given the genetic and phenotypic structure of the population. Large-scale drug vs. cell line screens are systematically pushing this component forward (see e.g. ref. 44). And finally, long-term success depends on the ability to monitor the evolution of a target population and act rationally based on this information, the topic of this paper.