Fine-mapping additive and dominant SNP effects using group-LASSO and Fractional Resample Model Averaging

Abstract

Genomewide association studies sometimes identify loci at which both the number and identities of the underlying causal variants are ambiguous. In such cases, statistical methods that model effects of multiple SNPs simultaneously can help disentangle the observed patterns of association and provide information about how those SNPs could be prioritized for follow-up studies. Current multi-SNP methods, however, tend to assume that SNP effects are well captured by additive genetics; yet when genetic dominance is present, this assumption translates to reduced power and faulty prioritizations. We describe a statistical procedure for prioritizing SNPs at GWAS loci that efficiently models both additive and dominance effects. Our method, LLARRMA-dawg, combines a group LASSO procedure for sparse modeling of multiple SNP effects with a resampling procedure based on fractional observation weights; it estimates for each SNP the robustness of association with the phenotype both to sampling variation and to competing explanations from other SNPs. In producing a SNP prioritization that best identifies underlying true signals, we show that: our method easily outperforms a single marker analysis; when additive-only signals are present, our joint model for additive and dominance is equivalent to or only slightly less powerful than modeling additive-only effects; and, when dominance signals are present, even in combination with substantial additive effects, our joint model is unequivocally more powerful than a model assuming additivity. We also describe how performance can be improved through calibrated randomized penalization, and discuss how dominance in ungenotyped SNPs can be incorporated through either heterozygote dosage or multiple imputation.

INTRODUCTION

Genomewide association studies (GWAS) have been highly successful at identifying short chromosomal regions (loci) harboring causal variants affecting complex disease. At these identified loci, significant associations of single nucleotide polymorphisms (SNPs) with the trait, as judged by single marker testing, are often numerous; yet in many cases, the pattern of association, considered jointly with inspection of the LD structure, clearly implicates a few SNPs (genotyped or imputed) that best represent the underlying causal variants [Edwards et al. 2013]. In other cases, the pattern of association and LD structure is so complex that both the number and identities of such best representative SNPs are ambiguous [e.g., Strange et al. 2010]; this ambiguity is problematic because it provides a poorly informed starting point for subsequent experimental or annotation-based follow-up.

At these more complex loci, there is a compelling case for reanalysis using procedures that model multiple SNP effects simultaneously. In theory, such multi-SNP methods should lead not only to more robust estimates of each SNP’s effect but also should better distinguish which SNPs represent independent signals worthy of subsequent prioritization [Stephens and Balding 2009; Wang et al. 2012]. In practice, however, such multi-SNP analysis is typically of an informal nature, restricted to, for example, conditional regressions on top-scoring associations producing statistics that, though superficially decisive (e.g., declaring the presence or absence of multiple signals) are also unreliable, in that they would be expected to vary dramatically in different samples from the same population (see well-established arguments in, e.g., Buckland et al. 1997). Although more sophisticated multi-SNP methods based on general statistical procedures for variable selection can provide more robust or moderated inference, these methods are much less often applied and their results less often reported. This may be in part because such methods, in balancing a more complicated set of statistical priorities, make trade offs between computational convenience and biological comprehensiveness that can seem severe, arbitrary, and/or omitting of important features.

One biological feature routinely omitted in methods currently proposed for multi-SNP analysis is genetic dominance. Instead, it is common to assume additive-only genetics — that is, where the effect of each SNP’s minor allele is strictly additive in relation to its count [Kooperberg et al. 2010; Ballard et al. 2010; Segura et al. 2012]. This assumption of additivity is likely motivated by convenience: Although modeling both additive and dominance effects together in the single marker setting is straightforward [Yeager et al. 2007; Li et al. 2009; Zheng et al. 2011], in the multi-SNP setting it can be hard to achieve gracefully. In particular, each SNP is ideally represented by a pair of variables, but these variables are often highly correlated with each other. For reasons of speed or simplicity, the burden of these additional complications typically leads to dominance being ignored [see, e.g., Guan and Stephens 2011].

The presence of genetic dominance, or equivalently genetic recessivity, is nonetheless a standard assumption made when modeling complex traits in plants and model organisms [Lynch and Walsh 1998; Neale et al. 2008]. Dominance is also commonly recognized in human genetics: it is a well-studied feature of monogenic disorders such as cystic fibrosis and phenylketonuria; it has been shown to contribute significantly to broad-sense heritability in cohort studies [Ober et al. 2001]; and it has been shown to have a substantial role in the form of recessivity leading to inbreeding depression in height [McQuillan et al. 2012]. Moreover, dominance has been shown to capture with greater accuracy (and higher statistical significance) the effects at some disease susceptibility loci in human GWASs of blood pressure [Org et al. 2009], cancer [Antoniou et al. 2009], and kidney disease [Okamoto et al. 2011].

Modeling that ignores dominance will in many cases provide inference that is nonetheless adequate: For instance, when the local genetic architecture is in fact mostly additive; or when, in the sample under study, dominant-acting loci are anyway observed on only two genotypes (and thus well-modeled by an additive effect). Historically, assuming additivity even in single marker tests was a reasonable trade-off when primarily using tagging SNPs. In that setting, dominant-acting causal SNPs can present an additive-like signal if and when detected through a tagging SNP in low to moderate LD [Chapman and Clayton 2007].

In modern genetic association, however, with genotypes available at high density, and when strong genetic dominance is present, modeling effects at single SNPs under additive-only assumptions can fail badly [Kim et al. 2010]. By implication, when applied in this context, multi-SNP models that fail to capture dominance can give more weight to weak additive associations modeled well than to strong dominance signals modeled poorly; when deciding among candidates for further investigation, this risks systematic prioritization of the wrong SNPs.

In this paper we propose a multi-SNP method that uses joint modeling of additive and dominance effects to characterize more accurately the genetic architecture of loci identified in standard GWAS, producing a reprioritization of SNPs that is enriched for true signals relative to single marker and additive-only multi-SNP analyses. Our method builds on our previous work in this area: We take our existing multi-SNP method LLARRMA [Valdar et al. 2012] (reviewed in Methods), which reprioritizes SNPs under the assumption of additive-only genetics, and we introduce several coordinated extensions that allow it to model dominance. The original LLARRMA combined LASSO-penalized regression with resampling in order to estimate how frequently each SNP at a locus would be included in a sparse multi-SNP model in a random sample from the population. This led to a prioritization of SNPs based on the stability of each SNP’s association with the phenotype, with stability judged with regard to both sampling variation and competition from other SNPs that may be in high LD. In this paper, we incorporate dominance through two (necessarily linked) elaborations: 1) each SNP, previously represented by a single additive-effect predictor, is now modeled as a pair of variables subject 4 to joint shrinkage and selection via a group LASSO penalty; and 2) the resampling procedure, previously subsampling, is generalized to ensure that the dimension of the predictor matrix, and thereby the dimensions of the fitted LASSO model, between resamples remains constant. This latter elaboration, which we term “fractional resampling” and which is related to the Bayesian bootstrap [Rubin 1981], helps resolve a general problem with the application of resampling-based methods to data sets in which some levels of a categorical predictor have low frequency — that is, where some genotypes necessary for defining a modeled effect are rare to the point of being entirely absent in a large proportion of ordinary resamples. Additionally, we investigate the use of randomized LASSO penalization (after Meinshausen and Bühlmann 2010) as a means to stabilize behavior of the LASSO when applied to subsets of SNPs in extremely high LD, incorporating this feature into our procedure as an option that, once calibrated to the data under study, can provide inference that is even more robust.

METHODS

We start by describing a standard linear model for estimating the additive and dominance (recessive) effects of m SNPs at a broad genomic locus (hereafter, “locus”) identified by GWAS of a quantitative outcome in n individuals; we then describe a statistical procedure to identify a subset of m_q SNPs that might best represent the underlying causal variants using penalized regression combined with a resampling procedure. For convenience we define a “true signal” as the SNP that most strongly tags an underlying causal variant, a “background” SNP to be a SNP that is not a true signal, and an optimal analysis as one that distinguishes true signals from background SNPs within a locus. Throughout, we assume the following setup: that the locus has been previously identified by an initial genomewide scan (e.g., using single marker regression); that the m SNPs may be in high LD; and that m_q < m < n. Notationally, we represent the true (but unknown) status of the SNPs using the binary vector γ = (γ₁, …, γ_m), where γ_j = 1 if SNP j is a true signal and γ_j = 0 otherwise.

STATISTICAL MODEL

Let y = (y₁, …, y_n) be the n-vector of quantitative outcomes for the n individuals, and define the “additive” matrix A as an n × m matrix containing the minor allele count for each of the m genotyped SNPs — that is, for a given SNP j with alleles q (major allele) and Q (minor allele), the ith element a_ij is 0, 1, and 2 for genotypes qq, qQ and QQ respectively. The “dominance” matrix D is defined to be another n × m matrix indicating for each SNP j whether the genotype of individual i is a heterozygote; in particular, d_ij = I_{{ai j =1}} (as in, eg, Servin and Stephens 2007). The phenotype y_i of individual i is modeled by a linear regression of the 2m predictors as follows:

$$y_i=\mu +{\mathbf{a}}_{i,\ast }^{\mathrm{T}}{\mathit{\beta }}_a+{\mathbf{d}}_{i,\ast }^{\mathrm{T}}{\mathit{\beta }}_d+{\epsilon }_i,$$ (1)

where μ is the intercept, a_i,* and d_i,* are the ith rows of A and D respectively, β_a and β_d are the corresponding m-vectors of additive and dominance effects respectively, and ε_i ~ N(0, σ²).

General Penalized Likelihood Framework

Our primary goal is not to distinguish which SNPs are additive or dominant but rather to identify the m_q true signal SNPs, regardless of their genetic mode of action. For SNPs selected to be included in the model it is then a secondary goal to estimate additive and dominance components of their effects. In order to achieve these goals, we adopt penalized likelihood approach that adapts ideas from the Bayesian bootstrap [Rubin 1981], the group LASSO [Yuan and Lin 2006], and the randomized LASSO [Meinshausen and Bühlmann 2010]. Details of the penalized likelihood framework are given below; further discussion and motivation follow.

Let = {y,A,D} represent the observed data, and let ${\mathit{\beta }}^{\mathrm{T}}=[{\mathit{\beta }}_a^{\mathrm{T}},{\mathit{\beta }}_d^{\mathrm{T}}]$ be the vector of additive and dominance SNP effects. Let the vector θ = (μ, σ²) collect all nuisance parameters and, optionally, any covariate effects. For 1 ≤ i ≤ n let L(β, θ; y_i, a_i,*, d_i,*) be the likelihood of observation y_i given parameters β and θ, and genotype predictors a_i,* and d_i,*. Given a sample weight vector w = (w₁,…,w_n) with w_i ∈ [0, ∞), define the weighted log-likelihood as

$$\ell (\mathit{\beta },\mathit{\theta };\mathbf{w},\mathcal{D})=\sum _{i=1}^n{w}_{i}logL(\mathit{\beta },\mathit{\theta };y_i,{\mathbf{a}}_{i,\ast },{\mathbf{d}}_{i,\ast }).$$ (2)

When all weights w_i are equal to 1, the weighted log-likelihood reduces to the ordinary log-likelihood; for binary weights w_i ∈ {0, 1}, the weighted log-likelihood is the log-likelihood of a subsample consisting of those observations i for which w_i = 1; for normally distributed traits Eq 2 simplifies to a weighted residual sum of squares.

In real data, for a given SNP j, the additive and dominance vectors a_*,,j and d_*,j (i.e., the jth columns of A and D respectively) will often be highly correlated. To avoid this correlation producing numerically unstable results, it is advantageous to moderate the estimation of each non-zero pair {β_a,j, β_d,j} through some form of joint shrinkage. We achieve this by structured penalization based on the group LASSO, which forces pre-specified groups of parameters to enter or leave the model together, and performs shrinkage of effects within each group. In more detail, we employ a weighted penalty of the form

$$\text{pen}(\mathit{\beta };\mathbf{r})=\sum _{j=1}^m{r}_j^{-1}\sqrt{{\beta }_{a,j}^2+{\beta }_{d,j}^2},$$ (3)

where r₁, …, r_m ∈ (0, ∞) are SNP-specific weights.

Describing both observation-specific and SNP-specific weights collectively as a “perturbation”, 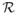= {w, r}, and letting λ > 0 be a parameter balancing the tradeoff between the log-likelihood and the penalty, our estimate of additive and dominance effects is given by

$$\widehat{\mathit{\beta }}(\lambda ,\mathcal{R};\mathcal{D})=\underset{\mathit{\beta }}{\text{argmin}}\left\{-\underset{\mathit{\theta }}{min}\ell (\mathit{\beta },\mathit{\theta };\mathbf{w},\mathcal{D})+\lambda ·\text{pen}(\mathit{\beta };\mathbf{r})\right\}.$$ (4)

When all values in perturbation 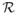are equal to 1, the estimate β̂(λ, 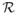; 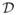) coincides with that of the group LASSO [Yuan and Lin 2006] with a natural grouping of additive and dominance effects for each SNP.

Permutation-based selection of the penalty parameter

The penalty parameter λ in Eq 4 controls the degree of sparsity (and shrinkage) in the model, with larger values causing a greater number of SNPs to be excluded. To choose a suitable value of λ for inference we use the discovery-based “permutation selection” criterion proposed in Valdar et al. [2012], which was based on a proposal of Ayers and Cordell [2010]. Let π₁ (y),…, π_S (y) be S permutations of the response y, and define π_s ( 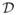) = {π_s (y),A,D} be a version of 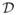in which the response y is replaced by its sth permutation. For a given perturbation 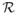, let λ_s be the smallest value of penalty λ for which each entry of β̂(λ, 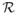;π_s ( 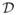)) is zero. The permutation selection value of λ is defined as the median of the λ_s values,

$$\widehat{\lambda }(\mathcal{R},\mathcal{D})=\text{Median}({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_S.).$$ (5)

For stable estimation of this median, we find that in real data settings S = 20 (as in Valdar et al. 2012) is adequate, and we use that value here.

Definition of an included SNP

For a fixed perturbation 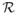, the jth SNP is defined as being “included” if either its additive or dominant effect is estimated to be non-zero. Formally, if β̂_a,j and β̂_d,j are the additive and dominance effects for SNP j estimated in β̂(λ, 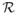; 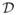) where λ = λ̂( 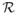, 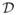), then we define the inclusion indicator of SNP j to be

$${\widehat{\gamma }}_j(\mathcal{R},\mathcal{D})=\{\begin{array}{ll}0\hfill & \text{if}{\widehat{\beta }}_{a,j}={\widehat{\beta }}_{d,j}=0\hfill \\ 1\hfill & \text{otherwise}\hfill \end{array}.$$ (6)

Calculating this for SNPs j = 1, …,m leads to the binary m-vector of SNP inclusions γ̂( 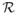, 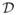) = (γ̂₁ ( 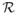, 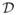),…, γ̂_m( 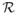, 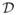)), which estimates the true vector of inclusions γ.

FRACTIONAL RESAMPLE MODEL AVERAGING

Model averaging rationale

Frequentist methods for variable selection commonly used in this context, including stepwise selection, LASSO, and informal conditional regression, typically yield a single, categorical decision about which SNPs should be included in the model, that is, a hard estimate of γ; but a statement of that estimate’s frequentist properties, namely how much it would be expected to vary in alternate, random, finite samples from the population (i.e., akin to a standard error), is analytically unavailable and so goes unreported. This is unfortunate because the set of SNPs selected, along with any inferences conditioning on that set (e.g., the jointly considered SNP effects), is usually highly sensitive to sampling (see well-established arguments in, e.g., Buckland et al. 1997), and reporting it as if otherwise is at best optimistic, and at worst misleading. Faced with this, one option is to switch to using Bayesian methods, which explicitly model posterior uncertainty about higher order inference, following appropriate specification of priors (e.g., Guan and Stephens 2011); another, which we consider here, is to stay within the frequentist framework but estimate relevant frequentist properties of the selection procedure by means of resampling.

Rather than using LASSO-based model selection to estimate γ directly, we therefore instead use multiple estimates of γ obtained from alternative realizations of the data to help identify those SNPs whose association with the phenotype is stable, both to model selection and sampling variation. In our previous work, these alternative data sets were generated by bootstrapping or subsampling the observations, and optionally using a multiple imputation step to fill in any missing data [Valdar et al. 2006, 2009, 2012]. That general approach we termed resample model average (RMA) to reflect the fact that it generalizes bagging [Breiman 1996] and bootstrap model averaging [Buckland et al. 1997] (see also Utz et al. 2000). In RMA, statistics of interest are collected on each resample (and imputation) and then averaged (or otherwise summarized) to give a final, aggregate estimate. In the context of fine-mapping SNPs at a locus: for each SNP j we estimate the long-run average frequency E(γ_j) that its association with the phenotype would survive model selection, describing this as its resample model inclusion probability (RMIP; Valdar et al. 2009). In Valdar et al. [2012] we developed an RMA method based on the LASSO (termed LLARRMA, for LASSO local automatic regularization RMA) to reprioritize SNP associations at a locus (or “hit region”, in that paper’s terminology) under an additive genetic model; here we extend that work to incorporate modeling of dominance.

Extending the additive model to incorporate dominance, however, poses challenges for RMA: Aggregating the results of model selection and estimation over repeated bootstraps or subsamples of data 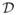is problematic when 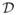contains predictors that are constant among a large fraction of individuals. For example, SNPs with a small number of individuals representing their homozygous minor allele genotype (ie, QQ) will have indistinguishable additive and dominance components in some resamples but not others; rarer SNPs with few examples of variant individuals may become entirely monomorphic. In either case, SNPs with low frequencies for some genotypes will not be representable in the same way between resamples, leading to a change in dimensionality of β or γ̂ that complicates the definition and interpretation of statistics such as RMIPs that are based on aggregation.

Resample model averaging using fractional observation weights

To overcome the problem of rare predictors, we introduce a generalization of RMA, fractional resample model averaging (FReMA), based on fractional data weights. Let w⁽¹⁾, …,w^(K) ∈ (0, ∞]ⁿ be vectors of non-negative sample weights drawn independently from a fixed weighting distribution W(·). For each k = 1, …, K, define the following quantities: the kth perturbation 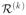= {w^(k), r^(k)}, where r^(k) = 1_m unless otherwise stated; the penalty λ̂^(k) = λ̂( 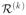, 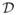); the vector of estimated effects β̂^k) = β̂(λ̂^(k), 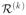; 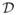); and the vector of SNP inclusions γ̂^(k) = γ̂( 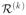, ). Performing K independent fractional resamples gives the m × K matrix of inclusions Γ = [γ̂⁽¹⁾, γ̂⁽²⁾, ···, γ̂^(K)]. From this matrix, we estimate the fractional resample model inclusion probability (FReMIP) of SNP j as

$${\widehat{\text{FReMIP}}}_j=\frac{1}{K}\sum _{k=1}^K{\widehat{\gamma }}_j({\mathcal{R}}^{(k)},\mathcal{D})=\frac{1}{K}\sum _{k=1}^K{\widehat{\gamma }}_j^{(k)}=\frac{1}{K}\sum _{k=1}^K{\mathrm{\Gamma }}_{jk},$$ (7)

which approximates the expectation of γ_j over repeated samples from the same weighting distribution. Similarly, for any function g(β), such as, for example, a predicted phenotype or a SNP effect, we can obtain a FReMA estimate as ĝ = K⁻¹ Σ_k g(β̂^(k)).

Weighting distributions for which $w_i^{(k)}=0$ with probability zero fix the dimensionality of the data, and thereby the dimensionality of β and γ̂, across resamples because they ensure that every observation participates (to a lesser or greater extent) in the likelihood. For normally distributed traits, sample weighting is equivalent to some phenotype values being treated as if they were measured with less precision, since the weighting in Eq 2 becomes equivalent to respecifying the residuals in Eq 1 as ε_i ~ N(0, σ²/w_i).

Proposed weighting density: independent uniforms

We propose to sample the weight of each data point independently from the range 0 to 1, that is, to draw $w_i^{(k)}\stackrel{\text{iid}}{\sim }\text{Unif}(0,1)$. This can be seen as a smoothed version of subsampling. Under this setting, the effective sample size of each fractional resample, which we define to be the total weight $n^{(k)}={\sum }_{i=1}^n{w}_i^{(k)}$, has expectation $\mathrm{E}(n^{(k)})=\frac{1}{2}n$ and, for reasonable values of n, has approximate distribution $\mathrm{N}(\frac{1}{2}n,{(12n)}^{-1})$. Moreover, the proportion of total data weight n^(k) attributed to any one observation will generally be of order 1/n with maximum proportion of order 2/n.

Alternative weighting densities: subsampling and bootstrapping

The weighting density W is defined loosely, and encompasses subsampling, non-parametric bootstrapping and the Bayesian bootstrap, among others. Specifically, when W(·) is generated by permuting φn ones and (φ − 1)n zeros for some proportion φ, then FReMA is equivalent to subsample model averaging (e.g., Valdar et al. 2009, 2012); when W(·) = Multinomial(n⁻¹1_n, n), such that $w_i^{(k)}\in \{0,1,\dots ,n\}$ subject to n^(k) = n, FReMA is equivalent to bootstrap model averaging (eg, Buckland et al. 1997); and when W(·) = Dirichlet(1_n), such that $w_i^{(k)}\in [0,n]$ subject to n^(k) = n, it is equivalent to model averaging based on the Bayesian bootstrap [Rubin 1981; Clyde and Lee 2001]. The maximum proportion of weight attributed to any one individual varies among these alternatives: for subsampling it is constant at 1/n, but for the bootstrap and Bayesian bootstrap it is considerably greater (of order 6/n or more).

Terminology for resampling

Despite the fact that FReMA generalizes RMA, for the purposes of this article we will henceforth reserve the terms “fractional resample”, FReMIP and FReMA exclusively for procedures and outcomes that involve weighting distributions capable of producing non-integer weights (eg, independent uniform weighting and the Bayesian bootstrap). For continuity with previous work, we will retain the terms RMA and RMIP when referring to subsampling or bootstrapping (ie, integer weight resamples), and will use “resample” to mean an integer or non-integer weight resample.

SELECTING AMONG HIGHLY CORRELATED SNPS: THE RANDOMIZED GROUP-LASSO

When the LASSO is applied to a set of highly correlated SNPs that all strongly associate with the phenotype, it will tend to select a small subset arbitrarily. The effect of this arbitrariness on inference is mitigated by resampling only somewhat. For instance, in the extreme case of high correlation in the population leading to some pairs of SNPs having a perfect correlation in the sample, subsequent resampling will simply replicate this perfect correlation, with any arbitrary selections between the two SNPs being similarly replicated.

A modification of the LASSO that helps address this issue was proposed by Meinshausen and Bühlmann [2010]. In their “randomized LASSO”, the penalty applied to each predictor in each resample is chosen at random from {λ, λ/c}, for some pre-specified c ∈ [0, 1] (see also Bühlmann and van de Geer 2011). Here we employ a “randomized group LASSO” in which SNP-specific weights ${\mathbf{r}}^{(k)}=(r_1^{(k)},\dots ,r_m^{(k)})$ are drawn independently in each resample as r_j = {c, 1} with equal probability. Incorporating this additional randomization step into our procedure has minor consequences for computation time (see Supplemental Material).

Empirical tuning of the randomization penalty

We find that the optimal choice of randomization parameter c depends on the correlation structure of the data, and so we recommend dataset-specific calibration. Moreover, because of the additional variability induced in the estimation, we recommend a minimum of K = 250 resamples, with more preferred. Based on preliminary simulations using the locus dataset described below, we find that optimal performance is achieved with c ∈ [0.6, 0.8] (see Supplemental Material); in the applications of the randomized LASSO described subsequently we therefore set c = 0.7.

LLARRMA-RDAWG NOMENCLATURE

To help assess how much each proposed extension to LLARRMA contributes to performance, we use the naming convention in Table 1, suffixing “LLARRMA” with a string of letters indicating which genetic model, weighting density and effect penalization is in place. Thus, “LLARRMA-dawg” applies fractional resampling to additive and dominance (recessive) effects grouped through a penalty applied to each SNP, and “LLARRMA-rdawg” additionally incorporates penalty randomization to help break ties between tightly linked SNPs. By contrast, “LLARRMA-sa” corresponds to the original, additive-only subsampling procedure of Valdar et al. [2012].

Table 1.

Nomenclature for modeling and resampling procedures used in the paper.

Character	Description
r	Randomized LASSO penalization
s	Resampling by subsampling
w	Resampling by fractional subsampling
a	Additive effects
d	Dominance/Heterosis effects
g	‘a’ and ‘d’ modeled as a grouped effect

COMPETITOR METHOD: SINGLE MARKER REGRESSION

Our model averaging approach calculates a score (an RMIP, or its generalization, a FReMIP) that prioritizes each SNP in the identified locus. We compare the ability of those scores to discriminate true signals from background SNPs, not only between different variations of LLARRMA, but also with the standard GWAS alternative: single marker regression, as used in, for example, PLINK [Purcell et al. 2007]. In single marker regression, we fit a linear model to each SNP with either additive only, or additive and dominance effects as in Eq 1, and report the score of the SNP as −log₁₀ P (“logP”), where P is the p-value from a likelihood ratio test against an intercept-only model. For comparison of LLARRMA-sa with multi-SNP procedures based on Stability Selection and Bayesian model averaging we refer the reader to Valdar et al. [2012].

SIMULATION FRAMEWORK

Simulation was used to assess how well each method could discriminate SNPs with additive and/or dominance effects from those with no effect in GWAS loci of complex LD. Performance was examined under seven different settings (“locus effect architectures”), each corresponding to a scenario in which a different mix of additive and dominance effects were present. Simulations were structured as follows: first, 500 loci, each comprising 376 SNPs on 2500 individuals, were simulated based on real GWAS data; for each simulated locus, five SNPs were randomly selected to be true signals; true signals were then assigned effects according to the simulated effect architecture; the effects of the five true signals were combined with random noise to generate a quantitative phenotype owing on average 5.8% of its variance to the true signals; phenotype and genotype data were analyzed by LLARRMA, its extensions, and single-marker regression to produce scores (logP, RMIP, or FReMIP) for each SNP; and the abilities of these scores to discriminate the true signals from background SNPs were assessed. Details of specific steps follow.

Genotypes

Loci were simulated to have an LD structure mimicking that of a real reference dataset. The reference dataset in this case comprised genotypes for 2,016 individuals on 376 SNPs in the contiguous 11 39.063723-40.985321 Mb segment on chromosome 22 from the human GWAS of WTCCC [2007] (LD structure shown in Fig 1) (Note: This is a trimmed version of the ’58 data used in Valdar et al. 2012). Genotypes for new loci were generated as follows: haplotypes were inferred for each individual in the reference dataset using fastPHASE [Scheet and Stephens 2006]; these haplotypes were passed to HAPGEN2 [Su et al. 2011], together with necessary map and legend files from the HapMap project [The International HapMap 3 Consortium 2010] (specifically these files were from HapMap 3 [release 2] NCBI build 36 [dbSNP b126]); HAPGEN2 was then used to generate haplotypes and corresponding genotypes for 376 SNPs on 2500 new individuals.

Figure 1.

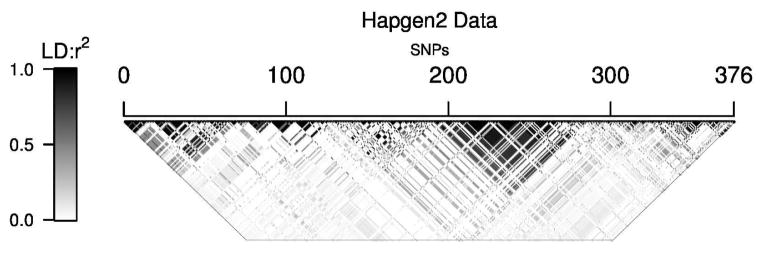
LD structure used by HAPGEN2 to create simulated genotype data. Shading indicates pairwise LD between SNPs, ranging from white (r² = 0) to black (r² = 1).

Placement of true signals

For each simulated locus, five SNPs = {q₁,…, q₅} ⊂ {1, …,m} were selected to be true signals. Selection was at random, subject to the minor allele frequency (MAF) of any chosen SNP being at least 0.1; this bounded the genotype frequency of the homozygous minor allele (required to model dominance) to 0.01, ensuring that estimation of dominance was meaningful.

SNP effects and locus effect architecture

True signals were assigned effects based on the simulated locus effect architecture. Seven such architectures were considered: additive effects only (architecture A); dominance of minor alleles (B); dominance of major alleles (C); heterosis (D); a mixture of dominance types (E); and mixtures of additive and dominance that are mostly additive (F) or mostly dominant (G). Architectures were defined by the SNP effect types they included. Specifically, for a given locus/architecture combination, each true signal was designated one of five SNP effect types — additive, or one of four subcategories of dominance (first six columns of Table 2) — in a probabilistic manner, with the probabilities of each type being architecture-dependent (listed in the last seven columns of Table 2, where blank cells “-” denote probability zero). For example, under setting A only additive effects are assigned; under setting G additive effects are assigned with probability 0.3, with heterosis and general dominance assigned with probabilities 0.1 and 0.6 respectively. Once an effect type of some SNP q has been designated, its corresponding effects were assigned in a stochastic fashion: Additive effect β_a,q and dominance effect β_d,q are calculated according to the rules in columns 2 and 3 in Table 2, where, independently for each simulation trial and for each locus, we first draw sign variable $B~\text{Bernoulli}(\frac{1}{2})$ and dominance variable δ randomly from {−1.25, −1, −0.75, −0.5, 0.5, 0.75, 1, 1.25}, and then draw effect variable β_q ~ N(1.35(−1)^B, 0.02²), .

Table 2.

Additive and dominance effects for simulated true signals.

SNP effect type	Effects parameters SNP q		Genotype value			Locus effect architecture
	Additive	Dominance	qq	qQ	QQ	A	B	C	D	E	F	G
Additive	βq	0	0	βq	2βq	1	-	-	-	-	0.6	0.3
Minor allele dominant	βq	βq	0	2βq	2βq	-	1	-	-	-	-	-
Major allele dominant	βq	−βq	0	0	2βq	-	-	1	-	-	-	-
Heterosis	0	βq	0	βq	0	-	-	-	1	-	0.1	0.1
General dominance	βq	δβq	0	(1 + δ)βq	2βq	-	-	-	-	1	0.3	0.6

Phenotypes and signal to noise ratio

Phenotypes were simulated based on the linear model in Eq 1. For a prescribed set of SNP effects β_a and β_d, we calculate the expected phenotype E(y_i) for each individual i and then add residual error ε_i ~ N(0, σ²) to obtain simulated phenotype y_i. The residual error variance σ² is chosen to produce an expected signal to noise ratio of σ⁻²β^TVar([A,D])β = 1/16. This level of noise on average produces a locus explaining about 5.8% of the phenotypic variance, which is comparable to that observed in Warren et al. [2012] and Dastani et al. [2012].

Evaluating performance: initial ROC curve and initial AUC

Methods are compared based their ability to discriminate true signals from background SNPs, with performance evaluated formally using receiver operator characteristic (ROC) curves. The way ROC curves are defined and used can vary between studies [Krzanowski and Hand 2009]. Here, we follow the procedures and calculations described previously in Valdar et al. 2012, which focus on the “initial ROC curve” and maximizing the corresponding initial area under curve (AUC): the “initial ROC” curve is defined as the segment of the ROC curve in which between zero and 5% of the included SNPs are false positives; the “initial AUC” is the area underneath, proportionally rescaled to the range [0,1] such that an initial AUC of 1 is ideal whereas an initial AUC of 0.025 corresponds to selection based on random guessing. Examination of the initial ROC curve is, in our view, more relevant to GWAS practice than examination of the “full” ROC curve for the following reason: the initial AUC credits enrichment of true signals among only the top-scoring SNPs; unlike the full AUC, it gives no credit to, for example, a method that detects all true signals exclusively within the middle ranks of its discoveries.

COMPUTATION

All analyses were performed in R [R Development Core Team 2012], with the glmnet package [Friedman et al. 2010] used for fitting LASSO models and the grplasso package [Meier 2009] for group LASSO models. For the purposes of the simulation study, the number of resamples used by each LLARRMA-based method was limited to K = 250.

RESULTS

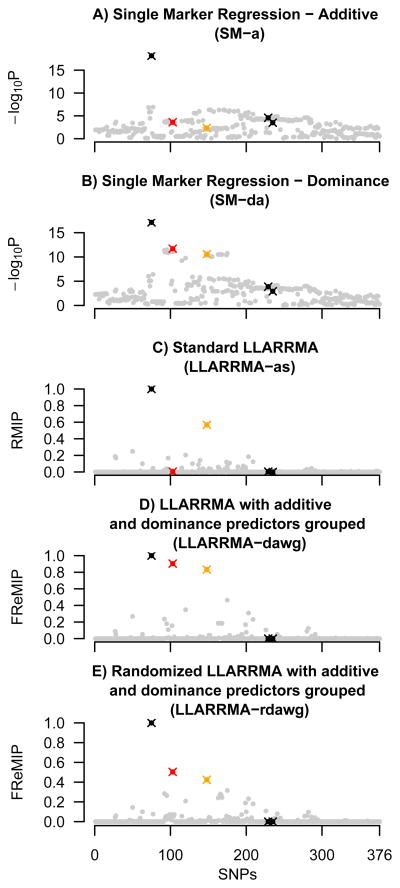
Example output from a single simulation under setting G is shown in Figure 2. In this simulation, the locus includes both additive and dominance effect true signals. For five of the methods considered, Figure 2 plots SNP location against SNP score (logP, RMIP or FReMIP); true signals are shown as crosses colored black (additive effects), orange (major allele dominant), and red (minor allele dominant), with background SNPs in gray. Moving from left to right in the locus: the leftmost true signal, a SNP with an additive effect, is easily identified by all methods; the two dominance effect signals (red and orange) are given low priority by additive-only methods (SL-a and LLARRMA-as), but higher priority in methods that explicitly model dominance; the two rightmost true signals, additive effects that (at least in this example) are in repulsion, are essentially undetectable by any method. For this particular simulated locus, multi-SNP modeling (bottom three plots) is seen to act like a filter, assigning lower priorities to background SNPs that would otherwise detract attention from the true signals; in other examples, the nature of the reprioritization can be very different, and so general behavior of these methods is best considered through examining results from a large number of trials, as described below.

Figure 2.

Results of five methods applied to an example dataset from simulation study G. Plots show SNP location in a simulated locus against SNP score, where SNP score is defined for single marker methods (sub plots A, B) as −log₁₀ of the p-value (logP), and for multi-SNP methods as the inclusion probability (RMIP or FReMIP). SNPs for which a true signal was simulated are shown as crosses, in black (additive effect), orange (major allele dominant), and red (minor allele dominant); all other (background) SNPs are shown gray dots.

LOCI WITH ADDITIVE-ONLY EFFECTS

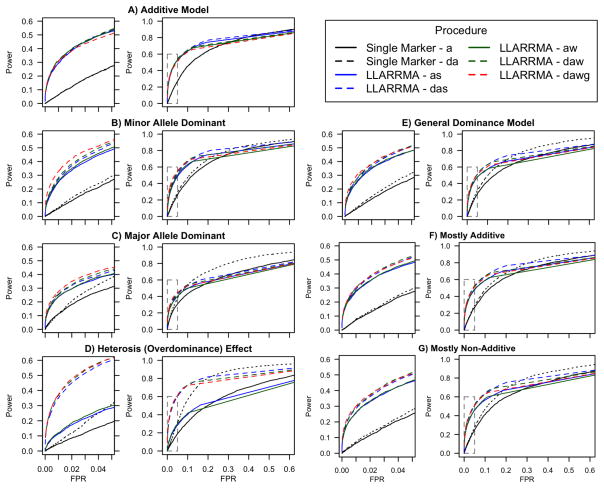
It was important for us to examine whether the incorporation of dominance effect parameters might lead to reduced power when dominance was absent. In Figure 3a we therefore assess the performance of the LLARRMA variations against each other and against single marker regression for additive only loci. Figure 3a contains two subplots: rightmost is the ROC curve plotting power (the proportion of true signals declared as influential) against false positive rate (FPR; the proportion of background SNPs declared as influential) for each method over a range of possible cutoffs of the SNP score; leftmost is a zoom-in of the ROC curve for FPR≤0.05, which we call the “initial ROC” curve. The initial ROC curve, and the area under it (the “initial AUC”, rescaled to range [0,1]) are our primary performance measures (see Methods); values of the initial AUC are listed for each simulation in Table 3.

Figure 3.

Initial and full ROC curves plotting discriminatory power of single marker and multi-SNP (LLARRMA) methods under seven simulation settings. Each setting (A–G) corresponds to the presence of a a different underlying genetic architecture for the locus, and plots both the full ROC curve (right) and its zoom-in (the initial ROC; left); better performance in each case is indicated by a greater area under the initial ROC curve. For clarity, only multi-SNP methods using constant penalization are shown.

Table 3.

Mean percentage of maximum initial AUC for all simulation studies (all standard errors < 0.26). For each simulation study, best performing method (or methods when other methods are not statistically different from the best method) in bold; best among those with constant penalization are underlined.

Locus effect architecture (simulation study)	Single marker regression		LLARRMA Constant penalization					LLARRMA Randomized penalization
	-a	-da	-as	-das	-aw	-daw	-dawg	-ras	-rdas	-raw	-rdaw	-rdawg
Additive (A)	14.6	14.6	39.1	39.4	39.8	40.1	38.5	41.2	41.3	42.5	42.7	41.4
Minor Dom. (B)	13.8	15.6	34.4	37.4	35.6	38.7	42.0	36.3	39.1	38.0	40.9	45.4
Major Dom. (C)	19.4	22.3	30.1	32.1	30.4	32.9	34.8	32.0	33.2	32.5	34.4	36.9
Heterosis (D)	10.1	15.4	18.3	45.3	19.5	47.0	47.4	19.1	46.5	20.8	49.1	50.3
General Dom. (E)	14.9	17.1	35.1	37.4	35.6	38.2	38.8	37.4	39.7	38.3	40.8	42.5
Mostly add. (F)	14.9	15.9	35.7	38.3	36.2	39.1	38.7	37.7	40.0	38.5	41.0	41.3
Mostly non-add. (G)	13.5	15.0	33.8	37.2	34.0	38.0	38.3	35.7	39.0	36.5	40.2	41.3

As shown in Figure 3a and Table 3, the LLARRMA-based methods are considerably more powerful than single marker regression; but when compared with each other, at least for this additive-only locus, the LLARRMA-based methods are about evenly matched. Among methods using constant penalization, a slight advantage over other methods is seen for LLARRMA-daw (i.e., LLARRMA using fractional resampling and additional ungrouped predictors for dominance). Methods using randomized penalization performed consistently better, and among these the most successful were the ungrouped, FReMA-based LLARRMAraw and LLARRMA-rdaw. Results under constant penalization have been separated from those under randomized penalization to reflect the fact that the latter require an additional, potentially arduous data-dependent calibration (see Methods). Under the additive-only setting described here, group penalization conferred little advantage nor disadvantage to discriminatory power.

LOCI WITH DOMINANCE-ONLY EFFECTS

When the simulated locus contained only dominance signals, best performance in the initial AUC was seen for multi-SNP methods using the grouped-penalty (Figure 3B–E and Table 3), specifically: LLARRMA-dawg among methods using a constant penalization; LLARRMA-rdawg among methods using randomized penalization; and LLARRMA-rdawg over both types of penalization (Table 3). The degree of outperformance varied with the type of dominance simulated, with the most extreme form — heterosis (simulation D) — producing the most striking contrasts: Under heterosis, additive-only models failed badly; adding a dominance term, especially in conjunction with fractional resampling, rescued performance (Table 3, Figure 3d). More generally, simulations B-E revealed several clear trends: single marker regression with additive-only effects is inferior to single marker regression incorporating dominance; this in turn, perhaps surprisingly, is inferior to multi-SNP methods with additive-only effects; those in turn (less surprisingly) are inferior to multi-SNP methods incorporating dominance. Among multi-SNP methods, the incorporation of grouped penalization, randomized penalization, or (ideally) both, leads to a small but consistent performance increment.

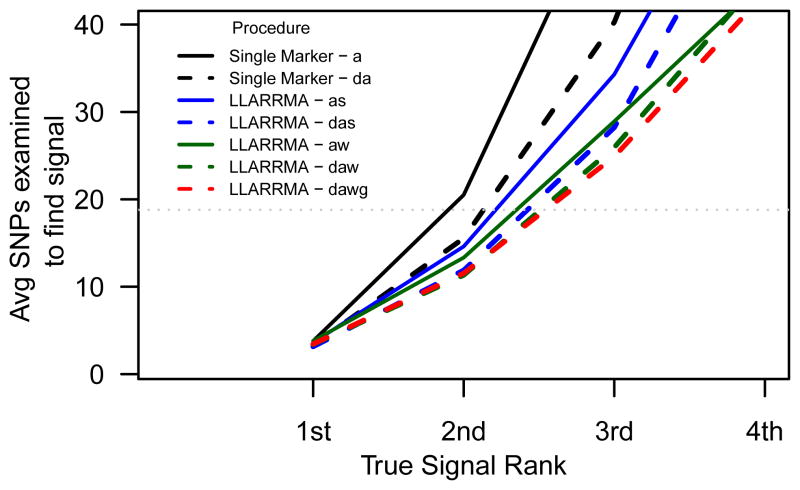
Identifying multiple true signals in a locus of complex LD inevitably requires examining some number of false positives; superior analysis methods will be those for which that number is typically few. For each analysis method, we calculated the average number of SNPs that would need to be examined in order to find k true signals. This average is plotted in Figure 4 for k = 1, …, 4, with results shown for single marker regression and the constant-penalty LLARRMA methods. (Results for detecting the full k = 5, and those using randomized penalization, are omitted for legibility). When it comes to detecting the first (k = 1) of five true signals, we observe little difference between the methods; for detecting the second, third and fourth (k = 2, …, 4) true signals, single marker regression quickly falls behind the multi-SNP methods, of which the FReMA-based, group-penalized LLARRMA-dawg is seen to be slightly more efficient for these simulations.

Figure 4.

The average number of SNPs that must be examined to find the first, second, third, fourth, and fifth true signal in simulation E. Dotted gray line indicates 5% of the SNPs in the locus.

LOCI WITH ADDITIVE AND DOMINANCE EFFECTS

Under the potentially more common setting of both additive-only and dominance effect SNPs, results were more consistent with the simulations of dominance (B–E) than of additive-only loci (A): Incorporating dominance effects in the model significantly improved performance; the use of grouped and randomized penalties also each produced a small but consistent improvement. In particular, when true dominance effects exist, incorporating dominance in the model was most effective when modeled with additive effects as a group.

DISCUSSION

We describe a statistical model selection procedure that better characterizes the genetic architecture at loci identified in GWAS by exploiting both additive and dominance components of each SNP’s genetic effect. We show that when it comes to discriminating additive-only true signals from background SNPs, there is no disadvantage associated with including dominance parameters, at least in our penalized regression framework; when, on the other hand, dominance effects are actually present — even in combination with significant additivity — we find that modeling both additive and dominance, either through a group penalty or as independently penalized predictors, produces a substantial improvement in discriminatory power.

The fact that additional power would be gained through more flexible or comprehensive modeling of effects at individual loci should not, in principle, be surprising: Dominance (or recessivity) is defined by its deviation from additivity; the more dominance signal present, the less effectively it will be captured by an additive model. In older GWAS focusing on indirect association through tagging SNPs, incorporating dominance effects adds little value since dominance, when identified by proxy through variants in low to moderate LD, resembles an additive signal [Chapman and Clayton 2007]. In modern settings, however, when genotypes are available at higher density (or in the limit all variants are observed or well-imputed), where dominance effects are not attenuated in this way, and where complex LD can result in a locus showing multiple variants of similar significance, comprehensive modeling is more crucial. In our multi-SNP setting, where SNPs are reprioritized on the basis of their ability to compete with each other for a position in a sparse multi-SNP model, additive-only modeling gives dominance SNPs a competitive disadvantage; as shown in our simulations, this translates to poorer discrimination of true signals when dominance is present to any degree.

Dominance is modeled in our regression setting using a standard parameterization based on orthogonal contrasts that splits each biallelic effect into separate additive and dominance components (also used by, e.g., Servin and Stephens 2007). An alternative parameterization, also standard in genetic analysis, is based on ANOVA-style treatment contrasts whereby each genotype is modeled as a treatment category with its own effect, with one of these categories (usually homozygote qq) chosen as a baseline (e.g., Yang et al. 2010). The choice of parameterizing one way or the other does not affect how well a single or multi-SNP model fits in terms of its likelihood; they are equivalent in this respect, and equivalently powerful. The choice does matter, however, when these coefficients representing the SNP effect are estimated subject to a penalty, such as the LASSO or group LASSO. In simulations reported in Supplementary Material, we show that LLARRMA-dawg using the orthogonal additive/dominance parameterization outperforms the genotype category parameterization in six out the seven genetic architectures tested here, with the degree of outperformance in five of these being dramatic. As discussed in the context of Bayesian priors by Servin and Stephens [2007], penalization imposes constraints that can strongly favor the fit of one parameterization over the other; under group LASSO penalization, we find that the orthogonal additive/dominance split used here confers substantially greater power and discrimination.

Despite its potential value, incorporating dominance into the fine-scale analysis of GWAS loci will likely require a slight shift in the use of results from SNP imputation. Imputation is a stalwart of GWAS, used to estimate genotypes of SNPs that either failed on the array or that were not genotyped explicitly, and thereby expanding considerably the set of SNPs available for identifying associations. The underlying statistical models used to perform the imputation, by their construction, distinguish all three genotypic classes of a SNP, and give probabilities for each. However, in practice, information on these three genotypic classes is not fully exploited by subsequent analyses. In particular, the imputation of a SNP, which estimates (at least) three probabilities (p = {p_qq, p_qQ, p_QQ}) that correspond to two non-redundant parameters, is most often reduced to a single value: an allele dosage (p_qQ + 2p_QQ). Although this allele dosage is intuitive and simple to incorporate into analyses, it represents a loss of information: The SNP effect is represented only in its additive component, whereas the dominance component (for example, representable as heterozygote dosage p_qQ), regardless of whether it would have provided important signal, is discarded. For modeling dominance with imputed SNPs in LLARRMA (and its variations), we offer two options: 1) additive and dominance inputs can be substituted by their dosage and heterozygote dosage (as above) respectively; or, our preferred option when feasible, 2) in each resample, genotypes of imputed SNPs can be directly sampled, either as multinomial draws from their marginal probabilities p or, better, from the full phased haplotype-based posterior (as available in, e.g., Scheet and Stephens 2006, and performed in Servin and Stephens 2007 and Valdar et al. 2012).

In reporting results from our reprioritization methods, we have focused not on identifying a single, best, multi-SNP model, which under realistic conditions would be highly sample-dependent, but rather on estimating for each SNP a measure that reflects the robustness of its association, both to finite sampling and competition from alternative multi-SNP models. Our (fractional) resample model inclusion probabilities — RMIPs or FReMIPs — are superficially analogous to the posterior model inclusion probabilities generated by Bayesian variable selection procedures, but in fact have a wholly frequentist motivation: They reflect variability in an estimator with respect to finite sampling, where the estimator in this case is our group LASSO model and where sample-to-sample variability is emulated via resampling of the original data. The role played by resampling is therefore crucial to the practical utility of our approach.

In our previous resample model averaging procedure, LLARRMA, in which SNPs were modeled under additive-only assumptions [Valdar et al. 2012], resampling was performed using subsampling. When extending LLARRMA to model dominance, however, we encountered a shortcoming of resampling when applied to model selection on data sets in which some predictors have categories that are rarely observed: When SNPs have some genotype classes observed at low (but non-zero) frequencies, subsampling (or equivalently bootstrapping) can lead to a reduction in the number of predictors associated with its effect. This means that rare variants can become monomorphic, and three-genotype SNPs, for which additive and dominance effects are distinguishable, can be converted into two genotype SNPs, for which additive and dominance cannot be separated. Although within a resample this change in effective dimension can be addressed by simply reducing the set of predictors from which included loci are chosen, when aggregating fitted models across resamples, it creates an additional level of incomparability that we find undesirable. Specifically, we aim to approximate the results of a hypothetical study that quantifies how much the sparse subset selected from a fixed (and non-sparse) candidate set of SNP predictors will vary with different samples of individuals drawn from the same population; but inducing variability in both the selection and the candidate set from which selection is made makes the resulting inclusion probabilities harder to interpret. To address this issue, we develop a smooth generalization of the resampling procedure itself — fractional resampling — that allows the candidate set to stay constant, permitting multi-SNP additive and dominance modeling even when the minor allele frequencies of those SNPs are low.

We find in simulation that using fractional resampling in place of subsampling leads to a consistent increase in discriminatory power; this is not only in settings where subsampling is likely to alter the candidate set (i.e., when modeling additive and dominance) but also in settings where subsampling should be unproblematic (i.e., when applying additive-only multi-SNP models). Our generalization of subsampling to fractional resampling is similar in spirit to the generalization of the non-parametric bootstrap to the Bayesian bootstrap [Rubin 1981]: In the Bayesian bootstrap, the bootstrap’s discrete multinomial weights are smoothed to a continuous dirichlet weighting; in fractional resampling, the effective 0 or 1 weights of subsampling are smoothed to fractions drawn from a uniform distribution on [0,1]. Moreover, both can be formulated as specific examples of the weighted likelihood bootstrap [Newton and Raftery 1994]. Given the choice, however, we prefer our subsampling-based strategy over the Bayesian bootstrap because the latter allows a potentially much larger number of duplicates of some observations — a feature that we find hard to justify in the human genetics context (and a feature also criticized at length in Rubin 1981). On the other hand, if subsampling can be viewed as approximately like drawing from Beta(a, a) where a = 1/∞, then fractional resampling as we implement it here (i.e., a = 1) lies somewhere between subsampling and the application of a constant half-weight (i.e., a = ∞); thus despite the strong empirical performance of using Beta(1, 1), we acknowledge that other ways to generate fractional weights are also worth investigating.

Our results suggest that, when it comes to discriminating multiple true signals among highly correlated background SNPs, performance of the LASSO-based RMA procedures can be consistently improved by randomization of the penalty parameter. This randomization, whereby in each resample approximately half of the predictors are given a weakened penalty, acts to break ties and redistribute advantages between SNPs in extremely high LD; in doing so, it helps compensate for the fact that the extreme correlations in the original sample are likely overstated and more likely to occur in resamples than in (true) new samples from the population. Nonetheless, the extent of the improvement depends on the value of the randomization parameter, c. In particular, we found that although performance in full AUC was relatively insensitive to the choice of c (a result consistent with Meinshausen and Bühlmann [2010], who advocated choosing c ∈ [0.2, 0.8]), performance in the initial AUC, our preferred metric, was far more sensitive to c: Randomized penalization improved on constant penalization only for c ∈ [0.6, 0.8]. How these values generalize will require further examination, but for now we conservatively recommend manual calibration via simulation to a given SNP dataset. Moreover, to average over the additional layer of randomization, LLARRMA using randomized (as opposed to constant) penalization requires a larger number resamples to obtain comparably stable RMIP or FReMIP estimates.

Our LLARRMA-dawg procedure can be though of as a multi-SNP association model embedded within a resample model averaging scheme; as such, it can be extended in a number of ways. The association model described here uses linear regression for a quantitative phenotype, but this is trivially extended to logistic regression for case/control phenotypes (as in the original LLARRMA of Valdar et al. 2012), or to any generalized linear model to which the LASSO or group LASSO can be applied. Within our association model, we penalize effects using the group LASSO, but this could be replaced by more sophisticated type of penalization. For example, Yang et al. 2010 describe a related SNP selection method that incorporates not only additive and dominance effects but also epistasis, all via the adaptive group LASSO; their procedure uses a different parameterization of additive and dominance than ours and returns only a single best model rather than an ensemble of models, but it could in theory be embedded in our FReMA framework to yield comparable model-averaged results. Our association model focuses on grouped effects for single SNPs but it could be extended to consider different types of grouped effects, such as differential effects of local haplotype combinations, structural variants, or combinations of rare variants within a gene or LD block. For the last of these, our FReMA framework could also be used to provide model-averaged inference for existing single-solution rare variant selection procedures such as those of Zhou et al. [2010], Ayers et al. [2011], Ayers and Cordell [2013] or Larson and Schaid [2014]. In this case, a given procedure would be applied in full to multiple independent fractional resamples, with each such resample defined through a reweighting of the likelihood component (as in Eq 2); the results of each application would then be aggregated in the manner described for Eq 7.

In summary, we describe a frequentist procedure, and its variations, to reprioritize genetic associations at loci containing multiple additive and dominance signals. The authors will provide an implementation of the proposed procedures in the R-package R/FReMA as soon as is practicable.