Skip to main content
PMC home page
Genome Research logoLink to Genome Research
. 2015 Feb;25(2):268–279. doi: 10.1101/gr.178756.114

Efficient inference of population size histories and locus-specific mutation rates from large-sample genomic variation data

Anand Bhaskar 1,2, YX Rachel Wang 3, Yun S Song 1,2,3,4
PMCID: PMC4315300  PMID: 25564017

Abstract

With the recent increase in study sample sizes in human genetics, there has been growing interest in inferring historical population demography from genomic variation data. Here, we present an efficient inference method that can scale up to very large samples, with tens or hundreds of thousands of individuals. Specifically, by utilizing analytic results on the expected frequency spectrum under the coalescent and by leveraging the technique of automatic differentiation, which allows us to compute gradients exactly, we develop a very efficient algorithm to infer piecewise-exponential models of the historical effective population size from the distribution of sample allele frequencies. Our method is orders of magnitude faster than previous demographic inference methods based on the frequency spectrum. In addition to inferring demography, our method can also accurately estimate locus-specific mutation rates. We perform extensive validation of our method on simulated data and show that it can accurately infer multiple recent epochs of rapid exponential growth, a signal that is difficult to pick up with small sample sizes. Lastly, we use our method to analyze data from recent sequencing studies, including a large-sample exome-sequencing data set of tens of thousands of individuals assayed at a few hundred genic regions.

The demography of an evolving population strongly influences the genetic variation found within it, and understanding the intricate interplay between natural selection, genetic drift, and demography is a key aim of population genomics. For example, the human census population has expanded more than 1000-fold in the last 400 generations (Keinan and Clark 2012), resulting in a state that is profoundly out of equilibrium with respect to genetic variation. Recently, there has been much interest in studying the consequences of such rapid expansion on mutation load and the genetic architecture of complex traits (Gazave et al. 2013; Lohmueller 2014; Simons et al. 2014). Estimating the population demography is necessary for developing more accurate null models of neutral evolution in order to identify genomic regions subject to natural selection (Williamson et al. 2005; Boyko et al. 2008; Lohmueller et al. 2008). The problem of inferring demography from genomic data also has several other important applications. In particular, the population demography is needed to correct for spurious genotype-phenotype associations in genome-wide association studies due to hidden population substructure (Marchini et al. 2004; Campbell et al. 2005; Clayton et al. 2005), to date historical population splits, migrations, admixture, and introgression events (Gravel et al. 2011; Li and Durbin 2011; Lukić and Hey 2012; Sankararaman et al. 2012), to compute random match probabilities accurately in forensic applications (Balding and Nichols 1997; Graham et al. 2000), for examples.

A commonly used null model in population genetics assumes that individuals are randomly sampled from a well-mixed population of constant size that evolves neutrally according to some model of random mating (Ewens 2004). However, several recent large-sample sequencing studies in humans (Coventry et al. 2010; Fu et al. 2012; Nelson et al. 2012; Tennessen et al. 2012) have found an excess of single nucleotide variants (SNVs) that have very low minor allele frequency (MAF) in the sample compared to that predicted by coalescent models with a constant effective population size. For example, in a sample of ∼12,500 individuals of European descent analyzed by Nelson et al. (2012), >74% of the SNVs have only one or two copies of the minor allele, and >95% of the SNVs have an MAF <0.5%. On the other hand, assuming a constant population size over time, Kingman’s coalescent predicts that the number of neutral SNVs is inversely proportional to the sample frequency of the variant (Fu 1995). Keinan and Clark (2012) have suggested that such an excess of sites segregating with low MAF can be explained by recent exponential population growth. In particular, a rapid population expansion produces genealogical trees that have long branch lengths at the tips of the trees, leading to a large fraction of mutations being limited to a single individual in the sample. Motivated by these findings and rapidly increasing sample sizes in population genomics, we here tackle the problem of developing an efficient algorithm for inferring historical effective population sizes and locus-specific mutation rates using a very large sample, with tens or hundreds of thousands of individuals.

At the coarsest level, previous approaches to inferring demography from genomic variation data can be divided according to the representation of the data that they operate on. Full sequence-based approaches for inferring the historical population size such as the works of Li and Durbin (2011) and Sheehan et al. (2013) use between two and a dozen genomes to infer piecewise constant models of historical population sizes. Since these approaches operate genome wide, they can take into account linkage information between neighboring SNVs. On the other hand, they are computationally very expensive and cannot be easily applied to infer recent demographic events from large numbers of whole genomes. A slightly more tractable approach to inferring potentially complex demographies involves comparing the length distribution of identical-by-descent and identical-by-state tracts between pairs of sequences (Palamara et al. 2012; Harris and Nielsen 2013).

The third class of methods, and the one that our approach also belongs to, summarizes the variation in the genome sequences by the sample frequency spectrum (SFS). The SFS of a sample of size n counts the number of SNVs as a function of their mutant allele frequency in the sample. Since the SFS is a very efficient dimensional reduction of large-scale population genomic data that summarizes the variation in n sequences by n − 1 numbers, it is naturally attractive for computational and statistical purposes. Furthermore, the expected SFS of a random sample drawn from the population strongly depends on the underlying demography, and there have been several previous approaches that exploit this relationship for demographic inference. Nielsen (2000) developed a method based on coalescent tree simulations to infer exponential population growth from single nucleotide polymorphisms that are far enough apart to be in linkage equilibrium. Coventry et al. (2010) developed a similar coalescent simulation-based method that additionally infers per-locus mutation rates and applied this method to exome-sequencing data from ∼10,000 individuals at two genes. Nelson et al. (2012) have also applied this method to a larger data set of 11,000 individuals of European ancestry (CEU) sequenced at 185 genes to infer a recent epoch of exponential population growth. The common feature of all these methods is that they use Monte Carlo simulations to empirically estimate the expected SFS under a given demographic model, and then they compute a pseudo-likelihood function for the demographic model by comparing the expected and observed SFS. The optimization over the demographic models is then performed via grid search procedures. More recently, Excoffier et al. (2013) have developed a software package that employs coalescent tree simulations to estimate the expected joint SFS of multiple subpopulations for inferring potentially very complex demographic scenarios from multipopulation genomic data. The problem of demographic inference has also been approached from the perspective of diffusion processes. Given a demographic model, one can derive a partial differential equation (PDE) for the density of segregating sites at a given derived allele frequency as a function of time. Gutenkunst et al. (2009) used numerical methods to approximate the solution to this PDE, while Lukić et al. (2011) approximated this solution using an orthogonal polynomial expansion. The coalescent-based method of Excoffier et al. (2013), fastsimcoal, and the diffusion-based method of Gutenkunst et al. (2009), ∂a∂i, can infer the joint demography of multiple subpopulations with changing population sizes and complex patterns of migration between subpopulations.

In this paper, we focus on the problem of inferring the effective population size as a function of time for a single randomly mating population. As mentioned above, our method is based on the SFS. By restricting our inference to a single population, we are able to compute the expected SFS exactly, rather than using Monte Carlo simulations or solving PDEs numerically. Briefly, we utilize the theoretical work of Polanski et al. (2003) and Polanski and Kimmel (2003), which relate the expected SFS for a sample of size n from a single population to the expected waiting times to the first coalescence event for all sample sizes ≤n. We show that the latter quantities can be computed efficiently and numerically stably for very large sample sizes and for an arbitrary piecewise-exponential model of the historical effective population size. Further, our method utilizes the technique of automatic differentiation to compute exact gradients of the likelihood with respect to the parameters of the effective population size function, thereby facilitating optimization over the space of demographic parameters. These techniques result in our method being both more accurate and more computationally efficient than ∂a∂i and fastsimcoal. In what follows, we carry out an extensive simulation study to demonstrate that our method can infer multiple recent epochs of rapid exponential growth and estimate locus-specific mutation rates with a high accuracy. We then apply our method to analyze data from recent sequencing studies.

Results

In what follows, we perform extensive validation of our method on simulated data using several sets of demographic models similar to those inferred by recent large-sample studies. We also apply our method to the neutral region data set of Gazave et al. (2014) and the exome-sequencing data set of Nelson et al. (2012) to detect signatures of recent exponential population growth.

Simulated demographic models

To validate our inference algorithm, we simulated data under the coalescent with recombination using the simulation program ms (Hudson 2002) with the following two demographic scenarios:

  • Scenario 1: This demographic scenario models two ancestral population bottlenecks followed by an epoch of exponential growth. We simulated data sets with several values for the growth duration t1 and per-generation growth rate r1 such that the population expansion factor Inline graphic is fixed at 512, which is close to the estimated population expansion factor inferred by Nelson et al. (2012) in the CEU subpopulation. The ancestral population bottlenecks reflect the out-of-Africa bottleneck and the European-Asian population split, and these parameters were set to those estimated by Keinan et al. (2007). The population size functions for this scenario are shown in Figure 1A.

  • Scenario 2: In this scenario, there are two epochs of exponential growth, the older of which (called epoch 2) lasts for t2 = 300 generations with a growth rate of r2 = 1% per generation, and a recent epoch (called epoch 1) of more rapid growth lasting t1 = 100 generations with a growth rate of r1 = 4% per generation. This model also incorporates the two ancestral population bottlenecks inferred by Keinan et al. (2007) and is shown in Figure 1B.

Figure 1.

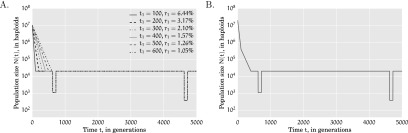
Figure 1.

Open in a new tab

Population size N(t) as a function of time (measured in generations) for (A) several choices of t1 and r1 in Scenario 1, and (B) Scenario 2. The present time corresponds to t = 0.

For each demographic scenario, we simulated several data sets using the coalescent simulator ms (Hudson 2002) with 10,000 diploid individuals and 100 unlinked loci each of length 10 kb, while using a realistic recombination rate of 10−8 per base per haploid per generation within each locus. We used a mutation rate of 2.5 × 10−8 per base per haploid per generation at each locus.

Maximum likelihood estimation (MLE) of demographic parameters

We applied our method to estimate the exponential growth rate and onset times for Scenario 1 and Scenario 2 while assuming that the details of the ancestral population bottlenecks are known. We did not try to estimate the ancestral population bottlenecks because our focus was on inferring recent population expansion events which are not detectable with small sample sizes. To infer ancient demographic events such as bottlenecks, we think that genome-wide methods such as those of Li and Durbin (2011) and Sheehan et al. (2013) will be more powerful. Figure 2, A and B shows violin plots of the inferred values of the duration and rate of exponential growth for each of the simulation parameter settings in Scenario 1, with the joint distribution over the inferred parameters shown in Supplemental Figure S1. In each simulation parameter combination in Scenario 1, the population expands by a factor of 512 in the epoch of recent exponential growth. The solid red curves in Supplemental Figure S1 represent the exponential growth parameter combinations that have this same population expansion factor, while the dashed red curves are the parameter combinations having 25% higher and lower population expansion factors. As can be seen from the tight clustering of points along the red curves in Supplemental Figure S1, the jointly inferred exponential growth parameter combinations quite accurately reflect the exponential population expansion factor—i.e., when the inferred growth onset time is large, the inferred growth rate is correspondingly lower, so that the population expands by the same factor in the inferred demographic model as in the true demographic model. Similarly, Figure 2, C and D shows the marginal distribution of the inferred values of the growth onset times and rates for each of the two epochs in Scenario 2, with the joint distribution of the inferred parameters for each of the two epochs shown in Supplemental Figure S2. Since most points in Supplemental Figure S2 fall within the dashed red curves, this indicates that the population expansion factors from the inferred estimates match the true population expansion factor in each epoch quite well.

Figure 2.

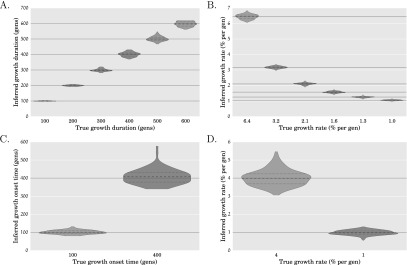
Figure 2.

Open in a new tab

Performance of our method on simulated data. Each violin plot is generated using 100 simulated data sets with 100 unlinked loci of 10 kb each over 10,000 diploid individuals. The gray solid horizontal lines indicate the true values for the simulation parameters. The median inferred parameter values, indicated by dashed black lines, match the true parameter values very well. Panels A and B, respectively, show violin plots of the duration and rate of exponential growth in the population size for each of the six simulation parameter settings of Scenario 1, illustrated in Figure 1A. Panels C and D show violin plots of the onset times (t1 and t2) and exponential growth rates (r1 and r2) for the two epochs of exponential growth in Scenario 2, illustrated in Figure 1B.

We also applied the coalescent simulation-based method of Excoffier et al. (2013), fastsimcoal, to the same simulated data sets used with our method above. Since we are working with large sample sizes here, for computational reasons we restricted fastsimcoal to use 200 and 500 coalescent tree simulations per likelihood function evaluation for Scenario 1 and Scenario 2, respectively, and at most, 40 rounds of conditional expectation maximization (ECM cycles). Figure 3 shows the results of running fastsimcoal on the simulated data sets for Scenario 1. We do not show the results of running fastsimcoal on the data sets for Scenario 2 because there was a huge variance in the estimated parameters. Note that in their work, Excoffier et al. (2013) use 105 coalescent tree simulations per likelihood function evaluation and 20–40 ECM cycles. There is substantially more bias in the estimated growth onset times and more uncertainty in the growth rates compared to our method (see Fig. 2A,B), which should decrease if one uses more coalescent tree simulations to evaluate the likelihood at each point. However, if we had used 105 trees per likelihood computation as was done in Excoffier et al. (2013), the inference would have taken an estimated 21 CPU days per data set for Scenario 1 and 47 CPU days per data set for Scenario 2 on average. In contrast, our method took on average ∼1.5 CPU minutes per data set for Scenario 1 and 20 CPU minutes per data set for Scenario 2.

Figure 3.

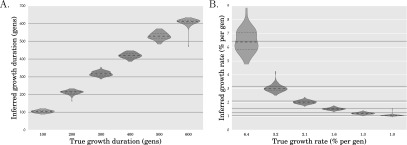
Figure 3.

Open in a new tab

Performance of fastsimcoal (Excoffier et al. 2013) on simulated data for Scenario 1. Panels A and B, respectively, show violin plots of the inferred duration and rate of exponential growth in the population size for 100 simulated data sets for each of the simulation parameter settings in Scenario 1. These are the same simulated data sets used to generate Figure 2, A and B and Supplemental Figure S1. The gray solid horizontal lines indicate the true values for the simulation parameters. When applying fastsimcoal, due to computational reasons we used 200 and 500 coalescent tree simulations for Scenario 1 and Scenario 2 per likelihood function estimation and limited the number of rounds of conditional expectation maximization (ECM cycles) to 40. On one of these 100 simulated data sets, their method appeared to have a runaway behavior and produced unreasonable estimates after 40 ECM cycles; this data set was excluded from these plots.

Estimation of per-locus mutation rates

Our method can compute the MLE for the mutation rate at each locus while estimating the optimal population size function parameters (see Equation 8 in Methods). The inferred mutation rates for each set of parameters in Scenario 1 and Scenario 2 are shown in Supplemental Figure S3. Since the mutation rates are estimated using the inferred demography, uncertainty in the demographic estimates will lead to uncertainty in the mutation rate estimates, as can be seen for the estimates for Scenario 2 in Supplemental Figure S3. For Scenario 1 with t1 = 100 gens and r1 = 6.4% per gen, we also simulated data sets where the mutation rate at each locus is randomly chosen from the range 1.1 × 10−8 to 3.8 × 10−8 per base per gen per haploid, and then held fixed across all the simulated data sets. This is the range of mutation rates estimated from family trio data by Conrad et al. (2011). Figure 4A shows the performance of our method on simulated data sets with 100 loci each of length 10 kb and demonstrates that our procedure can accurately recover the mutation rates.

Figure 4.

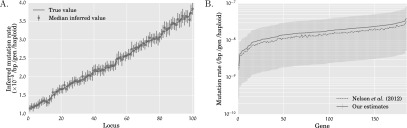
Figure 4.

Open in a new tab

Mutation rates inferred by our method. (A) Inferred mutation rates for simulated data sets with 100 loci from 10,000 diploids under Scenario 1 with t1 = 100 and r1 = 6.4%. The mutation rates at the 100 loci were drawn randomly from the range [1.1 × 10−8, 3.8 × 10−8]. The loci are sorted in ascending order of the simulated mutation rates. The increasing solid line indicates the mutation rates used in the simulation, while the circle and the vertical bars, respectively, denote the median and one standard deviation of the inferred mutation rate over 100 simulated data sets. (B) Inferred mutation rates for each of the 185 genes in the exome-sequencing data set of Nelson et al. (2012). The solid line connects our point estimates for the mutation rate, while the light vertical bars denote 95% confidence intervals that were constructed by a resampling block bootstrap procedure with 1000 bootstrap samples. The dashed line connects the point estimates of the mutation rate inferred by Nelson et al. (2012). While the mutation rates estimated by our method and that of Nelson and coworkers are very close to each other, the mutation rates estimated by our method are systematically higher at each locus owing to the lower population expansion rate inferred by our method.

Estimation of confidence intervals

Our inference algorithm described in Methods assumes that the sites within each locus are unlinked, in which case the function 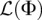Inline graphic given in Equation 9 is a true log-likelihood function. However, since actual genomic data (and our simulated data sets) involve nontrivial linkage within a locus, the function 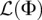Inline graphic in Equation 9 is a composite log-likelihood function. Hence, the asymptotic confidence interval expressions in the “Confidence intervals” section of Methods will not necessarily be well calibrated. To understand this issue a bit better, we simulated data sets under Scenario 1 with t = 100 gens and r1 = 6.4% per gen. We generated data sets with a sequence length of 106 bp by simulating 106/m unlinked loci of length m bp each and with a recombination rate of 10−8 per base per gen per haploid. We did this for m ∈ {100, 103, 104} bp. By linearity of expectation, the expected total number of segregating sites is independent of the locus length m. Hence, for small locus lengths m, we expect fewer segregating sites per locus and thus more independence between the segregating sites across the sequence. In such cases, we expect the function in Equation 9 to be close to the true log-likelihood function. Figure 5, A and B shows asymptotic confidence intervals for the inferred growth onset times and growth rates over 100 simulated data sets. According to those figures, the asymptotic confidence interval procedure in Methods is close to an idealized confidence interval estimation procedure when the locus length m is shorter than 1 kb. For longer locus lengths of m = 10 kb, we performed a resampling block bootstrap procedure with 200 bootstrap resamples per data set to estimate confidence intervals for the exponential population growth parameters. As shown in Figure 5, C and D, the bootstrap confidence intervals are much more faithful to an idealized confidence interval estimation procedure and are better calibrated than those produced by the asymptotic confidence interval estimation procedure.

Figure 5.

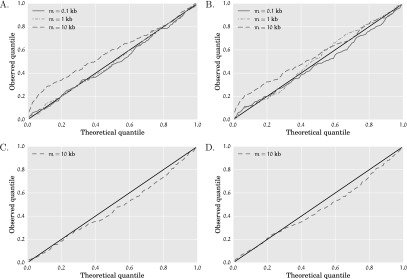
Figure 5.

Open in a new tab

Calibration plots for asymptotic (A,B), and bootstrap (C,D) confidence intervals of the duration and rate of exponential growth for Scenario 1 with t1 = 100 gens and r1 = 6.4% per gen for 200 simulated data sets of 10,000 diploids, each with 100 unlinked loci of length m. For each confidence level α on the x-axis, the y-axis counts the fraction of data sets where the true parameter estimates lie outside the 100(1 − α)% predicted confidence interval. The straight black lines denote the plot that would be obtained from an idealized confidence interval estimation procedure. (A,B) Asymptotic confidence interval calibration plots for the inferred (A) duration and (B) rate of exponential growth. As the locus length m increases, linkage disequilibrium causes the composite log-likelihood approximation in Equation 9 to become increasingly inaccurate, thus leading to poorly calibrated asymptotic confidence intervals for m = 10 kb. (C,D) Bootstrap confidence interval calibration plots using 200 bootstrap replicates per simulated data set for the inferred (C) duration and (D) rate of exponential growth. The bootstrap confidence intervals are much better calibrated than those produced by the asymptotic confidence interval estimation procedure.

Application to real data I: neutral regions

The data set of Gazave et al. (2014) consists of 15 carefully curated loci from 500 individuals of European ancestry that were sequenced at a high coverage depth of 295×. These loci were chosen to be distant from known or potential coding regions, as well as regions believed to be under selection. These 15 loci contain 1688 segregating sites that were sequenced in at least 450 individuals. Gazave and coworkers employed coalescent simulations to fit several demographic models incorporating recent exponential population growth to this data set. In their models, they assumed that the ancient European demography has two population bottlenecks that were inferred by Keinan et al. (2007). Incidentally, these are also the same bottlenecks that were used in our simulation study (Scenarios 1 and 2) described above. Gazave and coworkers’ best-fit model (Model II) had a growth rate of 3.38% per generation starting about 140 generations in the past.

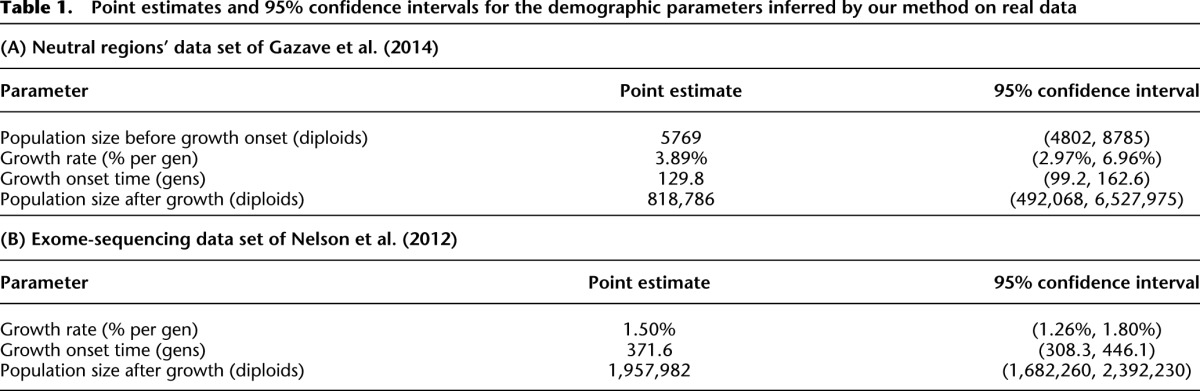
We applied our inference program to fit a model of exponential growth while fixing the parameters of the two ancient bottlenecks to the values inferred by Keinan et al. (2007). We inferred the following three parameters: the rate and the onset time of recent exponential growth, and the population size just before the onset of exponential growth. We inferred that the population grew exponentially at a rate of 3.89% per generation starting 130 generations in the past, resulting in a present effective population size of about 820,000 individuals. Supplemental Figure S4 shows the inferred demographic model, while Table 1A summarizes the point estimates and 95% confidence interval for the inferred parameter values. The confidence intervals for the demographic parameters were generated using 1000 block bootstrap resamples. These confidence intervals have significant overlap with those estimated by Gazave et al. (2014) in their best-fit model. To get a sense of the goodness of fit of our inferred demographic model, we generated 104 bootstrap replicates by drawing samples from a multinomial distribution given by the expected SFS of our inferred demographic parameters and then computing the Pearson χ2 test statistic on each of these replicates and using the expected counts given by the expected SFS of the inferred parameters. This gives us an empirical distribution for the Pearson χ2 statistic under the null hypothesis that the data are generated according to the PRF model with demographic parameters given by our inferred parameters. We did not use the asymptotic χ2 distribution because the cell counts corresponding to the intermediate and tail entries of the SFS were too low. Of the bootstrap replicates, 99.94% have a larger χ2 statistic than that for the observed data, indicating that we cannot reject our inferred demographic model at the 5% significance level.

Table 1.

Point estimates and 95% confidence intervals for the demographic parameters inferred by our method on real data

graphic file with name 268tbl1.jpg

Open in a new tab

Application to real data II: exome-sequencing

Nelson et al. (2012) sequenced more than 14,000 individuals from several case-control studies at 202 coding regions that are of interest for drug targeting. This data set includes the SFS of a sample of 11,000 individuals of European ancestry containing ∼2600 segregating sites among ∼43,000 fourfold degenerate sites in 185 genes (Nelson et al. 2012, Database S3). Using the demographic estimates of Schaffner et al. (2005) for modeling the ancient demography of the CEU population, Nelson and coworkers employed the coalescent simulation-based approach of Coventry et al. (2010) to fit an epoch of recent exponential growth to their data. They estimated that the effective population size of the CEU subpopulation expanded from 7700 individuals 375 generations ago to ∼4 million individuals at the present time at a rate of ∼1.68% per generation.

We also applied our method to this data set to infer an epoch of recent exponential growth. In particular, we inferred the onset time and the rate of recent exponential population growth while fixing the population size before the onset of growth and the parameters of the two bottlenecks in the ancient demography to those estimated by Schaffner et al. (2005). We computed empirical confidence intervals for these parameter estimates using a resampling block bootstrap procedure with 1000 bootstrap resamples. Our point estimates and 95% confidence intervals for the demographic parameters are summarized in Table 1B with the inferred effective population size function shown in Supplemental Figure S5. We estimated that the effective population size grew exponentially from 7700 individuals 372 generations ago (95% CI: [308, 446] generations) to about 1.96 million individuals (95% CI: [1.68, 2.39] million) at the present time at a rate of ∼1.50% per generation (95% CI: [1.26%, 1.80%] per generation). To measure the goodness of fit of our inferred demographic model, we performed a similar procedure to that described in the previous section. Creating an empirical distribution for the Pearson χ2 statistic using 104 bootstrap replicates drawn from a multinomial distribution given by the expected SFS of our inferred demographic parameters, we found that 75.7% of the simulation replicates had a larger χ2 test statistic than that of the data, indicating that we cannot reject our inferred demographic model at the 5% significance level.

There are several reasons for the difference in demographic estimates between our method and that of Nelson et al. (2012). First, the coalescent simulations of Nelson and coworkers were performed assuming that all sites within a locus are completely linked, while we make the opposite extreme assumption that all sites are freely recombining and evolve independently. Second, Nelson and coworkers used 400 simulated coalescent trees to approximate the likelihood for each combination of demographic parameters, resulting in a noisy likelihood surface. Our method, in contrast, uses exact computation to determine the expected SFS for a given demographic model. Third, they computed the log-likelihood on a discretized grid of demographic parameters, which might result in their procedure being far from the maximum likelihood estimate if the log-likelihood function is fairly flat. Our approach mitigates this problem by employing sophisticated gradient-based algorithms that can adapt their step size to the likelihood landscape.

We also estimated the mutation rate at each locus using our method (see Equation 8 in Methods). Figure 4B shows our mutation rate estimates and 95% confidence intervals and compares them to those reported by Nelson et al. (2012). Our estimates are close to those of Nelson and coworkers while being systematically larger. This systematic difference can be explained by noting that our inferred population growth rate is slower than that inferred by Nelson and coworkers, resulting in a higher mutation rate being needed to explain the same number of rare variants.

Discussion

Before one can perform any meaningful demographic inference from SFS data, it is worth examining whether the statistical problem is well defined. Myers et al. (2008) showed that, in general, the historical effective population size function is not uniquely determined by the SFS, no matter how large the sample size considered. In particular, they showed that there are infinitely many population size functions that can generate the same expected SFS for all sample sizes. While this nonidentifiability result might seem like a barrier to statistical inference, it was recently shown (Bhaskar and Song 2014) that if the effective population size function does not oscillate too often, a condition that is met for several widely used demographic model families such as piecewise-exponential functions, then the expected SFS of a sample of moderate size can uniquely identify the underlying population size function. More precisely, Bhaskar and Song (2014) showed that any family of population size functions is identifiable using the expected SFS of a sample of n sequences as long as suitably time-rescaled versions of every pair of functions in the family do not “cross” (i.e., change the sign of their pointwise difference) each other more than n − 2 times.

The theoretical results of Bhaskar and Song (2014) apply to the case where the expected SFS of a model is available as data. However, the empirical SFS obtained from a finite genome may be noisy and may not have converged to the expected SFS. In such a case, using a large number of segregating sites from a large sample size may help with inference. In this paper, we developed a method that can leverage genomic variation data from samples involving tens of thousands of individuals to infer piecewise-exponential models of recent changes in the effective population size.

Similar to the SFS-based demographic inference methods of Nielsen (2000), Coventry et al. (2010), and Excoffier et al. (2013), we also work in the coalescent framework rather than in the diffusion setting. However, our method differs from existing methods in several ways. First, our method is based on an efficient algorithmic adaption of the analytic theory of the expected SFS for deterministically varying population size models that was developed by Polanski et al. (2003) and Polanski and Kimmel (2003). This is in contrast to expensive Monte Carlo coalescent simulations employed by the aforementioned coalescent-based methods. As a result, our approach is much more efficient and allows us to more thoroughly search the space of demographic models of interest. In a related work, Marth et al. (2004) developed analytic expressions for the expected SFS of piecewise-constant population size models and used them for inferring piecewise-constant population size histories for European, Asian, and African-American populations. However, their analytic expressions are not numerically stable for sample sizes larger than about 50 individuals and, moreover, do not extend to more general population size models. On the other hand, our approach utilizes numerically stable expressions for the expected SFS developed by Polanski and Kimmel (2003) which extend to arbitrary variable population size models.

Second, our method uses the Poisson Random Field (PRF) approximation proposed by Sawyer and Hartl (1992). Under this approximation, the segregating sites within a locus are assumed to be far enough apart to be completely unlinked. This is also the same approximation made by numerical and spectral methods for inference under the Wright-Fisher diffusion process (Gutenkunst et al. 2009; Lukić et al. 2011), and by the coalescent method of Excoffier et al. (2013) At the other extreme, the method of Coventry et al. (2010) assumes that all the segregating sites in a locus are completely linked and hence share the same underlying genealogy. Both these model simplifications—the assumption of perfectly linked or completely independently evolving sites within a locus—are biologically unrealistic. However, as we demonstrated in our results on simulated data, our method can recover demographic parameters accurately even when the data are generated under realistic recombination rates that are inferred from human genetics studies. Working in the PRF model also confers on our method a significant computational benefit. Under this assumption, we can derive efficiently computable expressions for the maximum likelihood estimate of the mutation rates at each locus. This contrasts with coalescent simulation-based methods where either the mutation rate is assumed to be known (Excoffier et al. 2013) or a grid search has to be performed over the mutation rates (Coventry et al. 2010; Nelson et al. 2012). This makes our method orders of magnitude more efficient.

Third, our method has advantages over the diffusion-based methods of Gutenkunst et al. (2009) and Lukić et al. (2011). By working in the coalescent framework, the running time of our method is independent of the population size. Furthermore, by leveraging analytic and numerically stable results for the expected SFS under the coalescent, our computations are exact. On the other hand, the method of Gutenkunst et al. (2009) must carefully discretize the allele frequency space to minimize the accumulation of numerical errors, while the method of Lukić et al. (2011) has to choose a suitable order for the spectral expansion of the transition density function of the diffusion process.

Finally, since our method is based on a likelihood function that is computed exactly, we can take advantage of the technique of automatic differentiation (Griewank and Corliss 1991) to compute exact gradients of the likelihood function. This is one of the key novel features of our approach and obviates the need for doing a grid search over the parameters. Instead, we take advantage of efficient gradient-based algorithms for optimization over the space of demographic parameters.

Our method is especially suited for inferring details of recent demographic expansion, since the SFS from large samples contains much information about recent rapid population growth. While in theory our method can also be applied to estimate parameters of ancient population demography such as ancient population bottlenecks, there might be more uncertainty in these parameter estimates compared to estimates from methods that use full or partial haplotype information (Li and Durbin 2011; Palamara et al. 2012; Harris and Nielsen 2013; Sheehan et al. 2013; Steinrücken et al. 2013). We recommend using our method by fixing the ancestral demographic parameters using estimates obtained by other means or by running our method with several parameter combinations for the ancient demography. Our method also assumes that the regions being analyzed are subject to neutral evolution. However, even neutrally evolving sites that are located close to regions under selective pressure would be subject to hitchhiking or background selection, and the inferred demographic and mutation parameters would need to be interpreted accordingly. For the application of our method, we chose to examine the data set of Gazave et al. (2014) because those sites were chosen to be distant from coding regions and regions believed to be under selective constraint.

Our approach suggests several directions for future research. It would be interesting to investigate other families of parametric population size functions that might better fit human genetic data. For example, Reppell et al. (2014) studied more general population growth models that allow for super- and subexponential growth through the incorporation of an acceleration parameter. Such richer parametric families might allow one to fit demographic models with a smaller number of growth epochs to the data. It is easy to extend our method to such parametric families, since the only dependence on the functional form of the population size function is in the integral expressions given in the Supplemental Material. More generally, the analytic theory underlying our computation of the expected SFS extends to an arbitrary variable population size model, and hence our method can be easily extended to perform inference under any parametric demographic model that is identifiable from the expected SFS of a finite sample; general bounds on the sample size sufficient for identifiability were obtained by Bhaskar and Song (2014).

It would also be useful to extend the analytic coalescent theory of the SFS to more realistic demographic models that incorporate multiple populations with migrations and time-varying population sizes. This would enable one to develop demographic inference algorithms that are potentially more efficient and accurate than coalescent simulation-based methods or numerical diffusion-based methods. The method we developed is limited to inferring the effective population size of a single randomly mating subpopulation. If the sampled individuals in fact belong to different subpopulations, the distribution of variants observed in the sample would strongly depend on the details of the population structure, and this would consequently also impact the results of the inference procedure. For example, if the subpopulations are well-mixed (i.e., close to being panmictic), the inferred population size function might closely approximate the sum of the sizes of the subpopulations from which the sample is drawn. At the other extreme, if the migration rates between the subpopulations are extremely low, most of the variants would be segregating within a single subpopulation with very few variants being present in multiple subpopulations. The inferred population size function would then strongly depend on the proportion of samples drawn from each subpopulation and their corresponding demographic histories. In general, the effect of population structure on the inference would depend strongly on the underlying demography, and care must be taken when applying our method to samples drawn from highly structured populations.

A natural extension to the SFS, which captures variation in samples from multiple subpopulations, is the joint population SFS which counts the number of segregating sites in the sample as a function of the sample allele frequency in each subpopulation. Chen (2012) has developed analytic expressions for the expected joint population SFS of multiple subpopulations when the migrations are instantaneous exchanges of individuals between subpopulations. Even more fundamentally, it would be interesting to characterize the statistical identifiability of complex demographic models from the joint population SFS of random samples.

Another direction for research is to understand how the uncertainties in the inference of different parameters are related to each other. For example, the violin plots in Figure 2, A and B show that when there is more uncertainty in the inference of the exponential growth rate, there is less uncertainty in the inference of the growth duration, and vice versa. A similar observation can be made from Figure 2, C and D for the inference of the exponential growth parameters of the two epochs in Scenario 2. It would be interesting to understand if there is a fundamental quantifiable uncertainty relation that is independent of the inference algorithm, or if this behavior is specific to our inference procedure.

Methods

In this section we provide an overview of our method. The involved computational details are provided in the Supplemental Material. In our work we utilize automatic differentiation (Griewank and Corliss 1991), a technique that allows one to compute exact gradients numerically without requiring explicit symbolic expressions for the gradient. This technique has not been widely adopted in population genetics, so we include a brief exposition of it here.

Model and notation

We assume that our data are drawn according to Kingman’s coalescent from a single panmictic population having population size N(t) haploids at time t, where t is increasing in the past. Without loss of generality, we assume that the sample is drawn from the population at the present time t = 0. We shall also assume the infinite-sites model of mutation, where mutations occur at a low enough rate that any segregating site in the sample has experienced at most one mutation event.

The data we wish to analyze, denoted by 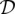Inline graphic, consist of the sample frequency spectrum (SFS) for n haploid (or n/2 diploid) individuals at each of L loci located sufficiently far apart along the genome. The SFS at locus l is a vector 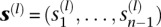Inline graphic, where 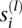Inline graphic is the number of segregating sites which have i copies of the mutant allele among the n alleles at that site. We are also given the length m(l) of each locus l. For notational convenience, let 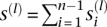Inline graphic be the total number of segregating sites in the sample at locus l. Given the data 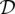Inline graphic, our goal is to infer the haploid effective population size function N(t) and the per-base locus-specific mutation rates μ(l). We use Φ to denote a vector of parameters that parameterize the family of piecewise-exponential demographic models. Note that such a family also contains piecewise-constant population size functions. While we describe our method assuming knowledge of the identities of the ancestral and mutant alleles, we can just as easily work with the folded SFS which counts the segregating sites as a function of the sample minor allele frequency, if the identity of the ancestral allele is not known.

Likelihood

Let us first restrict attention to a single locus l. For a locus with length m bases and per-base per-generation mutation rate μ, let θ/2 denote the population-scaled mutation rate for the whole locus. Specifically,

graphic file with name 268eq1.jpg

where Nr denotes a reference population size which is used as a scaling parameter.

We wish to compute the probability of the observed frequency spectrum s = (s1, …, sn−1) at locus l under the infinite-sites model. (We omit the superscript l for ease of notation.) If all the sites in the locus are completely linked and the n individuals in the sample are related according to the coalescent tree T, then the probability of observing the frequency spectrum s is given by

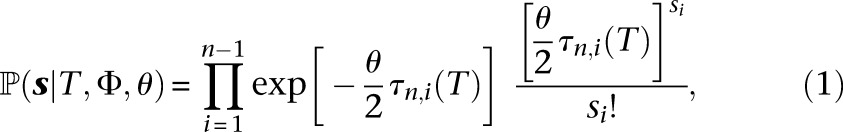graphic file with name 268e1.jpg

where τn,i(T) is the sum of the lengths of branches in the coalescent tree T which subtend i descendant leaves. The explanation for Equation 1 is as follows: In the infinite-sites mutation model, mutations occur on the coalescent tree according to a Poisson process with rate θ/2, where every mutation generates a new segregating site. A mutation creates a segregating site with i mutant alleles if and only if it occurs on a branch that subtends i descendants in the sample. To avoid unwieldy notation, we drop the dependence on the tree T for the branch lengths τn,i(T). To compute the probability of the observed frequency spectrum s, we need to integrate Equation 1 over the distribution f(T|Φ) of n-leaved coalescent trees T under the demography Φ. Let 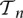Inline graphic denote the space of coalescent trees with n leaves. Then, abusing notation, the probability 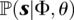Inline graphic can be written as

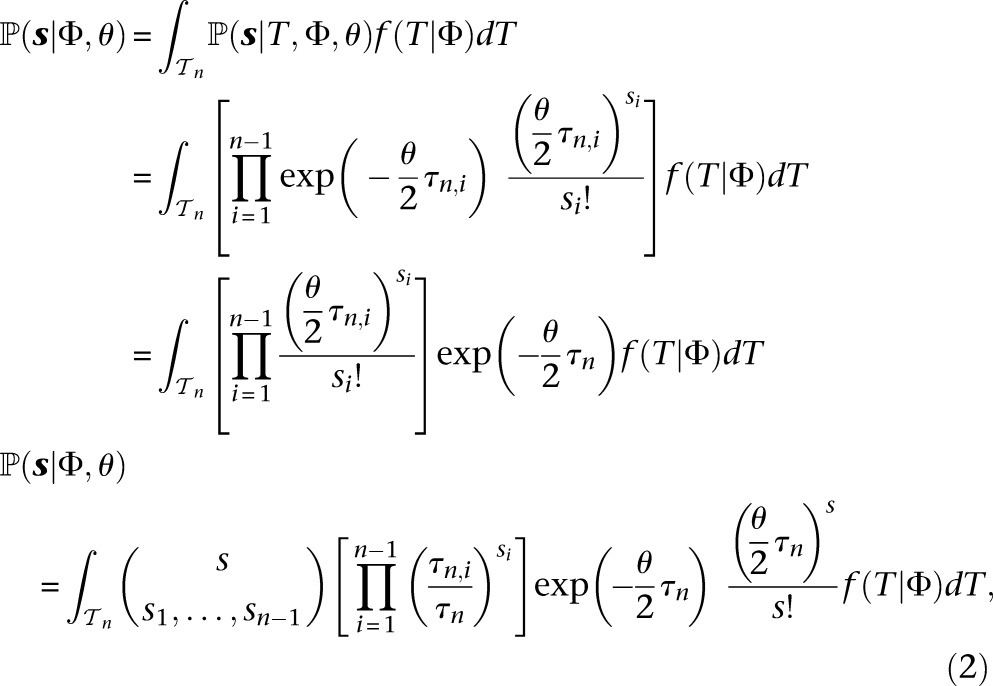graphic file with name 268e2.jpg

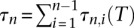where Inline graphic. In Equation 2, Inline graphic, the total branch length of the tree T on n haploid individuals. It is not known how to efficiently and exactly compute Equation 2, even when Φ represents the constant population size demographic model. Most works approximate the integral in Equation 2 by sampling coalescent trees under the demographic model Φ. In order to find the MLE for θ, they must repeat this Monte Carlo integration for each value of θ in some grid.

Poisson Random Field approximation

In our method we use the Poisson Random Field (PRF) assumption of Sawyer and Hartl (1992), which assumes that all the sites in a given locus are completely unlinked, and hence the underlying coalescent tree at each site is independent. Under this assumption, the probability of the observed frequency spectrum s is given by

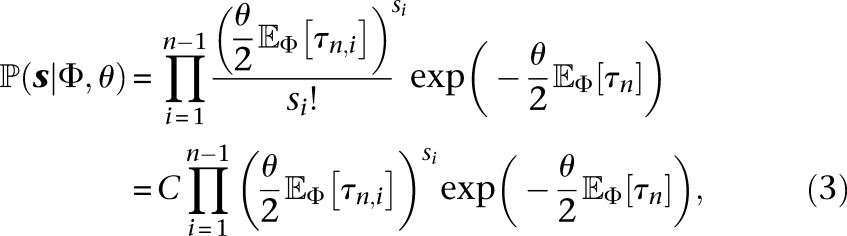graphic file with name 268e3.jpg

where the expectations 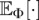Inline graphic in Equation 3 are taken over the distribution on coalescent trees with n leaves drawn from the demographic model parameterized by Φ, and 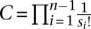Inline graphic is a data-dependent constant that can be ignored for maximum likelihood estimation.

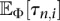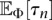Hence, under the PRF approximation, the problem of computing the likelihood in Equation 3 reduces to that of computing the expectations Inline graphic and Inline graphic for the demographic model given by Φ. Using analytic results for the SFS for variable population sizes developed by Polanski et al. 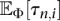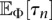(2003) and Polanski and Kimmel (2003), we can develop an efficient algorithm to numerically stably and exactly compute Inline graphic and Inline graphic for a wide class of population size functions 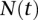Inline graphic. In this work, we consider inference in the family of piecewise-exponential functions with either a prescribed or variable number of pieces. 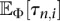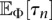The details of computing Inline graphic and Inline graphic for such a class of population size functions is given in the Supplemental Material. Inference under other families of parametric demographic models can just as easily be performed if one can efficiently compute the integral expressions given in the Supplemental Material.

Taking logarithms on both sides in Equation 3, we get the following log-likelihood for the demographic model Φ and mutation rate θ at this locus:

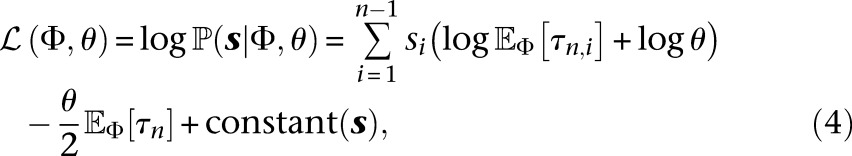graphic file with name 268e4.jpg

where constant (s) depends on s but not on the parameters Φ, θ.

Assuming the loci are all completely unlinked, the log-likelihood for one locus given in Equation 4 can be summed across all loci l = 1, …, L to get a log-likelihood for the entire data set 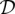Inline graphic:

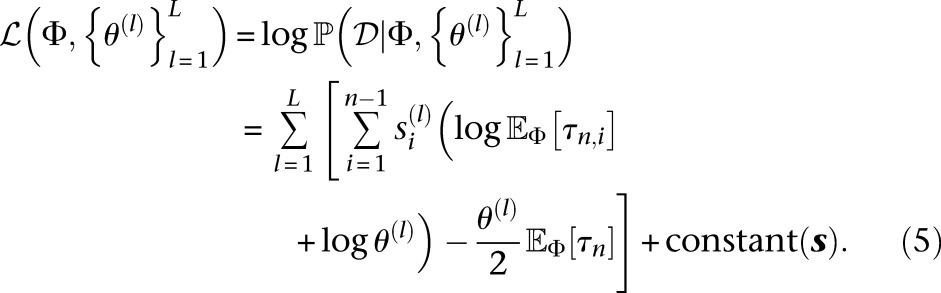graphic file with name 268e5.jpg

It is easy to see that 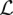Inline graphic is a concave function of the mutation rates θ(l), since the Hessian H of Inline graphic with respect to θ = (θ(1), …, θ(L)) is given by

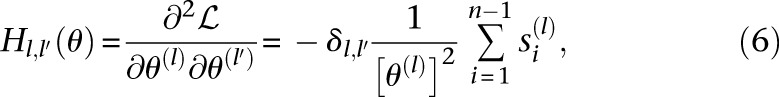graphic file with name 268e6.jpg

showing that H(θ) is negative definite for all θ ≻ 0. Hence, the mutation rates of the loci that maximize 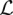Inline graphic are the solutions of

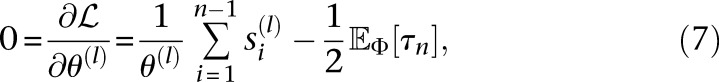graphic file with name 268e7.jpg

yielding the following maximum likelihood estimate for the mutation rate θ(l) at locus l given the demographic model:

graphic file with name 268e8.jpg

Note that for a constant population size, Equation 8 is the same as Watterson’s estimator 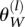Inline graphic for the mutation rate (Watterson 1975), namely

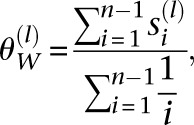graphic file with name 268eq2.jpg

since for a constant population size, 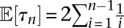Inline graphic. Substituting the MLE for θ(l) in Equation 8 into Equation 5, we obtain the log-likelihood with the optimal mutation rates:

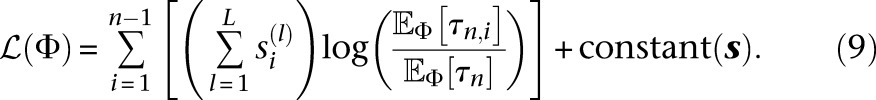graphic file with name 268e9.jpg

If we define the discrete probability distributions 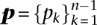Inline graphic and ξn 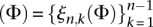Inline graphic by

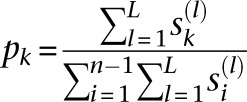graphic file with name 268eq3.jpg

and

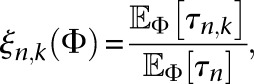graphic file with name 268eq4.jpg

then we see that the demographic model 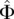Inline graphic that is the MLE of the likelihood function 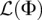Inline graphic in Equation 9 is given by

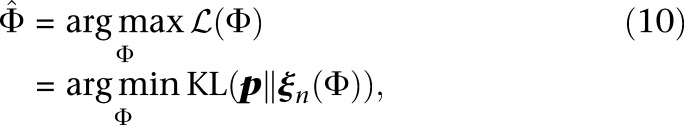graphic file with name 268e10.jpg

where KL(P ‖ Q) denotes the Kullback-Liebler divergence of distribution Q from P.

Hence, for a given demographic model Φ, we can compute the log-likelihood using Equation 9 and infer the optimal mutation rate at each locus independently according to Equation 8. We compute the gradient of 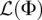Inline graphic with respect to Φ using automatic differentiation (Griewank and Corliss 1991), detailed below. Once we have access to the gradient of 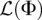Inline graphic, we can more efficiently search over the space of demographic models using standard gradient-based optimization algorithms.

Some computational details

For a sample of size n and a piecewise-exponential demographic model with M epochs, the terms 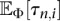Inline graphic in Equation 9 can be computed in O(nM) time for each value of the index i, 1 ≤ i ≤ n − 1. Hence, the time complexity for evaluating the log-likelihood function in Equation 9 is O(n2M). However, since we would like to use our method for large sample sizes on the order of tens to hundreds of thousands of individuals, in practice, and for the study reported in Results, we evaluate Equation 9 by using only the leading entries of the SFS which account for some significant fraction of the segregating sites in the observed sample. In particular, for the results on simulated and real data sets reported in Results, when computing the KL divergence in Equation 10, we use the first k entries of the SFS which account for a fraction f = 90% of the segregating sites in the observed data while collapsing the remaining n − k − 1 SFS entries into one class. It is an important open question to understand how such a binning strategy affects demographic inference procedures that operate on frequency spectrum data. We examine this issue empirically in Section 2 of the Supplemental Material.

Confidence intervals

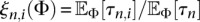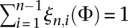If we ignore the fact that we are using the PRF assumption to treat the sites within each locus as freely recombining, Equation 9 is the log-likelihood function of L independent samples from a multinomial distribution with n − 1 categories and probabilities ξn(Φ) = (ξn,1(Φ), …, ξn,n−1(Φ)), where Inline graphic, and Inline graphic. Since the probability models specified by the likelihood function 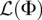Inline graphic are identifiable for a sufficiently large sample size n that depends on the number of parameters being inferred (Bhaskar and Song 2014), and since ξn(Φ) is differentiable with respect to Φ, it follows from the asymptotics of maximum likelihood estimators that

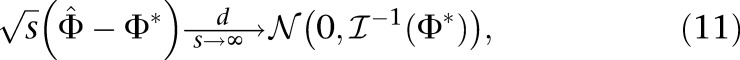graphic file with name 268e11.jpg

where Φ* is the true underlying demographic model, and 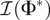Inline graphic is the expected Fisher information matrix of a single observation. The elements of 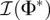Inline graphic are given by

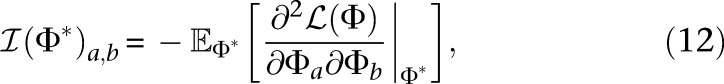graphic file with name 268e12.jpg

where Φi denotes the ith element of the demographic parameter vector Φ. For the log-likelihood function 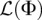Inline graphic in Equation 9, using 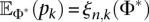Inline graphic, it is straightforward to show that Equation 12 simplifies to

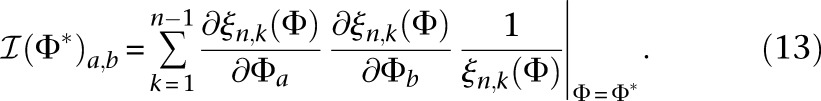graphic file with name 268e13.jpg

We calculate the partial derivatives in Equation 13 via automatic differentiation during the computation of p(Φ) (Griewank and Corliss 1991). This allows us to construct asymptotic empirical confidence intervals for Φ*. An asymptotic 100(1 − α)% confidence interval for the parameters of Φ* is given by

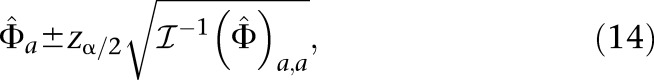graphic file with name 268e14.jpg

where zα/2 is the 100(1 − α/2)th percentile of a standard normal distribution.

If the loci being analyzed are long with low levels of intralocus recombination, then Equation 9 is a composite log-likelihood function rather than a true likelihood function. In such cases, we compute empirical confidence intervals for the demographic parameters using a nonparametric block bootstrap procedure (Efron and Tibshirani 1986). In particular, we subsample L loci with replacement from the original data set of L loci, where each locus is sampled with probability proportional to the number of segregating sites in it. We examine the performance of the asymptotic confidence interval procedure and the block bootstrap on simulated data in Results.

Automatic differentiation

Since our inference algorithm and asymptotic confidence interval estimation procedure rely heavily on computing gradients via automatic differentiation, we briefly describe this technique here to keep the paper self-contained. Automatic differentiation (AD) is a powerful technique for computing the gradient (and higher-order derivatives) of a mathematical function that is implemented in a computer program. The basic idea in AD is to track the values and gradients of the intermediate variables in a computer program evaluated at the desired value of the independent variables, where the chain rule of calculus is repeatedly employed to compute the gradients. For example, suppose we had the mathematical function f(x) = sin(x2 + x) that is implemented via the following computer function f(x):

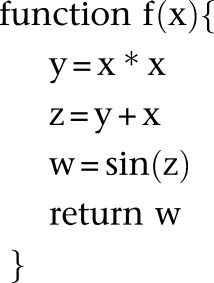graphic file with name 268eq5.jpg

To calculate the numerical value of df/dx, we augment the intermediate variables in this program to create a new variable per existing variable that will track the derivative with respect to x, evaluated at the value passed for the argument x. In particular, in this program, we define x′ = dx/dx (which will be trivially initialized to 1), y′ = dy/dx, z′ = dz/dx, and w′ = dw/dx. Suppose we wish to evaluate f and its gradient (with respect to x) at x = 1/2. The desired df/dx evaluated at x = 1/2 is equal to w′ evaluated at x = 1/2. The key idea in AD is to evaluate y′, z′, and w′ at the same time that y, z, and w are being evaluated for the input variable value x = 1/2. These augmented variables y′, z′, and w′ can be computed using the chain rule of calculus. The evaluation of the original and augmented variables of the function at x = 1/2 proceeds as follows:

graphic file with name 268eq6.jpg
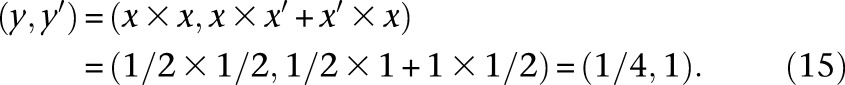graphic file with name 268e15.jpg
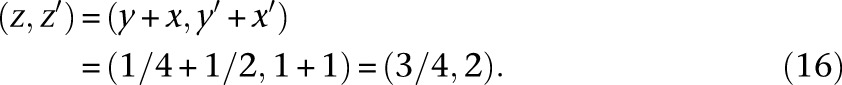graphic file with name 268e16.jpg
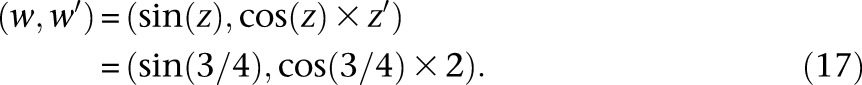graphic file with name 268e17.jpg

Note that the chain rule was invoked in Equations 15, 16, and 17 to calculate y′, z′, and w′ at x = 1/2. Using features of modern programming languages such as function and operator overloading, the chain rule calculations for common mathematical functions can be abstracted away in a library, thus requiring minimal changes to the user’s program. In our demographic inference software package, we used the AD library ADOL-C (Walther and Griewank 2012).

AD offers advantages over both symbolic and numerical methods for gradient evaluation. Since one does not have to derive and implement potentially complicated expressions for the symbolic gradient of the original mathematical function, AD helps reduce the chances of implementation errors. At the same time, AD computes exact gradients as opposed to approximate numerical methods like finite-difference schemes. The description provided above is called forward-mode AD; there are also other evaluation orders for the terms in the chain rule computation in AD. We refer the interested reader to Griewank and Corliss (1991) for a more detailed survey of this topic.

Software availability

We have implemented the algorithms described in this paper in an open-source software package called fastNeutrino, which stands for fast Ne (effective population size) and mUTation Rate Inference using aNalytic Optimization. It is publicly available at http://fastneutrino.sourceforge.net.

Supplementary Material

Supplemental Material
supp_25_2_268__index.html (1KB, html)

Acknowledgments

A.B. thanks Andrew Chan for helpful discussions at the initial stages of this work. We also thank John Novembre and Darren Kessner for sharing their demographic estimates on the exome-sequencing data set, and Alon Keinan and Li Ma for sharing the SFS of the neutral regions data set. We thank Nick Patterson and two anonymous reviewers for their suggestions that helped to improve the manuscript. A.B. and Y.S.S. acknowledge the generous support of the Simons Institute for the Theory of Computing, where much of this manuscript was completed while the authors were participating in the 2014 program on “Evolutionary Biology and the Theory of Computing.” A.B. thanks Hideki Innan for hosting him while the final version of this work was completed under a short-term postdoctoral fellowship from the Japan Society for the Promotion of Science. This research is supported in part by NIH grants R01-GM094402 and R01-GM108805, a Packard Fellowship for Science and Engineering, and a Simons-Berkeley Research Fellowship.

Footnotes

[Supplemental material is available for this article.]

Article published online before print. Article, supplemental material, and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.178756.114.

References

  1. Balding DJ, Nichols RA. 1997. Significant genetic correlations among Caucasians at forensic DNA loci. Heredity 78: 583–589. [DOI] [PubMed] [Google Scholar]
  2. Bhaskar A, Song YS. 2014. Descartes’ rule of signs and the identifiability of population demographic models from genomic variation data. Ann Stat 42: 2469–2493. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Boyko AR, Williamson SH, Indap AR, Degenhardt JD, Hernandez RD, Lohmueller KE, Adams MD, Schmidt S, Sninsky JJ, Sunyaev SR, et al. . 2008. Assessing the evolutionary impact of amino acid mutations in the human genome. PLoS Genet 4: e1000083. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Campbell CD, Ogburn EL, Lunetta KL, Lyon HN, Freedman ML, Groop LC, Altshuler D, Ardlie KG, Hirschhorn JN. 2005. Demonstrating stratification in a European American population. Nat Genet 37: 868–872. [DOI] [PubMed] [Google Scholar]
  5. Chen H. 2012. The joint allele frequency spectrum of multiple populations: a coalescent theory approach. Theor Popul Biol 81: 179–195. [DOI] [PubMed] [Google Scholar]
  6. Clayton DG, Walker NM, Smyth DJ, Pask R, Cooper JD, Maier LM, Smink LJ, Lam AC, Ovington NR, Stevens HE, et al. . 2005. Population structure, differential bias and genomic control in a large-scale, case-control association study. Nat Genet 37: 1243–1246. [DOI] [PubMed] [Google Scholar]
  7. Conrad D, Keebler J, DePristo M, Lindsay S, Zhang Y, Casals F, Idaghdour Y, Hartl C, Torroja C, Garimella K, et al. . 2011. Variation in genome-wide mutation rates within and between human families. Nat Genet 43: 712–714. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Coventry A, Bull-Otterson LM, Liu X, Clark AG, Maxwell TJ, Crosby J, Hixson JE, Rea TJ, Muzny DM, Lewis LR, et al. . 2010. Deep resequencing reveals excess rare recent variants consistent with explosive population growth. Nat Commun 1: 131. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Efron B, Tibshirani R. 1986. Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy. Stat Sci 1: 54–75. [Google Scholar]
  10. Ewens W. 2004. Mathematical population genetics: I. Theoretical introduction, 2nd ed. Springer, New York. [Google Scholar]
  11. Excoffier L, Dupanloup I, Huerta-Sánchez E, Sousa VC, Foll M. 2013. Robust demographic inference from genomic and SNP data. PLoS Genet 9: e1003905. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Fu YX. 1995. Statistical properties of segregating sites. Theor Popul Biol 48: 172–197. [DOI] [PubMed] [Google Scholar]
  13. Fu W, O’Connor TD, Jun G, Kang HM, Abecasis G, Leal SM, Gabriel S, Altshuler D, Shendure J, Nickerson DA, et al. . 2012. Analysis of 6,515 exomes reveals the recent origin of most human protein-coding variants. Nature 493: 216–220. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Gazave E, Chang D, Clark AG, Keinan A. 2013. Population growth inflates the per-individual number of deleterious mutations and reduces their mean effect. Genetics 195: 969–978. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Gazave E, Ma L, Chang D, Coventry A, Gao F, Muzny D, Boerwinkle E, Gibbs RA, Sing CF, Clark AG, et al. . 2014. Neutral genomic regions refine models of recent rapid human population growth. Proc Natl Acad Sci 111: 757–762. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Graham J, Curran J, Weir B. 2000. Conditional genotypic probabilities for microsatellite loci. Genetics 155: 1973–1980. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Gravel S, Henn BM, Gutenkunst RN, Indap AR, Marth GT, Clark AG, Yu F, Gibbs RA, Bustamante CD, Altshuler DL, et al. . 2011. Demographic history and rare allele sharing among human populations. Proc Natl Acad Sci 108: 11983–11988. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Griewank A, Corliss GF. 1991. Automatic differentiation of algorithms: theory, implementation, and application. Society for Industrial and Applied Mathematics, Philadelphia, PA. [Google Scholar]
  19. Gutenkunst RN, Hernandez RD, Williamson SH, Bustamante CD. 2009. Inferring the joint demographic history of multiple populations from multidimensional SNP frequency data. PLoS Genet 5: e1000695. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Harris K, Nielsen R. 2013. Inferring demographic history from a spectrum of shared haplotype lengths. PLoS Genet 9: e1003521. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Hudson R. 2002. Generating samples under a Wright–Fisher neutral model of genetic variation. Bioinformatics 18: 337–338. [DOI] [PubMed] [Google Scholar]
  22. Keinan A, Clark AG. 2012. Recent explosive human population growth has resulted in an excess of rare genetic variants. Science 336: 740–743. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Keinan A, Mullikin JC, Patterson N, Reich D. 2007. Measurement of the human allele frequency spectrum demonstrates greater genetic drift in East Asians than in Europeans. Nat Genet 39: 1251–1255. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Li H, Durbin R. 2011. Inference of human population history from individual whole-genome sequences. Nature 475: 493–496. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Lohmueller KE. 2014. The impact of population demography and selection on the genetic architecture of complex traits. PLoS Genet 10: e1004379. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Lohmueller KE, Indap AR, Schmidt S, Boyko AR, Hernandez RD, Hubisz MJ, Sninsky JJ, White TJ, Sunyaev SR, Nielsen R, et al. . 2008. Proportionally more deleterious genetic variation in European than in African populations. Nature 451: 994–997. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Lukić S, Hey J. 2012. Demographic inference using spectral methods on SNP data, with an analysis of the human out-of-Africa expansion. Genetics 192: 619–639. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Lukić S, Hey J, Chen K. 2011. Non-equilibrium allele frequency spectra via spectral methods. Theor Popul Biol 79: 203–219. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Marchini J, Cardon LR, Phillips MS, Donnelly P. 2004. The effects of human population structure on large genetic association studies. Nat Genet 36: 512–517. [DOI] [PubMed] [Google Scholar]
  30. Marth G, Czabarka E, Murvai J, Sherry S. 2004. The allele frequency spectrum in genome-wide human variation data reveals signals of differential demographic history in three large world populations. Genetics 166: 351–372. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Myers S, Fefferman C, Patterson N. 2008. Can one learn history from the allelic spectrum? Theor Popul Biol 73: 342–348. [DOI] [PubMed] [Google Scholar]
  32. Nelson MR, Wegmann D, Ehm MG, Kessner D, Jean PS, Verzilli C, Shen J, Tang Z, Bacanu S-A, Fraser D, et al. . 2012. An abundance of rare functional variants in 202 drug target genes sequenced in 14,002 people. Science 337: 100–104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Nielsen R. 2000. Estimation of population parameters and recombination rates from single nucleotide polymorphisms. Genetics 154: 931–942. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Palamara PF, Lencz T, Darvasi A, Pe’er I. 2012. Length distributions of identity by descent reveal fine-scale demographic history. Am J Hum Genet 91: 809–822. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Polanski A, Kimmel M. 2003. New explicit expressions for relative frequencies of single-nucleotide polymorphisms with application to statistical inference on population growth. Genetics 165: 427–436. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Polanski A, Bobrowski A, Kimmel M. 2003. A note on distributions of times to coalescence, under time-dependent population size. Theor Popul Biol 63: 33–40. [DOI] [PubMed] [Google Scholar]
  37. Reppell M, Boehnke M, Zöllner S. 2014. The impact of accelerating, faster than exponential population growth on genetic variation. Genetics 196: 819–828. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Sankararaman S, Patterson N, Li H, Pääbo S, Reich D. 2012. The date of interbreeding between Neandertals and modern humans. PLoS Genet 8: e1002947. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Sawyer SA, Hartl DL. 1992. Population genetics of polymorphism and divergence. Genetics 132: 1161–1176. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Schaffner S, Foo C, Gabriel S, Reich D, Daly M, Altshuler D. 2005. Calibrating a coalescent simulation of human genome sequence variation. Genome Res 15: 1576–1583. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Sheehan S, Harris K, Song YS. 2013. Estimating variable effective population sizes from multiple genomes: a sequentially Markov conditional sampling distribution approach. Genetics 194: 647–662. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Simons YB, Turchin MC, Pritchard JK, Sella G. 2014. The deleterious mutation load is insensitive to recent population history. Nat Genet 46: 220–224. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Steinrücken M, Paul JS, Song YS. 2013. A sequentially Markov conditional sampling distribution for structured populations with migration and recombination. Theor Popul Biol 87: 51–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Tennessen JA, Bigham AW, O’Connor TD, Fu W, Kenny EE, Gravel S, McGee S, Do R, Liu X, Jun G, et al. . 2012. Evolution and functional impact of rare coding variation from deep sequencing of human exomes. Science 337: 64–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Walther A, Griewank A. 2012. Getting started with ADOL-C. In Combinatorial scientific computing (ed. Schenk O), pp. 181–202. Chapman and Hall/CRC, London. [Google Scholar]
  46. Watterson G. 1975. On the number of segregating sites in genetical models without recombination. Theor Popul Biol 7: 256–276. [DOI] [PubMed] [Google Scholar]
  47. Williamson SH, Hernandez R, Fledel-Alon A, Zhu L, Nielsen R, Bustamante CD. 2005. Simultaneous inference of selection and population growth from patterns of variation in the human genome. Proc Natl Acad Sci 102: 7882–7887. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental Material
supp_25_2_268__index.html (1KB, html)
supp_gr.178756.114_Supplemental_M_aterial.pdf (764.4KB, pdf)

Articles from Genome Research are provided here courtesy of Cold Spring Harbor Laboratory Press

RESOURCES