Abstract
The ability to measure the properties of proteins at the single-molecule level offers an unparalleled glimpse into biological systems at the molecular scale. The interpretation of single-molecule time series has often been rooted in statistical mechanics and the theory of Markov processes. While existing analysis methods have been useful, they are not without significant limitations including problems of model selection and parameter nonidentifiability. To address these challenges, we introduce the use of nonparametric Bayesian inference for the analysis of single-molecule time series. These methods provide a flexible way to extract structure from data instead of assuming models beforehand. We demonstrate these methods with applications to several diverse settings in single-molecule biophysics. This approach provides a well-constrained and rigorously grounded method for determining the number of biophysical states underlying single-molecule data.
Introduction
Proteins are the fundamental unit of computation and signal processing in biological systems. Understanding the biophysical mechanisms that underlie protein conformational change remains an important challenge in the study of biological systems. The ability to measure the properties of proteins at the single-molecule level offers an unparalleled glimpse into biological systems at the molecular scale. This was first achieved with ion channel proteins using the patch-clamp technique (1) and has been extended to soluble proteins using optical methods such as single-molecule fluorescence resonance energy transfer (FRET) (2) and optical tweezers (3). Such single-molecule time series reveal stochastic dynamics indicative of rapid transitions between semistable conformational states separated by free-energy barriers. This leads to a natural interpretation of these time series within the context of statistical physics and the theory of Markov processes. Markov models fit well within the conceptual framework of protein conformational change, yielding mechanistic models with a finite number of discrete energetic states. In practice, such time series, inevitably obscured by experimental noise and other obfuscations, are often analyzed using hidden Markov models (4,5). While this approach has been widely successful, it is not without important limitations.
Contemporary methods for the analysis of single-molecule time series suffer from problems of model selection bias and parameter identifiability. Analysis typically begins with the investigator positing some mechanistic model: the lens through which the data are to be interpreted. Generally, we must postulate the existence of some number of biophysically relevant states and perhaps even their interrelationships. For example, in the study of ion channel gating, a typical analysis requires postulating a particular mechanistic scheme consisting of a specified state space and connectivity, and using a maximum likelihood approach to estimate the relevant parameters of that scheme, given the data (5–7). However, in most applications, the number of relevant biophysical states is not obvious from the data and is not known beforehand. In fact, it is likely that an experiment was performed with the purpose of uncovering the existence and details of hidden molecular states. Therefore, the choice of a particular model has a very strong effect on the analysis and interpretation of the data.
Methods for aiding in this problem of model selection have been proposed for a variety of experimental settings, and generally have relied on model comparison via maximizing likelihood or penalized maximum likelihood such as the Akaike information criterion (8–12). The strategy with such methods is motivated by parsimony: the goal is to find the model that provides the best explanation of the data, yet remains the least complex. Although parsimony is likely a useful guiding principle, these methods leave us with no rigorous way of quantifying our confidence in models relative to each other; we must rely on ad hoc comparison of models based on Akaike information criterion score or similar methods. Additionally, maximum likelihood methods are generally unable to detect parameter nonidentifiability, where disparate regions of parameter space might yield identical data, a pitfall that is increasingly common as researchers pursue models of higher complexity (13–15). Although they have been quite useful, likelihood-based approaches for modeling single-molecule time series suffer from important drawbacks.
Here, to our knowledge, we introduce a novel approach for the analysis of single-molecule time series that circumvents the problem of model selection by using nonparametric Bayesian inference. The goal of these methods is to use a class of probability models that are so flexible that we are able to extract structure from data instead of assuming models beforehand. These methods have become widely used in the machine learning community to handle challenging problems such as document modeling (16), speaker diarization (17), and image processing (18), among many others. The approach relies on the theory of random probability measures and in particular, we use the Dirichlet process to provide an infinite dimensional probability model that has well-defined properties for modeling finite data. This infinite model subsumes the set of all possible models, but in fitting finite data, we learn which of the infinite model components are actually necessary to provide a good explanation of the data. The properties of Dirichlet process models yield parsimony while preventing overfitting, allowing us to discover what process most likely generated the data, instead of assuming it. Importantly, this Bayesian approach provides estimates of all parameters, their uncertainty, and their identifiability. Finally, because our infinite dimensional model is a probability distribution with well-known properties, we gain a quantification of parameter confidence for different models that can be used for model comparison.
We demonstrate the use of nonparametric Bayesian inference with three cases from single-molecule biophysics. Using a Dirichlet process mixture model, we show that dwell-times from single ion channel recordings can be modeled nonparametrically in order to discover the number of biophysical states hidden in the data. We then describe the hierarchical Dirichlet process hidden Markov model and apply this model to time series from electrophysiology, single-molecule FRET, and single-molecule photobleaching. Finally, we introduce the hierarchical Dirichlet process aggregated Markov model that allows us to nonparametrically analyze single ion channel time series and discover hidden biophysical states without specifying a model. These methods provide a flexible and powerful framework for the analysis of diverse types of single-molecule data.
Materials and Methods
Electrophysiology
HEK293 cells were cultured following standard protocols. Wild-type BK channel cDNA was transiently transfected into HEK cells with Lipofectamine 2000 (Invitrogen, Carlsbad, CA). As an optical marker, Enhanced green fluorescent protein was cotransfected. Recordings of single BK channels were performed 2–4 days after transient transfection. Voltage-clamp was performed on inside-out patches pulled from HEK cells at room temperature. Patch electrode resistances were 1–2 MΩ and the electrode solution contained 6 mM KCl, 136 mM KOH, 20 mM HEPES, 2 mM MgCl2, and was pH-adjusted to 7.2 using MeSO3H. Bath solution contained 6 mM KCl, 136 mM KOH, 20 mM HEPES, 0.01 mM Crown Ether ((+)-(18-Crown-6)-2,3,11,12-tetracarboxylic acid), and pH was adjusted to 7.2 using MeSO3H. Additionally, EGTA was added to buffer calcium and varying amounts of CaCl2 were added. Free calcium concentrations were measured using a calcium-sensitive electrode. Recordings were performed with an Axopatch 200A amplifier (Axon Instruments, Jakarta, Indonesia; distributed by Molecular Devices, Eugene, OR) and digitized using an ITC-16 A/D converter. Single channel traces were sampled at 100 kHz and analog-filtered at 10 kHz, and collected using the software PATCHMASTER (HEKA Electronik, Lambrecht, Germany).
FRET
The single-molecule FRET data were kindly contributed by Christy Landes and David Cooper at Rice University. The data were collected using procedures similar to those reported in Ramaswamy et al. (19). The agonist-binding domain of the NMDA receptor was expressed and purified using standard procedures. Streptavidin acted as a linker between a biotin-PEG slide and the biotin-conjugated anti-histidine antibody bound to the NMDA subunit. A PBS solution containing 250 nM protein tagged with biotin-conjugated anti-histidine monoclonal antibody was then added. The dye attachment sites were mutated at T193 and S115 to cysteine residues. The NMDA agonist binding domain was in the presence of saturating concentrations of glycine and thus should be fully bound with agonist. To obtain the smFRET trajectories for the individual protein molecules, a 10 × 10-μm area of the sample was scanned to spatially locate 20–25 molecules. The fluorescence signals of the donor and the acceptor were collected until the fluorophores were photobleached. Photon counts were collected from two avalanche photodiodes tuned to the wavelengths for acceptor and donor light, which were then processed to remove background signal and crosstalk from the signals and FRET efficiency was calculated using standard methods. The emission intensity trajectories were collected at 1-ms resolution and later binned to 10-ms time steps.
Photobleaching
The single-molecule photobleaching data were collected as described in Bankston et al. (20), which is briefly replicated here: Xenopus oocytes were injected with varying ratios of TRIP8b and HCN2 mRNA. Total internal reflection fluorescence movies were acquired using a model no. TE2000-E microscope with a high numerical aperture objective (100×, 1.49 N.A.; Nikon, Melville, NY) and the Evolve 512 EMCCD camera (PhotoMetrics, Huntington Beach, CA), with a pixel resolution of 9.37 pixels/micron. Oocytes were illuminated with a 488-nm argon laser from Spectra-Physics (Santa Clara, CA). An image stack of 800–1200 frames was acquired at 30–50 Hz. The first five frames after opening of the laser shutter were averaged, and the background was subtracted using the rolling-ball method in the software IMAGEJ (National Institutes of Health, Bethesda, MD). The image was then lowpass-filtered with a two-pixel cutoff, and thresholding was applied to find connected regions of pixels that were above threshold. A region of interest of 6 × 6 pixels was placed around the center of the spot. Spots smaller than 3 pixels and larger than 15 pixels were discarded manually. Finally, the summed fluorescence intensity inside the 6 × 6 region of interest was measured and plotted versus time.
Data analysis
The models and algorithms used for data analysis are described in detail in the next section. Analysis for the Dirichlet process mixture of exponentials was performed using scripts written in the software R (The R Project for Statistical Computing, www.r-project.org). For the hierarchical Dirichlet process hidden Markov model, the beam sampling implementation of van Gael et al. (21) was used (code available at mloss.org/software/view/205/). For the hierarchical Dirichlet process aggregated Markov model, scripts were written in the software MATLAB (The MathWorks, Natick, MA). Code has been made available as the Supporting Material.
Theory
Nonparametric Bayes
Methods of nonparametric Bayesian inference rely on a class of flexible probability distributions known as random probability measures. Although there is an extensive literature on random probability measures of all flavors (22,23), we focus on the Dirichlet process. The Dirichlet process, DP(α, H), is a distribution on distributions (24). It has two parameters: a scalar α, which is referred to as the concentration parameter; and a probability distribution H. Draws from DP(α, H) are random probability measures that are centered on H and whose variance about H is controlled by α. A useful representation of a draw from a Dirichlet process is the stick-breaking process of Sethuraman (25). A random probability measure, G, is drawn from a Dirichlet process as
| (1) |
| (2) |
where all θi values are independent and identically distributed samples from the base distribution H, and the weights satisfy the stick-breaking construction,
for νk ∼ Beta(1,α). Imagine breaking a stick of unit length into an infinite number of segments in the following way: Break the stick at a random location w1 ∼ Beta(1,α) and associate with this weight a random draw from H, θ1 ∼ H. The remaining length of the stick is now 1 − w1. Again, draw ν2 ∼ Beta(1,α) and break the remaining length of the stick at this location, such that w2 = (1 – w1)ν2 and associated with this weight is another independent and identically distributed draw from the base measure, θ2 ∼ H. This process is repeated infinitely with the result that the probability mass is distributed across a countably infinite number of segments, hence,
where the notation denotes a point-mass at location θi. For convenience, we denote the sequence w1, w2, w3,…, which satisfies the stick-breaking construction as w ∼ GEM(α) (26). The expectation of the size of each weight, E[wi], decreases geometrically with i, such that only finitely many wi occupy nearly all the probability mass while infinitely many others occupy negligible probability. From Eq. 2, G is an infinite mixture of components each with probability mass wi located at θi. Note that G is a discrete probability distribution, even though H might be continuous.
Dirichlet process mixture models
Because a draw from the Dirichlet process is discrete, it can be awkward when used with data known to be drawn from a continuous distribution. A common variation is a Dirichlet process mixture model (DPMM), where G is convolved with some parametric continuous distribution (27). Because G is a discrete distribution, this convolution results in a mixture model with an infinite number of components. The data yi are drawn from a DPMM as
| (3) |
| (4) |
| (5) |
We now imagine that each data point is drawn from one of an infinite number of components, each one parameterized by θj. Due to the properties of the stick-breaking process, only finitely many wj occupy nearly all the probability mass, while infinitely many others occupy negligible probability mass. Because the data yi values are sampled from the probabilities wj, a natural clustering is induced in the data. In principle, the number of inferred clusters could range between two extremes: there could be one cluster from which all the data are drawn, or there could be N clusters, each data point being drawn from its own component. Obviously, neither of these of these extremes is particularly useful. Most commonly, we infer with high posterior probability the presence of some small number of clusters , where .
Model inference
In all the modeling applications that follow, we estimate the relevant joint posterior distributions using Markov chain Monte Carlo sampling (MCMC) (28). The strategy is that we can estimate an arbitrarily complex posterior distribution by drawing independent and identically distributed samples from it. Generating samples from the posterior is achieved by constructing a Markov chain whose limiting distribution is the desired posterior and then simulating this Markov chain for a finite number of iterations. Constructing Markov chains with a desired limiting distribution is achieved with the Gibbs sampling schemes described throughout this section.
As an example of a mixture model, later we will model dwell-times from single ion channel recordings using a mixture of exponential distributions. In this case, p(y|θ) is an exponential distribution with unknown scale parameter θ. If we do not know how many components (mixtures) are in the data, we can use DPMM to model an infinite mixture
| (6) |
Inference with this infinite mixture model is achieved with the following Gibbs sampling scheme. We initially describe the relevant conditional posterior distributions for sampling a finite mixture of exponential distributions, and then describe how sampling is performed with the infinite mixture model. For a given finite mixture model with K components, we are interested in computing the marginal posterior distributions of θ1, θ2,…, θK and w1, w2,…, wK. The likelihood is a mixture of exponential distributions,
| (7) |
| (8) |
For the prior on each θ, we use a conjugate Gamma-distribution, Ga(A,B). For a single-component exponential distribution with a Gamma-prior, the posterior distribution of scale parameter θ is
| (9) |
| (10) |
For the mixture model, we introduce a latent indicator variable, si, which serves to label each data point according to the component from which it was likely drawn. Using these indicator variables, the posterior of θ is extended to multiple components. Let Aj be set of all i such that si = j. Then the posterior over θj goes as
| (11) |
| (12) |
For each si, we sample the conditional posterior of datapoint yi belonging to each of the K components from a multinomial distribution,
| (13) |
| (14) |
The cluster weights, wj, are drawn from the standard Dirichlet distribution,
| (15) |
For any mixture model with K components, the conditional posterior distributions described above specify an efficient Gibbs sampler for calculating the posterior distributions of all model parameters. With a Dirichlet process mixture model, sampling si from a multinomial distribution with K components is likely to be impossible as K → ∞. However, even though θ1, θ2, θ3… is infinitely long, the Dirichlet process induces a natural clustering such that the data are drawn from a finite set, θ∗. During any particular iteration of Gibbs sampling, let k∗ denote the number of components that are represented in θ∗. Then data point yi might be sampled from one of the k∗ clusters that are already represented, or to one of the infinitely many other clusters that are not yet represented, but all of which together occupy finite probability mass. Sampling the indicator variables si goes as
| (16) |
where the superscript, −, indicates a conditioning variable without the data point in consideration, yi. Thus, the indicator variables sample from each existing component with probability proportional to the perceived size of each component, and generate a new component with probability proportional to α. If we use a conjugate model, then computing the integrals in Eq. 16 is simple and this scheme can be used for sampling from an infinite number of clusters. In this case of DP mixture of exponentials, we indeed can utilize the conjugacy between exponential and Gamma-distributions and the previous method can be used for inference. Alternatively, we prefer to use the slice sampling method of Walker (29) because it is used for more complex models discussed later.
Recall that, generally, our mixture model posits that the data are drawn from an infinite mixture of parametric distributions,
| (17) |
We augment this model by adding a latent variable u, drawn from a uniform distribution, such that the joint model is
| (18) |
where I(…) is the indicator function and takes value 1 when its argument is true and 0 otherwise. Note that if we integrate Eq. 18 with respect to u (marginalization), the result is the original model (Eq. 17), i.e.,
This marginalization will be achieved with MCMC sampling of u, and we therefore retain the original model (Eq. 17) in which we were interested. Most importantly, because all wj values are <1, any particular draw of u partitions the infinite set of wj into two sets: a finite set for which wj > u and an infinite set for which wj < u. By incorporating this augmented model into the Gibbs sampler, we can sample u in order to only represent finitely many clusters at each iteration, yet the aggregate sampling marginalizes the model back to that of Eq. 17. For each iteration, we draw u1,…,uN uniformly on the intervals and represent k′ clusters where
| (19) |
Each iteration is simply a finite mixture model, and the number of mixture components fluctuates over the course of Gibbs sampling to integrate over the infinite number of clusters.
Demonstration
Fig. 1 shows an example of using this infinite mixture model. At top left, a simulated dataset (N = 500) was drawn from a mixture of four exponential distributions. The four components had scale parameters, θj, equal to {0.001, 0.01, 0.1, 10}. Data points are plotted logarithmically to aid in visualization, and a kernel density estimate is shown. When shown in this way, we might guess by eye that there are distinct clusters in the data, but we would be unsure of how many. Using a DP mixture of exponentials allows us to posit an infinite model and then learn how many clusters are actually in the data. Shown at top right is the number of components in the infinite model that are represented throughout the course of Gibbs sampling. The model initializes with an arbitrary number of clusters, but quickly converges to the correct number. The bottom row of Fig. 1 shows the marginal posterior distributions for each of the θj that remain in the model. The true values of each θj are shown as red vertical lines. Using the DP mixture of exponentials, we were able to correctly learn the number of clusters in the data, and also get an accurate quantification of the relevant model parameters and their uncertainty.
Figure 1.
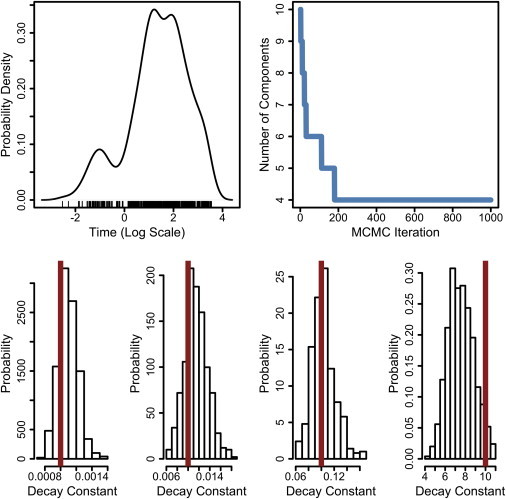
Demonstration of Dirichlet process mixture of exponentials. (Top left) Simulated data (N = 500) drawn from a mixture of four exponential distributions with scale parameters, θj, equal to {0.001, 0.01, 0.1, 10}, plotted logarithmically. A kernel density of estimate of the sampled data points is also shown. (Top right) Result of modeling this dataset with DP mixture of exponentials: the infinite model converges to four components. (Bottom) Marginal posterior distributions of all θj values that remain in the model. (Red vertical lines) True values. Algorithm parameters: α = 1.
Infinite hidden Markov model
Hidden Markov models (HMMs) have enjoyed vast application in many areas of science and engineering due to their flexibility and predictive ability (4). In this time-series model, we now index each data point as discrete time points t. It is assumed that observable data, yt, is an obfuscation of a hidden dynamical process that we cannot directly access. In particular, it is assumed that the system of interest has access to K different hidden states (1, 2,…,K) and transitions stochastically between states. The dynamics of the system are fully captured by the transition probability matrix π, where each element πi,j is equal to p(st = j|st−1 = i), the probability of a transition to state j at time t, given that the system was in state i at time t − 1. Atop these dynamics, it is assumed that each hidden state, s, has a distinct emission distribution, . Therefore, the system transitions stochastically according to π, and each observation is a random draw from . Because of the Markov property, the joint probability of all hidden states and observations can be written as
| (20) |
Although HMMs have been widely useful, a major limitation is that we must specify how many hidden states, K, are in the model. To overcome this barrier, the infinite hidden Markov model (iHMM) was introduced (30)—a model that was later generalized and termed the “hierarchical Dirichlet process hidden Markov model” (31,32). In this model, the number of hidden states is left unknown, and the transition matrix, π, is modeled nonparametrically using the hierarchical Dirichlet process. Each row of π is a draw from a Dirichlet process and thus specifies the probability of transitioning to each of a countably infinite number of other hidden states. However, this idea alone would not constitute a useful HMM. Consider that each πi is drawn from DP(α,β). Because each πi is almost surely discrete, there would be zero probability that any of the πi share any θ in common. Said differently, each πi quantifies transitions to an infinite number of hidden states, but there is no mechanism to ensure that the rows of π transition to any of the same states. In order to ensure the all the rows of π are coupled, the hierarchical Dirichlet process was introduced (31). Here, each row πi is drawn from a DP with base distribution β. This base distribution, β, is itself a draw from a Dirichlet process, which ensures that each πi is drawing from the same infinite set of hidden states (atoms). This process can be described as
| (21) |
| (22) |
| (23) |
| (24) |
The goal is then to learn the number of hidden states from a particular time series.
Model inference
We initially describe a Gibbs sampling scheme for parameter inference with finite HMMs, and then describe the implementation used for the iHMM. Gibbs sampling methods for HMMs have been described elsewhere (33,34), and we only briefly discuss the basic components. For these examples, we imagine our observations are normally distributed random variables and that each hidden state corresponds to a distinct mean θi and precision τi, such that
Again, let Ai denote the set of all t for which st = i. For the means, θi, we use a conjugate prior normal distribution N(a, b). For each θi,
| (25) |
where
| (26) |
| (27) |
With a conjugate Gamma-prior, p(τi) = Ga(c, d), on the precisions, τi,
| (28) |
where
| (29) |
| (30) |
Conditioned on the previous samples of hidden states s1,…,sN, sampling the transition matrix, π, is simple. We use the standard Dirichlet distribution with parameter vector [m,…,m] as a conjugate prior for rows of the transition matrix, i.e., p(πi) = Dir(m,…,m). Let matrix N track the number of transitions between hidden states i and j such that
Then each row of π is sampled as
| (31) |
Finally, the hidden states, st, are sampled using the forward-filter-backward-sampler method (33). We refer the reader to Scott (33) and Rosales (34) for a more detailed description of this sampling scheme for HMMs. The basic idea is that we combine the traditional forward-backward method (4) with a Gibbs sampling approach. The result is an effective way to generate posterior samples of s1, s2,…,sN, which is the last component we needed in our HMM Gibbs sampler. Thus, for any hidden Markov model of fixed size, K, this Gibbs sampler allows us to calculate posterior distributions of all relevant parameters.
Generalizing this model to the infinite case will proceed similarly as with the mixture model. Again, the problem is that we now wish to consider the probability of transitions to each of an infinite number of hidden states, a computation that we cannot perform in our existing Gibbs sampler. However, using the hierarchical Dirichlet process hidden Markov model, we can sample from both the instantiated hidden states as well as the infinitely many other hidden states that have yet to be sampled (31),
| (32) |
The sampling scheme works well, but it was noted that because Markov-type models will inherently have very high correlation between the latent variables, this form of Gibbs sampling could mix very slowly. To remedy this, the beam sampler for iHMMs was proposed (21). This implementation combines the dynamic programming approach described previously (33) with the slice sampling approach of Walker (29). The model is augmented to include latent variables u1,…,uN in order to limit the computation to a finite number of hidden states at each iteration of MCMC. Sampling st at each iteration becomes
| (33) |
| (34) |
Thus, ut splits the infinite state space into two partitions: an infinite set for which , and a finite set for which . Therefore, needs only to be computed with respect to a finite number of states.
As with the infinite mixture model, we can use to compute at each iteration the number of hidden states that must be represented, k′, then we proceed with the Gibbs sampler just described for finite HMMs. Again, throughout the course of MCMC, resampling results in fluctuations in the number of hidden states represented such that the aggregate of all MCMC samples results in integration over the infinite number of states. Sampling for β is performed using standard sampling methods for hierarchical Dirichlet process models (31).
Infinite aggregated Markov model
In the iHMM, it was assumed that each hidden state corresponds to a distinct emission distribution, . In some cases, we might want to model a degeneracy such that multiple hidden states share the same emission distribution. In this infinite aggregated Markov model (iAMM) (35), we imagine that the hidden states appear as aggregated into one of A distinct emission distributions such that A < K. We augment the iHMM with an indicator variable, at ∈{1, 2, …, A}, that specifies which aggregate each data point is drawn from such that . In this case, we cannot identify different states by their emission distributions, but aim to infer the hidden states based on differences in their dynamics. In the next section, this model is applied to data from single ion channel recordings and A is fixed to be two. It is our intention with the iAMM that the number of aggregates, A, is known beforehand, and we mean to infer the number of hidden states within each aggregate.
The use case for the iAMM will be the analysis of single ion channel recordings, for which we add one additional feature to the model. Previous authors extended the infinite hidden Markov model framework by allowing for a strong preference for models with state-persistence (32). That is, we assume the timescale of system dynamics is significantly slower than the data sampling rate. In this way, we are interested in solutions to the data where the system stays in each state for multiple time samples and we are intentionally not interested in models where states have nearly zero dwell-time before transitioning. This certainly seems to be the case with ion channels, where from dwell-time distributions, we imagine that the channel tends to stay in each state for multiple time samples (at least). Following Fox et al. (17), we employ a sticky-iAMM by biasing probability mass onto the diagonal elements of the transition matrix π. By ensuring nonzero probability mass on the diagonal of π, we exclude models where states transition arbitrarily quickly to other states. To achieve this, we make a slight alteration to the algorithm described in the previous section. We add a hyper-parameter κ, the magnitude of which tunes the stickiness of the resulting Markov model. Each row of π is drawn from a Dirichlet process, with the diagonal elements biased by κ,
| (35) |
and the rest of the algorithm remains the same. Incorporating uncertainty in κ into the sampling model should be possible in principle (36), but we prefer to use a fixed value. In experiments with simulated data, κ = 100 works well, and we use this same value for all ion channel data analyzed in the Results (see the Supporting Material for a discussion of Dirichlet process parameters).
An example of the sticky-iAMM, meant to mimic single ion channel recordings, is shown in Fig. 2. For simulating data, we use A = 2 and K = 4, and use transition dynamics π such that the two states within each aggregate have very different transition probabilities. A sample of such data is shown at the top of Fig. 2 (gray trace), and we can even see by eye that within each emission distribution are events that have very long durations and other events with have very brief durations. By using the sticky-iAMM to analyze this time series, we can infer how many states are hidden within the two aggregated states.
Figure 2.
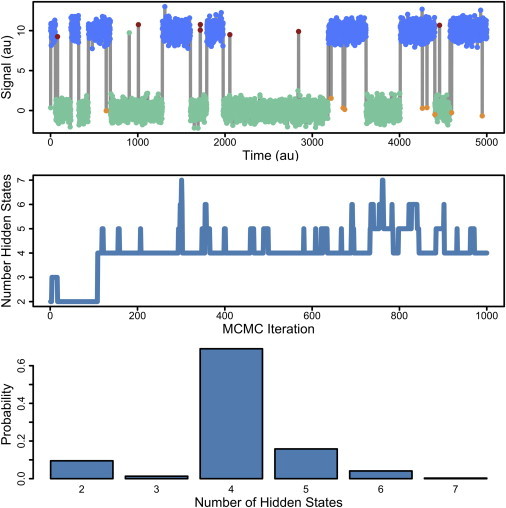
Demonstration of the iAMM. (Top) Simulated data from a four-state process with two closed and two open states with different dynamics. Each of the states differ in their exit rate—we can even tell by eye that there is a short-lived state and a long-lived state, for both open and closed. Colors correspond to the inferred state-assignments when this time series is modeled with the iAMM; we find the number of hidden states correctly and correctly label each data point. (Middle) The number of hidden states over the course of MCMC simulation. (Bottom) The posterior distribution over the number of hidden states. There is high probability that this time series was generated from a four-state process. Algorithm parameters: α = 1, γ = 1, and κ = 100.
The result of this model is shown as the colors in the top of Fig. 2; each datapoint is colored according to the hidden state from which it was likely drawn. With the infinite model, we are able to correctly identify that there are four states with distinct dynamics and are able to label all the data points: open states as red and blue, and closed states as green and gold. The middle of Fig. 2 is a plot of the number of hidden states represented throughout the course of MCMC. Fig. 2 (bottom) shows the posterior distribution over the number of hidden states, and we see that high posterior probability is placed on there being four hidden states within this time series. Therefore, we are able to accurately infer the number of hidden states within this aggregated Markov process time series.
Results
Single ion channel dwell-time distributions
We first demonstrate the use of infinite mixture models to analyze dwell-time distributions from single BK channel recordings. The BK channel has been studied extensively by many groups and detailed mechanistic models have been put forth to explain the effects of voltage and calcium on channel gating (37–40). This detailed understanding of BK channel gating provides an excellent testbed for the use of these proposed analysis methods.
As a first step to analyzing single ion channel records, we can deconstruct the time series into sojourns within closed states and open states (6). To do this, we first denoise, or idealize, the single channel data by classifying each datapoint as corresponding to either closed or open. The simplest method for this would be choosing a threshold of halfway between the average open and closed current levels and then classifying each data point relative to this threshold (41). This simple method works fairly well, although one must be wary of artifacts such as threshold-crossing due to poor signal/noise and correcting for missed events (41). We prefer an alternative approach, where we treat the time series as a two-state hidden Markov model. Here, the open and closed states correspond to different levels of current obscured by noise, each with different variability.
Note that the threshold method would yield very similar results to any model with a symmetric noise distribution, but makes the assumption that the current variance is the same for both open and closed states. We prefer not to make that assumption, and so model closed and open states corresponding to normal distributions each with distinct mean and variance. Using the Gibbs sampling approach described in the Theory, we utilize a latent indicator variable s1,…,sN to denote the state assignment for each data point. Thus, after MCMC inference, the indicator variables s1,…,sN yield the idealized trajectory through the hidden states. This Bayesian approach to idealization of ion channel records has been used previously and was thoroughly compared to previous methods (34,42), so we omit such a discussion here (see the Supporting Material for a demonstration of the idealization method). With an idealized trace, we simply count how many consecutive samples are spent in a state before transitioning to the other state; this is a dwell time in one of the states. Decomposing the whole recording in this way yields a distribution of dwell-time events in the open state and in the closed state.
The theory of Markov processes indicates that the ensemble of dwell times should be exponentially distributed, if there is truly only one closed state and one open state. However, while a single channel time series implies the presence of only two conductance states, the distribution of dwell-times often indicates that there exist multiple states appearing as closed or open, yet which have measurably distinct dynamics. Given that we have measured a set of dwell-times, interpretation of this data is simply a matter of fitting to a (potentially) multicomponent mixture of exponential distributions. If we can decide how many components are in the data, then many methods might be used for estimating the parameters of a finite mixture model (6,43).
Much effort has been put into data transformations and other methods for deciphering how many components exist in single channel dwell-time distributions (43,44). Discovering the number of components within such data is an ideal use for Dirichlet process mixture models. As described in the Theory, we imagine that the data yi values are drawn from an infinite number of exponential components by using a Dirichlet process prior on the mixture weights:
| (36) |
| (37) |
| (38) |
By using this infinite model to fit our finite data, we are able to discover the number of components in the data, instead of assuming it. In the Theory, we described an efficient Bayesian method of analyzing a finite mixture of exponential distributions as well as a sampling method for a Dirichlet process mixture model. We demonstrated that this infinite model could indeed discover the number of components in simulated data drawn from mixtures of exponential distributions, and it could also provide accurate estimates of the relevant parameters and their uncertainties (see Fig. 1).
This method can be applied to dwell-times from BK channel recordings at various holding voltages. Fig. 3 shows dwell-time distributions from 5 s of data from a BK channel in 6 μM calcium held at several voltages. These dwell-time distributions have been analyzed using an infinite mixture of exponential distributions so that we can discover the number of components in the data, instead of presupposing it or fitting many different models sequentially. In Fig. 3, the aggregates of dwell-times are visualized as histograms and the probability density of each component is shown atop the histogram. Finally, the total probability density from all components is shown as the gray trace, which overlays well with the observed histograms. We are able to extract from these data the number of hidden components (see Fig. S3 in the Supporting Material for posterior distributions) and find that these results are consistent with what is previously known about the BK channel. For example, we see that with the three increasing holding voltages, the infinite mixture model indicates the emergence of measurably distinct open states. Additionally, we have a rigorous estimate of the timescale parameter for each component, and can see that the alterations in mean dwell time (as a function of voltage) are consistent with previous findings (45). This task of determining the number of significant components in dwell-time distributions is easily accomplished using a Dirichlet process mixture model (see Discussion for comparison with previous methods).
Figure 3.
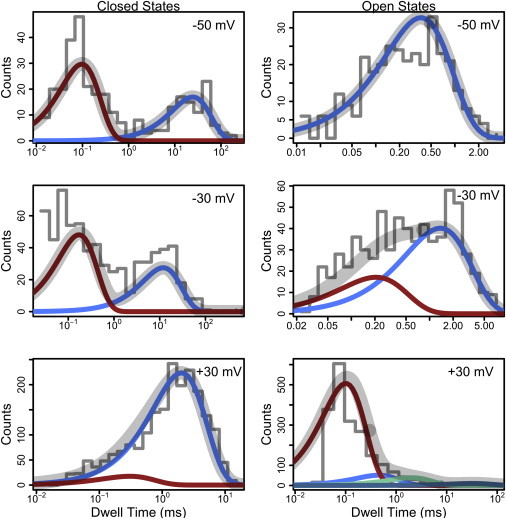
Dwell-time distributions and infinite mixture models. These dwell-times, plotted logarithmically for visualization, are from 5 s of a BK channel at 6 μM calcium and various holding voltages. Distributions of dwell-time are analyzed with an infinite exponential mixture model in order to discover how many components are in the data. The raw data are visualized in the histograms, and the probability density of each component is shown atop the histogram. Finally, the total probability density from all components is shown as the gray trace in each panel. Algorithm parameters: α = 1.
Application of iHMM to single-molecule time series
HMMs have enjoyed vast application in many areas of science and engineering due to their flexibility and predictive ability (4). For stochastic time series arising from single-molecule measurements, we now index each data point with discrete time t, and we might imagine that the observations yt are normally distributed random variables and that each hidden state corresponds to a normal distribution with a different mean and precision such that
As described in the Theory, a nonparametric Bayesian extension of this HMM framework is the hierarchical Dirichlet process hidden Markov model (30,31). Using this model, we do not fix the number of hidden states before data analysis, but instead we can learn the likely number of hidden components within the data. Example uses of this model are shown in Fig. 4. The top of Fig. 4 shows an electrophysiological recording from a patch that contains an unknown number of BK channels. The holding voltage is negative, so downward deflections of current indicate events of ion channel opening. From this multichannel patch, we might want to estimate the number of channels in the patch and the average open probability.
Figure 4.
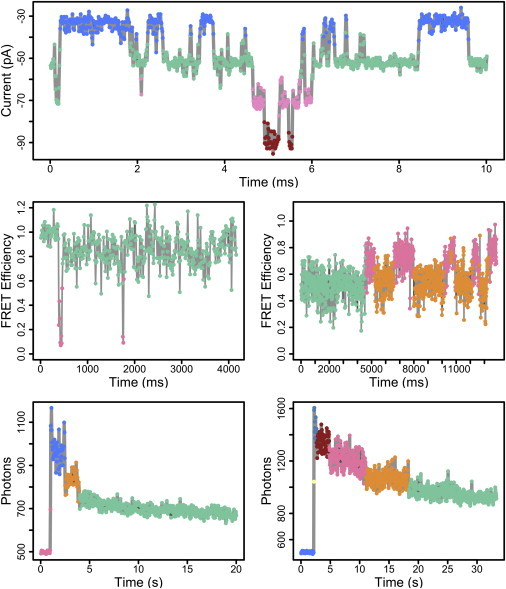
Application of iHMM to single-molecule time series. (Top) Electrophysiological recording of a patch containing multiple channels and downward current deflections indicate channel opening events. (Middle) Traces from single-molecule FRET. (Bottom) Traces from single-molecule photobleaching. In each case, the data points are colored corresponding to the hidden state from which they are likely drawn. Algorithm parameters: α = 1 and γ = 1.
When different numbers of channels are open at different times, we observe distinct levels of current, obscured by electrical noise. Thus, we can use an iHMM approach to learn how many distinct current levels exist in the time series and the number of channel openings seen. After iHMM modeling, each data point is colored corresponding to the hidden state from which it is likely drawn. It is clear that we are able to correctly detect the number of distinct levels of current and infer the number of open channels seen in this patch. In this particular case, the signal/noise of the recording is quite high and we could perform this task by eye fairly easily, but it serves as a general demonstration of the kinds of data that are well suited for the iHMM.
As a more challenging application, we use the iHMM to denoise single-molecule FRET traces and decipher distinct conformational states and transitions. Fig. 4 (middle) shows such single-molecule FRET traces recorded from the agonist-binding domain of the NMDA receptor (see Materials and Methods). In the traces shown, we can see that the FRET efficiency indicates the molecules tend to reside within distinct conformational states for tens of milliseconds before transitioning to other states. However, the noise in this data makes it difficult to tell when these transitions occur and, more importantly, how many conformational states are observed within each trace. We can use the iHMM to analyze these traces in order to detect the presence of significant conformational states. The data traces are overlaid with colors according to the hidden state from which each data point was likely drawn.
The iHMM is able to decipher distinct conformational states based on both the properties of the emission distribution (mean and variance) and the dynamics of the states. Even if a state is visited extremely rarely (such as in the left trace), we are able to confidently assert the existence of distinct conformational states. Additionally, we could use the posterior distribution over the number of hidden states as a simple way to quantify confidence in an interpretation of the data (see Fig. S6). An interesting extension of this model would be to combine an ensemble of different traces into a hierarchal model (46). In such a model, we imagine each trace provides a brief snapshot of some underlying hidden distribution from which all the traces are drawn. Then the traces, taken in aggregate, provide information about the total conformational space and transition dynamics. Future work remains to be done in this area.
As a final application, we turn to single-molecule photobleaching. In this setting, we observe photon counts over time and are interested in detecting photobleaching events that reveal themselves as sudden decreases in photon intensity. We are particularly interested in counting the number of photobleaching events in a data trace. This setting is well suited for the iHMM because we want to detect transitions between an unknown number of states (corresponding to bleaching events). Fig. 4 (bottom) shows example traces from fluorophore-tagged TRIP8b proteins (see Materials and Methods). We can see that photobleaching events are apparent, but in regimes of low signal/noise, it might be quite difficult to tell by eye when bleaching events occur. After analysis with the iHMM, the data points are colored corresponding to the hidden state to which they were assigned. The poster distributions over the number of inferred transitions are shown in Fig. S7. It is clear that the iHMM is an excellent tool for this task. Even in settings where photobleaching events are very difficult to detect by eye (right), the iHMM is able to identify likely transitions in the data. Using the iHMM provides a rigorous and unbiased method to analyze all these single-molecule time series.
Application of iAMM to single ion channel recordings
Next, we demonstrate the use of the iAMM to analyze single ion channel recordings. We previously analyzed BK single channel data by deconstructing the time series into dwell-times and fitting exponential mixture models. This approach throws away much information because it treats each dwell-time as an independent draw from an underlying mixture of exponential distributions. A preferable method is to model each time point in the Markov-type model (5). In the Theory, we introduced the iAMM, where we assume degeneracy such that multiple hidden states share an emission distribution. We demonstrated that the iAMM (more precisely, the sticky-iAMM; see the Theory) can be used to learn the number of hidden states from an AMM time series (Fig. 2). We now apply this to single BK data, where we see stochastic transitions between open and closed states of the channel but suspect there exist more than two hidden states. Using the iAMM, we can learn the presence of open and closed states in the time series, instead of assuming this beforehand.
For Fig. 5, we have used 1 s of a recording of a single BK channel in 110 μM calcium held at +30 mV. The top row of Fig. 5 visualizes the posterior distribution over the number of hidden states and we see that we infer, with high posterior probability, the presence of four hidden states. Fig. 5 (middle) shows the data trace that was analyzed and the colors correspond to the hidden state from which each data point was likely drawn. This analysis reveals one open state and three closed states. We can see that there is a fast closed state (green) and a measurably slower closed state (red). Additionally, there is an extremely slow closed state (pink), of which we have only one observation, but are easily able to infer its existence due to its distinct temporal dynamics. The bottom trace is the same data at an expanded timescale. Encouragingly, we are able to detect the presence of distinct hidden states based solely on their dynamical differences in single ion channel recordings.
Figure 5.
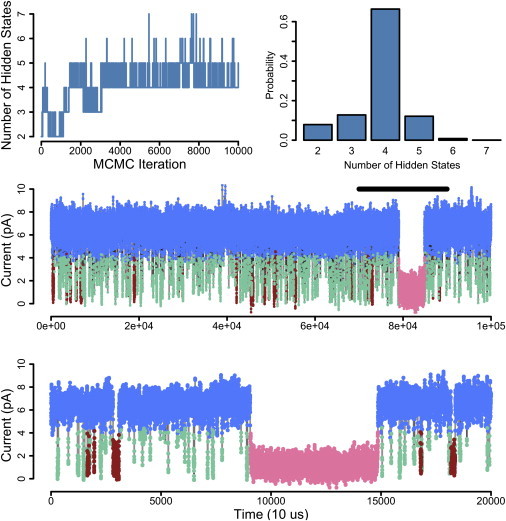
Application of iAMM to BK data. (Top row) Relating to posterior distribution of number of hidden states; it seems that this data has four hidden states. (Middle) Data trace labeled for the hidden states. The iAMM finds one open state (blue), and three closed states. For the closed states, the fastest timescale state (green) is different enough from a slower one (red) that we are able to identify them as distinct. Additionally, an extremely slow closed state (pink) is identified. (Bottom) Same data at an expanded scale. Algorithm parameters: α = 1, γ = 1, and κ = 100.
Before continuing, we describe a general barrier to the analysis of single channel recordings that the iAMM is still unable to surpass with this dataset. Kienker (35) noted that with aggregated Markov models, the space of potential mechanisms that can adequately fit any given equilibrium data set is nonidentifiable. In particular, it was shown that the transition matrix π of any given AMM exists among a (possibly infinite) equivalence class of other , which would all produce identical data. Not only might it be impossible to derive a unique estimate of π from data, but the members of such an equivalence class span a continuous range of , including members with entirely different connectivities between the hidden states. Hence, the problem of model selection is exacerbated, because many different models (different connectivities) can be transformed into one another and would all fit the data equally well. In fact, the only way to circumvent nonidentifiability in aggregated Markov models is to presuppose a particular connectivity. Often, such a constraint on the connectivity between the states allows typical inference methods, such as maximum likelihood (5) or Gibbs sampling (34), to yield a unique estimate of π conditioned on a particular model. However, because our goal has been to avoid the prespecification of models, the iAMM approach will inevitably suffer from this model nonidentifiability when fitting equilibrium time series. Indeed, all existing methods for single channel analysis (5,6) will still be plagued by this nonidentifiability, because any particular model we choose will only specify a large equivalence class of models. It is likely that this nonidentifiability can be overcome by using nonstationary methods (35,47–50), and future work remains to be done in this area.
Despite this limitation, the iAMM approach can still be used to gain qualitative insights and to test the algorithm against what is previously known about the BK channel. In order to visualize the results, we cast the inferred state topology into a canonical form that is representative of, and unique to, a particular equivalence class. Several such canonical forms have been proposed including uncoupled form (35), manifest interconductance rank form (51), reduced dimensions form (52), and maximum entropy form (53). Because we are using canonical forms solely for visualization, and not to estimate the resulting transition rates, we use the Kienker uncoupled form due to its simplicity. Here, the connectivity is shown in the simplest form where none of the states of the same aggregate are connected to each other. That is, open states are only connected to closed states and closed states are only connected to open states.
Fig. 6 shows the result of using the iAMM to analyze several BK recordings at 6 μM and 110 μM calcium. The data visualized here represents a small fraction of the full trace used for model inference, which was 1 s of data (105 samples) in each case. At left, the data traces are shown with data points colored corresponding to the hidden state from which they are likely drawn. In the middle column, the model inferred from each trace is shown in Kienker uncoupled form. Again, while the state topology shown here is but one of many that could explain the data with high posterior probability, the visualization is used here to convey the general complexity of the gating mechanism that generated each trace. At right, the posterior distribution over the number of hidden states is shown. At very low holding voltages, open probability is very low, but also the available state space explored by the channel is quite simple, with one open state and a fast and a slow closed state.
Figure 6.
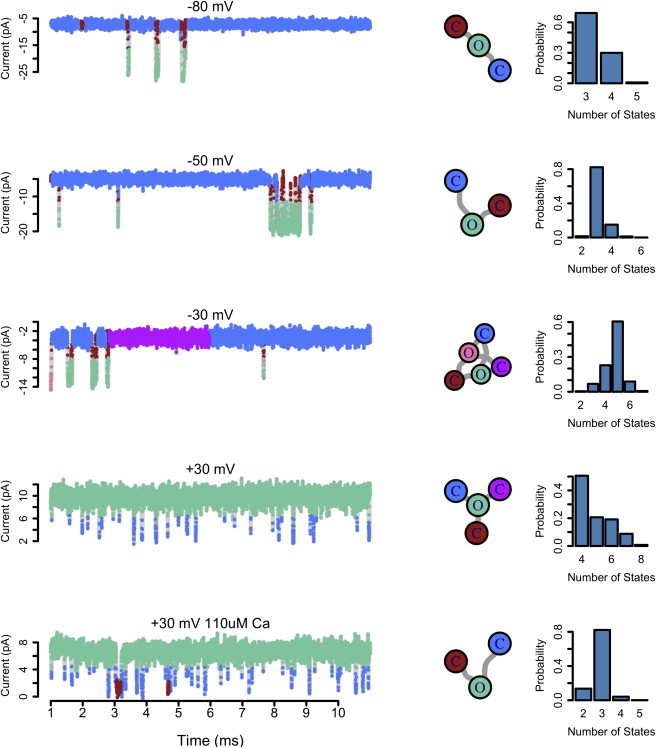
Recordings from a BK channel at multiple holding voltages and calcium concentrations analyzed using the sticky-iAMM. (Left) Data points are colored corresponding to the hidden state from which they were drawn in the inferred model. (Middle) The inferred model for each trace, visualized in Kienker uncoupled form. (Right) The posterior distribution over the number of hidden states for each trace. Algorithm parameters: α = 1, γ = 1, and κ = 100.
As the holding voltage is increased, not only does open probability increase, but also we detect the presence of more open and closed states. The increase in voltage affects channel function not only by shifting the open probability, but also by allowing the channel to access a more complex state space. As holding voltage is increased further, and open probability begins to saturate at a high value, the complexity of channel gating decreases as the channel accesses fewer conformational states. The last trace in Fig. 6 is at +30 mV and 110 μM calcium, which is in an extreme corner of BK’s activation range. The open probability is very high, and in this extreme range the complexity is decreased, because the channel mostly occupies a single open state with infrequent sojourns to just two closed states. In each trace, we see that the channel accesses a subset of a master state space. Consistent with what is known about the BK channel (39,45,54), we see that in the extreme ranges of voltage and calcium, characterized by either very high or very low open probability, the channel gating landscape is the least complex. Conversely, in the middle of the activation range, the gating scheme is most complex, with the channel accessing a diversity of open and closed states. Using a nonparametric Bayesian approach, we were able to recover this fundamental principle of channel gating, by discovering structure hidden within these time series.
Discussion
The study of protein biophysics has been greatly aided by the emergence of single-molecule experimental techniques, but developing rigorous and general tools for the analysis of such data remains an open challenge. We have described the use of nonparametric Bayesian inference, a powerful paradigm that has gained recent popularity in the statistics and machine learning communities, and which has been applied successfully for many difficult problems in science and engineering. These tools allow us to side-step the problems of model selection and user bias and instead allow us to discover significant structure in data, instead of assuming it beforehand. This framework was demonstrated with diverse settings in single-molecule biophysics, with models including nonparametric mixture models, hidden Markov models, and aggregated Markov models and data sets including single channel electrophysiology, single-molecule FRET, and single-molecule photobleaching. This paradigm provides a powerful basis to enhance the study of protein biophysics.
An important factor to consider with the methods proposed here is that of computation time. In general, Bayesian methods that employ MCMC require considerable computation because the sampling is designed to thoroughly explore posterior distributions. However, it is important to note that the Dirichlet process models described here do not incur additional computational complexity as compared to any Gibbs sampling approach for a finite model. Thus, the advances afforded by using nonparametric Bayes come at negligible additional computational cost relative to a more familiar Bayesian model. The computational complexity, then, is simply that of a typical Gibbs sampler for each of the use cases we describe. For a model with N data points and K hidden states, each Gibbs sampling iteration for the mixture model and the hidden Markov models has complexity (NK2).
As a benchmark, we describe the computation time required for the examples we have explored (with a 2 GHz Intel i7 processor (Mountain View, CA)). The mixture models with small datasets (such as Fig. 1) can be computed in <1 s. With the single channel dwell times (Fig. 3), we observed on the order of thousands of events, which could be computed in tens of minutes. The iHMM examples shown in Fig. 4 each consisted of a very short time series, and took on the order of minutes to compute. The single channel traces for the iAMM were quite long, on the order of 106 data points, and computation time was ∼10 h for each trace. These examples were executed with nonoptimized code written in high level languages (R and MATLAB) and computation speed will be improved considerably over time. Additionally, variational Bayes methods (55) and online methods (56) can be used to mitigate computation time with large datasets.
We demonstrated a basic use of nonparametric Bayesian inference by using a Dirichlet process mixture model to analyze dwell-times from single ion channel recordings. Using this infinite mixture model, it is possible to discover how many hidden clusters lay within the data and in this way, the number of hidden states could be learned, instead of assumed. For the case of ion channel dwell-times, much emphasis has been placed on optimal methods for analyzing such data (6,7,35,41,43). Recently, Landowne et al. (44) described a method to fit dwell-time data without knowing the number of components. This is similar in goal to the infinite mixture model described here. Their approach, grossly paraphrased, consists of beginning with a number of components that are very large (they used 20); iteratively using maximum likelihood to optimize the timescale and weight parameters of each component; removing clusters that are deemed to be too similar in timescale (they chose 2%) or too small in weight (they chose 10−5); and continuing this process of removing clusters until the log-likelihood is no longer improved. They demonstrate that their approach works very well to correctly identify the number of components in simulated data as well as BK channel data. Their approach, while convincingly demonstrated and validated, is not based on a rigorously defined mixture model, but instead consists of iterative hypothesis testing, ad hoc thresholds, and parameter optimization until the fit to data no longer improves.
In contrast to this, the Dirichlet process mixture model is rigorously defined over an infinite set of mixture components, and has well-studied properties that guarantee a clustering of the data. With ion channel data, a small number of distinct clusters are detected with high posterior probability. By sampling the space of all mixture models, we calculate the posterior distribution over the number of clusters in the data and can quantify our confidence in an interpretation of the data. Further, by sampling the full posterior (as opposed to simply seeking a maximum likelihood estimate), we can address parameter nonidentifiability, a pitfall that is sure to be problematic for exponential mixtures and small sample sizes.
In addition to channel data, Landowne et al. (44) test out their methods with classic datasets that have been deemed to be extremely challenging. They show that their method does very well in all cases to correctly detect the number of components. For comparison and validation, Fig. 7 shows the result of using an infinite mixture model to analyze each of these data sets. “Boliden 3” corresponds to a mixture of four exponentials where each component has higher timescale parameter and larger weight. “Boliden 4” is a mixture of four exponentials where one of the components has smaller weight than the adjacent components. Fig. 7 shows the result of using the infinite mixture model to analyze N = 10,000 data points drawn from each mixture, using the parameter values reported in Tables 2 and 3 of Landowne et al. (44).
Figure 7.
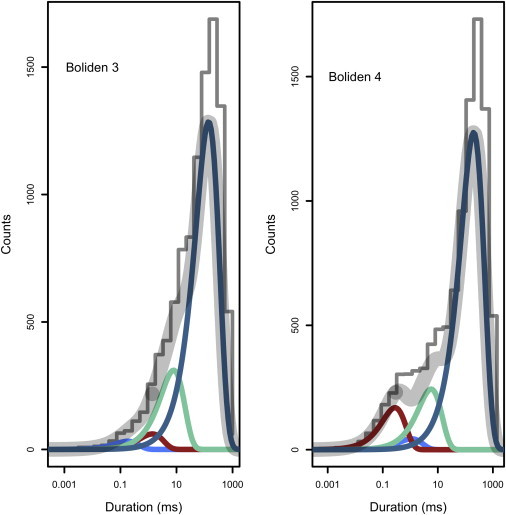
Demonstration of the infinite exponential mixture model with data sets discussed in Landowne et al. (44). “Boliden 3” corresponds to a mixture of four exponentials where each component has a higher timescale parameter and larger weight. “Boliden 4” is a mixture of four exponentials where one of the components has smaller weight than the adjacent components. Using the parameter values reported in Landowne et al. (44), 104 data points are drawn from each mixture and analyzed using the infinite model. We are able to correctly recover the number of components and the relevant parameters. Algorithm parameters: α = 1.
It is clear that we infer, with high posterior probability, the correct number of components in each case. A more direct comparison of the parameters inferred by the two methods is shown in Fig. S4. Importantly, we can detect the presence of these components using only 104 data points, which is a 1000-fold smaller sample size than the 107 samples used in Landowne et al. (44). Although it is clear that the approach of Landowne et al. (44) works very well with large datasets (and is almost certainly faster than an MCMC-based approach), they discuss the limitations of their hypothesis-testing based approach when faced with inadequate sample size. In this small-sample regime, the Bayesian approach presented here will be better able to detect significant components in the data.
A generalization of mixture models might be one where we do not assume each datapoint is drawn independently from the underlying distributions, but instead we assume there is dependency between successive data points which is governed by some Markov process. Such a hidden Markov model has been a popular tool for modeling time series from ion channels and single-molecule FRET (5,57,58), especially with recent Bayesian methods (14,34,59,60). We showed how the nonparametric Bayesian extension, the hierarchical Dirichlet process hidden Markov model, can be successfully applied to a single-molecule time series. Using an iHMM to analyze multichannel patch recordings allows us to estimate the number of channels and open probability in noisy electrophysiological data.
Additionally, we used the same model to analyze data from the increasingly popular method of single-molecule FRET. In this case, we are interested in detecting distinct conformational states, as manifest in the noisy FRET efficiency signal. We can use the iHMM to analyze these traces in a typical hidden Markov approach, but without assuming the number of distinct states or their properties. Finally, we showed that single-molecule photobleaching traces can be analyzed with the iHMM in order to detect bleaching steps. Especially in cases of poor signal/noise, the iHMM provides a principled method to analyze such data. Generally, using the infinite hidden Markov model provides a rigorous and unbiased method to interpret stochastic single-molecule time series.
We showed that a special case of the iHMM, the infinite aggregated Markov model, could be used to analyze single ion channel recordings in order to detect the existence of hidden conformational states. We showed that this approach can be used to infer the presence of distinct open and closed states that differ only in their dynamics. Further, when this approach is applied to BK channel recordings at multiple calcium concentrations and holding voltages, the inferred gating schemes recapitulate basic principles regarding the complexity of BK channel gating. However, with the equilibrium single channel traces, we are still limited by nonidentifiability and cannot infer a unique and reliable estimate of the connectivity between these hidden states. Previous authors have shown the benefits of globally analyzing large data sets in aggregate or of incorporating nonstationary stimulus protocols (35,40,47–50). We suspect that such a strategy, coupled with an iAMM approach, may help considerably to overcome the barrier of nonidentifiability and be able to extract accurate and reliable models of ion channel gating from single-molecule recordings. Future work remains to be done in this area.
Acknowledgments
The authors thank Christy Landes and David Cooper for contributing the single-molecule FRET data, and Peter Müller and Jonathan Pillow for helpful discussions.
This work was supported by National Institutes of Health grant No. R01-NS077821 to R.W.A.; K.E.H. is supported by a predoctoral fellowship from the American Heart Association.
Supporting Material
References
- 1.Hamill O.P., Marty A., Sigworth F.J. Improved patch-clamp techniques for high-resolution current recording from cells and cell-free membrane patches. Pflugers Arch. 1981;391:85–100. doi: 10.1007/BF00656997. [DOI] [PubMed] [Google Scholar]
- 2.Weiss S. Measuring conformational dynamics of biomolecules by single molecule fluorescence spectroscopy. Nat. Struct. Biol. 2000;7:724–729. doi: 10.1038/78941. [DOI] [PubMed] [Google Scholar]
- 3.Svoboda K., Schmidt C.F., Block S.M. Direct observation of kinesin stepping by optical trapping interferometry. Nature. 1993;365:721–727. doi: 10.1038/365721a0. [DOI] [PubMed] [Google Scholar]
- 4.Rabiner L. A tutorial on hidden Markov models and select applications in speech recognition. Proc. IEEE. 1989;77:257–286. [Google Scholar]
- 5.Qin F., Auerbach A., Sachs F. Maximum likelihood estimation of aggregated Markov processes. Proc. Biol. Sci. 1997;264:375–383. doi: 10.1098/rspb.1997.0054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Colquhoun D., Hawkes A.G. On the stochastic properties of single ion channels. Proc. R. Soc. Lond. B Biol. Sci. 1981;211:205–235. doi: 10.1098/rspb.1981.0003. [DOI] [PubMed] [Google Scholar]
- 7.Horn R., Lange K. Estimating kinetic constants from single channel data. Biophys. J. 1983;43:207–223. doi: 10.1016/S0006-3495(83)84341-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Horn R. Statistical methods for model discrimination. Applications to gating kinetics and permeation of the acetylcholine receptor channel. Biophys. J. 1987;51:255–263. doi: 10.1016/S0006-3495(87)83331-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ball F.G., Sansom M.S. Ion-channel gating mechanisms: model identification and parameter estimation from single channel recordings. Proc. R. Soc. Lond. B Biol. Sci. 1989;236:385–416. doi: 10.1098/rspb.1989.0029. [DOI] [PubMed] [Google Scholar]
- 10.Liebovitch L.S., Tóth T.I. The Akaike information criterion (AIC) is not a sufficient condition to determine the number of ion channel states from single channel recordings. Synapse. 1990;5:134–138. doi: 10.1002/syn.890050207. [DOI] [PubMed] [Google Scholar]
- 11.Wagner M., Timmer J. Model selection in non-nested hidden Markov models for ion channel gating. J. Theor. Biol. 2001;208:439–450. doi: 10.1006/jtbi.2000.2230. [DOI] [PubMed] [Google Scholar]
- 12.Csanády L. Statistical evaluation of ion-channel gating models based on distributions of log-likelihood ratios. Biophys. J. 2006;90:3523–3545. doi: 10.1529/biophysj.105.075135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Siekmann I., Sneyd J., Crampin E.J. MCMC can detect nonidentifiable models. Biophys. J. 2012;103:2275–2286. doi: 10.1016/j.bpj.2012.10.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Calderhead B., Epstein M., Girolami M. Bayesian approaches for mechanistic ion channel gating. In: Schneider M., editor. In Silico Systems Biology. Springer; New York: 2013. [DOI] [PubMed] [Google Scholar]
- 15.Hines K.E., Middendorf T.R., Aldrich R.W. Determination of parameter identifiability in nonlinear biophysical models: a Bayesian approach. J. Gen. Physiol. 2014;143:401–416. doi: 10.1085/jgp.201311116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Blei D., Griffiths T., Tennenbaum J. Hierarchical topic models and the nested Chinese restaurant process. Adv. Neural Inf. Process. Syst. 2004;16:17–24. [Google Scholar]
- 17.Fox E., Sudderth E., Willsky A. A sticky HDP-HMM with application to speaker diarization. Ann. Appl. Stat. 2011;5:1020–1056. [Google Scholar]
- 18.Kivinen J., Sudderth E., Jordan M. IEEE Conference on Computer Vision. Institute of Electrical and Electronics Engineers (IEEE); New York: 2007. Learning multiscale representations of natural sciences using Dirichlet processes; pp. 1–8. [Google Scholar]
- 19.Ramaswamy S., Cooper D., Jayaraman V. Role of conformational dynamics in α-amino-3-hydroxy-5-methylisoxazole-4-propionic acid (AMPA) receptor partial agonism. J. Biol. Chem. 2012;287:43557–43564. doi: 10.1074/jbc.M112.371815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bankston J.R., Camp S.S., Zagotta W.N. Structure and stoichiometry of an accessory subunit TRIP8b interaction with hyperpolarization-activated cyclic nucleotide-gated channels. Proc. Natl. Acad. Sci. USA. 2012;109:7899–7904. doi: 10.1073/pnas.1201997109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.van Gael J., Saatci Y., Ghahramani Z. Proceedings of the 25th International Conference on Machine Learning. Association for Computing Machinery (ACM); New York: 2008. Beam sampling for the infinite hidden Markov model; pp. 1088–1095. [Google Scholar]
- 22.Hjort N., Holmes C., Walker S. Cambridge University Press; New York: 2010. Bayesian Nonparametrics. [Google Scholar]
- 23.Mueller P., Rodriguez A. Vol. 9. Institute of Mathematical Statistics; Beachwood, OH: 2012. Nonparametric Bayesian Inference. (Institute of Mathematical Statistics Monograph Series). [Google Scholar]
- 24.Ferguson T. A Bayesian analysis of some nonparametric problems. Ann. Stat. 1973;1:209–230. [Google Scholar]
- 25.Sethuraman J. A constructive definition of Dirichlet process priors. Stat. Sin. 1994;4:639–650. [Google Scholar]
- 26.Pitman J. Poisson-Dirichlet and GEM invariant distributions for split-and-merge transformations of an interval partition. Combin. Probab. Comput. 2002;11:501–514. [Google Scholar]
- 27.Lo A. On a class of Bayesian nonparametric estimates. I: Density estimates. Ann. Stat. 1984;12:351–357. [Google Scholar]
- 28.Hines, K. E. A primer on Bayesian inference for biophysical systems. Biophys. J. In review. [DOI] [PMC free article] [PubMed]
- 29.Walker S. Sampling the Dirichlet mixture model with slices. Simul. Comput. 2007;36:45–54. [Google Scholar]
- 30.Beal M., Ghahramani Z., Rasmussen C. The infinite hidden Markov model. Adv. Neural Inf. Process. Syst. 2002;14:577–584. [Google Scholar]
- 31.Teh Y., Jordan M., Blei D. Hierarchical Dirichlet processes. J. Am. Stat. Assoc. 2006;101:1566–1581. [Google Scholar]
- 32.Fox E., Sudderth E., Willsky A. Proceedings of the 25th International Conference on Machine Learning. Association for Computing Machinery (ACM); New York: 2008. An HDP-HMM for systems with state persistence. [Google Scholar]
- 33.Scott S. Bayesian methods for hidden Markov models: recursive computing in the 21st century. J. Am. Stat. Assoc. 2002;97:337–351. [Google Scholar]
- 34.Rosales R.A. MCMC for hidden Markov models incorporating aggregation of states and filtering. Bull. Math. Biol. 2004;66:1173–1199. doi: 10.1016/j.bulm.2003.12.001. [DOI] [PubMed] [Google Scholar]
- 35.Kienker P. Equivalence of aggregated Markov models of ion-channel gating. Proc. R. Soc. Lond. B Biol. Sci. 1989;236:269–309. doi: 10.1098/rspb.1989.0024. [DOI] [PubMed] [Google Scholar]
- 36.Escobar M., West M. Bayesian density estimation and inference using mixtures. J. Am. Stat. Assoc. 1995;90:577–588. [Google Scholar]
- 37.Cox D.H., Cui J., Aldrich R.W. Allosteric gating of a large conductance Ca-activated K+ channel. J. Gen. Physiol. 1997;110:257–281. doi: 10.1085/jgp.110.3.257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Rothberg B.S., Magleby K.L. Voltage and Ca2+ activation of single large-conductance Ca2+-activated K+ channels described by a two-tiered allosteric gating mechanism. J. Gen. Physiol. 2000;116:75–99. doi: 10.1085/jgp.116.1.75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Horrigan F.T., Aldrich R.W. Coupling between voltage sensor activation, Ca2+ binding and channel opening in large conductance (BK) potassium channels. J. Gen. Physiol. 2002;120:267–305. doi: 10.1085/jgp.20028605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Rosales R.A., Varanda W.A. Allosteric control of gating mechanisms revisited: the large conductance Ca2+-activated K+ channel. Biophys. J. 2009;96:3987–3996. doi: 10.1016/j.bpj.2009.02.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Colquhoun D., Sigworth F. Fitting and analysis of single-channel records. In: Sakmann B., Neher E., editors. Single Channel Recording. Plenum Press; New York: 1983. [Google Scholar]
- 42.Siekmann I., Wagner L.E., 2nd, Sneyd J. MCMC estimation of Markov models for ion channels. Biophys. J. 2011;100:1919–1929. doi: 10.1016/j.bpj.2011.02.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Sigworth F.J., Sine S.M. Data transformations for improved display and fitting of single-channel dwell time histograms. Biophys. J. 1987;52:1047–1054. doi: 10.1016/S0006-3495(87)83298-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Landowne D., Yuan B., Magleby K.L. Exponential sum-fitting of dwell-time distributions without specifying starting parameters. Biophys. J. 2013;104:2383–2391. doi: 10.1016/j.bpj.2013.04.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Talukder G., Aldrich R.W. Complex voltage-dependent behavior of single unliganded calcium-sensitive potassium channels. Biophys. J. 2000;78:761–772. doi: 10.1016/S0006-3495(00)76634-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.van de Meent J., Bronson J., Wiggins C. Hierarchically-coupled hidden Markov models for learning kinetic rates from single molecule data. J. Mach. Learn. Res. 2013;28:361–369. [PMC free article] [PubMed] [Google Scholar]
- 47.Sigworth F.J. Covariance of nonstationary sodium current fluctuations at the node of Ranvier. Biophys. J. 1981;34:111–133. doi: 10.1016/S0006-3495(81)84840-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Conti F., Hille B., Nonner W. Non-stationary fluctuations of the potassium conductance at the node of Ranvier of the frog. J. Physiol. 1984;353:199–230. doi: 10.1113/jphysiol.1984.sp015332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Millonas M.M., Hanck D.A. Nonequilibrium response spectroscopy of voltage-sensitive ion channel gating. Biophys. J. 1998;74:210–229. doi: 10.1016/S0006-3495(98)77781-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Milescu L.S., Akk G., Sachs F. Maximum likelihood estimation of ion channel kinetics from macroscopic currents. Biophys. J. 2005;88:2494–2515. doi: 10.1529/biophysj.104.053256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Bruno W.J., Yang J., Pearson J.E. Using independent open-to-closed transitions to simplify aggregated Markov models of ion channel gating kinetics. Proc. Natl. Acad. Sci. USA. 2005;102:6326–6331. doi: 10.1073/pnas.0409110102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Flomenbom O., Silbey R.J. Utilizing the information content in two-state trajectories. Proc. Natl. Acad. Sci. USA. 2006;103:10907–10910. doi: 10.1073/pnas.0604546103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Li C., Komatsuzaki T. Aggregated Markov models using time series of single molecule dwell times with minimum excessive information. Phys. Rev. Lett. 2013;111:1–5. doi: 10.1103/PhysRevLett.111.058301. [DOI] [PubMed] [Google Scholar]
- 54.Rotherberg T. Identification in parametric models. Econometrica. 1971;39:577–591. [Google Scholar]
- 55.Blei D., Jordan M. Proceedings of the 21st International Conference on Machine Learning. Springer; New York: 2004. Variational methods for the Dirichlet process. [Google Scholar]
- 56.Wang, C., J. Paisley, and D. Blei. 2011. Online variational inference for the hierarchical Dirichlet process. In Proceedings of the 14th International Conference on Artificial Intelligence and Statistics. 752–760. http://machinelearning.wustl.edu/mlpapers/papers/AISTATS2011_WangPB11.
- 57.Andrec M., Levy R.M., Talaga D.S. Direct determination of kinetic rates from single-molecule photon arrival trajectories using hidden Markov models. J. Phys. Chem. A. 2003;107:7454–7464. doi: 10.1021/jp035514+. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.McKinney S.A., Joo C., Ha T. Analysis of single-molecule FRET trajectories using hidden Markov modeling. Biophys. J. 2006;91:1941–1951. doi: 10.1529/biophysj.106.082487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Bronson J.E., Fei J., Wiggins C.H. Learning rates and states from biophysical time series: a Bayesian approach to model selection and single-molecule FRET data. Biophys. J. 2009;97:3196–3205. doi: 10.1016/j.bpj.2009.09.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Taylor J.N., Makarov D.E., Landes C.F. Denoising single-molecule FRET trajectories with wavelets and Bayesian inference. Biophys. J. 2010;98:164–173. doi: 10.1016/j.bpj.2009.09.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


