Self-Calibrated Line-Scan STED-FCS to Quantify Lipid Dynamics in Model and Cell Membranes

Abstract

Only a limited number of noninvasive techniques are available to directly measure the dynamic behavior of lipids in model and cell membranes. Here, we explored whether a commercial instrument could be used for fluorescence correlation spectroscopy (FCS) under pulsed stimulated emission depletion (STED). To overcome issues with photobleaching and poor distinction between confocal and STED signals, we implemented resonant line-scan STED with filtered FCS, which has the additional benefit of autocalibrating the dimensions of the point-spread function and obtaining spatially resolved molecular mobility at subdiffraction resolution. With supported lipid bilayers, we achieved a detection spot radius of 40 nm, although at the expense of decreased molecular brightness. We also used this approach to map the dynamics of Atto646N-labeled sphingomyelin and phosphatidylethanolamine in the plasma membrane. Despite the reliability of the method and the demonstration that photobleaching and the photophysical properties of the dye did not influence diffusion measurements, we found great heterogeneities even within one cell. For both lipids, regions of high local density correlated with slow molecular diffusion, indicating trapping of Atto646N-labeled lipids. Future studies with new dyes are needed to reveal the origin of the trapping.

Introduction

Various concepts of membrane organization, such as the lipid raft hypothesis, have elevated lipids from simple membrane building blocks to regulatory elements (1). It is certainly now appreciated that lipids in biological bilayers can actively contribute to domain formation and membrane compartmentalization (2). However, the tools and techniques for studying lipid domains and the dynamic behavior of lipids in native cell membranes are still in their infancy and consequently relatively little is known about the size, geometry, diversity, and assembly/disassembly rates of lipid domains and complexes, and the ability of these entities to attract and retain other membrane proteins. The limited number of techniques that can be applied equally to model and cell membranes has made it exceedingly difficult to identify which physical mechanisms observed in model membranes are dominant in cell membranes, and how the diversity of cellular lipids preconditions membranes for specific biophysical processes. Often lipid manipulations such as cholesterol depletion are used to infer a role for lipids in distinct biological functions, but in complex membranes, interpretation of the data is often not straightforward (3). Alternatively, the distribution and dynamics of membrane proteins are interpreted as evidence of an underlying lipid organization (4). Thus, it is not surprising that many membrane models still await direct and vigorous testing.

In our opinion, there are two breakthrough technologies that have provided direct insights into the dynamics of single lipids in the plasma membrane of live, unfixed cells. Both employ fluorescent lipid analogs and require a highly sophisticated imaging setup, so experiments involving these approaches have rarely been repeated and expanded to an extended range of lipids. These two technologies are 1) single-molecule tracking at extremely high acquisition speeds to identify lipid hop diffusion (5), in support of the picket-fence membrane model proposed by Kusumi et al. (6); and 2) stimulated emission depletion combined with fluorescence correlation spectroscopy (STED-FCS) (7), in which the reduction of the FCS excitation spot can be used to apply the FCS law (8) and reveal the differential trapping of sphingomyelin (SM) over phosphatidylethanolamine (PE) in cholesterol-dependent domains.

Given that STED instruments are now commercially available, we investigated whether we could implement the STED-FCS technique in such a fashion as to obtain robust and reproducible results regarding lipid diffusion in model and cell membranes. In STED, so-called fluorescence superresolution is achieved by overlaying the excitation beam of a conventional confocal laser scanning microscope with a second laser beam, which reversibly switches off the fluorescence emission in the outer regions of the diffraction-limited focal spot of the excitation laser, thereby reducing the point-spread function (PSF) and vastly improving the spatial resolution (9). In utilizing STED for lipid measurements, we were particularly concerned about the photobleaching effect of the powerful STED laser, since these experiments need to be conducted in live, unfixed cells. In addition, since depletion by the STED laser may not result in 100% suppression of fluorescence, the overall emitted light from the sample may be the sum of the fluorescence from the center of the STED doughnut (the superresolution fluorescence that we refer to here as the central spot emission) and the incompletely suppressed fluorescence from the doughnut region of the STED beam (referred to here as the ring emission) (10), decreasing the achievable spatial resolution.

To date, improved lateral resolution by STED has mainly been used in point-acquisition STED-FCS studies (11,12), for STED raster image correlation spectroscopy (STED-RICS) (13), and more recently for pair-correlation analysis (14). By reducing the free diffusion time across the detection spot, the smaller detection spot offered by STED improves the observation window of transient molecular immobilization toward the millisecond timescale, provided the precision and accuracy of the STED-FCS acquisition are sufficiently high. It is well described that point confocal FCS acquisitions require precise calibration of the detection volume (15) and precise z positioning when the lateral diffusion of lipids in membranes is measured (16). Several solutions for the spot size calibration problem have been implemented (16,17). The most practical solution for lateral diffusion measurements is to use scanning FCS (18), particularly line-scan FCS (LS-FCS) (19), which is compatible with commercial instruments. Moreover fast scanning inherently reduces photobleaching of the dye because it reduces the probability of excitation from the triplet state into higher-energy states (20).

Background signals, such as scattered light, detector afterpulsing, and thermal noise, can corrupt the amplitude and shape of autocorrelation functions, leading to errors in the quantification of dye concentrations and time constants of fast dynamics (21). An elegant way to remove the unwanted contributions to the FCS curves is to filter out the background signal based on the time response after pulsed excitation. Enderlein and Gregor (21) showed that photon filtering (weighting) based on the nanosecond time patterns of the fluorescent and background signals can efficiently remove the detector afterpulsing contribution to correlation curves. Štefl et al. (22) demonstrated that photon filtering can be used to extract correlation curves for particular regions of the confocal detection volume, provided the nanosecond time patterns differ at different locations of the confocal volume.

Inspired by solutions developed for traditional confocal FCS, we implemented a fast resonant line scanning and fluorescence filtering approach to overcome the calibration, photobleaching, and background issues encountered with STED-FCS. By calculating spatiotemporal correlations using a newly developed fast correlation algorithm, we can obtain the exact PSF dimension so that the diffusion measurements become autocalibrated and parameters such as fluorophore concentrations, brightness, and diffusion coefficients can be plotted relative to the measured excitation spot area. The fluorescence filtering removes the background signals, which improves the achievable resolution. Additionally, spatially resolved molecular diffusion data are obtained along the scanned line. We applied STED-LS-FCS measurements to DOPE-Atto647N and SM-Atto647N in Cos7 cells and found great heterogeneities even within one cell, where the local concentration of the fluorophores correlated inversely with the diffusion coefficient for both lipids. This meant that fitting of spatiotemporal correlation functions would require one to detect subtle differences between PE and SM dynamics. Hence, we explored other, diffusion-model-free analyses of the same spatiotemporal correlation data, such as image mean-square displacement (iMSD), that might be useful for bridging the data obtained by FCS and single-particle tracking (23).

Theory

A detailed Theory section is provided in the Supporting Material.

Materials and Methods

Fluorescent lipid analogs

1,2-Dioleoyl-sn-glycero-3-phosphocholine (DOPC) was purchased from Avanti Polar Lipids (Alabaster, AL). DOPE-Atto647N was obtained from ATTO-TEC (Siegen, Germany). Oregon Green 488 DHPE was obtained from Life Technologies. SM-Atto647N was a kind gift from Christian Eggeling, University of Oxford.

Supported lipid bilayers

First, we prepared a 1 mM mixture of DOPC with DOPE-Atto647N, with a ratio of fluorescent dye to lipids of 1:100,000. The organic solvent was evaporated under a stream of nitrogen and the resulting thin lipid film was kept for 2 h under vacuum. The dried lipid film was subsequently hydrated with 10 mM HEPES buffer (150 mM NaCl, pH 7.4) and the solution was extensively vortexed for at least 2 min until multilamellar vesicles were formed. Next, the cloudy solution was extruded by 21 passages through a membrane with a 100 nm pore size (Avanti Polar Lipids), yielding a suspension of large unilamellar vesicles (LUVs). The LUV suspension was diluted in Ca²⁺-containing buffer (10 mM HEPES, 150 mM NaCl, 1 mM CaCl₂, pH 7.4) and incubated on glass surfaces for 30 min. Glass coverslips were used both without and with cleaning (a 20 min exposure to 1 mM NaOH in a sonication bath). Supported lipid bilayers (SLBs) were rinsed to remove excess lipid vesicles and used immediately.

Cell experiments

Cos-7 cells were cultured in high-glucose Dulbecco’s modified Eagle’s medium (DMEM; Invitrogen) supplemented with 10% fetal calf serum. Cells were plated into a 35 mm glass-bottom culture dish (Proscitech) 24 h before experiments were conducted.

To label cells with fluorescent lipid analogs, 100 nmol of DOPE-Atto647N or SM-Atto647N in chloroform was dried under a nitrogen stream and redissolved in 20 μl of absolute ethanol by vigorous vortexing. The lipids were diluted to 100 μM with 100 μM defatted bovine serum albumin (BSA; Sigma Aldrich, Australia). The defatted BSA solution was prepared in phenol red-free, 10 mM HEPES-buffered DMEM (Life Technologies, Australia). Cultured cells were washed with ice-cold HEPES-buffered DMEM three times before addition of 50 μM of a lipid-BSA complex solution. Cells were incubated with the lipid-BSA mixture for 30 min and unbound lipids were removed by washing the cells with HEPES-buffered DMEM three times. Finally, the cells were imaged in HEPES-buffered DMEM containing 10% fetal calf serum.

STED-FCS hardware setup

For STED-LS-FCS acquisitions, a commercial Leica SP5 microscope with a near-infrared pulsed STED module and an 8 kHz resonant scanner was used. The excitation sources were pulsed diode lasers (LDH-P-635 and LDH-P-FA-530B) driven by a PDL 800-B (all from PicoQuant, Germany), and the depletion beam was provided by a wavelength-tunable Ti-Sapphire laser (Mai Tai; Spectra Physics). The excitation power varied from 5 to 20 μW and the maximum depletion power was 100 mW for a 750 nm wavelength at the objective back aperture at a frequency of 80 MHz. We mostly used 750 nm rather than 780 nm depletion because it was more than twice as efficient in depleting fluorescence, albeit at the expense of a 10-fold higher anti-Stokes excitation background, which was limited by the available depletion laser power. When a higher signal/noise ratio (SNR) was preferred over the improved resolution, we used depletion at 780 nm. There was no difference in diffusion-related parameters between the data obtained with either depletion wavelength. Synchronization of the excitation and depletion pulses was realized by means of a software-adjustable delay box (Leica). Minor modifications to the excitation path were needed, including insertion of a laser cleanup filter HQ640/10 (Chroma) to suppress the laser diode background, and installation of a motorized microscrew-based control of the excitation intensity (Schaefter and Kirchhoff, Germany) to change the excitation intensity without modifying the excitation pulse time profile. A STED-optimized 100× oil immersion objective with NA 1.4 and 1 Airy unit pinhole size was used. Emitted fluorescence passed an internal 700 nm short-pass filter and an external 680/40 bandpass filter (Chroma), coupled through an optical fiber to a MicroTime200 main optical unit (PicoQuant) containing SPAD detectors (τ-SPAD [PicoQuant, Germany] or PDM [Micro Photon Devices, Italy]). Single photon detection events were saved in a time-tagged time-resolved (TTTR) format with a photon-counting module (PicoHarp300; PicoQuant). In the TTTR data, each photon was encoded by its arrival time after the start of the acquisition, its arrival time after a laser excitation pulse, and its detector number. Additionally, line start markers provided by the Leica trigger box were inserted into the TTTR file for image or LS reconstruction.

After we found the region of interest with xy scans, we increased the zoom to a line length of 5.15 μm (80% of amplitude). Next, we initiated continuous bidirectional confocal xt scanning with minimized page breaks and optimized the z position by minimizing the apparent PSF width, which corresponds to placing the membrane properly into the focused beam waist. After this membrane focusing procedure, we activated the STED laser and started the TTTR data acquisition. Usually, data acquisition took ∼1 min for one STED power setting. However, when we tried to reach the minimum spot size using the full laser power at 750 nm depletion (with reduced SNR), the data acquisition was extended up to 5 min.

STED-FCS software

Imaging and setup of the xt scans, including STED alignment, were done using standard LAS AF software. For single photon data acquisition in TTTR format, and for online visualization of temporal and spatial correlation functions and other LS-FCS output parameters, an acquisition program with a user interface was written in LabVIEW (NI). The program uses a dll library provided by PicoQuant to operate the PicoHarp300 photon-counting unit and a custom-written dll library for fast spatiotemporal correlations developed in C/C++ (MVS2010; Microsoft). The offline version of this software allows for batch correlations of LS-FCS data in various data formats, application of filtered FCS, correlation data fitting, and iMSD analysis.

Correlation function fitting

The fluorescence cross-correlation function g(t,δ) between two laterally displaced foci along the x axis by a distance δ is given by (6,24)

$$g\left(t,\delta \right)=g_{\infty }+{\epsilon }_1{\epsilon }_{2}c\int d{\mathit{r}}_1\int d{\mathit{r}}_{2}U\left({\mathit{r}}_2\right)p\left({\mathit{r}}_2-{\mathit{r}}_1-\mathit{x}\delta ,t\right)U\left({\mathit{r}}_1\right),$$ (1)

where g_∞ is the constant offset; ε is the factor that describe the overall excitation power and detection efficiency in the detection volume; c is the concentration of the molecules; U(r) is the molecule detection function (MDF), which gives the position-dependent probability of detecting a fluorescence photon from a molecule at position r (which is equal to the PSF if the molecule responds linearly to excitation intensity); and p(r₂ − r₁ − xδ,t) denotes the probability density that a molecule will move from position r₂ to position r₁ + xδ within time t.

Approximating the MDF by a two-dimensional (2D) Gaussian profile and assuming multiple components freely diffusing within the plane, the correlation function takes the form

$$g\left(t,\delta \right)=g_{\infty }+{\sum }_{i=1}^n{A}_i\frac{1}{4D_{i}t+{\omega }^2}{e}^{\left(\frac{-{\delta }^2}{4D_{i}t+{\omega }^2}\right)},$$ (2)

where n is the number of components, A is the amplitude, D is the diffusion coefficient, and ω is the 1/e² radius of the Gaussian beam profile. The full width at half-maximum (FWHM) parameter, which is often used to describe the lateral resolution, is equal to FWHM = 1.177 × ω. Since the time resolution of the LS is 63 μs and typical triplet relaxation times are on the microsecond timescale, we did not include a triplet term into our model.

If the diffusion is not Brownian, the probability density that a molecule will move from one position to another differs from Green’s function for the free diffusion. An example of how this probability density changes and a description of the correlation function when molecules are subject to transient binding at random locations are provided in Dertinger et al. (25).

To fit the intensity-normalized temporal autocorrelation function at different points along the scanned line, we used a simple model for one-component diffusion:

$$G\left(t\right)=G_{\infty }+\frac{1}{PN}\frac{1}{1+\frac{4Dt}{{\omega }^2}},$$ (3)

where G_∞ is the correlation function offset, PN is an average particle number in the detection spot, ω is the spot radius, and D is the diffusion coefficient. To estimate the average molecular transit time through the detection spot without any a priori assumption of the diffusion mode, we first fitted the spatial correlation at each lag time to a Gaussian profile to obtain the dependency of the amplitudes on the lag time. The curve was then smoothed with the cubic spline method, and an interpolated value at which the curve decayed to 50% of its zero lag time extrapolated value was read out.

We obtained iMSD plots by fitting a single Gaussian profile to spatial correlations at varying lag times, extrapolating the spot radius to the zero lag time, and subtracting the obtained initial radius from the radii at varying lag times.

Results and Discussion

One of the main limitations of quantitative STED measurements is that the PSF dimensions depend on the user-adjusted power of the STED laser and the efficiency of the depletion, which in turn depends on the fluorescent probe as well as on the sample and the focus z position relative to the membrane. To make STED-FCS measurements robust, one must avoid recording each data set with a different PSF and a different degree of suppression of the confocal signal. Hence, recording the STED resolution with a different sample (e.g., with fluorescent beads) is often not practical or reliable, and careful calibration curves need to be recorded (12). These are required because for many measurements, and particularly for the quantification of molecular dynamics and interactions, it is necessary to know the dimensions and localization of the PSF (11).

Here, we used LS-FCS (Fig. 1) to obtain the spatiotemporal correlation function with sufficient sampling, which enabled us to obtain the effective radius of PSF directly from the spatial correlation extrapolated to zero lag time without the need for external calibration. For LS-FCS acquisition of fluorescent lipids (here DOPE-Atto647N) in the plasma membrane, only cells with a sufficiently low labeling density are suitable for correlation analysis (<100 molecules per detection spot is optimal; Fig. 1 a). With the plasma membrane adherent to the glass coverslip in focus, we selected a region of interest and chose a line within the region (Fig. 1 b). We switched the acquisition mode to a continuous bidirectional LS, i.e., an xt scan, and visualized the LS as a kymograph (sometimes also called an intensity carpet; Fig. 1 c). The kymograph helped us check the quality of the acquired data. In principle, a kymograph acquired by any imaging format allows one to calculate the spatiotemporal correlation function (19).

Figure 1.

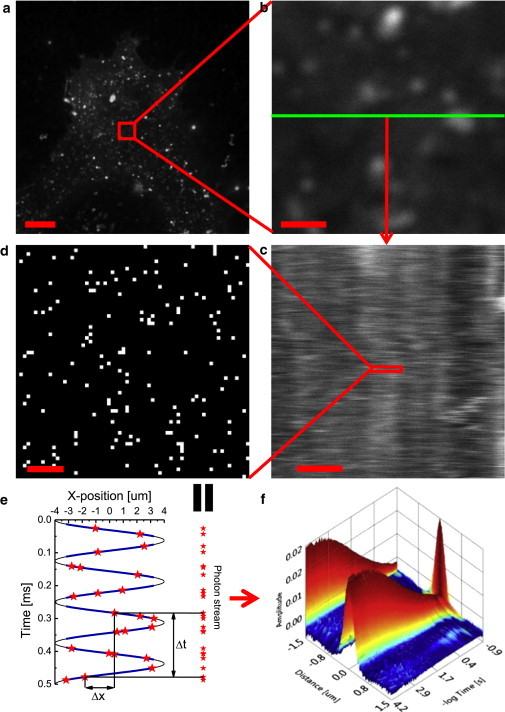
Principles of LS-FCS. (a and b) Intensity images of the plasma membrane adjacent to a glass coverslip in a COS7 cell labeled with DOPE-Atto647N (640 nm excitation at 5 μW). The scale bar represents 10 μm and 1 μm, respectively. (b) The highlighted region (red square in a, 5 μm × 5 μm) is used to select the position of the LS (green line). (c) Kymograph representing the time evolution of the fluorescence intensity along the scanned line. The scale bar represents 1 μm. A total of 2,170,000 lines were sampled for 137 s at 63 μs per line. At full resolution, each line consists of 2,852 nonequally spaced points. (d) A zoomed region of the kymograph reveals the scarcity of detected photons. The scale bar represents 100 nm. (e) Individual photons (stars) are recorded in a TTTR format and the arrival time of each photon is converted into its exact position along the scanned line (blue lines; the black line indicates movement of the scanner). The time and position differences, ∂t and ∂x, respectively, from which spatiotemporal correlation curves are calculated are shown for a selected pair of photons. (f) Spatiotemporal autocorrelation for DOPE-Atto647N in a COS7 cell from the image shown in (a) and (b) at confocal (i.e., diffraction-limited) resolution. The projections along the space and time axes are provided to highlight the shape of the autocorrelation function reflecting the time decay and PSF profile, respectively. To see this figure in color, go online.

The correlation function can be calculated by direct multiplication (19) or by a fast Fourier transform (FFT) (26). However, the size of the kymograph at full resolution made it difficult for us to obtain correlation functions from our data by FFT. A 1 min acquisition produces a kymograph of 512 × 960,000 points, which simply takes too long to be processed by FFT on a standard PC. Direct multiplication is also computationally demanding, but it allows for implementation of the multiple-tau algorithm combined with histogramming, similar to the point FCS correlation algorithm described by Felekyan et al. (27). Inspecting the single-line data in more detail revealed that most of the points of the full-resolution kymograph contained zero photons (Fig. 1 d). We therefore switched from image-like acquisition to a single-photon acquisition mode using a TTTR format (Fig. 1 e). In this mode, every detected photon was assigned a time (t) from the start of the acquisition in multiples of pulsed laser periods, a time (τ) from the excitation laser pulse with picosecond time resolution, and the detector number (d). We could recover the position of the scanner at the time of photon detection using inserted markers, which indicated the start of each scanned line. We then obtained the spatiotemporal correlation function by counting the number of occurrences for a given time (∂t) and position (∂x) difference (Fig. 1 f). Hence, this data acquisition format has the additional benefit that the exact position of each photon is known and no binning is required to generate the kymograph. The raw correlation histogram was subsequently corrected for nonlinear motion of the resonant scanner, uneven intensity distribution along the scanned line, and homogeneous photobleaching (Fig. S1). The approach was verified with simulations (Fig. S1), and imaging of nonmobile beads had no temporal or spatial correlations with this approach (Fig. S2). The correlation algorithm is not restricted to TTTR data and can also be used for fast correlation of xt scans exported as TIFF images (Fig. S3).

The spatial autocorrelation extrapolated to zero lag time corresponds to a convolution of the PSF with itself (shown as a projection along the time axis in Fig. 1 f). Approximating the PSF by a Gaussian, the convolution is also a Gaussian with the radius equal to the square root of two times the PSF radius (as can be seen from Eq. S15 for t = 0; see the Theory section in the Supporting Material). Hence, the correlation function directly gives us the effective PSF size without the need for additional calibration experiments. The correlation function at the zero distance is equal to the standard point FCS autocorrelation function (shown as a projection along the distance axis in Fig. 1 f and Eq. S15 for δ = 0).

Compared with point FCS acquisition, LS-FCS sacrifices superior time resolution for spatial resolution and averaging. Point FCS allows one to calculate the correlation function at the repetition frequency of the pulsed laser (or the time resolution of the acquisition board for continuous wave (CW) excitation), which was 12.5 ns here for pulsed Ti-Sa STED-FCS. The time resolution of LS-FCS is given by the frequency of the scanner, which was 63 μs for a 7.92 kHz bidirectional scan. The limitation of LS-FCS is that the average residence time of the diffusing molecule in the detection volume must be longer than this time resolution. The diffusion coefficient for lipid translational diffusion in cellular membranes is on the order of ≤2 μm²s⁻¹, which results in a correlation time of 5 ms for a diffraction-limited spot of 200 nm radius, and a correlation time of 200 μs for an STED spot of 40 nm radius. This means that LS-FCS at 7.92 kHz scan frequency and spot sizes down to 40 nm can be used to assess lipid diffusion in cells. An additional consideration is the SNR for correlation functions, which is given not only by the brightness of the molecules and the background signal but also by the number of events that caused the fluctuations of the fluorescence signal during the data acquisition. In the case of diffusion measurements, the event that causes fluctuations is the passage of a molecule through the detection spot. Although in general an LS and a point measurement acquire a similar amount of photons, by collecting the signal over larger area, the LS averages more molecular passages. The better averaging of the correlation function allows for shorter acquisition times, especially for slowly diffusing species.

The LS can be considered as a one-dimensional variant of RICS (28,29). In a standard RICS experiment, a series of xy images are taken and correlations between neighboring pixels within each image are calculated. The main difference between RICS and LS-FCS is the time and spatial sampling, and hence the resulting spatiotemporal correlation function. In a typical RICS experiment, the time sampling is limited to a couple of points at tens-of-microseconds timescales for neighboring pixel correlations, a couple of points at millisecond time resolution for neighboring lines correlations, and a couple of points at second time resolution for subsequent frames correlations. In contrast to continuous time sampling from 63 μs to seconds in LS-FCS, this sampling is not sufficient to obtain the PSF radius directly from the spatial correlation and must be a known parameter. LS-FCS seems to be a suitable compromise between point FCS and RICS, since it offers a medium spatial averaging with medium temporal resolution and the additional advantage of self-calibration of the PSF radius.

A severe problem in performing accurate STED measurements is background signals that can come from scattered excitation and STED light, dark counts and afterpulsing of the detector, anti-Stokes excitation by STED beam, and incomplete suppression of the fluorescence in the STED doughnut. The latter is fluorescence (here termed ring emission) that is emitted before the depletion is completed (Fig. 2 a), in case of a pulsed depletion or before the depletion is sufficiently high for CW depletion. Such unwanted background signals decrease the resolution (Figs. 2 e and S4) and in quantitative FCS measurements lead to an overestimation of the number of the fluorescent molecules.

Figure 2.

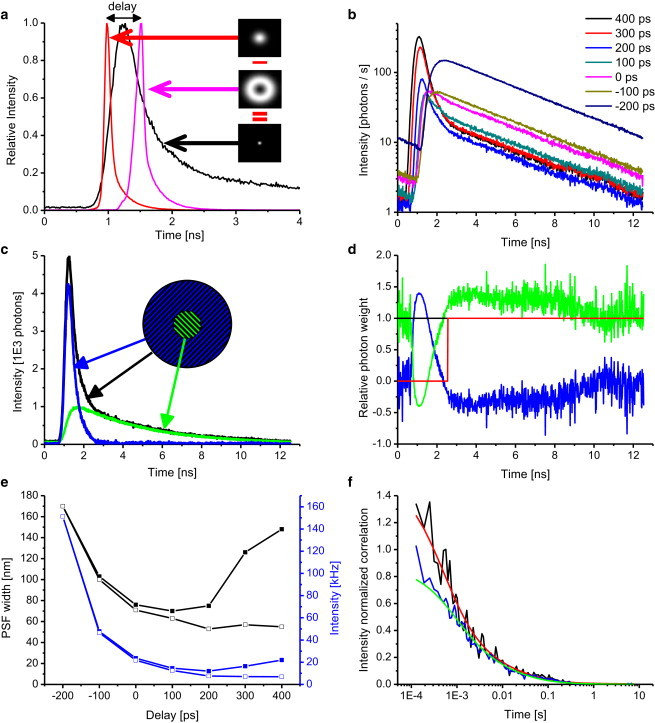
STED-FCS with photon weighting improves the spatial resolution and SNR. (a) Scheme of the pulsed STED excitation-depletion principle. A focused diffraction-limited 640 nm excitation pulse of 100 ps FWHM (red line) is followed by a 750 nm doughnut-shaped STED pulse of 200 ps FWHM (pink line). The molecules in the outer ring of the excitation spot are switched off, leading to an improvement in spatial resolution. The overall detected fluoresce decay (black line) depends on the delay between the excitation and depletion pulse, and on the excited-state lifetime of the fluorophores. (b) TCSPC histograms of DOPE-Atto647N fluorescence in SLBs (DOPC/DOPS at 4:1) for various time delays between the excitation pulse (640 nm, 100 ps FWHM, 10 μW) and the Ti-Sa STED pulse (750 nm, 200 ps FWHM, 50 mW). (c) The overall TCSPC histogram (black line) from an experiment with an efficient STED depletion can be decomposed into a normally decaying component (green line) originating from fluorescence of nondepleted molecules located in the central region and a fast-decaying component (blue line) stemming from the ring region before fluorescence depletion. (d) Photon-weighting filters calculated from the TCSPC histogram (shown in c) for superresolved (green) and ring (blue) photons that go into the spatiotemporal correlation function calculation. Unlike photon gating (red line), photon weighting keeps the overall intensity constant (black line). (e) Dependence of the spatial resolution (black line) and fluorescence intensity (blue line) on the delay between excitation and depletion pulses before (solid squares) and after (open squares) application of the photon-weighting filters shown in (d). The best resolution is achieved for delays longer than 200 ps with the ring fluorescence removed by photon weighting. Data are described in (b). (f) Comparison of temporal correlation decays at zero spatial difference obtained for a 200 ps delay between excitation and depletion pulses without (blue line) and with (black) photon weighting. Removal of the ring fluorescence increases the amplitude and shortens the correlation time. To see this figure in color, go online.

To minimize the problem with ring emission, we exploited the time-correlated single photon counting (TCSPC) features of the TTTR data acquisition. We generated TCSPC histograms that showed that the photon distribution over time depends on the delay between excitation and depletion pulses (Fig. 2 b). The ring emission itself was a fast component in the decay curves (Fig. 2 c) and the contribution of the ring emission to the overall signal depended on the delay between excitation and depletion pulses (Fig. 2, a and b). The more overlapping the pulses were, the more the ring emission was decreased, but it was impossible to remove it completely. The drawback of minimizing the ring emission by higher overlapping of excitation and depletion pulses is that this also lowers the STED efficiency. This is because fluorophores that are excited at the end of the excitation pulse are only exposed to parts of the depletion pulse, so the efficient STED power is lowered and consequently the spatial resolution is decreased. An optimal depletion pulse should arrive only after the excitation pulse is completed, which leads to an increased ring emission, again leading to a decrease in resolution. In practice, one needs to balance these two effects to obtain the highest possible resolution. In our case, the optimal delay was 100 ps when the ring fluorescence was not removed from the correlation function (solid symbols in Fig. 2 e).

Removal of the ring fluorescence was previously achieved by nanosecond time gating for STED imaging experiments (10), CW STED-FCS acquisition (30), and recently for pulsed STED-FCS experiments (31). The trick behind the time gating is simple: only photons that arrive after the ring fluorescence has decayed are used to calculate the correlation function. However, a more accurate means of distinguishing between photons from the central zero-STED spot and ring emission is photon filtering, an approach that was previously used in fluorescence lifetime correlation spectroscopy (32,33) and more recently in fluorescence spectral correlation spectroscopy (34). In filtered FCS, each photon is weighted according to a filter that splits the signal into its various contributions (here the central spot emission and ring emission, and potentially also the uniform background fluorescence) based on their fluorescence decay patterns. This is possible because the fluorescence decay patterns differ for these two emissions (Fig. 2 c). The filters constructed from these decay curves (Fig. 2 d) are then used during the calculation of the spatiotemporal correlation functions. We split the original raw correlation function into four filtered correlation functions (Fig. S4) and found that the autocorrelation of the central spot emission with itself had the best spatial resolution. The improvement in spatial resolution due to removal of the ring emission by photon filtering is demonstrated in Fig. 2 e. Without filtering, the best resolution in this experiment was 70 nm with a 100 ps delay, whereas with filtering, the resolution was 55 nm for a delay of ≥200 ps. The fact that the resolution stayed constant for longer delays after application of the photon filters is in agreement with our assumption that the ring emission is the cause of the decreased spatial resolution. The amount of removed ring emission is the difference between the intensities before and after filtering (Fig. 2 d, blue curves).

The advantage of filtering over gating is that all photons, even those emitted simultaneously with the background, are used. On the other hand, filtering introduces additional uncertainty and thus decreases the SNR. In general, both gating and filtering achieve similar resolution provided that the afterpulsing of the detector is low, as was the case here. Only in the extreme case of high depletion power (100 mW) and low apparent molecular brightness could we observe a slightly better performance for filtering (improvement from 45 to 40 nm; data not shown), as it also removed the contribution from afterpulsing photons (22). Thus, the main difference between gating and filtering is the SNR of the correlation curves. For dyes with long fluorescent lifetimes (such as Atto647N used in this study) and pulsed depletion, the differences are small. For dyes with a short lifetime, filtering achieves a better SNR than gating. The most significant difference in terms of SNR between gating and filtering can be expected for CW STED depletion with pulsed excitation. Our simulations show that for the same resolution, the relative standard deviation of correlation curves obtained by filtering was almost two times lower than that obtained with gating (Fig. S5).

The primary purpose of STED-FCS is to extend variable-spot FCS (vsFCS) below the diffraction limit (35). In vsFCS, the diffusion coefficients are measured at different length scales and the diffusion mode of the studied molecules is deduced from the dependence of the obtained diffusion coefficients on the measurement spot size (8). Typical modes include free Brownian diffusion, confined diffusion due to domains or meshwork, and temporary binding to immobile structures. For the latter, the sensitivity of the method depends on the ratio of the timescale of the molecular transit time to that of the binding/unbinding event (Fig. S6). If the binding/unbinding event is much faster than the time it takes the molecule to diffuse through the detection spot, it is difficult to distinguish between fast diffusion with temporary trapping and slow diffusion without trapping. Shrinking the detection spot size can thus shorten the average transition time and increase the sensitivity of vsFCS to fast binding/unbinding, as demonstrated by Mueller et al. (7).

We tested the STED-vsFCS approach on SLBs labeled with DOPE-Atto647N (Fig. 3). The increase in STED power led to a narrowing of the spatial correlation function, a shortening of the time decays, and an increase in amplitude (Fig. 3, a–d). The spatiotemporal correlation functions were fitted to a 2D free-diffusion model with two components (Eq. S15). From the spatial correlations extrapolated to zero lag time, a dependency of the PSF radius on the STED laser power was obtained (Fig. 3 e). The shrinking of the detection spot size down to 40 nm was accompanied by a decrease in the apparent molecular brightness. This effect can be explained by nonzero STED intensity in the center of the STED doughnut. Knowing the effective PSF size, we could plot the apparent particle number (Fig. 3 f) and diffusion coefficients (Fig. 3 g) as a function of the central spot area. The particle number scaled linearly with the spot area unless the latter had a radius of <70 nm. The deviation from linearity at small spot sizes can be explained by the decrease in molecular brightness, since a lower ratio of noncorrelating background to correlating signal increases the apparent particle number. The two diffusion coefficients obtained for the fast and slow fractions differed in their dependence on the spot area (Fig. 3 g). The fast diffusion coefficient remained constant, indicating free diffusion. The slow diffusion coefficient decreased with the spot size, indicating temporary binding. It is possible that positively charged DOPE-Atto647N dye becomes transiently arrested on the negatively charged glass surface (25). Hence, this experimental example illustrates both the accuracy and sensitivity of STED-vsFCS measurements obtained using our approach of line scanning and photon weighting.

Figure 3.

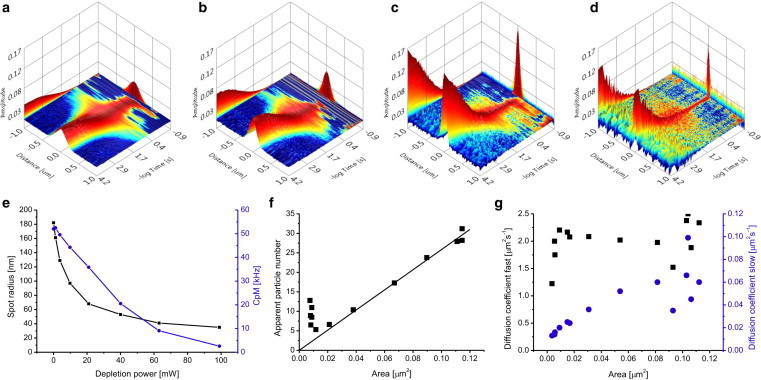
STED-vsFCS. (a–d) Spatiotemporal correlations for DOPE-Atto647N in SLBs on glass (DOPC/DOPS 4:1, lipid/dye 20,000:1,640 nm excitation at 10 μW) at increasing STED powers: (a) 0 mW, (b) 5 mW, (c) 20 mW, and (d) 100 mW. (e) Dependence of the effective spot radius (black squares) and apparent molecular brightness (blue circles) on STED power. The spot radius decreased from 185 nm to 40 nm at the expense of lower molecular brightness. (f) The apparent particle number of DOPE-Atto647N is plotted against the spot area. The black line represents the theoretical linear dependence of the particle number on the spot area. (g) The spatiotemporal correlation functions at different STED powers were fitted to a two-component model. The obtained fast (black squares) and slow (blue circles) diffusion coefficients are plotted against the spot area to create a vsFCS plot. To see this figure in color, go online.

It is well known that the quality of confocal FCS data acquired on planar membranes crucially depends on the relative axial position of the focal plane and the sample (16). Although LS-FCS mitigates the error of the diffusion coefficient coming from wrong focusing by its internal calibration, we decided to investigate how the STED-FCS data are influenced by changing the axial z position at high STED powers (Fig. S7). The dependencies of the spot radius (black squares) and the apparent molecular brightness (red triangles) on the z position clearly indicated that there was only a small region in which the measurement was optimal. If the focus is below the membrane, the apparent molecular brightness decreases strongly, which spoils the SNR of the correlation function. If the focus is above the membrane, the molecular brightness also decreases, although not so steeply, and the spatial resolution is compromised as the spot radius increases. The optimal region in these experiments occurred within a 200 nm zone in the axial direction, meaning that a stable stage is required for these measurements (i.e., stage or objective drift should be <200 nm over the acquisition).

An often-discussed issue with STED measurements is the influence of the intensive STED beam on the photophysics and photobleaching of the fluorophores. To demonstrate that the shortening of the correlation function is indeed due only to the diffusion and smaller detection spot size, and not to higher rates of switching into dark states, we adopted a novel (to our knowledge) fit-free concept called area integrated correlation function (AICF) for STED-LS-FCS data. The AICF integrates the values of the spatiotemporal correlation function over the area for varying lag times. In the case of line scanning, the spatiotemporal correlation function is obtained for only one dimension and hence we assume that the correlation function is symmetric within the xy plane. For any kind of 2D diffusion, whether Brownian or anomalous, the AICF profile is constant over time as the molecules remain fluorescent within the plane. An AICF profile that decays over time is indicative of other processes, such as out-of-plane diffusion (three-dimensional diffusion), intersystem crossing, and photobleaching. All of these processes cause molecules to disappear from the plane, which leads to the temporal decay of AICF on the timescale of the underlying process. The AICF profile of DOPE-Atto647N in SLBs on glass at various STED powers (Fig. S8, solid lines) indicates that the initial STED power-dependent decay of temporal autocorrelation functions (Fig. S8, dashed lines) was due to 2D diffusion and not to the photophysical properties of the dye or photobleaching. The changes in the AICF at longer times can be attributed to the increased SNR associated with wider and lower amplitudes in the spatial correlation function.

Having demonstrated the suitability and accuracy of this approach in model membranes, we applied line-scan filtered STED-FCS to cells to further test the method in live biological specimens. We measured and calculated the spatiotemporal correlations with and without STED for a glycophosphatidylinositol (GPI)-anchored protein tag labeled with Atto647N in plasma membrane of HeLa cells (Fig. 4, a and d), for DOPE-Atto647N in plasma membrane of COS7 cells (Fig. 4, b and e), and for a membrane-targeted fluorescent protein (Lck10-TagRFP657) in plasma membrane of COS7 cells (Fig. 4, c and f). For DOPE-Atto647N in plasma membrane of COS7 cells, we reached a resolution of 50 nm, which is similar to that obtained in pure lipid bilayers. For GPI-SNAP-Atto647N, we reached a resolution of 60 nm. With the recently introduced far-red emitting fluorescent protein TagRFP657 (36), we achieved better results with 532 nm excitation than with 640 nm excitation, which allowed us to capture a larger part of the emission spectrum. The resolution for the fluorescent protein improved from 160 nm in confocal mode to 95 nm in STED mode.

Figure 4.

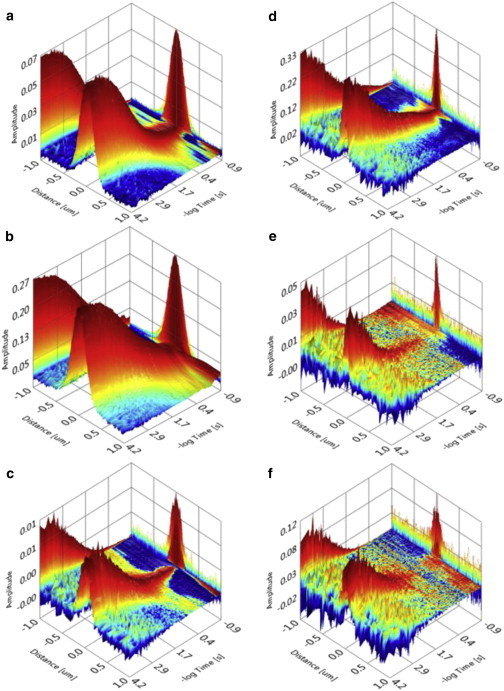
Examples of STED-LS-FCS in cells. (a–c) Spatiotemporal correlation functions at a confocal resolution of 170–200 nm of (a) GPI-SNAP-Atto647 in a HeLa cell (640 nm excitation at 5 μW), (b) DOPE-Atto647 in a COS7 cell (640 nm excitation at 5 μW), and (c) Lck10-TagRFP647 in a COS7 cell (532 nm excitation at 5 μW). (d–f) Spatiotemporal correlation functions with STED for (d) GPI-SNAP-Atto647 in a HeLa cell (640 nm excitation at 10 μW, 750 nm depletion at 30 mW) resulting in a resolution of 70 nm; (e) DOPE-Atto647 in a COS7 cell (640 nm excitation at 10 μW, 750 nm depletion at 50 mW) at 60 nm resolution; and (f) Lck10-TagRFP647 in a COS7 cell (532 nm excitation at 20 μW, 750 nm depletion at 50 mW) with 95 nm resolution. To see this figure in color, go online.

Mueller et al. (7) showed that DOPE-Atto647N diffused freely in plasma membrane, whereas SM-Atto647N was subject to temporary binding. We also acquired vsFCS data for DOPE-Atto647N and SM-Atto647N in plasma membrane of COS7 cells. We fitted the spatiotemporal correlation functions by a two-component model and plotted the slow and fast diffusion coefficients versus the effective PSF size (Fig. 5, a and b). We could not observe any trends for either lipid because of the huge scatter in the data (Fig. 5, a and b). Therefore, we attempted to discover the source of the scatter. To rule out the possibility that errors were introduced by fitting the data to a two-component model, which may not accurately describe the lipid diffusion modes, we utilized a model-free approach and plotted the average transit time versus the spot area (Fig. S9). However, no trend or clear distinction between DOPE-Atto647N and SM-Atto647N could be seen. There are many possible reasons for this discrepancy between our study and previously published reports (7,11,12), including the use of different cell types (see Conclusions for more details).

Figure 5.

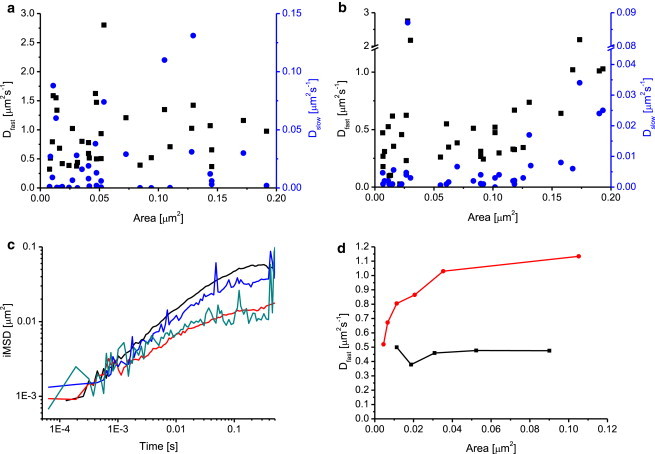
STED-vsFCS in cells. (a and b) The spatiotemporal correlation functions at different STED powers, obtained from COS7 cells labeled with DOPE-Atto647N (a) and SM-Atto647N (b), were fitted by a two-component model and the obtained fast (black squares) and slow (blue circles) diffusion coefficients are plotted against the spot area. Each data point represents one STED-LS-FCS acquisition. Data from three different days, with an average of 10 measurements per day, are shown. (c) iMSD curves corresponding to data presented in (a) and (b) are averaged for DOPE-Atto647N and SM-Atto647N, and for confocal (black and red lines, respectively) and STED acquisitions (blue and dark green curves, respectively). (d) Single-line STED-vsFCS experiments for DOPE-Atto647N in COS7 cells (black line) and SM-Atto647N in COS7 membrane lawn (red line). Line acquisitions at different STED powers were acquired along the same line within one sample. The spatiotemporal correlation functions were fitted to a two-component model and the obtained fast diffusion coefficients were plotted against the spot area. To see this figure in color, go online.

Another method for evaluating spatiotemporal correlation data that does not a priori require diffusion models is iMSD (23). This method assesses the time evolution of the MSD of diffusing molecules as the difference between the width of the spatial correlation distribution at the given lag time and the extrapolated distribution width for zero lag time. The widths of the spatial correlation distribution are obtained by fitting single-component Gaussian functions.

The average iMSD curves obtained from the same spatiotemporal correlation data (Fig. 5 c) indeed suggest a difference in diffusion between DOPE-Atto647N and SM-Atto647N in cells. The initial slope at short times, proportional to the diffusion coefficient, is similar, but the iMSD curve for SM-Atto647N levels off earlier and at shorter distances than DOPE-Atto647N. Here, we used only one Gaussian function to fit the PSF at any lag time. If there are fast- and slow-diffusing populations, the one-Gaussian fit will return an average PSF width, which depends on the fraction of molecules belonging to either population and also on the lag time. The longer the lag time, the higher is the contribution of the slow fraction to the average PSF width. Taking this interpretation of iMSD plots into account, the earlier leveling off for SM-Atto647N compared with DOPE-Atto647N suggests a higher fraction of slow SM than DOPE molecules. The smaller iMSD values for SM-Atto647N at long lag times could be caused by the much lower mobility of the slow fraction or by the smaller size of the underlying confinement structures.

Similarly to FCS analysis, iMSD analysis could benefit from the smaller PSF size under STED conditions. Smaller detection volumes enhance the relative difference in apparent diffusion coefficients between the bound and free fractions, making the difference detectable. Transient restriction of molecular diffusion leads to irregular widening of the spatial correlation profile, which requires the use of multiple Gaussian functions to describe its profile at times shorter than the time constant of the transient immobilization process. We tested a two-component Gaussian fit of spatial correlations under STED conditions, but the fit parameters were too correlated and did not allow us to quantify the binding kinetics and reveal any qualitative differences in diffusional properties of SM-Atto647N and DOPE-Atto647N. We propose that a fitting-free analysis of the spatial correlation distributions at different lag times (e.g., based on higher-moments analysis) could potentially provide information on the kinetics of transient immobilization that would complement the results of a STED-FCS analysis. It is possible that the large scatter in the vsFCS plot (Fig. 5, a and b) of data obtained in cells represents either variations in the membranes themselves or uncertainties in the measurements. To test the robustness of the method in cells, we acquired the full set of vsSTED-FCS data along a single line. As data acquisition for one PSF size (i.e., STED power) typically takes 1–3 min, the single-line vsSTED-FCS experiments took >10 min. Such long acquisition times are impractical because cells can move and fluorophores can bleach during the acquisition. Fig. 5 d shows two examples in which we successfully acquired the full vsSTED-FCS series. The constant diffusion coefficient for the fast fraction of DOPE-Atto647N in a COS7 cell (black squares) suggests that the method was sufficiently robust, and diffusion of the fast fraction of DOPE-Atto647N molecules was not obstructed. The second example for SM-Atto647N (red circles) shows a case in which the apparent diffusion coefficient of the free fraction changed with the spot size, suggesting a temporary binding of the DOPE-Atto647N molecules.

Given the reliability of the measurements themselves, we examined the heterogeneity of diffusion coefficients within a cell in more detail (Fig. 6). The intensity profiles along the scanned line within single acquisitions of DOPE-Atto647N and SM-Atto647N were rarely constant. To find out whether and how heterogeneities in dye density affected the diffusion coefficient, we calculated the temporal correlation functions at different positions along the scanned line, fitted them to a one-component model (Fig. 6, a and b), and plotted the local diffusion coefficients (red circles), dye particle numbers (blue squares), and fluorescence intensity (black line) against the position in the scanned line for both DOPE-Atto647N and SM-Atto647N (Fig. 6, c and d). Interestingly, there was a high level of correlation between intensity and particle number, which inversely correlated with the diffusion coefficient. This was observed for both DOPE-Atto647N and SM-Atto647N, and indicates local trapping of Atto647N-labeled molecules, which was independent of the lipid species to which Atto467N was attached. It should be noted that the transiently trapped dye molecules remained mobile. Also, the presence and amount of trapping did not depend on time after the lipid staining, and trapping was present even in the fresh samples taken directly from ice, which suggests that trapping is probably not caused by endocytosis of the Atto647N-labeled lipid molecules. Surprisingly, cells stained with DOPE-Oregon Green 488 did not show this behavior (Fig. S10). As with Atto647N, the intensity profile of DOPE-Oregon Green 488 was not constant and the particle number varied accordingly. However, the diffusion coefficient for DOPE-Oregon Green 488 remained constant within the experimental error, whereas this was not the case for the two Atto647N-labeled lipids (Fig. 6, c and d). Therefore, we cannot rule out the possibility that the cellular heterogeneities that caused the scatter in the vsFCS plots (Fig. 5, a and b) were caused by the Atto647N fluorophore itself.

Figure 6.

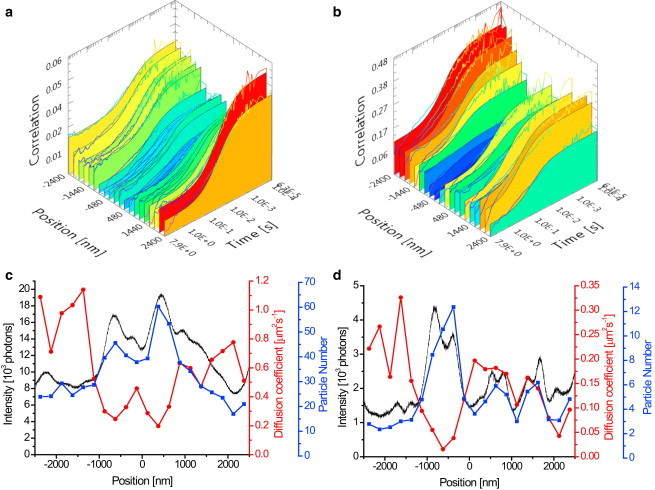
Spatially resolved LS-FCS. (a and b) Examples of temporal autocorrelation functions and their single-component fit at different points along the scanned line for DOPE-Atto647N (a) and SM-Atto647N (b) in two COS7 cells. Data were acquired at confocal resolution (640 nm excitation at 5 μW). Each of 20 curves is an average of a 250-nm-long line segment. (c and d) Typical spatial profiles of diffusion coefficients (red line) and particle numbers (blue line) obtained from single-component fits at different points along the scanned line shown in (a) and (b), and the corresponding fluorescence intensity (black line) for DOPE-Atto647N (c) and SM-Atto647N (d) in COS7 cells. To see this figure in color, go online.

Conclusions

Here, we utilized a commercial STED microscope with fast resonant line scanning to overcome the key problems of STED-FCS quantification. Our goal was to establish a robust measurement tool for lipid diffusion and, more generally, for biological systems in which transient immobilization of diffusing molecules occurs on timescales shorter than or comparable to the diffusion time of these molecules through the diffraction-limited detection spot. Squeezing down the detection spot significantly shortens the diffusion time but does not change the binding constant of the immobilization. To achieve more reliable STED-FCS measurements and easier quantification, we combined STED excitation with LS-FCS (18,19), which allowed us to determine the PSF size directly from the data and obtain spatially resolved diffusion maps along the scanned line with subdiffraction resolution. Further, we implemented filtered FCS to improve the spatial resolution using TCSPC-based photon filtering, which removes the contributions of nondepleted background fluorescence from the ring regions of the excitation spot. Importantly, this approach also reduces photobleaching and thus enables measurements in bilayers and cells. To our knowledge, we developed a new correlation algorithm to speed up the calculation of high-resolution spatiotemporal correlation functions and tested its robustness against immobile fraction, nonlinear scanning, and homogeneous photobleaching artifacts. We also tested the influence of the axial position on STED-LS-FCS readout parameters and applied AICF to show that the shortening of correlation function with increasing STED power is due to diffusion and not to photobleaching or the photophysics of the dye.

We demonstrated improvements by establishing the spatiotemporal correlation function for lipids and proteins in model and cell membranes. We routinely achieved an effective PSF width of 50 nm in model and cell membranes for Atto647N-labeled lipids. In both model and cell membranes, the spatiotemporal correlation functions required a model with at least two components for fitting. Despite the reliability of the measurements, we found a great heterogeneity in the vsFCS for Atto647N-labeled SM and DOPE both between and within cells. Along a scanned line, the diffusion coefficients of DOPE-Atto647N and SM-Atto647N correlated inversely with local dye concentrations, strongly suggesting that Atto647N-labeled lipids become temporarily trapped. This observation is in agreement with the hydrophobicity and positive charge of Atto647N, which makes the dye prone to sticking to a glass surface and also to unspecific binding to various cellular components (37). The fact that we could detect this heterogeneity, whereas previous point STED-FCS studies did not (11,12), could be due to significant differences between LS-FCS and point FCS with respect to the impact of photobleaching on the data. The LS obtains the same overall number of photons from a larger number of molecules, resulting in slower local photobleaching rates and superior averaging. With a stationary beam, a bleaching of transiently trapped molecules before they can diffuse away can be expected, and this could prevent one from observing heterogeneity within the sample. Moreover, the slow fraction of diffusing lipids may be less visible in single-point temporal correlation decays and may only become significant when the full spatiotemporal correlation function is analyzed. We should also point out the lipid probes used here are no longer commercially available, so it was not possible to ensure that our probes were identical to those used in the previous studies (7,11,12). Only new STED-compatible fluorophores will reveal whether such trapping is caused by Atto647N interacting with the glass surface or is indeed an intrinsic feature of cell membranes. If it is the latter, a large number of reliable and sensitive measurements will be needed to reveal the complex structure of the cell membranes that cause the lipid trapping behavior. We propose that STED-LS-FCS with the appropriate fluorophores and dependable hardware could provide such data.

Author Contributions

A.B. designed and performed research, contributed analytic tools, analyzed data, and wrote the paper. Y.M. performed research, analyzed data, and contributed to writing of the paper. K.G. designed research and wrote the paper.

Supporting Citations

References (38–43) appear in the Supporting Material.