A Major Controversy in Codon-Anticodon Adaptation Resolved by a New Codon Usage Index

Abstract

Two alternative hypotheses attribute different benefits to codon-anticodon adaptation. The first assumes that protein production is rate limited by both initiation and elongation and that codon-anticodon adaptation would result in higher elongation efficiency and more efficient and accurate protein production, especially for highly expressed genes. The second claims that protein production is rate limited only by initiation efficiency but that improved codon adaptation and, consequently, increased elongation efficiency have the benefit of increasing ribosomal availability for global translation. To test these hypotheses, a recent study engineered a synthetic library of 154 genes, all encoding the same protein but differing in degrees of codon adaptation, to quantify the effect of differential codon adaptation on protein production in Escherichia coli. The surprising conclusion that “codon bias did not correlate with gene expression” and that “translation initiation, not elongation, is rate-limiting for gene expression” contradicts the conclusion reached by many other empirical studies. In this paper, I resolve the contradiction by reanalyzing the data from the 154 sequences. I demonstrate that translation elongation accounts for about 17% of total variation in protein production and that the previous conclusion is due to the use of a codon adaptation index (CAI) that does not account for the mutation bias in characterizing codon adaptation. The effect of translation elongation becomes undetectable only when translation initiation is unrealistically slow. A new index of translation elongation I_TE is formulated to facilitate studies on the efficiency and evolution of the translation machinery.

FOLLOWING empirical documentation of the correlation between codon usage and tRNA abundance (Ikemura 1981a,b, 1982, 1992), many studies have demonstrated a strong relationship not only between codon adaptation and gene expression (Coghlan and Wolfe 2000; Comeron and Aguade 1998; Duret and Mouchiroud 1999; Xia 2007) but also between experimentally modified codon usage and protein production (Haas et al. 1996; Ngumbela et al. 2008; Robinson et al. 1984; Sorensen et al. 1989). These results have led to the explicit formulation of codon-anticodon coevolution and adaptation theory (e.g., Akashi 1994; Moriyama and Powell 1997; Ran and Higgs 2012; Xia 1998, 2008), which states that (1) protein production is rate limited by both translation initiation and elongation efficiency, (2) codon usage and tRNA anticodons coevolve to adapt to each other, resulting in increased production of correctly translated proteins, and (3) the increased elongation efficiency and accuracy represent the driving force for the highly expressed genes to acquire a high degree of codon-anticodon adaptation. These studies not only advanced our understanding of the joint effect of mutation and selection on codon usage (Chithambaram et al. 2014a,b; Palidwor et al. 2010) but also resulted in improved computational tools for characterizing codon usage and codon-anticodon adaptation (Sun et al. 2013; Xia 2007).

Whether translation elongation is a rate-limiting process in protein production has been controversial. Early theoretical considerations (Andersson and Kurland 1983; Bulmer 1990, 1991; Liljenstrom and von Heijne 1987) tended to favor the argument that translation elongation is not rate limiting in protein production but that translation initiation is. This hypothesis states that codon-anticodon adaptation and increased elongation efficiency are not related to protein production. Instead, the benefit of codon adaptation and increased elongation efficiency is to increase ribosomal availability for global translation.

To test these two alternative hypotheses, Kudla et al. (2009) engineered a synthetic library of 154 genes, all encoding the same green fluorescent protein in Escherichia coli but differing in synonymous sites [and consequently the degree of codon adaptation, as measured by codon adaptation index (CAI)]. All sequences share an identical 5′-UTR that is 144 nt long, so there is no variation in the Shine-Dalgarno sequence. Because the engineered genes all encode the same protein, it is justifiable to use protein abundance as a proxy for protein production (assuming that protein molecules sharing the same amino acid sequence have the same degradation rate).

Kudla et al. (2009) interpreted minimum folding energy (MFE), computed from sites −4 to +37 (where ribosomes position themselves at the initiation codon), as a proxy for initiation efficiency. The rationale for using MFE as a measure of translation initiation is that an initiation codon would be inaccessible if it were embedded in a strong secondary structure and that accessibility of the initiation codon is a key determinant of translation initiation efficiency (Nakamoto 2006). A stable secondary structure in sequences flanking the start codon has been shown experimentally to inhibit translation initiation (Osterman et al. 2013). MFE can be computed by using DAMBE (Xia 2013), which implements the RNA folding library from the Vienna RNA package (Hofacker 2003).

Kudla et al. (2009) interpreted CAI as a proxy for translation elongation. If both translation initiation and translation elongation contribute to translation efficiency, then protein production is expected to depend on both MFE and CAI. If only translation initiation is important, then protein production will depend only on MFE. These authors found that MFE accounts for 44% of the variation in protein production but that CAI is essentially unrelated to protein production. They concluded, consequently, that “translation initiation, not elongation, is rate-limiting for gene expression” (Kudla et al. 2009, p. 258).

The conclusion by Kudla et al. (2009), however, is based on two critical assumptions: (1) that MFE and CAI are good proxies of translation initiation and elongation efficiencies, respectively, and (2) that the effect of translation elongation is independent of translation initiation. The problem with the second assumption has been pointed out recently (Supek and Smuc 2010); Tuller et al. (2010) reanalyzed the data in addition to providing an overwhelming amount of additional empirical evidence to demonstrate the joint effect of both translation initiation and translation elongation on protein production. In short, the protein production rate is expected to increase with elongation efficiency only when translation initiation is efficient. If translation initiation is slow, then an increasing elongation rate is not expected to increase protein production. Kudla et al. (2009) ignored the dependence of elongation effect on translation initiation.

However, the results reported by Tuller et al. (2010) are not much different from those of Kudla et al. (2009). The key finding from the reanalysis (Tuller et al. 2010) is that the effect of codon usage bias on protein production is only marginally significant when translation initiation (with MFE as proxy) is controlled for. The partial correlation between codon usage bias and protein production is only marginally significant (P = 0.04), accounting for less than 3% of the total variation in protein abundance. This finding simply reinforces the original conclusion of Kudla et al. (2009) that the effect of codon usage and translation elongation on protein production is negligible relative to that of translation initiation (with MFE as proxy), which accounts for 44% of the total variation in protein production.

CAI by Kudla et al. (2009) and translation adaptation index (tAI) by Tuller et al. (2010) as proxies for translation elongation efficiency are both problematic and can lead to serious bias, as will be illustrated in the next section. In this paper, I develop a new CAI that accommodates the background mutation bias. I found that translation elongation accounts for about 17% of total variation in protein production.

Necessity of a New Translation Elongation Index

Many gene-specific codon usage indices have already been formulated and improved, including CAI (Sharp and Li 1987; Xia 2007), tAI (dos Reis et al. 2004) and several indices that are based on coding sequences only, such as the effective number of codons ${\widehat{N}}_{\text{c}}$ (Wright 1990) and its improved versions (Novembre 2002; Sun et al. 2013) and the codon deviation coefficient (CDC) (Zhang et al. 2012). The first two have been used frequently as proxies for translation elongation efficiency, whereas the others are typically not related to translation rate. For example, in contrast to CAI and tAI, which are at least positively correlated with the protein production data in Kudla et al. (2009), CDC is negatively correlated with protein production, although the correlation is not significant (r = −0.1254, P = 0.1211).

The problem with tAI is that codon usage bias is not always inferable from tRNA gene copy numbers or experimentally measured tRNA abundance because codon and anticodon do not always pair as expected according to the wobble or extended wobble hypothesis (Crick 1966; Grosjean et al. 2007, 2010). For example, inosine is expected to pair best with C and U, less with A (partly because of the bulky I-/A pairing involving two purines), and not with G. However, tRNA^Val/IAC from rabbit liver pairs better with the GUG codon than with other synonymous codons (Jank et al. 1977; Mitra et al. 1977). Similarly, the Bacillus subtilis genome codes a tRNA^Ala/GGC for decoding GCY codons, but the GCC codon that forms the Watson-Crick base pair with the anticodon is not used as frequently as the GCU codon, which wobble-pairs with the anticodon. One might argue that based on previous studies (Fiers and Grosjean 1979; Grantham et al. 1981; Grosjean et al. 1978; Ikemura 1981a), the intermediate binding strength between codon and anticodon is optimal, especially for highly expressed genes. A weak binding at the third codon position is preferred, with strong binding occurring at the first two codon positions, and a strong binding at the third codon position is preferred, with weak binding occurring at the first two codon positions. Thus, GCU is preferred by anticodon GGC because of the strong binding at the first two codon positions. However, this explanation does not work for Gly, where four tRNA^Gly/GCC genes are present for decoding GGY codons, and GGC is used more frequently than GGU (Sun et al. 2013). Furthermore, codon-anticodon base pairing is known to be context dependent (Lustig et al. 1989), for example, a wobble cmo⁵U in the anticodon of tRNA^Pro; tRNA^Ala and tRNA^Val can read all four synonymous codons in the respective codon family, but the same cmo⁵U in tRNA^Thr cannot read C-ending codons (Nasvall et al. 2007). For this reason, the optimal codon usage is likely better approximated by the codon usage of highly expressed genes than by what we can infer based on codon-anticodon pairing. Consistent with this proposition, CAI, which is based on the codon usage of highly expressed genes (HEGs), performs better in predicting protein production or abundance than other indices based on tRNAs (Coghlan and Wolfe 2000; Comeron and Aguade 1998; Duret and Mouchiroud 1999).

CAI has its own problems, however. Other than those outlined previously (Xia 2007), it often leads to a wrong interpretation of tRNA-mediated selection. I illustrate this problem here with the Ala codon subfamily GCR (where R stands for either A or G). The frequencies of GCA and GCG in E. coli HEGs, as compiled and distributed with EMBOSS (Rice et al. 2000), are 1973 and 2654, respectively, which may lead one to think that the E. coli translation machinery prefers GCG over GCA. However, the codon frequencies of GCA and GCG for E. coli non-HEGs are 25,511 and 43,261, respectively. Thus, GCA is relatively more frequent in E. coli HEGs than in E. coli non-HEGs. This suggests that mutation bias favors GCG but that tRNA-mediated selection favors GCA, which is relatively more preferred by E. coli HEGs. This interpretation is corroborated by the E. coli genome encoding three tRNA^Arg genes for GCR codons, all with a UGC anticodon forming a perfect Watson-Crick base pair with codon GCA.

For the NNR or NNY codon family or subfamily, we first define P_i.HEG and P_i.non-HEG as the proportion of codon i within its R- or Y-ending family for E. coli HEGs and non-HEGs. For example, take data for codons GCA and GCG in Table 1

$$\begin{array}{l}{P}_{\text{GCA}\text{.HEG}}=\frac{N_{\text{GCA}\text{.HEG}}}{N_{\text{GCR}\text{.HEG}}}=\frac{1973}{1973+2654}=\text{0}\text{.42641}\\ P_{\text{GCA}\text{.non-HEG}}=\frac{N_{\text{GCA}\text{.non-HEG}}}{N_{\text{GCR}\text{.non-HEG}}}=\frac{25,511}{25,511+43,261}=0.37095\\ S_{\text{GCA}}=\frac{P_{\text{GCA}\text{.HEG}}}{P_{\text{GCA}\text{.non-HEG}}}=1.1495;S_{\text{GCG}}=\frac{P_{\text{GCG}\text{.HEG}}}{P_{\text{GCG}\text{.non-HEG}}}=0.9118\end{array}$$ (1)

where S_GCA and S_GCG may be viewed as relative codon frequencies of HEGs corrected for the “background” non-HEGs. Codon i is considered selected for if S_i > 1 and against if S_i < 1. Thus, codon GCA is considered selected for because, according to Equation 1, S_GCA > 0. This insight would be obscured if we were to use codon frequency data from only E. coli HEGs or only non-HEGs, which would have suggested that codon GCA is selected against. The S_i values for the sense codons in E. coli are listed in Table 1.

Table 1. Codon frequency (CF) for E. coli highly expressed genes (HEGs) and non-HEGs, as well as the computed S_i values according to Equation 1.

AA	Codon	CFHEGa	CFnon-HEGb	Si
A	GCA	1973	25,511	1.1495
A	GCG	2654	43,261	0.9118
A	GCC	1306	33,463	0.5646
A	GCU	2288	18,526	1.7865
C	UGC	475	8,397	1.1541
C	UGU	270	6,802	0.8098
D	GAC	2786	23,226	1.5125
D	GAU	2345	41,472	0.7130
E	GAA	4683	49,154	1.1180
E	GAG	1459	22,920	0.7470
F	UUC	2229	20,332	1.7637
F	UUU	872	29,556	0.4746
G	GGA	118	10,786	0.7282
G	GGG	267	14,842	1.1975
G	GGC	2987	37,418	0.8210
G	GGU	3583	30,154	1.2221
H	CAC	1160	12,144	1.7105
H	CAU	477	17,170	0.4975
I	AUA	22	5,926	0.0000
I	AUC	3488	30,787	1.5592
I	AUU	1640	39,788	0.5673
K	AAA	4129	41,696	1.0469
K	AAG	1050	13,057	0.8502
L	CUA	54	5,258	0.1275
L	CUG	5698	66,130	1.0694
L	CUC	541	14,591	1.2085
L	CUU	357	14,679	0.7927
L	UUA	210	18,739	0.7639
L	UUG	333	18,273	1.2422
M	AUG	2444	35,527	0.0000
N	AAC	2832	26,674	1.5850
N	AAU	539	23,652	0.3402
P	CCA	474	11,046	0.5779
P	CCG	2509	29,125	1.1601
P	CCC	38	7,443	0.2235
P	CCU	343	9,235	1.6258
Q	CAA	550	20,405	0.4975
Q	CAG	2548	36,780	1.2788
R	AGA	21	2,880	0.9782
R	AGG	13	1,681	1.0374
R	CGA	34	4,837	1.2807
R	CGG	33	7,370	0.8158
R	CGC	1530	28,473	0.6413
R	CGU	2995	25,528	1.4001
S	AGC	1015	20,868	1.3432
S	AGU	168	11,802	0.3931
S	UCA	189	9,614	0.9119
S	UCG	275	11,909	1.0711
S	UCC	1110	10,649	0.8950
S	UCU	1320	10,217	1.1094
T	ACA	181	9,527	0.7719
T	ACG	526	19,197	1.1132
T	ACC	2533	29,335	0.9108
T	ACU	1286	10,950	1.2389
V	GUA	1329	13,513	1.5053
V	GUG	1784	34,133	0.8000
V	GUC	824	19,972	0.4993
V	GUU	2669	22,297	1.4485
W	UGG	819	19,945	0.0000
Y	UAC	1569	15,094	1.5503
Y	UAU	865	21,207	0.6083

^aTaken from the Ecoli_high.cut file distributed with EMBOSS 6.4 (Rice et al. 2000) representing a compilation of codon usage from known highly expressed E. coli K12 genes.

^bMean codon frequencies from four sequenced E. coli K12 genomes (NC_010473, NC_020518, NC_007779, and NC_000913) minus CF_HEG.

The index of translation elongation I_TE is then calculated in a way similar to CAI except that the computation is applied to NNR and NNY codon subfamilies:

$$w_{\text{i}}=\frac{S_{\text{i}}}{\text{Max}(S_{\text{i}})},e.g.,w_{\text{GCA}}=\frac{1.1495}{1.1495}=1,w_{\text{GCG}}=\frac{0.9118}{1.1495}=0.7932$$ (2)

$$I_{\text{TE}}=e^{{\displaystyle \sum _{\text{i}=1}^{N_{\text{s}}}{F}_{\text{i}}\ln w_{\text{i}}}/{\displaystyle \sum _{\text{i}=1}^{N_s}{F}_{\text{i}}}}$$ (3)

where F_i is the frequency of codon i, and N_s is the number of sense codons (excluding those in single-codon families). For example, AUG for methionine, AUA for isoleucine, and UGG for tryptophan in the standard genetic code are excluded from computing I_TE. Just like CAI, tAI, and ${\widehat{N}}_c$, I_TE is a gene-specific index of codon usage bias.

The main reason for dividing codons into the R- and Y-ending groups is that for genes encoded by the nuclear genome, the R-ending codons are typically decoded by two types of tRNA species (one with a wobble C and the other with a wobble U), whereas the Y-ending codons are decoded typically by a single type of tRNA species with either a wobble G or a wobble A modified to inosine, but never by both (Grosjean et al. 2007; Marck and Grosjean 2002). For this reason, the R- and Y-ending codons, even within a single fourfold codon family, are subject to different tRNA-mediated selection and therefore should be treated separately. However, for comparative purposes, I have chosen to include the other two alternative approaches for computing I_TE, that is, one with compound six- and eightfold codon families broken into two- and fourfold codon families and the other lumping all synonymous codons into one codon family. A new version of DAMBE (Xia 2013) has been uploaded with all three approaches included. One may access the function by clicking on “Seq.Analysis|Codon usage|Index of translation elongation.”

One may note that CAI is a special case of I_TE when there is absolutely no codon usage bias in non-HEGs in all codon subfamilies. That is, when N_GCA.non-HEG = N_GCG.non-HEG, N_GCC.non-HEG = N_GCU.non-HEG, and so on. The range of I_TE is the same as CAI, that is, between 0 and 1. The reason for separating synonymous codons into R- and Y-ending codon subfamilies is that they are typically translated by different tRNAs and subject to different mutation bias. I have outlined the problems of lumping synonymous codons together and illustrated the benefit of treating R- and Y-ending codons separately elsewhere (Sun et al. 2013; Xia 2007).

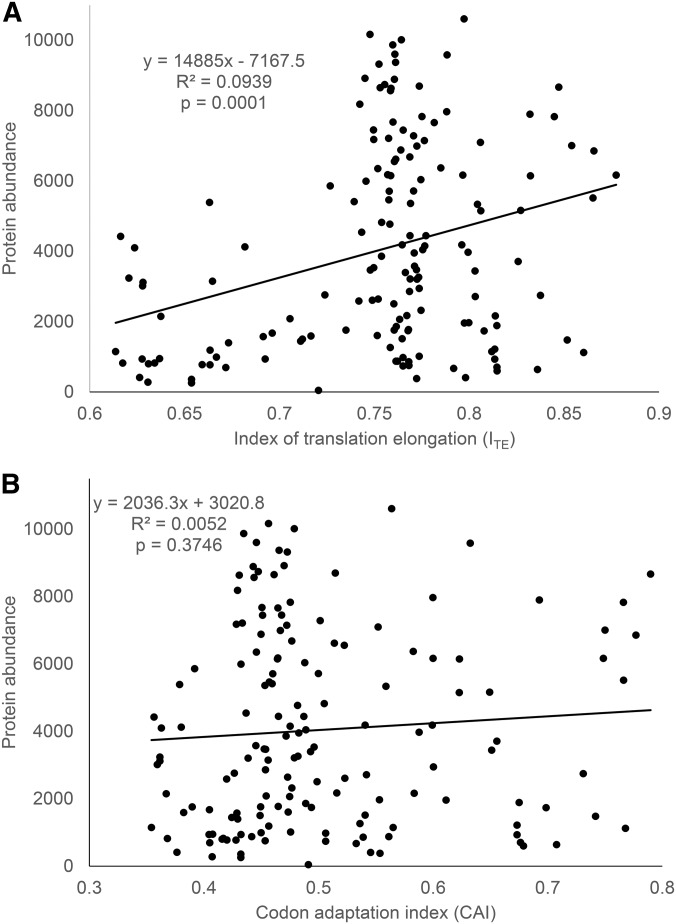
The relationship between protein abundance and I_TE (Figure 1a) for the data from Kudla et al. (2009) is contrasted with that between protein abundance and CAI (Figure 1b). There are three points worth highlighting. First, a highly significant relationship between protein abundance and translation elongation is revealed by the new I_TE, accounting for nearly 10% of the total variation in protein abundance (P = 0.0001) (Figure 1a). In contrast, no relationship exists between protein abundance and CAI (Figure 1b). Second, when I_TE is small (e.g., I_TE < 0), protein abundance is generally low, which suggests that translation elongation is limiting. Third, a large I_TE (efficient translation elongation) does not imply high protein production because translation initiation is also limiting. A large I_TE will lead to increased protein production only if translation initiation is also efficient.

Figure 1.

Relationship between protein abundance (measured by GFP normalized fluorescence; data kindly provided by Dr. Plotkin) and translation elongation efficiency I_TE, contrasting with that between protein abundance and CAI (codon adaptation index).

One may argue that I_TE should be computed without the first 36 bases because these sites have already been used in computing MFE. I have computed codon frequencies and I_TE without the first 36 bases (designated I_{TE_shortCDS}) and added this to Supporting Information, Table S1. I_{TE_shortCDS} and I_{TE_full-lengthCDS} (the original I_TE with full-length CDS) are almost perfectly correlated (r = 0.9976).

Conceptual Framework for Evaluating the Effect of Translation Initiation and Elongation

It is only genes with efficient translation initiation that are expected to increase protein production with improved codon-anticodon adaptation. If we express the protein production rate Prot as a linear function of elongation efficiency I_TE, that is,

$$Prot=a+b{I}_{\text{TE}}$$ (4)

we would expect the slope b to change with initiation efficiency. A low initiation efficiency implies little benefit for high I_TE, and b should be close to 0. In contrast, elongation efficiency would become rate limiting with high translation initiation efficiency, and we would expect b to increase with translation initiation efficiency.

I tested these predictions by using the original data in Kudla et al. (2009) with the same proxies that they used for Prot and translation initiation; that is, Prot was measured by normalized GFP fluorescence level and translation initiation efficiency by MFE of the sequences flanking the initiation codon, from sites −4 to +37. I replaced their CAI by I_TE as a proxy for translation elongation efficiency. I followed the practice of Tuller et al. (2010) by ranking Prot (designated as rProt in supporting information, Table S1, which contains all relevant data for the following analysis).

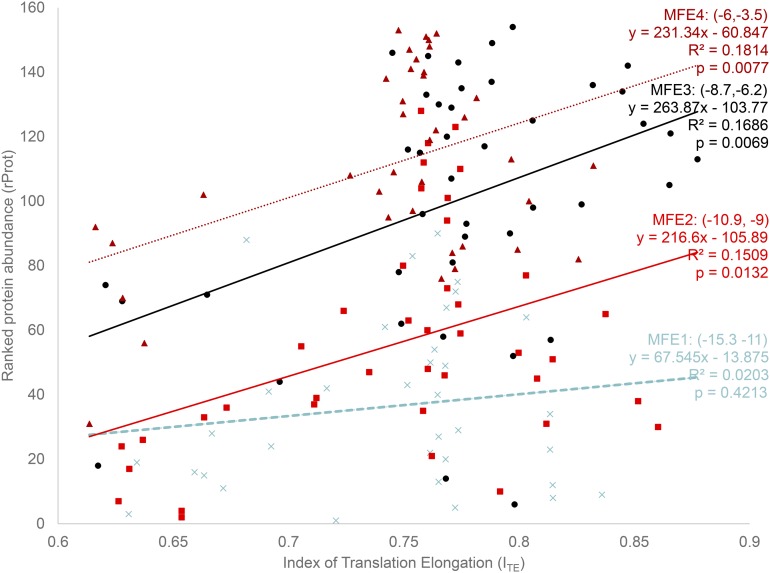
I binned the MFE into four categories, (−15.3, −11), (−10.9, −9), (−8.7, −6.2), and (−6, −3.5), representing translation initiation from the lowest to the highest and designated as MFE1–MFE4 (Figure 2). The intervals were chosen in such a way that all MFE values fall into four roughly equal-sized groups, with within-group MFE being as small as possible. The benefit of binning is that one can exclude the MFE variable so that the effect of I_TE can be modeled more explicitly. If MFE is included as an independent variable, then it becomes difficult to isolate the effect of I_TE because I_TE and MFE may interact with each other in unexpected ways. It is for this same reason that Tuller et al. (2010) also used binned analysis for this data set.

Figure 2.

Ranked protein abundance rProt (protein abundance is measured by GFP normalized fluorescence; data kindly provided by Dr. Plotkin) increases with translation elongation efficiency I_TE, except for the group with extraordinarily strong secondary structure at the 5′ end (the MFE1 group). rProt also increases with decreasing stability of secondary structure, with MFE1 having the most stable and MFE4 the weakest secondary structure. The range of MFE is indicated for each of the four MFE groups.

In the MFE1 group, translation initiation is the lowest, and we should expect little increase in protein production with translation elongation efficiency (I_TE), that is, a weak relationship between I_TE and rProt. This is consistent with the empirical result (Figure 2), where the relationship between I_TE and rProt is not statistically significant in the MFE1 group (b = 67.545, P = 0.4213) (Figure 2), with I_TE accounting for only 2% of total variation in ranked protein abundance (rProt). In contrast, when translation initiation is more efficient in groups MFE2–MFE4, rProt increases significantly with I_TE, with the simple linear model consistently accounting for about 17% of the total variation in rProt (Figure 2, with b varying from 216.60 to 263.87). Thus, the contribution of translation elongation (I_TE) to protein production is much greater than previously documented for this data set, that is, no (Kudla et al. 2009) or less than 3% of the total variation in protein production (Tuller et al. 2010).

Alternatively, one may rank MFE as an index of translation initiation (I_TI) so that a more negative MFE (more stable secondary structure) will have a smaller I_TI and fit the data to the following model:

$$rProt=b_0+b_1\cdot I_{\text{TI}}+b_2\cdot I_{\text{TI}}\cdot I_{\text{TE}}$$ (5)

The effect of I_TE can be evaluated by testing the hypothesis that b₂ = 0. Because protein abundance is measured by fluorescence levels (Kudla et al. 2009), b₀ in Equation 5 represents the background fluorescence. The fitted model is

$$\begin{array}{l}rProt=26.2286-1.2035I_{\text{TI}}+2.4960I_{\text{TI}}\cdot I_{\text{TE}}\\ \text{=}26.2286+(2.4960I_{\text{TE}}-1.2035)I_{\text{TI}}\end{array}$$ (6)

This model accounts for 56.0% of total variation in rProt. The P-value associated with b₂ is 0.00000004. The fitted model in Equation 6 suggests that when elongation efficiency is low (e.g., I_TE < 0.4822), increasing I_TI would either have no effect or a negative effect on protein production. The negative effect could be generated when ribosomes collide/interfere with each other when initiation is efficient but elongation is not.

Discussion

Many codon optimizing and deoptimizing experiments have used both prokaryotic and eukaryotic translation systems and consistently have suggested an increased translation rate with optimized codon usage and a reduced translation rate with deoptimized codon usage (Haas et al. 1996; Ngumbela et al. 2008; Robinson et al. 1984; Sorensen et al. 1989). Kudla et al. (2009) are exceptional in claiming that translation efficiency is not limited by elongation rate or codon usage bias. However, as shown in this paper, the claim is false for two reasons. First, the authors ignore the interaction between translation initiation and translation elongation. Second, CAI is an inadequate proxy for measuring translation elongation.

While theoretical models can fail to capture the essence of reality, experimental models can fail the same way. Tuller et al. (2010) have pointed out that the average MFE in the sequences of Kudla et al. (2009) is extraordinarily low. The average MFE is only −8.87, with a range from −15.3 to −3.5. Among the 4320 annotated coding sequences in the E. coli K12 strain (NC_000913), the MFE for the segment between sites −4 and +37 has a mean of −5.23, with only 16 sequences with MFE values smaller than −15.3 but 1278 sequences with MFE values greater than −3.5. Thus, the MFE1 group in Figure 2 is not representative of the real data and should be excluded in interpreting the effect of elongation on protein production for most genes.

I also wish to point out that the data of Kudla et al. (2009) also suffer from unrealistically small variation in elongation efficiency. The CAIs for the experimental sequences are all smaller than 0.6 according to Figure 2A in Kudla et al. (2009). More than 1000 E. coli genes have CAIs greater than 0.6. This means that the experimental sequences in Kudla et al. (2009) all have relatively low elongation efficiency, and the data set therefore is inadequate for a fair assessment of the effect of elongation on protein production. The fact that even such a limited variation in translation elongation efficiency can still demonstrate a highly significant effect of elongation rate on protein production represents strong evidence that protein production depends heavily on elongation efficiency and codon adaptation.

It is also problematic to attribute the effect of MFE all to translation initiation, as did Kudla et al. (2009). While a stable secondary structure embedding the initiation codon will surely affect translation initiation, it may well hinder translation elongation as well. This would suggest that the effect of MFE on protein production could be due to both translation initiation and translation elongation. That is, translation elongation as characterized by I_TE may well account for more than about the 17% shown in Figure 2.

In summary, the hypothesis that translation efficiency is limited by both translation initiation and translation elongation is strongly supported by the empirical evidence, with translation elongation accounting for about 17% of total variation in protein production. The new index of translation elongation I_TE is far superior to the conventional CAI or tAI as a proxy for translation elongation efficiency. The original conclusion by Kudla et al. (2009) that translation elongation does not contribute to protein production is based on an inadequate analysis aggravated by as an inadequate index of codon usage bias.