Abstract
This paper presents a formulation of controlled geometric reduction with one degree of underactuation for mechanical systems with an unactuated cyclic variable subject to passive damping. We show that the first control term in the fully actuated case reduces to passive joint-velocity feedback, which can be equivalently provided by viscous friction. The underactuated control strategy is applied to a five-link 3D biped with a hip, torso, knees, and unactuated yaw at the foot contact point. We show asymptotically stable walking in the presence of passive yawing for realistic friction coefficients.
I. INTRODUCTION
Human walking is a dynamic task involving distinct phases of static instability. Motor control of this task is challenged by different forms of underactuation during a gait cycle. A dynamic walking biped engages in controlled falling during single-support phase, where gravity and momentum propel the center of mass along a pendular arc causing the support foot to passively rotate about different contact points from heel-strike to toe-off. In addition to pitching in the sagittal plane-of-motion, body dynamics induce yawing about the gravity vector at these contact points. The human ankle joint provides substantial actuation in the sagittal plane through plantar/dorsiflexion and some actuation in the frontal plane through inversion/eversion, but internal/external rotation (i.e., yaw) of the stance leg is mostly passive [1].
Different control strategies have been proposed to confront these forms of underactuation in walking robots. Works based on hybrid zero dynamics model the foot/ankle as a point with passive degrees of freedom (DOFs) [2]–[5]. This method has produced walking without ankle actuation on the planar testbeds RABBIT [3] and MABEL [4], and recent work has simulated 3D walking with yaw rotation [5].
Controlled geometric reduction [6]–[10] uses symmetry-based momentum constraints to create zero dynamics corresponding to planar bipeds that are known to have passively stable gaits (i.e., gravity-powered walking down shallow slopes [11]). This approach exploits the natural existence of limit cycles in the sagittal plane as a sufficient condition for generating gaits in actuated 3D bipeds. Feet with fixed yaw are modeled in [10] to demonstrate that reduction-based control is robust to phases of underactuation associated with non-flat foot contact with ground. However, this body of work has not considered the steady form of underactuation associated with passive yaw rotation.
This paper derives an underactuated formulation of controlled reduction that produces 3D walking in the presence of passive yawing. We constrain our investigation to a fixed contact point by modeling the biped with point feet. Section II introduces the momentum constraints induced by cyclic variables (i.e., invariants in dynamics) and passive joint-velocity feedback. We use these constraints in Section III to show that controlled reduction can be achieved with an unactuated cyclic variable subject to passive damping. This controller produces locally exponentially stable walking gaits for a five-link 3D biped in Section IV. We conclude in Section V with discussion and future work.
II. LAGRANGIAN MECHANICS AND SYMMETRY
We consider the class of n-DOF mechanical systems with configuration space 𝒬 = ℝn, where the state (q, q̇) in tangent bundle T𝒬 ≅ ℝ2n consists of configuration q ∈ 𝒬 and tangential velocity q̇ ∈ ℝn. The system dynamics are derived from the Lagrangian ℒ : T𝒬 → ℝ, given in coordinates by
| (1) |
where 𝒱(q) is the potential energy and n × n symmetric, positive-definite M(q) is the mass/inertia matrix. System integral curves satisfy the Euler-Lagrange (E-L) equations
| (2) |
where τ ∈ ℝn contains the external joint torques. This second-order system of ordinary differential equations gives the dynamics for the actuated mechanism in phase space T𝒬:
| (3) |
where n × n-matrix C(q, q̇) contains the Coriolis/centrifugal terms, vector N(q) = ∇q 𝒱(q) contains the potential torques, and n × m-matrix B (full row rank) maps actuator input vector u ∈ ℝm to joint torques τ = Bu ∈ ℝn for m ≤ n.
Conservation Laws
Symmetry of the system Lagrangian implies a conservation law by Noether’s theorem [12], i.e., a physical quantity of the system is conserved by the dynamics. We are interested in conservation laws that can be expressed as nonholonomic constraints of the form
| (4) |
where Jc ∈ ℝk × n has rank k < n. The system dynamics restricted to the invariant level-set
| (5) |
then correspond to lower-dimensional zero dynamics. We now discuss the kind of symmetries that we will use to design a desirable submanifold 𝒵 for controlled reduction.
Cyclic Variables
Let Lagrangian ℒ be defined in coordinates of configuration space 𝒬 = 𝔾 × S, where 𝔾 = ℝk is the configuration symmetry group and S = ℝn − k is the shape space. We are interested in symmetries of ℒ characterized by cyclic variables qc ∈ 𝔾, such that
| (6) |
If these cyclic variables are free from external and actuator forces, equations (2) and (6) imply that the generalized momenta pc = ∇q̇c ℒ conjugate to the cyclic coordinates are constant. The dynamics then evolve on the invariant level-set (5) of these conserved momentum quantities, where Jc = [Ik × k 0k × n − k]M and b(q) = μ for some constant vector μ. Routhian reduction uses these constraints to directly relate full-order integral curves on phase space T𝒬 to reduced-order integral curves on phase space TS, and vice versa.
In the case of mechanical systems, often only the world coordinates are cyclic, e.g., position and orientation of the stance foot. However, extensive symmetries known as recursively cyclic variables exist in subsystems of open kinematic chains, a general property proven in [7], [8]. The rigid-body inertia matrix M can be expressed in relative coordinates to be independent of (cyclic) variable q1. The lower-right fn − 1 × n − 1 submatrix is additionally independent of q2, and the lower-right n − 2 × n − 2 submatrix is independent of q3. This nested cyclic structure holds recursively through the inertia matrix until a branch in the kinematic chain [8].
Many systems have an unactuated cyclic variable and actuated shape variables (e.g., bipedal runners in flight phase), for which stability can be achieved by breaking the momentum conservation law with a rotary spring in the cyclic coordinate [13]. We will instead use passive damping to replace the existing conservation law with a new functional momentum law that controls the cyclic variable.
Controlled Momentum Constraints
Our controlled version of Routhian reduction shapes the conservation laws arising from cyclic variables [6]–[8], [14]. These controlled momentum constraints will uniquely describe the dynamics of the constrained coordinates qc ∈ ℝk in terms of the reduced coordinates qr ∈ ℝn − k, where .
Although the generalized momentum is typically defined as p̃ ≔ ∇q̇ ℒ = Mq̇, multistage controlled reduction exploits the recursively cyclic structure of the inertia matrix by considering the momentum p ≔ M̂ q̇, where matrix M̂ is defined by upper-triangular blocks from M:
| (7) |
where M̂c ∈ ℝk × k is the upper-triangular part of the top-left k × k submatrix in M, and Mc,r ∈ ℝk × (n − k), Mr ∈ ℝ(n − k) × (n × k) are, respectively, the top-right and bottom-right submatrices in M. The first k momentum terms are
| (8) |
which we wish to constrain in order to control coordinates qc to neighborhoods around set-points q̄c ∈ ℝk (cf. [14]):
| (9) |
| (10) |
where gain matrix K ∈ ℝk × k is constant, diagonal, and positive-definite. These momentum constraints define the smooth, invariant, (2n − k)-dimensional submanifold 𝒵q̄c as in (5), where Jc = [M̂c Mc,r] has row rank k and b = − K(qc − q̄c) is continuously parameterized by q̄c.
Due to the recursively cyclic and upper-triangular structure of M̂, it is easily shown that scaling matrices have no dependence on configuration elements q1,…i in row i, for i ∈ 1,.., k. We then see that equation (10) represents a homogeneous first-order linear system in qc with time-varying coefficients based on trajectories (qr(t), q̇r (t)). The diagonal blocks of inertia matrix M are positive definite, implying that is also positive definite. System (10) then has negative gain linearity in qc, by which we can prove the existence of a unique T-periodic orbit in a neighborhood about q̄c given the existence of a T-periodic orbit . We can similarly prove that asymptotic convergence to the reduced orbit implies asymptotic convergence to the constrained orbit [14]. These constraints decompose the control problem into upper triangular form, allowing us to construct limit cycles for locomotor patterns in a manner analogous to forwarding/backstepping [15].
The first of these k constraints is achieved with passive joint-velocity feedback (e.g., viscous damping from friction), which we will exploit in underactuated controlled reduction.
Lemma 1: Letting q1 in configuration vector q correspond to the first DOF and , then passive feedback
| (11) |
in system (2) implies the functional conservation law
| (12) |
for some constant q̄1 satisfying initial boundary condition
| (13) |
Proof: Recursively cyclic M and imply that q1 is cyclic, so plugging (11) into (2) implies ṗ1 = − K1q̇1. Momentum p1 is no longer conserved as a constant but rather as a function by the fundamental theorem of calculus:
Given (13), then p1(t) = −K1(q1(t)− q̄1) for all t ≥ t0.
Remark 1: Every initial condition has an associated conservation law, so we have rendered invariant infinitely-many submanifolds, each parameterized by q̄1:
| (14) |
This so-called foliation of manifold T𝒬 will be the result of underactuated controlled reduction in Section III.
Lemma 1 suggests that viscous damping, whether from a mechanical damper or friction, will be helpful in enforcing the constraints needed for controlled reduction.
III. CONTROLLED GEOMETRIC REDUCTION
We now render the reduced dynamics (e.g., the sagittal plane of a biped) decoupled from the coordinates constrained by (9). Although Lagrangian/energy shaping is used in [6], [7], we will instead insert joint accelerations that directly enforce the desired constraints and decouple the reduced coordinates as in the fully actuated approach of [9].
Constraint Jacobian Jc = [M̂c Mc,r] maps joint velocities to momenta in first-order constraint (4), but this Jacobian can also map joint accelerations to torques. We take the time-derivative of (4) to obtain the second-order constraint
| (15) |
where J̇c = [M̂̇c Ṁc,r] and ḃ = −Kq̇c. This second-order constraint, which does not depend on set-point q̄c, renders invariant infinitely-many first-order submanifolds 𝒵q̇c in a foliation of T𝒬. This includes all possible conservation laws provided by passive feedback in Lemma 1.
We now design joint accelerations q̈d ∈ ℝn that enforce (15) and follow a reference acceleration within the constraint nullspace. This can be interpreted in terms of hierarchical operational space control [16], where constraint enforcement is the primary task and tracking q̈ref is a secondary task that complies with the primary. All solutions for this desired acceleration can be given by
| (16) |
where denotes any generalized inverse of Jc (i.e., a matrix such that .
Since Jc is full row rank, we can choose an inverse of the form , where W ∈ ℝn × n is a positive definite weight matrix that manipulates how accelerations q̈ref are projected into the null space of the constraints. We choose W = M̂−T to find that , so the nullspace projector takes the simple form
| (17) |
This choice of weight matrix (and nullspace projector) renders orthogonal the projections of the constrained and unconstrained dynamics (recall that Jc is defined by M̂, and M̂W = WM̂ = I). We can now express desired accelerations (16) in terms of the partitions
| (18) |
where v ∈ ℝk−1 is an auxiliary control term in the constrained dynamics. We see that nullspace projector (17) has removed any dependence on q̈cd – the first k coordinates instead evolve according to the constraints – leaving command over the reference acceleration q̈rd in the decoupled reduced partition. This term also appears in the constrained partition, which will provide synchrony between different planes-of-motion in our biped application, i.e., the constrained orbit will have the same period as the reduced orbit.
In order to impose joint accelerations (18), we first define the fully-actuated inverse dynamics controller
| (19) |
Applying control (19) to system (3), the closed-loop dynamics are finally decomposed into upper-triangular form (18).
Although second-order constraint (15) is always enforced under (19), initial conditions determine one of infinitely-many first-order constraints (4). System (18) possesses a symmetry with respect to set-points of the constrained coordinates. This may be desirable in some coordinates, e.g., biped dynamics should be invariant with respect to yaw/heading on a flat surface. We can achieve this foliation of T𝒬 even if the first DOF is unactuated, provided that it is subject to viscous damping from passive forces.
Proposition 1: Letting v = 0, the first term of control (19) reduces to passive feedback (11), i.e., [1 0]τ⊥ = −K1q̇1.
Proof: Plugging (18) into (19) and noting that , we first evaluate
Because q1 is a cyclic variable of the Lagrangian and thus the potential energy, . The definition of Coriolis matrix C (computed from M) can be invoked to show that .
Hence, the first control term can be provided by passive forces instead of actuation. This term enforces the second-order constraint with respect to q1 by Lemma 1, and the remaining control terms in (19) need only know the friction coefficient in (11) to enforce the remaining k − 1 second-order constraints. Any given solution trajectory belongs to a submanifold defined by some first-order constraint (4), and we can invoke Lemma 1, specifically (13), to determine the specific vector q̄c parameterizing this submanifold.
We let the initial conditions determine q̄1 in this manner, but the remaining k − 1 constrained coordinates can be controlled to desired set-points through auxiliary input v. We wish to render globally exponentially attractive the surface 𝒵k−1 defined by the last k − 1 first-order constraints of (4), where 𝒵q̄c ⊂ 𝒵k−1. This is equivalent to zeroing k − 1 outputs y ≔ [0 I](Jcq̇ − b), so we will feedback linearize the associated output dynamics into the exponentially stable system ẏ = −Ly, for some positive-definite gain matrix L ∈ ℝk−1 × k−1. In terms of the constraints this system is
| (20) |
Plugging (18) into q̈, we solve for the linearizing control law:
| (21) |
This proportional controller is zero when restricted to the constraint surface, i.e., v|𝒵k−1 = 0, allowing us to invoke Proposition 1. Letting torque map B = [0 I]T in system (3), the underactuated version of (19) is finally given by
| (22) |
We will see that the biped’s discontinuous impact events tend to violate first-order constraints (4), i.e., 𝒵k−1 is not hybrid invariant, but subcontroller (21) will correct these errors shortly after each impulsive event.
IV. FIVE-LINK 3D BIPED RESULTS
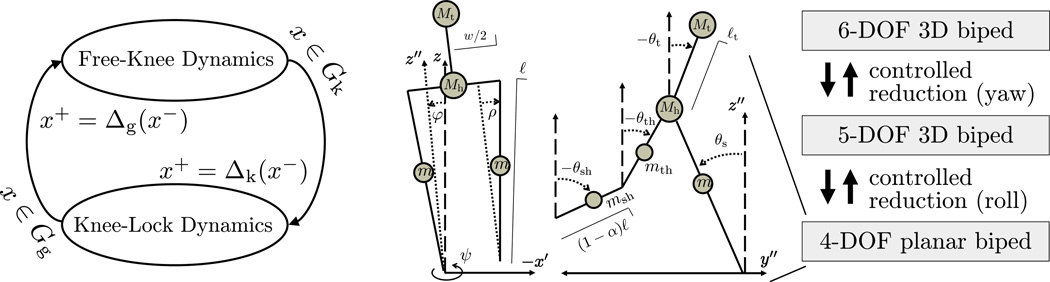
The 3D biped model in Fig. 1 has two phases during single-support: a knee-swing phase with six DOFs and a knee-lock phase with five DOFs. The knee of the stance leg remains locked during that leg’s entire single-support cycle. We assume the biped walks on a flat surface with sufficient Coulomb friction to prevent slipping and non-zero viscous friction in the yaw DOF. This can be interpreted as a point foot in contact with a textured surface or as a flat foot with passive elements in the yaw DOF of the ankle (e.g., tissue).
Fig. 1.
Diagrams of the 3D biped’s hybrid system ℋ (left), frontal and sagittal planes (middle), and controlled reduction (right). The first stage reduces the yaw DOF of the transverse plane, and the second stage reduces the lean DOF of the frontal plane, yielding the dynamics of the sagittal-plane biped.
This biped has coordinates q = (ψ, φ, θT)T in configuration space 𝒬 = ℝ6, where ψ, φ ∈ ℝ are respectively the heading/yaw and roll/lean variables at the stance foot, and vector θ = (θs, θt, θth, θsh)T contains the sagittal-plane (pitch) variables for the stance leg, torso, swing thigh, and swing shank, respectively. Knee-lock phase provides θth ≡ θsh. Yaw is the first DOF in the kinematic chain and is defined about the gravity vector on a flat surface, implying that variable ψ is cyclic in both kinetic and potential energy.
The system state is x = (qT, q̇T)T in domain D, defined as the subset of T𝒬 such that the swing foot height is nonnegative. We assume that both knee-strike and ground-strike impact events are instantaneous and perfectly plastic, resulting in transitions between the six and five DOF dynamics according to hybrid system ℋ of Fig. 1. The ground-strike guard Gg is defined as the set of states in D where the swing foot height is zero, and its reset map Δg(x) is computed following the method of [2]. The knee-strike guard Gk is the set of states in D where θth − θsh = 0, and its reset map Δk(x) is computed as in [17]. Bilateral symmetry across the sagittal plane provides that hybrid dynamics are mirrored between left and right leg stance, where the signs of hip width w and angle ρ are flipped at ground strike.
Model-Specific Controller
We partition this model’s configuration into constrained coordinates qc = (ψ, φ)T and reduced coordinates qr = θ. Ankle yaw is unactuated, cyclic, and subject to viscous damping as in (11). Each phase of ℋ has an associated controller (22), which switches with the model during walking. Control gains are uniform across phases, and control torques are saturated at Umax.
Lean is the only constrained coordinate that is controlled by output linearizing control (21) to a specific set-point, φ̄ = 0 corresponding to upright. We build pseudo-passive walking gaits by closing an outer feedback loop that inserts sagittal-plane dynamics into the unconstrained accelerations of (18):
| (23) |
where vpd = −kpθt − kd θ̇t is a torso controller and we have virtually rotated the gravity vector to mimic downhill dynamics (slope angle β = 0.06 rad) on flat ground [18]. This slope-changing “controlled symmetry” exploits passive limit cycles to render system (18) strictly minimum phase.
Simulation Results
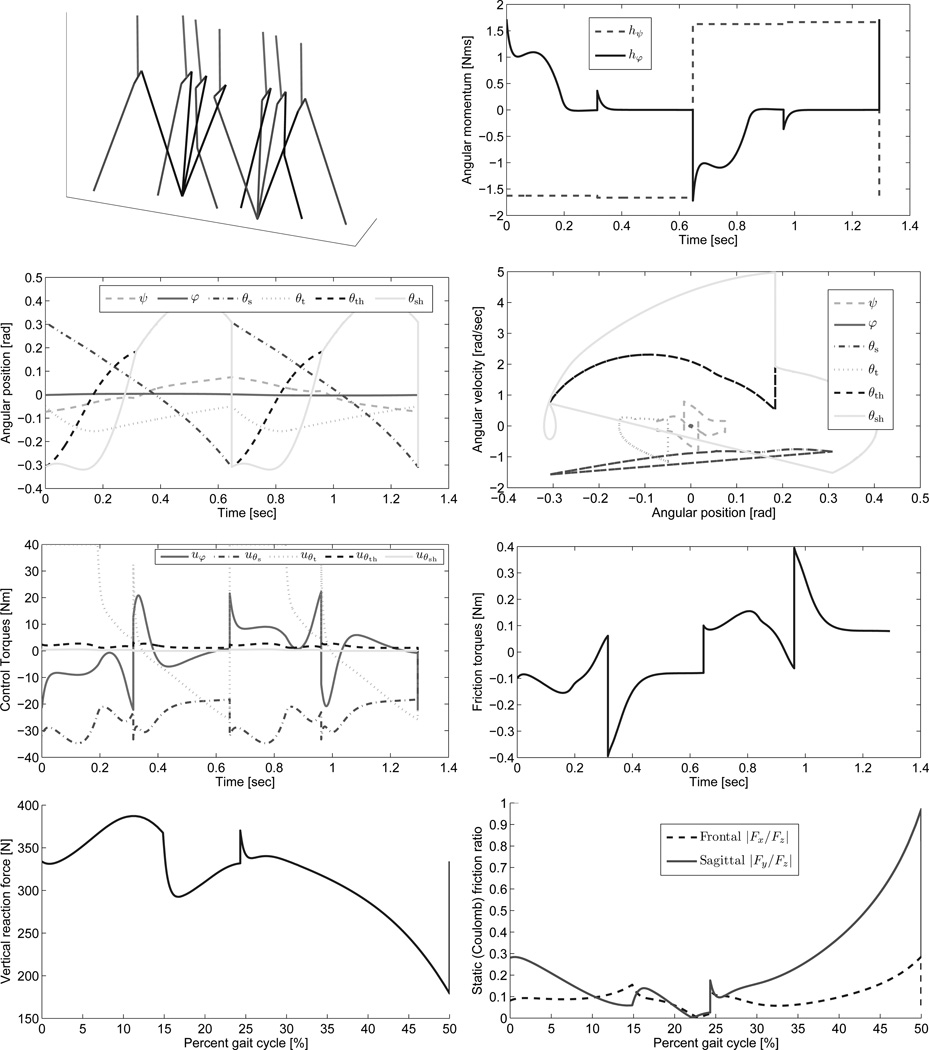
We set the rotational friction coefficient to K1 = 0.5 and adopt the parameters given in Fig. 2. Recall that system ℋ under (22) is invariant with respect to heading, implying that no isolated orbits exist in the given coordinate system. We therefore analyze the hybrid system modulo yaw, for which a hybrid limit cycle may exist with respect to the change in heading over two steps.
Fig. 2.
Gait animation (top left), conserved quantity errors (top right), joint trajectory (middle left), phase portrait (middle right), saturated control torques (lower middle left), yaw friction torque (lower middle right), vertical ground reaction force (bottom left), and Coulomb friction ratios (bottom right). A supplemental downloadable movie of this 3D walking simulation is available at: http://vimeo.com/20956363.
Model : Mt = 15 kg, ℓt = 0.55 m, Mh = 10 kg, m = 5 kg, mth = 0.7m, msh = 0.3m, ℓ = 1 m, α = 0.5, w = 0.2 m, ρ = 0.0564 rad
Gains : K1 = 0.5, K2 = 25, L = 68, kp = 700, kd = 265, β = 0.06 rad, Umax = 40 Nm
x* ≈ (−0.0741, −0.0016, 0.3089, −0.0498, −0.3084, −0.3084, 0.2008, 0.0450, −0.8307, −1.1639, 0.7324, 0.7324)T
1) Gait stability: We show the existence and local exponential stability of a hybrid limit cycle by the method of Poincaré sections [3]. Defining a return map P : Gg → Gg between intersections with the ground-strike guard, we find a fixed-point x* = P2(x*) corresponding to the hybrid limit cycle shown in Fig. 2. We numerically linearize the Poincaré map P2 about x* to show that all eigenvalues are within the unit circle (|eig|max = 0.58), confirming exponential stability of the discrete system and thus the hybrid system.
The yaw conserved quantity hψ = [1 0]Jcq̇ + K1ψ is piecewise constant throughout the walking gait in Fig. 2, switching signs every double-support transition due to the biped’s heading about ψ = 0. The hybrid dynamics in fact stabilize the relative difference between these output values. Recall that a constant value of hψ does not imply that yaw is constant, but rather that the biped rotates toward some heading ψ̄ parameterizing the first-order constraint (4) during that continuous phase. Directional changes in yaw correspond to jumps in hψ at discrete events, and the resulting yaw trajectory in Fig. 2 resembles internal/external rotation of the tibia during human walking [1, Fig. 1–15].
The control and joint trajectory plots in Fig. 2 also show that the biped leans and yaws in the direction of the swing leg after the knee-lock event. The passive damping element in the yaw DOF contributes two orders of magnitude less torque than the actuators, but yaw motion remains bounded and stable due to our momentum constraints.
2) Viscous friction: We next examine the effect of viscous friction coefficient K1, which enters into control (22). Decreasing the coefficient from K1 = 1, instability ensues for coefficients smaller than K1 = 0.4, which demonstrates that the yaw DOF requires a certain degree of damping for gait stability. The smallest maximum eigenvalue modulus is 0.518 for K1 = 0.7. We also find that yaw range-of-motion increases as we decrease the damping coefficient.
3) Gait efficiency: Integrating q̇T Bu to obtain the net work per step, we find that the specific average mechanical power is 0.52 W/kg. Moreover, the specific mechanical cost of transport (work done per unit weight per unit distance) is cmt = 0.037, which compares favorably with popular walking robots such as the Cornell biped at cmt = 0.055 and Honda ASIMO at cmt = 1.6 [19]. By choosing momentum constraints based on symmetries and reinserting the original planar dynamics, our inverse dynamics approach retains the energetic efficiency that is characteristic of dynamic walking.
4) Contact constraints: Bipedal locomotion is unilaterally constrained in the ground reaction forces (GRF). In order to validate the fixed-base assumption in our simulations, we need to show that the GRF vector F = (Fx, Fy, Fz)T keeping the stance foot fixed satisfies two conditions: the vertical GRF component remains strictly positive, i.e., Fz (t) > 0 for all t, and the GRF vector remains within the friction cone, i.e., |Fx (t)/Fz(t)|, |Fy (t)/Fz(t)| < η for all t with Coulomb friction coefficient η = 1 (e.g., rubber feet). We verify these conditions (Fig. 2) using the procedure outlined in [2].
V. CONCLUSIONS
By proving that the first control term reduces to passive feedback, we have shown that controlled reduction can be achieved with one degree of underactuation in the presence of viscous damping from friction. This underactuated control strategy produced asymptotically stable walking for a five-link 3D biped with passive yawing at the foot contact point.
Future work will construct steering gaits for motion planning applications [20]. Our controller does not provide direct control of heading set-point ψ̄, but a desired lean set-point φ̄ can be forced by output linearizing law (21). This angle can be chosen to lean into the direction of the desired heading.
The human-like yawing in our simulations was based on anthropomorphic ankle actuation, where viscous damping comes from passive elements such as tissues or ground friction. We unexpectedly found that the inclusion of knees in the model contributed to more natural GRF curves in Fig. 2, such as the double hump in vertical force that is characteristic of human walking. The addition of feet is not necessary for this profile but would likely improve the comparison.
Our walking model was not intended to be validated as human-like behavior, but it can be studied for insight into fundamental biped mechanics, such as the emergence of asymmetry [21]. This will guide the design of human subject experiments and ultimately novel interventions for locomotor deficits caused by stroke, amputation, or spinal injury.
Acknowledgments
This project has been funded in part with Federal funds from the National Center for Research Resources (NCRR), National Institutes of Health (NIH), through the Clinical and Translational Science Awards Program (CTSA), a trademark of DHHS, part of the Roadmap Initiative, “Re-Engineering the Clinical Research Enterprise.” Northwestern University UL1RR0254741. Content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH. This research was also partially supported by NSF Grants IIS-1018167 and CMS-0510119.
REFERENCES
- 1.Rose J, Gamble JG. Human Walking. 3rd ed. New York, NY: Lippincott Williams & Wilkins; 2006. [Google Scholar]
- 2.Westervelt ER, Grizzle JW, Koditschek DE. Hybrid zero dynamics of planar biped walkers. IEEE Trans. Automatic Control. 2003;48(1):42–56. [Google Scholar]
- 3.Westervelt ER, Grizzle JW, Chevallereau C, Choi JH, Morris B. Feedback Control of Dynamic Bipedal Robot Locomotion. New York, NY: CRC Press; 2007. [Google Scholar]
- 4.Sreenath K, Park HW, Poulakakis I, Grizzle JW. A compliant hybrid zero dynamics controller for stable, efficient and fast bipedal walking on MABEL. Int. J. Robotics Research. 2010 OnlineFirst. [Google Scholar]
- 5.Shih C, Grizzle JW, Chevallereau C. From stable walking to steering of a 3D bipedal robot with passive point feet. Robotica. 2010 to appear. [Google Scholar]
- 6.Ames AD, Gregg RD, Spong MW. IEEE Conf. on Decision and Control. New Orleans, LA: 2007. A geometric approach to three-dimensional hipped bipedal robotic walking; pp. 5123–5130. [Google Scholar]
- 7.Gregg RD, Spong MW. Reduction-based control of three-dimensional bipedal walking robots. Int. J. Robotics Research. 2010;26(6):680–702. [Google Scholar]
- 8.Gregg RD, Spong MW. IEEE Conf. on Decision and Control. Shanghai, China: 2009. Reduction-based control of branched chains: Application to three-dimensional bipedal torso robots; pp. 8166–8173. [Google Scholar]
- 9.Gregg RD, Righetti L, Buchli J, Schaal S. IEEE Int. Conf. Humanoid Robots. Nashville, TN: 2010. Constrained accelerations for controlled geometric reduction: Sagittal-plane decoupling in bipedal locomotion. [Google Scholar]
- 10.Sinnet R, Ames AD. IEEE Conf. on Decision and Control. Shanghai, China: 2009. 3D bipedal walking with knees and feet: A hybrid geometric approach; pp. 3208–3213. [Google Scholar]
- 11.Goswami A, Thuilot B, Espiau B. A study of the passive gait of a compass-like biped robot: Symmetry and chaos. Int. J. Robotics Research. 1998;17(12):1282–1301. [Google Scholar]
- 12.Marsden JE, Ratiu TS. Introduction to Mechanics and Symmetry. 2nd ed. New York, NY: Springer; 2002. [Google Scholar]
- 13.Grizzle JW, Moog CH, Chevallereau C. Nonlinear control of mechanical systems with an unactuated cyclic variable. IEEE Trans. Automatic Control. 2005;50(5):559–576. [Google Scholar]
- 14.Gregg RD. Ph.D. dissertation. University of Illinois at Urbana-Champaign; 2010. Geometric control and motion planning for three-dimensional bipedal locomotion. [Google Scholar]
- 15.Sepulchre R, Janković M, Kokotović PV. Constructive Nonlinear Control. New York, NY: Springer-Verlag; 1997. [Google Scholar]
- 16.Sentis L, Khatib O. Synthesis of whole-body behaviors through hierarchical control of behavioral primitives. Int. J. Humanoid Robotics. 2005;2(4):505–518. [Google Scholar]
- 17.Asano F, Yamakita M. Extended PVFC with variable velocity fields for kneed biped. IEEE Int. Conf. Humanoid Robots. 2000 [Google Scholar]
- 18.Spong MW, Bullo F. Controlled symmetries and passive walking. IEEE Trans. Automatic Control. 2005;50(7):1025–1031. [Google Scholar]
- 19.Collins SH, Ruina A. IEEE Int. Conf. Robotics and Automation. Barcelona, Spain: 2005. A bipedal walking robot with efficient and human-like gait; pp. 1983–1988. [Google Scholar]
- 20.Gregg RD, Bretl TW, Spong MW. IEEE Int. Conf. Robotics and Automation. Anchorage, AK: 2010. Asymptotically stable gait primitives for planning dynamic bipedal locomotion in three dimensions; pp. 1695–1702. [Google Scholar]
- 21.Gregg RD, Dhaher Y, Lynch KM. IEEE Int. Conf. Engineering in Medicine and Biology Society. Boston, MA: 2011. Functional asymmetry in a five-link 3D bipedal walker. [DOI] [PMC free article] [PubMed] [Google Scholar]