Properties of selected mutations and genotypic landscapes under Fisher’s Geometric Model

Abstract

The fitness landscape – the mapping between genotypes and fitness – determines properties of the process of adaptation. Several small genotypic fitness landscapes have recently been built by selecting a handful of beneficial mutations and measuring fitness of all combinations of these mutations. Here we generate several testable predictions for the properties of these small genotypic landscapes under Fisher’s geometric model of adaptation. When the ancestral strain is far from the fitness optimum, we analytically compute the fitness effect of selected mutations and their epistatic interactions. Epistasis may be negative or positive on average depending on the distance of the ancestral genotype to the optimum and whether mutations were independently selected, or co-selected in an adaptive walk. Simulations show that genotypic landscapes built from Fisher’s model are very close to an additive landscape when the ancestral strain is far from the optimum. However, when it is close to the optimum, a large diversity of landscape with substantial roughness and sign epistasis emerged. Strikingly, small genotypic landscapes built from several replicate adaptive walks on the same underlying landscape were highly variable, suggesting that several realizations of small genotypic landscapes are needed to gain information about the underlying architecture of the fitness landscape.

Introduction

Sewall Wright (1932) introduced the metaphor of “fitness landscapes” to think about evolutionary processes. A fitness landscape is defined by a set of genotypes, the mutational distance between them and their associated fitness. Populations are abstracted into groups of particles that navigate on this landscape (Orr 2005). In this regard, the process of adaptation by natural selection depends on the structure of the fitness landscape. Many fundamental features of adaptation depend on whether the landscape is smooth or rugged, and on the level of epistasis between genotypes on the landscape (note that these two properties are related, Weinreich et al. 2005, Poelwijk et al. 2011). For examples, levels and type of epistasis determine the probability of speciation (Gavrilets 2004, Chevin et al. 2014) and the benefits of sexual reproduction (Kondrashov and Kondrashov 2001; de Visser et al. 2009; Otto 2009; Watson et al. 2011). The ruggedness of the landscape determines the repeatability and predictability of adaptation (Kaufmann 1993; Colegrave and Buckling 2005; Chevin et al. 2010; Salverda et al. 2011).

It is now possible to explore the fitness landscapes of microbial species using several experimental methods. A common type of experiment consists in isolating a number of mutants and measuring the fitness of genotypes with either a single mutation or various combinations of mutations. The most fascinating of these experiments are perhaps those considering a small number (L) of mutations and reconstructing all possible genotypes (2^L genotypes) from the wild type to the evolved (reviewed in Weinreich et al. 2013; Lee et al. 1997, de Visser et al. 1997, Whitlock and Bourguet 2000, Lunzer et al. 2005, Weinreich et al. 2006, O’Maille et al. 2008, Lozovsky et al. 2009, da Silva et al. 2010, Chou et al. 2011, Khan et al. 2011). The properties of these reconstructed fitness landscapes determine whether adaptation was constrained to follow the particular sequence of mutations that indeed evolved in the experiment, or whether mutations could have evolved in any order with similar probabilities.

The experimental data can be interpreted in the light of various theoretical fitness landscape models. Many models directly define the mapping between individual genotypes and fitness (“discrete” fitness landscape models). The simplest is the additive model, whereby the log-fitness is the sum of additive contributions by individual loci. This model results in no epistasis and a very smooth landscape. At the opposite extreme, the “House of Cards” model (Kingman 1978) assumes that the fitness of each genotype is drawn independently of other genotypes in some distribution. This model results in a highly epistatic and rugged landscape. In between these two extremes, two models where the roughness is a tunable parameter have been designed. The “Rough Mount Fuji” model assumes that log-fitness of a genotype is the sum of additive contributions from mutations and a House of Cards random component (Franke et al. 2011, Szendro et al. 2013). Kauffman’s NK model assumes that fitness results from the sum of contribution of N loci, and the contribution of each locus is determined by the allelic status of this locus and K interacting loci (often its neighbors) (Kauffman and Levin 1987, Draghi and Plotkin 2013). The contributions of these sets of loci are themselves drawn independently in some distribution. The NK model encompasses all scenarios from the additive model (when K = 0) to the full House of Cards model (when K = N). In the House of Cards, Rough Mount Fuji and NK models, epistasis is a linear combination of the random components of the fitness landscape.

A very different family of fitness landscape models specifies fitness by mapping genotypes to a set of phenotypes that are themselves under selection. The most famous of these is Fisher’s geometric model (Fisher 1930). In Fisher’s model, individuals are characterized by a number of continuous phenotypes that are under stabilizing selection towards a single fitness peak in the multivariate phenotypic space. Mutations fuel the process of adaptation by generating new genotypes with different phenotypic values. One fundamental difference with the discrete models described above and phenotypic models is that in the latter, epistasis emerges from the non-linearity of the phenotype to fitness map, and not from random components.

In spite of the diversity of fitness landscape models, relatively little work has attempted to confront directly these models with experimental data. The “Rough Mount Fuji” model is able to reproduce a diversity of patterns observed in experimental fitness landscapes (Szendro et al. 2013). The NK model has been used to interpret landscapes of RNA or protein folding, and in particular to interpret the levels of autocorrelation of the landscape (Fontana et al. 1993, Rowe et al. 2010). Fisher’s model has been increasingly popular to interpret experimental data, perhaps because it is sufficiently simple to allow mathematical analysis and very fast simulations. Fisher’s model successfully predicts the distribution of selection coefficient of random mutations (Martin and Lenormand 2006), levels of epistasis (Martin et al. 2007, Gros et al. 2009, Rokyta et al. 2011), levels of dominance (Manna et al. 2011), the drift load (Tenaillon et al. 2007, Gros and Tenaillon 2009), and the dynamics of mean fitness in experimental lines (Perfeito et al 2014). Moreover, it has been shown recently that Fisher’s model emerges under a set of relatively general “first principles” that describe the underlying metabolic network and developmental process of an organism (Martin 2014). Fisher’s model has been used predominantly to interpret results on fitness effects of single mutations or pairs of mutations, and these mutations were often considered as newly arising random mutations and thus not filtered by selection. But so far no predictions have been developed for the properties of experimental genotypic landscapes under Fisher’s model. Generating such predictions raises several challenges. First, the phenotypic layer between genotypes and fitness makes it is less straightforward to generate prediction for the properties of genotypic landscapes under Fisher’s model than under genotypic models. Second, most experiments use mutations that arise under the action of natural selection, either naturally or in experiment (Lee et al. 1997, Sanjuan et al. 2004, Rokyta et al. 2011, O’Maille et al. 2008, Lozovsky et al. 2009, Chou et al. 2011, Khan et al. 2011). This raises a theoretical challenge because selected mutations are a non-random sample of all mutations. For example, selection has been shown to bias the prevalence and type of epistasis among mutations (Draghi and Plotkin 2013). Some experiments have used random mutations (de Visser et al. 1997, Whitlock and Bourguet 2000, Sanjuan et al. 2004) and there is a recent interest in high-throughput random mutations approaches (e.g., Costanzo et al. 2010, Hietpas et al. 2011, Firnberg et al 2014), but even protocols designed to identify “random” mutations often involve selection at some stage (Bataillon and Bailey 2014). Third, the precise protocol used to isolate mutations potentially impacts the reconstructed genotypic landscape. In some experiments, each of the mutations was selected independently in distinct populations (Sanjuan et al. 2004, Rokyta et al. 2011). In others, all mutations arose sequentially in the same population (Lee et al. 1997, O’Maille et al. 2008, Lozovsky et al. 2009, Chou et al. 2011, Khan et al. 2011). The properties of selected mutations potentially depends on the genetic background in which they arise (because of epistasis), thus on the details of the protocol used to isolate them.

Here we combine a new analytical approximation and simulations to address these challenges and generate predictions for the properties of genotypic landscapes under Fisher’s model. We focus on selected mutations and we contrast several protocols (independently selected vs. co-selected mutations). We analyze the properties of selected mutations at several scales. We begin by introducing Fisher’s fitness landscape model and derive new analytical results on the properties and fitness effect of single selected mutations. In a second step, we derive predictions for the distribution of the coefficient of epistasis and the fraction of sign epistasis among two mutations. Last, we explore the properties of genotypic landscapes that include a larger number of mutations.

1. Model and methods

1.1 Fisher’s geometric model

We use Fisher’s fitness landscape model to define the relationship between genotypes, phenotypes, and fitness. We assume Gaussian stabilizing selection on a set of phenotypes. In mathematical terms, setting the optima at 0 for all phenotypes without loss of generality, the fitness of an individual with phenotype vector z is:

$$W\left(z\right)=\exp (-z^T\mathbf{S}z)$$ (1)

where S is a matrix representing the variance-covariance structure of selection. The diagonal elements determine the strength of direct stabilizing selection on each of the phenotypes, and the off-diagonal elements represent correlative selection between phenotypes. Mutations are assumed to affect all phenotypes to the same extent (universal pleiotropy). Specifically, the effects of each new mutation on the set of phenotypes are randomly drawn in a multivariate normal distribution with variance-covariance matrix M. Thus, each new mutation is unique and the pool of available mutations is infinite. We discuss later on the consequences of relaxing this assumption.

Since both S and M are positive semi-definite matrices, it is always possible to find a linear transformation of the phenotypic space, ensuring that in the transformed space all phenotypes are independent for selection (S becomes a diagonal matrix) and all phenotypes are independent and have equal variance by mutation (M becomes proportional to the identity matrix) (Waxman and Welch 2005, Martin and Lenormand 2006). The fitness function in the transformed space simplifies into $W\left(z\right)=\exp (-{\Sigma }_{i=1}^n{\lambda }_i{z}_i^2)$ where the λ_i are the eigenvalues of S.M. The dimension of the phenotype vector and the matrix,, represents the “complexity” of the organism in a phenotype space where selection acts independently along axes. For simplicity, we now assume an isotropic landscape, that is λ₁ = ⋯ = λ_n = 1.

1.2 Effect of selected mutations on phenotypes and fitness

An approximation

We assume that the ancestral strain in which mutations arise is located far from the optimum relative to the size of mutations, and we develop a novel approximation to describe the properties of selected mutations arising in this ancestral strain. This approximation is suitable to understand and interpret many situations relevant to experimental evolution, where the ancestral strain is grown in a novel environment to which it is initially poorly adapted. We set the ancestral strain at position $\{\sqrt{-\log \left[W_0\right]},0,0\dots ,0\}$ in the phenotypic space, where W₀ is the fitness of the ancestral strain. This assumption is made without loss of generality because of the isotropy of the landscape.

The distribution of phenotypic effects of random mutations {dz₁,dz₂,…,dz_n} follows a multivariate normal distribution $N(\mathbf{0},{\sigma }_{mut}^2{\mathbf{I}}_n)\left(N\right(.,.)$ denotes the normal distribution and I_n is the identity matrix of dimension n). ${\sigma }_{mut}^2$ is the mutational variance which quantifies the size of mutations in the phenotypic space. To understand how selection biases this distribution, we assume that the ancestral strain is sufficiently far from the optimum relative to the size of mutations that selection acts mainly along the first phenotypic axis that links the ancestral strain to the optimum (“main axis of selection”), and that all phenotypic changes along orthogonal directions cause negligible fitness changes. Thus, the phenotypic effects of mutations along axes 2 to n, {dz₂,dz₃,… dz_n} are distributed according to $N(\mathbf{0},{\sigma }_{mut}^2{\mathbf{I}}_{n-1})$ just as random mutations. To determine how selection impacts the distribution of phenotype effects of mutations along the main axis of selection, we assume that the population size N is large and the input of new mutations is small (i.e., Nμ << 1, where μ is the mutation rate), such that adaptation proceeds under a “strong selection – weak mutation” (SSWM) regime (Kimura 1983, Gillespie 1991). In this regime, there is no standing genetic variation, such that adaptation over this landscape is only enabled by new mutations arising within a genetically homogenous population. Deleterious mutations have a negligible probability to fix in the population, and the next beneficial mutation to invade is the realization of a random drawing among the pool of beneficial mutations where each beneficial mutation has a probability proportional to its selection coefficient to be chosen (Patwa and Wahl 2008). Because the selection coefficient of a mutation is linearly related to the phenotypic effect on the main axis (s = −2z_0,1 dz₁, Appendix), under the SSWM regime the scaled phenotypic effect along the first phenotype $-d{z}_1∕{\sigma }_{mut}^2$ is distributed according to a χ₂ distribution. χ_i denotes chi distribution with i the degrees of freedom: this is the distribution of the norm of vectors of dimension i drawn in a standard normal distribution, which must not be confused with the chi squared distribution, which is the distribution of the squared norm.

The geometry of selected mutations

It is more intuitive to translate these algebraic results in geometrical terms. A mutation and its fitness effect is characterized by its norms ||dz|| and its angle with the main axis of selection θ (see fig 1). We found that selected mutations are slightly larger than random mutations. In mathematical terms, the norm of selected mutations (the size of the mutation in the phenotypic space) scaled by the mutational standard deviation σ_mut is distributed according to a χ_n+1, while that of random mutations is a χ_n. Of course, the norm of mutations is larger in a more complex space because mutations modify the phenotype in many dimensions. Thus, to compare properties of selected mutations and genotypic landscapes across several complexities of the phenotypic space while keeping the same distance to the optimum, we scale the standard deviation as ${\sigma }_{mut}=\overline{\mid \mid dz\mid \mid }\Gamma \left(\frac{n}{2}\right)∕\left(\sqrt{2}\Gamma \left(\frac{n+1}{2}\right)\right)$, where Γ(.) is the gamma function and $\overline{\mid \mid dz\mid \mid }$ is the average norm of random mutations (constant across complexities). This relationship converges for large complexity to ${\sigma }_{mut}=\overline{\mid \mid dz\mid \mid }∕\sqrt{n}$, such that the average fitness effects of random mutations (equal to $-n{\sigma }_{mut}^2$) is also constant across complexities. We use this scaling for the simulations, but our analytical results are general with respect to the potential relationship between σ_mut and n. As a consequence of this scaling, the major effect of increasing complexity is to reduce the variance of the norm (fig. 1).

Figure 1.

The geometry of selected mutations in Fisher’s fitness landscape for various complexities of the phenotypic space. The left panel represents an isotropic landscape with n = 3. The log-fitness isocline in the phenotypic space is a sphere centered at the origin $\left(\log \right[W\left[z\right]]=-{\Sigma }_{i=1}^n{z}_i^2)$. The vertical axis is the main axis of selection. The ancestral strain and the optimum are shown as black points. A beneficial mutation is shown as a plain arrow. The geometry of the mutation is characterized by the norm ||z|| and by the angle between the mutations and the main axis of selection θ. On the right panel, the distribution of these quantities is shown for complexities n = 3, n = 10, n = 100. The mutational variance σ_mut was normalized such that the expected norm is the same for all complexities. At higher complexities, mutations tend to be almost orthogonal to the main axis of selection (θ → π/2) and to exhibit very little variation in their norm.

We also found that selected mutations point in the direction of the optimum when complexity is low, but that they point increasingly in a direction orthogonal to the optimum as complexity increases (the distribution of θ becomes concentrated around π/2), such that mutations pointing directly towards the optimum (θ = 0) become extremely rare (Appendix, fig. 1). This change in orientation at high complexity is due to the overwhelming importance of other phenotypic directions relative to the “main axis of selection”. In complex organisms, because of pleiotropy, beneficial mutations cause small changes on a myriad of other phenotypes as a side effect of changing the phenotypic value on the “main axis of selection”. This effect of complexity was previously noted in the context of random mutations (Hartl and Taubes 1998, Poon and Otto 2000).

1.3 Stochastic, individual-based simulations

To verify the analytical results, we simulated a population under selection, mutation and genetic drift under Fisher’s model. The population is of constant size N_e = 10⁷ and is initially composed of a single genotype whose position is drawn at random on the fitness isocline W₀ (the ancestral strain is maladapted on all phenotypic axes).

The number of individuals of each genotype after selection is drawn in a multinomial distribution with parameters N_e and $\left\{p\right({\mathbf{z}}_1\left)W\right({\mathbf{z}}_1)∕\stackrel{‒}{W},\dots ,p({\mathbf{z}}_g\left)W\right({\mathbf{z}}_g)∕\stackrel{‒}{W}\}$, where z_i is the phenotypic vector for genotype i, p(z_i) is the frequency of genotype i, W(z) is the fitness function given by Fisher’s model, g is the number of genotypes in the population, and $\stackrel{‒}{W}$ is the mean fitness $\stackrel{‒}{W}={\Sigma }_{i=1}^{g}p\left({\mathbf{z}}_i\right)W\left({\mathbf{z}}_i\right)$. In the simulations, we set the norm of random mutations, constant across complexity, to $\overline{\mid \mid dz\mid \mid }=0.1$.

Following selection, the number of mutations that affect an individual’s genome is given by a Poisson distribution with parameter μ = 10⁻⁹. The phenotypic effects of each mutation are drawn in a multivariate normal distribution (0, I_n) following the assumptions of Fisher’s model.

The low value of N_μ ensures that adaptation occurs by successive selective sweeps of beneficial mutations. We iterated the following life cycle until the desired number of mutations had fixed in the population or t_max = 10⁷ generations was reached. The output of a run was discarded when the desired number of mutations was not reached at t_max. This should not alter significantly our results, as it only happened for a very small fraction of runs.

2. Results

2. 1 Distribution of fitness effects of selected mutations

Under the SSWM regime and assuming the wild type is far from the optimum, the normalized fitness effects of selected mutations are distributed as a χ₂ (Appendix). In mathematical terms,

$$\begin{array}{cc}\hfill f^{\ast }\left(s\right)=& \frac{s}{4{\sigma }_{mut}^2(-\log [W_{00}\left]\right)}{\mathrm{e}}^{\frac{-s^2}{8{\sigma }_{mut}^2(-\log [W_{00}\left]\right)}}\text{if}S>0\hfill \\ \hfill f^{\ast }\left(s\right)=& 0\text{otherwise}\hfill \end{array}$$ (2)

This density is essentially the distribution of fitness effects of random mutations, weighted by their probability of fixation (assumed to be proportional to the selection coefficient s in the SSWM regime). The most frequent mutations to evolve have an intermediate fitness effect, because they represent the best compromise between occurring frequently and enjoying a high selection coefficient (Kimura 1983). The mean of this distribution is $\sqrt{2\pi }{\sigma }_{mut}\sqrt{-\log \left[W_0\right]}$ and the standard deviation is $\sqrt{2(4-\pi )}{\sigma }_{mut}\sqrt{-\log \left[W_0\right]}$. Under our assumptions, the distribution of fitness effects does not directly depend on complexity (although it would depend indirectly on complexity through the scaling). Indeed only the main axis of selection determines fitness, so the number of other phenotypic directions, assumed to be neutral, does not matter. Interestingly the coefficient of variation of the selection coefficient is $\sqrt{(4-\pi )∕\pi }\approx 0.52$ and is independent of initial fitness and the effect of mutations in the phenotypic space.

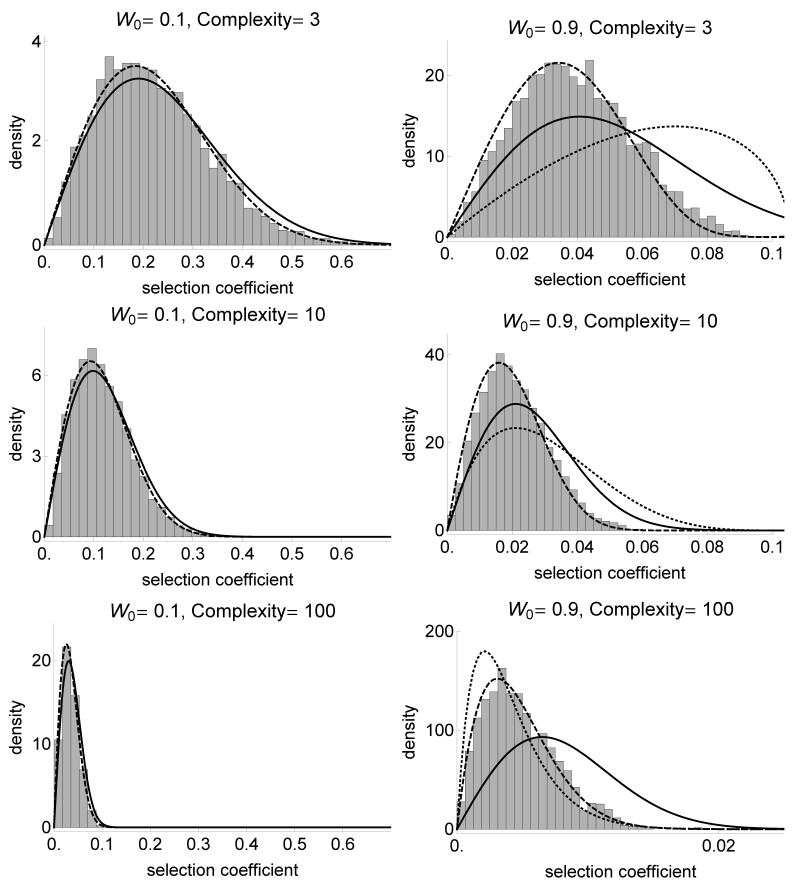
This analytical result was found to be a good approximation when compared with the results of stochastic, individual-based simulations, when the ancestral strain is far from the optimum (W₀= 0.1) (fig. 2). We also compared this approximation to two other approximations for the distribution of fitness effects of selected mutations in Fisher’s model. The first is the beta distribution based on extreme value theory (Martin and Lenormand 2008). This approximation does not depend on the phenotypic effects of mutation σ_mut but depends strongly on the complexity of the organism n (Appendix, equation S3d). It performs well when the ancestral strain is very close to the optimum (W₀₀ = 0.99; not shown), and indeed even with W₀₀ = 0.99 it is not very accurate. The second approximation is the gamma approximation based on a moment-matching method, which is always very accurate (Martin and Lenormand 2006; fig. 2; Appendix, equation S3c).

Figure 2.

Distribution of the selection coefficient under Fisher’s model for various fitnesses of the ancestral strain W₀ (left: far from the optimum, right: near the optimum) and various complexities of the phenotypic space (from bottom to top). The line is the χ₂ analytical approximation (equation 2), the dashed line is based on the gamma approximation developed in Martin and Lenormand (2006) (Appendix) and the dotted line for W₀ = 0.9 is the beta approximation developed in Martin and Lenormand (2008). Selection coefficient is calculated for 10000 selected mutations. σ_mut is scaled such that the average norm of the mutational effect on phenotype is constant equal to 0.1 across complexities. The population size is N = 10⁷ and the mutation rate μ = 10⁻⁹.

Given our analytical results on the properties of individual selected mutations in Fisher’s model, our goal now is to determine the emerging properties of genotypic landscapes composed of several mutations. Towards this goal, we next investigate the properties of pairs of mutations.

2. 2. Properties of pairs of mutations in Fisher’s landscape

Epistasis coefficient among selected mutations

We first examine the distribution of the epistasis coefficient, which quantifies non-multiplicative interactions for fitness between two mutations. The epistasis coefficient between two mutations is defined as $e=\log \left[\frac{W_{11}{W}_{00}}{W_{01}{W}_{10}}\right]$ where W₁₁ is the fitness of the double mutant and, W₀₁, W₁₀ are that of the two single mutants (the fitness of the ancestral strain is now denoted W₀₀ for clarity, because it bears the “0” allele at two loci). In Fisher’s fitness landscape model, it can be shown that epistasis is proportional to the scalar product of the effects of the two mutations in the phenotypic space (Martin et al. 2007):

$$e=-2\sum _{i=1}^{n}d{z}_{i}d{z}_i^{\prime }$$ (3)

where dz_i and dz_i′ are the phenotypic effect of two mutations on phenotype i. It has been shown previously that the coefficient of epistasis of random (newly arising) mutation does not depend on the fitness of the ancestral strain and is distributed as a N(0,4nσ⁻⁴) (Martin et al. 2007). Here we derive similar results for the distribution of the epistasis coefficient between selected mutations.

First we investigate the distribution of epistasis among two mutations that evolved in independent replicates. Specifically, we assume that each replicate starts with a monomorphic population of fitness W₀₀ and is let to evolve until one mutation arises and fixes.

The epistasis coefficient (equation 3) can be decomposed as the sum of a “selected epistasis” component which emerges from selection along the main axis of selection (first axis), and an independent “random epistasis” component, contributed by all other orthogonal axes and which we characterize using the approximation developed by Martin et al. (2007) (details in Appendix).

We find, assuming a SSWM regime and a wild type far from the optimum, that the mean and variance of the distribution of epistasis are:

$$\begin{array}{cc}\hfill \mathrm{E}\left(e\right)=& -\pi {\sigma }_{mut}^2\hfill \\ \hfill \mathrm{V}\left[e\right]=& (4n+12-{\pi }^2){\sigma }_{mut}^4\hfill \end{array}$$ (4)

These results reveal that the average epistasis is negative, meaning that two independent mutations that both bring the population closer to the optimum along the first axis tend to interact negatively for fitness. As complexity increases, the variance of the distribution of epistasis among selected mutations converges to the variance among random mutations, because effectively neutral phenotypes contribute increasingly more to epistasis. Importantly, as long as the distance to the optimum is large, epistasis among selected mutations does not depend on the fitness of the ancestral strain, just as for random mutations.

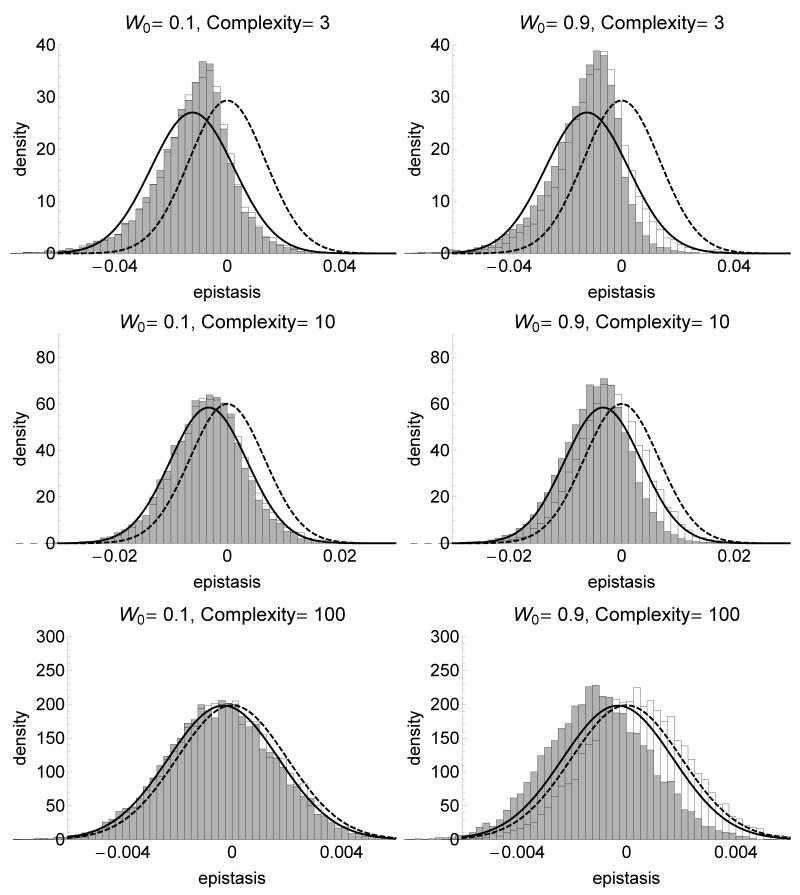
Figure 3 shows the predicted distribution of epistasis along with results of simulations described above. In general, our analytical approximations capture correctly the average and variance of epistasis when the population is initially not too close of the optimum (fig. 3, sup. fig.). It is worth noting that the impact of complexity on epistasis, which is apparently missing in equation 4, comes from the scaling of σ_mut with n that keeps the norm of random mutations constant across complexities. This scaling ${\sigma }_{mut}~1∕\sqrt{n}$ (when n is large) causes both the average and variance of epistasis to be proportional to 1/n. If we impose no particular scaling, the average epistasis is indeed constant across complexities (sup. fig.).

Figure 3.

Distribution of the epistasis coefficient e between two independently selected mutations (grey) and for co-selected mutations (white) for various fitnesses of the ancestral strain W₀ (left: far from the optimum, right: near the optimum) and complexities of the phenotypic space (from bottom to top). The plain line is the analytical approximation for independently selected mutations based on a normal distribution with mean and variance given by equation (4), and the dashed line is the normal approximation for random (newly arising) mutations (Martin et al. 2007). For independently selected mutations, the first mutations sweeping through the population in each of 20000 independent replicates were selected, and epistasis coefficient is calculated for 10000 independent pairs of selected mutations. For co-selected mutations, the first two mutations sweeping through the population in each of 10000 independent replicates were selected, resulting in 10000 independent epistasis coefficients. σ_mut is scaled such that the average norm of the mutational effect on phenotype is constant equal to 0.1 across complexities. The population size is N = 10⁷ and the mutation rate μ = 10⁻⁹.

Slight discrepancies with the predictions arise when the ancestral strain is close to the optimum relative to the size of mutations. Epistasis among independently selected mutations tends to be more negative than predicted analytically. Near the optimum, the selected mutations are more constrained to follow the direction of the optimum (θ is closer to 0 than expected) and this causes more negative epistasis on average. This “canalization” also causes a reduction in variance of epistasis close to the optimum.

Next we determine the distribution of epistasis arising between two mutations that arise and sweep to fixation sequentially in the same ancestral strain (“co-selected mutations”). We found that co-selected mutations have a distribution of epistasis very similar to that of independently selected mutations when the ancestral strain is far from the optimum; but that this distribution can be significantly shifted towards positive values of epistasis when the ancestral strain is closer to the optimum (fig. 3).

A simple argument explains why epistasis among co-selected mutations is distributed just as epistasis among independently selected mutations. Recall that epistasis is defined as $e=\log \left[\frac{W_{11}{W}_{00}}{W_{01}{W}_{10}}\right]$, where W₁₀ and W₀₁ are the fitness of genotypes with the first and second mutation respectively. We have shown that when the ancestral strain is sufficiently far from the optimum, the distribution of phenotypic effects of selected mutations is independent of the position of the ancestral strain (Appendix, equation S3a). If following fixation of the first mutation, the single mutant is still sufficiently far from the optimum, the second mutation will have the same distribution of phenotypic effects as the first mutation. Thus, the epistatic coefficient, which is related to phenotypic effects through equation (3), will be the same among co-selected mutations than among independently selected mutations.

The shift of epistasis towards more positive values when the ancestral strain is closer the optimum is due to antagonistic pleiotropy. Indeed, close to the optimum, changes in the phenotypic directions orthogonal to selection are not neutral but selected against. A selected mutation will bring the population closer to the optimum along the main direction of selection at the cost of antagonistic pleiotropy in the other phenotypes. When a second mutation arises in the background of the first, it will compensate for these antagonistic effects. This compensation generates positive epistasis between the two mutations. When complexity n is high, many phenotypes are available for that compensation effect to operate and positive epistasis becomes more pervasive (fig. 3). The observation that epistasis between selected mutations is negative for low complexity but positive for large complexity has been noted previously (Chevin et al. 2014).

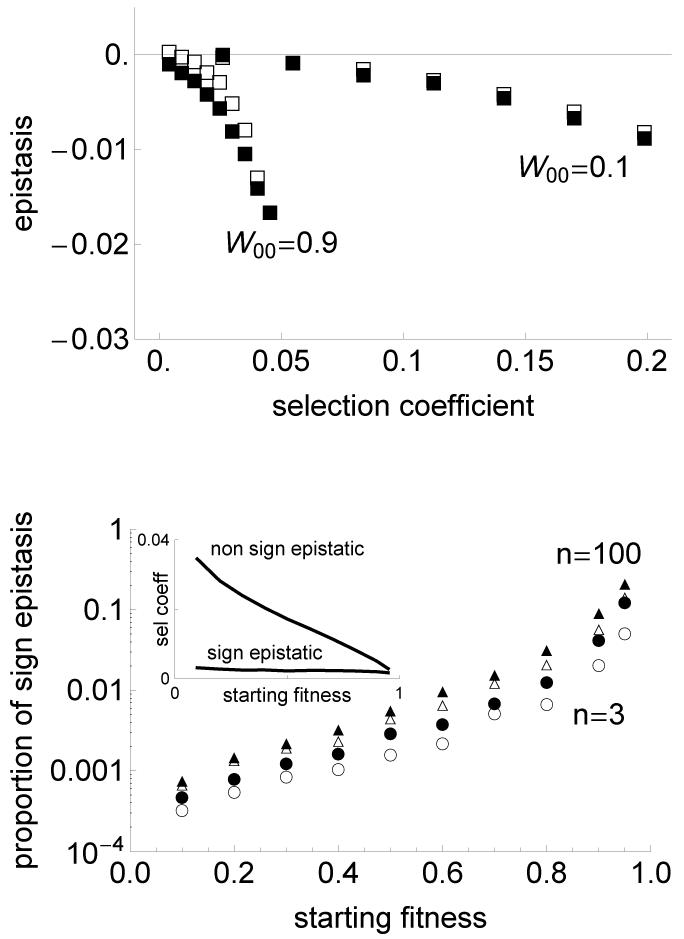
Lastly we found, in accordance with previous studies (Velenich and Gore 2014), that mutations conferring larger selective advantage exhibit more negative epistasis (fig. 4).

Figure 4.

Relationship between epistasis and the selection coefficient. Top panel: average epistasis coefficient between pairs of mutations as a function of the average selection coefficient of the two mutations, when W₀₀ = 0.1 and W₀₀ = 0.9, between independently selected mutations (filled squares) and co-selected mutations (open squares). For each parameter set, the selection coefficients were binned in 10 intervals of size (s_max − s_min)/10 and the average epistasis was computed for each of these bins when at least 10 pairs of mutations were present. For all curves complexity n = 10 (relationships are similar for other values of n). Bottom panel: Fraction of sign epistasis between two independently selected mutations (filled symbols) and between two co-selected mutations (open symbols). This is shown for complexities of the phenotypic space n = 3 (circles) and 100 (triangles). Inset shows the average coefficient of selection among non sign epistatic mutations (top curve) and sign epistatic mutations (bottom curve), as a function of the starting fitness, for complexity n = 3 and independently selected mutations (curves are similar for other parameters and selection procedure). The fraction of sign epistasis is calculated among at least 2000 independent pairs of mutations. Other parameters as in fig. 3.

Analytical predictions for selection and epistasis coefficients are important because these predictions can be directly compared to experimental data. These coefficients are also theoretically important to predict the dynamics of adaptation. However, they are difficult to relate to other properties such as the roughness and accessibility of the genotypic landscape. Such properties are determined by sign epistasis – the fact that mutations are beneficial in some background but deleterious in other backgrounds (Weinreich et al. 2005), which is not directly related to the epistasis coefficient. In the following part, we investigate the fraction of sign epistasis among selected mutations in Fisher’s model.

Sign epistasis among selected mutations

For independently selected mutations, we find that a mutation will present sign epistasis in the ancestral background vs. the background with another mutation when the selection coefficient is small and the epistasis coefficient is sufficiently negative (Appendix). Clearly, this condition will be increasingly easier to fulfill as the ancestral strain is closer to the optimum because the selection coefficient becomes smaller on average, and epistasis become more shifted towards negative values. Similarly, for co-selected mutations, because the epistasis coefficient is more positive on average among co-selected mutations, the first mutation should more rarely be sign epistatic. Thus sign epistasis is predicted to be less frequent among co-selected than among independently selected mutations. The effect of complexity on the fraction of sign epistasis is harder to predict, because both the selection and epistasis coefficients tend to be concentrated around 0 as complexity increases.

Our predictions are confirmed by stochastic simulations: sign epistasis is much more frequent when the fitness of the ancestral strain is higher, both in independently selected and co-selected mutations (fig. 4). Moreover, we found that sign epistasis is more frequent in a more complex phenotypic space. As much as 20% of sign epistasis occurred between independently selected mutations when W₀₀ = 0.95 and n = 100. This large fraction of sign epistasis may seem at first surprising since Fisher’s model is a completely smooth phenotypic landscape. Even more strikingly, this large fraction of sign epistasis emerges in the absence of optimum overshooting. Optimum overshooting – the fact that individual mutations are so large that their combined effects are deleterious (fig. 5) – can generate sign epistasis in Fisher’s model, but is not present for the values of parameters we chose because the ancestral strain is always too far away from the optimum relative to the size of mutations. To understand what causes sign epistasis, we looked more specifically at the properties of sign epistatic mutations and found that, on average, these mutations had larger norm, smaller selection coefficient and were more orthogonal to the main direction of selection (θ is closer to π/2). In other words, sign epistatic mutations are mutations of very small fitness effect with large antagonistic pleiotropy. Such mutations have a small beneficial effect in the background in which they evolve, but they easily become deleterious in another background (fig. 5). In more complex organisms, there are much more phenotypic axes along which antagonistic pleiotropy can arise, explaining why sign epistasis is more frequent.

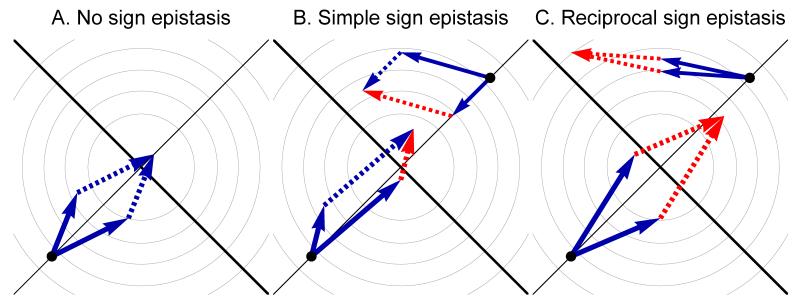
Figure 5.

The geometry of sign epistasis among two mutations in a two-dimensional Fisher’s fitness landscape model. The light gray lines are the fitness isoclines and the black lines are the phenotypic axes. Beneficial and deleterious mutations are shown respectively as blue and red arrows in the phenotypic space. In panel A, the two mutations are beneficial in the ancestral background and in the background with the other mutation (no sign epistasis). In panels B and C, two examples of pairs of sign epistatic mutations are shown. In B, one of the mutations is deleterious in the background with the other mutation (simple sign epistasis). In C, both mutations are deleterious in the background with the other mutation (reciprocal sign epistasis). In B and C, sign epistasis may occur by antagonistic pleiotropy (up, right) or optimum overshooting (bottom, left).

To conclude, a smooth phenotypic landscape such as that of Fisher’s model may generate high amounts of sign epistasis among mutations because of antagonistic pleiotropy, and especially so in complex organisms. This suggests that Fisher’s model has the potential to generate quite rough genotypic landscapes. In the following we explore this possibility by considering genotypic landscapes composed of a larger number of mutations.

2. 3. A great diversity of genotypic fitness landscapes is expected under Fisher’s phenotypic model

Several experiments study the properties of the fitness landscape by examining the genotypic landscape encompassing an ancestral genotype and a set of evolved genotypes differing from the ancestor by a small number of mutations L (typically 4-5 mutations). The genotypic landscape is composed of 2^L genotypes with all possible combinations of these mutations. Because of the stochasticity of the evolutionary process (stochasticity of mutations and genetic drift), a single underlying fitness landscape will generate a distribution of possible genotypic landscapes depending on the L mutations that are sampled. Thus, in the next part, we characterize the distribution of possible genotypic landscapes as a function of the parameters of the underlying fitness landscape (W₀ and n), when mutations are independently selected or co-selected.

Statistics summarizing the properties of a genotypic landscape

We use two commonly used statistics to summarize the properties of genotypic landscapes. The first is the fraction of sign epistasis among all pairs of genotypes separated by two mutations (as already investigated for the simpler case of two mutations in part 2.2 above). This proportion is 0 in an additive landscape and expected to be 2/3 among random mutations in a House of Cards model. Our simulations show it reaches 70 to 90% among independently selected mutations in the House of Cards model (not shown). The second statistic is the roughness to slope ratio (Carneiro and Hartl 2010, Szendro et al. 2013). This measure quantifies how well the landscape can be described by a linear model where mutations additively determine fitness. Specifically, the linear model is:

$$W^{\left(fit\right)}=c_0+\sum _{j=1}^L{c}_j{a}_j$$ (6)

where the sum is over all L loci, c_j is the effect of the mutation at the jth locus on fitness, and a_j is an indicator variable which is 0 or 1 if the jth locus is wild type or mutated respectively. The c_j are estimated by least square regression. The slope is the defined as the average additive effect of mutations, $s=\frac{1}{L}{\Sigma }_{j=1}^L\mid c_j\mid$, and the roughness is the residual variance that quantifies the fit of the linear model, $r=\sqrt{2^{-L}{\Sigma }_{genos}{(W-W^{\left(fit\right)})}^2}$. The roughness to slope ratio r/s is 0 when the fit of an additive model is perfect, and becomes very large in a House of Cards model.

Distribution of the statistics

We first investigated the distribution of the two above statistics when starting from an ancestral strain with fitness W₀₀ = 0.1, and when selecting five mutations according to the two sampling protocols described above (mutations occurring either independently in different replicates, or co-selected). We found that Fisher’s fitness landscape consistently generates a genotypic landscape very close to a smooth, additive landscape when the ancestral strain is far from the optimum relative to the size of mutations (W₀₀ = 0.1 and ${\overline{\mid \mid z\mid \mid }}_{rand}=0.1$). Specifically, there is no sign epistasis in more than 95% of landscapes and the roughness to slope ratio is always very close to 0. Interestingly, the genotypic landscape is closer to additive in phenotypic landscapes of higher complexity (lower r/s ratio) (fig. 6). This is because the deviation from strict additivity is due to the curvature of the fitness landscape, which appears smaller in more complex landscapes because the effects of mutations in the direction of the optimum are smaller.

Figure 6.

The distribution of the roughness to slope ratio and the fraction of sign epistasis over 1000 genotypic fitness landscapes generated with 5 mutations. Top left panel: distribution of roughness to slope ratio when W₀₀ = 0.1, for three levels of complexity, for independently selected mutations (distributions for co-selected mutations are very similar). In these conditions, there is no sign epistasis in more than 95% of the landscapes. Top right panel: distribution of the statistics in independently selected (blue) vs. co-selected mutations (purple). Bottom panel: distribution of the statistics for different levels of complexity (n = 3, n = 10, n = 100 in blue, red, green) in independently selected mutations (left) and co-selected mutations (right). Statistics corresponding to three experimental landscapes are superimposed (C: Chou et al. 2011, K: Khan et al. 2011, W: Weinreich et al. 2006).

In a second step, we investigated genotypic landscapes that emerge when the ancestral strain is fitter (W₀₀ = 0.9). Three general tendencies emerge from the distribution of these statistics (fig. 6). First, complexity does not affect much the distribution of the statistics. Again, this is because we scale the norm of mutations such that the expected norm is constant across complexity. Second, the properties of the genotypic landscapes depend strongly on the sampling protocol. Specifically landscapes generated from independently selected mutations tend to be more rough than those generated from co-selected mutations. Indeed, landscapes with co-selected mutations include at least one evolutionarily accessible path from the initial genotype to the genotype of maximal fitness, and tend to exhibit mutations of smaller effect on average, which generates less rough genotypic landscapes. Third, and more strikingly, a great diversity of genotypic landscapes may be generated with the same underlying fitness landscape because of the inherent stochasticity of the evolutionary process (fig. 6, 7).

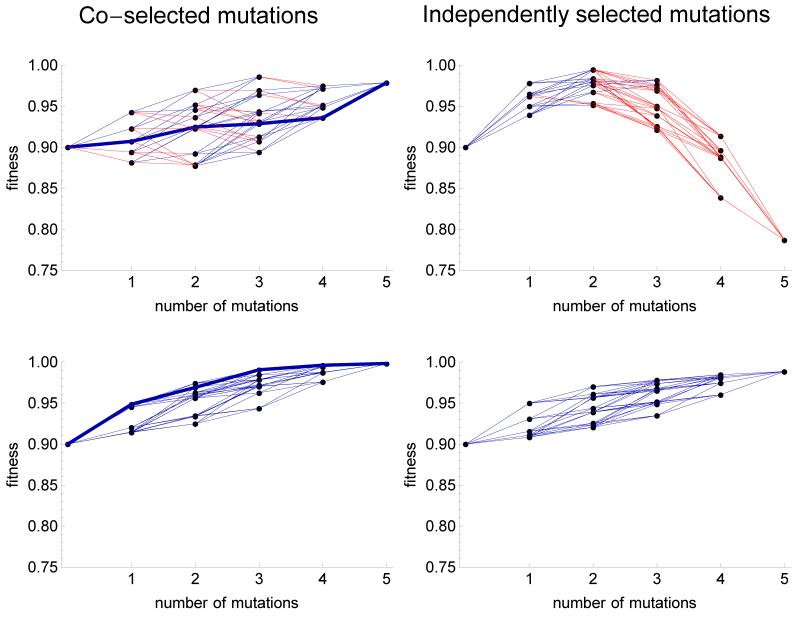
Figure 7.

Rough (top) and smooth (bottom) fitness landscapes obtained with 5 co-selected (left) or independently selected (right) mutations in Fisher’s model, with the same parameters (n = 3, W₀₀ = 0.9). Fitness of the 2⁵ = 32 genotypes is shown as a function of the number of mutations relative to the ancestor. The black points represent genotypes’ fitnesses, and the blue and red links are beneficial and deleterious mutations respectively. The thicker links represent the evolutionary path that was actually taken in the simulation, for co-selected mutations. In some cases, the genotypic landscape generated by independently selected mutations reflects quite clearly the presence of an optimum in fitness.

Discussion

Main results

Fisher’s fitness landscape is a smooth phenotypic landscape with stabilizing selection towards a single optimum. Yet non-trivial properties of individual random mutations and their interactions emerge from that model. In the present paper, we have explored the properties of genotypic fitness landscapes generated by adaptive mutations in Fisher’s fitness landscape model and developed analytical predictions that apply when the ancestral strain is far from the optimum.

First, selected mutations may point in the direction of the optimum in simple organisms, but in more complex organisms they are often almost orthogonal to the main direction of selection because of the numerous pleiotropic effects of mutations. The fitness effects of selected mutations follow a χ distribution with 2 d.f., independent of the complexity, with an invariant coefficient of variation of approximately 0.5.

Second, the epistasis coefficient among pairs of selected mutations is on average negative when the ancestral strain is far from the optimum. When the ancestral strain is close to the optimum, the epistasis coefficient is on average more strongly negative between independently selected mutations. For co-selected mutations, epistasis is negative on average in landscapes of low complexity but can become positive when complexity gets very high. Sign epistasis – the fact that a mutation may be beneficial or deleterious depending on the background in which it appears–may be common in Fisher’s model, especially when the ancestral strain is close to the optimum relative to the size of mutations. The cause of sign epistasis in Fisher’s model when far from the optimum is antagonistic pleiotropy, whereby the combination of pleiotropic effects in multiple phenotypic directions are deleterious in the double mutant. As a consequence, sign epistasis occurs more frequently in more complex organisms.

Third, we explore how these properties of pairs of mutations scale up to the global properties of genotypic landscapes made of all combinations of mutations between an ancestral strain and an evolved genotype. When the ancestral strain is far from the optimum, these empirical landscapes are smooth and very similar to an additive landscape. However, when the ancestral strain is close to the optimum, the landscape can encompass some roughness, especially when mutations have been independently selected. Even though all landscapes have a major additive component, an appreciable variety of empirical genotypic landscapes can be observed across different replicate simulations using the same set of parameters.

Critical assumptions

Our analytical results rely on several assumptions. First we assumed that the landscape is isotropic, that is the eigenvalues of SM (the product of the selection matrix and the mutation matrix) are all identical. Recent work suggests that the isotropic landscape emerges under a relatively general set of “first principles” (Martin 2014). Our analytical results may be extended to anisotropic landscape when the ancestral strain is maladapted only on one phenotype (Appendix, sup. fig.), but it remains to be explored how the outcomes are modified when the landscape is anisotropic and when the ancestral strain is maladapted on several phenotypes. Simulations suggest that anisotropy may alter the average value of epistasis (sup. fig.). Second we assume universal pleiotropy, whereby each mutation affects all phenotypes of the organism. We predict that restricted pleiotropy will reduce the fraction of sign epistasis and the roughness of small genotypic landscapes. Indeed, if restricted pleiotropy only makes the norm of mutations smaller (Lourenço et al. 2010), then the optimum will appear further away in the phenotypic space and sign epistasis will be less common. If restricted pleiotropy also reduces the complexity of the sub-space affected by mutations (Chevin et al. 2010), antagonistic pleiotropy will be less common and this will also make sign epistasis less common. Also, note that we scale the mutational effect such that complexity does not affect the expected norm of mutations in the phenotypic space. With a different scaling such that the norm of mutations is larger in a more complex space, an even greater impact of complexity on sign epistasis and roughness is expected. Third, we assume that the pool of available beneficial mutations is infinite: each mutation that can occur and fix in the population is unique. If the number of available beneficial mutations were reduced, we expect less variation across replicate genotypic landscapes because the same beneficial mutations will be sampled several times across replicates. However this effect will be important only when the number of beneficial mutations is very reduced, and is likely to be irrelevant in a number of contexts where the pool of available beneficial mutations is of the order of tens or hundreds (Salverda et al. 2011, Tenaillon et al. 2012, Schenk et al. 2013). This confirms the relevance of continuous (phenotypic) landscapes (Achaz et al. 2014) and implies that an empirical landscape built from a handful of mutations is a single random sample among all possible sets of adaptive mutations. The last important assumption is that of “Strong Selection – Weak Mutation” regime. Under this regime, adaptation occurs by successive fixation of beneficial mutations. If the mutation rate and/or population size are large (Nμ >> 1), several beneficial mutations will compete in the population (clonal interference) and beneficial mutations of larger fitness effect on average will fix. Thus, genotypic landscapes may also vary depending on the evolutionary regime, a possibility that would be worth exploring in future work.

Comparison with previous theoretical work

Our study complements previous work. Draghi and Plotkin (2013) studied the patterns of epistasis along adaptive walks in Kauffman’s NK model and in a simulated RNA folding landscape, and examined the implications of their results for in the light of experimental data from bacterial populations. They found a predominance of antagonistic (negative) epistasis in the early steps of adaptation and of synergistic (positive) epistasis later on. This result is very similar to our finding that co-selected mutations tend to interact negatively for fitness far from the optimum, but positively close to the optimum (fig. 3). Both illustrate the limited number of options left for adaptation when close the optimum (Greene and Crona 2014). Draghi and Plotkin’s observation stems directly from the finiteness of the genotypic space. Close to the optimum, there are very few beneficial mutations; if one of these mutations fixes, it is very likely that adaptation will proceed further through other beneficial mutations that were “unlocked” by the fixation of the last beneficial mutation. In Fisher’s model, in contrast, more positive epistasis close to the optimum is due to the fact that most beneficial mutations exhibit antagonistic pleiotropy. The second mutation compensates for antagonistic pleiotropy of the first mutation. In our model this effect is observed in particular in more complex organisms where compensation operates in multiple phenotypic directions.

Testing our predictions with experimental data

Our analytical and simulation results generate a number of testable predictions for experimental work. We qualitatively compared several of these predictions with published data, and we found that in general the available data is in good agreement with Fisher’s model.

First, we tested the prediction that the coefficient of variation of the distribution of fitness effect of selected mutation is approximately 0.5 (equation 2). Two data sets on adaptation of E. coli to minimum glucose medium (Rozen et al. 2002) and adaptation of Pseudomonas aeruginosa to rifampicin (MacLean et al. 2010) are suitable to test this prediction. We found the distribution of fitness effects of selected mutations in these datasets has c_v = 0.44 and c_v = 0.42 respectively, which is in relatively good agreement with the prediction.

Second, our results on the distribution of epistasis among pairs of selected mutations suggest that complexity of the organism and the mutational variance could be estimated from data. This approach has been suggested using the distribution of fitness effects of random mutations (Martin et al. 2007). Yet with random mutations, n and σ_mut could not be estimated independently. Here on the contrary, the mean and variance of the distribution give access to n and σ_mut independently. For example, the coefficient of variation of epistasis is equal to $-\sqrt{\frac{4}{{\pi }^2}n+\frac{12}{{\pi }^2}-1}$, from which the complexity n can inferred. Moreover, the distribution of the selection coefficient can be used to infer the initial fitness W₀₀ (equation 2). We computed n and σ_mut for Methylobacterium adapting to methanol medium (Chou et al. 2011). In that dataset, the strain was initially extremely maladapted and four beneficial mutations were quickly selected. Using the distribution of epistasis among these pairs of mutations we found n = 8 and ${\sigma }_{mut}^2=0.007$.

Third, we tested whether the distribution of statistics characterizing the full genotypic landscape was compatible with the predictions of Fisher’s model. We developed three predictions: first mutations arising in an ancestral strain far from the optimum relative to the size of mutations generate a close-to-additive fitness landscape, while mutations arising in a fitter background generate more rough landscapes. To test this prediction, we compared the fraction of sign epistasis and roughness to slope ratio for two published experimental landscapes (Chou et al. 2011, Khan et al. 2011) that differ in their initial maladaptation, as the first one exhibits an increase in fitness of 100% over 600 generations while the other one fitness increased of 30% over 2000 generations. As expected the landscape starting from a better-adapted strain (Khan et al. 2011) exhibited more sign epistasis and a higher roughness to slope ratio than the landscape starting from a very poorly adapted strain (Chou et al. 2011) (fig. 6). The second prediction is that the properties of genotypic landscapes depend on the procedure by which mutations are sampled (Szendro et al. 2013), and in particular that co-selected mutations tend to show less epistasis than independently selected mutations. Chou et al.’s dataset is also meeting this prediction. While mutations arising in the same replicate exhibited little sign epistasis (Chou et al. 2011), mutations occurring in independent populations exhibited substantial levels of antagonistic and sign epistasis (Chou et al. 2014). In this system all mutations resulted in a decrease of the expression of an operon carried on a plasmid. The combined effects of two mutations occurring independently resulted in too low levels of expression, hence lower fitness. In addition, the genotypic landscape reconstructed in Weinreich et al. (2006), which comprises 5 mutations which did not all evolve together (only some combinations of these mutations were found together in the same population) exhibits a high fraction of sign epistasis and roughness to slope ratio compatible with independently selected mutations in Fisher’s model. It is encouraging to note that the joint values of the two statistics in the three experimental landscapes we examined fall squarely in the density of points generated with Fisher’s model (fig. 6). However the relationship between the two statistics could be a property exhibited by many fitness landscapes and not a specific prediction of Fisher’s model. Indeed Szendro et al. (2013) find a similar relationship in the “Rough Mount Fuji” model (see their fig. 4). The third prediction on genotypic landscapes under Fisher’s model is that, when close to the optimum or when mutations have effects large enough to get close to the optimum, a wide diversity of genotypic landscapes may emerge as independent realizations of stochastic sampling of a set of mutations evolved on a single underlying landscape. This is in line with the experimental results of Schenk et al. (2013), who show that several genotypic landscapes of adaptation to cefotaxime resistance in the enzyme TEM-1 β-lactamase have distinct properties. Sign epistasis and roughness were contingent on the sample of mutations used to build the landscape (Schenk et al. 2013) and generated a diversity of landscapes strikingly similar to the ones plotted in figure 7. To our knowledge, there are no other examples of such replicate landscapes, but we should keep in mind that stochasticity in the emergence and evolutionary fate of mutations may explain a substantial amount of variability observed among empirical landscapes. This variability is not necessarily due to different properties of the underlying fitness landscape. It will be important to design statistical tools that make more precise what information on the underlying landscape is contained exactly in a small genotypic landscape.

To summarize, the good agreement between our qualitative predictions and experimental data, and the diversity of landscapes that Fisher’s model may generate, suggest that Fisher’s model may be used as a flexible tool to describe the relationship between genotypes and fitness. Specifically, although Fisher’s model is based on a smooth phenotypic space, it may actually be used to interpret experimental evolution results where very short adaptive walks and highly rugged genotypic landscapes are observed (e.g., Gifford et al. 2011). These limitations call for more flexible and more robust methods to estimate the parameters of Fisher’s model from experimental data. Of course, it would also be necessary to compare more rigorously the explanatory power of different fitness landscape models. For example, the “Rough Mount Fuji” model (Szendro et al. 2013) or the NK model (Franke et al. 2011) are also able to explain a diversity of patterns observed in experimental data. The analytical and simulation results presented here are a step forward towards this goal. But Fisher’s model appears as a good candidate to standardize and unify a growing and disparate body of experimental work.

Supplementary Material

S1

Supplementary figure

Mean (left graphs) and variance (right graphs) of the epistasis coefficient as a function of the fitness of the ancestral strain for several scenarios (rows). In each graph, mean or variance of epistasis is shown between independently selected mutations (closed symbols) and co-selected mutations (open symbols), and for complexities of the phenotypic space (circles), 10 (squares) and 100 (triangles). The lines are the analytical approximation for n = 3 independently selected mutations. First row: main model, the isotropic landscape (λ₁ = λ₂ = ⋯ = λ_n = 1), the ancestral strain is maladapted along the first axis and a scaling between σ_mut and n ensures that the norm of random mutations is constant across complexities (||dz|| = 0.1). Second row: as main model, but σ_mut = 0.1 for all n (no scaling). Third row: anisotropic landscape where selection is heterogeneous. Selection on the ith phenotype is, ${\lambda }_i=0.5+\frac{i-1}{n-1}$, and the ancestral strain is maladapted along the first axis. The approximation is given by equation (S14). Fourth row: anisotropic landscape where selection is heterogeneous. Selection on the ith phenotype is ${\lambda }_i=0.5+\frac{i-1}{n-1}$, and the ancestral strain is maladapted along all axes equally. This is compared with the approximation given by equation (4) (isotropic model with all λ_i equal to 1). The epistasis coefficient is calculated among at least 2000 independent pairs of mutations. Other parameters as in fig. 3.

Appendix for “Properties of selected mutations and genotypic landscapes under Fisher’s Geometric Model”

1. Properties of selected mutations

Distribution of phenotypic effects and selection coefficient of fixed mutations

We use the following fitness function to define the relationship between phenotypes and fitness: $W\left[z\right]=\exp [-{\Sigma }_{i=1}^n{\lambda }_i{z}_i^2]$, where z_i is the phenotype i, λ_i is the strength of selection on phenotype i and n is the total number of phenotypes (the complexity). In the Appendix we derive analytical results where the λ_i are kept unspecified, but in the main text, for simplicity, we restrict the analysis to the isotropic landscape λ₁ = ⋯ = λ_n = 1. We assume the phenotype of the ancestral strain is $\{\sqrt{-(1∕{\lambda }_1)\log \left[W_{00}\right]},0,0\dots ,0$ where W₀₀ is the fitness of the ancestral strain. We make the approximation that selection operates only along the first phenotypic axis (this approximation works best when the ancestral strain is far from the optimum). As a consequence, selection affects the distribution of phenotypic effects of selected mutations along the first axis only, and the distribution of phenotypic effects along all other n−1 directions is exactly the same as the distribution of random phenotypic effects (i.e., $N(0,{\sigma }_{mut}^2)$ where N stands for the normal distribution).

To derive the distribution of selected phenotypic effects along the first axis, we assume we are in a “strong selection – weak mutation” regime. In this regime, the next beneficial mutation to fix in the population is obtained by a random drawing among the pool of beneficial mutations, with each mutation is weighted by its selection coefficient (Kimura 1983). Thus, the distribution of selected phenotypic effect will be the distribution of random phenotypic effect weighted by the selective effect of the mutation along the first axis. To derive the distribution of phenotypic effects along the first axis, we need to know what is the selection coefficient acting on a mutant with effect on the first phenotype dz₁. This is given by:

$$s_1=\underset{log-fitnessofmutant}{\overset{-{\lambda }_1{(z_{0,1}+d{z}_1)}^2}{\underbrace{}}}+\underset{log-fitnessofwildtype}{\overset{{\lambda }_1{z}_{0,1}^2}{\underbrace{}}}=-2{\lambda }_1{z}_{0,1}d{z}_1-{\lambda }_{1}d{z}_1^2$$ (S1)

with $z_{0,1}=\sqrt{-(1∕{\lambda }_1)\log \left[W_{00}\right]}$. Thus, the distribution of phenotypic effects along the first direction is given by the product of the selection coefficient $-2{\lambda }_1{z}_{0,1}d{z}_1-{\lambda }_{1}d{z}_1^2$ and the distribution of phenotypic effects of random mutations ${\mathrm{e}}^{\frac{-d{z}_1^2}{2{\sigma }_{mut}^2}}$ (Fisher 1930, Kimura 1983), that is:

$$\begin{array}{cc}\hfill g\left(d{z}_1\right)=& \frac{1}{k}(-2{\lambda }_1{z}_{0,1}d{z}_1-{\lambda }_{1}d{z}_1^2)\mathrm{e}\frac{-d{z}_1^2}{2{\sigma }_{mut}^2}\text{if}d{z}_1<0\hfill \\ \hfill g\left(d{z}_1\right)=& 0\text{otherwise}\hfill \end{array}$$ (S2a)

where κ is a normalizing constant. Similarly the distribution of fitness effect of fixed mutations is given by:

$$\begin{array}{cc}\hfill f^{\ast }\left(s\right)=& \frac{1}{{\kappa }^{\prime }}sf\left(s\right)\text{if}s>0\hfill \\ \hfill f^{\ast }\left(s\right)=& 0\text{otherwise}\hfill \end{array}$$ (S2b)

where κ′ is another normalizing constant and f(s) is the distribution of fitness effects of random mutations.

Assuming mutation effects on the phenotype are small relative to the distance to the optimum, we may ignore the $d{z}_1^2$ term in (S2a), and the selection coefficient is directly proportional to the phenotype at the first axis s ≈ −2λ₁,z_0,1dz₁. In this case the distribution of phenotypic effects of mutations along the first axis simplifies to:

$$\begin{array}{cc}\hfill g\left(d{z}_1\right)=& \frac{-d{z}_1}{{\sigma }_{mut}^2}{\mathrm{e}}^{\frac{-d{z}_1^2}{2{\sigma }_{mut}^2}}\text{if}d{z}_1<0\hfill \\ \hfill g\left(d{z}_1\right)=& 0\text{otherwise}\hfill \end{array}$$ (S3a)

The above expression reveals that −d z₁/σ_mut follows a χ₂ (χ_i denotes a chi distribution with i degrees of freedom). Similarly the distribution of selection coefficients of selected mutations is:

$$\begin{array}{cc}\hfill f^{\ast }\left(s\right)=& \frac{s}{4{\sigma }_{mut}^2{\lambda }_1(-\log [W_{00}\left]\right)}{\mathrm{e}}^{\frac{-s^2}{8{\sigma }_{mut}^2{\lambda }_1(-\log [W_{00}\left]\right)}}\text{if}s>0\hfill \\ \hfill f^{\ast }\left(s\right)=& 0\text{otherwise}\hfill \end{array}$$ (S3b)

Which gives equation (2) of the main text when λ₁ is set to. The coefficient normalized by $4{\sigma }_{mut}^2{\lambda }_1(-\log [W_{00}\left]\right)$ follows a χ₂. Note that several others approximations for f(s) may be plugged into equation (S2b) to find other approximations for the fitness effects of selected mutations (e.g., the normal distribution of Waxman and Peck 1998, Lourenço et al. 2011, or the gamma distribution of Martin and Lenormand 2006). For example, in the isotropic case (no heterogeneity in selection, λ₁ = ⋯ = λ_n = 1) we used the displaced gamma distribution proposed by Martin and Lenormand and obtained the following distribution:

$$\begin{array}{cc}\hfill f^{\ast }\left(s\right)=& \frac{1}{\kappa }s\frac{1}{\Gamma \left(\beta \right){\alpha }^{\beta }}{(-s-\log [W_{00}\left]\right)}^{\beta -1}{\mathrm{e}}^{\frac{-s-\log \left[W_{00}\right]}{\alpha }}\text{if}0<s<-\log \left[W_{00}\right]\hfill \\ \hfill f^{\ast }\left(s\right)=& 0\text{otherwise}\hfill \end{array}$$ (S3c)

where $\alpha =\frac{2(1+2∊){\sigma }_{mut}^2}{1+∊}{\lambda }_e$, $\beta =\frac{n_e}{2}\frac{{(1+∊)}^2}{1+2∊}$ with $∊=\frac{-\log \left[W_{00}\right]}{n_e{\sigma }_{mut}^2}$ and κ is a normalizing constant (with a lengthy expression). We also compared these analytical predictions with the beta distribution based on Extreme Value Theory (Martin and Lenormand 2008), given by:

$$\begin{array}{cc}\hfill f^{\ast }\left(s\right)=& s\frac{{\left(1+\frac{s}{\log \left[W_0\right]}\right)}^{\frac{n}{2}-1}}{\beta [2,\frac{n}{2}]\log {\left[W_0\right]}^2}\text{if}0<s<-\log \left[W_0\right]\hfill \\ \hfill f^{\ast }\left(s\right)=& 0\text{otherwise}\hfill \end{array}$$ (S3d)

Geometry of selected mutations

The algebraic results derived above can be translated in geometric terms. The angle between a selected mutation and the first phenotypic axis can be calculated as:

$$\theta ={\tan }^{-1}\left[\frac{\sqrt{{\sum }_{i=2}^{n}d{z}_i^2}}{\sqrt{d{z}_1^2}}\right]$$ (S4)

where the numerator is the norm of the resultant vector of the phenotypic space in all “neutral directions (phenotypic directions 2 to n), and the denominator is the norm of the vector in the first phenotypic direction (under selection). Because both the numerator and the denominator follow χ distributions when appropriately scaled, the quantity $\frac{2}{n-1}\tan {\left[\theta \right]}^2$ is distributed according to a F-distribution with degrees of freedom n − 1 (corresponding to the numerator) and 2 (corresponding to the denominator) when appropriately scaled. It follows a relatively simple expression for the distribution of the angle θ:

$$f\left(\theta \right)=(n-1)\cos \left[\theta \right]{\sin }^{n-2}\left[\theta \right]\text{for}\theta \in [0,\frac{\pi }{2}]$$ (S5)

Lastly, the norm of selected mutations scaled by σ_mut is distributed according to a chi distribution with degrees of freedom (n + 1). This follows from the fact that the effect along the first phenotype normalized by σ_mut is χ₂ while all other effects (along the n − 1 other phenotypes) are $N(0,{\sigma }_{mut}^2)$ distributed. Thus the sum of squares is a ${\chi }_{n+1}^2$ and the norm is a χ_n+1.

These geometrical results can be extended to describe the relationship between two independently selected mutations. Whatever the complexity of the phenotypic space, it is possible to represent the relationship between two independent mutations and the optimum in a 3-dimensional space. This can be done using the Gram-Schmidt process, which generates an orthonormal basis for this 3-dimensional space in which the norm and angles are conserved (note that this space will of course be different for each pair of mutations considered). The relative disposition of the two mutations in the 3D space is characterized by their norms, the angles they have with the main direction of selection, and the angle between the two mutations when projected on a plane orthogonal to the main axis of selection (the azimuth). Because the fitness effect of a mutation does not change when it revolves around the main axis of selection, this angle is well characterized by the distribution of angles of random mutations for n − 1 phenotypic directions, that is (Poon and Otto 2000):

$$f\left(\psi \right)=\frac{\Gamma \left(\frac{n-1}{2}\right)}{\sqrt{\pi }\Gamma \left(\frac{n-1}{2}\right)}\sin {\left[\psi \right]}^{n-3}\text{for}\psi \in [0,\pi ]$$ (S6)

The angles of the two mutations with the main axis of selection, which we call θ and θ′ together with the azimuth ψ are sufficient to find the angle between two mutations α:

$$\cos \left[\alpha \right]=\sin \left[\theta \right]\sin \left[{\theta }^{\prime }\right]\cos \left[\psi \right]+\cos \left[\theta \right]\cos \left[{\theta }^{\prime }\right]$$ (S7)

where θ and θ′ lie in $[0,\frac{\pi }{2}]$ and ψ in [0, π]. Although we know the distribution of θ, θ′ and ψ, we were not able to derive explicitly the distribution of α. The average of the distribution of cos [α] is $\frac{\pi }{4}\frac{\Gamma {\left(\frac{n+1}{2}\right)}^2}{\Gamma {\left(1+\frac{n}{2}\right)}^2}$. This average is a decreasing function which is equal to 4/9 when n = 3 and tends to 0 as the complexity increases. Hence, the distribution of cos[α] becomes increasingly concentrated around 0 as the complexity increases (i.e., the distribution of α is concentrated around π/2). Thus, in a very complex phenotypic space two independent mutations tend to be perpendicular in the phenotypic space.

2. Distribution of epistasis among selected mutations

Epistasis among two mutations is defined as:

$$e=\log \left[\frac{W_{11}{W}_{00}}{W_{01}{W}_{10}}\right]$$ (S8)

Where W₀₀ = W₀ is the fitness of the ancestral strain, W₁₁ is the fitness of the double mutant, and W₁₀ and W₀₁ are the fitnesses of the two single mutants. Under Fisher’s model of adaptation where the fitness of a genotype characterized by n phenotypes z_i with i ∈ [1, n] is given by ${\mathrm{e}}^{-{\Sigma }_{i=1}^n{\lambda }_i{z}_i^2}$, epistasis reduces to (Martin et al. 2007):

$$e=-2\sum _{i=1}^n{\lambda }_{i}d{z}_{i}d{z}_i^{\prime }$$ (S9)

where dz_i and dz_i′ are the phenotypic effects of two independent mutations that evolved in this background. Equation (S9) gives equation (3) of the main text when the λ_i are set to 1.

Under our approximation, we can partition epistasis into a component due to mutational effect along the first (selected) axis and a component due to mutational effect along all other axes:

$$e=\underset{e_{sel}}{\overset{-2{\lambda }_{1}d{z}_{1}d{z_1}^{\prime }}{\underbrace{}}}\underset{e_{neutral}}{\overset{-2\sum _{i=2}^n{\lambda }_{i}d{z}_{i}d{z_i}^{\prime }}{\underbrace{}}}$$ (S10)

The second component follows the distribution of neutral epistasis for n − 1 phenotypes. This can be approximated by a normal distribution with mean 0 and variance $4(n-1){\stackrel{‒}{\lambda }}^2{\sigma }^4$ where the average $\overline{{\lambda }^2}$ is taken over phenotypes 2 to n − 1 (Martin et al. 2007). The first component is the product of two independent random variables following the distribution given by (S3a). It can be shown using the standard formula for the probability density function of two independent random variables that the probability density function of this component is:

$$\begin{array}{cc}\hfill p\left(e_{sel}\right)=& \frac{-e_{sel}}{4{\lambda }_1^2{\sigma }_{mut}^4}{Y}_0\left(\frac{-e_{sel}}{2{\lambda }_1{\sigma }_{mut}^2}\right)\text{if}{e}_{sel}<0\hfill \\ \hfill p\left(e_{sel}\right)=& 0\text{if}{e}_{sel}>0\hfill \end{array}$$ (S11)

where Y₀(.) is a Bessel function of the second kind (it is defined as the solution of a differential equation). The total density of epistasis is thus a convolution between the function defined in (S11) and the density of a $N(0,4(n-1\left)\overline{{\lambda }^2}{\sigma }^4\right)$:

$$h\left(e_{sel}\right)={\int }_{-\infty }^0\left(\frac{1}{2\sqrt{2\pi (n-1)\stackrel{‒}{{\lambda }^2}{\sigma }_{mut}^2}}-\exp \left[\frac{-{(e-e_{sel})}^2}{2\ast 4(n-1)\stackrel{‒}{{\lambda }^2}{\sigma }_{mut}^4}\right]\right)\left(\frac{-e_{sel}}{4{\lambda }_1^2}{\sigma }_{mut}^4{Y}_0\left[\frac{-e_{sel}}{2{\lambda }_1{\sigma }_{mut}^2}\right]\right)d{e}_{sel}$$ (S12)

We were not able to find a simpler expression for this convolution. But as the number of phenotypes increases, epistasis should increasingly look like a normal distribution with proper mean and variance, because all non-selected phenotypes will progressively have more weight in the convolution. The mean and the variance of epistasis can be found by summing up the mean and variances of the two components of epistasis. The mean and variance of selected epistasis are:

$$\begin{array}{cc}\hfill \mathrm{E}\left[e_{sel}\right]=& -\pi {\lambda }_1{\sigma }_{mut}^2\hfill \\ \hfill \mathrm{V}\left[e_{sel}\right]=& (16-{\pi }^2){\lambda }_1^2{\sigma }_{mut}^4\hfill \end{array}$$ (S13)

Epistasis corresponding to the selected component is always negative. The mean and variance of total epistasis are:

$$\begin{array}{cc}\hfill \mathrm{E}\left[e\right]=& -\pi {\lambda }_1{\sigma }_{mut}^2\hfill \\ \hfill \mathrm{V}\left[e\right]=& \left(4\right(n-1)\stackrel{‒}{{\lambda }^2}+(16-{\pi }^2\left){\lambda }_1^2\right){\sigma }_{mut}^4\hfill \end{array}$$ (S14)

Equation (S14) gives equation (4) of the main text when the λ_i are set to 1.

3. Sign epistas selected mutations

For independently selected mutations, the relationships W₁₀ > W₀₀ and W₀₁ > W₀₀ must hold in a strong selection, weak mutation regime, because the mutations are both beneficial in the ancestral strain. Thus, the first mutation is sign epistatic if and only if W₁₁ < W₀₁ (an analogous condition holds for the second mutation). This condition is equivalent to log(W₁₁) − log(W₀₁) < 0, equivalent to:

$$\underset{e}{\overset{\log \left(W_{11}\right)+\log \left(W_{00}\right)-\log \left(W_{01}\right)-\log \left(W_{10}\right)}{\underbrace{}}}+\underset{s_{\left(1\right)}}{\overset{\left(W_{10}\right)-\log \left(W_{00}\right)}{\underbrace{}}}=e+s_{\left(1\right)}<0$$ (S15)

Thus, a selected mutation is sign epistatic with another mutation, relative to the ancestral background, if and only if the sum of its selection coefficient and its epistasic coefficient is negative.

For co-selected mutations, the relationships W₁₀ > W₀₀ and W₁₁ > W₁₀ must hold. Thus the first mutation is sign epistatic if and only if W₁₁ < W₀₁, and the second mutation is sign epistatic if and only if W₀₁ < W₀₀ to the condition expressed in (S15) and the second condition is equivalent to log(W₀₁) − log(W₀₀) < 0, equivalent to:

$$\underset{-e}{\overset{-\log \left(W_{11}\right)-\log \left(W_{00}\right)+\log \left(W_{01}\right)+\log \left(W_{10}\right)}{\underbrace{}}}+\underset{s_{\left(2\right)}}{\overset{\log \left(W_{11}\right)-\log \left(W_{10}\right)}{\underbrace{}}}=-e+s_{\left(2\right)}<0$$ (S16)

where s₍₂₎ denotes the selection coefficient of the second mutation. Note that reciprocal sign epistasis cannot happen between co-selected mutations, because it would imply that W₁₁ < W₀₀.