Empirical Bayes MCMC Estimation for Modeling Treatment Processes, Mechanisms of Change, and Clinical Outcomes in Small Samples

Abstract

Objective

The current analysis demonstrates of the use of empirical Bayes estimation methods with data-derived prior parameters for studying clinically intricate process-mechanism-outcome linkages using structural equation modeling (SEM) with small samples.

Method

The data were obtained from a small subsample of 23 families receiving Functional Family Therapy (FFT) for adolescent substance abuse during a completed randomized clinical trial. Two or three video recorded FFT sessions were randomly selected for each family. The middle 20-minute portion of each session was observed and coded. A SEM was specified examining the influence of a select set of observed therapist behaviors on pre- to post-treatment change in mother-reports of family functioning and, in turn, pre- to post-treatment change in adolescent reports of adolescent marijuana use and delinquent behavior. The SEM was implemented using empirical Bayes estimation with data-derived maximum likelihood (ML) prior parameters and Markov Chain Monte Carlo (MCMC) estimation of the joint posterior distribution.

Results

The EB SEM results indicated that a relatively high proportion of individually focused general interventions (i.e., seek information, acknowledge) as well as relationally focused meaning change interventions by therapists during sessions of FFT were predictive of pre- to post-treatment increases in levels of family functioning as reported by mothers in families of substance abusing adolescents. In turn, increases in mother-reported family functioning were predictive of reductions in levels of adolescent-reported delinquent behavior.

Conclusions

EB MCMC methods produced more stable results than ML, especially regarding the variances on the change factors in the SEM. EB MCMC estimation is a viable alternative to ML estimation of SEMs in clinical research with prohibitively small samples.

Modern day researchers in clinical psychology and related areas of social and behavioral science find themselves in a bind when proposing new research as well as planning and executing corresponding statistical analyses. On one hand, fundable clinical research proposals are required to include investigations of relatively sophisticated research questions and hypotheses which may address (a) mediators, moderators, and mechanisms of intervention effects, (b) comparisons between subgroups, clusters, or latent classes of treatment responders, (c) linkages between clinical processes and treatment outcomes, etc. On the other hand, the types of multivariate statistical models required for investigating such nuanced research questions impose sample size requirements that are typically well in excess of what is feasible within the budgets of federally funded clinical trials. Faced with these conflicting requirements and constraints, clinical researchers have had little recourse but to proceed as best they can with whatever sample size is feasible and “simply hope for the best” (Maxwell, 2004, p. 160).

Small sample sizes in clinical research impose severe restrictions on the scope and complexity of the statistical models that may be implemented, and hence the nature of the research questions that may be investigated. Multivariate structural equation modeling (SEM), which is arguably the most widely utilized analytic approach for testing hypotheses regarding mechanisms of clinical change, is particularly infeasible with small samples (Bollen, 1989, Hoyle, 2012; Kline, 2011). This is the case because the most commonly implemented estimation algorithm in SEM research, the method of maximum likelihood (ML), yields results which are asymptotically valid -- meaning that a large sample is required for trustworthy inference (Lee & Song, 2004; Lei & Wu, 2012; Nevitt & Hancock, 2004; Song & Lee, 2012). More precisely, the desirable statistical properties of ML estimators (i.e., consistency, efficiency, normality, unbiasedness) are predicated on the sample data following a multivariate normal distribution – a condition that is satisfied only in large samples even if the observed data values are univariate normally distributed (Lee, 2007, p. 68). In small samples, departures from multivariate normality render ML estimates unstable and biased to a potentially substantial degree. Other problems associated with ML estimation of SEMs in small samples include nonconvergence, improper solutions (e.g., negative variance estimates), and biased model fit indices (Boomsma, 1985; Boomsma & Hoogland, 2001; Chen, Bollen, Paxton, Curran, & Kirby, 2001; Gagné & Hancock, 2006; Marsh, Balla, & McDonald, 1988; Robert, 2007, p. 21).

Emergence of Bayesian Statistical Methods for Analyses Based on Small Samples

The problems associated with small sample sizes in clinical research have been recognized for many years with relatively few solutions emerging (Maxwell, 2004). Recently, however, researchers in clinical psychology and related areas have become more attuned to the benefits of Bayesian statistical methods for studies with small samples. Methodological books and papers touting the benefits of Bayesian methods compared to more conventional ML methods are appearing more regularly in the social and behavioral science research literature (e.g., Baldwin & Fellingham, 2013; Christensen, Johnson, Branscum, & Hanson, 2011; Congdon, 2006; Gill, 2008; Hoff, 2009; Kaplan & DePaoli, 2012; Muthén & Aspahouhov, 2012; Robert, 2007; Rupp, Dey, & Zumbo, 2004; Skrondal & Rabe-Hesketh, 2004, pp. 204–214). In contrast to ML estimation, Bayesian statistical methods do not rely on asymptotic properties of estimators for valid inference (Baldwin & Fellingham, 2013; Lee & Song, 2004; Muthén & Aspahouhov, 2012; Rupp et al., 2004). Rather, Bayesian statistical parameter estimates are stabilized by the influence of prior distributions, which are probability density functions expressing a-priori information about how model parameters are distributed in the population (Carlin & Louis, 2009; Gelman, Carlin, Stern, & Rubin, 2004; Gill, 2008; Robert, 2007). In Bayesian statistics, parameter estimates are obtained as precision-weighted averages of the observed data likelihood function and the prior distribution. Given a large sample containing relatively abundant information about the population parameters, the influence of the prior distribution may be substantially down-weighted relative to the observed data to the point where Bayesian and ML estimates converge. Given a small sample, however, containing relatively scant information about the population parameters, Bayesian estimates are more heavily weighted toward the prior. It is the influence of the prior distribution that helps stabilize and anchor Bayesian parameter estimates in the presence of small samples (Song & Lee, 2012, p. 36).

Bayesian parameter estimation and inference are based on and proceed from the joint posterior distribution of the model parameters which, as noted above, is computed according to Bayes’ theorem as a weighted average of the likelihood function and the prior. Bayesian point estimates typically are taken to be the mean, median, or mode of the posterior distribution. Inferences in Bayesian statistical analyses typically are based on credible intervals, akin to confidence intervals in the conventional frequentist statistical framework, which are constructed from posterior percentiles (e.g., the 2.5^th and 97.5^th posterior percentiles).

Bayesian methods for SEM analyses with small samples

Recently, Bayesian methods have been formulated and specified for SEM spearheaded by the work of Lee (2007) and colleagues (Lee & Song, 2004; Song & Lee, 2012; Song, Lu, Hser, & Lee, 2011. See also Congdon, 2006; Kaplan & Depaoli, 2012; Muthén & Asparouhov, 2012; Stern & Jeon, 2004; Van de Schoot, Hoijtink, Hallquist, & Boelen, 2012; Zhang, Hamagami, Nesselroade, & Grimm, 2007). In particular, Lee (2007) and Song and Lee (2012) explicated how a variety of SEMs can be implemented using the WinBUGS software program for Bayesian statistics (see Ntzoufras, 2009). The basic approach entails specifying the entire system of mathematical (linear or nonlinear) equations for the observed and latent variables (i.e., the measurement and structural models) in a given SEM. A prior distribution is specified for each unknown parameter in each equation. As discussed further on, the joint posterior distribution of the SEM parameters is then approximated using a Markov-Chain Monte Carlo (MCMC) sampling algorithm (Carlin & Louis, 2009; Gelman et al., 2004; Gilks, Richardson, & Spiegelhalter, 1996; Robert & Casella, 2004). Bayesian SEM can be implemented in any of several popular software packages specialized for Bayesian statistics including WinBUGS, R, MATLAB, and SAS PROC MCMC. In addition, the SEM software packages Mplus and Amos have incorporated Bayesian estimation capabilities (Lei & Wu, 2012).

Regarding the use of Bayesian methods for SEMs with small samples, a critical caveat is that the stabilizing influence of the prior distribution is a function of the amount of information contained in the prior (which, in turn, is a direct function of the prior precision). In order for the small-sample benefits of Bayesian methods to take effect, prior distributions must be informative, that is, they must contain substantive information about the population parameter values in a given statistical model (see Baldwin & Fellingham, 2013; Zhang et al., 2007). Typically, informative priors for model parameters are specified or elicited based on previous research and/or expert judgment (Carlin & Louis, 2009; Christensen et al., 2011). In most cases, however, prior information about the parameters of SEMs is not available or does not exist, in which case non-informative or diffuse priors may be utilized (Lee, 2007; Song & Lee, 2012). Non-informative priors carry minimal substantive information about how statistical parameter values are distributed in the population and therefore have little to no influence in Bayesian estimation when the sample size is moderate to large. As such, Bayesian estimation with non-informative priors typically yields results that are equivalent to those obtained using ML given at least a moderate sample size (Gelman et al, 2004, p. 61; Song & Lee, 2012, p. 37). In small samples, however, non-informative priors may have an appreciable impact on model parameter estimates despite being devoid of information about such parameters which, when coupled with a small sample data set similarly devoid of substantive information, may yield results that are quite unstable and implausible (Baldwin & Fellingham, 2013).

Data-derived prior parameters

In the absence of available prior information about SEM parameters, an alternative to specifying non-informative priors is to estimate prior parameters from the sample data (see Gelman et al., 2004, p. 121; Lee, 2007, p. 76; Song & Lee, 2012, pp. 39–40). Although estimating prior parameters from sample data is a distinct departure from a purely Bayesian orientation, many regard such a practice as permissible when no other source of prior information exists other than the sample data (see Gelman et al., 2004, pp. 120–121; Robert, 2007, pp. 478–479; Song & Lee, 2012, pp. 39–40). In cases where the prior parameters are estimated from the same data to be used in the analysis, the analysis is not regarded as fully Bayesian but rather as empirical Bayes (EB; Carlin & Louis, 2009). Lee and Song (2004) utilized data-derived prior estimates in a simulation study comparing EB and ML estimation of SEMs with small sample sizes (see also Lee, 2007, pp. 89–95). Their results indicated that EB methods incorporating data-derived prior parameter values produced more accurate and unbiased estimates than ML for SEMs with small samples.

Computational advantages of Bayesian Over ML estimation for SEM analyses with small samples

Although EB estimation does not incorporate information about model parameters apart from that contained in the data, there are significant computational advantages nonetheless of Bayesian statistical methods (either empirical Bayes or purely Bayesian) over ML for estimating and fitting SEMs in small samples (see Kaplan & DePaoli, 2012, p. 668; Muthén & Asparouhov, 2012; Skrondal & Rabe-Hesketh, 2004, p. 206). Foremost among these computational practicalities is the elimination of improper solutions or “Heywood cases” in SEM (Chen et al., 2001; Kline, 2011, p. 158). In particular, when sample sizes are small it is not unusual for ML estimation to produce negative estimates for variance parameters, which are impermissible values leading to improper solutions in SEM (Kolenikov & Bollen, 2012). A typical but unsatisfying remedy in the ML setting is to fix negative variance estimates to zero (Anderson & Gerbing, 1988, p. 417). Alternatively, one may impose interval restrictions on offending variance parameters such that the corresponding estimates are constrained to be greater than zero. Another possibility is to rescale variance parameters using some functional transformation [i.e., σ² = exp(θ)] and perform ML estimation based on the rescaled parameters. Although restriction and rescaling of SEM parameters effectively disallow impermissible estimates, such manipulations are known to give rise to convergence problems especially for relatively complex multivariate statistical models (see Chung, Rabe-Hesketh, Gelman, Liu, & Dorie, 2011, p. 3). Moreover, certain types of parameter restrictions and constraints, especially those on the boundary of the valid parameter space, may adversely impact tests of overall model fit in SEM (Savalei & Kolenikov, 2006).

The problem of negative variance estimates in SEM may be more directly addressed within a Bayesian statistical framework by specifying prior distributions for variance parameters that cover the valid parameter space (i.e., zero to infinity). Draws from the posterior distribution, simulated using MCMC sampling methods, are thereby restricted to the same space (Chung et al., 2011; Gelman, 2006; Muthén & Asparouhov, 2012; Skrondal & Rabe-Hesketh, 2004, p. 206). An associated advantage of MCMC simulation methods within a Bayesian statistical framework is the capacity to obtain parameter estimates for complex multivariate models which may be analytically intractable or difficult to optimize numerically using ML methods, especially given a small sample (Christensen et al., 2011; Gelman et al., 2004; Hoff, 2009; Lee, 2007; Song & Lee, 2012). Further details on these computational advantages of Bayesian over ML methods for small-sample SEM analyses are provided in section S1 of the online supplementary materials.

Overview of the Demonstration Analysis

The computationally facilitative features of Bayesian over ML estimation for SEMs with small samples, as opposed to the fundamental philosophical distinctions between Bayesian and more traditional frequentist methodologies, are the principal motivation for the proposals, recommendations, and prescriptions for the use of such methods in this paper. The remainder of this paper illustrates the use of EB statistical methods for analyses of clinical processes and mechanisms of change in clinical research, in which restrictive sample sizes are the norm rather than the exception. Specifically, EB methods are used to analyze clinical data from a small-sample pilot study of the link between observed therapist behaviors, pre- to post-treatment change in a targeted area of functioning (i.e., mechanism of change), and behavioral outcomes. The data for this pilot analysis were obtained from a completed randomized clinical trial of the effects of various forms of adolescent substance abuse treatment. Therapist behaviors during 2 or 3 therapy sessions were observed and coded for a small subsample of cases from the clinical trial. A SEM was specified linking the extensiveness of therapists’ use of a specific set of clinical interventions with pre- to post-treatment change in a targeted change mechanism, and, in turn, change in behavioral outcomes. This pilot analysis demonstrates how a complex SEM for studying therapy process-mechanism-outcome linkages may be implemented with a small sample using EB statistical methods which produce more stable results than conventional ML estimation.

Although Bayesian methods have been developed for SEMs (Kaplan & DePaoli, 2012; Lee, 2007; Muthén & Asparouhov, 2012; Song & Lee, 2012; Van de Schoot et al., 2012) as well as for studying mediational processes in non-clinical research (Enders, Fairchild, & MacKinnon, 2013; MacKinnon, 2008; Yuan & MacKinnon, 2009), no study in the clinical psychology literature has used Bayesian SEM methods to study clinical process-mechanism-outcome linkages in treatment research. This demonstration analysis is intended to provide clinical methodologists with a feasible approach for implementing SEMs to study process-mechanism-outcome linkages when only a small sample is available.

Method

Description of the sample and selection of video recorded therapy sessions

The data for the pilot analysis were obtained from a small subsample of cases receiving Functional Family Therapy (FFT) for adolescent substance abuse (Alexander & Parsons, 1982; Alexander, Waldron, Robbins, & Neeb, 2013; Waldron & Brody, 2010) during a completed NIH-funded randomized clinical trial conducted by Waldron and colleagues (Waldron, Slesnick, Brody, Turner, & Petersen, 2001). Briefly, the parent clinical trial was a study of the efficacy of FFT compared to individual and group cognitive-behavioral treatment for adolescent substance abuse. A full description of the study participants is provided in Waldron et al. (2001). Additional details on the clinical sample are provided in section S2 in the online supplemental materials.

For the current pilot study, video recorded FFT sessions were randomly selected from an archived collection of videotaped FFT sessions conducted during the course of the clinical trial. Two or three FFT sessions were randomly selected for each of 23 families randomly assigned to the FFT condition. The middle 20-minute portion of each session was observed and coded. A total of 63 FFT sessions was included in the pilot analysis. Ten recorded FFT sessions (15.9%) were cross-coded for purposes of assessing and monitoring interrater agreement.

Protocols and procedures for the protection of human subjects during the parent clinical trial were reviewed and approved by the institutional review board (IRB) at the University of New Mexico. The subsequent pilot study, which is the focus of this demonstration analysis, was reviewed and approved by the IRB at the Oregon Research Institute.

Self-Report Measures

As documented in Waldron et al. (2001), a battery of assessment instruments was administered at several time points before and after treatment during the parent clinical trial. The current pilot analysis incorporated only the pretreatment assessment and the post-treatment assessment which occurred approximately 4 months after the initiation of FFT.

Adolescent substance abuse

The percent days of adolescent marijuana use was measured on the Timeline Follow-Back interview (TLFB; Sobell & Sobell, 1992) -- Form 90D version (Miller & DelBoca, 1994). Briefly, the TLFB is a semi-structured interview pertaining to substance use behavior over a specific time interval (e.g., past 90 days). On each day of the assessment period, the type and amount of substance use is recorded based on retrospective self-reports. The interviewer utilizes a daily calendar and other types of memory aides to facilitate recall. In the current study, adolescent substance use frequency was assessed over the past 90 days prior to the pretreatment assessment. At the 4-month assessment the measurement window was extended to the date of the pretreatment assessment.

Although the TLFB was originally developed as a measure of alcohol use in adults, it has been used successfully as a measure of marijuana and other substance use among adolescents (Winters, 2003, 2006). In particular, the TLFB has been shown to exhibit sound psychometric properties in adolescent samples, and strong concordance with other self-report, parent-report, and biological measures of adolescent substance use (Dillon, Turner, Robbins, & Szapocznik, 2005; Donohue et al., 2004; Waldron et al., 2001).

Adolescent delinquent behavior

The second adolescent outcome variable examined in this pilot analysis was the severity of delinquent behavior problems based on adolescent reports on the delinquent behavior subscale of the 1991 version of the Youth Self-Report (YSR) (Achenbach, 1991). Briefly, the YSR assesses the degree to which each of 118 distinct behavior problems is characteristic of the adolescent. Each item has a 3-point response scale in which 0 = “not true”, 1 = “somewhat true”, and 2 = “very often true.” Item responses are summed to form eight behavior problem subscales, which in turn may be summed to form two overarching constructs known as internalizing and externalizing problem behavior. Achenbach (1991) specifies clinical cut-off scores for each behavior problem subscale as well as the two overarching construct scales. As a component of the CBCL family of instruments, the YSR has been used in thousands of studies and is one of the most well validated self-report measures of emotional and behavioral problems among youth (Achenbach, Dumenci, & Rescorla, 2002; Achenbach & Rescorla, 2001).

Family functioning

The quality of family functioning was assessed according to mothers’ reports on the Family Environment Scale (FES, Moos & Moos, 1994). The FES is a 90-item self-report scale assessing various dimensions of family functioning. Each item has a dichotomous true/false response scale. The items of the FES are summed to form 10 subscales composed of 9 items each. Subscale scores range from 0 to 9. Extensive validity and reliability data are reported in Moos and Moos (1994; see also Kronenberger, Thompson, & Morrow, 1997).

The FES has been shown to be a reliable and valid measure of family characteristics in research on adolescents (Foster & Robin, 1997). Moreover, the FES has been used successfully in studies of the efficacy of family-based interventions for substance abuse and conduct problems among youth (Kazdin, Siegel, & Bass, 1992; Kazdin & Whitley, 2006; Liddle, Rowe, Dakof, Ungaro, & Henderson, 2004; Santisteban et al., 2003).

Observational Measurement

Functional Family Therapy Coding and Rating Scale

In recognition of the need for a process research instrument for studying the effects of manual-based interventions in FFT, the author of this manuscript organized a two-day expert panel meeting of the primary developers and researchers of FFT.¹ The objective of the meeting was to begin designing a comprehensive instrument for coding and rating the presence of prescribed clinical interventions and processes during sessions of FFT. The discussions during this meeting (and over many subsequent months) culminated in the Functional Family Therapy Coding and Rating Scale (FFT CARS). As the name suggests, the FFT CARS contains both a micro-coding and a rating scale component. This demonstration analysis incorporates only the coding portion of the FFT CARS. The coding portion of the FFT CARS contains 24 intervention codes for classifying discrete therapist statements (see Table S1 in the online supplemental materials).² In addition, the FFT CARS contains four numerical codes for classifying the “frame of reference” of each therapist statement. Frame-of-reference codes on the FFT CARS describe the broad focus or subject matter of therapist statements which may include (a) individual – focused on thoughts, feelings, or behaviors of individual family members, (b) relational – focused on aspects of the behavioral interaction or quality of the relational bond between two or more family members or among the family as a whole, (c) therapist – focused on the thoughts, feelings, or behaviors of the therapist, or (d) neutral -- unrelated to any particular family member(s) or the family as a whole or the therapist. Altogether, each discrete therapist statement receives a 5-digit code on the FFT CARS where digit-1 corresponds to the identity of the speaker (which is always the therapist), digits-2 and -3 correspond to the intervention code, digit-4 is the frame of reference of the coded statement, and the digit-5 identifies the intended recipient of the coded statement. The FFT CARS is designed to assess a range of therapist interventions which are prescribed in the FFT model, as well as those that are proscribed in FFT and those which are common to most forms of behavioral treatment.

Coder selection and training

Two graduate level coders were recruited through local newspaper advertisements. Both coders were Caucasian females in their 20’s. One was a graduate student in clinical psychology and the other a pre-graduate student in the field of neuropsychology. Neither coder had any significant clinical experience nor any prior knowledge of the FFT model. The coders were thoroughly trained to use the FFT CARS to observe and code therapist behavior during sessions of FFT. A description of the coder training process is provided in section S3 of the online supplemental materials.

Data Analysis Plan

Creating therapist behavior variables based on the FFT CARS

The total amount of therapist talk-time, or the amount of time during which therapist was speaking, was totaled across the observed 20-minute segments of FFT for each family. Next, the proportion of therapist talk-time within each “intervention × frame-of-reference” category on the FFT CARS was computed. These proportions were used as observed variables in an SEM analysis of the link between therapist behavior in FFT and improvements in family functioning and adolescent behavior (see below).

Structural equation modeling analysis

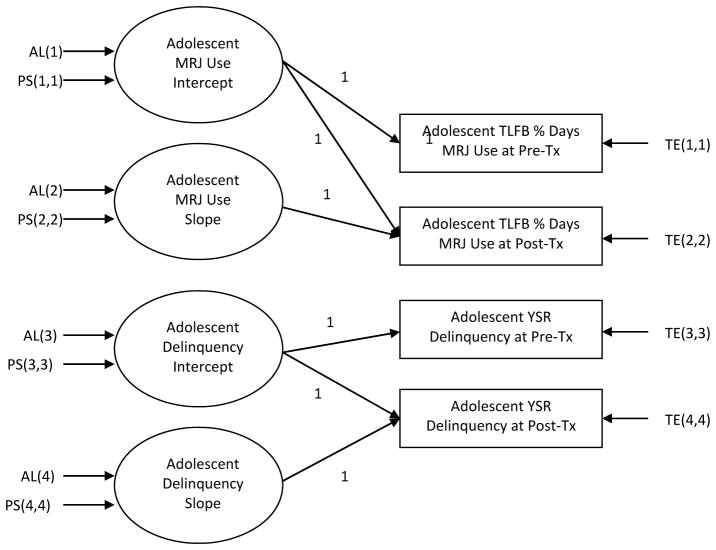
The complete SEM is displayed in Figures 1 through 4. In each figure, LISREL syntax and terminology is used to label all variables and parameters. Figure 1 contains a latent growth curve model (LGCM) estimating change in adolescent marijuana use and delinquency between the pre-treatment and 4-month assessments (see Bollen & Curran, 2006; Duncan, Duncan, & Stryker, 2006). The LGCM in Figure 1 models change in both marijuana use and delinquent behavior by regressing a set of longitudinal measurements for each behavioral outcome on two latent growth factors, respectively. The first latent growth factor for each behavioral outcome is called the intercept which estimates the level of the behavioral outcome at the pre-treatment assessment. The second growth factor for each outcome is called the slope which captures the amount of linear change between the pre-treatment and 4-month measurements. Each growth factor is summarized by a mean (the AL parameter) and a variance (the PS parameter). The mean intercept and slope are the average pre-treatment level and the rate of change, respectively, across all individuals in the sample. The corresponding growth factor variances capture individual heterogeneity around the growth factor means. The latent growth factors for adolescent marijuana use are measured by adolescent reports of the percentage of days of marijuana use over the past 90 days (or since the previous assessment) on the TLFB at the pre-treatment and 4-month assessments. The latent growth factors for adolescent delinquency are indicated by adolescent reports on the YSR delinquency subscale at these same time points.

Figure 1.

Latent growth curve model for change in adolescent marijuana use and delinquency. Parameter names expressed using LISREL syntax. (MRJ = marijuana use, TLFB = Timeline Follow-Back Interview, YSR = Youth Self-Report Scale). Parameter names expressed using LISREL syntax.

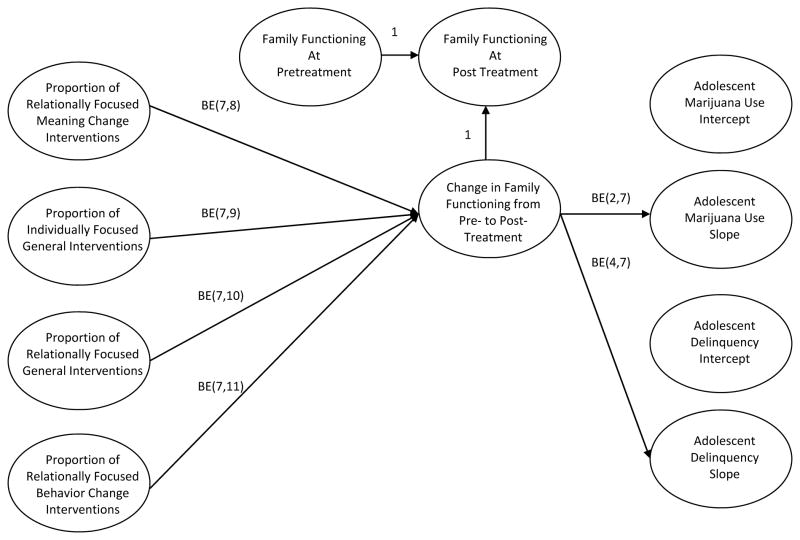
Figure 4.

Structural model of the effects of therapist behavior on change in family functioning and adolescent marijuana use and delinquency. Parameter names expressed using LISREL syntax

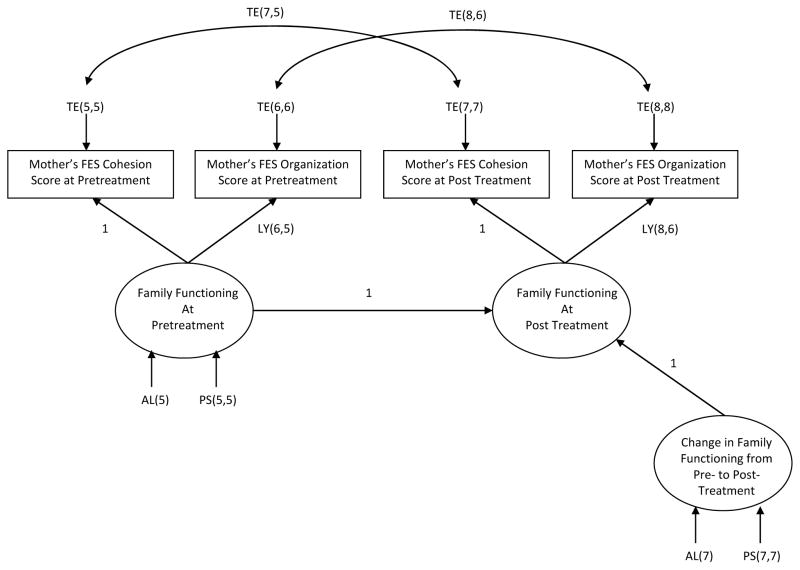
Figure 2 contains a latent change score model (LCSM) that estimates change in family functioning between the pre-treatment and 4-month assessments (see McArdle, 2009, pp. 587–589). Specifically, the LCSM contains a family functioning latent construct at both the pre-treatment and 4-month assessments which was operationalized by mothers’ reports on the FES cohesion and organization subscales at these respective assessment points. The construct labeled family functioning change captures the difference or the amount of change in the family functioning latent construct between the pre-treatment and 4-month assessments. The unit constraints on the regression paths leading to the family functioning at 4-months construct force the family functioning change construct to act as a latent difference score between the pre-treatment and 4-month family functioning constructs. The advantage of modeling latent rather than observed difference scores is that measurement error in the observed variables is removed from latent difference scores whereas observed difference scores contain measurement errors on the observed variables.

Figure 2.

Latent change score model for family functioning. Covariance between Family Functioning at Pre-Treatment and the Adolescent Marijuana Use Intercept in Figure 1 [PS(5,1)] not displayed. FES = Family Environment Scale.

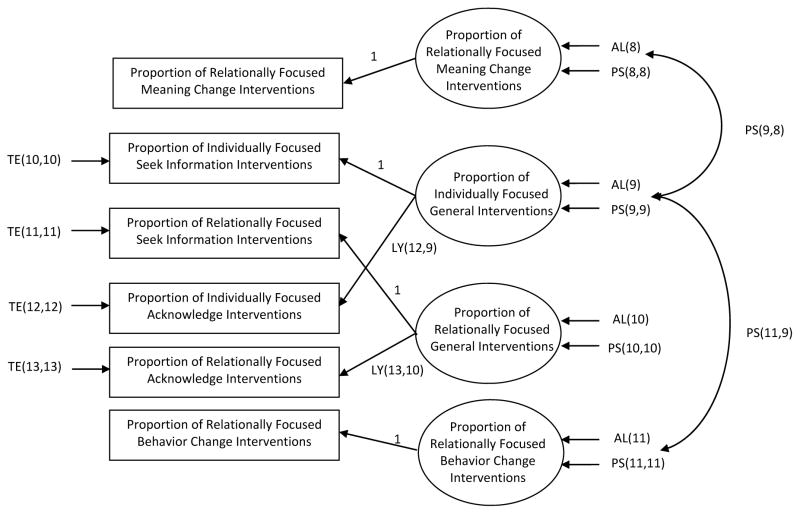
Figure 3 contains a measurement model for a select set of therapist intervention variables from the FFT CARS. Specifically, the measurement model for therapist interventions is comprised of four latent constructs including (a) relationally focused meaning change interventions which encompasses the proportion of therapist talk-time devoted to relabeling and reframing interventions,³ (b) individually focused general interventions which encompasses the proportion of therapist talk-time devoted to seeking information about or acknowledging the thoughts, feelings, or behavior of individual family members, (c) relationally focused general interventions which encompasses the proportion of therapist talk-time devoted to seeking information about or acknowledging aspects of the behavioral interactions or relational bonds between family members, and (d) relationally focused behavior change interventions which encompasses the proportion of therapist talk-time devoted to teaching new behavioral skills to enhance family functioning (e.g., communication, problem-solving, etc.). Constructs (b) and (c) listed above represent general types of interventions and therapist behaviors (i.e., seeking information and acknowledging) which are common to most any form of psychosocial or behavioral treatment. Constructs (a) and (d) represent therapist behaviors and interventions which are prescribed as core components of the FFT model (see Alexander et al., 2013).

Figure 3.

Measurement model for observed therapist behaviors during sessions of FFT. Parameter names expressed using LISREL syntax.

The measurement models in Figures 1–3 are linked together by regression parameters within the structural model displayed in Figure 4. Specifically, regression parameters between the therapist intervention latent constructs and the LCSM estimate the degree to which change in family functioning is predicted by each of the general and FFT-prescribed intervention constructs. In turn, regression parameters between the LCSM and the LGCM estimate the degree to which change in family functioning predicts change in adolescent marijuana use and delinquency between the pre-treatment and 4-month assessments. Collectively, the regression parameters within the structural model constitute an empirical investigation (as opposed to a formal experimental test) of a fundamental clinical hypothesis in FFT which is that higher proportions of relationally focused interventions, including both general (seek information and acknowledge) and FFT-prescribed (meaning change, behavior change) therapist behaviors lead to greater improvements in levels of family functioning from pre-to-post treatment. In turn, change in family functioning operates as a mechanism of change in adolescent behavioral problems including marijuana use and delinquency (see Alexander et al., 2013; Waldron & Brody, 2010).

Empirical Bayes SEM parameter estimation

The SEM shown in Figures 1–4 was fit to the data for the 23 adolescents and parents in the pilot sample using the EB statistical approach outlined previously. First, an initial fitting of the SEM employing robust ML estimation was implemented in the LISREL 8 software (Jöreskog & Sörbom, 1996–2001; Jöreskog, Sörbom, du Toit, & du Toit, 1999). Next, the resulting ML parameter estimates and robust standard errors were utilized as prior parameters in a subsequent fitting of the SEM using Bayesian statistical methods in the PROC MCMC package of the SAS/STAT 12.1 software (SAS Institute, Inc., 2012). As the name of the procedure suggests, PROC MCMC implements MCMC sampling methods to simulate observations from the posterior distribution using the Metropolis-Hastings algorithm (see section S1 in the online supplemental materials). The PROC MCMC programming code to execute the SEM is provided Figure S1 in the online supplemental materials (see also Baldwin & Fellingham, 2013). One hundred thousand simulated draws from the posterior were obtained for each parameter. The simulated draws were preceded by 2000 “burn-in” draws which were discarded from the analysis. To reduce temporal autocorrelation among the draws, the MCMC chain was thinned by including only every 20^th draw, yielding 5000 simulated posterior observations.

Specification of data-derived prior parameters

The SEM shown in Figures 1–4 contains a total of 46 free parameters (see lines 2–8 of the PROC MCMC program presented in Figure S1 in the online supplemental materials). In terms of LISREL parameter matrices, the SEM parameters include three factor loadings contained in the lambda-y (LY) matrix, 12 measurement errors on the observed variables contained along the diagonal of the theta-epsilon (TE) matrix, 10 latent variable means contained in the alpha (AL) matrix, 10 error variances on the latent variables contained along the diagonal of the psy (PS) matrix, six regression parameters estimating direct effects between latent variables contained in the beta (BE) matrix, three covariances between latent variables contained in the off-diagonal portion of the PS matrix, and two covariances between measured variables contained in the off-diagonal portion of the TE matrix. The entire model is expressed in terms of the y-model in LISREL, which is the set of parameter matrices associated with the endogenous or dependent variables (see Jöreskog & Sörbom, 1996–2001, p. 202; Rindskopf, 2012, p. 337). The x-model parameter matrices in LISREL associated with the exogenous or independent variables were not utilized in the SEM specification in order to simplify the presentation of the model. Moreover, expressing the SEM entirely within the LISREL y-model simplifies the matrix algebra involved in ML estimation because fewer distinct parameter matrices must be inverted during the computations.

To implement the SEM using EB estimation, all paths shown in Figures 1–4 were expressed as a system of linear equations in PROC MCMC, using LISREL syntax for parameter names (although any parameter naming syntax other than LISREL may be used. See lines 65–88 of the PROC MCMC program in Figure S1 in the online supplemental materials). Each estimated parameter in the model was assigned a prior distribution, the parameters of which were obtained from the robust ML solution of the preliminary model fitting in LISREL (see lines 10–64 of the PROC MCMC program in Figure S1 in the online supplemental materials). Prior distributions for all parameters in the LY, AL, and BE matrices were specified as normal with mean equal to the corresponding ML point estimate and standard deviation equal to the corresponding ML standard error estimate.

Regarding the variance and covariance parameters in the PS and TE matrices, the predominant practice is to specify an inverse-Wishart prior distribution which is the multivariate generalization of the inverse-gamma distribution and the conjugate prior for a multivariate normal covariance matrix (Gelman et al., 2004, p.87; Lee, 2007, p. 75, Lee & Song, 2004; Muthén & Asparouhov, 2012; Song et al., 2011; Zhang et al., 2007).⁴ Although the conjugacy of the inverse-Wishart renders it a computationally convenient prior for an SEM covariance matrix, it is a highly restrictive and inflexible prior specification (see Barnard, McCulloch, & Meng, 2000; Gelman et al., 2004, p. 483; Hsu, Sinay, & Hsu, 2012). In particular, an oft-cited limitation of the inverse-Wishart prior is that, because the precision of the entire matrix is determined by a single degrees-of-freedom parameter, it is not possible to specify varying levels of prior knowledge across variance-covariance elements. For this reason, numerous Bayesian methodologists have proposed more flexible approaches to specifying prior distributions for covariance matrices in multivariate statistical models (e.g., Barnard et al., 2000).

In the current demonstration analysis, an approach described by Muthén and Asparouhov (2012) was utilized to assign element-specific priors to each variance and covariance parameter in the PS and TE matrices. Specifically, Muthén and Asparouhov (2012, p. 317) discussed a prior specification approach for Gaussian (i.e., normal) covariance matrices (to which they referred simply as “Method 3”) in which each variance element along the diagonal of a given covariance matrix is assigned its own inverse-gamma prior and each off-diagonal covariance element is assigned its own normal prior. In the current analysis, however, rather than using inverse-gamma priors for the variance parameters, independent gamma (α, λ) priors were specified based on the recommendations of Chung et al. (2011), where α is the shape parameter and λ is the scale parameter of the gamma distribution. Chung et al. (2011) prefer the gamma over the inverse-gamma prior because the latter density function is flat (i.e., has a first derivative equal to zero) at the lower bound of zero, thereby eliminating very low posterior variance estimates even when such values are supported by the data (as often is the case when implementing multivariate SEMs with small samples). Chung et al. (2011) recommended using a gamma prior with α = 2 which ensures that (a) all posterior values are within the valid parameter space ranging from 0 to ∞, and (b) that the prior density function has a positive slope (i.e., is increasing) rather than a flat slope at the lower bound of zero. Additionally, given that α·λ equals the mean of the gamma distribution, λ for each prior variance parameter in the current analysis was set equal to the corresponding ML estimate divided by 2 to ensure the prior mean would equal the ML point estimate (see lines 13–24 and 34–43 of the PROC MCMC program in Figure S1 in the online supplemental materials). In cases where the ML point estimate for a given variance component is either negative or fixed to zero, then the least-squares estimate of the covariance between the measured indicator variables serves as a suitable value for λ for latent variables with two measured indicators.⁵ For latent variables with more than two measured indicators, λ may be set equal to the average of the pairwise least-squares covariance estimates among the observed indicators.

As noted above, Muthén and Asparouhov’s (2012) approach of specifying a distinct normal prior for each free covariance parameter in the off-diagonal portions of the PS and TE matrices was followed. The free covariance parameters in the PS and TE matrices were estimated in PROC MCMC by including those parameters as common terms in the measurement or structural equations for the corresponding observed or latent variables, respectively. Dagne, Howe, Brown, and Muthén (2002) demonstrated this “common term” approach to estimating covariance parameters in SEM (see p. 272). Dagne et al. (2002) showed that common parameters across model equations capture the shared variance between the corresponding dependent variables in the linked equations, with the variance of the common parameter representing the covariance between the dependent variables. In the current analysis, free covariance parameters between select pairs of observed or latent variables were included as common terms in the respective SEM equations (see lines 65, 69, 71, 72, 74, 79–82 of the PROC MCMC program in Figure S1 in the online supplemental materials). These covariance parameters were specified to have normal prior distributions with mean equal to the ML covariance point estimate and standard deviation equal to the corresponding ML standard error estimate. In order to preclude these covariance parameters from impacting the value and interpretation of the remaining terms in each model equation, the covariance terms were both added and subtracted within each equation so that their net impact on the remaining terms in each equation was zero.

Ensuring that estimated posterior covariance matrices are positive definite

An important consideration with regard to the element-specific approach to estimating SEM variances and covariances described above is verifying that the estimated posterior matrices (PS and TE in the current application) are positive definite (see Wothke, 1993). Although the prior inputs for the variance and covariance parameters in the EB estimation approach are obtained from the ML estimates of the corresponding matrices, which are by definition positive definite, the element-specific prior specification approach described above does not guarantee that positive definiteness is preserved in the posterior matrices. As such, the positive definiteness of the posterior estimates of the SEM covariance matrices should be explicitly verified. In general, a fairly straightforward way of verifying the positive definiteness of any covariance matrix is to obtain its Cholesky factorization (see Leon, 2009). In the current analysis, the Cholesky factorization of the PS and TE matrices was computed using the FCMP procedure of the BASE SAS software package (see Figure S2 in the online supplemental materials). Further details on positive definite covariance matrices and the Cholesky factorization may be found in section S4 in the online supplementary materials.

Results

Frequencies of FFT CARS Codes

Across the 63 coded FFT therapy sessions, 3733 discrete segments of therapist behavior were coded on the FFT CARS. Table S1 presents the frequency and percentage of each FFT CARS intervention code across the 63 pilot sessions (see online supplemental materials). It is evident from Table S1 that the overwhelming majority of coded therapist behaviors (63.6%) fell into the categories of seek information or acknowledge/clarify. The percentage of all other codes was no greater than 4.7% and many of the codes occurred at a rate of less than 2% of the total number of coded statements.

The frequencies in Table S1 made apparent the necessity to collapse across certain codes and to eliminate others from the analysis altogether. It was decided to condense the original FFT CARS intervention codes into nine aggregate codes including (a) provide expert information (treatment focus, give information), (b) meaning change (relabel, reframe), (c) seek information, (d) support, (e) acknowledge, (f) challenge, (g) direct session (in-session focus, structure/direct), (h) behavior change (teach skills, behavioral rehearsal, assign/review homework, reinforce skills, relapse prevention), and (i) talk/humor. Segments of therapist behavior assigned to any intervention code not included in this condensed list were trimmed from the analysis. Regarding the frame-of-reference codes assigned to each segment of therapist behavior, the overwhelming majority of coded segments were classified as either individual (53.1%) or relational (38.4%). Therapist behaviors receiving any other frame-of-reference code were trimmed from the analysis as well. The collapsing and elimination of certain FFT CARS codes reduced the number of coded segments of therapist behavior in the final analysis to 3333.

Coder Agreement

Agreement between coders was examined for the aggregate FFT CARS intervention codes as well as the individual/relational frame-of-reference codes. For the FFT CARS intervention codes we obtained κ = .60 (95% CI: .55 to .67). For the FFT CARS frame-of-reference codes we obtained κ = .41 (95% CI: .35 to .52). The level of agreement on the collapsed FFT CARS intervention codes was within the “substantial” range whereas agreement on the FFT CARS frame-of-reference codes was within the “moderate” range as specified by Landis and Koch (1977). Both these levels of agreement were deemed acceptable for purposes of these pilot analyses.

SEM Analysis

Model convergence

For both ML and MCMC, a necessary condition for valid and trustworthy inference is that the algorithms converge upon a stable set of estimates that do not fluctuate with further iterations. In the ML setting, convergence is a requirement for parameter estimates to be produced by SEM software programs. In the Bayesian setting, however, ascertaining whether MCMC algorithms have converged is far less straightforward given that output and estimates are produced regardless of whether convergence is achieved. Consequently, checking for convergence is an essential first-step in Bayesian analyses using MCMC estimation.

The most basic way of assessing MCMC convergence is to visually inspect trace plots of the posterior draws for each parameter in order to establish that the chain has fully traversed and sampled from the parameter space. A somewhat more systematic approach is to inspect numerical indices of convergence such as the lag-50 posterior autocorrelation (r_L50) and the Monte Carlo standard error (MCSE) for each parameter. Briefly, r_L50 is the correlation between the posterior draws at steps s and s + 50 in the MCMC chain. Values of r_L50 near 0 indicate that the chain has traversed and sampled from the entire parameter space, rather than getting stuck in a restricted region of that space, thereby increasing the likelihood of stable convergence. Along similar lines, the MCSE is defined as the standard error of the posterior mean for a given model parameter (see Ntzoufras, 2009, pp. 40–41). The MCSE is a measure of the magnitude of error or imprecision in the posterior mean associated with instability in the MCMC sampling algorithm (see Gelman et al., 2004, p. 277). MCMC convergence can be gauged by comparing MCSE to the posterior standard deviation (PSD). Small values of the MCSE/PSD ratio indicate that only a small portion of the variability in the draws from the posterior are attributable to sampling instability, with values of MCSE/PSD less than 0.10 being generally acceptable levels of imprecision in the posterior mean (see Schiller & Dendukuri, 2012).

Perhaps the most rigorous way to establish MCMC convergence is to run the chain numerous times from widely dispersed starting values. If the separate chains arrive at the same posterior distribution, then one may safely conclude that the MCMC algorithm converges to the true posterior. In the current analysis, the MCMC procedure was executed seven times from different starting values dispersed from −3 to +3 standard deviations from the mean of the prior distribution for parameters with normal priors. For parameters with gamma priors, the starting values were dispersed as a multiplicative function of the scale parameter λ. The convergence of the MCMC algorithm across the seven chains was assessed for each parameter using Gelman and Rubin’s (1992) R-hat (R̂) index (see also Gelman, 1996, pp. 136–137; Gelman et al., 2004, pp. 296–297). Briefly, R̂ is a function of the between-chain (B) and within-chain (W) variances, and is computed as the ratio of the upper and lower bound of the posterior standard deviation for a given parameter, where the upper bound is a weighted average of B and W and the lower bound is simply W (Gelman, 1996, p. 137). If MCMC algorithm has converged across all chains then these two bounds will be very close to one another, and the value of R̂ will be close to 1.0. Values of R̂ in excess of 1.1 suggest that convergence could be improved by further iterations of the MCMC chain.

PROC MCMC does not compute the R̂ index. However, R̂ may be obtained using the NLMIXED procedure of the SAS/STAT software. See section S5 as well as Figure S3 in the online supplementary materials for further details on obtaining R̂.

Table S2 in the online supplementary materials presents r_L50, the MCSE/PSD ratio, W, B, and R̂ for each parameter in the SEM. To summarize, across all 46 parameters r_L50 ranged in absolute value from 0.00 to 0.05 indicating minimal autocorrelation between posterior draws and good mixing of the chains and traversing of the parameter space for all parameters. Likewise, values of MCSE/PSD ranged from .01 to .09 indicating satisfactory levels of stability in the MCMC chain for all parameters. Finally, values of R̂ equaled 1.0 for all parameters, indicating convergence across the seven chains initiated from disparate starting values (i.e., the separate chains arrived at the same destination from different starting points). By all indications, it appeared that the MCMC algorithm achieved convergence for all SEM parameters, meaning that the simulated posterior values were drawn from the true posterior for each parameter.

Model fit

The parameters of the SEM shown in Figures 1 through 4 were estimated using the EB methods described above. The LISREL fit indices and statistics indicated that the SEM fit the data well from a frequentist perspective [Satorra-Bentler scaled χ² = 48.76, df = 76, p = .9936; RMSEA = 0.00; CFI = 1.00. See Yuan (2005) for a discussion of these measures of fit]. That is, the covariance matrix implied by the SEM showed strong concordance with the observed covariance matrix. From a Bayesian perspective, a good fitting SEM also exhibits strong concordance with the observed data. However, rather than comparing model-implied and observed covariance matrices as in the ML setting, Bayesian model fit is gauged by comparing the observed data with predicted values sampled from the posterior predictive distribution (PPD) of the measured variables (Gelman et al., 2004, p. 159; Gelman & Meng, 1996). Briefly, the PPD is a collection of predicted values (i.e., future observations) for the measured variables in a statistical model that are implied by the Bayesian estimates of the model parameters contained in the joint posterior distribution. The PPD is obtained mathematically by integrating (i.e., averaging) the observed data likelihood function with respect to the joint posterior. Samples of predicted values may be drawn from the PPD and compared to the observed sample data. Strong concordance between the predicted and observed data values suggest a good fitting model from a Bayesian perspective.

Due to space limitations, the assessment of model fit based on comparisons between the observed data and predicted values sampled from the PPD is detailed in section S6 in the online supplemental materials.

Model parameter estimates and inferences

Table S4 in the online supplemental materials presents the robust ML and EB parameter estimates. Consistent with results obtained by Zhang et al. (2007), there was substantial concordance between the ML parameter estimates and the posterior means and medians derived from the EB analysis, especially for the normally distributed parameters in the LY, the AL, and BE matrices (see also Kaplan & DePaoli, 2012, p. 668). In contrast, a number of the variance parameters for the measured and latent variables along the diagonals of the TE and PS matrices, respectively, appeared to be more accurately and credibly estimated using EB methods. In particular, the ML estimates of the variances on the latent variables capturing pre- to post-treatment change in adolescent marijuana use [PS(2,2)], delinquency [PS(4,4)] and family functioning [PS(7,7)] were fixed to zero in order to remediate negative estimates of these parameters -- presumably reflecting an insufficient amount of information contained in the sample data for stable estimation of these variances. Given the theoretical centrality of the pre-to-post treatment change constructs in the SEM, it is most unsatisfying to constrain the variances on these latent factors to zero for the sake of obtaining a proper solution. Encouragingly, in contrast to the ML solution, each of the aforementioned variance parameters was properly estimated within the EB estimation approach. The EB posterior means were 1102.80 for PS(2,2), 11.79 for PS(4,4), and 0.06 for PS(7,7), all of which are within the valid parameter space and are more plausible estimates of these variance components than the fixed value of zero.

As described previously, the positive definiteness of the element-specific posterior estimates of the PS and TE matrices was assessed by computing the Cholesky factorization of each matrix. For both matrices, the Cholesky factorization was successfully computed, thereby verifying that both posterior matrices were positive definite (See section S4 and Figure S2 in the online supplemental materials).

Regarding the clinical process-mechanism-outcome linkages examined in the SEM, EB results for the regression parameters in the structural portion of the SEM (Figure 4) suggest a positive effect of the following sets of therapist interventions on change in family functioning: (a) proportion of individually focused general interventions [BE(7,9) = 17.49, 95% credible interval: 6.41 – 28.29], and (b) the proportion of relationally focused meaning change interventions [BE(7,8) = 5.14, 95% credible interval: 0.64 – 9.77]. In turn, the posterior means and intervals for the effects of change in family functioning on adolescent behavioral outcomes indicated that pre- to post-treatment increases in mother reports of family functioning predicted concurrent decreases in adolescent reports of delinquent behavior [BE(4,7) = −2.04, 95% credible interval: −3.65 – −0.39]. Change in family functioning did not appear to independently predict change in adolescent marijuana use [BE(2,7) = −4.53, 95% credible interval: −17.06 – 8.27]. Overall, the results of the structural portion of the SEM suggest that relatively frequent use of individually focused general interventions (i.e., seek information, acknowledge/clarify) as well as relationally focused meaning change interventions by therapists during sessions of FFT independently predict of pre- to post-treatment increases in levels of family functioning as reported by mothers in families of substance abusing adolescents. In turn, increases in mother-reported family functioning are predictive of concurrent reductions in levels of adolescent-reported delinquent behavior.

Discussion

The current analysis is a demonstration of the use of empirical Bayes estimation methods with data-derived prior parameters for studying clinically intricate process-mechanism-outcome linkages using SEM with small samples which are typical in clinical research. This demonstration is intended to provide clinical methodologists and data analysts with a feasible alternative to ML estimation for multivariate SEMs addressing research questions regarding clinical processes and mechanisms of change in the presence of small samples. The strength of the EB approach detailed here is the stabilization of SEM parameter estimation using informative prior distributions with prior parameters derived from a preliminary model fitting using robust ML methods. Admittedly, referring to data-derived priors as “informative” is a misnomer given that such priors contain no information about the population parameter values apart from that already contained in the data. Nonetheless, the use of data-derived priors permits Bayesian estimation to proceed using MCMC estimation methods which afford considerable computational advantages over ML estimation with small samples. Foremost among these advantages is the elimination of improper SEM solutions containing impermissible values which often arise using ML estimation in small samples. A secondary computational advantage of EB MCMC estimation is the capacity to converge upon stable parameter estimates for large and complex SEMs which may be computationally intractable using ML estimation, especially given a small sample.

As noted previously, it is often the case that the results obtained using Bayesian methods are nearly identical to those obtained using ML estimation, as illustrated by the results of the current analysis (see Table S4 in the online supplemental materials). As such, one might question whether the added complexities of implementing EB MCMC methods yield any real benefits over and above more familiar and accessible ML methods. There are at least two reasons why EB MCMC methods are well worth the extra analytic effort even when yielding results very similar to ML. First, as noted previously, with small samples it is often the case that certain SEM parameter values, typically one or more latent factor variances, must be constrained or fixed to arbitrary and unrealistic values in order for ML estimation methods to converge upon a proper solution. In the current analysis, the variances of the latent factors in the SEM measuring change in adolescent behavior [PS(2,2), PS(4,4)] and family functioning [PS(7,7)] were fixed to zero in order for ML to properly converge. Given that the study of change is sine qua non within clinical intervention research, especially studies examining clinical processes and mechanisms of intervention effects, constraining or eliminating model parameters regarding change is highly undesirable. In particular, fixing change factor variances to zero precludes drawing inferences about individual differences or heterogeneity in change processes, and also hampers the ability to calculate effect sizes to gauge the magnitude and clinical significance of intervention effects (see Feingold, 2009). Calculations of statistical power to detect clinical effects are also substantially impeded by constraining change factor variances to zero. In contrast to the ML solution, the EB estimation procedure yielded valid estimates for all three change factor variances listed above. Even though most other EB parameter estimates were very close to the corresponding ML estimates, the capacity to estimate the change factor variances which were constrained to zero in the ML analysis is a very important and worthwhile advantage of EB over ML estimation of SEMs in small samples. A secondary benefit of supplementing ML with EB estimation of SEMs is that the EB estimates may help to cross-validate the ML solution, which must always be regarded as suspect when sample sizes are small.

Despite the aforementioned benefits and advantages of Bayesian methods over ML for fitting complex statistical models to data obtained from small samples, caution is warranted when utilizing the EB approach discussed in this paper. In particular, a well known criticism of Bayesian statistical methods, especially for small-sample research, is the degree of sensitivity (i.e., non-robustness) of the results to the specification of the prior distribution (see Carlin & Louis, 2009, pp. 5–9). In other words, in any Bayesian analysis the influence of the prior may substantially outweigh that of the observed data when sample sizes are small thereby raising concerns that the results may be driven or shaped primarily by the researcher’s subjective prior knowledge or beliefs rather than by empirical evidence. Given that the prior parameters in the EB approach presented herein are themselves data-derived, one might take some degree of assurance that the EB methodology pays sufficient homage to the frequentist statistical adage of “let the data speak for themselves.” Nevertheless, users of EB methods should be ever mindful that the data may have relatively little to say when the sample size is small, as is the case in the current demonstration analysis. As such, any set of statistical results based on a small sample, regardless of the method of estimation, should be regarded as preliminary and perhaps suggestive of hypotheses that may be more rigorously tested in subsequent research with larger samples.

Although EB estimation with data-derived prior parameters is not a new idea, detailed guidelines and examples of such analyses for small-sample studies are absent in the clinical psychology literature. In fact, the current analysis is the first application of EB SEM for studying theoretically and clinically intricate linkages among observed therapist behaviors, pre- to post-treatment change in primary intervention targets (i.e., mechanisms of change), and behavioral treatment outcomes. Given that many clinical methodologists and data analysts may be unfamiliar with Bayesian SEM methods in general, let alone EB SEM using data-derived prior parameters, the current demonstration analysis may provide valuable methodological instruction and guidance which, in turn, may promote more widespread use of EB SEM methods in clinical research involving prohibitively small samples.