Therapeutic mechanisms of high-frequency stimulation in Parkinson’s disease and neural restoration via loop-based reinforcement

Significance

We investigated the therapeutic mechanisms of high-frequency stimulation (HFS) in Parkinson’s disease by developing a computational model of the cortico-basal ganglia-thalamo-cortical loop in normal and parkinsonian conditions under the effects of stimulation at several frequencies. We found that the stimulation injected in the loop elicits neural perturbations that travel along multiple pathways with different latencies and rendezvous in striatum (one of the basal ganglia). If the stimulation frequency is high enough, these perturbations overlap (reinforcement) and cause more regular, stimulus-locked firing patterns in striatum. Overlap is maximal at clinically relevant HFS and restores more normal activity in the remaining structures of the loop. This suggests that neural restoration and striatal reinforcement may be a therapeutic merit and mechanism of HFS, respectively.

Abstract

High-frequency deep brain stimulation (HFS) is clinically recognized to treat parkinsonian movement disorders, but its mechanisms remain elusive. Current hypotheses suggest that the therapeutic merit of HFS stems from increasing the regularity of the firing patterns in the basal ganglia (BG). Although this is consistent with experiments in humans and animal models of Parkinsonism, it is unclear how the pattern regularization would originate from HFS. To address this question, we built a computational model of the cortico-BG-thalamo-cortical loop in normal and parkinsonian conditions. We simulated the effects of subthalamic deep brain stimulation both proximally to the stimulation site and distally through orthodromic and antidromic mechanisms for several stimulation frequencies (20–180 Hz) and, correspondingly, we studied the evolution of the firing patterns in the loop. The model closely reproduced experimental evidence for each structure in the loop and showed that neither the proximal effects nor the distal effects individually account for the observed pattern changes, whereas the combined impact of these effects increases with the stimulation frequency and becomes significant for HFS. Perturbations evoked proximally and distally propagate along the loop, rendezvous in the striatum, and, for HFS, positively overlap (reinforcement), thus causing larger poststimulus activation and more regular patterns in striatum. Reinforcement is maximal for the clinically relevant 130-Hz stimulation and restores a more normal activity in the nuclei downstream. These results suggest that reinforcement may be pivotal to achieve pattern regularization and restore the neural activity in the nuclei downstream and may stem from frequency-selective resonant properties of the loop.

High-frequency (i.e., above 100 Hz) deep brain stimulation (HFS) of the basal ganglia (BG) and thalamus is clinically recognized to treat movement disorders in Parkinson’s disease (PD) (1–4), but its therapeutic mechanisms remain unclear (5, 6).

Early hypotheses about HFS were derived from the rate-based model of the BG function (7, 8) and postulated the disruption of the output of the BG-thalamic system via either the inactivation of neurons in the stimulated site (target) (9–15), which would provide an effect similar to a surgical lesion, or the abnormal excitation of axons projecting out of the target (16–19), which would disrupt the neuronal activity in the structures downstream, including any pathophysiological activity (20).

More recently, an ever-growing number of experiments in PD humans and animal models of Parkinsonism has indicated that HFS affects the firing patterns of the neurons rather than the mean firing rate both in the target and the structures downstream (18, 19, 21–31) and it replaces repetitive low-frequency (i.e., ≤50 Hz) bursting patterns with regularized (i.e., more tonic) patterns at higher frequencies (25, 26). It has been proposed that increased pattern regularity of neurons in the target may be therapeutic (5, 32–37), but it is still unknown how this regularity comes about with HFS.

It has been suggested that an increased pattern regularity can deplete the information content of the target output and this lack of information would act as an “information lesion” (33) and prevent the pathological activity from being transmitted within the BG-thalamic system (22, 33, 36). As a result, an information lesion in the target [typically, one among the subthalamic nucleus (STN), internal globus pallidus (GPi), or thalamus] would have effects similar to those of a destructive lesion in the same site, which has been reported to alleviate the movement disorders (38).

Instead, studies (32, 34, 35, 37) have suggested that an increased pattern regularity of the BG output partly compensates the PD-evoked impairment of the information-processing capabilities of the thalamo-cortical system, and this restores a more faithful thalamic relay of the sensorimotor information (35, 39).

Although intriguing, these hypotheses remain elusive on (i) the neuronal mechanisms that would elicit pattern regularization (e.g., why regularization would be relevant only for HFS) and (ii) the effects that increased regularity would have on the cortico-BG-thalamo-cortical loop.

It has been hypothesized that pattern regularization occurs because axons projecting out of the target follow the pattern of the stimulus pulses (40, 41) and, given the segregated organization of the BG-thalamic connections (42), it has been assumed that pattern regularization percolates straightforward from the target to the structures immediately downstream (34, 36). However, this representation of the pattern regularization as a “local” effect can hardly be reconciled with the fact that HFS of any structure of the cortico-BG-thalamo-cortical loop is therapeutic for at least some movement disorders (1–4, 43–47), nor does it explain why stimulation at frequencies above 160–180 Hz is not necessarily therapeutic despite the fact that the regularity of the axonal patterns may increase (48, 49). Moreover, coherence in the 8–30-Hz band among neurons across different structures may decrease under HFS but not for lower frequencies (26, 50–52), which suggests the emergence of diffused changes in neuronal activity that would be hardly accounted for with purely local effects.

There is emerging evidence, instead, that HFS affects multiple structures simultaneously. First, it has been shown that deep brain stimulation (DBS) may antidromically activate afferent axons and fibers of passage (53–59), thus reaching structures not immediately downstream. Second, studies (57, 58) observed in 6-hydroxydopamine (6-OHDA)-intoxicated rats that the antidromic effects increase with the stimulation frequency and peak around 110–130 Hz. Third, it has been shown in 1-methyl-4-phenyl-1,2,3,6-tetrahydropyridine (MPTP)-intoxicated nonhuman primates (NHPs) that STN DBS may evoke similar poststimulus responses in different BG structures, both downstream from and upstream to the STN (5, 27, 28, 30, 60). Finally, it has been reported that the cortico-BG-thalamo-cortical system consists of multiple sets of reentrant, interconnected, and partially overlapping neuronal loops (5, 42, 61, 62), which means that the structures upstream to the target (e.g., the striatum) may play an important role in the therapeutic mechanisms of HFS.

Altogether, these results suggest that (A) pattern regularization is a global effect that exploits the closed-loop nature of the cortico-BG-thalamo-cortical system and selectively emerges only for specific HFS values, and that (B) the therapeutic merit of pattern regularization has to deal with the restoration of a more normal functionality of the entire cortico-BG-thalamo-cortical loop rather than with variations in the information content of one specific structure.

We explored hypotheses (A) and (B) and assessed the system-wide effects of DBS by constructing a computational model of the cortico-BG-thalamo-cortical loop in both normal and parkinsonian conditions and by simulating the effects of STN DBS both at low (20–80 Hz) and high (100–180 Hz) frequencies. The model includes populations of single-compartment neurons and interneurons from motor cortex, striatum, GPi, and thalamus according to a network topology derived from the NHP anatomy, and it simulates both the orthodromic and antidromic effects of DBS. As a result, this model reproduced both average activity and discharge patterns of single units in NHP and rats under normal and parkinsonian conditions, with and without DBS, for all modeled structures.

We show through numerical simulation that hypothesis (A) is significantly contributed by reinforcement mechanisms in the striatum. These mechanisms are selectively elicited by HFS, facilitate the percolation of regularized discharge patterns from the striatum to the GPi, and have a primary role in (B), because the percolated striato-pallidal input combines with the local effects of STN DBS to restore the thalamic relay function (63).

Results

We modeled the “direct pathway” in the cortico-BG-thalamo-cortical loop (7, 8) (a schematic is shown in Fig. S1) by using single-compartment neurons from the motor cortex [200 pyramidal neurons (PYNs) and 20 fast-spiking interneurons (FSIs)], dorsolateral striatum [i.e., putamen, 200 medium spiny neurons (MSNs) and 20 parvalbumin-positive interneurons (PPIs)], GPi [200 pallidal neurons (PANs)], and ventrolateral thalamus [200 thalamocortical neurons (TCNs) and 40 reticular neurons (RENs)].

The activity of the remaining BG nuclei was subsumed in the input delivered to the GPi neurons and it varied in normal and PD conditions (64). The connections between neurons were chosen consistently with the neuronal anatomy in NHPs and the synaptic conductances were randomized across the entire network to increase the pattern variability of the neurons at rest (SI Notes 1 and 2).

DBS in the subthalamic area may elicit direct effects on the GPi [monosynaptic orthodromic activation (17)], putamen [both monosynaptic orthodromic activation and antidromic activation of striatonigral projections (5, 65–67)], cortex [antidromic activation of cortico-subthalamic projections (53, 56–58)], and thalamus [antidromic activation of cortico-subthalamic collaterals to the thalamus (31)]. We simulated these effects by applying a delayed depolarizing current pulse for each DBS pulse to the PANs, MSNs, PYNs, and TCNs. The lag between current pulses and DBS input varied according to the depolarization mechanism (orthodromic vs. antidromic) and structure, and the pulse amplitudes were randomly distributed to simulate the stochastic effects of both antidromic and orthodromic propagation (17, 18, 58) (Fig. S2 and SI Note 3).

Regular DBS (i.e., constant interpulse interval) was applied at 20, 50, 80, 100, 130, 160, and 180 Hz. Nonregular DBS (i.e., interpulse intervals following a gamma distribution; SI Note 3) with average frequency of 130 Hz was also applied. For each combination of disease condition and DBS setting, three instances of the model were generated and each instance was simulated for 32,000 ms. The first 2,000 ms of each simulation were neglected to let the model reach steady-state conditions and results were averaged across the model instances.

Normal vs. Parkinsonian Conditions at Rest.

Figs. 1–5 report the population-averaged results for the projecting neurons in the GPi (PANs), putamen (MSNs), cortex (PYNs), and thalamus (TCNs), respectively, under normal and PD conditions at rest. Each population was $N=$600 neurons (i.e., total number of neurons across three model instances). The multifarious effects of the PD-elicited loss of dopamine on the D_1–5 dopaminergic receptors on the MSNs and on the interneurons in the putamen (68) were simulated by varying the maximal conductance of the M-type potassium currents in the MSNs and the activity of the PPIs. We also changed the stochastic distribution of the inputs delivered to the GPi neurons, thus simulating the effects of the loss of dopamine on the GPe–STN subsystem (SI Note 2).

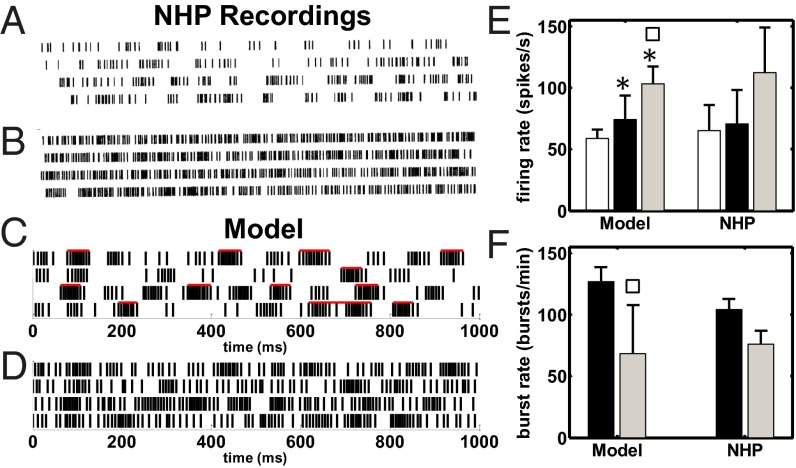
Fig. 1.

(A–D) Raster plot of a GPi neuron under PD conditions at rest (A and C) and with STN HFS (B and D). A and B are from an MPTP-treated NHP (modified with permission from ref. 17). C and D are from a pallidal neuron in our model. Red bars in C denote estimated bursts. (E) Population-average firing rate (mean$\pm$ SD) of the GPi neurons under normal (white), PD (black), and PD with STN HFS (PD+HFS, gray) conditions in our model and NHPs. (F) Population-average burst rate (mean $\pm$ SD) of the GPi neurons under PD (black) and PD+HFS (gray) conditions in our model and NHPs. Population-average burst rate of the GPi under normal condition is 20.9 ± 4.7 bursts per minute (mean ± SD). Rates for NHPs in E and F are reported in refs. 17 and 71 and ref. 23, respectively. Asterisks (squares) show significant differences normal vs. PD and PD+HFS (PD vs. PD+HFS), one-way ANOVA with Tukey–Kramer post hoc test,$P<0.001$. HFS is 136 Hz in the NHPs (B, E, and F) and 130 Hz in our model (D–F).

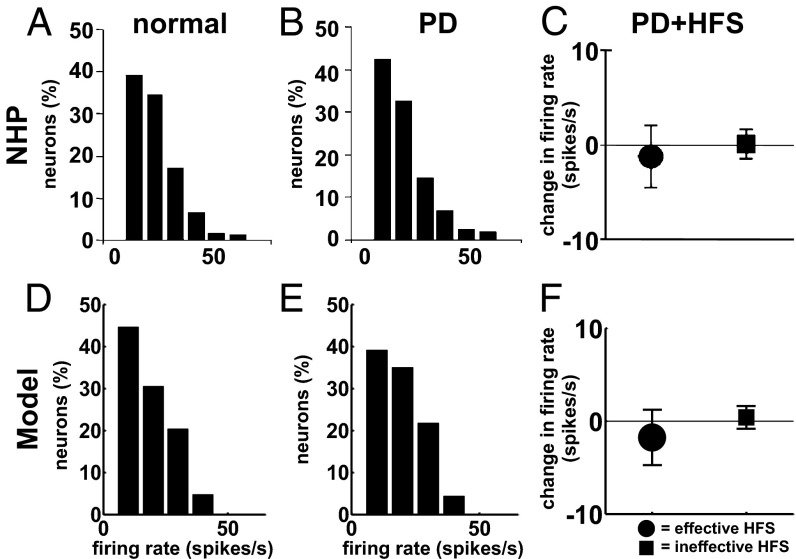
Fig. 5.

Firing rate of TCNs in the ventrolateral thalamus of NHPs (A–C) and in our model (D–F) under normal, PD, and PD with STN HFS (PD+HFS) conditions. (A, B, D, and E) Histograms of mean firing rates under normal (A and D) and PD (B and E) conditions at rest. (C and F) Population-average (mean$\pm$SD) variation of the firing rate of the TCNs at the transition from PD to PD+HFS conditions when the amplitude of the DBS pulses is therapeutically effective (circles) or ineffective (squares) (SI Note 3). STN HFS is 136 Hz in C and 130 Hz in F. A and B are modified with permission from ref. 78, and C is modified with permission from ref. 31.

As a result, the simulated PANs showed a 56% increment of the population-averaged pairwise cross-correlation at the transition from normal to PD conditions (SI Note 4 and 5), 26% increment in the average firing rate (Fig. 1E), and an increased incidence of the bursting mode, thus reproducing experimental results in refs. 17 and 69–71 for NHPs. A comparison between simulated and actual NHP single units from ref. 17 is reported in Fig. 1 A and C.

The percentage of time spent by PANs in bursts raised from $9.1\pm 2.3\%$ (normal) to $22.3\pm 4.0\%$ (PD), the percentage of GPi spikes belonging to bursts raised from 13.9$\pm$3.4% to 58.5$\pm$ 16.0% (mean$\pm$S.D.), and the population-average rates (firing and burst rate) were comparable to the values in refs. 17, 23, and 71 for both normal and MPTP-treated NHPs (Fig. 1 E and F). Furthermore, the spectral analysis of the spiking patterns showed that, under PD conditions, the PANs had exaggerated oscillations either in the 4- to 8-Hz band (tremor band, 60% of the population) or in the 10- to 15-Hz band (beta band, 40% of the population), Fig. 2 A and B. These oscillations were caused by a combination of the input from putamen (72) and the input from the GPe–STN subsystem (73). The frequency bands of the oscillations and the ratio between the number of neurons with tremor- and beta-band oscillations were consistent with experiments in refs. 51, 52, 69, and 70 (Fig. 2C).

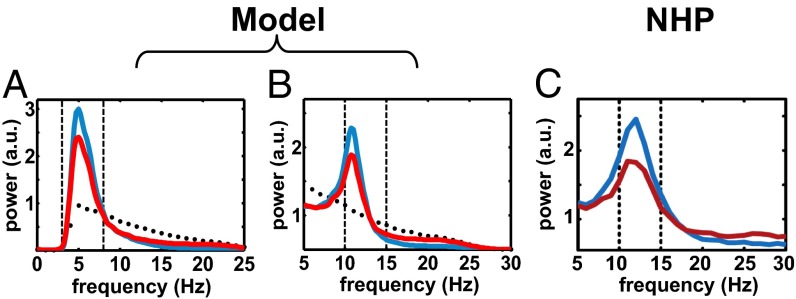
Fig. 2.

(A and B) Population-average normalized power spectrum density (PSD) of tremor-band-oscillatory (A) and beta-band-oscillatory (B) GPi neurons in our model under normal (black dots), PD (blue line), and PD+HFS (red line) conditions. (C) Population-average normalized PSD of beta-band-oscillatory GPi neurons from a NHP under PD (blue line) and PD+HFS (red line) conditions. HFS is 130 Hz in A and B and 125 Hz in C. C is modified with permission from ref. 51.

Under PD conditions, the modulation of M-type potassium currents and the reduced GABAergic input from the striatal interneurons affected the activity of the MSNs. Overall, 72% of the MSNs (490 out of 600) increased the average firing rate (t test,$P<0.05$), which is consistent with refs. 74 and 75, whereas the remaining neurons decreased it. As a result, even though the mean firing rate increased, there was a larger variability of the spiking patterns across the population (Fig. 3 A and B) and an increased level of pairwise cross-correlation (SI Note 5).

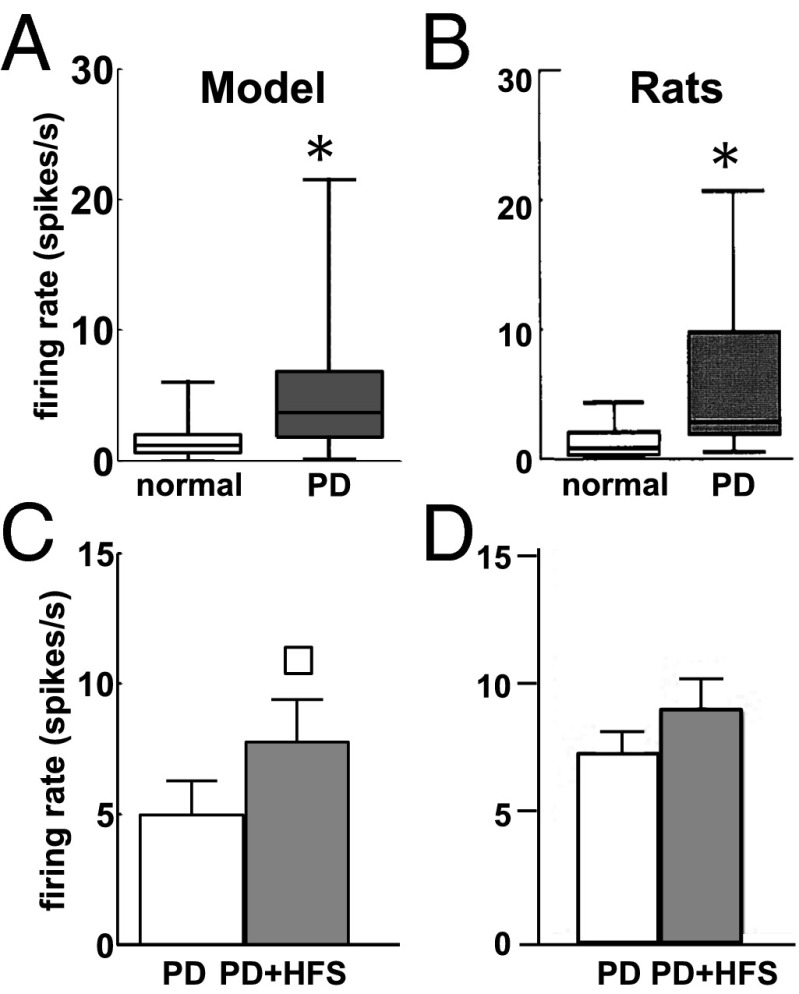
Fig. 3.

(A and B) Box plots of the firing rate of MSNs in our model (A) and in Sprague–Dawley rats (B) under normal (white) and PD (gray) conditions. In each box plot, the median value (black line), 25th and 75th percentiles (bar limits), and 10th and 90th percentiles (error bars) are shown. (C and D) Population-average firing rate (mean$\pm$SD) of the MSNs in our model (C) and Sprague–Dawley rats (D) under PD conditions (white) and PD with 130-Hz STN DBS (PD+HFS, gray). Asterisks in A and B and square in C denote significant differences (Wilcoxon rank-sum test,$P<0.001$). B and D are modified with permission from refs. 75 and 80, respectively.

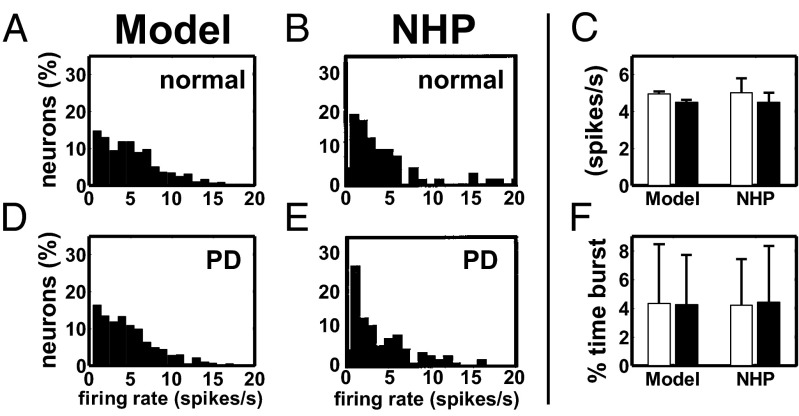
Overall, the changes in the striato-pallidal subsystem had minor effects on the average activity of the cortical and thalamic neurons. In cortex, the percentage of PYNs with random, regular, or bursty patterns mildly changed at the transition from normal to PD conditions (random: 270 vs. 290; regular: 97 vs. 121; bursty: 231 vs. 184; normal vs. PD; definition of the patterns is given in ref. 76 and SI Note 4), and nonsignificant changes (Wilcoxon rank-sum test, $P>0.05$) were reported for the distribution of the firing rates across the PYNs (Fig. 4 A, B, D, and E), the population-average firing rate (Fig. 4C), and the percentage of time spent in burst activity (Fig. 4F), consistently with ref. 76 (M1 group). We measured the fraction of power allocated in the 8–30-Hz band for each PYN and we found that this fraction increased in 331 out of 600 PYNs when under PD conditions, which is consistent with the increment of oscillations in that band reported by ref. 76. The average increment in the 8–30 Hz power across these 331 PYNs was 5.9 ± 6.0% (mean ± SD, range: 0–53.9%) and resulted in no prominent oscillation in that band, which is consistent with the analysis of single unit recordings of MPTP-treated NHPs reported in ref. 52.

Fig. 4.

Histograms of single unit mean firing rates under normal (A and B) and PD (D and E) conditions for the PYNs in our model (A and D) and in the M1 cortex of a NHP (B and E). (C) Population-average firing rate (mean$\pm$SEM) of the PYNs in normal (white) and PD (black) conditions in our model and in the M1 cortex of an NHP. (F) Population-average percentage of time (mean$\pm$SD) spent by PYNs in bursts in our model and in the M1 cortex of an NHP. Data for NHPs in C and F are reported in refs. 102 (animal Z) and 76, respectively. Histograms in B and E are modified with permission from ref. 102.

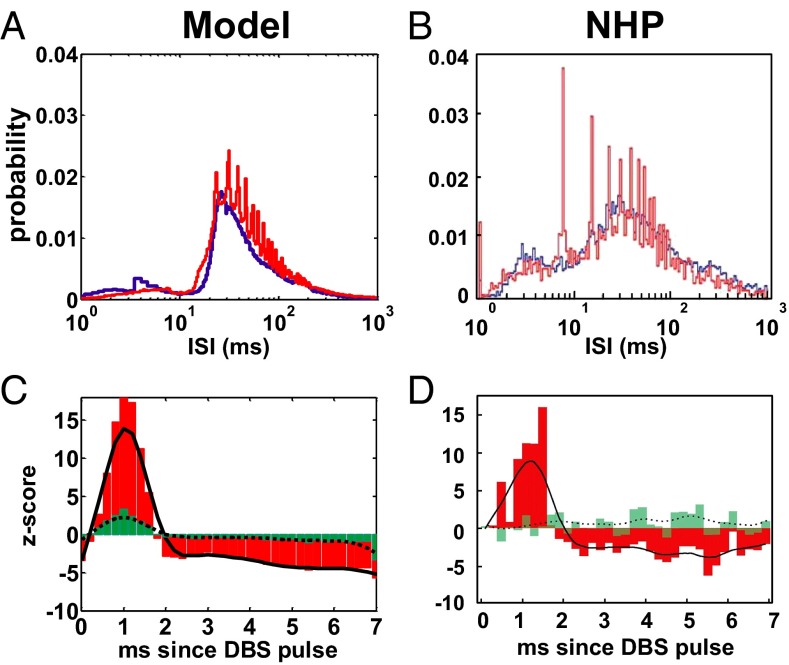
Analogously, the sample distribution of the mean firing rates across the population of TCNs was similar in normal and PD conditions and reproduced experimental results in refs. 77–79 for nontremulous NHPs (Fig. 5 A, B, D, and E). Moreover, the majority of TCNs preserved a random discharge pattern and the number of bursty TCNs remained small across the disease conditions, whereas the number of regular TCNs decreased (random, bursty, and regular pattern: 471 vs. 527, 51 vs. 32, and 70 vs. 41 TCNs, respectively, normal vs. PD conditions), consistently with the trend reported in ref. 78. On the other hand, the loss of dopamine had an effect on the oscillations of the TCN discharge pattern: 224 out of 600 TCNs had a significant change in the interspike interval (ISI) histogram (t test,$P<0.05$), with an enhanced bimodal distribution of the ISIs in PD conditions and peaks around 3 ms and 30 ms (Fig. 6 A and B), consistently with data from MPTP-treated NHPs (31). Correspondingly, the difference between the power spectrum of the spike trains under normal and PD conditions [mean square error (MSE) in the 3–100-Hz band] was significant (Fig. 7A,$P<0.001$).

Fig. 6.

(A and B) ISI histogram of the TCNs in our model under PD conditions (A) and in a MPTP-treated NHP (B) at rest (i.e., no DBS applied, blue lines) and under effective STN HFS (red lines). (C and D) Population-averaged PSTH of the TCNs in A (C) and B (D), respectively, for effective STN HFS. HFS is 130 Hz in A and C and 136 Hz in B and D. Red bars and black line in C and D indicate the PSTH (bin: 0.2 ms) and its envelope (i.e., a smoothing running average of the PSTH), respectively, for effective HFS. Green bars and dotted line in C and D indicate the PSTH and its envelope, respectively, for ineffective HFS. Definition of “effective” and “ineffective” HFS is in ref. 31. B and D are reproduced with permission from ref. 31.

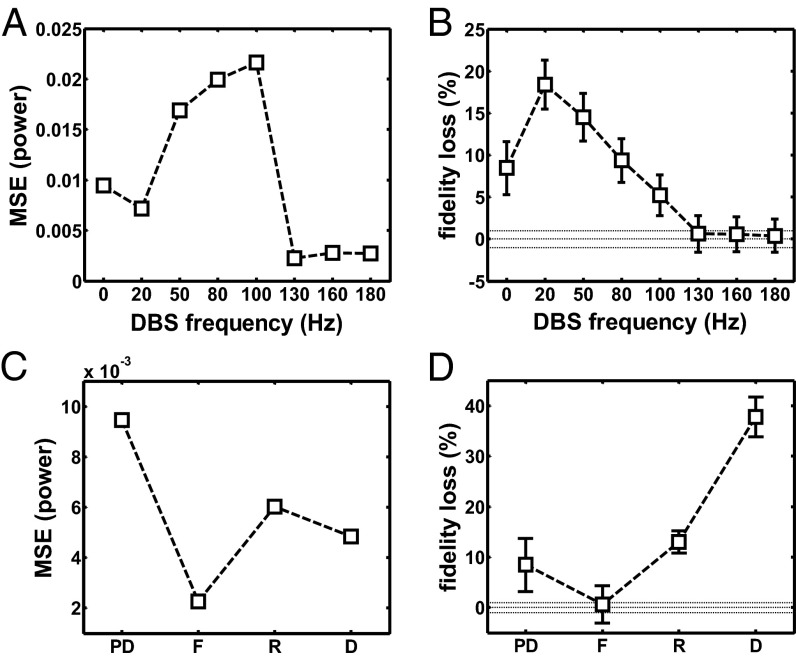
Fig. 7.

(A) MSE in the band [3, 100] Hz between the population-average power spectrum density of the TCNs in normal and PD conditions with regular DBS vs. the DBS frequency. (B) Population-average loss in fidelity (mean$\pm$SEM) of the TCNs over the value in normal conditions due to PD and regular STN DBS at several frequencies. In A and B, 0-Hz DBS means no DBS. The definition of loss in fidelity is in SI Note 4. (C and D) MSE in the band [3, 100] Hz (C) and average loss in fidelity (D) (mean $\pm$ SEM) of the TCNs over the value for the normal case due to PD conditions and various DBS settings. Dotted lines in B and D indicate the reference value (i.e., no increment) and 99% confidence bounds. Settings: D, PD conditions and regular 130-Hz STN DBS applied (only orthodromic effects on GPi); F, PD conditions and regular 130-Hz STN DBS applied (antidromic and orthodromic effects included); PD, PD conditions and no DBS; R, PD conditions and irregular 130-Hz STN DBS applied.

Direct Effects of STN DBS on the GPi, Thalamus, Cortex, and Putamen.

STN DBS at 130 Hz (range: 125–136 Hz) has been reported to restore movement disorders in MPTP-treated NHPs and 6-OHDA–treated rats (5, 15, 17, 23, 28, 31, 51, 57, 80).

In our model under PD conditions, 130-Hz STN DBS affected the GPi PANs by inducing more regular firing patterns, higher average firing rates, and lower burstiness (Fig. 1 B, E, and F), with results matching experimental observations in refs. 17 and 23 (Fig. 1 D–F). The percentage of time spent in bursts and the percentage of spikes belonging to bursts dropped to 14.8$\pm$6.7% and 27.7$\pm$15.5% (mean$\pm$SD), respectively, and the oscillations in the tremor and beta band were significantly attenuated (Wilcoxon rank-sum test,$P<0.001$), consistently with results in ref. 51 (Fig. 2).

STN DBS at 130 Hz also affected the remaining structures in the model under PD conditions. The population-average firing rate significantly increased (t test,$P<0.001$) for the MSNs (Fig. 3 C and D) and PYNs (Fig. S3) and it mildly decreased for the TCNs (Fig. 5 C and F), whereas individual TCNs either significantly increased (77 out of 600) or decreased (339 out of 600) the firing rate (t test,$P<0.05$), consistently with experiments in refs. 31, 57, and 80. Furthermore, the ISI histogram for the TCNs moved from a continuous distribution to a multimodal distribution with peaks corresponding to multiples of the DBS interpulse interval (Fig. 6 A and B), whereas the spectral content of the TCN spike trains was affected in a way that compensated for the changes induced by the PD conditions and returned to a value close to normal conditions (MSE was minimal and $\cong$ 0, Fig. 7A).

The firing pattern of the TCNs, however, remained significantly different from normal when 130-Hz STN DBS was applied. These neurons tended to fire an action potential with short latency (1–2 ms) after each DBS pulse [z-score >2.58, which corresponds to a P value$P<0.01$ (18)] as in ref. 31 (Fig. 6 C and D) and were entrained to similar patterns, as suggested by the fact that ∼80% of the TCNs were likely to fire a poststimulus action potential with the same latency (Fig. S4B). The population-average pairwise cross-correlation, instead, decreased by 16.7% and was similar to the normal case (less than 1% difference, SI Note 5).

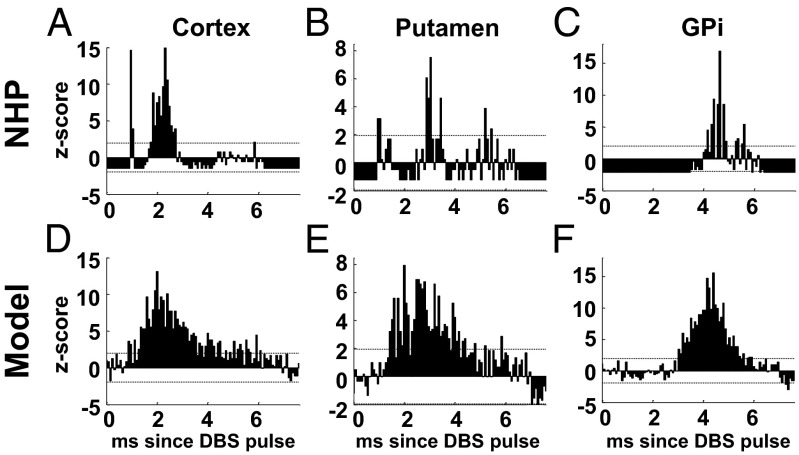
Analogously to the TCNs, PYNs in the cortex, PANs in the GPi, and MSNs in the putamen were consistent with single unit recordings in refs. 5, 28, 30, 57, and 58, i.e., they showed a patterned poststimulus response and an increased likelihood of firing action potentials with short latency after each DBS pulse (Fig. 8), despite the fact that the average firing rate remained significantly lower than the DBS frequency (Fig. S3).

Fig. 8.

PSTH (bin size: 0.08 ms) of a PYN (A and D), an MSN (B and E), and a PAN (C and F) from an MPTP-treated NHP (A–C) and in our model (D–F) under PD conditions and 130-Hz STN DBS. Dotted lines in A–F denote 95% confidence bounds. The single unit recordings used to compute the histograms in A–C are from M1 cortex, putamen, and GPi and were part of the dataset analyzed in refs. 28, 86, and 30, respectively.

These results were determined by a combination of low stimulation efficacy and distal effects. As in refs. 18 and 57, we focused on each structure and we measured the DBS efficacy as the fraction of STN DBS pulses that result into a poststimulus spike of the neurons in that structure. We found that, for the given amplitudes of the DBS-evoked postsynaptic currents (SI Note 3), only 35% of the DBS pulses at 130 Hz elicited a poststimulus spike in the pallidal neurons and only 3.5–6.8% elicited a spike in TCNs, PYNs, or MSNs, thus limiting the increase of the average firing rate. Nonetheless, the poststimulus currents to the cortex, thalamus, and putamen were pivotal to achieve the early (i.e., latency of 1–2 ms) poststimulus excitation in Fig. 6 C and D and Fig. 8 (compare with Fig. S5, where these currents were blocked), thus indicating that the distal effects of STN DBS (i.e., the antidromic activation of cortico-subthalamic projections, orthodromic activation of cortico-thalamic collaterals of these cortico-subthalamic projections, orthodromic activation of subthalamo-striatal projections, and antidromic activation of the striatonigral projections) are pivotal to the overall change in pattern reported in the BG structures.

STN HFS Elicits Thalamic Restoration.

We tested several DBS frequencies in the range 20–180 Hz on our model under PD conditions and we assessed the effect of stimulation on the thalamic activity (Fig. 7). Compared with the rest conditions, the spectral MSE for the TCNs either increased or did not significantly change for nontherapeutic DBS (20–100 Hz), whereas it dropped for DBS above 100 Hz (Kruskal–Wallis test with Tukey–Kramer post hoc test,$P<0.001$) (Fig. 7A).

Correspondingly, we assessed the fidelity of the TCNs in relaying cortical inputs (63), which has been proposed in refs. 34 and 35 as a measure of the restoration of the normal thalamic function. We found that the amount of misresponses to the cortical inputs (fidelity loss, see definition in SI Note 4) increased under PD conditions and this increment was worsened by low-frequency DBS (20–50 Hz) and mildly compensated by nontherapeutic DBS (80–100 Hz), which indicate an overall deterioration of the relay performance (Fig. 7B). Instead, the loss in fidelity was significantly reduced for DBS at frequencies above 100 Hz (Kruskal–Wallis test with Tukey–Kramer post hoc test, $P<0.001$) and achieved values $\cong$ 0, thus indicating a restoration of the normal thalamic relay performance. Interestingly, the restoration of the spectral activity and the thalamic performance required both the regularity of the DBS input and the contribution of the distal effects of STN DBS. To prove this, we compared the spectral MSE for the TCNs (Fig. 7C) and the loss in fidelity (Fig. 7D) caused by PD conditions under no DBS (PD in Fig. 7 C and D), regular 130-Hz STN DBS (F and D), and irregular 130-Hz STN DBS (R). For settings R, the DBS input was a memoryless point process with instantaneous rate following a gamma function (130$\pm$78 Hz, mean$\pm$SD; SI Note 3 and ref. 36), whereas settings D and F included the subthalamo-pallidal orthodromic effects of DBS on the GPi only (D) and both the orthodromic and antidromic effects of DBS on the GPi, cortex, putamen, and thalamus (F), respectively. Fig. 7 C and D shows that both the MSE and the loss in fidelity were minimal and close to 0 (i.e., the normal conditions were restored, $P<0.01$) only in settings F, whereas both the lack of the antidromic effects (D) and the lack of DBS regularity (R) were unable to compensate the effects caused by the PD conditions.

Striatal Reinforcement As a Mechanism of HFS-Elicited Thalamic Restoration.

Fig. 7 indicates that any DBS frequency above 100 Hz can produce some level of compensation of the effects of PD on the thalamic function but results are maximized for 130-Hz DBS. Hence, we hypothesized that this frequency selectivity depends on the closed-loop nature of the cortico-BG-thalamo-cortical system and the overlap of several pathways in the striatum (Fig. S1).

We analyzed the firing pattern of the MSNs in our model under PD conditions and STN DBS by constructing the bi-PSTH (poststimulus time histogram) for several DBS frequencies (Fig. 9). Differently from the PSTH (Fig. 6 C and D and Fig. 8), which estimates the likelihood of poststimulus spikes normalized to the prestimulation activity (18), the bi-PSTH is a 2D histogram whose generic element ($x,y$) focuses on two consecutive DBS pulses and estimates the likelihood that the first spike after the first pulse and the first spike after the second pulse occur with latency of$x$ and$y$ ms, respectively (SI Note 4), thus estimating the dispersion of the poststimulus latencies across consecutive DBS pulses and assessing the entrainment of the pattern to DBS.

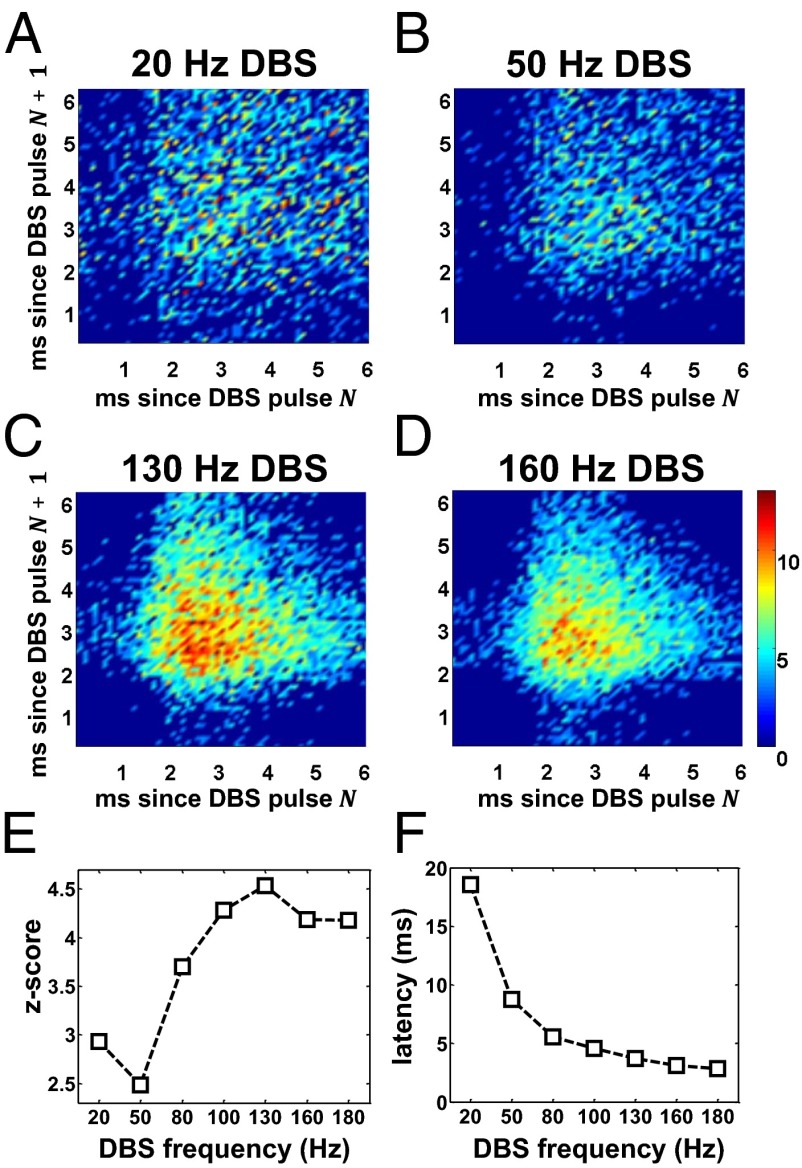
Fig. 9.

(A–D) Population-average bi-PSTH (time bin: 0.1 ms) of the MSNs under PD conditions when regular STN DBS at 20 Hz (A), 50 Hz (B), 130 Hz (C), and 160 Hz (D) is applied. (E) Average z-score of the bi-PSTH of the MSNs over all of the pairs of latencies ($x,y$), with 1$<x<$5.3 ms and 1$<y<$5.3 ms, estimated for several DBS frequencies under PD conditions. (F) Population-average latency of the first poststimulus spike of the MSNs under PD conditions and STN DBS at several frequencies. Color scale in D also applies to A–C and indicates the z-score for each combination of poststimulus latencies. Only the z-scores above 2.58 (i.e.,$P<0.01$) are plotted.

We found that the latencies were highly dispersed for low-frequency DBS and nonsignificantly different from the baseline prestimulation condition (Fig. 9 A and B), whereas for high-frequency DBS (i) the firing pattern was characterized by a small set of latencies, (ii) all these latencies were close to the propagation latency of the DBS pulses toward the MSNs (Fig. S2), and (iii) the neurons were entrained to the DBS input (Fig. 9 C and D).

Unlike for the other high-frequency values we noted that for 130-Hz DBS the range of paired latencies ($x,y$) with significant likelihood ($P<0.001$) was minimal. The average z-score, instead, was maximal and significantly different from the z-score estimated for the other DBS frequencies (Fig. 9E, one-way ANOVA with Tukey–Kramer post hoc test,$P<0.001$), thus indicating that the level of entrainment was overall maximized.

To assess whether the entrainment was just an effect of the DBS-elicited direct input to the MSNs (i.e.,$I_{DBS}$ in Fig. S2), we measured the population-average latency of the first poststimulus spike (Fig. 9F). Results indicate that the latency decreased monotonically with the DBS frequency and plateaued at the value of the propagation latency of the direct effects of DBS, presumably because the number of DBS inputs$I_{DBS}$ increases with the DBS frequency while the duration of interpulse intervals decreases. The entrainment, instead, occurs if distinct neurons respond with similar latencies and discharge patterns to a common subthreshold input. Typically, this is a consequence of an increased level of excitability of the neurons (i.e., higher subthreshold membrane voltage), which may actually enhance the effects of low-amplitude currents$I_{DBS}$ and make the poststimulus latencies more uniform.

We investigated the origins of the increased excitability of the MSNs by assessing the timing of the PYNs and TCNs that project on the MSNs. In particular, we inquired whether the excitability was just a consequence of the increased firing rate of the cortical input to the MSNs or rather an effect of the percolation of DBS stimuli through the pallido-thalamo-striatal and pallido-thalamo-cortico-striatal pathways (Fig. S1). To this purpose, we applied irregular 130-Hz STN DBS (as for settings R in Fig. 7 C and D) and we found that, despite the fact that the average firing rate of the cortical and thalamic neurons was higher for irregular than regular 130-Hz DBS (PYNs: 10.5$\pm$4.3 Hz vs. 8.9$\pm$4.5 Hz; TCNs: 16.3$\pm$11.6 Hz vs. 12.4$\pm$11.3 Hz; t test,$P<0.001$), the average z-score of the bi-PSTH of the MSNs was lower ($P<0.001$) and the range of poststimulus latencies was larger (4.95$\pm$7.49 ms vs. 3.69$\pm$1.98 ms,$P<0.001$). Overall this indicates that the excitability of the MSNs and their entrainment to the DBS input were inferior for irregular DBS.

The origins of this likely stem from the fact that, for any given MSN$n$, the activity of the PYNs and TCNs projecting on$n$ had distinct DBS-dependent patterns before each spike of$n$ (Fig. 10 A and B). In particular, the PAN and TCN patterns were unrelated for irregular DBS (uniform distribution, Fig. 10B) whereas PANs and TCNs tended to fire simultaneously 8–10 ms before the neuron$n$ under regular DBS, thus evoking concurrent depolarizing currents in$n$. Moreover, because the thalamo- and cortico-striatal synapses have long decay times (∼10 ms, Table S1), the sum of the TCN- and PYN-evoked currents was able to combine with the antidromic effects of DBS (Fig. 8E), thus further increasing the depolarization of the MSNs. Overall, these results indicate that the effects of DBS on the putamen depend on the timely overlap between inputs from different pathways (reinforcement) and were maximized at the signature frequency of 130 Hz, which likely represents a resonant frequency of the overall cortico-BG-thalamo-cortical loop.

Fig. 10.

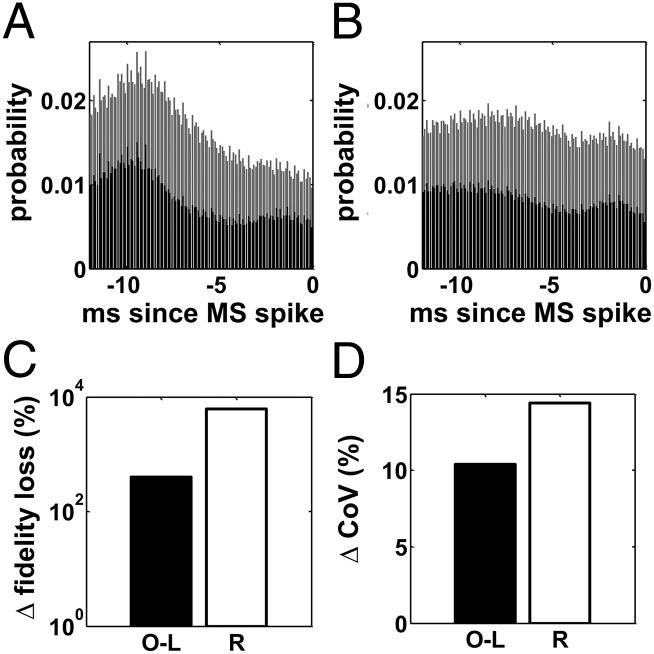
(A and B) Population-average time histogram (time bin: 0.1 ms) of the TCNs (black) and PYNs (gray) projecting onto MSNs in the 12 ms preceding a spike of the target MSN (0 ms is when the spike arrives) under PD conditions when regular (A) and irregular (B) 130-Hz STN DBS is applied. (C) Change of average loss in fidelity of the TCNs at the transition from settings F to O-L and R, respectively. (D) Change of population-averaged coefficient of variation (CoV) of the PANs at the transition from settings F to O-L and R, respectively. Settings: F, PD conditions and regular 130-Hz STN DBS applied (as in Fig. 7); O-L, PD conditions and regular 130-Hz STN DBS applied, with the effects of the MSNs on the PANs blocked and replaced by a surrogate input (open-loop simulation); R, PD conditions and irregular 130-Hz STN DBS applied.

The fact that the level of entrainment of the MSNs and the level of restoration of the TCNs had a similar pattern when varying the DBS frequency and settings (Figs. 7 and 9) suggests that the projection of the MSNs onto the PANs may be relevant. To assess the impact of the striatal entrainment on the pallido-thalamic system, we simulated the network model under PD conditions and regular DBS at 130 Hz but we blocked the synaptic input from the MSNs to the GPi PANs (open-loop simulation). The lack of striatal inhibition was compensated by applying a surrogate input current$\widehat{I}\left(t\right)$ to the PANs.$\widehat{I}\left(t\right)$ was obtained by averaging the striato-pallidal synaptic currents over the available PANs (SI Note 1) and shuffling uniformly the values of this average current over time. In this way, the average level of inhibition provided by the MSNs to the PANs was preserved, whereas the propagation of the oscillatory pattern of the striato-pallidal input was prevented, thus assessing the impact of the closed-loop organization of the cortico-BG-thalamic system over the open-loop effects of STN DBS on the GPi neurons.

We found that, even though the average firing rate of the TCNs mildly changed because of the surrogate input to the GPi (open-loop: 12.1$\pm$11.2 Hz; closed-loop: 12.4$\pm$11.3 Hz), the spectral MSE of the TCNs increased by ∼10% over the value in the closed-loop simulation and, perhaps more importantly, the relay performance was significantly lower (i.e., the loss in fidelity increased by ∼200%, Fig. 10C).

To understand the mechanisms of this, we measured the discharge pattern of the PANs in the open-loop simulation. We found that, even though the instantaneous discharge rate of the PANs increased because of the lack of patterned GABAergic input from the MSNs (Fig. S6), the regularity of the pattern decreased, that is, the coefficient of variation [which measures the variability of the discharge pattern (33)] raised by ∼15% (Fig. 10D). This suggests that the pattern of the striato-pallidal input was important to maximize the restoration of the normal thalamic function.

Discussion

In the past 15 years there has been great effort to understand the effects of HFS on single neurons and neuronal populations, and to explain how these effects could relate to the restoration of movement disorders. Recordings from PD patients, MPTP-treated NHPs, and 6-OHDA–treated rats have recently shown that (i) the regularity of the stimulation (i.e., using constant interpulse intervals) and the high frequency are both relevant to achieve motor restoration (5, 36, 48, 81); (ii) STN and GPi neurons have exaggerated bursting and oscillatory firing patterns under PD conditions, which may correlate with the movement disorders (6, 52); (iii) HFS results into a more regular (i.e., tonic) firing of the neurons in both the stimulated site and the structures downstream from it (15, 17, 22, 23, 25, 26); and (iv) the measures of firing regularity (e.g., entropy, coefficient of variation, etc.) correlate with the reduction of movement disorders (22, 32, 33, 36, 49). Altogether i–iv led to hypothesize that the regularization of the firing patterns could be a mechanism through which motor restoration is achieved (33, 34), even though it remains elusive how HFS regularizes the firing patterns and what the effect of pattern regularization on the cortico-BG-thalamo-cortical loop is.

Computational studies (40, 41) have suggested that the pattern regularization depends on the axons projecting out of (or passing by) the stimulated site, that is, these axons may initiate action potentials at a fixed latency from the DBS pulses, thus resulting in a firing pattern that mimics the DBS pattern. This has led researchers to hypothesize that GPi and thalamocortical neurons gain more regular firing patterns because of the regularization of the presynaptic input from the STN (in case of STN HFS) and GPi (in case of GPi HFS), respectively (32–36). That is, pattern regularization is a “local” effect of HFS. However, this does not explain why the effects of stimulation would percolate to structures not directly receiving input from the stimulated axons for HFS but not for lower frequencies (24), and why, despite the fact that the regularity of the firing patterns of the stimulated axons increases with the stimulation frequency (41), the clinical benefits decrease for stimulation frequencies above 130–160 Hz (48, 49).

Our results, instead, indicate that the pattern regularization is likely a “system” effect, that is, it occurs because DBS elicits time-locked stimuli (i.e., stimuli with a fixed lag from the DBS pulse) in different structures and these stimuli eventually overlap in a gathering site (the putamen), thus causing a suprathreshold depolarization that none of them would be able to produce individually (reinforcement). The resultant regularized pattern of the striatal cells would then reenter the loop via the striato-pallidal projections and would combine with the local effects of HFS, thus sustaining itself and spreading within the GPi.

This indicates that the pattern regularization is presumably a by-product of the simultaneous occurrence of several conditions. First, it is pivotal that the cortico-BG-thalamic system forms a network of parallel, nonreciprocal, and intersecting loops (42, 62), because this lets suprathreshold DBS stimuli (which are locally applied in one structure, e.g., STN, GPi, etc.) propagate through different pathways and eventually rendezvous in a gathering site. Second, it is important that DBS elicits time-locked stimuli in the loops (41, 59) and that each loop has its own path of polysynaptic connections, because this locks the latency between any pair of stimuli passing through the gathering site (61). To clarify this point we note that a STN DBS pulse evokes an orthodromic stimulus in the GPi neurons (latency ∼3 ms) and a (perhaps antidromic) stimulus in the MSN (latency ∼2 ms), respectively (Fig. S1). The stimulus received by the GPi, though, propagates through the loop via polysynaptic connections (pallido-thalamic and thalamo-striatal synapses) and reenters the putamen. Because of the nature of these connections (synapses from GPi are GABAergic and elicit a spike in the TCN via rebound mechanisms) and the time constant of the striatal synapses, the overall time required by the orthodromic stimulus to percolate back to the putamen will be ∼17 ms. This suggests that if two consecutive DBS pulses were applied ∼15 ms apart one from one another, the stimulus due to the first pulse and propagated along the pallido-thalamo-striatal pathway would reach the putamen at the same time as the stimulus due to the second pulse that propagates straight to the MSNs, thus eliciting reinforcement. Therefore, consistently with the observations in refs. 48, 61, and 62, our simulations suggest that a regular DBS train at ∼67 Hz (i.e., the reciprocal of 15 ms), 130 Hz (reciprocal of 7.6 ms, half of 15 ms), and so on, engages this reinforcement mechanism. Note that our model is tuned on data from NHPs and 130-Hz DBS is reported as one of the most therapeutic for MPTP-treated NHPs (e.g., 5, 17, 23, 24, 26, 27, 30, 31).

The fact that reinforcement would make an impact on the whole loop only for DBS frequencies above 100 Hz instead depends on the duration of the poststimulus pattern. As reported in ref. 5, in fact, the poststimulus effects of a DBS pulse on the neuronal pattern vanish within 7–8 ms, thus letting the loop return to its abnormal prestimulus activity. Hence, 130 Hz is the first frequency for which both the reinforcement occurs and the neuronal pattern cannot turn to pre-DBS values.

Overall, these observations suggest that, even though there is a range of DBS frequencies that is likely therapeutic, there is a frequency within this range (e.g., 130 Hz in our model) that may achieve maximal restoration and that depends on the specific neural anatomy of the subject under treatment (i.e., human vs. NHP or rat).

Furthermore, because of its “system” nature, the proposed reinforcement-based mechanism is not affected by the specific location where the DBS lead is actually inserted (e.g., thalamus, STN, GPi, etc.). More precisely, because the concurrent effects of DBS on the STN, GPi, putamen, thalamus, and cortex contribute each and every one to the activation of the reinforcement, the location of the DBS lead determines which pathways are activated either orthodromically or antidromically, and hence it defines the minimum latency between consecutive pulses that allows reinforcement. This would explain why HFS of virtually every structure of the cortico-BG-thalamic system can restore at least some of the PD disorders (1–4, 43, 45, 47) and why the specific high frequency used may vary with the DBS target.

Finally, reinforcement can contribute to understanding the effect of pattern regularization on the cortico-BG-thalamo-cortical loop. The hypotheses so far [e.g., information lesion, thalamic relay restoration, etc. (33–35)] rely on the assumption that HFS must have some sort of similarity to destructive lesions. However, this hardly reconciles with the fact that there are structures (e.g., GPe) wherein applying HFS is clinically effective whereas a destructive lesion can elicit Parkinsonism (19, 47). Also, the aforementioned hypotheses are consistent with a representation of the cortico-BG-thalamo-cortical loop as a hierarchic feed-forward system where single neurons conceptually substitute for entire structures (5, 81). However, this representation is challenged by the fact that coherent frequency-specific oscillations may spread through the entire loop during Parkinsonism (52, 82) and HFS can have a decoupling effect among the various structures of the loop (51).

Our simulations, instead, suggest that the poststimulus modulation induced by HFS disrupts the ongoing firing patterns of each structure in the cortico-BG-thalamo-cortical loop (Figs. 6 C and D and 8, and refs. 28, 30, and 31) and the disruption may facilitate the attenuation of PD-related oscillations. In the case of thalamus, the attenuation would stem from a reduced bursting activity in the pallido-thalamic subsystem and a concurrent increase of the cortico-thalamic excitation. As a result, the relay performance of the thalamocortical neurons increases despite an attenuation of the average firing rate, and the power content of the GPi neurons in the beta frequency band decreases, which is consistent with results in 6-OHDA–treated rats and MPTP-treated NHPs under HFS (51, 57).

Distal Effects of DBS Contribute to the Reinforcement.

Our computational model assumes that (i) DBS may depolarize presynaptic terminals along with efferent axons from the stimulated site, (ii) this depolarization can lead to an activation of cortical, thalamic, and striatal neurons, even though with a very low probability, and (iii) the stimuli delivered to each neuron have a stochastic distribution.

These assumptions reflect recent evidence from computational and experimental studies. In particular, 3D reconstructions of the brain anatomy and DBS lead have been combined with multicompartment models of the neurons and fibers around the DBS electrode in refs. 54, 55, and 59, thus showing that, for therapeutic DBS amplitudes, the electric field induced by DBS in the brain can depolarize myelinated axons and passing fibers outside the stimulation target. The computational study (83) and the in vitro study (84) have also shown that the depolarization of myelinated axons and presynaptic terminals may cause antidromic action potential propagation, which can activate neurons that are upstream of the stimulated site, and numerical simulations (85) have shown that the activation of fibers of passage during STN and GPi HFS can increase the thalamic relay performance under PD conditions. Furthermore, single unit recordings in 6-OHDA–treated rats (57, 58) and MPTP-treated NHPs (28, 31, 86) have shown early (∼1 ms) poststimulus spikes in cortical, striatal, and thalamic neurons during STN HFS, which is consistent with an antidromic activation of the cortico-subthalamic fibers. Finally, a count of the DBS pulses that actually result in poststimulus spikes in cortical neurons (28, 57) indicated that the efficacy of the antidromic stimuli in depolarizing neurons was generally mild.

However, little attention has been paid thus far to the therapeutic significance that these distal effects of STN HFS may have on the motor cortex, thalamus, and striatum. Our results suggest that, although limited (i.e., the probability of having a suprathreshold antidromic stimulus is small in each neuron in our model), the antidromic activation is fundamental to the reinforcement. First, the antidromic stimuli increase the rest membrane potential right after every DBS pulse, thus resulting in an increased poststimulus neuronal excitability. Second, for therapeutic HFS frequencies, this subthreshold increase of membrane potential may combine with the diffused postsynaptic depolarization caused by the orthodromic projections from motor cortex and thalamus in striatum, and this may lead to the patterned poststimulus activation of the MSNs. Finally, the recurrent subthreshold increase of the membrane potential in the cortical, striatal, and thalamic neurons tends to mask the ongoing subthreshold oscillations in the beta band, which ultimately contributes to suppress the exaggerated PD-related beta oscillations.

Interestingly, this latter point suggests that, even though the origins and the significance of the beta oscillations in the pathophysiology of Parkinsonism remain debated (52), the antidromic activation elicited by HFS might provide a contribution to the suppression of the beta oscillations by involving different structures (striatum, cortex, etc.) simultaneously. Although speculative, this spatially distributed suppression mechanism could reconcile different (and apparently conflicting) indications in refs. 57, 82, and 87–89 about which structure should be primarily targeted to suppress the beta oscillations.

Model Limitations and the Role of Other Pathways.

We developed a network-based model of the cortico-BG-thalamo-cortical loop that includes populations of single-compartment neurons from the motor cortex, ventrolateral thalamus, GPi, and putamen, and we subsumed the activity of the GPe and STN in the net input to the GPi neurons. The GPe–STN subsystem has a fundamental role in the pathophysiology of PD and several studies have described the multifarious effects of DBS on the subthalamic and pallidal neurons (e.g., 12–15, 17, 22, 23, 26, 29). However, because the goals of our work were to (i) study the effects of DBS on a closed-loop neuronal system for several stimulation frequencies and (ii) understand the neuronal mechanisms of therapeutic HFS, we decided to model only a finite number of loops involving the BG, cortex, and thalamus. Furthermore, even though the GPe and STN inputs may contribute to the spontaneous activity of the GPi neurons at rest (64), it has been reported that under STN HFS, the subthalamo-pallidal projections entrain to the stimulation frequency (41), thus masking the reentrant effects of the cortex onto the STN neurons and of the striatum onto the GPe neurons. Based on these considerations, the current lack of the GPe–STN subsystem in our model has limited impact, and replacing the currently simulated net subthalamo-pallidal synaptic input to the GPi with the actual GPe–STN subsystem is expected to have minor impact on our results or even to facilitate the propagation of the reinforcement effects. In fact, there is evidence that PD-elicited exaggerated oscillations in the range of 8–30 Hz primarily affect the indirect pathway, propagate through the GPe-STN subsystem, and are attenuated in the GPe and STN by HFS (50, 72, 82). In our model, though, the input to the GPi neurons that subsumes the GPe–STN activity is not modulated by HFS, that is, our results are achieved despite the fact that we are neglecting the therapeutic effects of HFS on the indirect pathway. Furthermore, HFS has been reported to decouple the oscillatory pattern of the GPi and the STN–GPe subsystem (51), but we did not explicitly model it. It is therefore reasonable to speculate that, if the effects of HFS on the STN–GPe subsystem were modeled, the attenuation of the pathologic oscillations in the GPi would have been larger than shown in Fig. 2, and the reduction of the STN–GPe oscillatory input to the GPi would have facilitated the percolation through the direct pathway (64) (i.e., the reinforcement-driven MSN pattern would propagate toward the GPi and thalamus in a more effective way).

Another limitation in our model is the simplified representation of the motor cortex, thalamus, GPi, and putamen. Studies on single unit recordings from NHPs and PD patients have shown that different subtypes of pyramidal, thalamocortical, and pallidal neurons may have different patterns under PD conditions and DBS (76, 79, 90–92), and MSNs in the striatum may respond differently to the loss of dopamine depending on the prominent expression of D₁ or D₂ receptors (68). Our model focused on small neural populations with homogeneous properties and reproduced only a subset of the multifarious effects of Parkinson’s disease and DBS. This would have little impact on the main results, though, because the mechanisms we explored primarily exploit the fact that DBS pulses modify the ongoing pattern of relevant neurons (i.e., pyramidal, thalamocortical, and medium spiny) within the cortico-BG-thalamo-cortical loop by inducing a common poststimulus response (Fig. 8) which, for these neurons, resulted independent of the specific prestimulation activity. Finally, there is evidence in NHPs and rats of GABAergic projections from the GPe to the motor striatum (93, 94). Although numerically limited, these projections have diffusive organization in the striatum and might determine a strong, DBS-locked inhibitory input to the striatal neurons, as recently proposed (95). However, because the reinforcement mechanism described above would primarily contribute to the early poststimulus activation of the MSNs along the direct pathway and because this pallido-striatal inhibitory input would be mediated by polysynaptic connections, it is plausible that the resultant effect would not reduce the poststimulus antidromic depolarization of the MSNs. More likely, instead, this pallido-striatal input would contribute to further attenuate the exaggerated oscillations in the range of 8–30 Hz and it would account for the late poststimulus inhibition (∼6–7 ms after the DBS pulse) that has been observed in striatal neurons from MPTP-treated NHPs (5, 86) and that is not entirely captured by our model.

Materials and Methods

Network Model.

We developed a network of 880 single-compartment model neurons. The equations and parameters for each model neuron are as in refs. 96 (TCNs and RENs), 97 (PYNs and FSIs), 87 (PANs), and 72 (MSNs) and are reported in SI Note 1. The PPI model is as in ref. 98 with the ionic conductances from the soma compartment in ref. 99. The ratio of PYNs to FSIs (200:20) is as in ref. 100 and accounts for the high electrical connectivity of the cortical interneurons, which is not explicitly modeled. The ratio of MSNs to PPIs (200:20), instead, was chosen such that (i) the number of distinct PPIs projecting onto each MSN and (ii) the number of distinct MSNs reached by each PPI were as in ref. 101. Details about the network connectivity are in SI Note 1.

Each neuron was endowed with a constant current ($I_{bias}$) to simulate the background excitation and a Gaussian noise with zero mean and SD$\sigma$ to simulate the subthreshold membrane voltage fluctuations (±5 mV) (Table S1). The transition from normal to PD conditions in the network model is described in SI Note 2 and shown in Fig. S7. Briefly, we mimicked the effects of dopamine depletion on the excitability of the MSNs and PPIs in the putamen and we reproduced the altered input from the subthalamo-pallidal subsystem to the PANs in the GPi.

We simulated the effects of STN DBS on the subthalamofugal axons projecting onto the GPi by applying depolarizing current pulses to the PANs. Duration of each pulse was fixed, and the amplitude followed a Gaussian distribution and could be either supra- or subthreshold. Similarly, we simulated the antidromic effects of STN DBS on the thalamus, cortex, and putamen by applying depolarizing current pulses with normally distributed amplitudes to the TCNs, PYNs, and MSNs, respectively. See details in SI Note 3.

Computational Tools.

The model network was simulated at room temperature (36 °C). Numerical simulations were programmed in C++ and run on a six-core Intel Xeon workstation (3.5 GHz per core). The differential equations were integrated via the midpoint method with time step 0.01 ms. Results were analyzed in MATLAB R2013a (The MathWorks, Inc.). We implemented published algorithms to compute firing and burst rates, poststimulus histograms, power spectrum densities, cross-correlation, and thalamic relay fidelity. A full description of the implementation is given in SI Note 4.