Abstract
Cell polarity underlies many aspects of metazoan development and homeostasis, and relies notably on a set of PAR proteins located at the cell cortex. How these proteins interact in space and time remains incompletely understood. We performed a quantitative assessment of polarity establishment in one-cell stage Caenorhabditis elegans embryos by combining time-lapse microscopy and image analysis. We used our extensive data set to challenge and further specify an extant mathematical model. Using likelihood-based calibration, we uncovered that cooperativity is required for both anterior and posterior PAR complexes. Moreover, we analyzed the dependence of polarity establishment on changes in size or temperature. The observed robustness of PAR domain dimensions in embryos of different sizes is in agreement with a model incorporating fixed protein concentrations and variations in embryo surface/volume ratio. In addition, we quantified the dynamics of polarity establishment over most of the viable temperatures range of C. elegans. Modeling of these data suggests that diffusion of PAR proteins is the process most affected by temperature changes, although cortical flows appear unaffected. Overall, our quantitative analytical framework provides insights into the dynamics of polarity establishment in a developing system.
Introduction
A widespread mechanism to polarize cells in metazoan organisms relies on generating spatially restricted domains of protein enrichment at the cell cortex below the plasma membrane. Such cortical polarization is important for many aspects of cellular behavior and development, including asymmetric cell division, cell migration, and determination of body axes (reviewed in (1)). Defects in cortical cell polarity have been associated with a variety of disease conditions, including cancer (reviewed in (2)).
The core molecular players of cortical polarity were identified in the nematode Caenorhabditis elegans, where their inactivation results in PARtitioning defective phenotypes characterized by impaired asymmetric cell division (3). In the wild-type (WT) ∼50 μm-long C. elegans embryo, cortical polarity is established during the first cell cycle, thereby defining the anterior-posterior embryonic axis. Initially, the so-called anterior PAR complex, consisted of PAR-3, PAR-6, and PKC-3, occupies the entire cortex in a uniform manner, whereas the posterior components PAR-2, PAR-1, and LGL-1 are cytoplasmic (reviewed in (4)). The actomyosin network, a central constituent of the cell cortex, is uniformly tensed at this stage. Shortly thereafter, symmetry is broken in the vicinity of the centrosomes through a local reduction in cortical tension at the presumptive posterior pole (5–7). This initiates an anterior-directed cortical flow that promotes clearance of the anterior PAR complex from the posterior side, as well as binding of PAR-2, PAR-1, and LGL-1 to the thus depleted region of the posterior cortex (8,9). Thereupon, the first phase of polarity establishment (hereafter referred to as initiation) continues for ∼5 min through retraction of the anterior domain and concomitant expansion of the posterior domain until the two each occupy approximately half of the embryo cortex (8). The second phase of polarity establishment (hereafter referred to as maintenance) follows, during which the anterior and posterior domains remain stationary for ∼10 min until the first mitotic division takes place.
Polarization in one-cell stage C. elegans embryos relies on the mutual inhibition between the anterior and the posterior PAR proteins, leading to the formation of two nonoverlapping cortical domains (10,11). Such mutual inhibition and, more generally, polarity establishment, have been the subjects of mathematical models that capture the essence of the underlying molecular interactions (12–14). Although several parameters characterizing these processes were measured experimentally (15), the parameters governing mutual inhibition were assigned empirically to enable modeling (13), leaving uncertainties concerning the underlying mechanism. Regardless of the mathematical model, polarity establishment must be robust to changes in size and temperature. C. elegans embryos that are ∼30 μm- to ∼75 μm-long are viable and give rise to fertile adults (16,17). Therefore, scaling of the PAR domains must take place, although the extent to which this is the case has not been investigated. Moreover, because C. elegans can develop between ∼10°C and ∼25°C (18), polarization must also tolerate temperature variations, but how this occurs has not been investigated either. Here, we address these and related outstanding issues by combining quantitative microscopy with mathematical modeling, thus yielding important insights into polarity establishment dynamics in C. elegans embryos.
Materials and Methods
Worm strains, cell cycle timing, and RNAi
All C. elegans strains were maintained at 24°C according to standard procedures (19). For recordings performed at 20°C and 13°C, the strains were shifted to a lower temperature at least 1 h before imaging. The transgenic strain expressing green fluorescent protein (GFP) fusion proteins were kindly provided as follows: mCherry::PH (OD70 (20)) by Karen Oegema, GFP::PAR-2(RNAi resistant); par- 2(ok1723) animals (JH2951 (21)) by Fumio Motegi, GFP::PAR-2(RNAi resistant) (TH129 (22)) by Anthony Hyman, GFP::PAR-2 (KK866 (8)) by Kenneth Kemphues, and VIT-2::GFP (RT130 (23)) by the Caenorhabditis Genetics Center.
Determination of three key events during the first cell cycle was performed by visual inspection of the recordings and their timing defined as follows: pseudocleavage furrow, maximal ingression of the pseudocleavage furrow; pronuclear meeting, first contact between pronuclei; cytokinesis, cleavage furrow initiation.
The bacterial RNAi feeding strain for C27D9.1 was obtained from the C. elegans ORFeome RNAi library (gift from Jean-François Rual and Marc Vidal, Harvard Medical School, Boston, MA). The bacterial RNAi feeding strain for ani-2 was obtained from the Ahringer RNAi library (24). Bacteria were prepared as described (25) and fed to starved L1 animals for 48 h at 24°C.
Time-lapse microscopy and temperature control
GFP::PAR-2(RNAi resistant); par-2(ok1723); mCherry-PH (GZ1056) nematodes were dissected in tempered osmotically balanced blastomere culture medium (26). Embryos were imaged using multichannel time-lapse differential interference contrast (DIC) and fluorescence microscopy on a Zeiss Axioplan 2 with a 63× oil objective and a 6% neutral density filter to attenuate the 103 W Arc Mercury epifluorescent source. The microscope and the 1392 × 1040 pixels 12-bit Photometrics CoolSNAP ES2 camera were controlled by μManager (27). Images were taken every 10 s with the following exposure time: DIC, 100 ms; GFP, 500 ms; mCherry, 250 ms. The focus was manually adjusted during the recordings to remain close to the mid-embryo focal plane.
For WT recordings, an additional Fast response temperature control unit (GP205, EMBL (28)) was used to obtain very stable temperature conditions. The samples were mounted as detailed by the manufacturer on 22 × 40 × 0.14 mm coverslips and the stage filled with desalted water. To obtain an optimal DIC image despite the copper grid present 1 mm below the slide, an achromatic condenser head P 0.90 S1 from Leica was adapted to the Zeiss Axioplan 2.
Otherwise WT VIT-2::GFP worms were prepared similarly but imaged on a PerkinElmer Spinning-Disk Confocal equipped with a 60× oil objective and an 488 nm Argon laser. Images were taken every second on a Hamamatsu EMCCD C9100-50 camera with an exposure time of 250 ms. The focus was manually adjusted during the recordings to keep the imaging plane focused on the male pronucleus. VIT-2::GFP ani-2(RNAi) and VIT-2::GFP C27D9.1(RNAi) embryos were imaged in a similar manner but on a Yokogawa Spinning-Disk CSU-W1 equipped with a 60× oil objective and a Hamamatsu EMCCD ImagEM B/W camera.
All recordings were performed under controlled temperature conditions. ani-2(RNAi) and C27D9.1(RNAi) recordings were acquired in an air-conditioned room at 23°C, VIT-2::GFP in another room kept at 22°C.
Results
Monitoring polarity establishment
To challenge and potentially improve extant mathematical models, we performed multichannel time-lapse recordings of polarity establishment in 140 embryos, monitoring the posterior cortical domain with GFP::PAR-2 at a frame rate of 0.1 Hz (Fig. S1, A–C, in the Supporting Material; Movie S1; Materials and Methods). To avoid nonphysiological levels of PAR-2, we used a strain expressing GFP::PAR-2 (21) in a par-2(ok1723) deletion mutant background to remove endogenous PAR-2. These worms are fully viable and fertile, attesting to the functionality of the fusion protein. In addition, immunofluorescence analysis showed that cortical PAR-2 levels in this strain are closer to the WT than in a previously used strain expressing GFP::PAR-2 on top of endogenous PAR-2 (13) (Fig. S1, D–F). We crossed the newly obtained worms with transgenic animals expressing mCherry::PH (20) to visualize the plasma membrane in the entire embryo and acquired a collection of high spatial and temporal data sets including five recording conditions (Fig. S1 G). This provides a unique resource for a quantitative study of polarity establishment, including upon size or temperature perturbations.
Quantifying polarity establishment
To precisely measure polarity establishment in every embryo, we combined ASSET (29), a fully automated segmentation and standardization algorithm, with a signal quantification method developed specifically for this study (see the Supporting Material). ASSET first identifies the embryo eggshell in the DIC channel (Fig. 1 A) and then locates the cell membrane using the mCherry::PH signal (Fig. 1 B). Thereafter, the DIC and mCherry::PH segmentations are smoothed and used to guide GFP::PAR-2 signal detection (Fig. 1, C and D). The signal intensity along the membrane (Fig. 1 E) is then quantified after separation from the cytoplasmic signal, from the eggshell autofluorescence and from the noise (Fig. S1, H–M). The GFP::PAR-2 cortical signal was thus determined for every frame, yielding a high-resolution kymograph of polarity establishment represented in absolute distance (Fig. 1 F).
Figure 1.
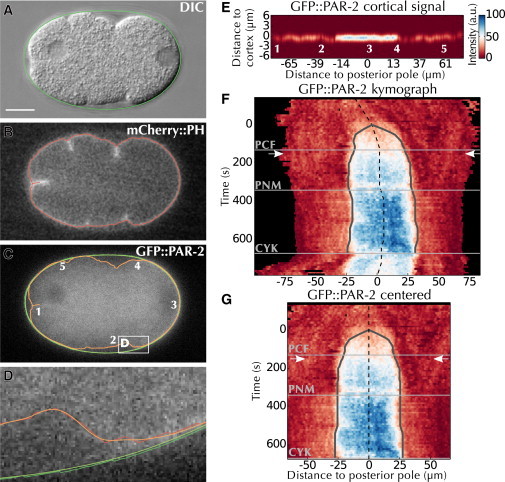
Quantifying polarity establishment. (A–D) Automated segmentation using ASSET. ASSET first (A) identifies the eggshell (green) in the DIC image, and then (B) segments the cell membrane (red) in the mCherry::PH image, and finally (C) transposes these two segmentations (green and red) to the GFP::PAR-2 channel and smoothes them (light green and orange). The white box delimits the area magnified in (D). Numbers in (C) and (E) denote corresponding locations. (D) Magnification of area delimited in (C) by the white box. (E) Perpendicular quantification of GFP::PAR-2 fluorescence in frame C (Fig. S1, H–M). (F) Kymograph of the recording containing the frame shown in (A)–(C) (see Movie S1), overlaid with automatic detection of the domain center (dashed line) and of domain expansion (gray line). Horizontal lines: cell cycle events (see Materials and Methods); arrows: position of the frame shown in (A)–(E). Black areas correspond to locations outside the embryo. (G) Final kymograph after centering and cropping, overlaid with landmarks as in (F). CYK, cytokinesis; PCF, pseudocleavage furrow; PNM, pronuclear meeting.To see this figure in color, go online.
During polarity establishment, a process referred to as posteriorization centers the growing posterior domain to the closest pole of the embryo (30,31). Because we focused this study on the expansion of the posterior domain, we normalized for posteriorization by automatically detecting the center and the extent of the expanding GFP::PAR-2 domain in the kymographs (Fig. 1, F and G, and Supporting Material). Together, the previous steps enabled us to robustly determine the dynamics of GFP::PAR-2 accumulation at the cell cortex in 140 embryos.
A model with newly measured cortical flows faithfully captures the experimental data
To quantitatively assess how the spatial and temporal dynamics of PAR-2 predicted from mathematical models matches our kymographs, we developed a likelihood score (Eq. S1 and the Supporting Material). The extant model we initially considered ((13), termed M1) is one-dimensional, assuming rotational symmetry along the longitudinal embryonic axis, and simulates the concentration of both anterior and posterior complexes at the cortex over space and time. This model accounts for binding and unbinding of the complexes to the cortex, protein diffusion within the cortex, and cortical flows, all of which have been determined experimentally (15). In addition, the model embeds mutual inhibition between the two complexes, which involves nonlinear interactions with cooperativity exponents α and β that have not been determined experimentally (Eq. S2, Eq. S3 and the Supporting Material).
To assess the performance of M1, the 47 WT recordings performed at 24°C were averaged after temporal registration to reduce variability between kymographs (Figs. 2 A and S2, A and B). The resulting average was in qualitative agreement with M1 using the published parameter values (Figs. 2 B and S2, C and D; Table S1 (13)). However, the salient leading edge enrichment and concomitant overshooting reported previously (13) was observed to a much lesser extent in our experiments (Fig. 2 B, arrowheads, compare with Fig. 2 A). We considered whether the more salient enrichment might result from the excess of total PAR-2 in the previous analysis (see Fig. S1 E). However, we found that simulating an excess of posterior versus anterior complexes still resulted in notable leading edge enrichment (Fig. S3, A–C). Therefore, we set out to investigate further what in the model may cause such discrepancy with the experimental results. In a first approach that minimizes the changes with respect to the original model M1, we tested whether individual parameters, including those that had been experimentally determined previously (15), needed to be adjusted (Fig. S3, D–W). However, none of the tested parameter variations could reduce the salient leading edge enrichment and the concomitant domain overshooting (Fig. S3). Given that the four parameters governing mutual inhibition between anterior and posterior components (i.e., kAP, α, kPA, and β) were not measured experimentally, we reasoned that reoptimizing all these four parameters simultaneously (into a model termed M1∗) could reduce the discrepancies with the data. We found that, although this improved the simulation at the leading edge, the predicted initiation phase of polarity establishment was still not in agreement with the experimental data (Fig. S2 E). We thus decided to explore whether another minimal modification to M1 could reduce this leading edge while keeping the model as close as possible to the published experimental parameter values. Because of the importance of cortical flows in the early dynamics of polarity establishment (9), and because the two-dimensional (2D) cortical flow velocity map accompanying M1 stems from only a few measurements (13), we considered whether this could be the source of the observed discrepancy.
Figure 2.
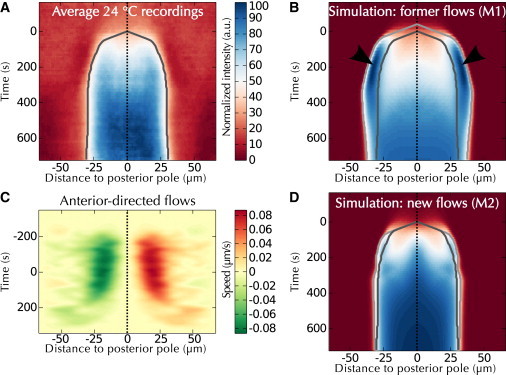
Model with newly measured cortical flows faithfully captures the experimental data. (A) Average GFP::PAR-2 protein distribution during polarity establishment at 24°C (n = 47), overlaid with segmentation of domain center (dashed line) and domain expansion (dark gray). Time zero in this figure: onset of polarity establishment, as identified by domain segmentation. (B) Polarity establishment as predicted by M1 (Table S1 (13)), overlaid with the segmentation of this prediction (light gray) and of our experimental data (dark gray). Arrowheads indicate leading front enrichment not observed in (A). (C) Cortical flows measured using VIT-2::GFP particle tracking (Fig. S4 and the Supporting Material). (D) Polarity establishment as predicted by M2 (i.e., M1 with flows shown in C), overlaid with landmarks similar to (B). Note the strong dampening of leading edge enrichment. To see this figure in color, go online.
We thus set out to estimate cortical flows anew. We used the movements of subcortical VIT-2::GFP yolk granules as a proxy (32), because we anticipated that the high number of granules that can be analyzed in this manner compared to the lower number of nonmuscle myosin (NMY-2) foci should generate a more accurate 2D cortical velocity map, in particular close to the site of polarity initiation (see the Supporting Material). This approach enabled us to detect ∼450 particles per frame (i.e., over 1.7 million particles in total, Figs. S4 and S5). The resulting 2D velocity map (∼0.08 μm/s at the maximal location, Fig. 2 C) is characterized by slightly slower flows than those stemming from previous measurements based on NMY-2::GFP (∼0.11 μm/s on average, Table S2 (9,13,33)), while being analogous to earlier one-dimensional measurements based on manual tracking of individual yolk granules (∼0.07 μm/s, Table S2 (34,35)) as well as with measurements performed using particle image velocimetry as an alternative means to quantify flows (Fig. S6 and (32)). Of importance, incorporating the newly determined 2D cortical flows into a revised version of the original mathematical model M1 (termed M2) drastically dampened the previously noted leading edge enrichment (Figs. 2 D and S2, G and H). Therefore, model M2 provides a more accurate quantitative description of polarity establishment in the WT.
Cooperativity of both anterior and posterior components is required to account for polarity establishment
Among the model parameters (Table S1 and Eqs. S2 and S3 in the Supporting Material), those governing mutual inhibition between anterior and posterior components (i.e., kAP, α, kPA, and β) do not rely on experimental measurements, but were chosen empirically to allow for a stable initial homogeneous anterior state and a stable final polarized state (13). Given that other combinations of values can give rise to such behaviors (13), we decided to use M2 to infer those four values from our data set. Because our data set provides data on the dynamics of the posterior domain and merely infers parameter values of the anterior domain, we set out to test whether such inferences are precise. To this end, we conducted simulation experiments using the same maximum-likelihood optimization procedure applied for the actual data, which demonstrated that the inferences derived for the anterior domain are indeed precise (Fig. S7, Eq. S1, and Supporting Material). We thus could identify the most likely values independently for each embryo (Fig. 3), and hence obtained the distribution of parameters that can give rise to polarity establishment (Fig. S8). Correlation analysis of the estimated parameters (Fig. S8 O (36)) confirmed the need for tightly coregulated mutual inhibition rates kAP and kPA (Fig. S8 G), as previously derived analytically (13), while revealing covariance between the other parameters of the mathematical model.
Figure 3.
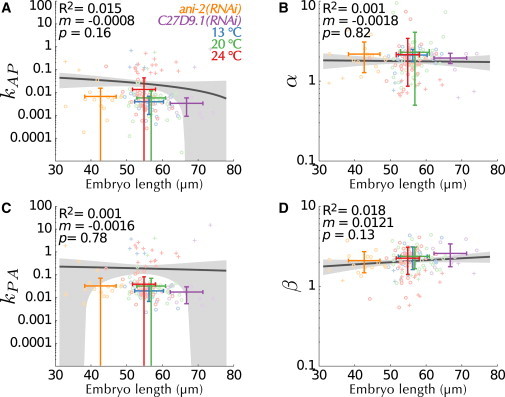
Cooperativity of both anterior and posterior components is required for polarity establishment. (A–D) Best values for the unmeasured mutual inhibition parameters {(A) kAP, (B) α, (C) kPA, (D) β} was identified in each embryo by an optimization procedure. Values detected as outliers (see the Supporting Material) are depicted using crosses and removed from the calculation of the mean as well as from the parameter distribution (Fig. S8). Values are color-coded with respect to their recording condition and overlaid with the corresponding average and standard deviation. Shown are the linear regression (dark gray line) with the corresponding 95% confidence interval (light gray area), the correlation coefficient R2 that reports the fraction of variance explained by the linear regression, the slope of the correlation m and the p-value (Student’s two-tailed t-test for the coefficient m). To see this figure in color, go online.
The average estimated values provided insights into the mutual inhibition process, both in terms of the rates and cooperativity exponents. First, the two mutual inhibition rates were significantly smaller than the formerly proposed values (kAP = 0.008 ± 0.017 and kPA = 0.030 ± 0.035 compared to 0.19 and 2, respectively, Fig. 3, A and C, and Table S3 (13), all ± represent standard deviations). Such smaller rates reflect reduced mutual inhibition and are required to account for the low GFP::PAR-2 signal on the anterior half (Fig. S2, I and K, lighter red, compared to Fig. S2, C and G, dark red). Second, our analysis revealed a difference in the value of one of the exponents compared to that previously chosen. α describes the cooperative action of posterior proteins toward inhibiting the anterior complex, and vice-versa for β (see the Supporting Material). Values >1 for α or β indicate nonlinear biochemical kinetics such as oligomerization (37) or multisite phosphorylation (38). Our data confirms that the hypothesized cooperativity for the anterior complex (β = 2 in (13,14)) is necessary to explain the data (β = 2.30 ± 0.74, Fig. 3 D). In addition and of importance, in contrast to previous conclusions (α = 1 in (12–14)), our results predict that cooperativity in the posterior domain is also required (α = 2.17 ± 1.28, Fig. 3 B). This suggests a nonlinear mechanism involved in the exclusion by posterior proteins of the anterior complex.
Fixed protein concentration combined with changes in surface/volume ratio underlies domain scaling
We next investigated how polarity can be established seemingly normally over a wide range of embryo sizes (16,17). Here, we define perfect scaling as a situation where the relative size of the posterior domain is independent of embryo size. To probe the degree to which scaling operates in vivo, we quantified the extent of the posterior domain in smaller embryos generated using RNA-interference (RNAi)-mediated depletion of the anillin gene ani-2 (n = 16, Fig. 4, A and B (16)), in WT embryos (n = 47, Fig. 4, C and D), as well as in larger embryos generated using RNAi-mediated depletion of the open reading frame C27D9.1 (n = 11, Fig. 4, E and F (39)). We found that the size of the posterior domain scaled with membrane length, albeit not perfectly (Fig. S9 A).
Figure 4.
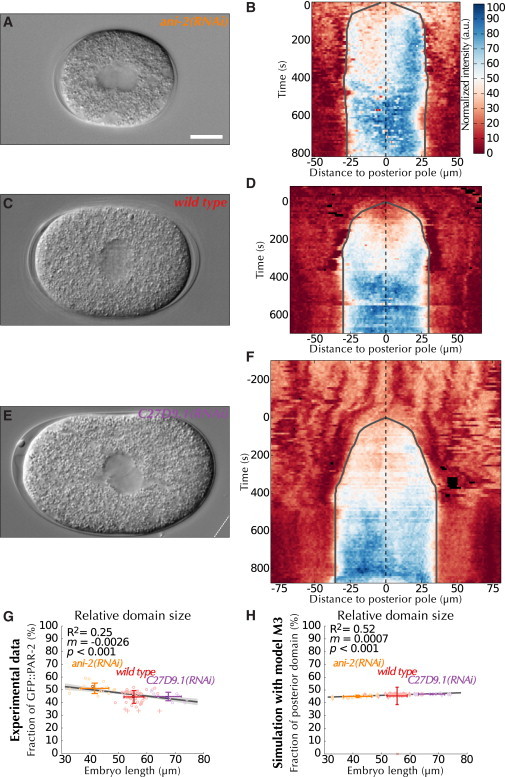
Fixed protein concentration and changes in surface/volume ratio underlie domain scaling. (A, C, and E) DIC images representing the median embryo of each recording condition and (B, D, and F) corresponding kymographs, overlaid with landmarks similar to Fig. 1. The white dashed line in E delimits the boundary of the raw image. (G) Linear regression (dark gray line) performed on the length of the embryo versus the fraction of the membrane spanned by GFP::PAR-2, overlaid with landmarks similar to Fig. 3. The darker circles indicate the locations of the median recordings depicted in (A)–(F). (H) Same as (G), but quantifying the extent of the posterior domain as predicted by M3 (i.e., using the values calibrated with the median recordings). To see this figure in color, go online.
We next studied whether the mathematical model could reproduce such behavior. Scaling is anticipated from the model because the size of the posterior domain is governed mathematically by the relative abundance of anterior versus posterior proteins (13), which should be independent from cell size given that oocytes derive from a common syncytium. To assess the actual degree of scaling in the model, we simulated M2 with the estimated parameters for mutual inhibition (see Fig. 3). M2 indeed predicts that domain length increases with membrane length (Fig. S9 C). However, scaling is imperfect, with smaller embryos showing proportionally larger posterior domains (Fig. S9 D), as anticipated because the surface/volume ratio φ, which decreases for larger cells (see the Supporting Material), dictates the protein pool available to bind the membrane (Eq. S3 in the Supporting Material).
Intriguingly, the scaling observed experimentally is even less precise than the model predictions (Fig. S9 B, compare with Fig. S9 D), raising the possibility that the model does not capture the full impact of cell size on polarity establishment. One process that may contribute further to size dependence is cortical flow. Indeed, extending the assumption of fixed protein concentrations to components of the actomyosin cytoskeleton, we deduced that the magnitude of cortical flows could be inversely proportional to φ (see the Supporting Material). To test this hypothesis, we determined cortical flows both in smaller ani-2(RNAi) (n = 6) and larger C27D9.1(RNAi) embryos (n = 8), which were analyzed in conjunction with cortical flows in the WT. As shown in Fig. S9, E and F, we did not observe a correlation between cortical flows and either embryo length, or surface/volume ratio. Therefore, because we sought to derive a single model able to capture the entire data set, we explored whether some of the unmeasured parameters would need to be optimized. We thus recalibrated the model (i.e., optimized kAP, α, kPA, and β) using together the median embryo from the small, normal and large data sets (Fig. 4 G and Supporting Material). Although the resulting model (M3, Table S3) matches the experimentally measured domain length using a single set of parameter values (Fig. S9 G), it does not fully capture the correlation between embryo length and relative domain size (Fig. 4 H). This suggests that an additional mechanism involved in domain scaling has not been incorporated into the model. Irrespective of these small variations, the four mutual inhibition parameters in M3 were similar to those obtained with M2 (Table S3), reinforcing our conclusion that cooperativity is needed for both anterior and posterior components. Overall, our results suggest that scaling is an intrinsic property of PAR proteins, which arises mainly from the combination of fixed protein concentrations and variations in surface/volume ratio.
Diffusion is the process most affected by temperature changes and exhibits an Arrhenius-type behavior
We next investigated how polarity establishment depends on temperature. Because temperature influences most molecular processes, all the parameters of the mathematical model could a priori depend on temperature. We thus considered that the three types of molecular mechanisms embedded in the model (i.e., protein diffusion, biochemical reactions, and cortical flows) might be affected differently by variations in temperature. To explore this possibility, we performed recordings at three temperatures spanning most of the viable range for C. elegans (13°C, 20°C, 24°C, Fig. 5, A–C) (18). Our analysis uncovered three changes with increased temperature: 1) a significant acceleration in the pace of polarity initiation (Fig. 5 D); 2) a loss of steepness in the gradient of the posterior domain during the maintenance phase (Fig. 5 E, arrowheads, (40)); and 3) a slight contraction of the relative length of the posterior domain (Fig. S10 C). To identify the source of these three modifications, we mimicked the impact of temperature on each group of related rates in the mathematical model using a scaling factor λ set to 1 at 20°C (see the Supporting Material).
Figure 5.
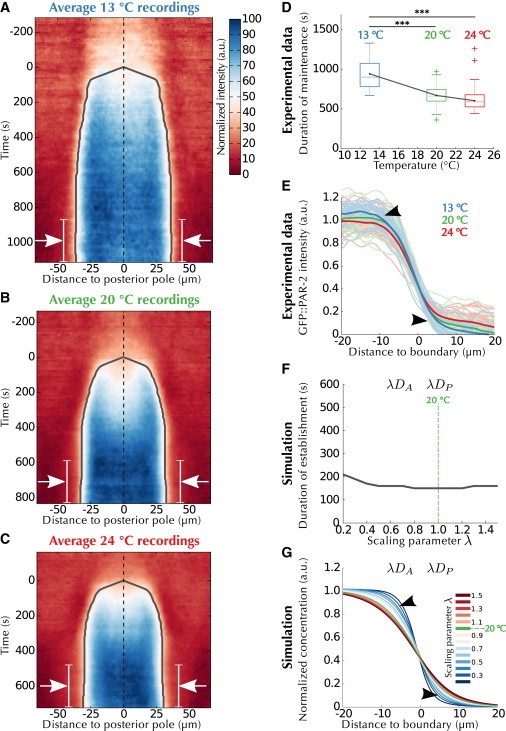
Diffusion is the process most affected by temperature. (A–C) Average kymographs of polarity establishment at the indicated temperatures, overlaid with landmarks similar to Fig. 1. Arrows: portion of the maintenance stage (white line) averaged for the profiles displayed in (E). (D) Quantification of duration of the maintenance phase (see the Supporting Material) at the three temperatures, overlaid with tests of significance (Student’s two-tailed t-test). (E) Profiles of GFP::PAR-2 signal during maintenance (arrows in A–C) at different temperatures. Thin lines: individual profiles; thick lines: average of each condition. Each set of curves (i.e., each recording temperature) is statistically different from each other (p < 0.001, adaptive Neyman test (40)). Arrowheads: variations predicted by the model (see G). (F) Quantification of the time required for polarity maintenance as in (D) when the values of the diffusion parameters DA and DP are scaled by the factor λ. Note that the x axes in (D) and (F) cannot be directly compared; however, a similar trend is observed. (G) Profiles simulated by the model as in (F) and aligned as in (E). To see this figure in color, go online.
We varied λs for the parameters representing protein diffusion (DA and DP), biochemical reactions (kA+, kA−, kAP, kP+, kP−, and kPA), or cortical flows (ν) (Fig. S10, D–R, and Table S4). The exponents α and β were assumed to be unaffected by temperature, and the new flow measurements were used (M3). We found that varying the membrane binding rates (kA+, kP+, Fig. S10, G–I) reproduced both the contraction of relative domain length (Fig. S10 I) and the acceleration in polarity initiation (Fig. S10 H) but not gradient steepening (Fig. S10 G). Variations in cortical unbinding rates (kA−, kP−, Fig. S10, J–L) predicted only gradient steepening (Fig. S10 J), whereas variations in cortical flows reproduced only the acceleration in polarity initiation (ν, Fig. S10, P–R). Moreover, variations in the mutual inhibition rates (kAP, kPA, Fig. S10, M–O) had almost no effect on the contraction of relative domain length (Fig. S10 O). By contrast, variations in diffusion could reproduce all three modifications (DA, DP, Figs. 5, F and G, and S10 F), suggesting that diffusion is the main process underlying the observed alterations in polarity establishment upon temperature changes.
To relate the scaling factors λ to the actual temperatures and to assess the contribution of parameters other than diffusion, we considered three increasingly complex mechanisms: 1) constant value for each temperature, e.g., in temperature-compensated cortical fluidity (41,42); 2) Arrhenius-type dependence for each temperature, e.g., in metabolic rates kinetics (43,44); and 3) independent values for each temperature, an arbitrary temperature dependence. These relations were hypothesized for the three types of molecular mechanisms encapsulated in the model. We then assessed the performance of different combinations of temperature mechanisms (Fig. S11 and the Supporting Material). The best model, selected using the Akaike information criterion with a correction or AICc (45), revealed again that diffusion is most sensitive to variations in temperature (Fig. S11 A). In addition, the selected model indicates that protein diffusion and biochemical reactions have Arrhenius-like kinetics (see the Supporting Material). Interestingly, in almost all models (Fig. S11, except Fig. S11 D), flows are independent of temperature, suggesting the existence of a compensation mechanism for cortical flows. We also conducted a parameter sensitivity analysis, which uncovered that polarity establishment is most robust to variations in diffusion parameters (Fig. S12, E and I). Such buffering of fluctuations in diffusion speeds indicates that significant variations in parameter value are required for a noticeable effect on polarization, hence providing an explanation for the identified strong dependence of diffusion on temperature.
Overall, we conclude that diffusion is more sensitive to variations in temperature than biochemical reactions, and that cortical flows appear to be largely constant within the studied temperature range.
Discussion
We performed a quantitative analysis of polarity establishment in the early C. elegans embryo combining live imaging and mathematical modeling. To extend and further calibrate an extant mathematical model (M1 (13)), we first refined estimates of cortical flows, which are essential to account for the early dynamics of polarity establishment (M2, Fig. 6 A). Using an optimization method, we estimated previously unspecified parameters characterizing the mutual inhibition terms. Using our unique data on embryos of varying sizes, we derived a model that also accounts for part of the observed scaling of the PAR domains (M3, Fig. 6 B). Finally, we extended this model so that it also predicts temperature dependence of polarity establishment using Arrhenius-like equations (M4, Fig. 6, C and D). The lower magnitude of the variations predicted by the model following changes in size or temperature raises the possibility that some parameters did not converge to optimal values. However, the smoothness of the scoring function (Fig. S12) combined with the efficient convergence of the optimization (Fig. S7) render this hypothesis unlikely. Instead, we suggest that these remaining differences reflect simplifications inherent to mathematical modeling.
Figure 6.
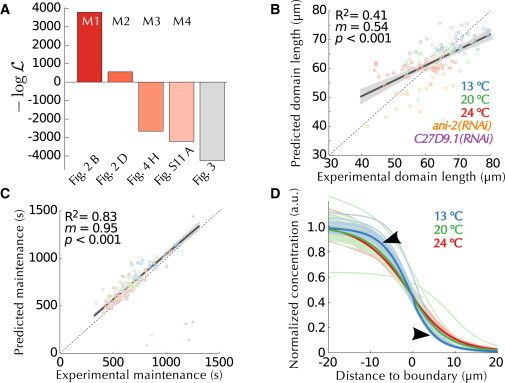
Predictions of the mathematical model obtained from size and temperature perturbations. (A) Performance (negative log-likelihood score) of the successive modifications of the mathematical model with an indication of the model used (above) and of the corresponding figure panel (below). The right-most gray bar corresponds to optimization of each embryo individually (Fig. 3) and is displayed for comparison. (B) Comparison between the experimental data and the predictions of the optimized model (M4) when the size of each embryo is used (color-coded as indicated). (C) Comparison between the experimental quantification of the duration of the maintenance phase and the predictions of M4. (D) Maintenance profiles simulated by the optimized model at different temperatures, to be compared with Fig. 5E. To see this figure in color, go online.
Indeed, the model from which our own analysis stems (13) did not consider certain aspects of polarity establishment. This includes the existence of other players of polarity establishment such as PAR-5 (46) or CDC-42 (47), potential feedback between polarity and cortical flows (8,35), and the individual dynamics of the different members of the anterior and posterior complexes. Nevertheless, we believe that the level of detail considered here is the most suitable mathematical representation of polarity establishment given the currently available experimental evidence. Of importance, such abstractions are important to reduce the number of parameters and permit their identifiability (Fig. S12). Moreover, despite its simplicity, model M1, and by extension its new variants M2–M4, can account for the behavior of various mutant/RNAi conditions that affect polarity establishment, including polarization in a no-flow regime or following changes in the ratio of anterior versus posterior proteins (13). A quantitative analysis in such embryos following the approach presented here should help further characterize the proposed mathematical model. In particular, studying polarity establishment upon depletion of proteins known to modulate the size of the domains, such as PAR-4 (48) or MEX-5/6 (8), would be highly informative.
Our work underscores the importance of cortical flows in the spatial and temporal dynamics of polarity establishment. Introducing newly determined flow values corrected spurious enrichment at the leading edge of the posterior domain (Fig. 2). Why was such an enrichment reported in embryos expressing GFP::PAR-2 in addition to endogenous PAR-2 (13)? Conceivably, PAR-2 levels could influence cortical flow velocity, through the anterior complex that can promote actomyosin contractility (9). In this scenario, higher PAR-2 levels may exclude anterior components more efficiently, hence increasing their concentration on the anterior. As for embryos expressing NMY-2::GFP (9), we suggest that higher levels of total NMY-2 cause increased cortical flows. Alternatively, it is conceivable that the manual tracking of NMY-2::GFP might have been biased toward selection of faster particles. Our analysis confirms that cortical mutual inhibition coupled to an overall fixed pool of proteins can explain the observed scaling and thus robustly pattern embryos of different sizes.
This model can also adapt to variations in temperature by incorporating an Arrhenius equation for the diffusion coefficient and the various reaction rates. The Arrhenius relation for diffusion relates to the viscosity of the medium (i.e., the cell cortex here, see the Supporting Material). Such an Arrhenius dependence is valid for an amorphous substance such as glass-like materials or colloidal gels (49) and has been observed in bacteria (50), indicating that biological material can exhibit such a type of viscous behavior. Whether the cortex of C. elegans displays similar features will be interesting to explore. Intriguingly, our results for cortical flows (Fig. S11) suggest relative insensitivity to variations in temperature, whereas cortical viscosity, which has been postulated to be an important factor in cortical flow dynamics (33), is predicted to be significantly affected by such variations. One potential explanation for this apparent conundrum is that variations in viscosity are balanced by changes in contractility throughout the probed temperature range.
Our approach combining a large data set with maximum-likelihood optimization allowed us to infer previously unspecified parameters governing mutual inhibition. Of importance, we found cooperativity of both anterior and posterior complexes to be required for polarity establishment. A previous model (14) proposed cooperativity between anterior proteins, in line with the evolutionarily conserved protein-protein interaction site in PAR-3 proteins that governs oligomerization (51). Here, we propose in addition that cooperativity is needed among posterior domain proteins. The underlying molecular tenets remain to be discovered, but may result from a different mechanism than in the anterior domain because no evidence of oligomerization has been reported among posterior components. One possibility is cooperative binding (37) between one or several of the posterior PAR proteins and the 14-3-3 protein PAR-5, which is necessary for efficient mutual inhibition (46). Alternatively, multisite phosphorylation of PAR-3 by PAR-1 (21) could provide such nonlinearity (38).
In conclusion, we performed a quantitative analysis of polarity establishment in C. elegans embryos that allowed us to identify hitherto undetermined parameters and refine a mathematical model to better account for variations in size and temperature. In addition and of importance, the automated pipeline that we developed provides an analytical framework adequate to investigate both the dynamics and the impact of other molecular players involved in polarity establishment.
Author Contributions
S.B., P.G., and F.N. designed the research; S.B. performed the experiments, with help from C.B.; S.B. implemented ASSET and the automated quantification procedures; S.B., P.G., and F.N. analyzed the data and wrote the manuscript.
Acknowledgments
We are grateful to Fumio Motegi for the transgenic animals expressing GFP::PAR-2; par-2(ok1723), as well as to Jonathan Bieler, Aude Blanchoud, Alessandro De Simone, Aitana Neves, and Virginie Hamel Hachet for useful comments on the manuscript. We also thank Nathan Goehring and Stephan Grill for insightful discussions on their model, as well as the MathWorks community and the Bio-Formats (52) for useful pieces of code.
This work was supported by grants from Josy Marty-Echec au Cancer de la Broye to S.B., from SystemsX.ch IPhD 51PH_0125979 to P.G. and F.N., as well as from the Swiss National Science Foundation to P.G. (3100A0-122500/1).
Supporting Material
The recorded channels are (top) DIC, (middle) mCherry::PH, and (bottom) GFP::PAR-2; the raw data are displayed in each case. This recording corresponds to the frames used in Figs. 1 and S1 and has been accelerated 60 times.
Supporting Citations
References (53–66) appear in the Supporting Material.
References
- 1.Thompson B.J. Cell polarity: models and mechanisms from yeast, worms and flies. Development. 2013;140:13–21. doi: 10.1242/dev.083634. [DOI] [PubMed] [Google Scholar]
- 2.Martin-Belmonte F., Perez-Moreno M. Epithelial cell polarity, stem cells and cancer. Nat. Rev. Cancer. 2012;12:23–38. doi: 10.1038/nrc3169. [DOI] [PubMed] [Google Scholar]
- 3.Kemphues K.J., Priess J.R., Cheng N.S. Identification of genes required for cytoplasmic localization in early C. elegans embryos. Cell. 1988;52:311–320. doi: 10.1016/s0092-8674(88)80024-2. [DOI] [PubMed] [Google Scholar]
- 4.Gönczy P. Mechanisms of asymmetric cell division: flies and worms pave the way. Nat. Rev. Mol. Cell Biol. 2008;9:355–366. doi: 10.1038/nrm2388. [DOI] [PubMed] [Google Scholar]
- 5.Motegi F., Sugimoto A. Sequential functioning of the ECT-2 RhoGEF, RHO-1 and CDC-42 establishes cell polarity in Caenorhabditis elegans embryos. Nat. Cell Biol. 2006;8:978–985. doi: 10.1038/ncb1459. [DOI] [PubMed] [Google Scholar]
- 6.Schonegg S., Hyman A.A. CDC-42 and RHO-1 coordinate acto-myosin contractility and PAR protein localization during polarity establishment in C. elegans embryos. Development. 2006;133:3507–3516. doi: 10.1242/dev.02527. [DOI] [PubMed] [Google Scholar]
- 7.Jenkins N., Saam J.R., Mango S.E. CYK-4/GAP provides a localized cue to initiate anteroposterior polarity upon fertilization. Science. 2006;313:1298–1301. doi: 10.1126/science.1130291. [DOI] [PubMed] [Google Scholar]
- 8.Cuenca A.A., Schetter A., Seydoux G. Polarization of the C. elegans zygote proceeds via distinct establishment and maintenance phases. Development. 2003;130:1255–1265. doi: 10.1242/dev.00284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Munro E., Nance J., Priess J.R. Cortical flows powered by asymmetrical contraction transport PAR proteins to establish and maintain anterior-posterior polarity in the early C. elegans embryo. Dev. Cell. 2004;7:413–424. doi: 10.1016/j.devcel.2004.08.001. [DOI] [PubMed] [Google Scholar]
- 10.Etemad-Moghadam B., Guo S., Kemphues K.J. Asymmetrically distributed PAR-3 protein contributes to cell polarity and spindle alignment in early C. elegans embryos. Cell. 1995;83:743–752. doi: 10.1016/0092-8674(95)90187-6. [DOI] [PubMed] [Google Scholar]
- 11.Boyd L., Guo S., Kemphues K.J. PAR-2 is asymmetrically distributed and promotes association of P granules and PAR-1 with the cortex in C. elegans embryos. Development. 1996;122:3075–3084. doi: 10.1242/dev.122.10.3075. [DOI] [PubMed] [Google Scholar]
- 12.Tostevin F., Howard M. Modeling the establishment of PAR protein polarity in the one-cell C. elegans embryo. Biophys. J. 2008;95:4512–4522. doi: 10.1529/biophysj.108.136416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Goehring N.W., Trong P.K., Grill S.W. Polarization of PAR proteins by advective triggering of a pattern-forming system. Science. 2011;334:1137–1141. doi: 10.1126/science.1208619. [DOI] [PubMed] [Google Scholar]
- 14.Dawes A.T., Munro E.M. PAR-3 oligomerization may provide an actin-independent mechanism to maintain distinct par protein domains in the early Caenorhabditis elegans embryo. Biophys. J. 2011;101:1412–1422. doi: 10.1016/j.bpj.2011.07.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Goehring N.W., Hoege C., Hyman A.A. PAR proteins diffuse freely across the anterior-posterior boundary in polarized C. elegans embryos. J. Cell Biol. 2011;193:583–594. doi: 10.1083/jcb.201011094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Maddox A.S., Habermann B., Oegema K. Distinct roles for two C. elegans anillins in the gonad and early embryo. Development. 2005;132:2837–2848. doi: 10.1242/dev.01828. [DOI] [PubMed] [Google Scholar]
- 17.Hara Y., Kimura A. Cell-size-dependent spindle elongation in the Caenorhabditis elegans early embryo. Curr. Biol. 2009;19:1549–1554. doi: 10.1016/j.cub.2009.07.050. [DOI] [PubMed] [Google Scholar]
- 18.Anderson J.L., Albergotti L., Phillips P.C. Does thermoregulatory behavior maximize reproductive fitness of natural isolates of Caenorhabditis elegans? BMC Evol. Biol. 2011;11:157. doi: 10.1186/1471-2148-11-157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Brenner S. The genetics of Caenorhabditis elegans. Genetics. 1974;77:71–94. doi: 10.1093/genetics/77.1.71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kachur T.M., Audhya A., Pilgrim D.B. UNC-45 is required for NMY-2 contractile function in early embryonic polarity establishment and germline cellularization in C. elegans. Dev. Biol. 2008;314:287–299. doi: 10.1016/j.ydbio.2007.11.028. [DOI] [PubMed] [Google Scholar]
- 21.Motegi F., Zonies S., Seydoux G. Microtubules induce self-organization of polarized PAR domains in Caenorhabditis elegans zygotes. Nat. Cell Biol. 2011;13:1361–1367. doi: 10.1038/ncb2354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Schonegg S., Constantinescu A.-T., Hyman A.A. The Rho GTPase-activating proteins RGA-3 and RGA-4 are required to set the initial size of PAR domains in Caenorhabditis elegans one-cell embryos. Proc. Natl. Acad. Sci. USA. 2007;104:14976–14981. doi: 10.1073/pnas.0706941104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Grant B., Hirsh D. Receptor-mediated endocytosis in the Caenorhabditis elegans oocyte. Mol. Biol. Cell. 1999;10:4311–4326. doi: 10.1091/mbc.10.12.4311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kamath R.S., Fraser A.G., Ahringer J. Systematic functional analysis of the Caenorhabditis elegans genome using RNAi. Nature. 2003;421:231–237. doi: 10.1038/nature01278. [DOI] [PubMed] [Google Scholar]
- 25.Kamath R.S., Martinez-Campos M., Ahringer J. Effectiveness of specific RNA-mediated interference through ingested double-stranded RNA in Caenorhabditis elegans. Genome Biol. 2001;2 doi: 10.1186/gb-2000-2-1-research0002. RESEARCH0002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Shelton C.A., Bowerman B. Time-dependent responses to glp-1-mediated inductions in early C. elegans embryos. Development. 1996;122:2043–2050. doi: 10.1242/dev.122.7.2043. [DOI] [PubMed] [Google Scholar]
- 27.Edelstein A., Amodaj N., Stuurman N. Computer control of microscopes using μManager. Curr. Protoc. Mol. Biol. 2010;Chapter 14 doi: 10.1002/0471142727.mb1420s92. Unit14.20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Gorjánácz M., Mattaj I.W., Rietdorf J. Some like it hot. Imaging Microsc. 2007;9:28–29. [Google Scholar]
- 29.Blanchoud S., Budirahardja Y., Gönczy P. ASSET: a robust algorithm for the automated segmentation and standardization of early Caenorhabditis elegans embryos. Dev. Dyn. 2010;239:3285–3296. doi: 10.1002/dvdy.22486. [DOI] [PubMed] [Google Scholar]
- 30.Goldstein B., Hird S.N. Specification of the anteroposterior axis in Caenorhabditis elegans. Development. 1996;122:1467–1474. doi: 10.1242/dev.122.5.1467. [DOI] [PubMed] [Google Scholar]
- 31.Rappleye C.A., Tagawa A., Aroian R.V. The anaphase-promoting complex and separin are required for embryonic anterior-posterior axis formation. Dev. Cell. 2002;2:195–206. doi: 10.1016/s1534-5807(02)00114-4. [DOI] [PubMed] [Google Scholar]
- 32.Niwayama R., Shinohara K., Kimura A. Hydrodynamic property of the cytoplasm is sufficient to mediate cytoplasmic streaming in the Caenorhabditis elegans embryo. Proc. Natl. Acad. Sci. USA. 2011;108:11900–11905. doi: 10.1073/pnas.1101853108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Mayer M., Depken M., Grill S.W. Anisotropies in cortical tension reveal the physical basis of polarizing cortical flows. Nature. 2010;467:617–621. doi: 10.1038/nature09376. [DOI] [PubMed] [Google Scholar]
- 34.Hird S. Cortical actin movements during the first cell cycle of the Caenorhabditis elegans embryo. J. Cell Sci. 1996;109:525–533. doi: 10.1242/jcs.109.2.525. [DOI] [PubMed] [Google Scholar]
- 35.Cheeks R.J., Canman J.C., Goldstein B. C. elegans PAR proteins function by mobilizing and stabilizing asymmetrically localized protein complexes. Curr. Biol. 2004;14:851–862. doi: 10.1016/j.cub.2004.05.022. [DOI] [PubMed] [Google Scholar]
- 36.Bieler J., Pozzorini C., Naef F. Whole-embryo modeling of early segmentation in Drosophila identifies robust and fragile expression domains. Biophys. J. 2011;101:287–296. doi: 10.1016/j.bpj.2011.05.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Colotti G., Boffi A., Chiancone E. Cooperativity and ligand-linked polymerisation in Scapharca tetrameric haemoglobin. In: Bolognesi M., Prisco G., Verde C., editors. Dioxygen Binding and Sensing Proteins. Milano; Springer, Milan: 2008. pp. 107–119. [Google Scholar]
- 38.Gunawardena J. Multisite protein phosphorylation makes a good threshold but can be a poor switch. Proc. Natl. Acad. Sci. USA. 2005;102:14617–14622. doi: 10.1073/pnas.0507322102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Sönnichsen B., Koski L.B., Echeverri C.J. Full-genome RNAi profiling of early embryogenesis in Caenorhabditis elegans. Nature. 2005;434:462–469. doi: 10.1038/nature03353. [DOI] [PubMed] [Google Scholar]
- 40.Fan J., Lin S. Test of significance when data are curves. J. Am. Stat. Assoc. 1998;93:1007–1021. [Google Scholar]
- 41.Sinensky M. Homeoviscous adaptation—a homeostatic process that regulates the viscosity of membrane lipids in Escherichia coli. Proc. Natl. Acad. Sci. USA. 1974;71:522–525. doi: 10.1073/pnas.71.2.522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Hazel J.R., Williams E.E. The role of alterations in membrane lipid composition in enabling physiological adaptation of organisms to their physical environment. Prog. Lipid Res. 1990;29:167–227. doi: 10.1016/0163-7827(90)90002-3. [DOI] [PubMed] [Google Scholar]
- 43.Gillooly J.F., Brown J.H., Charnov E.L. Effects of size and temperature on metabolic rate. Science. 2001;293:2248–2251. doi: 10.1126/science.1061967. [DOI] [PubMed] [Google Scholar]
- 44.Dell A.I., Pawar S., Savage V.M. Systematic variation in the temperature dependence of physiological and ecological traits. Proc. Natl. Acad. Sci. USA. 2011;108:10591–10596. doi: 10.1073/pnas.1015178108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Hurvich C.M., Tsai C.-L. Regression and time series model selection in small samples. Biometrika. 1989;76:297–307. [Google Scholar]
- 46.Morton D.G., Shakes D.C., Kemphues K.J. The Caenorhabditis elegans par-5 gene encodes a 14-3-3 protein required for cellular asymmetry in the early embryo. Dev. Biol. 2002;241:47–58. doi: 10.1006/dbio.2001.0489. [DOI] [PubMed] [Google Scholar]
- 47.Gotta M., Abraham M.C., Ahringer J. CDC-42 controls early cell polarity and spindle orientation in C. elegans. Curr. Biol. 2001;11:482–488. doi: 10.1016/s0960-9822(01)00142-7. [DOI] [PubMed] [Google Scholar]
- 48.Hung T.J., Kemphues K.J. PAR-6 is a conserved PDZ domain-containing protein that colocalizes with PAR-3 in Caenorhabditis elegans embryos. Development. 1999;126:127–135. doi: 10.1242/dev.126.1.127. [DOI] [PubMed] [Google Scholar]
- 49.Doremus R.H. Viscosity of silica. J. Appl. Phys. 2002;92:7619–7629. [Google Scholar]
- 50.Parry B.R., Surovtsev I.V., Jacobs-Wagner C. The bacterial cytoplasm has glass-like properties and is fluidized by metabolic activity. Cell. 2014;156:183–194. doi: 10.1016/j.cell.2013.11.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Li B., Kim H., Kemphues K. Different domains of C. elegans PAR-3 are required at different times in development. Dev. Biol. 2010;344:745–757. doi: 10.1016/j.ydbio.2010.05.506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Linkert M., Rueden C.T., Swedlow J.R. Metadata matters: access to image data in the real world. J. Cell Biol. 2010;189:777–782. doi: 10.1083/jcb.201004104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Abràmoff M., Magalhães P., Ram S. Image processing with ImageJ. Biophotonics Int. 2004;11:36–42. [Google Scholar]
- 54.Amer A., Dubois E. Fast and reliable structure-oriented video noise estimation. IEEE Trans. Circ. Syst. Video Tech. 2005;15:113–118. [Google Scholar]
- 55.Bellman R. On the theory of dynamic programming. Proc. Natl. Acad. Sci. USA. 1952;38:716–719. doi: 10.1073/pnas.38.8.716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Olver F.W.J., Lozier D.W., Boisvert R.F., Clark C.W. Chapter 19: Elliptic integrals. In: Olver F.W.J., Lozier D.W., Boisvert R.F., Clark C.W., editors. NIST Handbook of Mathematical Functions. Cambridge University Press; New York, NY: 2010. pp. 514–516. [Google Scholar]
- 57.Hansen N., Ostermeier A. Completely derandomized self-adaptation in evolution strategies. Evol. Comput. 2001;9:159–195. doi: 10.1162/106365601750190398. [DOI] [PubMed] [Google Scholar]
- 58.Lagarias J.C., Reeds J.A., Wright P.E. Convergence properties of the Nelder–Mead simplex method in low dimensions. SIAM J. Optim. 1998;9:112–147. [Google Scholar]
- 59.Filzmoser P., Maronna R., Werner M. Outlier identification in high dimensions. Comput. Stat. Data Anal. 2008;52:1694–1711. [Google Scholar]
- 60.Laidler K.J. Chemical kinetics and the origins of physical chemistry. Arch. Hist. Exact Sci. 1985;32:43–75. [Google Scholar]
- 61.Kawai M., Kido T., Ishiwata S. Temperature change does not affect force between regulated actin filaments and heavy meromyosin in single-molecule experiments. J. Physiol. 2006;574:877–887. doi: 10.1113/jphysiol.2006.111708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Jaqaman K., Loerke D., Danuser G. Robust single-particle tracking in live-cell time-lapse sequences. Nat. Methods. 2008;5:695–702. doi: 10.1038/nmeth.1237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Olivo-Marin J.-C. Extraction of spots in biological images using multiscale products. Pattern Recognit. 2002;35:1989–1996. [Google Scholar]
- 64.Smith C.S., Joseph N., Lidke K.A. Fast, single-molecule localization that achieves theoretically minimum uncertainty. Nat. Methods. 2010;7:373–375. doi: 10.1038/nmeth.1449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Hird S.N., White J.G. Cortical and cytoplasmic flow polarity in early embryonic cells of Caenorhabditis elegans. J. Cell Biol. 1993;121:1343–1355. doi: 10.1083/jcb.121.6.1343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Tseng Q., Duchemin-Pelletier E., Théry M. Spatial organization of the extracellular matrix regulates cell-cell junction positioning. Proc. Natl. Acad. Sci. USA. 2012;109:1506–1511. doi: 10.1073/pnas.1106377109. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
The recorded channels are (top) DIC, (middle) mCherry::PH, and (bottom) GFP::PAR-2; the raw data are displayed in each case. This recording corresponds to the frames used in Figs. 1 and S1 and has been accelerated 60 times.


