Splicing of designer exons informs a biophysical model for exon definition

Abstract

Pre-mRNA molecules in humans contain mostly short internal exons flanked by longer introns. To explain the removal of such introns, exon recognition instead of intron recognition has been proposed. We studied this exon definition using designer exons (DEs) made up of three prototype modules of our own design: an exonic splicing enhancer (ESE), an exonic splicing silencer (ESS), and a Reference Sequence (R) predicted to be neither. Each DE was examined as the central exon in a three-exon minigene. DEs made of R modules showed a sharp size dependence, with exons shorter than 14 nt and longer than 174 nt splicing poorly. Changing the strengths of the splice sites improved longer exon splicing but worsened shorter exon splicing, effectively displacing the curve to the right. For the ESE we found, unexpectedly, that its enhancement efficiency was independent of its position within the exon. For the ESS we found a step-wise positional increase in its effects; it was most effective at the 3′ end of the exon. To apply these results quantitatively, we developed a biophysical model for exon definition of internal exons undergoing cotranscriptional splicing. This model features commitment to inclusion before the downstream exon is synthesized and competition between skipping and inclusion fates afterward. Collision of both exon ends to form an exon definition complex was incorporated to account for the effect of size; ESE/ESS effects were modeled on the basis of stabilization/destabilization. This model accurately predicted the outcome of independent experiments on more complex DEs that combined ESEs and ESSs.

INTRODUCTION

For most mammalian genes, transcription produces pre-mRNA molecules that include exons and introns; the introns are removed and the exons are spliced together. The cellular splicing machinery identifies the boundaries between exons and introns with extreme accuracy. Early studies showed that the sequences at these boundaries (Mount 1982) are fundamental contributors to their recognition. However, it was later realized that these sequences by themselves are not enough since many sequences that resemble the consensus are ignored in the process of splicing while others that show less similarity are used (Sun and Chasin 2000).

Two alternative ideas have been implicit in thinking about the early recognition of splice sites (De Conti et al. 2013). In the first approach, intron definition, each intron is recognized as a unit and removed; the exons are joined as a result. In the second approach, exon definition, each exon is recognized as an entity and joined to another similarly recognized exon; the intron is removed as a result. Therefore, in both approaches the ends of the intervening intron must be paired, requiring intron definition. The difference lies in the initial recognition of either an intron or an exon. Systematic changes in intron lengths showed that intron definition prevails when a central intron is <200–250 nt; beyond this length exon definition takes place (Fox-Walsh et al. 2005). More than 75% of human exons are flanked by two introns that exceed this threshold and alternative exon skipping occurs predominantly in this group (Fox-Walsh et al. 2005). Thus the elucidation of just how exons are defined, i.e., recognized as an entity, is important for understanding splicing as a fundamental step in gene expression.

The development of in vitro splicing (Dignam et al. 1983; Krainer et al. 1984) has led to a detailed picture of the biochemistry of splicing and to the identification of myriad proteins regulating this process. However, this tool works well only with short introns and systems with only a single such intron are routinely used. Accordingly, splicing substrates with internal exons that are surrounded by long introns have usually been abbreviated by removing large chunks of the introns and frequently further abridged to comprise only two exons. Even with these restrictions, the rate of intron removal is lower in vitro than in vivo (Hicks et al. 2005) and is lower yet for long introns in vitro (Lazarev and Manley 2007). These limitations in splicing long introns are present even in current transcription-splicing coupled systems (Lazarev and Manley 2007). Therefore, modifications to the in vitro assay or the development of new tools to complement it would be useful for the study of exon definition.

Factors that affect inclusion of an exon in the final mRNA molecule include the strengths of the 5′ and 3′ splice sites (SSs) and the presence of regulatory sequences both in the exon (exonic splicing enhancers, ESEs; and exonic splicing silencers, ESSs) and in the intron (intronic splicing enhancers, ISEs; and intronic splicing silencers, ISSs). More recently, the involvement of transcription kinetics (Dujardin et al. 2013) and chromatin structure (Luco et al. 2011) have been demonstrated. Many of these factors have been studied by systematic variation (Graveley et al. 1998; Luco et al. 2010; Shepard et al. 2011) and in model systems functional networks of interacting proteins bound to regulatory sequence elements have been discovered (Li et al. 2007; Martinez and Lynch 2013).

However, a set of general principles that would allow “finding splice sites within a wilderness of RNA” (Black 1995) still eludes us, as is evidenced by our inability to predict these sites within typical long transcripts. Although reasonable models for several pieces of the puzzle have been put forward, new approaches may be needed (Roca et al. 2013).

We have chosen to explore splicing using a reductionist point of view, attempting to segregate individual parameters governing splicing so as to identify fundamental biophysical principles involved and their parameters. Toward this end we have created simplified exon sequences of our own design (“designer exons” or DEs). A key feature in the design of these exons was the capability to vary the parameters of exon length, ESE/ESS number, and ESE/ESS position without otherwise changing the sequence characteristics of the exon. We found that these parameters include both simple and complex components but that both can be modeled to conform to straightforward molecular mechanisms.

RESULTS

DEs: effect of size

The exon definition model for splice site recognition (Berget 1995) maintains that internal exons will be chosen for inclusion only if they have acceptable splice sites at both ends, suggesting a physical interaction between the two ends of the exon. Thus the distance between the two ends of the exon could be an important parameter for the realization of this interaction. Consistent with this idea internal exon size in humans is limited, with <4% being >300 nt (Berget 1995). The effect of exon size on splicing has been tested in the past, but the experimental exon expansions changed the quality as well as the length of the test exons. Thus splicing in those experiments could well have been affected by the quality and not necessarily the quantity of the added sequence (Chen and Chasin 1994; Sterner et al. 1996). Since DEs can be expanded by adding identical sequence modules, chosen to avoid exonic regulatory elements, the contribution of parameters other than length should be diminished.

To assess the effect of size on exon inclusion we constructed a series of 3-exon minigenes containing a DE as the central exon flanked by introns of 299 and 635 nt (Fig. 1; Supplemental Fig. S1). Both introns are longer than the size often cited for intron definition (200–250 nt, [Fox-Walsh et al. 2005]), although intron 1 is close to this size. However, neither of these introns is removed by intron definition, since mutations that knock out or weaken the splice sites of these introns have never been seen to result in intron retention ((Carothers et al. 1993; Chen and Chasin 1993) and results therein). Importantly, in the experiments presented here in which scores of exon skipping results were visualized by gel electrophoresis of PCR products, we never saw any evidence of intron retention (data not shown and Supplemental Fig. S12).

FIGURE 1.

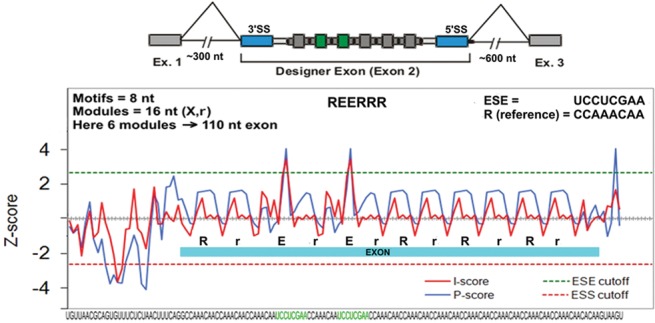
Construction of designer exons (example). From the bottom: the RNA sequence with two 8-nt ESE motifs in green. Above that is a plot of the computationally predicted enhancer/silencer strengths of each overlapping eight-mer using two different criteria: red or blue (Zhang and Chasin 2004). The dashed lines indicate cutoffs used for classifying a sequence as an ESE (green) or ESS (red). The exon is indicated by a blue bar, where E refers to the ESE motif and R or r refers to the reference motif, with the lower case indicating its use as a spacer. At the top of the graph is an abbreviated version of the motif composition in which the spacer r motifs have been omitted. Finally, at the top of the panel is a cartoon showing the overall structure of a minigene containing a DE, with the splice sites in blue and the ESE motifs in green.

The DEs are composed exclusively of repeats of the 8-nt Reference Sequence CCAAACAA inserted between positions +1 (3′SS) and −5 (5′SS); those remaining bases at the 5′ and 3′ ends are parts of the splice sites or necessary “linker” sequences. We previously called this Reference Sequence “neutral,” as it is not predicted (Zhang and Chasin 2004) to be either a putative exonic splicing enhancer (PESE) or a putative exonic splicing silencer (PESS) and it had relatively little effect on the splicing of a test exon (Zhang et al. 2009). More importantly this sequence has the property of not “creating” either a predicted ESE or a predicted ESS when all overlapping eight-mers formed by self-concatenation are considered (Zhang et al. 2009). However, in the analysis presented here it appears to have weak silencing activity (see below); we therefore refer to it as the Reference Sequence (R), since the effects of the ESEs and ESSs used were evaluated by substituting them for the Reference Sequence.

The exon sizes used here ranged from 14 to 302 nt in steps of 32. In preliminary experiments, we found that the levels of exon inclusion for DEs of intermediate size (110 nt) made up exclusively of Reference Sequences and using our original DE splice sites were too low to be useful (<10 percent spliced in, psi). Strengthening the sequence at the 3′SS from the original wild-type UCUCUAACUUUCAG/G (consensus value, CV [Shapiro and Senapathy 1987] = 81.0) to UCUCUUUUUUUCAG/G (CV = 93.1) or the sequence at the 5′SS from the original wild-type CAA/GUAAGU (CV = 88.4) to CAG/GUAAGU (CV = 99.9) increased the psi of these intermediate size DEs to above 75%. The effect of size on each of these two constructs was then examined in HEK293 cells. Splicing was assessed by RT-QPCR after transient transfection and also after site-specific integration into a unique chromosomal location (see Materials and Methods).

As shown in Figure 2, the points describing the inclusion of DEs display an optimum size range for exon inclusion, with inclusion levels dropping off dramatically both below and above this range. The optimum range depended on the nature of the splice site sequences, being ∼45–80 nt for exons with a strong 3′SS and 80–110 nt for those with a strong 5′SS. Interestingly, not just the optimum but the entire curve was shifted along the x-axis according to the splice site sequences used. Although exon inclusion efficiencies differed at most points depending on the splice site sequences, the shapes of the curves are remarkably similar. A stronger 3′SS favored the inclusion of shorter exons whereas a stronger 5′SS favored the inclusion of longer exons. For example, compare the effects of the different splice site sequences on DEs of 46 and 142 nt in Figure 2. To assess the extensibility of these results to a chromosomal context, we engineered a cell line where DE minigenes could be placed by stable transfection exclusively at a defined location in the genome (see Supplemental Material); we call these exons chromosomal DEs. A series of exons bearing the strong 3′SS yielded a curve closely resembling that for transient transfections (Supplemental Fig. S2). The interdependence between the quality of a splice site sequence and size-dependent efficiency of exon inclusion is surprising and will be revisited in the Discussion.

FIGURE 2.

Exon inclusion has an optimum size range. Inclusion levels (psi) of DEs in transient transfections. DEs consist of Reference Sequences and have either a strong 3′SS (filled symbols) or a strong 5′SS (open symbols). The splice site sequences and consensus scores are shown. See Supplemental Figure S2 for inclusion levels of DEs in a chromosomal context. Error bars: SEM, n ≥ 3. The curves were generated by a model developed in the last section of the text.

DEs: effect of ESE position

Interactions that take place in exon definition have been shown to be facilitated by exonic splicing enhancers (Blencowe 2000; Chasin 2007). To assess the effect of enhancers on DE inclusion, we chose as a baseline framework a DE of 110 nt made up exclusively of Reference Sequence repeats and carrying wild-type splice sites, SS Set 7 (see Table 1). This exon yielded a psi of ∼7%, a suitably low value for observing the effect of enhancers. As a prototype ESE we used the sequence UCCUCGAA, previously shown to function as an ESE in both a natural and a designer exon (Zhang et al. 2009). Like the Reference Sequence this sequence has the property of not creating either a predicted ESS or a predicted ESE within the overlaps created by its insertion into the baseline DE. This ESE is the same prototype we used in our initial study of designer exons (Zhang et al. 2009). When this ESE was inserted into the baseline DE it was always flanked by two Reference Sequences, so as to satisfy the critical condition for which it was designed: to keep constant the local context into which it was placed. Thus we can consider the resulting DEs as being comprised of 16 nt modules each consisting of the reference eight-mer followed by either the ESE or another reference eight-mer. The baseline DE provides six evenly spaced nonoverlapping positions at which a 16-nt ESE module can be substituted. Later we will describe similar constructs bearing ESS sequences. To define the composition of a DE we will use the notation E for ESE, S for ESS and R for the Reference Sequence. So, for instance, we refer to the placement of an ESE at the second and third of the six available positions as REERRR (Fig. 1).

TABLE 1.

Effect of splice site sequences on exon inclusion

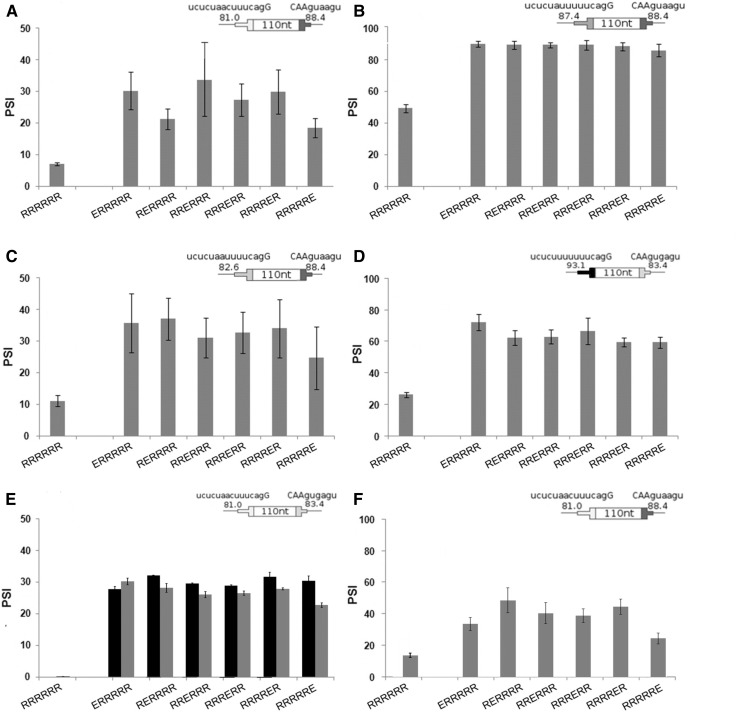
We first substituted a sole ESE at each of the six evenly spaced positions in the baseline DE and measured splicing after transient transfection. At each position the presence of the ESE caused a three- to fourfold increase in psi (P < 0.01) with respect to the baseline DE (Fig. 3A). Similar increases were seen for these exons in the chromosomal context (Supplemental Fig. S3A). The ESE was effective at each of the 6 positions. Indeed, there were no statistically significant psi differences between positions, except for three differences of ≤5% in the chromosomal DEs.

FIGURE 3.

Addition of a single ESE enhances inclusion level and is position independent. (A–F) Enhancement as a function of ESE position in four different splice site contexts. The cartoons show the consensus values for splice site sets used (Table 1). (A) SS Set 7; (B) SS Set 5; (C) SS Set 6; (D) SS Set 4. Error bars: SEM, n ≥ 3 except C, where n = 2. In all cases the psi of DEs with an ESE are significantly different from that without ESEs (t-test, P < 0.01), except for the right most position in C (P = 0.05). None of the 90 pairwise comparisons between ESEs at different positions showed significant differences (t-test, P > 0.05). See Supplemental Figure S3 for inclusion levels of DEs in a chromosomal context. (E) ESEs corresponding to SRSF1 (black columns) and SRSF7 (gray columns) binding sites in a DE with SS Set 8. (F) An ESE corresponding to an SRSF2 binding site in a DE with SS Set 7.

ESEs are often thought of as acting by enhancing the recruitment of components of the splicing machinery to a nearby splice site. In this view they would be expected to show a position effect, being more important close to a weak splice site. The lack of a position effect here could be due to the incorrectness of this argument or to the possibility that the ESE is equally effective at enhancing the use of the 3′SS and the 5′SS, and so only appears to be position independent. To distinguish between these two ideas, we manipulated one or the other of the DE splice sites so as to create a range of differences between the two in terms of SS strength.

We tested seven combinations of three 5′ and four 3′SS sequences using transient transfection. We started with a DE with two relatively strong splice sites, having consensus values of 93.1 and 88.4 for the 3′SS and 5′SS, respectively. This exon was efficiently included even without an ESE (psi of ∼80%) and so was not useful for evaluating enhancement (Table 1, SS Set 3). We then weakened one or the other of the splice sites so as to produce a range of disparities between the 3′SS and the 5′SS strengths; the differences in strength (3′SS minus 5′SS) for the four tested pairs were +10, −1, −6, and −7, measured as CV. Weakening either the 3′SS or 5′SS reduced psi values to the 7%–50% range so that the effect of adding an ESE could be evaluated (Table 1, SS Sets 4–7). Once again no statistically significant difference was found for the effect of the ESE at the various positions: P-values were >0.10 for all pairwise comparisons (Fig. 3B,C,D; Table 1, last column). SS Set 5 was also tested in a chromosomal context; addition of a single ESE produced increases of similar magnitude to those found using transient transfections and was once again position independent (Supplemental Fig. S3B). These observations provide no support for the existence of a position effect for splicing enhancement by this ESE in these DEs.

As might have been expected, the DEs without ESEs spliced more efficiently as the strength of the splice site sequences increased (Table 1, column 7, R² of 0.81 for psi versus combined CV scores). Interestingly, the average increment in psi engendered by an ESE also increased with the combined CV score (R² = 0.96) in this range (psi of 7%–50% without the ESE).

This position independence result contrasts with other reports that suggest that the positions closest to the splice sites are the most effective for ESEs (Graveley et al. 1998; Fairbrother et al. 2004). This discrepancy could be explained by our use of an exonic sequence context designed to minimize factors other than distance when ESEs are placed at different positions. However, an alternative explanation is that the ESE we used, also carefully chosen for the same reason, happens to be a position-independent ESE, perhaps a minority type. To address this question we also tested three previously described ESEs, which correspond to the SR proteins SRSF1, SRSF2, and SRSF7. The exact sequences chosen (Table 2) were based on relative binding affinities reported in the CISBP database (Ray et al. 2013). Unlike our designed ESE, these ESE sequences are not immune from creating additional ESRs through overlaps with their insertion sites; however, those creations will be the same regardless of position. Each of these ESEs was tested singly in each of the same six positions described above. SRSF2 was tested using the same splice sites used for the designer ESE. SRSF1 and SRSF7 produced near 100% inclusion from any position with these splice sites. Therefore, these two ESEs were tested using somewhat weakened splice sites (Set 8, Table 1). SRSF1 and SRSF7 produced the same enhancement of splicing at each of the six positions (Fig. 3E). The same was true for SRSF2 at positions 1–5. SRSF2 at position 6, closest to the 5′SS, did exhibit a difference, but it yielded less, not more, enhancement (Fig. 3F). These results thus support the conclusion that many ESEs do not show an exonic position effect for splicing (see also Discussion).

TABLE 2.

ESEs tested for position dependence

DEs: effect of multiple ESEs

The sequence of our DEs allowed us to add an ESE while diminishing the chance of creating other regulatory sequences within overlapping sequences. It also allowed us to add multiple copies of an ESE while not adding any sequences that were not already present in a single ESE DE. It has been shown that the ESE strength or number inversely correlates with splice site strength in mammalian exons, i.e., ESEs can compensate for weak splice sites (Xiao et al. 2007; Ke et al. 2008). In addition, Hertel and Maniatis (1998) showed that the use of multiple downstream enhancer elements increased the use of a 3′SS in an additive manner when tested in vitro (Hertel and Maniatis 1998). We asked whether such additivity also holds true for the definition of an internal exon in vivo.

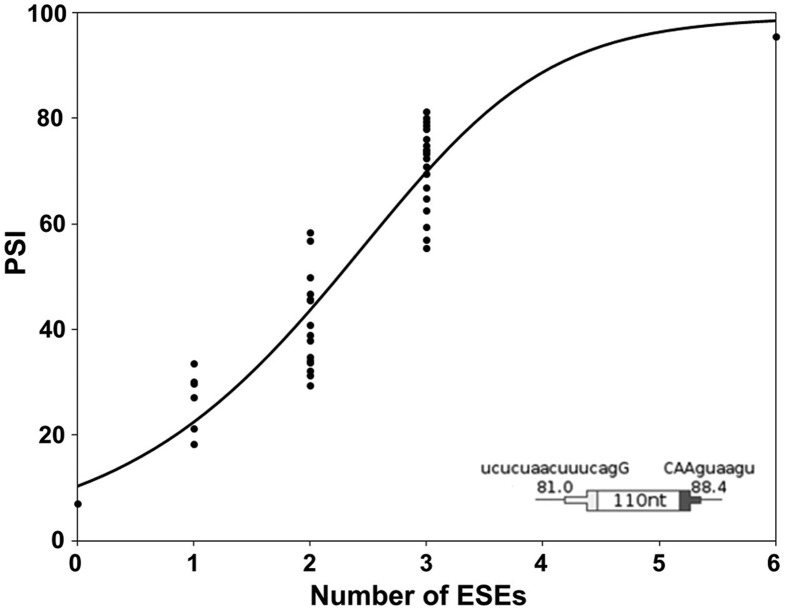
To assess the effect of multiple enhancers in a single exon, splicing of DEs with 0, 1, 2, 3, or 6 ESEs was measured using transient transfections. For these experiments we used SS Set 7 in Table 1, which was the same set used in our previous study of randomly constructed DEs (Zhang et al. 2009). The data for no ESEs and 1 ESE at all possible positions were shown in Figure 3A. The analogous data for all 36 combinations of positions for 2, 3, and 6 ESEs are summarized in Figure 4 and provided in detail in Supplemental Table S1. As was the case for one ESE, there was no strong or consistent position effect when 2 or 3 ESEs were present. Psi values increased with the number of ESEs in a near linear manner up to 3 ESEs (R² = 0.82) and leveled off when six ESEs were included. Ascribing the last point to saturation, these results are consistent with the additive model. The slope in the linear range was a moderate 20% per ESE added; this kind of limited enhancement enabled testing the effect of multiple ESEs.

FIGURE 4.

Inclusion levels of DEs increase with the number of ESEs present. The psi for all possible DE permutations with 0, 1, 2, 3, or 6 ESEs was measured (n ≥ 3). SS Set 7 was used. The curve was generated by a model developed in the last section of the text.

DEs: effect of ESS position

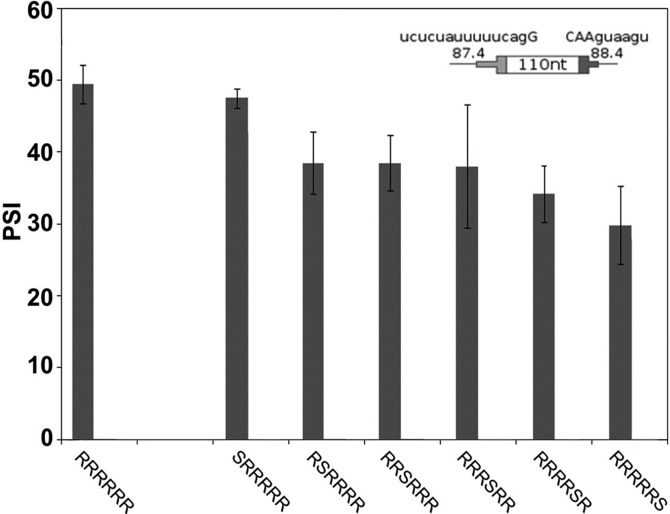
To study the effect of the position of an exon silencer sequence (ESS) we used SS Set 5 (Table 1), which provided a psi of ∼50% with no ESS present. The ESS sequence, CACAUGGU, was chosen so as to not create any other predicted splicing regulatory sequence when placed in the DE; this same ESS was used in our previous study (Zhang et al. 2009). A single ESS at positions 2–6 reduced the psi in transient transfections or in chromosomal DEs (Fig. 5; Supplemental Fig. S4). The ESS had no effect at the 5′ most position (position 1) and an apparently greater effect at the 3′ most position (position 6). These results suggest a difference between positions, a conclusion that is supported by considering the effects of multiple ESSs (see below).

FIGURE 5.

Addition of a single ESS decreases inclusion level and shows some position dependence. The psi for DEs with a single ESS are shown for transient transfections. SS Set 5 was used. Error bars: SEM, n ≥ 3. An ESS at positions 2, 3, 5, or 6 reduced the psi significantly compared with no ESS (P ≤ 0.03). There was no effect at position 1 and variability at position 4 did not allow a conclusion. The cartoon shows the consensus values for splice sites used. See Supplemental Figure S4 for inclusion levels of DEs in a chromosomal context.

DEs: effect of multiple ESSs

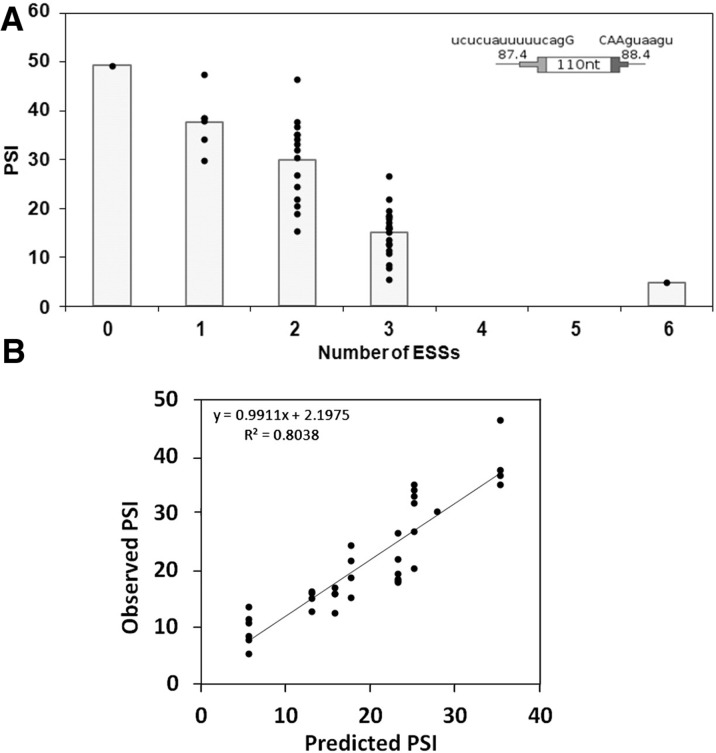
We next measured the effect of multiple ESSs, once again with the question of additivity in mind. The results of including 0, 1, 2, 3, or 6 ESSs in all 43 positional combinations are summarized in Figure 6A; the psi values are shown in Supplemental Table S1. Psi decreased approximately linearly from 50% to 15% as 1–3 ESSs were included in the exon (R² = 0.68); six ESSs resulted in 10-fold silencing, but showed signs of saturation (Fig. 6A). These results are consistent with an additive model in which each ESS contributes ∼12% drop in psi.

FIGURE 6.

Inclusion levels of DEs decrease with the number of ESSs present. (A) The psi for all possible permutations with 0, 1, 2, 3, or 6 ESSs were measured (n ≥ 3). SS Set 5 was used. The columns depict the average. Note that the data here are summarized using a column chart rather than a curve such as was used in Figure 4 for the ESEs. That curve was generated by a model that assumes position independence (see below), which is not the case for the ESSs. (B) The psi for all possible permutations with two and three ESSs were plotted against predictions based on the addition of the individual position effects of each ESS as measured in the single-ESS experiments (Fig. 5).

The simple relationship between ESS number and psi described above does not take into account possible position effects (see Fig. 5). Thus the relationship between psi and ESS number cannot be represented as simply as it was for the position-independent ESEs in Figure 4. To investigate this issue we allowed each ESS to exert a characteristic position effect, summing the effects of the individually positioned ESSs as measured in the single-ESS DE experiment:

$$\begin{array}{c}\text{Predicted}\text{psi}=\text{baseline}\\ +{\displaystyle {\sum }_{i=1}^6{P}_i(\text{psi}(i)-\text{baseline})},\end{array}$$ (1)

where baseline is the psi of the DE with no ESSs, i is an index number for positions 1–6, P_i is 1 if an ESS is present at position i and 0 otherwise, and psi(i) is the measured psi for a DE bearing a single ESS at position i. The observed psi measurements for all 35 two- and three-ESS DEs show a good agreement to these linear combination predictions (R² = 0.80) (Fig. 6B). In contrast, when we assumed that all positions were equivalent and used the average value for all the single-ESS DEs to predict psi then the R² value dropped to 0.56, supporting the position dependence observed in Figure 5. To explore this idea further, we examined the contributions of individual positions to this position effect by averaging all but one of the positions while retaining the position-specific contribution of that one. Retaining the position-specific contribution of the first or last positions increased the R² value from 0.56 to 0.68 or 0.72, respectively, while such retention at the internal positions 2–5 produced no increase in R². Thus it appears that positional information is important only for the two terminal positions, as was indicated by the significance tests of the data in Figure 5. Indeed, retention of the position effect of 1 and 6 alone returned the R² value to 0.80, the same as the value reached using all positional information. Taking all these data into account, it appears that an ESS at the first position has no effect, an ESS at the last position is the most effective and ESSs in the middle positions have intermediate effects that are equivalent and independent of their positions.

A biophysical model to explain splicing decisions

We designed our own exons so as to be able to isolate individual parameters that govern splicing decisions. While this reductionist approach dispenses with the complexity of natural exons, it has the advantage of making fundamental principles discernible. We next sought to develop a biophysical model that could explain the data produced by these ∼150 exon perturbations. The goal of this model was to assess whether the biophysical assumptions made were consistent with the parameters studied: size and ESE/ESS number and position.

The model is centered on exon definition as a decisive step in the recognition of most splice sites and assumes that this step requires the formation of an RNA–protein complex on the exon of interest. The number of pre-mRNA molecules in such a complex is determined by the balance between assembly and disassembly, which can be described by overall association and dissociation rate constants. Once assembled, complexed molecules can then proceed to a state of commitment to exon inclusion (Fig. 7A).

FIGURE 7.

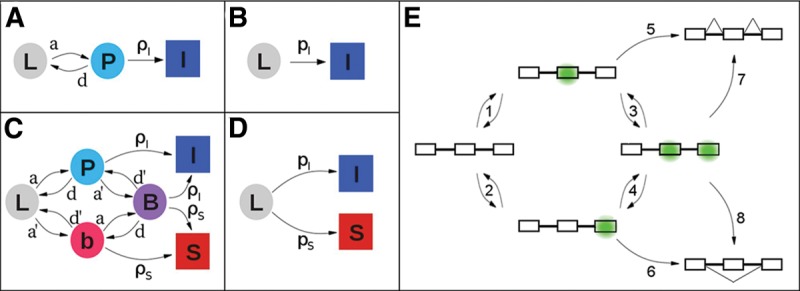
Complex kinetics can be described in simpler terms. The squares and circles represent different states of a pre-mRNA molecule: (L) “naked” transcript; (P) exon of interest in an exon definition complex (EDC) with the downstream exon either not present or present but not in an EDC; (b) downstream exon in an EDC with the exon of interest not in an EDC; (B) both exons in EDCs; (I) (inclusion) and (S) (skipping) represent molecules that have either committed to or achieved their respective splicing outcomes. The arrows represent transitions between states, and are labeled with rate constants: (a) and (d) association and dissociation, respectively, of the complex on the exon of interest; (a′) and (d′) the same for the downstream exon; (ρ_I) and (ρ_S) commitment to inclusion and skipping, respectively, of the exon of interest. (A) Model for the splicing reactions before time τ. Importantly, the transition from P to I is independent of the presence of exon 3. (B) Simplified model before time τ; p_I amalgamates a, d, and ρ_I. (C) Model for the splicing reactions after time τ. (D) Model after time τ simplified analogously to B. p_S amalgamates a′, d′, and ρ_S. See Supplemental Material for details. (E) Cartoon showing the states implied in C for a pre-mRNA molecule depicting EDCs (green). Steps 1–4 represent the formation or loss of EDCs; Steps 5–8 represent commitments to the splicing outcome shown.

We start with a set of assumptions that are listed in Supplemental Box 1 and focus on a cohort of pre-mRNA molecules (conceptually “tagged”) that are all in the same state of synthesis. To consider the choice between inclusion and skipping, it seems reasonable to consider the competition presented by the downstream exon. We define time τ as the time interval between the synthesis of the exon of interest and its downstream neighbor and consider separately the pre-τ and post-τ periods. For times prior to τ, there are three types of pre-mRNA molecules with respect to the exon of interest: naked L, complexed P, and committed to inclusion I (Fig. 7A). A set of differential equations relates the number of tagged L, P, and I molecules starting at t = 0:

$$\text{d}L\text{/}dt=\text{d}P-aL,$$ (2)

$$\text{d}P\text{/d}t=aL-(d+{\rho }_{\text{I}})P,$$ (3)

$$\text{d}I\text{/d}t={\rho }_{\text{I}}P,$$ (4)

where a and d are association and dissociation constants, respectively, and ρ_I is the rate at which complexed molecules commit to the included pathway. Since it is a cohort of previously tagged molecules that is being followed, rates of synthesis need not be considered.

For times starting at time τ the molecules can consider splicing the downstream exon to the upstream exon; i.e., skipping the exon of interest (Fig. 7C,E). A set of differential equations, analogous to the set for the pre-τ period, describes this situation (see Supplemental Material). Although we are most interested in the probability of exon inclusion, it is easier to calculate the probability of exon skipping, which provides the same information. The general solutions as well as some approximations and intermediate results are presented in Supplemental Material. Equation 5 describes the fraction of tagged molecules that skip the exon:

$$S_{\infty }\text{/}{L}_0\approx {\text{e}}^{-\text{pI}\tau }{p}_{\text{S}}\text{/(}{p}_{\text{S}}+p_{\text{I}}),$$ (5)

where L₀ represents the total number of molecules that were initially tagged, S_∞ is the final number of skipped molecules, τ is the time interval between the synthesis of the exon of interest and its downstream neighbor, p_I = ρ_I/(1 + d/a) and p_S = ρ_S/(1 + d′/a′); ρ_I and ρ_S are the rate constants for commitment to inclusion and skipping, respectively; and a, d, and a′, d′ are the association and dissociation constants for an exon definition complex of the exon in question and the downstream exon, respectively, as defined in Figure 7C.

If the rates of degradation of the included and skipped molecules are similar, Equation 5 provides approximations for the fraction of skipped and, by subtraction, of included untagged molecules at steady state. The form of Equation 5 lends itself to intuitive interpretation, and the focus on S provides insight into the roles of the different parameters (see below). The exponential decay term describes the commitment to inclusion that occurred during the pre-τ interval: molecules no longer available for skipping. The remaining fraction arises after time τ and reflects the competition between inclusion and skipping among those molecules capable of either. At this point the model predicts splicing outcomes in terms of an unspecified exon definition complex and of the ratios of rate constants p_I and p_S. We now turn to relating these terms to biophysical processes and to use the resulting model to predict psi values.

Modeling the DEs

Equation 5 should be applicable to the definition of any internal exon spliced using exon definition. In the case of natural exons there are many factors that could be in play and that are poorly understood. For instance, protein–protein interactions and pre-mRNA secondary or tertiary structure could well determine ρ, a, d, and/or τ. We did not consider such factors in applying this model to DEs, which represent a simplified framework for testing the validity of the model and for building more refined versions.

In order to apply Equation 5 to the DE data, we needed to model τ, p_I, and p_S. We consider τ and p_S to be constant for all DEs used, τ dependent on the transcription time and p_S dependent on the downstream exon. Thus we are left with p_I, which is ρ_I/(1 + d/a). A physical model for ρ_I is challenging, as this term describes the conversion of an initial complex to a commitment complex. It is not yet understood what commitment entails or how it is achieved. We therefore decided to focus on the formation of the initial complex itself, asking whether the effect of exon size, ESEs, and ESSs on its formation (a/d) can explain our data. That is, we assume that ρ_I, the rate constant for the conversion of an exon with an assembled complex to a committed exon, remains constant with respect to these three parameters. Equation 5 can be rewritten as Equation 6, which combines those terms that are not resolvable by the experiments we carried out and serves as the proving ground for fitting the data to the model:

$$\text{pso}\approx \text{100}{\text{e}}^{-T\text{/(1}+D\text{)}}/(1+C\text{/(1}+D\text{)),}$$ (6)

where pso denotes percent spliced out (i.e., skipped), T = ρ_Iτ, C = ρ_I/p_S, and D = d/a. We then focused on how all the different DE configurations affect D, the ratio of the disassociation and assembly rate constants of the initial complex, while T and C were taken to be constant.

We first sought an expression relating size and D, modeling the formation of an exon-spanning complex. We reasoned that in the simplest case, the formation of this complex is proportional to the probability of the two tethered ends of the exon having undergone a productive collision, which occurs when both ends of the exon are suitably occupied and they approach each other in the correct orientation through thermal movements. The ends will then be at a fitting distance from each other, y_i, as shown in Figure 9A, below. The movements of the ends of the exon were approximated using a worm-like chain model for the exonic RNA, as described in Supplemental Material.

FIGURE 9.

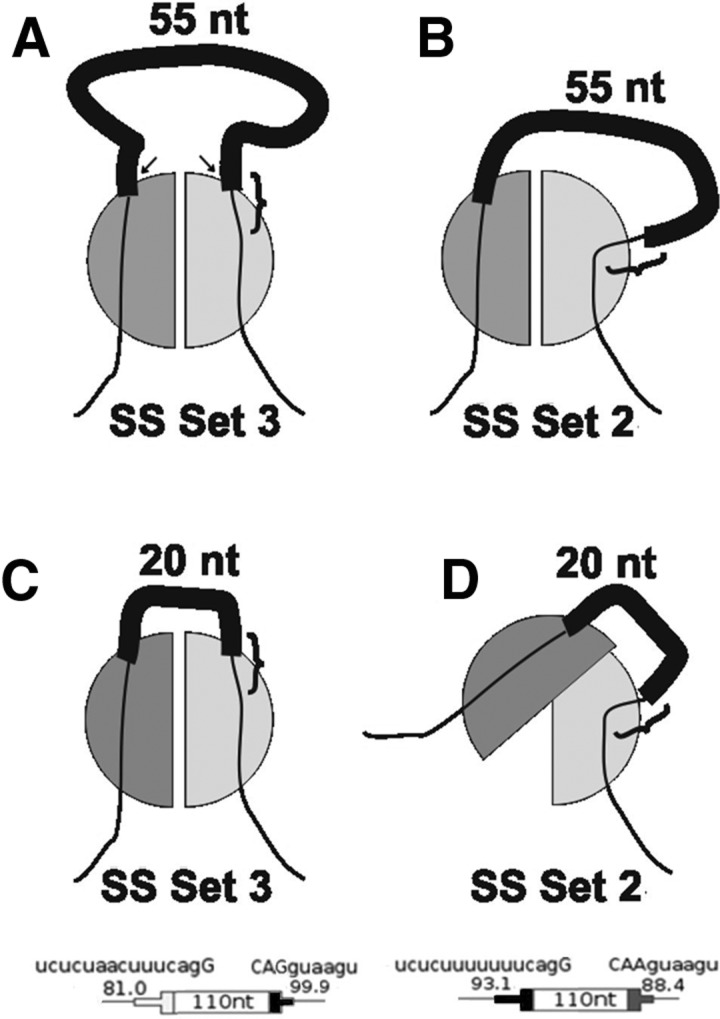
A model for exon end-to-end contact in exon definition. (A) Communication between the two ends of the exon is mediated by protein–protein interaction (half-circles). The line represents the pre-mRNA, with the thick black section being the exon, the thin black sections being the intronic flanks, and the 5′SS indicated by the curly brace. A 55 nt exon is accommodated by protein factors binding to the ends of the exon (e.g., U2AF65 and U1 snRNP). SS Set 3 is being used. The distance between the emerging ends of the RNA molecule (arrows), designated the fitting distance (y_i), was used to obtain an equation for the rate of formation of this complex. (B) A different splice site sequence (SS Set 2) could change the point and angle at which the pre-mRNA extends from a binding protein such that the fitting distance (y_i) is increased compared with SS Set 3. The 55 nt exon can accommodate this difference. (C) Same as A but with a shorter 20 nt exon. The short fitting distance of SS Set 3 still allows coupling of the protein factors. (D) Same as B but showing that the long fitting distance of SS Set 2 precludes coupling of the two protein factors when the exon is only 20 nt long.

We modeled the effect of enhancers by assuming that they act by increasing the stability of the complex (see Supplemental Material). Note that this choice is in contradistinction to other possibilities such as recruitment or improving catalysis. Multiple enhancers were modeled here as independent, leading to an exponential dependence of D on the number of enhancers present. A similar approach was taken for modeling the ESSs, which are considered to be disruptive to the complex and therefore decrease its stability. Since the ESS used showed a position-dependent effect, we divided the ESSs into three categories based on their position: first (position 1), intermediate (positions 2–5), and last (position 6). As in the case of the ESEs, multiple ESSs were modeled as independent of each other.

The effect of the Reference Sequences on stability also had to be considered, for it is unknown if they should be modeled as enhancers, silencers or something else. Since the effect of replacing Reference Sequences with ESEs was shown to be position-independent, the effect of individual Reference Sequences should also be position-independent. Extending the analogy with ESEs and ESSs, multiple Reference Sequences in a single exon were modeled as independent.

Taking all of this into account and modeling these size and stability effects as independent of each other gave the following approximation for D in Equation 6 (see Supplemental Material for a detailed description of its derivation):

$$D=K_i{Y}_i^{-2}{c}_{\text{E}}^{n_{\text{E}}}{c}_{\text{R}}^{n_{\text{R}}}{c}_{\text{SF}}^{n_{\text{F}}}{c}_{\text{SL}}^{n_{\text{L}}}{c}_{\text{SI}}^{n_{\text{I}}}{Z}^{3/2}{\text{e}}^{3Y_i{}^2/Z},$$ (7)

where Z is the size of the DE in nucleotides figuring 2 nt/nm (Chen et al. 2012), Y_i is y_i/√Kuhn length, n_E is the number of ESEs in the exon, n_R is the total number of Reference Sequences present, n_I is the number of nonterminal ESSs, and n_F and n_L are 1 if the first or last position, respectively, is occupied by an ESS and 0 otherwise. The c constants represent destabilization coefficients for the ESSs (c_SF, c_SL, c_SI), Reference Sequences (c_R) and ESEs (c_E). K_i is a constant that combines all remaining constants generated by each of the individual terms; the index i refers to the set of splice sites present.

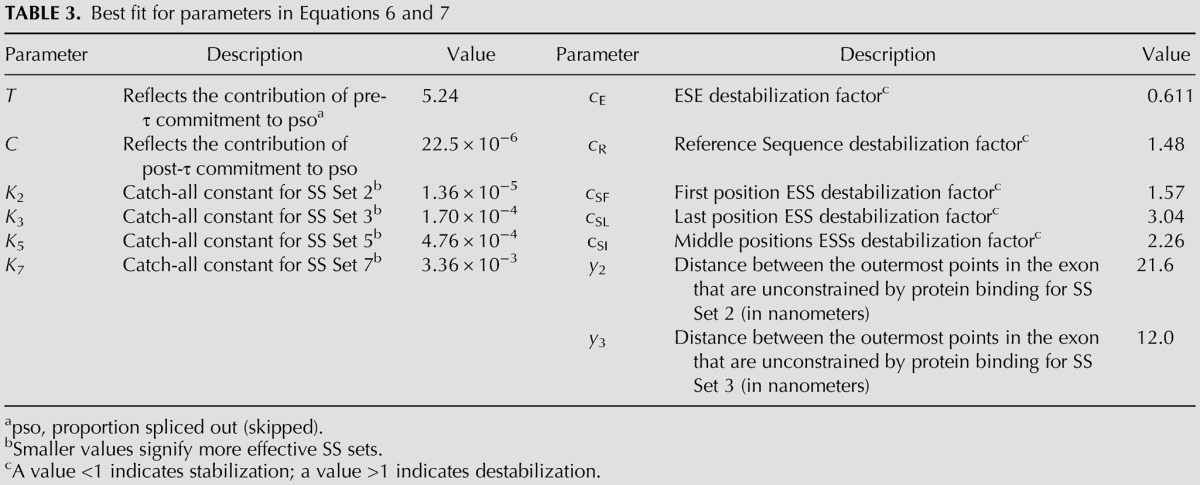
To optimize the values for K_i, y_i, and the c constants in Equation 7 we used BFGS, an iterative multivariate nonlinear optimization algorithm (Press et al. 2007), for minimizing the sum of the squared differences between predicted and observed pso values (see Materials and Methods). The BFGS algorithm is capable of simultaneously dealing with the 13 parameters listed in Table 3. The fitting distances y₂ and y₃ were discoverable from the data of the size perturbation experiments (Fig. 2). As there were no size perturbation data for SS Sets 5 and 7, we set y₅ and y₇ equal to y₃, based on the identity of the 5′SS in these 3 DEs. Evidence that this choice was appropriate is presented below. The data used for optimization are described in Materials and Methods and shown in Supplemental Table S1. The parameter set that emerged is shown in Table 3.

TABLE 3.

Best fit for parameters in Equations 6 and 7

Testing the model

That the model accurately predicts the results of these single parameter perturbation experiments can be seen in the good fits of the curves to the data in Figure 2 (for size) and Figure 4 (for ESEs); these curves were generated according to the predictions of the model and are not a simple heuristic fit. Additional fitting data can be seen in predicted versus observed relations for individual parameters (R² values of 0.86–0.99, Supplemental Fig. S5). While a good fit to these data is perhaps not surprising given the number of parameters that were optimized, it is nevertheless noteworthy that it was achieved notwithstanding the constraints imposed by the biophysically derived form of the equations.

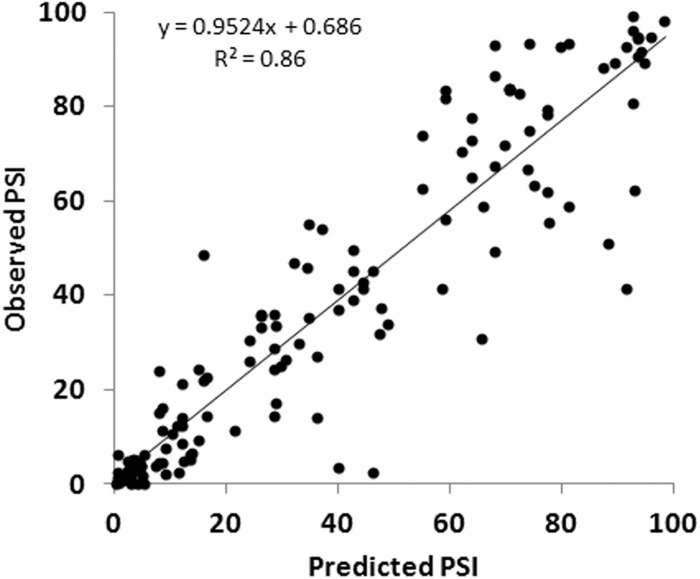
A more appropriate validation of the model is to test it against experimental data that were not used in its optimization. An extensive set of such data was available from our previous experiments with more complex designer exons that combined ESEs and ESSs as well as variable size (Zhang et al. 2009). These 142 DEs used SS Set 7, ranged from 62 to 270 nt in length and included sequence compositions such as SES, SSSE, EEESEE, etc. We asked whether our model could explain the behavior of these more complex DEs, despite the fact that it was optimized without using any exon in which an ESE and an ESS were present together. We refer to these previously studied DEs as “complex DEs.” Complex DEs differ in two additional ways from the present set of DEs: (1) In the present DEs, a different promoter and polyadenylation site were incorporated, as well as some additional mutations in the first and last exons (see Materials and Methods) and (2) semiquantitative endpoint RT-PCR was used in the older experiments as opposed to RT-QPCR used here. These caveats notwithstanding, the model worked quite well in predicting these untouched data, generating an R² of 0.86, a slope of 0.95 and an intercept of 0.69% (Table 4; Fig. 8). Beyond the high R² value, the close match to a slope of 1 and a y-intercept of 0 attest to the accuracy of the model. Although the R² value achieved was gratifying, some points were evidently not accurately predicted. There are two types of explanations for such discrepancies. The first is technical, due to the different contexts and methods used and to simple experimental error. The second may be due to limitations in the current model, which does not take into account possible ESE/ESS interactions or a role for possible secondary structures.

TABLE 4.

Testing the model on complex DEs

FIGURE 8.

The model accurately predicts the inclusion levels of DEs. Observed psi values are those previously reported for more complex DEs harboring combinations of ESEs and ESSs and being of varying lengths (Zhang et al. 2009). These 142 measurements represent an untouched data set not used for building the model. Psi values were predicted using the composition of the exons and Equations 6 and 7. Constants used were those derived from the single parameter experiments described here (Table 3).

We addressed three anticipated sources of discrepancy between the old and new data. First, because we examined the size dependence using SS Sets 2 and 3 (Table 1) we were able to discover the fitting distance y₂ and y₃ (Table 3). Since we did not have a fitting distance (y₇) for the splice site set used to generate the complex DEs, we tried setting it equal to y₂ or to y₃. Either value accurately predicted the results for ESE and ESS variation when restricted to DEs of a single fixed size (see below). However, in predicting the observations of the complex DEs that differ in size, y₃ was clearly superior to y₂ (R² of 0.86 versus 0.64). To further explore this issue, we used the BFGS routine to optimize the value for y₇ (as well as K₇) while keeping all other parameters constant. The optimized value for y₇ was 11.2 nm, close to that of y₃ (12.0 nm) and quite different from that of y₂ (21.6 nm). This BFGS-optimized value for y₇ performed no better than y₃ itself. Splice site Sets 3 and 7 share a common 5′SS, distinct from that of Set 2 (Table 1), implying that it is the 5′SS that is the determining factor in the shift observed in Figure 2 between the two size curves (see Discussion).

Second, we looked for evidence of ESE/ESS interaction by asking how well the model fared in predicting the splicing of complex DEs containing mixtures of ESEs and ESSs. To avoid any confounding effect of size, we examined 27 complex DEs 110 nt in length, which was the most common size class in the previous experiments. The model predicted the effect of multiple ESEs and ESSs very well in these DEs, with an R² of 0.96, a slope of 1.02 and an intercept of 3.29% (Supplemental Fig. S6). Since the model treats the effect of the ESEs and ESSs independently, we saw no evidence of interaction between these two regulatory elements.

Third, in looking at the observed versus predicted relationships in all complex DE size classes, we noticed that while all size classes showed good correlations (R² of 0.85–0.99), a systematic trend was revealed in their accuracy, as gauged by the slope of the best fit linear relationship. Beyond the 142-nt size class, the observed values progressively fell short of the predictions at a rate of ∼1% per additional nucleotide (Supplemental Fig. S7). We interpret this distortion as being at least partially due to a drop-off in PCR efficiency for longer templates, an artifact that is expected from the end point RT-PCR used for the older data but which was avoided by using RT-QPCR in the present study. Taking all these results together, the good overall fit seen suggests that the possible omission of some biological factors in the model is not having a substantial effect on any of these DEs.

DISCUSSION

We have described the splicing phenotypes of exons of our own design, each principally comprised of prototype eight-base sequence modules that represent an ESE, an ESS, or a Reference Sequence that resembles neither. Using these simplified exons as the central exon in three-exon minigenes, we independently and systematically measured the effect of exon size, ESE content, and ESS content on splicing. We found that there is a major effect of size on splicing. Both small and large exons are spliced less efficiently than exons of intermediate size. Lower efficiencies for the splicing of small exons (Black 1991; Dominski and Kole 1991; Hwang and Cohen 1997) and large exons (Peterson et al. 1994; Sterner et al. 1996; Borensztajn et al. 2006) have been observed previously. Surprisingly, when we used different splice site sequences, we found a striking difference in exon size dependence. One set showed a better efficiency for long exons while the other was better for short exons; that is, one dependency was shifted relative to the other.

Using a DE of a fixed size, the ESE sequence used increased psi equivalently from positions throughout the exon. This position independence was maintained even when the 3′SS or 5′SS was purposely weakened. Similar behaviors were also observed when ESEs for SRSF1, SRSF2, and SRSF7 were tested, with only minor decreases in efficiency in the positions closest to the splice sites. When multiple ESEs were used, enhancement of splicing increased proportionately before showing saturation as psi approached 100%. The ESS sequence, on the other hand, displayed some position dependence. Its effect was maximal when placed close to the 5′SS but showed almost no effect near the 3′SS. Intermediate positions showed a uniform intermediate effect. When multiple ESSs were present their combined effects increased proportionately with signs of saturation as the psi approached 0%. Thus neither the ESEs nor the ESSs used here showed signs of cooperative behavior.

Given that these DEs are recognized by exon definition, we devised a general equation for exon definition that incorporated several intermediate states along a splicing pathway: Equation 5. This equation predicts that lengthening τ, the time available for commitment exclusively to the included fate (e.g., by slowing synthesis), should increase psi; this kinetic effect has been observed previously in exon definition systems (Dujardin et al. 2013). Using these equations, we explored the potential of intuitive but novel mechanisms to explain our observations. While these observations have been obtained using a simplified exon we expect the underlying mechanisms to be applicable to the definition of natural exons as well since they are based on straightforward biophysical assumptions and are indeed supported by previous studies (see below). Similarly, even though these results were obtained targeting only a single type of ESE and ESS, the method used provides a framework for exploring these same parameters using additional motifs.

Although we originally chose the Reference Sequence on the basis of its predicted relative neutrality, we found that its presence is consistent with weak ESS activity (see Table 3). A survey of the binding affinities of seven-mers in the CISBP-RNA database (Ray et al. 2013) revealed 10 human proteins (of 91 in the database) that bind to seven-mers within CCAAACAACCAAACAA, a tandem pair of Reference Sequences. Of these five are associated with splicing: hnRNP K, hnRNP LL, hnRNP R, SRSF3, and SART3. HnRNP LL is known to cause skipping of CD45 exon 4 by binding to an exonic element (Topp et al. 2008) and so is consistent with it having ESS activity. Sequences that are completely neutral may indeed be rare.

The effect of size

It has been suggested that there is an interaction between U2AF and U1 snRNP not only across the intron (Michaud and Reed 1993) but also across the exon (Hoffman and Grabowski 1992; Reed 1996). We modeled this sort of interaction across the exon as an exon definition complex. Tethered collisions were used to model the formation of this complex (Fig. 9). Not all collisions will be productive; both ends of the exon must approach each other in the correct orientation in order to interact. The probability of a productive collision was modeled assuming the RNA behaves as a flexible worm-like chain. After the bound RNA sequences at the ends of this chain become associated the physical distance between these two ends becomes fixed (the fitting distance y_i defined in Fig. 9). The emerging equations predict that splicing efficiency should decrease for short exons and for long exons: If an exon is very short no collisions may be possible while for long exons the chance of a collision between the ends is low. By optimizing the fitting distance independently for each set of SSs used, we found that a difference in this parameter could predict the shift seen in Figure 2. The values for y₂ and y₃, 12 and 22 nm, respectively, are in the size range of the RNP complexes posited (Kastner and Luhrmann 1989; Pomeranz Krummel et al. 2009; Weber et al. 2010). Importantly, the 5′SS is the determinant factor, since y_i changed substantially only when the 5′SS changed. Three possibilities come to mind to explain this 5′SS sequence dependence: (1) a large conformational change in one or more of the proteins bound to these sequences. Although a difference of 9.6 nm (Table 3) seems large, protuberances of this size have been seen in U1 snRNP (Kastner and Luhrmann 1989; Pomeranz Krummel et al. 2009; Weber et al. 2010); (2) a small conformational change that enables one or more proteins to recruit an additional “bulging” factor; (3) a sequence-dependent change in the point or angle at which the pre-mRNA extends from U1 snRNP. These options can explain the changes for both short exons and long exons (as seen in the model-generated curves in Fig. 2). An illustration of option 3 in the case of short exons is shown in Figure 9. In the hypothetical situation shown, an exon of 55 nt can be recognized with either SS Set 2 or 3 (Fig. 9A,B). However, an exon of 20 nt can be recognized with SS Set 2 (Fig. 9C) but not with SS Set 3 (Fig. 9D), as a shift in the angle and point of exit when SS Set 3 is used causes this exon to be too short to allow interaction between protein complexes bound to each end. (Fig. 9D). Indeed, such a difference can be seen in two crystal structures of U1 snRNP bound to two different mRNA ligands (Pomeranz Krummel et al. [PDB ID 3CW1] 2009; Weber et al. [PDB ID 3PGW] 2010). Irrespective of any model, the 5′SS-dependent shift in size dependence seen in Figure 1 implies that the characterization of 5′SS strength is more complex than the degree of similarity to a consensus sequence.

Compared with these simplified exons, natural exons may be influenced by other factors. For instance, the collision rate between the exon ends could be increased (or decreased) by additional protein–protein interactions or by the formation of secondary structures. In this respect, DEs can provide a framework for investigating such individual influences. Finally, the mechanism proposed here for across-the-exon pairing of splice sites for exon definition could apply to across-the-intron pairing of splice sites for intron definition as well (see Supplemental Material).

The position independence of ESEs

The 8 nt ESE studied here acted with similar efficiency from any position within a 110 nt DE, whether it was enhancing a weakened 3′SS or a weakened 5′SS. That is, we saw no position effect within the exon. Incorporating this result by modeling ESE action without position dependence, we were able to predict the effect of single or multiple ESEs in the untouched data from complex DEs with good accuracy (Fig. 8). This result stands in contrast to the prevailing view that ESEs act by recruitment of the splicing machinery to a “nearby” splice site, i.e., position is a key general factor in splice site recognition. How can we reconcile our observations with this prevailing view? Support for position dependence comes from several types of experiments. There is evidence of interactions between activator proteins that bind ESEs and some of the proteins involved in the early steps of splicing (Kohtz et al. 1994; Staknis and Reed 1994). However, this result in and of itself does not show that a close distance is necessary for such an ultimate interaction. More to the point are the results of Graveley et al. (1998) who studied activation of a doublesex 3′SS by five different splicing activators placed at different downstream positions. The activators became progressively less effective when placed at the ends of progressively longer exons. While these results were clear, consistent and striking, they need not apply generally. There are notable differences between the conditions of those experiments and the experiments reported here. The Graveley et al. experiments studied longer distances than we did, using increments of 60–100 nt to a maximum of 300 nt compared with the five finer increments of 16 nt to a maximum of 110 used here. Thus it could be that if we had studied much longer distances we would have seen a position effect. However, the 110 nt exon we studied was close to the 122 nt median size of human internal exons (Lander et al. 2001). Importantly, the pre-mRNAs they used were comprised of only two exons, the second being a truncated version of an alternative terminal exon lacking a poly(A) signal. Thus those results may apply more to terminal exon definition than to internal exon definition. Additionally, since their terminal exons varied in size, the effects on splicing might have been due to size per se rather than to position relative to the 3′SS. In the DE experiment exon size was kept constant despite a change in ESE position. Another important difference lies in intron size: The intron between their two exons was only 114 nt long, making it a likely substrate for intron definition, whereas we focused on exon definition. Finally, the Gravely et al. experiments were done in vitro while we used transfection.

Support for a position effect for ESEs also comes from the bioinformatic analysis of Fairbrother et al. (2004), who showed that RESCUE-ESE sequences are ∼10% more frequent in the exonic 20 nt closest to the ends of exons (20 nt) compared with the next exonic 50 nt and that synonymous SNPs are ∼25% less frequent in these 20 nt edge regions. Even if these frequencies are entirely ascribable to splicing efficiency, these same data can also be interpreted as suggesting that in the majority of cases (i.e., 90% and 75%, respectively) RESCUE-ESEs and SNPs do not show a position effect. Moreover, there are other large sets of computationally or experimentally defined exonic splicing motifs that do not exhibit a preferential location at exon edges (Zhang et al. 2009; Ke et al. 2011). Finally, these authors searched for motifs that were enriched toward the ends of exons which might target a specific subset of ESEs. Alternatively, this positional bias might not represent a functional requirement for enhancement. The position of the ESE may be relative to other exonic features. Take, for example, the competition between the real 5′SS and some cryptic 5′SS located upstream in the exon. If an ESE functions within the exon in a position-independent fashion, placing this ESE between the two candidate SSs would be the only option that would be selective for the downstream 5′SS (assuming an ESE must function from within an exon). This scenario introduces an incidental positional bias that would favor positions closer to the real 5′SS without placing a positional requirement on the “function” of the ESE. Our direct observations, on the other hand, are not subject to such complexity.

A third type of experiment suggesting a position effect comes from the experiment of Goren et al. (2006), who placed motifs evolutionarily defined as exonic splicing regulators (ESRs) at different positions within a test exon. Depending on the position, these ESRs sometimes behaved as ESEs and sometimes as ESSs. However, most of this variability could be explained by the creation of new overlapping motifs that spanned the joint between the motif in question and its contextual flanks (Zhang et al. 2009; Ke et al. 2011) rather than to a position per se within the exon.

In the end, there may be no need to reconcile results such as those described above with our results: Some ESEs may be sensitive to position while others are not; that is, not all ESEs need to act via the same mechanism. Indeed, there are other examples of a lack of a position effect by splicing regulatory elements or proteins in this distance range. Lavigueur et al. (1993) saw equivalent splicing enhancements by an SRSF1-based enhancer at distances of 99, 187, and 293 nt, which finally succumbed at distances of 370 and 380 nt. And there are several reports of ESEs acting bidirectionally (Bourgeois et al. 1999; Selvakumar and Helfman 1999; Caputi et al. 2004). Also, proteins that bind to ESE need not be restricted to local interactions: SRSF1 can contact a branch point sequence across a distance of at least 50 nt (Shen et al. 2004).

The Graveley and Fairbrother papers are widely cited to support an intuitive picture in which a protein bound to an ESE situated close to a splice site recruits spliceosomal components to that splice site, a picture we expected to be confirmed by our experiments. Once we obtained the opposite results, we realized that much of the support for this idea lies in its reasonableness rather than in sufficiently discriminating data. In the designer exon experiments reported here, the local context for each ESE has been kept fixed, the sequences between the ESE and the splice sites have been kept few and uniform, and exon definition is taking place. In this controlled environment, we have been able to focus on the parameter of distance between an ESE and a splice site. We find no effect of distances in the range of typical of exon lengths, either for our primary ESE or three other ESEs. We conclude that distances in this range present no impediment to many, and possibly most, ESEs. It is important to note that none of our experiments addresses the question of intronic versus exonic positions.

Stabilization versus recruitment

ESE-induced increases in the yield of splicing complexes (Hoffman and Grabowski 1992) can be explained by stabilization or by recruitment. Changes in stability, expressed as the rate of dissociation (d in Fig. 7), respond exponentially to the number of ESEs. This stability model predicts a sigmoidal curve but with a near linear relationship between psi and the number of ESEs over much of the range examined and accounts for the saturation effect when >4 ESEs are used (Fig. 4). Interestingly, the sigmoidal behavior is explained without invoking cooperativity, being simply the result of the addition of the independent ESE contributions in the denominator of an exponent (Equations 6 and 7). The recruitment model leads to a negative exponential term and a nonsigmoidal curve that did not fit the data as well (see Supplemental Fig. S8; the sum of the squared differences of the points to the curve was 0.005 for the stability model but 0.026 for the recruitment model). Moreover, unlike the stability model the recruitment model performed poorly for the complex DEs (R² of 0.37 compared with 0.86). It is interesting to note that the model used here can account for the dependence of in vitro splicing efficiency on the number of doublesex enhancers (compare Supplemental Fig. S9 to Fig. 2D in Hertel and Maniatis 1998). This agreement with long-established data supports the idea that results using a prototype ESE of our own design reflect general mechanisms involved in splicing and may not be limited to internal exons. Recruitment and stabilization are not at all mutually exclusive; one can imagine recruitment of a factor followed by stabilization of the binding of that factor and/or the subsequent stabilization of a full exon definition complex.

Mechanistic interpretations

The model described here worked well to predict the splicing behavior of 140 designer exons that were not used in its derivation. A central feature of this model is an early irreversible step in exon recognition (exon commitment). It is widely believed that the regulation of splicing takes place at an early stage in splicing (Smith and Valcárcel 2000; Black 2003). In particular, Lim and Hertel (2004) demonstrated the pairing of splice sites across an intron is associated with an early irreversible step occurring after complex E and before or coincident with ATP-dependent complex A formation. This step could represent what we call here exon commitment. Commitment steps are common characteristics of biological processes, as exemplified for instance by cell determination during development and promoter clearance in transcription (Darzacq et al. 2007; Wada et al. 2009). Mechanistically, the exon commitment step proposed here could be the capture of an exon by a scaffold, such as the CTD of RNA polymerase II.

Undoubtedly there are elements that influence splicing in addition to those studied here: exon size, ESE content, and ESS content. We attempted to keep the influence of these other parameters unchanged, collecting their effects in a catch-all constant. This disregard notwithstanding, it is noteworthy that the predictions had such a high degree of accuracy. Further experiments could target other factors using the same theoretical framework. Possible routes for extending this model are to incorporate different and additional ESEs and ESSs, to use as an endpoint the formation of an exon definition complex itself (Robberson et al. 1990; Schneider et al. 2010) rather than splicing, and to examine later steps in splicing.

The values of the optimized equation coefficients used in the model (Table 3) show expected characteristics as well as some surprises. The coefficients for dissociation for ESEs (c_E) and ESSs (c_SF, c_SL, and c_SI) were less and greater than unity, respectively, as expected. We expected the coefficient for the Reference Sequence (c_R) to be close to unity if it was neutral, but obtained a value of 1.5. This value represents a significant contribution that cannot be ignored; that is, an arbitrary assignment of “neutrality” (1.0) to the Reference Sequence seriously weakens the model's predictive power (data not shown). Thus this Reference Sequence has a negative effect on the formation of the exon definition complex. The values obtained for c_E, c_R, c_SF, c_SI, and c_SL correspond to small incremental changes in threshold energies, explaining why multiple elements are required to effect large changes in psi.

K_i is a catch-all constant in Equation 7 that notably includes the effect of SS “strength.” SS Set 3 differs from Set 5 by only a single base in the 3′SS (see Table 1) and results in a 2.8-fold increase in K_i. Set 5 differs from Set 7 by two bases in the 3′SS and results in a 7.1-fold increase in K_i. Differences in the 5′SS were found to be substantially greater. Set 2 differs from Set 7 by only a single base in the 5′SS yet results in a ∼250-fold increase in K_i. The greater effect of the 5′SS suggests a more critical role of its sequence, as has been suggested before (Xiao et al. 2007).

Finally, T and C in Equation 6 provide an indication of the contributions of the pre-τ and the post-τ phases. The value for T represents the commitment to inclusion that takes place even before the third exon is synthesized while the value for C models the period after the third exon becomes available. As shown in Table 3, C is several orders of magnitude smaller than T, implying that by the time competition becomes possible, essentially no additional molecules commit to inclusion (i.e., all remaining molecules will skip exon 2). Indeed, setting C = 0 does not change the performance of the model (data not shown). This surprising result could be due to an unexplained relative weakness of these DEs compared with the downstream exon; or, more intriguingly, to a mechanism that was not considered when conceiving the model: that there is a restricted window of commitment time that is shorter than τ. Consequently, molecules that have not committed to inclusion within this window of time can no longer do so; paradoxically, they are, by default, “committed” to skipping even before the downstream exon is synthesized. The transcription time to the synthesis of the downstream exon here is only a matter of seconds, a time much shorter than the several minutes required for the splicing reaction itself (Kessler et al. 1993; Singh and Padgett 2009; Wada et al. 2009). Thus most of the time spent before the spliced product is formed is spent after the commitment step has been taken. A short commitment time might be dictated by the time an uncommitted exon with an exon definition complex can be captured by a putative hub bearing a committed upstream exon. If the hub is associated with the CTD of the RNA polymerase II, this time might be related to the time at which transcription of the downstream intron places the exon too far away to ensure a collision of the exon definition complex and the CTD. Four regimens can then be defined: the time involved in exon definition complex formation, which should be in the order of submilliseconds (Hyeon and Thirumalai 2012); the time required for commitment, seconds (as suggested in this paper); the time required to generate the spliced product, a few minutes (Kessler et al. 1993; Singh and Padgett 2009; Wada et al. 2009); and the time required to generate the final mRNA molecule, up to several hours.

MATERIALS AND METHODS

DE minigene construction

Detailed descriptions can be found in Supplemental Material. In outline, DEs were constructed by the sequential ligation of 32-mers comprised of two 16-mer units: RR, RE, ER, EE, RS, SR, and SS. These units were assembled in a “drafting” plasmid, using type IIS restriction sites flanking a central CCAAACA sequence, which is most of the R sequence. The finished DEs were cloned into a series of “receiving” plasmids that differed principally in their SS sequences. Each receiving plasmid contained a modified dhfr minigene controlled by a tet-responsive promoter and a SV40 poly(A) site; a start codon (a Kozak sequence), was placed in exon 3. Each receiving plasmid had a specific SS set and, in place of a DE, a specifically designed removable sequence/adapter: RA. Using BveI (Fermentas), this RA was removed, generating appropriate overhangs for seamless incorporation of the DEs constructed in the drafting plasmid.

The plasmid used in the generation of the cell line used for chromosomal incorporations, pMA-FW, contains a kanamycin resistance gene for initial selection, a promoterless puromycin resistance gene for subsequent selection of site-specific recombinations with DE-containing plasmids, a φC31 attP site and only the downstream portion of the modified dhfr minigene (including the last exon only). A single copy transfectant of HEK293 cells carrying a single integrated copy of this plasmid with the attP sequence as a site-specific target was then isolated. pMA-IC contains an attB site for site-specific recombination, a CMV promoter to drive the puromycin resistance gene after site-specific recombination, and the upstream half of the modified dhfr minigene for reconstitution of the full minigene (Supplemental Fig. S10; see Supplemental Material). Versions of this plasmid constructed with different DEs as exon 2 allowed the isolation of transfectant HEK293 populations carrying minigenes with different DEs.

QPCR measurements were calibrated using plasmids containing both an exon-included and an exon-skipped sequence. These coupled-standard plasmids were generated by incorporating cDNA for DE-skipped mRNA and either γ actin mRNA or mRNA that included a DE in the same plasmid. Purified plasmid was digested with EcoO109I (NEB) to generate a solution with equimolar amounts of each type of molecule. This solution provided a standard for relative quantification through QPCR. Included-skipped equimolar coupled-standards were used to calibrate the psi measurements, while actin coupled-standards allow a measurement of relative expression levels. (Supplemental Fig. S11; see Supplemental Material for details). End point PCRs were carried out in many cases; quantification of representative ethidium-stained agarose gels using Image J can be seen in Supplemental Fig. S12. These results were as expected from the RT-QPCR measurements.

Psi measurement

RNA was extracted from transfected cells and reverse transcribed. Serial dilutions of the equimolar coupled-standard were used for QPCR quantification and the ratio of DE-skipped to DE-included was obtained (S/I, or SOI). This ratio was used to obtain psi by the formula psi = 100/(1 + SOI). A similar protocol was followed for stable transfections including γ actin quantification (see Supplemental Material).

Transfection

Transient transfections were performed in modified HEK293 cells carrying a tTA gene (cMA-HEK293-tTA). RNA was extracted after 25 h. Stable transfections were performed in cMA-FW cells using a DE-containing pMA-IC plasmid and the plasmid coding for the site-specific recombinase pPGKPhiC31obpA (Addgene). After puromycin selection, the resulting site-specific recombinants were pooled and grown for RNA extraction (see Supplemental Material).

Cell lines

HEK293 cells were stably transfected with a plasmid coding for the tet-Off trans-activator (Gossen and Bujard 1992). A clone, cMA-HEK293-tTA, was chosen and used for all transient transfections. cMA-HEK293-tTA cells were electroporated using linearized pMA-FW plasmid. Clone cMA-FW was selected as one that had incorporated a single genomic copy of pMA-FW, had a high level of expression and showed an adequate level of site-specific recombination. This clone was used for all site-specific recombinations (see Supplemental Material).

Parameter optimization

The BFGS algorithm was adapted from Press et al. (2007), implementing walls to force all parameters to be nonnegative and using explicit gradient. A script was written in Perl for minimizing the sum of the squared differences between observed and predicted pso (Equations 6 and 7; see Supplemental Material).

CISBP survey

To associate an RNA binding protein to heptamers within the Reference Sequence we downloaded the binding intensity z-scores from the CISBP Website (Ray et al. 2013) and used a cutoff of 4.6 as a minimum z-score.

SUPPLEMENTAL MATERIAL

Supplemental material is available for this article.