A model-based reconstruction for undersampled radial spin echo DTI with variational penalties on the diffusion tensor

Abstract

Radial spin echo diffusion imaging allows motion-robust imaging of tissues with very low T2 values like articular cartilage with high spatial resolution and signal-to-noise ratio (SNR). However, in vivo measurements are challenging due to the significantly slower data acquisition speed of spin-echo sequences and the less efficient k-space coverage of radial sampling, which raises the demand for accelerated protocols by means of undersampling. This work introduces a new reconstruction approach for undersampled DTI. A model-based reconstruction implicitly exploits redundancies in the diffusion weighted images by reducing the number of unknowns in the optimization problem and compressed sensing is performed directly in the target quantitative domain by imposing a Total Variation (TV) constraint on the elements of the diffusion tensor. Experiments were performed for an anisotropic phantom and the knee and brain of healthy volunteers (3 and 2 volunteers, respectively). Evaluation of the new approach was conducted by comparing the results to reconstructions performed with gridding, combined parallel imaging and compressed sensing, and a recently proposed model-based approach. The experiments demonstrated improvement in terms of reduction of noise and streaking artifacts in the quantitative parameter maps as well as a reduction of angular dispersion of the primary eigenvector when using the proposed method, without introducing systematic errors into the maps. This may enable an essential reduction of the acquisition time in radial spin echo diffusion tensor imaging without degrading parameter quantification and/or SNR.

Introduction

Diffusion tensor imaging (DTI) provides insight into the amount of water diffusion anisotropy caused by oriented micro-structural barriers in the tissue. Thus DTI provides unique quantitative sensitivity in vivo to microscopic tissue integrity and function (1). In the anisotropic Gaussian diffusion model used in DTI, the diffusion properties in each voxel are described by a rank-2 symmetric diffusion tensor. Accurate measurement of the components of the diffusion tensor requires repeated acquisitions with different diffusion weightings and diffusion-encoding directions. Consequently, fast acquisition techniques such as the single shot EPI are widely used to acquire enough diffusion directions with reduced acquisition time. However, EPI has limited applicability in musculoskeletal (MSK) applications due to its sensitivity to off-resonance and the demands for high resolution. A paramount example of musculoskeletal applications where high resolution (≤0.7 mm) is needed is DTI of articular cartilage (≈4 mm in its thickest regions).

Assessment of the integrity of articular cartilage is considered key for the early diagnosis of osteoarthritis (OA). A comprehensive assessment of the cartilage matrix involves assessment of the two major components of the solid matrix of the cartilage: Proteoglycan content and collagen structure. Articular cartilage can stimulate proteoglycan synthesis but has very limited ability to repair damaged collagen, so changes in collagen are believed to be an indication of irreversibility (2, 3). While many MRI biomarkers have focus on the assessment of the proteoglycan content (e.g. sodium imaging (4), delayed Gadolinium enhanced MRI of articular cartilage (dGEMRIC) (5) or glycosaminoglycan chemical exchange saturation transfer imaging (gagCEST) (6)), only a partial evaluation of the collagen structure is possible with the existing biomarkers (T2 relaxation time (7) and the magnetization transfer (8)).

DTI of articular cartilage has been proposed as a biomarker for both proteoglycan (PG) content and collagen architecture (9). The key idea behind the use of DTI is that the various components of the cartilage matrix have different effects on the motion of water molecules. The collagen network favors the motion of water along the collagen fibers inducing anisotropy in the motion of water, which can be measured with fractional anisotropy (FA) (10–14). PG molecules, on the other hand, do not show a preferred orientation and therefore restrict the motion of water molecules equally in all directions. Thus, PG content only affects the mean diffusivity (MD) (11–15). Measurement of diffusion is also interesting from the physiological point of view, because diffusion is an essential mechanism for mechanical function of articular cartilage and for the transport of nutrients to the chondrocytes and for the removal of their metabolic waste product.

Ex vivo studies of DTI of articular cartilage have shown potential to assesses early cartilage damage with accuracy of 95%, and grade cartilage damage with accuracy of 75% using histology as a gold standard (16). First in vivo clinical studies have shown great promise of DTI for the early detection of osteoarthritis (17, 18). In particular, DTI showed an accuracy of 92% to detect changes on cartilage with unspecific changes in clinical images (17). However, these first clinical studies were performed at high field (7 T) using dedicated coils. Therefore there is a need for DTI methods to acquire high-quality diffusion measurements for articular cartilage.

Measurement of DTI of articular cartilage in vivo in clinical scanners is technically challenging due to the short T2 relaxation times (≈40 ms) and the submilimetric resolution required to resolve the cartilage anatomy (≈0.6 mm). Therefore, standard single-shot sequences like diffusion-weighted echo planar imaging (EPI) fail to deliver adequate image quality (18). To overcome these problems we have recently introduced a radial spin-echo diffusion tensor imaging (RAISED) sequence (16,19). The high SNR efficiency of spin echo sequences makes them specially suitable for the measurement of diffusion on a short-T2 tissue like articular cartilage. However, spin-echo sequences have intrinsically slow data acquisition rates, which typically results in very long acquisition times. The radial acquisition of the RAISED sequence is ideally suited for high undersampling of the data, so that the acquisition can be performed within the typical clinical scanning times.

Undersampled data acquisition is a well established principle to accelerate measurement time. However, due to the violation of the sampling theorem, this leads to aliasing artifacts when a conventional reconstruction technique is used. Parallel imaging (PI) (20–22) is one known way to address this issue, and was already used successfully in diffusion imaging (23). Another technique to reconstruct images from undersampled data is compressed sensing (CS), which has gained much popularity in recent years (24, 25). CS can also be combined with PI to achieve higher acceleration factors (e.g. (26–30)). However, it is also well known that the performance of CS is limited in cases where the fully sampled image already has low SNR, because noise compromises the ability of CS to separate between compressible ”true” image content and incoherent aliasing (25, 31). This makes the application of CS to diffusion-weighted imaging (DWI) challenging since diffusion-weighted images inherently have lower SNR. However, DTI has the advantage of a well defined signal model, which can be added to the CS framework in the form of a modelbased reconstruction. This concept was first applied for relaxometry (32-37). Both compressed sensing (38-40) and model-based reconstruction (41) were recently applied to reduce the measurement time of diffusion acquisitions as well. In addition, we recently demonstrated in related work on denoising that improved DTI maps can be obtained by performing nonlinear regularization directly in the domain of the diffusion tensor, instead of denoising the diffusion-weighted images followed by calculating tensor maps from denoised images (42).

In this work, we introduce a new image reconstruction technique for DTI which combines the concepts of PI, model based reconstruction and CS. An l1-norm-based sparsifying transform is used directly in the target quantitative domain, given by the elements of the diffusion tensor. Evaluation was performed by comparing the results to reconstructions from gridding, combined parallel imaging and compressed sensing, and a recently proposed model-based approach (41) both in terms of image quality and in terms of reliability of the quantitative values for phantom, MSK and brain applications.

Matlab source code for the method, along with sample data, will be provided on our website and on request ¹.

Methods

Theory of model based reconstruction and CS

The basic optimization problem for a combined CS-PI reconstruction of diffusionweighted images (prior to the inclusion of a specific diffusion model, which we will introduce below) can be written as follows:

$$F(x)={\sum _{n=1}^N\Vert E_n(x_n)-y_n\Vert }_2^2+{\alpha }_n{\Vert \mathrm{\Psi }{x}_n\Vert }_1.$$ [1]

In Eq. 1, E_n is the forward sampling operator for the nth diffusion-weighted image x_n, y_n is the corresponding k-space data and Ψ is a transform that promotes sparsity in a certain domain. Finite differences were used as the sparsifying transform in this work, which is equivalent to total-variation (TV) minimization (43). This choice was motivated by the favorable properties of TV when combined with radial sampling trajectories (25), but in principle an arbitrary transform can be used. N is the number of diffusion-weighted images. In the case of non-Cartesian imaging, E_n is comprised of multiplication by the coil sensitivity profile followed by a non-uniform fast Fourier transform (NUFFT) (44) along the particular sampling trajectory of the nth diffusion-weighted image. α > 0 is the regularization parameter. As signal intensities of the different x_n change depending on the b-values used and the signal values of the individual directions must be preserved with respect to each other, a proper balance of the two terms in Eq. 1 has to be ensured. This is achieved by scaling α by the ratio of the norm of the I₀ image to the norm of the diffusion-weighted images $({\alpha }_n=\alpha \frac{{\Vert x_n\Vert }_2}{{\Vert x_{I_0}\Vert }_2})$. This ensures proper balancing of the individual contributions to the sum in Eq. 1. Note that this scaling is only done once before the actual initialization of the iterative algorithm, using the signal values of the regridding reconstruction. In the DTI framework, the diffusion properties of the tissue are characterized by the diffusion tensor D, which is a rank-2 symmetric tensor:

$$D=\left(\begin{array}{ccc}{D}_{xx}& D_{xy}& D_{xz}\\ D_{xy}& D_{yy}& D_{yz}\\ D_{xz}& D_{yz}& D_{zz}\end{array}\right).$$ [2]

The tensor has 6 independent elements so that the minimum number of diffusionencoding directions N that must be acquired is 6. However, the estimation of the diffusion coefficients can be improved if more than 6 directions and more than a single b-value are acquired (45-47). This means that by directly reconstructing the tensor elements rather than proceeding through the intermediary of diffusionweighted images, the number of unknowns is reduced from N · n_x·n_y to 6 · n_x·n_y (n_x and n_y being the size of the grid the images are reconstructed to), resulting in an easier parameter-estimation problem (41,48). This step can also be seen as inherent compression by exploiting redundancies in the DWIs. The basic DTI signal model, which is integrated into the image reconstruction step in the proposed method, is given by:

$$x_n:=I_0{e}^{-b_n{\overrightarrow{g_n}}^{T}D\overrightarrow{g_n}}.$$ [3]

Here, I₀ is the non-diffusion-weighted image, x_n the diffusion-weighted image for diffusion-encoding direction n with diffusion weighting b_n and $\overrightarrow{g_n}$ its unitary direction vector. The extended forward operator Ẽ_n(D), which maps D to the k-space data of direction n, is then given by:

$$y_n={\stackrel{\sim }{E}}_n\left(D\right)=F{T}_n\left(I_0{e}^{-b_n{\overrightarrow{g_n}}^{T}D\overrightarrow{g_n}}{c}_n{e}^{-i{\mathrm{\Phi }}_n}\right).$$ [4]

A different NUFFT operator FT_n is applied for each diffusion direction, allowing the use of different k-space patterns for different directions. c_n is the complex coil sensitivity map for direction n, which must be estimated in a preprocessing step, and e^−iΦ_n describes phase errors due to macroscopic motion. For the purpose of iterative image reconstruction, the independent elements of the diffusion tensor D are written as a 6×1 vector [D_xx,D_yy,D_zz,D_xy,D_xz,D_yz]. This vector can also be extended to include images without diffusion weighting (I₀ images), which are then treated as unknowns as well. This extended form of the tensor is denoted by D̃. An extended version of the method recently presented in (41), adding iterative estimation of the I₀ image, arbitrary trajectories, phase correction and integration of coil sensitivities can therefore be formulated as follows:

$$\stackrel{\sim }{F}(\stackrel{\sim }{D})={\sum _{n=1}^N\Vert {\stackrel{\sim }{E}}_n(\stackrel{\sim }{D})-y_n\Vert }_2^2+{\alpha }_n{\Vert \mathrm{\Psi }{x}_n\Vert }_1.$$ [5]

Finally, a model-based optimization problem with regularization of the elements of D̃ can be formulated as follows:

$$\stackrel{\sim }{F}(\stackrel{\sim }{D})={\sum _{n=1}^N\Vert {\stackrel{\sim }{E}}_n(\stackrel{\sim }{D})-y_n\Vert }_2^2+\sum _{i=1}^{N_D}{\alpha }_i{\Vert \mathrm{\Psi }{\stackrel{\sim }{D}}_i\Vert }_1.$$ [6]

in both Eqs. 5 and 6 the first term evaluates the data fidelity of the current estimate, where the operator Ẽ_n maps the current estimate of the extended diffusion tensor to the corresponding k-space data y_n of the diffusion-weighted image x_n. i indexes the element of the unknown vector D̃. Identical to Eq. 1, α_i in Eq. 6 is scaled according to the norms of the signal intensities of the tensor elements generated from the gridding reconstruction $\left({\alpha }_i=\frac{{\Vert {\stackrel{\sim }{D}}_i^{\mathit{\text{grid}}}\Vert }_2}{{\Vert {\stackrel{\sim }{D}}_{N_D}^{\mathit{\text{grid}}}\Vert }_2}\right)$. Again, this means that the scaling is only done once before the initialization of the iterative algorithm. The numerical method that was chosen to minimize F̃ (D̃) is the gradient-descent (GD) algorithm:

$${\stackrel{\sim }{D}}_i^{k+1}={\stackrel{\sim }{D}}_i^k-t_i^k\frac{\partial \stackrel{\sim }{F}(\stackrel{\sim }{D})}{\partial {\stackrel{\sim }{D}}_i}$$ [7]

This very simple numerical scheme requires evaluation of the gradient of F̃ (D̃) with respect to D̃_i in each iteration step and updating of the individual elements of D̃_i according to the step sizes $t_i^k$.

Using the well-known relaxation for the l1-norm ${\Vert x\Vert }_1\approx \sqrt{x^{\ast }x+\mu }$ for a small μ > 0, it follows that $\frac{d{\Vert x\Vert }_1}{dx}\approx \frac{x}{\sqrt{x^{\ast }x+\mu }}$ (μ = 10^‒15 was used here). Following the derivations in (24,32,41) it can be shown that the gradient with respect to a specific element of the diffusion tensor is (* denoting the adjoint in equations 8 and 9):

$$\frac{\partial \stackrel{\sim }{F}(\stackrel{\sim }{D})}{\partial {\stackrel{\sim }{D}}_i}\approx \sum _{n=1}^N-2b{({\overrightarrow{g_n}}^T\overrightarrow{g_n})}_i{I}_0{e}^{-b_n{\overrightarrow{g_n}}^T\stackrel{\sim }{D}\overrightarrow{g_n}}\mathit{\text{Re}}\left\{c_n^{\ast }{e}^{i{\mathrm{\Phi }}_n}F{T}_n^{\ast }({\stackrel{\sim }{E}}_n(\stackrel{\sim }{D})-y_n)\right\}+{\alpha }_i{\mathrm{\Psi }}^{\ast }\frac{\mathrm{\Psi }{\stackrel{\sim }{D}}_i}{\sqrt{(\mathrm{\Psi }{\stackrel{\sim }{D}}_i)\ast (\mathrm{\Psi }{\stackrel{\sim }{D}}_i)+\mu }}.$$ [8]

The gradient with respect to the non-diffusion-weighted images is:

$$\frac{\partial \stackrel{\sim }{F}(\stackrel{\sim }{D})}{\partial {\stackrel{\sim }{D}}_{I_0}}\approx \sum _{n=1}^{N}2e^{-b_n{\overrightarrow{g_n}}^T\stackrel{\sim }{D}\overrightarrow{g_n}}\mathit{\text{Re}}\left\{c_n^{\ast }{e}^{i{\mathrm{\Phi }}_n}F{T}_n^{\ast }({\stackrel{\sim }{E}}_n(\stackrel{\sim }{D})-y_n)\right\}+{\alpha }_i{\mathrm{\Psi }}^{\ast }\frac{\mathrm{\Psi }{\stackrel{\sim }{D}}_i}{\sqrt{(\mathrm{\Psi }{\stackrel{\sim }{D}}_i)\ast (\mathrm{\Psi }{\stackrel{\sim }{D}}_i)+\mu }}.$$ [9]

The gradient used in the gradient descent update step in Eq. 7 is then comprised of N_D elements. In particular, if a single non-diffusion weighted image is aquired, 6 elements of the diffusion tensor, plus one non-diffusion weighted image. A single update step therefore consists of a simultaneous update of both the tensor elements and the I ₀ image. One issue of first-order methods such as GD is that the scaling of the gradients during the optimization can be poor. This is also true here when comparing the gradients of the tensor elements and the I₀ image, but it was also described for applications in relaxometry (32,34,36,37). This can lead to the need for a prohibitively large number of iterations. A workaround in our implementation is to scale the step-sizes of the iterations with the inverse of the norm of the individual gradients, leading to an adaptive step-size for gradient direction i and iteration number $k:t_i^k=\frac{t}{{\Vert {\stackrel{\sim }{D}}_i^k\Vert }_2}$.

Data acquisition and image reconstruction

Data acquisition for this work was performed on a clinical 3T scanner (MAGNETOM Skyra, Siemens Healthcare, Erlangen, Germany) with a diffusion-weighted radial spin-echo sequence (RAISED), which has been developed for DTI of articular cartilage (16,49). The RAISED sequence is a spin-echo sequence with a radial acquisition of k-space. Every diffusion-weighted image is acquired with a different set of radial trajectories, thus providing an overall less undersampled k-space over all b-values. It is a multi-slice sequence that excites all slices interleaved within the TR. To avoid slice cross-talk diffusion-weighting of of each slice is alternated within the TR, so that two consecutive slices never have the same diffusion-weighting. Spokes were equally distributed, go from $-k_r^{\mathit{\text{max}}}$ to $k_r^{\mathit{\text{max}}}$ and the polarity of the readout direction is alternated between successive spokes to improve the robustness of the sequence to residual off-resonant frequencies (e.g. residual fat signal). If the angle shift between two spokes is δ, the spokes were acquired with angles: 0, π + δ, 2δ, π + 3δ… Finally, each diffusion-weighted image is acquired with a different set of angles to provide optimal sampling of the outer part of k-space. We rotated the trajectory of each diffusion-weighted images by the angle δ(n - 1)/N_D (n denoting one individual diffusion weighting and N_D the total number of diffusion weightings), so that all spokes of all diffusion weighted images were equally distributed in the k-space with a gap of δ/N_D degrees.

Radial sequences are robust against macroscopic motion, however the diffusion sensitizing gradients induce phase inconsistencies that need to be corrected to produce high-quality images. Thus, the RAISED sequence includes a 2D low-resolution EPI motion-correction navigator acquired after each readout after refocusing the magnetization. The EPI readout is performed on a Cartesian grid with a matrix resolution of 32×32, a monopolar readout to avoid N/2 ghosting, partial Fourier of 5/8 and echo spacing of 5 ms.

For the forward operator we calculated the images as described by Miller et al. (50). 2D phase navigator maps were constructed separately for each spoke and channel of the receive-coil array. These phase maps were subtracted from the 2D back-projection of the corresponding spoke in each channel. The final images for each channel were calculated as the sum of all phase-corrected back-projections (50). All channels were combined using sum of squares. In the backward operator for each spoke and channel we added the Navigator phase to our image estimation and den multiply by the coil sensitivity, and then applied the FFT operator,

All reconstructions were carried out offline using Matlab (R2012b, The Math-Works Inc., Natick, MA, USA) implementations of four different reconstruction methods:

1. Conventional gridding using the NUFFT implementation from (44) and the phase correction approach described above.

2. A combined PI and CS reconstruction on the individual diffusion-weighted images (denoted as PI-CS DWI in the following sections), as described in Eq. 1.

3. A multi-coil, non-Cartesian version of (41). In addition, optimization of the I ₀ image, which was kept constant in (41) because it was fully sampled, is performed in the image reconstruction step as well, as described in Eq. 5. As this method utilizes a model-based reconstruction but applies the sparsifying transform on the diffusion-weighted images, it is denoted as Model DWI.

4. The proposed model-based approach with application of the sparsifying transform directly on the elements of the diffusion tensor (Eq. 6), denoted as Model DTI.

While all diffusion-weighted images were treated as a single dataset for the purpose of image reconstruction, the sparsifying transform was only applied in 2D, which means that no joint sparsity over the diffusion-encoding directions was enforced (see discussion for more details). The parameters of the GD algorithm were a starting step-size of t = 10^‒4 and 100 iterations. All three methods require determination of a regularization parameter, as is the case for almost all regularized or CS-based reconstruction methods. This parameter will depend on SNR, matrix size and sampling pattern, but once identified for a specific combination of sequence parameters can then usually kept constant in future examinations (24,25,29). In this study it was determined once for the different sequence parameters of the different experiments (matrix size, number of spokes) using exhaustive search, yielding values ranging from 5 ·10^‒5 to 3 · 10^‒4 (PI-CS DWI), 1 · 10^‒2 to 3 · 10^‒2 (Model DWI) and 1 · 10^‒3 to 3 · 10^‒3 (Model DTI). Once identified, these values were kept constant for the same type of acquisition. To estimate coil-sensitivity maps, reconstructions were performed using quadratic regularization on the gradient, followed by convolution with a smoothing kernel. These reconstructions were then divided by the sum of squares image, yielding a method that is fully autocalibrated and uses only the acquired DTI dataset to estimate the corresponding sensitivity map (25,29).

Image analysis and statistical evaluations

From the diffusion tensor, the mean diffusivity (MD) and the fractional anisotropy (FA) were calculated according to standard formulae: MD = (λ₁ + λ₂ + λ₃)/3, $FA=\sqrt{\frac{3}{2}}\frac{\sqrt{{({\lambda }_1-MD)}^2+{({\lambda }_2-MD)}^2+{({\lambda }_3-MD)}^2}}{\sqrt{{\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2}}$. In the case of the phantom measurements, the angular dispersion of the principal eigenvector was analyzed in the anisotropic region. For each different reconstruction method, the mean of all vectors was calculated, followed by a calculation of the dispersion angle θ to the mean vector. A region-of-interest (ROI) analysis was performed by calculating means and standard deviations in selected ROIs. Additional statistical evaluation was conducted for the phantom and brain experiments. Each nonlinear reconstruction was compared to the result given by gridding, but no comparisons of the individual methods with respect to each other (ANOVA) were performed. A Kolmogorov-Smirnov-test was performed to check for normal distribution of the samples in the ROI. If the data was normally distributed (p > 0.05) t- and F-tests were used to test for statistically significant differences of mean and variance. In cases when data was not normally distributed, the Wilcoxon-rank-sum-test and the Levene-test were used instead.

Phantom experiments

Measurements of an in-house built diffusion phantom consisting of polyethylene (Dyneema) fibers (51,52) at the center surrounded by water were performed with a 15 channel knee coil array. Sequence parameters were: TR=1500 ms, TE=39 ms, matrix=208×208, 61 spokes (corresponding to undersampling of $\frac{\pi }{2}\frac{208}{43}\approx 7.5$ at the edge of k-space $k_r^{\mathit{\text{max}}}$) with 416 samples along each readout, slice thickness=3 mm, 11 slices, b-values (200 and 400 s/mm²) and one single image with b-value 1 s/mm², in-plane resolution=0.7×0.7 mm², acquisition time t_acq=19:50 min, bandwidth=300 Hz/pixel, 6 diffusion-encoding directions for each b-value optimized with the downhill simplex algorithm (45), diffusion time=20 ms, duration of the diffusion gradients=17 ms, maximum gradient strength=39 mT/m. Data was acquired in axial, coronal and oblique at a 45 degree angle with respect to the anisotropic fiber bundle. A schematic drawing of the phantom, also indicating the three orientations where data was acquired, is presented in Fig. 1b.

Figure 1.

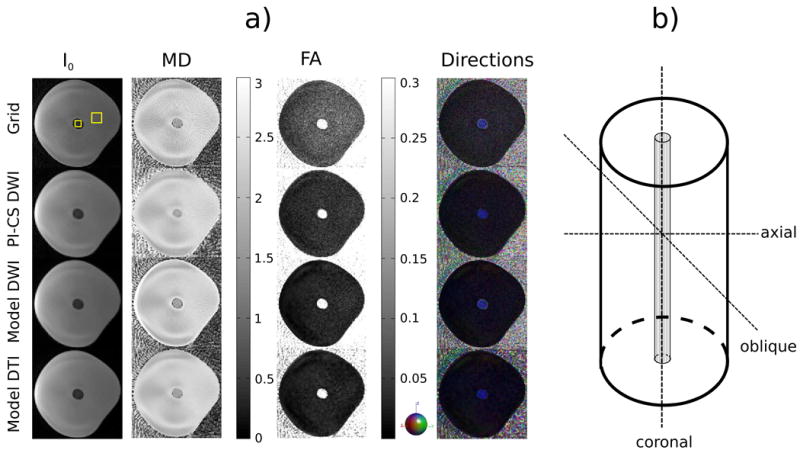
a) Axial I₀ image and maps of MD, FA and the color coded direction of the principal eigenvector of the phantom measurement with 61 spokes, two b-values and 6 diffusion-encoding directions for conventional gridding (Grid, first row), combined PI and CS on the diffusion-weighted images (PI-CS DWI, second row), model-based reconstruction with TV regularization of the diffusion-weighted images (Model DWI, third row) and model-based reconstruction with TV regularization of the tensor elements (Model DTI, fourth row). The ROIs used for the analysis in Table 1 are highlighted in the gridding reconstruction of the I₀ image. b) Schematic of the phantom. The orientations where data was acquired are shown as dashed lines. The Dyneema fibers are located at the center of the phantom and are responsible for the anisotropy in the central region of the images in a.

In-vivo experiments

Scans of the right knee and the brain of healthy volunteers (3 and 2 volunteers, respectively) were performed with a 15-channel knee coil array and the 16 head channels of a 20-channel head/neck coil array using the RAISED sequence. All measurements were approved by the institutional review board. The subjects provided written informed consent. Again 6 directions were used for each b-value, diffusion time=20 ms, duration of the diffusion gradients=17 ms and maximum gradient strength was 39 mT/m.

Scans of the right knee were performed with TE=39ms, b-values 150, 300 s/mm² and one single image with b-value 1 s/mm², matrix=208×208 and resolution=0.74×0.74 mm². 208 and 70 radial spokes (undersampling of $\frac{\pi }{2}\frac{208}{70}\approx 4.7$ at $k_r^{\mathit{\text{max}}}$) were acquired with 416 samples along each readout with slice thickness=3 mm and 11 slices. Scantime for the 208 spokes acquisition was 67:27 min and 22:42 min for 70 spokes. The goal of the 208 spokes acquisition was to serve as a reference measurements against which the undersampled acquisition could be compared. ROIs were manually drawn on the I₀ image around the femoral cartilage, tibial cartilage, and two sections of calf muscle tissue. A second experiment was designed to compare the performance of the individual reconstruction methods when using a different number of diffusion directions. Acquisitions were performed with 6 (t_acq=10:39 min) and 30 directions (t_acq=52:23 min) using a b-value of 300 s/mm².

For reference, acquisitions were also performed in the brain using the following protocol: TE=60 ms, b-value (1000 s/mm²) and one single image with b-value 1 s/mm², matrix= 196×196, resolution=1×1 mm² and 75 radial spokes (undersampling of $\frac{\pi }{2}\frac{196}{75}\approx 4.1$ at $k_r^{\mathit{\text{max}}}$) and acquisition time t_acq=15:46 min. A slice thickness of 3 mm with 11 slices was used and ROIs were manually drawn on the FA map in the splenum of the corpus callosum (high FA) and bilateral cortical gray matter (low FA). Mean values and standard deviations of DTI metrics within these ROIs were computed for each of the 4 reconstruction schemes.

It should be noted that the RAISED sequence is a multi-slice sequence. With the TR of 1500 ms used in our acquisitions a maximum of 21 slices can be acquired without additional increase in the scanning time. We chose a protocol with 11 slices to have representative slices from all knee cartilage regions.

Results

Phantom experiments

Figure 1 shows the I₀ image, MD, FA, and the color-coded direction of the principal eigenvector of the anisotropy-phantom measurement in axial direction with 61 spokes, two b-values for the reconstruction approaches described in the methods section (Gridding, PI-CS, Model DWI and Model DTI). In the case of I ₀ and especially MD, a noticeable reduction of streaking artifacts can be observed for all nonlinear reconstruction methods when compared to conventional gridding. FA and the color-coded directions show a pronounced reduction of noise, which is strongest in the two model-based approaches while still maintaining a sharper appearance of MD in comparison to PI-CS. It can also be observed that none of the nonlinear methods introduce a systematic error with respect to the direction of the principal eigenvector. The through-slice orientation of the polyethylene fibers, encoded in blue color, is preserved equally well for all reconstruction methods.

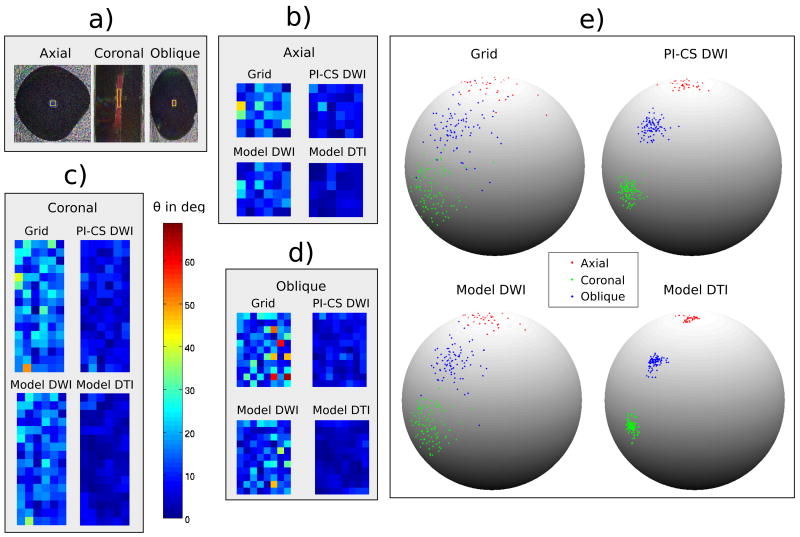
Figure 2 illustrates the dispersion of the principal eigenvector in the anisotropic region of the phantom for the three different scan orientations indicated in the schematic in Figure 1b (axial, coronal, oblique at a 45 degree angle with respect to the anisotropic fibers). The specific anisotropic ROIs where the dispersion analysis was performed are shown in subfigure a. The mean of all vectors in the ROI was calculated and the pixel wise deviation from the mean is plotted color coded in subfigures b, c and d for all reconstruction methods. Subfigure e is a 3D graphical illustration of the dispersion of the eigenvectors on a sphere.

Figure 2.

Dispersion of the principal eigenvector in the anisotropic region of the phantom for three different orientations (axial, coronal and oblique at a 45 degree angle with respect to the anisotropic fibers). While all nonlinear methods show a clear reduction of dispersion the effect is strongest for the proposed Model DTI approach. This behavior is consistent over the different orientations of the anisotropy. a) Color coded direction of the principal eigenvector for the three different orientations. b,c,d) Color coded deviations of the dispersion angle θ to the mean of all vectors in the ROI in degrees. e) Illustration of the dispersion of the eigenvectors in the ROIs.

While all nonlinear methods show a clear reduction of dispersion the effect is strongest for the proposed Model DTI approach. This behavior is consistent over the different orientations of the anisotropy.

The results of the ROI analysis in the highlighted regions in Figs. 1 and 2 are shown in Table 1. The number of voxels was 256 for the isotropic, and 36 for the anisotropic region. It can be observed that the values of MD are very consistent when comparing the different reconstruction methods and corresponds to a temperature of 23 °C (53), which was the room temperature in our scanner suite. The exception here is the PI-CS reconstruction, which exhibits a higher MD value. Given the homogeneous nature of the phantom, it is not surprising that all non-linear reconstructions showed a significant reduction of the standard deviation of MD as compared to gridding, which indicates reduction of noise and streaking artifacts due to undersampling.

Table 1.

ROI analysis of MD, FA and angular dispersion θ of the first eigenvector for the phantom measurements¹. See Fig. 1 for the ROIs used. t: t-test, F: F-test. p-values that are bold faced are statistically different from gridding (p < 0.05).

	Isotropic		Anisotropic
	Mean ± Std	p-values	Mean ± Std	p-values
MD Grid	2.33 ± 0.13	-	1.67 ± 0.22	-
MD PI-CS DWI	2.36 ± 0.05	t: < 10–3, F: < 10–15	1.75 ± 0.09	t: 0.03, F: < 10–6
MD Model DWI	2.32 ± 0.07	t: 0.46, F: < 10–15	1.68 ± 0.17	t: 0.75, F: 0.11
MD Model DTI	2.32 ± 0.03	t: 0.15, F: < 10–15	1.66 ± 0.05	t: 0.75, F: < 10–12
FA Grid	0.10 ± 0.03	-	0.36 ± 0.08	-
FA PI-CS DWI	0.04 ± 0.01	t: < 10–15, F: < 10–15	0.32 ± 0.04	t: < 0.01, F: < 10‒5
FA Model DWI	0.04 ± 0.01	t: < 10–15, F: < 10–15	0.32 ± 0.05	t: 0.01, F: < 0.01
FA Model DTI	0.03 ± 0.01	t: < 10–15, F: < 10–15	0.31 ± 0.02	t: < 10–4, F: < 10–10
θ Grid			14.93 ± 9.35	-
θ PI-CS DWI			7.20 ± 4.22	t: < 10–4, F: < 10–5
θ Model DWI			10.4 ± 6.32	t: 0.02, F: 0.02
θ Model DTI			4.14 ± 2.63	t: < 10–8, F: < 10–10

¹MD values are given in units of μ m²/ ms. FA values are dimensionless. Angular dispersion θ of first eigenvector is given in degrees.

The trend is similar for FA. For isotropic diffusion of free water an FA value of 0 is the physical expectation. Deviations from this value can be attributed to noise and aliasing artifacts and there is a significant reduction of both mean values and standard deviations for FA for all nonlinear methods. In the ROI defined over the anisotropic fibers significant reductions of both mean values and standard deviations of FA can be observed as well. All methods show significant reductions of the angular dispersion of the principal eigenvector (θ). Model DTI yields the lowest dispersions in comparison to all other methods.

In-vivo experiments

Figure 3 shows the reconstructions from a single sagittal slice visualizing the cartilage around the distal femur and tibial plateau of the right knee of a healthy volunteer. Gridding reconstructions are presented for both the 208 and the 70 spokes acquisition, as well as nonlinear reconstructions in the case of 70 spokes. Table 2 presents the corresponding values from the ROI analysis. The number of voxels was around 500 in the cartilage ROI and 850 in the two muscle regions. All nonlinear reconstructions show a reduction of streaking artifacts and noise as well as increased contrast and reduced numerical values for FA which is more consistent with the 208 spokes acquisition than the regular gridding reconstruction from 70 spokes (see discussion for more details).

Figure 3.

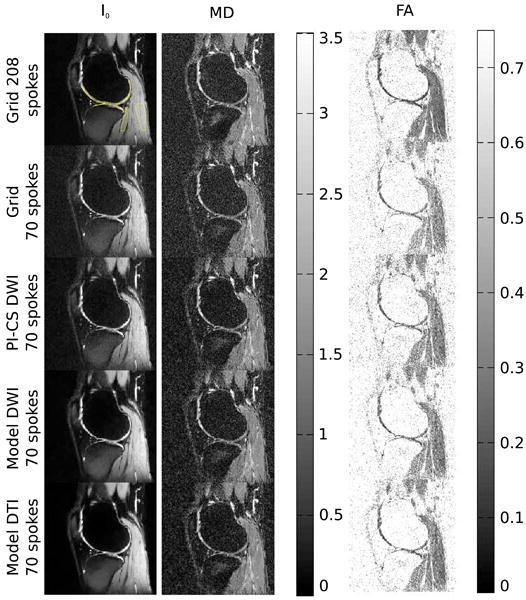
I₀ image and maps of MD and FA from measurements of the knee of a healthy volunteer with 208 and 70 spokes and two b-values for conventional gridding (Grid, first row 208 spokes, second row 70 spokes), combined PI and CS on the diffusion-weighted images (PI-CS DWI, third row), model-based reconstruction with TV of the diffusion-weighted images (Model DWI, fourth row) and model-based reconstruction with TV of the tensor elements (Model DTI, fifth row). The ROIs that were used for the evaluation of cartilage and muscle tissue in Table 2 are highlighted in the 208 spokes gridding reconstruction of the I₀ image.

Table 2.

ROI analysis of MD and FA of knee measurements¹. See text for details and figure 3 for the used ROIs.

	Cartilage	Muscle
	Mean ± Std	Mean ± Std
MD Grid 208 spokes	1.72 ± 0.45	1.70 ± 0.26
MD Grid 70 spokes	1.61 ± 0.47	1.62 ± 0.33
MD PI-CS DWI 70 spokes	1.61 ± 0.45	1.62 ± 0.28
MD Model DWI 70 spokes	1.57 ± 0.40	1.62 ± 0.25
MD Model DTI 70 spokes	1.54 ± 0.38	1.61 ± 0.22
FA Grid 208 spokes	0.25 ± 0.13	0.31 ± 0.11
FA Grid 70 spokes	0.41 ± 0.18	0.42 ± 0.15
FA PI-CS DWI 70 spokes	0.37 ± 0.17	0.37 ± 0.13
FA Model DWI 70 spokes	0.36 ± 0.17	0.37 ± 0.13
FA Model DTI 70 spokes	0.35 ± 0.16	0.35 ± 0.13

¹MD values are given in units of μm²/ ms. FA values are dimensionless.

Figure 4 shows the results from the comparison of 6 and 30 diffusion encoding directions and Table 3 presents the corresponding values from the ROI analysis in cartilage (≈500 voxels), two different muscle groups (≈900 and ≈500 voxels) and a small area of synovial fluid (≈50 voxels). Both model based approaches show a reduction of overall noise level in comparison to PI-CS. Quantitative evaluation displays stable MD values for the two model based methods. MD of PI-CS is increased, a finding that is in line with the phantom experiments. FA values again show the strongest trend of being decreased with Model-DTI. This effect is stronger for the 6 directions data, which is the more challenging experiment due to the significantly lower amount of data. It is worth noting that the FA values of Model-DTI with 6 directions are pronouncedly closed to the 30 directions results than those of all other methods. This effect can best be observed in synovial fluid with FA values of 0.12 ± 0.07 (30 directions gridding), 0.11 ± 0.07 (30 directions Model-DTI) and 0.13±0.05 (6 directions Model-DTI). In comparison, the values of the other methods are pronouncedly higher.

Figure 4.

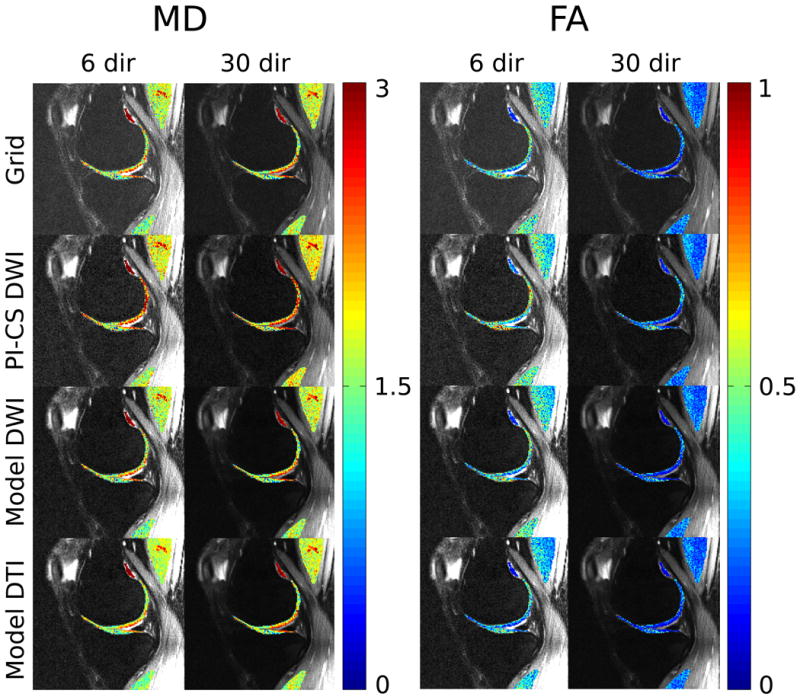
I₀ images with overlaid maps of MD and FA in cartilage and muscle from measurements of the knee of a healthy volunteer with 70 spokes using 6 and 30 directions for conventional gridding (Grid, first row), combined PI and CS on the diffusion-weighted images (PI-CS DWI, second row), model-based reconstruction with TV of the diffusion-weighted images (Model DWI, third row) and model-based reconstruction with TV of the tensor elements (Model DTI, fourth row). Quantitative values are presented in Table 3.

Table 3.

ROI analysis of MD and FA of knee measurements¹. See text for details and figure 4 for the used ROIs.

	Cartilage	Muscle 1	Muscle 2	Synovial fluid
	Mean ± Std	Mean ± Std	Mean ± Std	Mean ± Std
6 directions
MD Grid	1.77 ± 0.54	1.75 ± 0.39	1.51 ± 0.41	3.01 ± 0.23
MD PI-CS DWI	2.09 ± 0.61	1.89 ± 0.36	1.68 ± 0.38	3.24 ± 0.25
MD Model DWI	1.77 ± 0.54	1.75 ± 0.39	1.51 ± 0.41	3.01 ± 0.23
MD Model DTI	1.75 ± 0.44	1.75 ± 0.26	1.50 ± 0.26	2.96 ± 0.14
30 directions
MD Grid	1.78 ± 0.56	1.80 ± 0.35	1.65 ± 0.41	2.93 ± 0.35
MD PI-CS DWI	2.07 ± 0.60	1.93 ± 0.32	1.85 ± 0.35	3.08 ± 0.27
MD Model DWI	1.78 ± 0.56	1.80 ± 0.35	1.65 ± 0.40	2.93 ± 0.35
MD Model DTI	1.78 ± 0.53	1.80 ± 0.31	1.65 ± 0.36	2.92 ± 0.33
6 directions
FA Grid	0.42 ± 0.21	0.38 ± 0.14	0.47 ± 0.18	0.17 ± 0.06
FA PI-CS DWI	0.50 ± 0.23	0.40 ± 0.14	0.47 ± 0.15	0.24 ± 0.08
FA Model DWI	0.42 ± 0.21	0.38 ± 0.13	0.47 ± 0.18	0.17 ± 0.06
FA Model DTI	0.34 ± 0.17	0.31 ± 0.11	0.38 ± 0.13	0.13 ± 0.05
30 directions
FA Grid	0.24 ± 0.16	0.23 ± 0.08	0.26 ± 0.10	0.12 ± 0.07
FA PI-CS DWI	0.29 ± 0.19	0.24 ± 0.08	0.25 ± 0.09	0.16 ± 0.07
FA Model DWI	0.24 ± 0.16	0.23 ± 0.08	0.26 ± 0.10	0.12 ± 0.07
FA Model DTI	0.22 ± 0.16	0.23 ± 0.07	0.25 ± 0.09	0.11 ± 0.07

¹MD values are given in units of μm²/ ms. FA values are dimensionless.

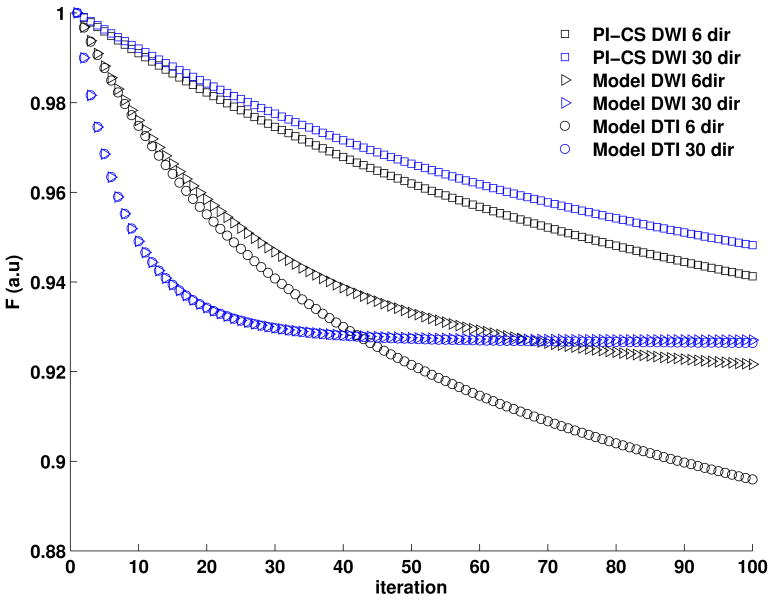
Figure 5 convergence plots of the different iterative reconstruction methods from Fig. 4. The convergence of Model-DWI and Model-DTI are very similar, and indicate proper convergence of the methods while convergence of PI-CS is slower. We did not observe a notable improvement in image quality with a higher number of iterations for PI-CS so we restricted the presented results to the same number of iterations for all three methods. It id interesting to note that the two model based methods converged faster for the 30 directions dataset than for the 6 directions dataset, while PI-CS did not show this effect.

Figure 5.

Convergence plots of the different iterative reconstruction methods from Fig. 4. The convergence of Model-DWI and Model-DTI are very similar, and indicate proper convergence of the methods while convergence of PI-CS is slower.

Figures 6 and 7 show reconstructions of a single mid-brain axial slice through the ventricles of a healthy volunteer. The most prominent effect is the reduction of noise in the FA map for the nonlinear reconstructions, which is highest for the two model-based methods. I₀ and MD show a reduction of streaking and ringing near the edges of the brain and a reduction of noise. PI-CS DWI and Model DTI show the same behavior in terms of preservation of fine details and sharp edges. In contrast, MD maps of Model DWI displays some degree of blurring and reduced detectability of fine structures.

Figure 6.

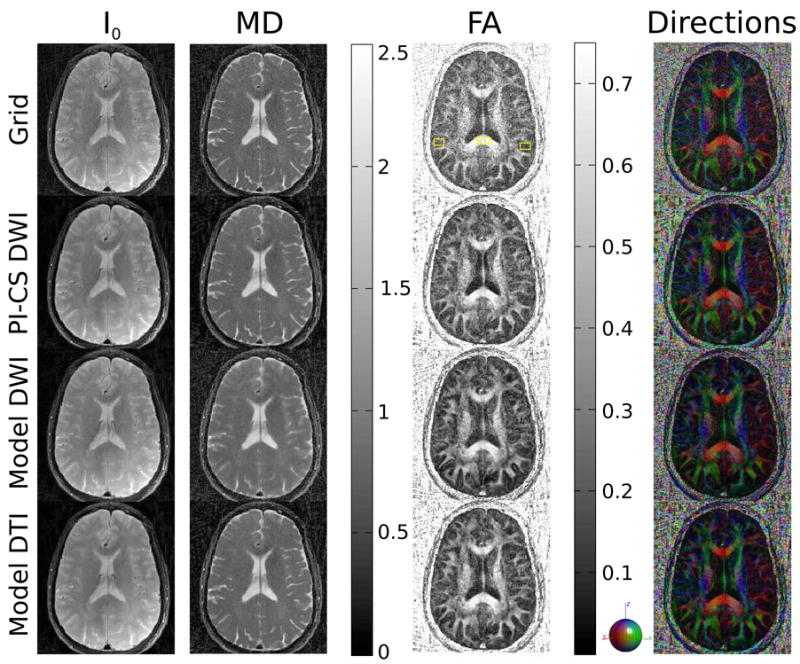
I₀ image and maps of MD, FA and the color coded direction of the principal eigenvector from 196-matrix 75 spokes brain measurements for conventional gridding (Grid, first row), combined PI and CS on the diffusion-weighted images (PI-CS DWI, second row), model-based reconstruction with TV of the diffusion-weighted images (Model DWI, third row) and model-based reconstruction with TV of the tensor elements (Model DTI, fourth row). The ROIs used for the analysis of the splenium of the corpus callosum and grey matter in Table 4 are highlighted in the gridding reconstruction of the FA map.

Figure 7.

An enlarged region from brain acquisitions in Figure 6. Note the pronounced reduction of noise in FA and direction color maps for all nonlinear reconstructions, which is strongest for the two model based methods. In the case of Model DWI this comes at the cost of blurring and a loss of fine details in the MD maps, an effect that does not occur in Model DTI.

ROI evaluations of the brain measurements are shown in Table 4. The number of voxels was ≈100 in the corpus callosum and ≈200 for the gray matter. MD values in both the corpus callosum and grey matter are very consistent for all reconstruction methods with the exception of Model DWI, which leads to an increase in MD. Similar to the results of the phantom measurements, FA is significantly decreased in gray matter, where the expected FA is lower, for all reconstructions. For white matter significant reductions of FA are only observed with model-DWI in comparison to gridding.

Table 4.

ROI analysis of MD and FA of the brain measurements¹. See text for details and Fig. 6 for the used ROIs. t: t-test, F: F-test, W: Wilcoxon-rank-sum test, L: Levene-test. p-value that are bold faced are statistically different from gridding (p < 0.05).

	Splenium CC		Grey Matter
	Mean ± Std	p-values	Mean ± Std	p-values
MD Grid	0.76 ± 0.10	-	1.02 ± 0.27	-
MD PI-CS DWI	0.76 ± 0.06	t: 0.95, F: < 10–5	1.02 ± 0.26	W: 0.93, L: 0.43
MD Model DWI	0.80 ± 0.06	t: < 10–3, F: < 10–5	1.04 ± 0.21	W: 0.04, L: < 10–3
MD Model DTI	0.76 ± 0.06	t: 0.82, F: < 10–5	1.02 ± 0.25	W: 0.86, L: 0.28
FA Grid	0.70 ± 0.09	-	0.24 ± 0.09	-
FA PI-CS DWI	0.67 ± 0.07	t: 0.04, F: < 10–2	0.21 ± 0.08	W: < 10–3, L: 0.14
FA Model DWI	0.63 ± 0.05	t: < 10–7, F: < 10–6	0.17 ± 0.08	W: < 10–15, L: 0.06
FA Model DTI	0.66 ± 0.06	t: < 10–2, F: < 10–3	0.18 ± 0.07	W: < 10–12, L: 0.01

¹MD values are given in units of μm²/ms. FA values are dimensionless.

With 100 GD iterations, we observed reconstruction times between 4 and 10 minutes for one slice of the different experiments on a regular desktop workstation (Intel Xeon X5647, 2.93GHz, 8 Cores, 12GB memory, Linux Kernel 3.5, Matlab 2012b 64 bit). Computation times dependent on matrix size, number of spokes, and number of receive channels but were nearly identical for the different reconstruction methods.

Discussion

The results of this work show that model-based nonlinear reconstruction with evaluation of the sparsifying transform directly in the domain of the the tensor elements outperforms conventional CS, applied to the individual diffusion-weighted images, in terms of the quality of the parameter maps for a range of different radial spin echo DTI experiments. This is in line with findings on retrospectively undersampled Cartesian fixed specimen data previously observed by Welsh et al. (41) and our own results from denoising (42). Our experiments did not show a risk of reduced accuracy of the DTI parameter maps when used with nonlinear reconstructions. However, in all reconstructions using (nonlinear) regularization or compressed sensing in general, there is a certain risk that small features are lost below the noise level if the acceleration is pushed too far that can not be recovered even though the reconstructed images appear to have a higher SNR. This potential problem is of course also present in the proposed method, but it is not unique to it.

In the case of isotropic diffusion of free water in the phantom, the value of 2.32 ± 0.03 μm²/ms corresponds well to the expected values for room temperature (53). The true FA is known to be zero, and model-based reconstruction methods lead to a statistically significant decrease in FA of free water from 0.10 ± 0.03 (gridding) to (CS-PI DWI and Model DWI) and 0.03 ±0.01 (Model DTI). This observed reduction likely reflects the lower residual streaking artifacts and noise in the nonlinear reconstructions, because MD is robust to noise while FA is easily biased in the presence of noise. The strongest improvements were seen for the dispersion of the principal eigenvector (Fig. 2). This result is also not surprising because this parameter is known to be most susceptible to changes in SNR.

For the in vivo experiments, interpretation of the results from the ROI analysis is less straightforward due to the lack of a standard reference. This is best observed when comparing the MD values of the 208 spokes vs. 70 spokes knee acquisitions. Due to the prolonged scantime of more than one hour in the 208 spokes case, some subject motion is inevitable even in the case of a healthy volunteer. This leads to residual phase inconsistencies that remain with the proposed phase correction scheme. This can also be attributed to the approximation of the ”unmixing-operator” in the phase correction step (50). Studies have shown that this approximation cannot generally guaranteed (54). As a result the values of MD are higher for the 208 spokes gridding reconstruction (cartilage 1.72±0.45 μm²/ms, muscle 1.70 ±0.26 μm²/ms) than for 70 spokes gridding (cartilage 1.61 ±0.47 μm²/ms, muscle 1.62 ± 0.33 μm²/ms). The reduction of streaking artifacts and noise leads to a slight decrease of MD for the nonlinear reconstructions in cartilage (strongest for Model-DTI, cartilage 1.54 ±0.38 μm²/ms) while values in muscle are similar for all reconstructions of the 70 spokes dataset. A similar trend can be observed when comparing the 30 directions and 6 directions data. While no definite statement can be made about the accuracy, these lower values are in line with the results from the literature. See for example (17,55) reporting values between 1.5 and 1.6 μm²/ms for knee cartilage and (56) for muscle.

Results of FA are consistent with the phantom measurements. Lowest values in cartilage are observed in the case of 30 directions (0.24 ± 0.16) and 208 spokes (0.25 ± 0.13) data. Due to increased noise, the values are significantly larger in the regridding reconstruction from the 6 directions data (0.42 ±0.21) and the 70 spokes data (0.41 ± 0.18). Again, there is a general trend of reduced FA in the case of the nonlinear reconstruction due to removal of streaking artifacts and noise. This effect is strongest for Model-DTI (Cartilage: 70 spokes: 0.35 ± 0.16, 6 directions: 0.34 ± 0.17). The area of synovial fluid in the 6 and 30 directions experiment is the closest to a gold standard reference that can be obtained. While the diffusion in this area will not be completely isotropic due to the small ROI the effect of partial volume effects, FA values are significantly lower than in the other tissues investigated, and results from Model-DTI show the highest consistency between the highly accelerated 6 directions experiment and the long-scantime 30 directions acquisition.

In the brain measurements, a general trend of reduced values for FA was observed with nonlinear reconstruction in gray matter. The general range of values of the measurements is in line with values reported in the literature. Studies that report comparable values include (57–60).

One of the main advantages of enforcing the TV penalty in tensor space (Eq. 6) as opposed to the diffusion weighted images (Eqs. 1 and 5), is that the regularization can only lead to potentially over or under-regularized results. These are immediately spotted by visual inspection of the results. In contrast, changes in the individual diffusion weighted images can lead to systematic errors, because even with adaptive regularization certain areas might be subject of slightly different regularization in different images. As the DWIs are subsequently used in the estimation of the tensor such potential inconsistencies can lead to systematic errors in the tensor maps, which are much harder to spot and generate more severe artifacts. This can best be observed in the increased MD and FA values in the 6 and 30 directions knee experiment (Fig. 4 and Tab. 3) of PI-CS. It is worth noting that our choice of TV as a sparsifying transform was motivated by previous work and its known properties on undersampled radial data. To facilitate comparison between the different methods, we also used it in the Model-DTI method where it is directly applied on the elements of the tensor. This neglects certain properties of the tensor maps, and it was already shown that for image processing based denoising, transforms like second oder TGV (29) outperform TV when working on the tensor elements (42). However, application of these more advanced methods to non-convex optimization problems is challenging and requires future advances in numerical methods.

Extensions and future work

One challenge of the model-based approaches is that the nonlinearity of the forward operator results in a non-convex optimization problem. This makes the numerical solution challenging and sensitive to initial values. In the current work, we used the gridding sum-of-squares reconstruction to initialize the optimizer. Another issue, mentioned already in the Theory section, is the potential poor scaling of the gradients during the numerical optimization, which has been described previously in the literature (32,34,36,37). Our approach to adaptively scale the step size with the norm of the gradients $\frac{\partial \stackrel{\sim }{F}(\stackrel{\sim }{D})}{\partial {\stackrel{\sim }{D}}_i}$ leads to acceptable reconstruction times for the experiments performed in this work. However, it is expected that higher numerical performance can be achieved with second-order methods like the iteratively-regularized Gauss-Newton method (30,61). In addition, very recent developments in the field of numerical optimization introduced algorithms that guarantee finding the global minimum of functionals that consist of the sum of a non-convex smooth function (the model based data term) and a convex non-smooth function (the TV term) (62). This is subject of ongoing research.

Previously proposed methods to accelerate diffusion acquisition with CS also suggested the application of a sparsifying transform across the dimension of the diffusion-encoding directions, e.g. dictionary based approaches (39) or methods based on distributed compressed sensing (40). While these approaches lead to a higher degree of sparsity due to the increased dimensionality, which is expected to improve reconstruction quality, we did not exploit compressibility in the diffusion dimension in this work because we observed a transfer of diffusion information between the individual images in preliminary experiments. However, recent work in mathematical image processing suggests that such an approach can be advantageous in the domain of the diffusion tensor (63), and a thorough evaluation of the integration of this additional dimension is currently ongoing. Such an additional dimension may be especially promising for applications where the number of diffusion encoding directions is much larger, as the redundancies in the data will be much larger in these situations.

The undersampled acquisition protocols used in this work aimed at the reduction of scan time. However, the proposed approach opens up possibilities to invest the scan time gained from k-space undersampling into either higher resolution or a larger number of diffusion-encoding directions (64–66). The different brain protocols presented here already illustrate the potential in this respect, but such optimizations will have to be investigated independently for each specific application. DTI is the preferred model for the diffusion in articular cartilage as well as many other musculoskeletal applications of diffusion (e.g. inter vertebral discs and muscle diffusion). Due to the short T2 of articular cartilage (around 40 ms), and the high in-plane resolution required, DTI of the cartilage is restricted to moderate diffusion-weightings with b-values lower than 500 s/mm². For such modest b-values the water diffusion is accurately characterized by the DTI framework, which assumes a Gaussian model for diffusion. In any case, our model-based approach could be extended to include non-Gaussian diffusion (e.g. diffusion-kurtosis imaging (67,68)), or advanced models like HARDI, Q-ball imaging or DSI (69–72). It is expected that the potential for improvements will be of even greater relevance for these advanced diffusion MRI techniques due to the much higher number of b-values and diffusion weighted images, which can reach up to 300 for diffusion spectrum imaging. However, this comes at the cost the higher complexity of the models which will make the numerical solution more challenging and computationally demanding.

Finally, the methodological developments in this work were performed with a limited number of volunteers (3 and 2 for knee and brain). Using the accelerated scan protocols, we are currently performing a follow up study with a larger number of patients and healthy controls.

In summary, this work describes a novel technique to accelerate diffusion imaging that uses a model-based reconstruction and applies a sparsifying transform directly on the diffusion tensor components. While it was demonstrated for radial spin echo acquisitions in this work, it is in principle applicable to arbitrary sampling patterns as long as aliasing artifacts are incoherent in the space of the selected transform domain. As the model-based reconstruction allows data acquisition in a clinically acceptable time of approximately 10 minutes without compromising image quality and fidelity of quantitative values, this provides a critical improvement towards clinical application of DTI of articular cartilage.

List of abbreviations

DWI

Diffusion weighted imaging

DWIs

Diffusion weighted images

DTI

Diffusion tensor imaging

CS

Compressed sensing

PI

Parallel imaging

ROI

Region of interest

MSK

Musculoskeletal