Scaling laws describe memories of host–pathogen riposte in the HIV population

Significance

A cure or a vaccine for HIV remains elusive, and HIV is not known to be cleared by natural immune responses. Thus, one can study how a virus evolves in humans in the absence of effective directed selection pressures and harness this knowledge to inform vaccine design. We find that the sequence space accessed by circulating HIV strains is characterized by sets of sequences related by collectively coupled mutations that evade host immunity (an informative lower-dimensional representation of sequence space). These sets of sequences represent stored memories of host–pathogen combat won by the virus (analogous to neural networks) and obey power law scaling. The collective escape pathways we reveal must be thwarted by an effective vaccine.

Abstract

The enormous genetic diversity and mutability of HIV has prevented effective control of this virus by natural immune responses or vaccination. Evolution of the circulating HIV population has thus occurred in response to diverse, ultimately ineffective, immune selection pressures that randomly change from host to host. We show that the interplay between the diversity of human immune responses and the ways that HIV mutates to evade them results in distinct sets of sequences defined by similar collectively coupled mutations. Scaling laws that relate these sets of sequences resemble those observed in linguistics and other branches of inquiry, and dynamics reminiscent of neural networks are observed. Like neural networks that store memories of past stimulation, the circulating HIV population stores memories of host–pathogen combat won by the virus. We describe an exactly solvable model that captures the main qualitative features of the sets of sequences and a simple mechanistic model for the origin of the observed scaling laws. Our results define collective mutational pathways used by HIV to evade human immune responses, which could guide vaccine design.

Viruses can infect humans to cause infectious diseases, which, on occasion, lead to outbreaks that reach pandemic proportions resulting in millions of deaths. One prominent example of such a virus is HIV. Vaccination, a procedure that aims to protect humans from infectious pathogens, is one of the greatest triumphs of modern medicine. Vaccines induce human immune responses that are specific for a pathogen, which then lie ready and waiting to abort infection. However, no effective vaccine for HIV exists, and there is no known example of HIV being cleared by natural human immune responses. This is because of the extraordinarily high mutability of the virus and its ability to rapidly down-regulate the human immune system (1, 2). The high mutability enables HIV to evade natural or vaccine-induced immune responses (2, 3), while down-regulation of the host immune system hinders the development of potent responses (2). This is in contrast to many other viruses that can often be cleared by effective natural responses and vaccinated against successfully (4). These viruses accumulate mutations in a directed fashion, guided by selective pressure due to successful vaccine-induced or natural immune responses (1, 5). The lack of effective natural immune responses or successful vaccines, and the enormous diversity of human immune pressures [e.g., T-cell responses (6)], implies that HIV has evolved in the human population in response to myriad, usually ineffective, immune responses. We set out to study the properties of such a virus population.

In past and current work (7–9), we have tried to define the functional constraints on HIV evolution with the practical goal of identifying its mutational vulnerabilities, and then harnessing this knowledge to inform vaccine design. Toward this end, we analyzed sequences of HIV proteins derived from virus samples extracted from diverse patients. Following a statistical approach pioneered in the study of neuronal networks (10, 11), we inferred a model for the probability of occurrence of mutant strains (a “prevalence landscape”) by maximizing the entropy of this inferred probability distribution subject to the constraints of reproducing the observed frequency of single and double mutations in the sequence data (8, 9). This model also accurately reproduces higher-order statistics characterizing the sequence data, such as the probability of observing sequences with a certain number of mutations, even though these quantities are not directly constrained in the inference procedure (Fig. S1 and SI Text). Theoretical studies suggest that, for HIV strains that are phylogenetically relatively close, the rank order of the prevalence of strains is the same as the rank order of their intrinsic replicative fitness (12). This may seem surprising because the viral sequences used to infer our model are samples obtained from patients during the course of nonequilibrium host–pathogen combat, and so the effective in-host fitness of a viral strain can be different from its intrinsic fitness. Although immune responses drive sequence evolution in each patient, they are a perturbative effect at the population level, making the rank order of prevalence and fitness statistically similar (12). This is because of the great diversity of human immune responses directed toward different regions of the viral proteome, and deleterious mutations made to evade the immune response in one host tend to revert upon transmission to another host (13). In vitro and in vivo studies testing our predictions for fitness support this conclusion (8, 9).

The maximum entropy model for the prevalence/fitness is described by the following:

$$P\left(\mathit{z}\right)=\frac{\exp \left(-H\left(\mathit{z}\right)\right)}{Q},\hspace{1em}H\left(\mathit{z}\right)=-{\displaystyle \sum _{i=1}^N{h}_i}{z}_i-{\displaystyle \sum _{i=1}^{N-1}{\displaystyle \sum _{j=i+1}^N{J}_{ij}}}{z}_i{z}_j,$$ [1]

where P(z) is the probability of observing a sequence of amino acids z = {z₁, z₂, …, z_N}, with N the total length of the protein sequence. Amino acids at each site i are identified as either consensus (z_i = 0) or mutant (z_i = 1). Here, the partition function Q ensures that the probabilities of all sequences sum to 1. The fields, h_i, and couplings, J_ij, in the Hamiltonian are obtained by fitting the observed probabilities of single and double mutations in sequences of HIV proteins (Methods). A positive coupling between a pair of sites implies that sequences with both sites mutated are observed more often than would be expected if mutations at these sites were independent. Thus, positive couplings indicate potentially synergistic or compensatory interactions between mutations. Mutations of both sites in a negatively coupled pair are observed less often than would be expected if the sites were independent, indicating a potential antagonistic or deleterious interaction between mutations at these sites. Similarly, point mutations are observed more often at sites with positive fields than at those with negative fields, when interactions with other sites in the sequence background are neglected. (Although related to epistasis, we emphasize that the overall effect of a particular mutation on fitness must be considered in the context of a particular sequence background: for example, mutation at a site i where the field h_i is positive may nonetheless lead to a decrease in viral fitness if there exist significant negative couplings between site i and other mutated sites in the sequence background.) For clarity and consistency, we use the language of fitness to describe the results presented below.

Results

We analyzed the HIV proteins Gag, Nef, protease, and integrase. Gag contains a number of structurally important HIV proteins, Nef proteins play a role in down-regulation of the human immune system, protease cuts HIV polyproteins into functional proteins, and integrase incorporates the viral genome into host DNA. These proteins are not exposed on virus particle’s surface; thus, they are primarily subject to immune attack by T cells. Peptides derived from viral proteins bound to HLA proteins are displayed on the surface of infected cells. T cells have a receptor on their surface called the T-cell receptor (TCR), which is different for each T-cell clone. If the TCR on a particular T-cell can bind strongly to a specific viral peptide–HLA complex, it can initiate a T-cell response leading to the death of the infected cell, cutting short viral replication. The Gag and Nef proteins are highly immunogenic and are frequently targeted by the immune response of diverse humans, whereas protease and integrase are targeted much less frequently (14, 15).

Because the inferred couplings J_ij have both positive and negative signs, the form of the Hamiltonian in Eq. 1 is reminiscent of spin glasses (16) and Hopfield models of neural networks (17). In Hopfield-like models, local maxima of the fitness landscape [i.e., local minima of the energy H(z)] in Eq. 1 play a special role: they act as attractors of the network dynamics. To discover analogous “attractor” sequences for HIV evolution, we evolved all available sequences through zero-temperature Monte Carlo simulations (SI Text). In this process, the identity of amino acids of the protein is sequentially changed following the direction of steepest increase in fitness until it can no longer increase. We found that the thousands of available sequences partitioned into a much smaller number of fitness peaks, a phenomenon that is not observed in test analysis of uncorrelated sequence data (SI Text). Intriguingly, this is similar to the proliferation of metastable states observed in some models of neural networks (11) and segments of antibody sequences (11, 18).

Properties of Fitness Peaks.

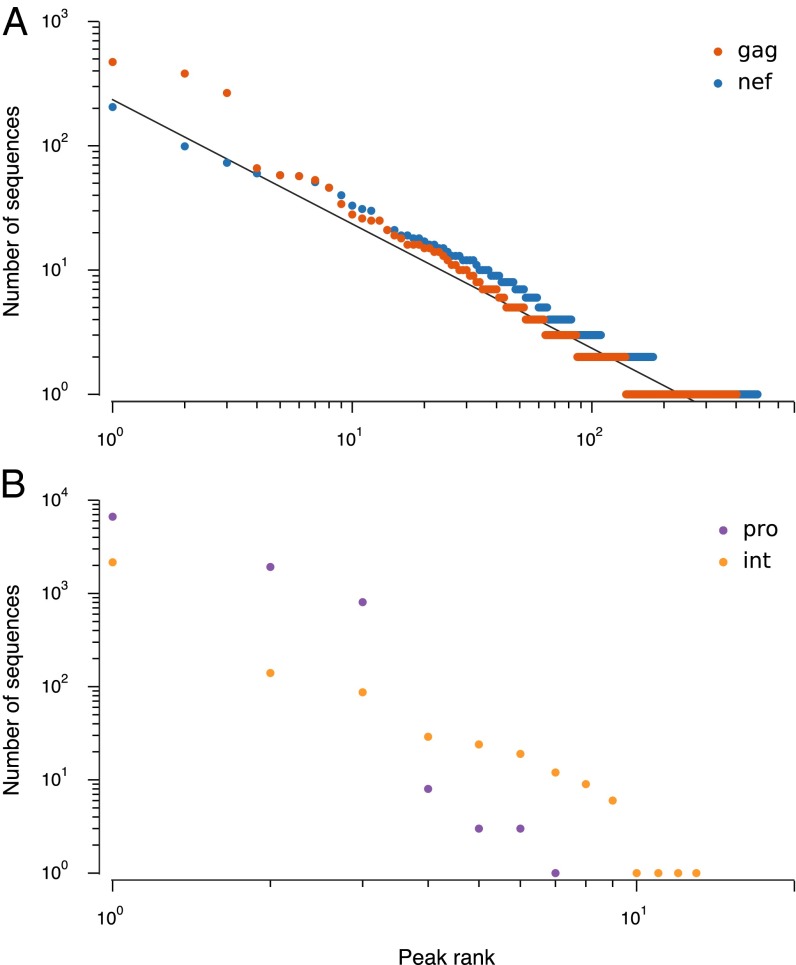
We rank ordered the fitness peaks by counting the number of sequences that lie on each peak, with the most populous peak ranked 1. For the immunogenic proteins Gag and Nef, the number of sequences on a fitness peak exhibits power law scaling as a function of the rank (Fig. 1A):

$$\omega \propto r^{-1},$$ [2]

where ω is the frequency with which sequences lie on a peak of rank r. The power law exponent of 1 observed here is similar to that observed in many other contexts, such as the frequency of word use in written text or the distribution of populations of cities in a country (19). For the weakly immunogenic proteins, protease and integrase, we do not observe power law scaling (Fig. 1B), and most sequences lie on a very small number of fitness peaks. This dramatic difference between the highly immunogenic proteins and the weakly immunogenic proteins is surprising, because at the level of single-site conservation there is little difference between Gag, protease, and integrase (Table S1).

Fig. 1.

Scaling laws describe the distribution of sequences across fitness peaks for highly immunogenic proteins, but not for those which are weakly immunogenic. (A) Sequences for Gag and Nef proteins are power law distributed across fitness peaks, with exponent ∼1 (maximum-likelihood estimate 1.04 for Gag and 1.02 for Nef; SI Text). For comparison, a power law with exponent 1 is shown in the background. Gag and Nef have a large number of peaks. (B) The distribution of sequences for the weakly immunogenic protease and integrase proteins is concentrated only on the top few fitness peaks. Far fewer peaks are observed in weakly immunogenic proteins compared with highly immunogenic proteins. For consistency, we use the same color conventions for Gag, Nef, protease, and integrase throughout.

To understand these findings, we have extensively characterized the fitness peaks. Each peak can be described by its frequency, rank, and the sequence to which all of the sequences that lie on the peak converge upon carrying out the zero-temperature Monte Carlo procedure (hereafter referred to as the peak sequence). A large fraction of mutations in peak sequences are typically shared by the sequences that lie on the peak. For Gag and Nef, roughly 70% and 80%, respectively, of mutations in a peak sequence are mutated in sequences that lie on the same fitness peak, on average (Fig. S2). Other mutations appear to be mostly ones that have lower fitness costs (Fig. S3). Importantly, mutations in peak sequences are strongly enriched in HLA-associated mutations, which are driven by host immune responses (20) (Fig. 2A and Fig. S4). The fraction of sites with HLA-associated mutations in Gag (23%) is much closer to the fraction of sites with HLA-associated mutations in protease (24%) and integrase (19%) than in Nef (50%), further highlighting the surprising similarity of the structure of fitness peaks in the highly immunogenic Gag and Nef proteins and in the weakly immunogenic protease and integrase.

Fig. 2.

Fitness peaks in the highly immunogenic proteins Gag and Nef exhibit similar properties. (A) All 402 fitness peaks in Gag and 491 fitness peaks in Nef are enriched in HLA-associated mutations (SI Text). Enrichment values are defined as the fraction of HLA-associated mutations in a peak sequence divided by the fraction of HLA-associated mutations in the whole protein. Vertical lines indicate maximum enrichment values, obtained if all mutations present in a peak sequence are HLA-associated. P values express the probability of obtaining at least as many HLA-associated mutations as actually observed in each peak sequence, assuming that these mutations were selected by chance (SI Text). Small P values suggest that HLA enrichment is not by chance. (B) Most peaks are distinct, with little overlap between sets of mutations in other fitness peaks. We define overlap as the number of mutations that the peak sequences have in common divided by the total number of mutations in both peak sequences combined. (C) We refer to mutations that occur in <20% (>20%) of fitness peaks as primary (secondary) mutations. Only a small fraction of sites are classified as secondary mutations (35 for Gag, 32 for Nef). Secondary mutations typically have small fields h_i, suggesting low fitness costs. (D) Average couplings between primary sites mutated within each peak sequence are strongly positive. (E) Average couplings between primary and secondary sites mutated in each peak sequence are weaker than those between primary sites alone, but mostly positive. (F) Average couplings between mutated sites in pairs of peaks are positive (compensatory) when the peaks strongly overlap, becoming more negative (deleterious) when the peaks are disjoint. Box plots describe the distribution of couplings between pairs of peak sequences grouped according to their overlap (SI Text).

The peak sequences themselves typically do not overlap strongly with one another (Fig. 2B), and pairs of peaks with low overlap are characterized by more negative couplings between the sites that are mutated (Fig. 2F). The typical overlap between peak sequences is larger than would be expected by chance, however, reflecting the strong enrichment of peak sequences in immune-driven HLA-associated mutations. Consistent with the low overlap observed between peak sequences, most mutations appear in only a few peak sequences (Fig. 2C). We refer to these as primary mutations. Primary mutations within peak sequences are associated with strong positive couplings in our inferred fitness landscape (Fig. 2D), suggesting that, due to compensatory effects, these mutations partially restore the fitness cost incurred by mutations driven by immune responses. Indeed, deleterious immune escape mutations and corresponding compensatory mutations identified experimentally (see ref. 21 and references therein) are represented in our peak sequences.

A small number of mutated sites appear in many peak sequences (35 in Gag and 32 in Nef are mutated in 20% or more of the peak sequences). These “secondary” mutations seem to incur relatively small fitness costs because the corresponding fields (h_i) at these sites tend to be small and positive (Fig. 2C). Peak sequences comprised of secondary mutations alone are very close to consensus. This suggests again that secondary mutations incur small fitness costs because few, if any, compensatory mutations are required. Deleterious (negative) couplings between secondary mutations prevent them from all appearing together on a single fitness peak. In peaks that also contain primary mutations, secondary mutations do play some compensatory role (Fig. 2E).

Collectively, these findings lead us to the following picture. Immune pressure imposed by humans drives HIV sequence evolution. Individuals with HLA genes that result in their T cells targeting similar regions of the proteome force similar mutations in proteins such as Gag and Nef, which often compromise viral fitness (21, 22). For the virus to remain viable (and therefore be observed in patients), other compensatory mutations are needed to restore these fitness costs. This is why the primary mutations in peak sequences are positively coupled and why peak sequences are enriched in HLA-associated mutations. The sequences that lie on the same fitness peak share many of this common set of mutations that confer escape from certain kinds of immune responses while maintaining virus viability through compensatory mutations; i.e., common collective effects define each fitness peak. Mutations in each sequence that are distinct from those that define its peak are likely to be nearly neutral variation superimposed on this critical set of shared mutations.

We may regard the set of fitness peaks as a useful lower-dimensional representation of sequence space that reflects the local collective compensatory pathways that HIV uses to successfully avoid diverse natural immune responses. The dynamics of Hopfield models of neural networks results in attractors that are stored memories of past stimuli. Given that our fitness landscape (Eq. 1) is analogous, the peaks we have defined may be considered to be attractors to which HIV evolves when forced to mutate in a certain way to successfully evade immune responses and maintain viability. Thus, they are stored memories of successful host–pathogen riposte in the HIV population.

We have confirmed that the properties of the fitness peaks described above are robust to finite sampling error or perturbation of the inferred fields h_i and couplings J_ij, and alternate choices for the starting sequences for the zero-temperature Monte Carlo simulations (see SI Text for details). The fitness peaks we obtain for various “perturbed” models, and the distribution of sequences across them, are similar to those presented here (Fig. S5). Furthermore, the scaling laws for the highly immunogenic Gag and Nef proteins (as well as the lack of power law scaling for protease and integrase) are preserved in the perturbed models. The observed overlap between fitness peaks, enrichment in HLA-associated mutations in peak sequences, and properties of the couplings within and between peak sequences are also consistent. These findings suggest that the features of the fitness landscapes we have described are robust to errors in the correlations due to finite sampling and to reasonable perturbations of the inferred fields and couplings.

A Simple Mathematical Model Describes Qualitative Features of the Fitness Peaks.

An exactly solvable simplified model captures some of the essential properties of the fitness peaks described above. We consider a protein of length N, with each peak α represented by a subset of N_α sites. Following Fig. 2B, we assume that there is no overlap between sites in different peak sequences. The sites in each peak are constrained such that a fraction m_α of the N_α sites are mutated in all sequences that lie on peak α, reflecting the typical overlap between peak sequences and the multiple sequence alignment (MSA) sequences that lie on each fitness peak (Fig. S2). This model can be cast in the same form as in Eq. 1, with uniform fields h_α for the sites in each peak α and average couplings J_α between them. We assume that a sequence belongs to only one fitness peak, which is enforced by strong negative couplings (deleterious interactions) between sites in different peak sequences.

In this model, the probability of finding a sequence on a particular fitness peak α is proportional to exp(F_α), where F_α is the free fitness (23) (free energy) of peak α. The free fitness is extensive, that is, $F_{\alpha }\propto N_{\alpha }$. Thus, in the limit that N becomes large with N_α increasing proportionally, only sequences lying on the fitness peak with the highest free fitness would be observed. If we want the probability of observing a sequence lying on any fitness peak to be nonvanishing in the large N limit, then the free fitness of each peak must be equal, at least up to small additive factors subleading in N. This condition leads to a constraint on the fields and couplings (SI Text):

$$-h_{\alpha }{m}_{\alpha }-N_{\alpha }{J}_{\alpha }{m}_{\alpha }^2+m_{\alpha }\log \left(m_{\alpha }\right)+\left(1-m_{\alpha }\right)\log \left(1-m_{\alpha }\right)=0.$$ [3]

Coupled with a self-consistency condition, this formula gives an equation for h_α and J_α as a function of m_α. Although this qualitative model is very simple, the couplings derived in this way are similar in size to those obtained for each peak using our fitness landscape, although the size of the fields is overestimated (SI Text and Fig. S6).

Origins of Power Law Scaling.

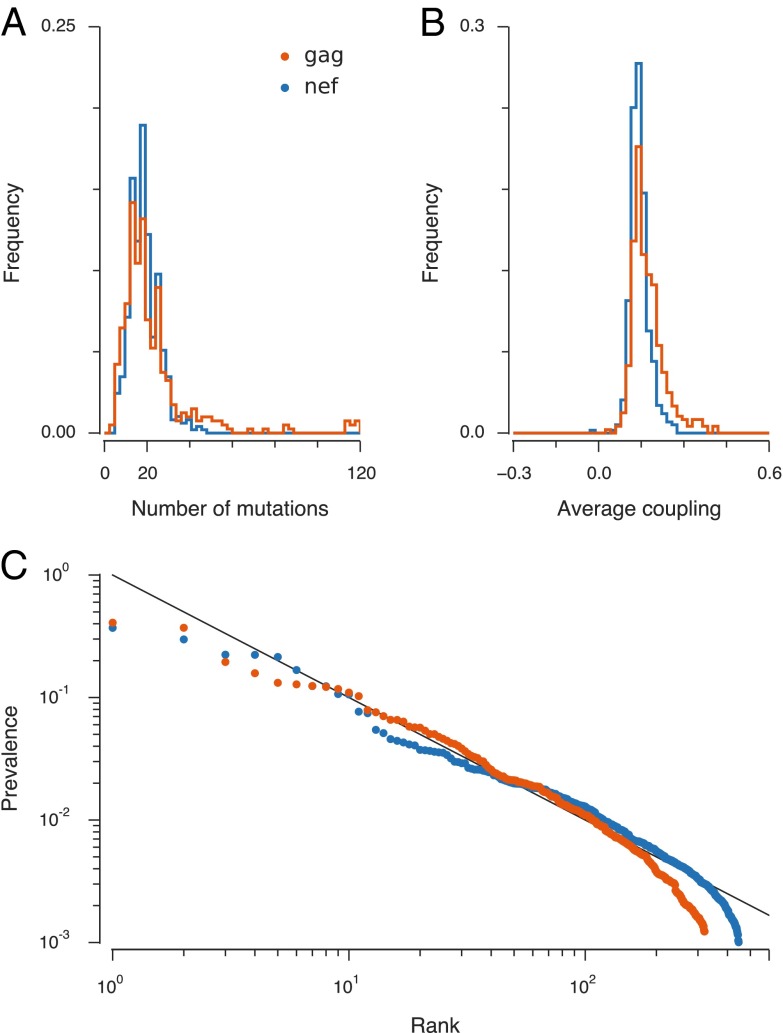
The observed power law scaling (absence of a typical number of sequences on fitness peaks) for the immunogenic proteins could be explained by the enormous diversity of HLA genes in the human population (22) and by the diversity of fitness constraints characterizing the peaks. The HLA haplotype of an individual determines the types of T-cell responses individuals are capable of mounting (22). The frequency of HLA haplotypes in the human population is also distributed as a power law (Fig. S7, haplotype data from ref. 24); so, the virus has not evolved to evade any special type of immune pressure imposed by most humans but has encountered diverse pressures. Additionally, the ease of evolving compensatory mutations corresponding to different fitness peaks may vary broadly because of the different numbers of mutations in peak sequences and networks of compensatory interactions between them (Fig. 3 A and B). A different number of strains (including multiple copies of the same strain) is compatible with each fitness peak because the constraints that must be satisfied vary between peaks. Therefore, a broad power law distribution of sequences across fitness peaks can result. Analogously in language, as new concepts and situations are encountered, new words are used. Because of the diversity of concepts and situations, there is no typical frequency of word use.

Fig. 3.

Scaling laws for immunogenic proteins can be recovered qualitatively through a simple model of viral growth incorporating the number of mutations and average coupling between sites in each peak sequence. (A) The distribution of the number of mutations in peak sequences in the Gag and Nef proteins. (B) The distribution of average couplings between mutated sites in peak sequences is centered around positive values. (C) A simple model of viral growth (Eq. 4) approximately reproduces the power law distribution of sequences across fitness peaks for Gag and Nef, with an exponential tail for high-ranked peaks. Here, the normalization of the prevalence (proportional to the number of sequences lying on each fitness peak) is arbitrary. For comparison, a power law with exponent 1 is shown in the background.

Because the weakly immunogenic proteins protease and integrase are not frequent immune targets, there is little pressure on them to broadly explore the sequence space. Thus, for these proteins we find very few fitness peaks, with most sequences residing on the top few peaks and a sharp falloff in the frequency of sequences on lower ranked peaks, and power laws do not emerge.

A simple model of viral growth incorporating the features described above yields distributions of sequences among fitness peaks consistent with the observed power law scaling. When under attack by the host immune system, viral growth is attenuated until the virus is able to accumulate mutations to evade the immune response and to compensate for loss of fitness due to deleterious escape mutations. The time needed for the virus to complete this adaptive process and grow robustly may differ depending on the number of mutations that must be generated—quantified in our lower-dimensional representation by the number of mutations in each peak sequence (N) and the average fraction (m) of these mutations present in sequences that lie on the same fitness peak—as well as the strength of the compensatory interactions between those mutations—quantified by the average coupling (J) between mutations in each peak sequence (Fig. 3 A and B). Following this adaptive process, the fitness of viable strains is expected to be distributed around a typical fitness, as strains with very low replicative capacity have rarely been isolated from patients and strains that far exceed the usual replicative capacity would kill the host (25). We assume that the fitness of viable strains is the same (f). We then estimate that the number of strains that lie on the ith fitness peak should be proportional to the population size of viable viruses following the adaptation period, assuming exponential growth:

$$n_i\propto \exp \left[f\left(t-T_i\right)\right],$$ [4]

where t is the time of observation and T_i is the time at which mutations satisfying constraints for peak i first emerge. The observation time, t, is likely distributed uniformly over a range, but we take it to be a constant; thus, our analysis below is independent of t. This deterministic equation applies after the strain has grown sufficiently so that it is not lost due to genetic drift. We ignore this establishment time.

We calculated T_i as the average time required for a sequence to accumulate the number of mutations characteristic of the ith fitness peak given the couplings between the sites that are mutated in the corresponding peak sequence. We have carried out our analyses requiring that either the full set of mutations (N), or the average mutated subset (mN), needs to evolve for a viable virus. Mutations are initiated at a constant rate, and they revert at rates that depend exponentially on the corresponding change in fitness, along with a suppression factor α that reflects the relative difficulty of reverting existing mutations versus making new ones (SI Text). Because new mutations are driven by immune pressure, we expect α < 1. We find that (26)

$$T_i={\displaystyle \sum _{k=0}^{N_i-1}\frac{1}{p_k}}+{\displaystyle \sum _{k=0}^{N_i-2}\frac{1}{p_k}}{\displaystyle \sum _{m=k+1}^{N_i-1}{\displaystyle \prod _{j=k+1}^m\frac{q_j}{p_j}}}\hspace{0.17em},$$ [5]

with N_i the number of mutated sites in peak i. Here, p_k and q_k are rates for the accumulation and reversion of mutations, respectively, when k sites in the sequence are mutated. These rates depend implicitly on α and the average coupling between mutations in the peak sequence (SI Text). Using the true numbers of mutations and couplings for the peak sequences (Fig. 3 A and B), we computed a set of T_i and the corresponding set of prevalences, n_i (Fig. 3C). When the reversion rate is small ($\alpha \lesssim 0.1$), we generically find a power law distribution consistent with the data (Fig. 3C), with the exponent roughly set by the parameter f. These results are not sensitive to the exact parameter values. We note that, although the computed prevalences n_i are correlated with the true number of sequences found to lie on each fitness peak i, the correspondence is not exact (Fig. S8). Here, our goal is not to reproduce exactly the true distribution, but rather to show that a simple model of this form readily generates a distribution of sequences across fitness peaks that is consistent with the true one.

This basic model captures the power law scaling observed in the data over most, but not the entire, range. However, it ignores the distributions of mutation rates, viable virus fitness (f), coupling strengths, and observation times (t), as well as the stochastic variation in establishment times (taken to be zero), whose inclusion could broaden the distribution predicted by the simplest model and mimic the data more closely. For example, choosing mutation rates from a uniform distribution, to mimic that different types of amino acid mutations are not equally likely, broadens the range over which power law scaling is observed (Fig. S9B). Conversely, if we use only a partial set of peak mutations to estimate T_i, we recover the power law over a more restricted range compared with using all peak mutations (Fig. S9A). This is because the width of the distribution of the entire set of peak mutations is larger.

Discussion

Our analyses have revealed some basic principles that describe how HIV has evolved in the human population to evade diverse immune responses. We find interesting analogies between these findings and properties of neural networks and scaling laws observed in diverse contexts. In addition, the finding that each fitness peak reveals a discrete class of compensatory pathways that HIV employs to evade immune responses while maintaining virus function may have practical consequences. Any useful vaccination strategy must avoid targeting regions of the HIV proteome wherein mutations that evade the vaccine-induced immune response can take advantage of the classes of compensatory pathways revealed by our analyses. An important future direction to explore is whether targeting residues belonging to distinct peak sequences that are negatively coupled to each other, while avoiding these compensatory pathways, is a useful criterion for rational immunogen design.

Methods

Our data consists of MSAs of HIV-1 clade B sequences for the proteins Gag, Nef, protease, and integrase, obtained from the Los Alamos National Laboratory HIV sequence database (www.hiv.lanl.gov). Accession numbers for all sequences are recorded in Dataset S1. As described in ref. 8, we converted these sequences into a binary form, writing each sequence from the MSA as a vector of binary variables z = {z₁, z₂, …, z_N}, where N is the total length of the amino acid sequence. Each binary variable z_i is set to 0 (1) if the amino acid at site i matches (does not match) the consensus amino acid at that site. Binarized MSA data for Gag, integrase, Nef, and protease are given in Datasets S2–S5, respectively.

We seek to infer a model that describes the observed distribution of sequences. To characterize the sequence distribution, we focus on the average frequency of single and double mutations. The simplest (maximum entropy) model capable of reproducing these frequencies is the Ising model, described in Eq. 1. We inferred an Ising model reproducing the observed mutation frequencies using the selective cluster expansion algorithm (27, 28) following the procedure outlined in ref. 28 and confirmed that the inferred model reproduces the statistics of the MSA (Fig. S1).