Abstract
Circuit quantum electrodynamics, consisting of superconducting artificial atoms coupled to on-chip resonators, represents a prime candidate to implement the scalable quantum computing architecture because of the presence of good tunability and controllability. Furthermore, recent advances have pushed the technology towards the ultrastrong coupling regime of light-matter interaction, where the qubit-resonator coupling strength reaches a considerable fraction of the resonator frequency. Here, we propose a qubit-resonator system operating in that regime, as a quantum memory device and study the storage and retrieval of quantum information in and from the Z2 parity-protected quantum memory, within experimentally feasible schemes. We are also convinced that our proposal might pave a way to realize a scalable quantum random-access memory due to its fast storage and readout performances.
Analogous to the classical computer processors, a quantum processor inevitably requires memory cell elements1,2,3,4 to store arbitrary quantum states in efficient and faithful manner. In particular, these memory devices might be needed and useful for storing and retrieving qubits in a fast timescale between the quantum processor and the memory elements, similar to a classical random-access memory5. That would require ability to store information for a short time with fast storage and readout responses. Here, we propose a quantum memory implemented on circuit quantum electrodynamics (cQED)6,7,8 with fast storage and retrieval responses. The memory cell operates in the ultrastrong coupling (USC) regime of light-matter interaction9,10,11, where the qubit-resonator coupling strength approaches a significant fraction of the resonator frequency. In addition, a key ingredient towards realizing our scheme is the existense of the Z2 parity symmetry12,13, which allows us to encode quantum information in partiy-protected states that are robust against certain environmental noises14,15.
In this report, we propose a scalable quantum memory cell element based on the cQED architecture, comprising of a superconducting flux qubit galvanically coupled9 to a microwave resonator. In particular, we study the storage and retrieval of single- and two-qubit states, while the input states are in the form of flying microwave photons16,17,18,19. These processes can be carried out with good fidelity even with the presence of noise. We are also convinced that our memory can be scaled up to store large number of qubits since the cQED architecture provides very high level of controllability20,21 and scalability22. In this way, we believe our proposal might pave a way towards scalable quantum random-access memory (QRAM)23,24 and distributed quantum interconnects25,26, which in turn might steer towards novel applications ranging from entangled-state cryptography27,28, teleportation29, purification30,31, fault-tolerant quantum computation32 to quantum simulations.
The qubit-resonator system operating in the USC regime, as shown in Fig. 1, exhibits a Z2 parity symmetry and its dynamics is governed by the quantum Rabi Hamiltonian13
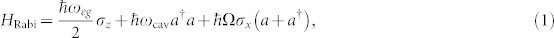 |
where ωeg, ωcav, and Ω stand for the qubit frequency, cavity frequency, and qubit-resonator coupling strength, respectively. In addition, a(a†) is the bosonic annihilation(creation) operator, and σx,z are the Pauli matrices of the qubit. A compelling feature of Hamiltonian (1) is that for ratios 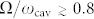 , the ground and first excited states can be approximated as
, the ground and first excited states can be approximated as
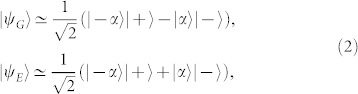 |
where |α〉 is a coherent state for the resonator field with amplitude |α| = Ω/ωcav, and 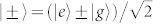 are the eigenstates of σx. The states |ψG/E〉 form a robust parity-protected qubit15 whose coherence time can be up to
are the eigenstates of σx. The states |ψG/E〉 form a robust parity-protected qubit15 whose coherence time can be up to 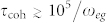 . In the following, we outline a protocol that allows storage and retrieval of quantum information to and from this qubit. It is achieved by adiabatically tuning the qubit-resonator coupling strength, from the Jaynes-Cummings (JC) to USC regime. In particular, we propose a USC memory cell element (see Fig. 1a) that can be designed by the flux-qubit architecture presented in Ref. 33, which provides a tunable qubit-resonator coupling (see Supplementary information). The latter can be implemented by using a superconducting quantum interference device (SQUID) as proposed for qubit-qubit coupling in Refs. 34, 35.
. In the following, we outline a protocol that allows storage and retrieval of quantum information to and from this qubit. It is achieved by adiabatically tuning the qubit-resonator coupling strength, from the Jaynes-Cummings (JC) to USC regime. In particular, we propose a USC memory cell element (see Fig. 1a) that can be designed by the flux-qubit architecture presented in Ref. 33, which provides a tunable qubit-resonator coupling (see Supplementary information). The latter can be implemented by using a superconducting quantum interference device (SQUID) as proposed for qubit-qubit coupling in Refs. 34, 35.
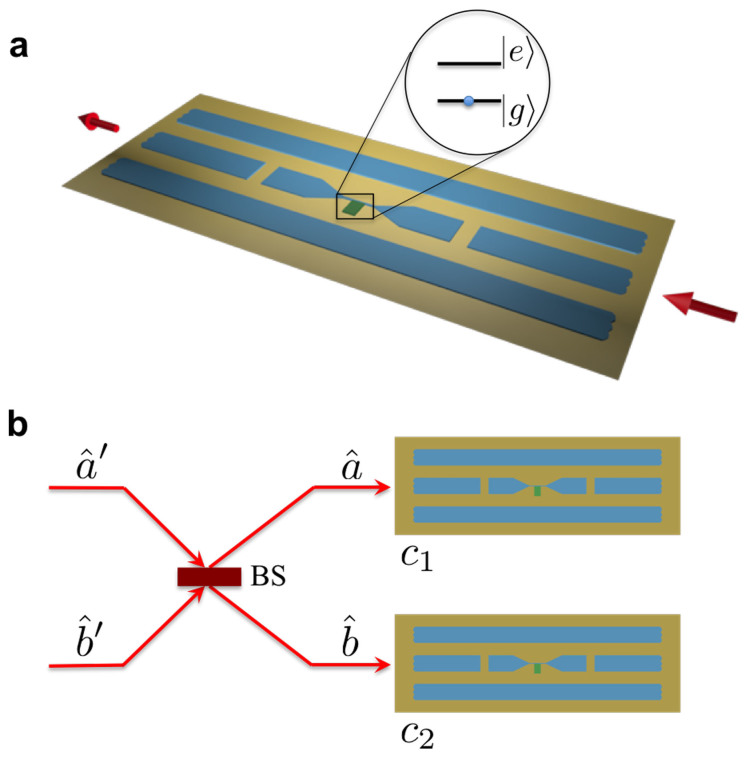
Figure 1. Schematic of circuit-QED design for storage and retrieval of an unknown single-and two-qubit states.
(a) A USC memory cell element, composed of a qubit-resonator system operating at the USC regime. (b) Two flying microwave photons, with modes 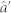 and
and 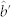 , come in and pass through a beam splitter (BS) implemented by a superconducting quantum interference device (SQUID) to form a two-qubit entangled state, which is then stored in two USC qubits located at a distance apart.
, come in and pass through a beam splitter (BS) implemented by a superconducting quantum interference device (SQUID) to form a two-qubit entangled state, which is then stored in two USC qubits located at a distance apart.
Results
Generating and catching flying qubits
Photons propagating through linear devices are well-suited as information carriers because they possess long coherence length and can be encoded with useful information. In our case, a flying microwave photon is generated from cQED platforms16,17,18,19, and a qubit is encoded in a linear superposition of zero (|0F〉) and one photon (|1F〉) Fock states. Recently, it has been pointed out in Ref. 19 that if a photonic wave packet emitted from a source has a temporally symmetric profile, it overcomes the impedance mismatch problem when a flying qubit impinges onto a resonator. With all these latest advancement in cQED technologies, we envision our memory cell be located on the pathway of a single microwave photon to accomplish quantum information storage (see Fig. 1).
Storage and retrieval processes
The storage of quantum information into our USC memory cell is realized within three steps. At first, we cool down the system to reach its ground state in the USC regime. Secondly, the qubit frequency is tuned to be off-resonant with the resonator frequency, i.e., ωcav > ωeg, while the qubit-resonator coupling stregth Ω is adiabatically tuned towards the strong coupling regime where 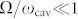 , where the coupling is much larger than any decoherence rate in the system. In this regime, the ground and first excited states of the qubit-resonator system are
, where the coupling is much larger than any decoherence rate in the system. In this regime, the ground and first excited states of the qubit-resonator system are  and
and 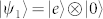 , respectively. Here, the states |g〉 and |e〉 stand for the ground and excited states of the qubit, while |0〉 stands for the vacuum state of the resonator. Since we have adiabatically tuned the coupling from the USC to the strong coupling regime, our initial USC ground state is then mapped to the JC ground state, i.e.,
, respectively. Here, the states |g〉 and |e〉 stand for the ground and excited states of the qubit, while |0〉 stands for the vacuum state of the resonator. Since we have adiabatically tuned the coupling from the USC to the strong coupling regime, our initial USC ground state is then mapped to the JC ground state, i.e., 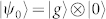 . At this stage, our memory cell is ready for information storage. When a flying qubit with an unknown quantum state |ΨF〉 = αF|0F〉 + βF|1F〉 comes in contact with the cell as shown in Fig. 1a, the encoded information from the flying qubit is transferred to the flux qubit due to the JC dynamics. Therefore, the state of our system becomes
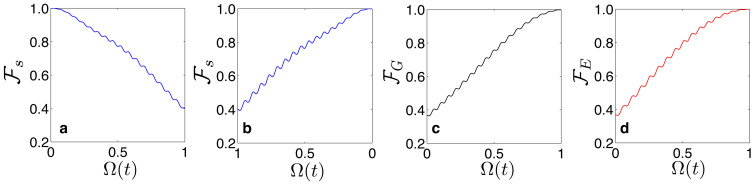
. At this stage, our memory cell is ready for information storage. When a flying qubit with an unknown quantum state |ΨF〉 = αF|0F〉 + βF|1F〉 comes in contact with the cell as shown in Fig. 1a, the encoded information from the flying qubit is transferred to the flux qubit due to the JC dynamics. Therefore, the state of our system becomes 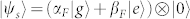 . At last, we turn on the qubit-resonator coupling adiabatically towards the USC regime. For simplicity, we consider a linear adiabatic switching scheme such that Ω(t) = (cos(f) − Δf sin(f)t/T)Ω0, with T total evolution time and f = ϕext/ϕ0. Here, ϕext is an external magnetic flux and ϕ0 = h/2e is the flux quantum (see Methods and Supplementary information for detailed definition). In Fig. 2a, b, we show the storage and retrieval processes for a quantum state |ψs〉 = αF|ψ0〉 + βF|ψ1〉, and Fig. 2c, d show the ground state |ψ0〉 and the first excited state |ψ1〉 adiabatically follow the instantaneous eigenstates such that |ψ0〉 → |ψG〉 and |ψ1〉 → |ψE〉. In this manner, we can encode important information onto the parity-protected qubit basis. Retrieval (decoding) process is reverse of the storage process and is achieved by adiabatically switching off the qubit-resonator coupling strength from the USC to SC regime.
. At last, we turn on the qubit-resonator coupling adiabatically towards the USC regime. For simplicity, we consider a linear adiabatic switching scheme such that Ω(t) = (cos(f) − Δf sin(f)t/T)Ω0, with T total evolution time and f = ϕext/ϕ0. Here, ϕext is an external magnetic flux and ϕ0 = h/2e is the flux quantum (see Methods and Supplementary information for detailed definition). In Fig. 2a, b, we show the storage and retrieval processes for a quantum state |ψs〉 = αF|ψ0〉 + βF|ψ1〉, and Fig. 2c, d show the ground state |ψ0〉 and the first excited state |ψ1〉 adiabatically follow the instantaneous eigenstates such that |ψ0〉 → |ψG〉 and |ψ1〉 → |ψE〉. In this manner, we can encode important information onto the parity-protected qubit basis. Retrieval (decoding) process is reverse of the storage process and is achieved by adiabatically switching off the qubit-resonator coupling strength from the USC to SC regime.
Figure 2. Fidelity plots.
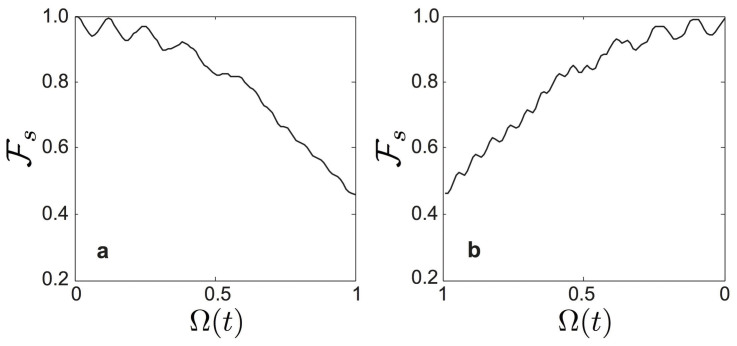
(a) Storage and (b) retrieval processes for a quantum state |ψs〉 = αF|ψ0〉 + βF|ψ1〉. In both cases, we plot the fidelity between the initial |ψ〉s and the instantaneous state |ψ(t)〉, i.e., 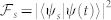 . Any arbitrary state |ψ〉 = u|ψ0〉 + v|ψ1〉 can be stored and retrieved with unit fidelity. (c) Fidelity between the approximated ground state in Eq. (2) and the instantaneous ground state
. Any arbitrary state |ψ〉 = u|ψ0〉 + v|ψ1〉 can be stored and retrieved with unit fidelity. (c) Fidelity between the approximated ground state in Eq. (2) and the instantaneous ground state 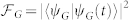 . (d) Fidelity between the approximated first excited state in Eq. (2) and the instantaneous first excited state
. (d) Fidelity between the approximated first excited state in Eq. (2) and the instantaneous first excited state 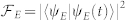 . For all the simulations, we choose the system parameters as ωcav = 1, ωeg = 0.1 ωcav, Ω0 = ωcav, and the total evolution T = 105/ωcav.
. For all the simulations, we choose the system parameters as ωcav = 1, ωeg = 0.1 ωcav, Ω0 = ωcav, and the total evolution T = 105/ωcav.
We note that the time for storage and retrieval of quantum information is several order of magnitude faster than the coherence time of the parity-protected qubit, which is about Tcoh ~ 40 μs for a coupling strength Ω0/ωeg ~ 1.515. For instance, if we consider a flux qubit with energy ωeg/2π ~ 2 GHz, and a cavity of frequency ωcav/2π ~ 5 GHz, our system reaches the USC regime with Ω0/ωcav = 0.6. For the linear adiabatic switching scheme with the above parameters, we estimate total time for storage/retrieval of a qubit is about 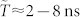 .
.
At the end of an adiabatic evolution, the state 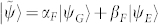 is desired. However, the state after the evolution might become
is desired. However, the state after the evolution might become 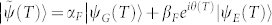 , with a relative phase θ(T) resulting from the dynamical and geometrical effects36. Hence, we need to keep track of a relative phase during the storage and retrieval processes.
, with a relative phase θ(T) resulting from the dynamical and geometrical effects36. Hence, we need to keep track of a relative phase during the storage and retrieval processes.
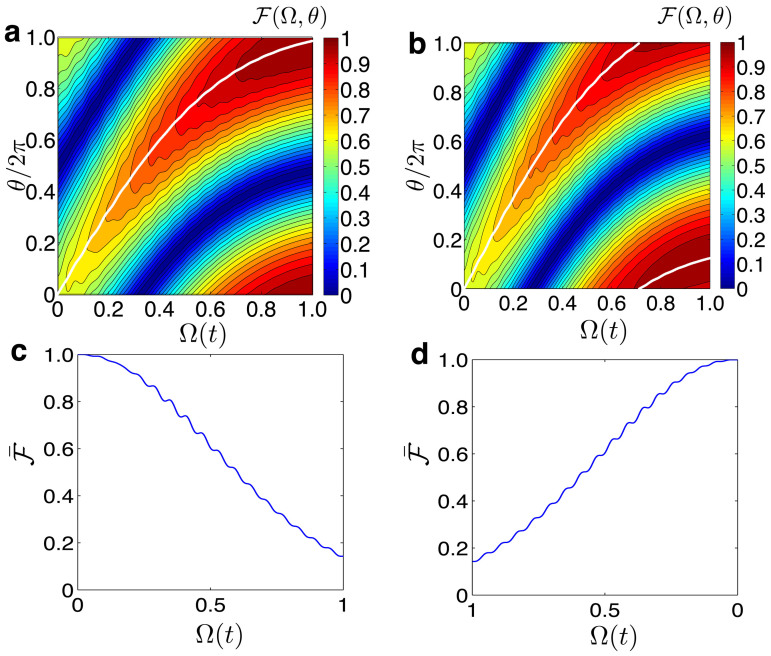
In order to find out which phase θ(t) optimizes the processes, in Fig. 3a, b, we plot the fidelity 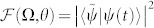 between the state
between the state 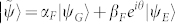 and the state |ψ(t)〉, which has adiabatically evolved from the initial state |ψs〉 = αF|ψ0〉 + βF|ψ1〉. In these simulations, we find the fidelity over the landscape of θ ∈ [0, 2π] versus the qubit-resonator coupling strength Ω(t), for two different total evolution time T = 105/ωcav (Fig. 3a), and T = 120/ωcav (Fig. 3b). White lines show the phase θopt, which optimizes the fidelity
and the state |ψ(t)〉, which has adiabatically evolved from the initial state |ψs〉 = αF|ψ0〉 + βF|ψ1〉. In these simulations, we find the fidelity over the landscape of θ ∈ [0, 2π] versus the qubit-resonator coupling strength Ω(t), for two different total evolution time T = 105/ωcav (Fig. 3a), and T = 120/ωcav (Fig. 3b). White lines show the phase θopt, which optimizes the fidelity 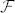 for both cases. Notice that the maximum fidelity and the optimal phase θ depend strongly on the system parameters and the total evolution time T. Thus, we require, for each USC memory cell, to find out the parameter T that maximizes the fidelity only once. When T is known, the cell can always be operated at that specific parameter for storing and retrieving unknown quantum states. Therefore, the time T might be a benchmark to characterize our potential USC quantum memory devices, in the same way as hard disk drives of the classical computer are being characterized by their seek time and latency.
for both cases. Notice that the maximum fidelity and the optimal phase θ depend strongly on the system parameters and the total evolution time T. Thus, we require, for each USC memory cell, to find out the parameter T that maximizes the fidelity only once. When T is known, the cell can always be operated at that specific parameter for storing and retrieving unknown quantum states. Therefore, the time T might be a benchmark to characterize our potential USC quantum memory devices, in the same way as hard disk drives of the classical computer are being characterized by their seek time and latency.
Figure 3.
(a) Contour plots of the fidelity 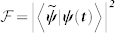 between the state
between the state 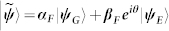 and the state |ψ(t)〉, which has adiabatically evolved from the initial state |ψs〉 = αF|ψ0〉 + βF|ψ1〉, when the total evolution time is set to T = 105/ωcav, and (b) when the evolution time is T = 120/ωcav. For the above cases, the black lines stand for the phase which maximized the fidelity
and the state |ψ(t)〉, which has adiabatically evolved from the initial state |ψs〉 = αF|ψ0〉 + βF|ψ1〉, when the total evolution time is set to T = 105/ωcav, and (b) when the evolution time is T = 120/ωcav. For the above cases, the black lines stand for the phase which maximized the fidelity 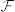 . In these simulations, the parameters are ωcav = 1, ωeg = 0.1 ωcav, and Ω0 = ωcav. (c) Storage process for an entangled state
. In these simulations, the parameters are ωcav = 1, ωeg = 0.1 ωcav, and Ω0 = ωcav. (c) Storage process for an entangled state 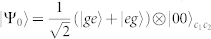 . (d) Retrieval process. In both cases, we plot the fidelity between the initial state |Ψ0〉, and the instantaneous state |ψ(t)〉,
. (d) Retrieval process. In both cases, we plot the fidelity between the initial state |Ψ0〉, and the instantaneous state |ψ(t)〉, 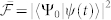 . In the simulations (c) and (d), we have chosen ωcav = 1, ωeg = 0.1 ωcav, Ω0 = ωcav, and the evolution time T = 105/ωcav.
. In the simulations (c) and (d), we have chosen ωcav = 1, ωeg = 0.1 ωcav, Ω0 = ωcav, and the evolution time T = 105/ωcav.
Additionally, storage and retrieval of entangled states in two separate USC cells is feasible. To demonstrate such a process, we let two bosonic fields to interact via the SQUID, simulating a Hong-Ou-Mandel setup37 as shown in Fig. 1b. Let us suppose that we have an initial state 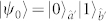 . After experiencing a beam splitter interaction, we have two-photon entangled state
. After experiencing a beam splitter interaction, we have two-photon entangled state 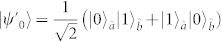 , which enters two cavities c1 and c2, each containing a flux qubit prepared in its ground state. This process allows the cavities to be prepared in the state
, which enters two cavities c1 and c2, each containing a flux qubit prepared in its ground state. This process allows the cavities to be prepared in the state 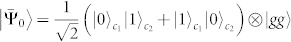 . Following the same procedure, we tune the qubits towards resonance with its respective cavity such that we arrive at the state
. Following the same procedure, we tune the qubits towards resonance with its respective cavity such that we arrive at the state 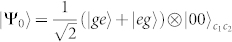 . With our protocol, the state is eventually mapped to a parity-protected state
. With our protocol, the state is eventually mapped to a parity-protected state  . In Fig. 3c, d, we show the numerical simulations for the storage and retrieval processes of the entangled state |Ψ0〉.
. In Fig. 3c, d, we show the numerical simulations for the storage and retrieval processes of the entangled state |Ψ0〉.
Discussion
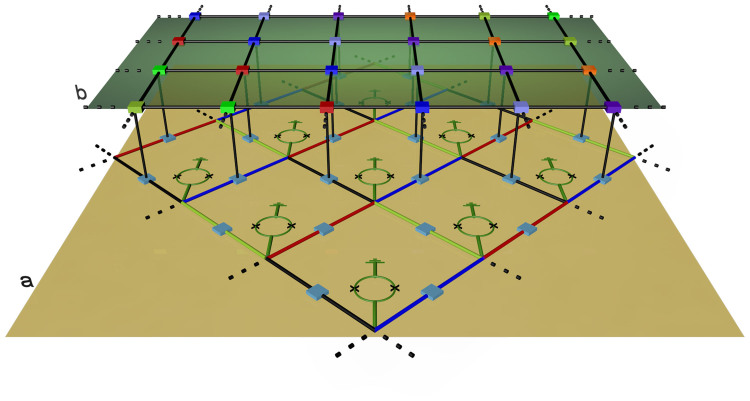
We have presented the basic tools for building a quantum memory based on a cQED architecture that operates in the USC regime of light-matter interaction. The storage/retrieval process for unknown quantum states, be single-qubit or two-qubit entangled states, can be accomplished by adiabatically switching on/off the qubit-resonator coupling strength. As a scope, we propose the large-scale quantum memory network shown in Fig. 4(a), where each edge of the memory network is constituted with our memory cell element. This architecture can pave the way for the implementation of a scalable QRAM, which might benefit from the fast storage and readout performances of superconducting circuits. In addition, each node in the network is connected to a SQUID that allows to selectively switch on/off interaction between neighbouring microwave cavities33,38, in order to implement quantum state transfer processes within the same layer (see Supplementary information). Ultimately, we would like to achieve a multilayer circuit architecture, where a quantum processor layer39 interfaces with the proposed memory layer as shown in Fig. 4.
Figure 4. A scalable quantum network.
(a) The light-matter interface operating at the ultrastrong coupling regime may be envisioned as a set of microwave cavities connected, at the nodes, by SQUID devices that allow to switch on/off the cavity-cavity interaction. Notice that each cavity is represented with different colors (red, black, blue and green) that stand for different lengths to assure the manipulation of specific pairwise interactions (see Supplementary information). In addition, on each edge of the memory array, there is a memory cell made of a USC entity (blue square) to store an arbitrary quantum information in a specific location. (b) Integrated quantum processor. A 2D cavity grid with a qubit distribution (rectangular boxes) represented in various colors is shown here. It was previously shown in Ref. 39 that such a cavity grid may provide a scalable fault-tolerant quantum computing architecture with minimal swapping overhead. Data transfer between the two layers may be done via cavity buses (vertical black colored lines connecting layer a and b).
Methods
Switchable quit-resonator coupling strength
In the cQED architecture composed of a flux qubit galvanically coupled to an inhomogeneous resonator, the Hamiltonian that describes the dynamics reads
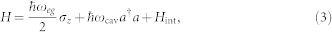 |
with an effective tunable interaction Hamiltonian
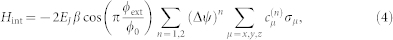 |
where EJ is the Josephson energy, β is a parameter that depends on the Josephson junctions size, ϕ0 = h/2e is the flux quantum, and ϕext is an external flux through a superconducting loop. The latter in turn allows to switch on/off the qubit-resonator coupling strength. Δψ stands for the phase slip shared by the resonator and the flux qubit. And, the coefficients 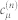 can be tuned33,34,35 at will via additional external fluxes (see Supplementary information).
can be tuned33,34,35 at will via additional external fluxes (see Supplementary information).
Adiabatic evolution
We obtain the effective system Hamiltonian 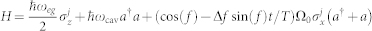 from Eqs. (3) and (4), if we consider an external flux that varies linearly with time according to
from Eqs. (3) and (4), if we consider an external flux that varies linearly with time according to 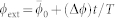 , where
, where 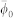 is an offset flux and Δϕ is a small flux amplitude.
is an offset flux and Δϕ is a small flux amplitude.
We remark that all our simulations presented so far assume no loss in both the qubit and resonator. Nonetheless, the open system analysis of a USC system40 can be carried out by studying dynamics of the microscopic master equation (see Supplementary information). In Fig. 5, we show numerical results for the storage and retrieval processes of an arbitrary superposed state |ψs〉 in presence of external noises. With our scheme and a simple decoherence model, we estimate fidelity of 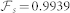 at the end of the retrieval process.
at the end of the retrieval process.
Figure 5. Fidelity plots.
(a) Storage process for a quantum state |ψs〉 = αF|ψ0〉 + βF|ψ1〉. (b) Retrieval process. In both cases, we plot the fidelity between the initial |ψ〉s and the instantaneous state |ψ(t)〉, i.e., 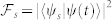 , while we introduce external noises Γx = Γy = Γz = 10−3ωeg and Γr = 10−4ωeg into our close system with the help of the microscopic derivation40. Here, Γx, Γy, Γz and Γr are rates of bit-flip noises, dephasing noise of the qubit, and the resonator relaxation, respectively. The system parameters are ωcav = 1, ωeg = 0.1 ωcav, Ω0 = ωcav, and the total evolution time is T = 105/ωcav.
, while we introduce external noises Γx = Γy = Γz = 10−3ωeg and Γr = 10−4ωeg into our close system with the help of the microscopic derivation40. Here, Γx, Γy, Γz and Γr are rates of bit-flip noises, dephasing noise of the qubit, and the resonator relaxation, respectively. The system parameters are ωcav = 1, ωeg = 0.1 ωcav, Ω0 = ωcav, and the total evolution time is T = 105/ωcav.
Author Contributions
All authors T.H.K., S.F., G.R., E.S. and L.-C.K. contributed equally to the results.
Supplementary Material
Supplementary Information for
Acknowledgments
The authors acknowledge support from the National Research Foundation & Ministry of Education, Singapore; Spanish MINECO FIS2012-36673-C03-02; UPV/EHU UFI 11/55; Basque Government IT472-10; and CCQED, PROMISCE, SCALEQIT EU projects. We also thank Lorenzo Maccone and Seth Lloyd for their helpful comments.
References
- Pritchett E. J. & Geller M. R. Quantum memory for superconducting qubits. Phys. Rev. A 72, 010301 (2005). [Google Scholar]
- Morimae T. Low-temperature coherence properties of Z2 quantum memory. Phys. Rev. A 81, 022304 (2010). [Google Scholar]
- Reim K. F. et al. Single-Photon-Level Quantum Memory at Room Temperature. Phys. Rev. Lett. 107, 053603 (2011). [DOI] [PubMed] [Google Scholar]
- Saito S. et al. Towards Realizing a Quantum Memory for a Superconducting Qubit: Storage and Retrieval of Quantum States. Phys. Rev. Lett. 111, 107008 (2013). [DOI] [PubMed] [Google Scholar]
- Jaeger R. C. & Blalock T. N. Microelectronic Circuit Design (McGraw-Hill, Dubuque, 2003). [Google Scholar]
- Blais A., Huang R. S., Wallraff A., Girvin S. M. & Schoelkopf R. J. Cavity quantum electrodynamics for superconducting electrical circuits: An architecture for quantum computation. Phys. Rev. A 69, 062320 (2004). [Google Scholar]
- Chiorescu I. et al. Coherent dynamics of a flux qubit coupled to a harmonic oscillator. Nature 431, 159 (2004). [DOI] [PubMed] [Google Scholar]
- Wallraff A. et al. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 431, 162 (2004). [DOI] [PubMed] [Google Scholar]
- Bourassa J. et al. Ultrastrong coupling regime of cavity QED with phase-biased flux qubits. Phys. Rev. A 80, 032109 (2009). [Google Scholar]
- Niemczyk T. et al. Circuit quantum electrodynamics in the ultrastrong-coupling regime. Nature Phys. 6, 772 (2010). [Google Scholar]
- Forn-Díaz et al. Observation of the Bloch-Siegert shift in a qubit-oscillator system in the ultrastrong coupling regime. Phys. Rev. Lett. 105, 237001 (2010). [DOI] [PubMed] [Google Scholar]
- Casanova J., Romero G., Lizuain I., García-Ripoll J. J. & Solano E. Deep Strong Coupling Regime of the Jaynes-Cummings Model. Phys. Rev. Lett. 105, 263603 (2010). [DOI] [PubMed] [Google Scholar]
- Braak D. Integrability of the Rabi Model. Phys. Rev. Lett. 107, 100401 (2011). [DOI] [PubMed] [Google Scholar]
- Douçot B., Feigel'man M. V., Ioffe L. B. & Ioselevich A. S. Protected qubits and Chern-Simons theories in Josephson junction arrays. Phys. Rev. B 71, 024505 (2005). [Google Scholar]
- Nataf P. & Ciuti C. Protected Quantum Computation with Multiple Resonators in Ultrastrong Coupling Circuit QED. Phys. Rev. Lett. 107, 190402 (2011). [DOI] [PubMed] [Google Scholar]
- Houck A. A. et al. Generating single microwave photons in a circuit. Nature 449, 328 (2007). [DOI] [PubMed] [Google Scholar]
- Yin Y. et al. Catch and Release of Microwave Photon States. Phys. Rev. Lett. 110, 107001 (2013). [DOI] [PubMed] [Google Scholar]
- Wenner J. et al. Catching Shaped Microwave Photons with 99.4% Absorption Efficiency. Phys. Rev. Lett. 112, 210501 (2014). [Google Scholar]
- Srinivasan S. J. et al. Time-Reversal Symmetrization of Spontaneous Emission for High Fidelity Quantum State Transfer. Phys. Rev. A 89, 033857 (2014). [Google Scholar]
- Barends R. et al. Superconducting quantum circuits at the surface code threshold for fault tolerance. Nature 508, 500 (2014). [DOI] [PubMed] [Google Scholar]
- Jeffrey E. et al. Fast Accurate State Measurement with Superconducting Qubits. Phys. Rev. Lett. 112, 190504 (2014). [DOI] [PubMed] [Google Scholar]
- Chow J. M. et al. Implementing a strand of a scalable fault-tolerant quantum computing fabric. Nature Comm. 5, 4015 (2014). [DOI] [PubMed] [Google Scholar]
- Giovannetti V., Lloyd S. & Maccone L. Quantum Random Access Memory. Phys. Rev. Lett. 100, 160501 (2008). [DOI] [PubMed] [Google Scholar]
- Giovannetti V., Lloyd S. & Maccone L. Architectures for a quantum random access memory. Phys. Rev. A 78, 052310 (2008). [DOI] [PubMed] [Google Scholar]
- Cirac J. I., Ekert A. K., Huelga S. F. & Macchiavello C. Distributed quantum computation over noisy channels. Phys. Rev. A 59, 4249 (1999). [Google Scholar]
- Kimble H. J. The quantum internet. Nature 453, 1023 (2008). [DOI] [PubMed] [Google Scholar]
- Ekert A. K. Quantum cryptography based on Bell's theorem. Phys. Rev. Lett. 67, 661 (1991). [DOI] [PubMed] [Google Scholar]
- Bennett C. H. Quantum information and computation. Phys. Today 48(10), 24 (1995). [Google Scholar]
- Bennett C. H. et al. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 70, 1895 (1993). [DOI] [PubMed] [Google Scholar]
- Bennett C. H. et al. Purification of Noisy Entanglement and Faithful Teleportation via Noisy Channels. Phys. Rev. Lett. 76, 722 (1996). [DOI] [PubMed] [Google Scholar]
- Deutsch D. et al. Quantum Privacy Amplification and the Security of Quantum Cryptography over Noisy Channels. Phys. Rev. Lett. 77, 2818 (1996). [DOI] [PubMed] [Google Scholar]
- Nigg S. E. & Girvin S. M. Stabilizer Quantum Error Correction Toolbox for Superconducting Qubits. Phys. Rev. Lett. 110, 243604 (2013). [DOI] [PubMed] [Google Scholar]
- Romero G., Ballester D., Wang Y. M., Scarani V. & Solano E. Ultrafast Quantum Gates in Circuit QED. Phys. Rev. Lett. 108, 120501 (2012). [DOI] [PubMed] [Google Scholar]
- Makhlin Y., Scöhn G. & Shnirman A. Josephson-junction qubits with controlled couplings. Nature 398, 305 (1999). [Google Scholar]
- Grajcar M., Liu Y.-X., Nori F. & Zagoskin A. M. Switchable resonant coupling of flux qubits. Phys. Rev. B 74, 172505 (2006). [Google Scholar]
- Berry M. V. Quantal Phase Factors Accompanying Adiabatic Changes. Pros. R. Soc. Lond. A. 392, 45–47 (1984). [Google Scholar]
- Lang C. et al. Correlations, indistinguishability and entanglement in HongOuMandel experiments at microwave frequencies. Nature Phys. 9, 345 (2013). [Google Scholar]
- Felicetti S. et al. Dynamical Casimir effect entangles artificial atoms. Phys. Rev. Lett. 113, 093602 (2014). [DOI] [PubMed] [Google Scholar]
- Helmer F. et al. Cavity grid for scalable quantum computation with superconducting circuits. Europhys. Lett. 85, 50007 (2009). [Google Scholar]
- Ridolfo A., Leib M., Savasta S. & Hartmann M. J. Photon Blockade in the Ultrastrong Coupling Regime. Phys. Rev. Lett. 109, 193602 (2012). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Information for