Metabolic theory predicts whole-ecosystem properties

Significance

A theory is presented which shows how the metabolism of individual organisms controls the flow of carbon through ecosystems. The theory synthesizes top-down, ecosystem-level and bottom-up, organism-level approaches to ecological energetics and material cycles. The theory predicts a very simple straight-line relationship between residence time of carbon molecules and the ratio of whole-ecosystem biomass to primary productivity. This and additional predictions for total throughfow and recycling are supported by numerical models and data from real ecosystems. The theory provides a powerful way to understand the roles of organisms in ecosystem processes at scales from local habitats to the biosphere. Such an understanding is important for addressing the impacts of human-caused changes in climate, land use, and biodiversity.

Abstract

Understanding the effects of individual organisms on material cycles and energy fluxes within ecosystems is central to predicting the impacts of human-caused changes on climate, land use, and biodiversity. Here we present a theory that integrates metabolic (organism-based bottom-up) and systems (ecosystem-based top-down) approaches to characterize how the metabolism of individuals affects the flows and stores of materials and energy in ecosystems. The theory predicts how the average residence time of carbon molecules, total system throughflow (TST), and amount of recycling vary with the body size and temperature of the organisms and with trophic organization. We evaluate the theory by comparing theoretical predictions with outputs of numerical models designed to simulate diverse ecosystem types and with empirical data for real ecosystems. Although residence times within different ecosystems vary by orders of magnitude—from weeks in warm pelagic oceans with minute phytoplankton producers to centuries in cold forests with large tree producers—as predicted, all ecosystems fall along a single line: residence time increases linearly with slope = 1.0 with the ratio of whole-ecosystem biomass to primary productivity (B/P). TST was affected predominantly by primary productivity and recycling by the transfer of energy from microbial decomposers to animal consumers. The theory provides a robust basis for estimating the flux and storage of energy, carbon, and other materials in terrestrial, marine, and freshwater ecosystems and for quantifying the roles of different kinds of organisms and environments at scales from local ecosystems to the biosphere.

In most ecosystems, energy and materials flow through trophic networks comprised of plant primary producers, animal consumers, and microbial decomposers (Fig. 1). The individual organisms that make up these networks control the storage and flux of energy, carbon, and other materials. Consequently, a theoretical framework that can account for how different kinds of organisms and ecosystems affect fluxes and stores of energy and materials in ecosystems is central to understanding the carbon cycle of the biosphere and to predicting the impacts of human-caused changes in climate, land use, and biodiversity (1–3). Although it has long been recognized that different kinds of organisms play important roles in the processing of energy and materials in ecosystems, existing treatments are incomplete. Most studies have focused on particular trophic levels, such as primary producers or herbivores, specific ecosystem types, such as tropical forest or pelagic marine, or single species, such as top predators or ecosystem engineers (4–14). Still missing is a simple mechanistic theory that can make precise, quantitative predictions based on the mechanistic relationships between traits of the organisms in the different trophic levels and whole-ecosystem properties, such as carbon flux or recycling.

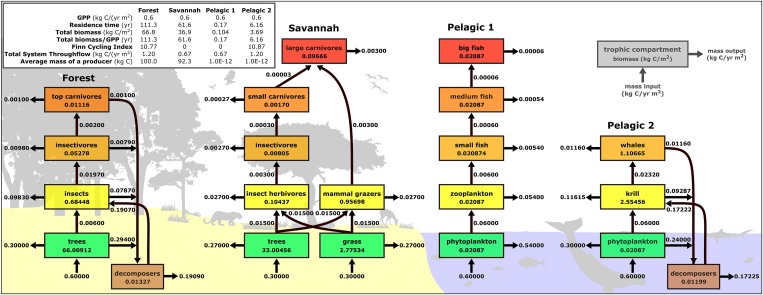
Fig. 1.

Examples of four idealized trophic networks used for numerical analysis showing pathways of carbon flow from primary producers through successive trophic levels of animal consumers to top predators; Forest and Pelagic 2 networks also have cycling via a decomposer loop. Numbers in each box give total biomass in the trophic compartment (kg C/m²), and the arrows in and out of each box give the flux of biomass (kg C/y⋅m²) in and out of the compartment, respectively. Details of model construction and simulation are in Materials and Methods, with additional parameter values in SI Appendix, Table S1 and Fig. S1: Forest (model 2a); Savannah (model 7a), Pelagic 1 (model 3), and Pelagic 2 (model 6a).

Two main theoretical frameworks have been used to quantify and synthesize information on energy and material cycling in ecosystems. Systems theory (15, 16) is a top-down approach that quantifies the fluxes and stores of energy or materials among functional compartments and derives emergent whole-ecosystem properties, including average residence times of carbon and other molecules, total system throughflow (TST; the sum of all flows in the system), and the Finn cycling index (FCI; the percentage of organic carbon that is recycled through the decomposer loop). Metabolic theory (17, 18) is a bottom-up approach that quantifies the fluxes and stores of energy and materials within organisms and uses the scaling of metabolic rate with body size and body temperature to predict structural and functional characteristics at multiple levels of organization from individual organisms to ecosystems (6, 19–24). Both approaches are grounded in universal physical laws and established biological principles.

In this paper, we synthesize these two frameworks to show how the traits of individual organisms give rise to ecosystem properties. Our analytical mathematical and numerical simulation models show how residence times of carbon in ecosystems vary with the body size and temperature of the constituent organisms and how TST and FCI are determined by primary production and carbon flows between organisms. We use data on carbon fluxes in organisms and ecosystems to test the assumptions and predictions of the theory. The approach can be expanded straightforwardly to analyze many aspects of the flux and storage of energy and materials in the biosphere.

Theory

The carbon cycle in the biosphere, and in the organisms, populations, food webs, and ecosystems that comprise the biosphere, is controlled by biological metabolism. Individual organisms take up carbon compounds from the environment, transform and retain them within their bodies, and ultimately release them back into the environment (Fig. 1). Carbon and energy budgets are intimately related. Carbon dioxide, water, and solar energy are incorporated into the high-energy bonds of organic compounds of plant producers during photosynthesis. When the organic bonds are broken during respiration, plants, animal consumers, and microbial decomposers obtain usable energy in the form of ATP.

In any organism, population, trophic compartment, or ecosystem where the flux of carbon is in steady state, the rate of uptake equals the rate of loss and the total number of molecules within the system remains constant. At steady state, the loss rate equals the uptake rate, so the average residence time of carbon molecules in the system ($\widehat{t}$) is then equal to total biomass (B, in carbon units) divided by the uptake rate (P)

$$\widehat{t}=B/P.$$ [1]

This follows straightforwardly from mass balance (SI Appendix; we use the $\widehat{t}$ notation to indicate average residence time at steady state). Rate of carbon uptake is the rate of gross primary production in autotrophic cyanobacteria, algae, and higher plants, which obtain energy from sunlight, and the rate of gross assimilation in heterotrophic bacteria, fungi, and animals, which obtain energy by consuming living or dead biomass. These uptake rates scale similarly to the metabolic rates of the organisms (17, 25), which are usually measured in units of power but can equally well be expressed in units of carbon. Following Eq. 1, the average residence time (${\widehat{t}}_{ind}$) of a carbon molecule in an individual organism with uptake rate (P_ind) and body mass (M_ind) is

$${\widehat{t}}_{ind}=M_{ind}/P_{ind}.$$ [2]

Residence time of carbon varies among organisms by orders of magnitude, from minutes in some microbes to centuries in some plants (17, 26). Most of this variation can be understood using metabolic scaling theory and allometry, where the metabolic rates of individuals characteristically scale as a power function of body mass and an exponential function of temperature

$$P_{ind}=P_0{M}_{ind}^{\beta }{e}^{-E/kT},$$ [3]

where P₀ is a normalization constant that varies between taxa and environments, β is the mass scaling exponent, E is an activation energy that gives the temperature dependence, k is Boltzmann’s constant; and T is temperature in kelvin (17, 27, 28). Average residence time of carbon molecules within an individual is obtained by substituting Eq. 3 into Eq. 2, giving

$${\widehat{t}}_{ind}=M_{ind}/P_{ind}=M_{ind}/\left(P_0{M}_{ind}^{\beta }{e}^{-\left(E/kT\right)}\right)=P_0^{-1}{M}_{ind}^{1-\beta }{e}^{E/kT}.$$ [4]

Metabolic theory and available data suggest β is ∼3/4 (17), so Eq. 4 predicts that whole-organism rates of carbon uptake increase ∼15 orders of magnitude with the ∼20 orders of magnitude increase in body size from microbes to trees and whales. Consequently, carbon residence times should scale as α = 1 − β or ∼1/4, increasing by about five orders of magnitude over the same size interval (Fig. 2A). Theory and available data suggest that E is ∼0.65 eV (i.e., rates increase about 2.5 times with every 10°C) (17, 27–29), meaning that uptake rates increase and residence times decrease exponentially with temperature, varying by about 40-fold over the range 0–40 °C (Fig. 2D).

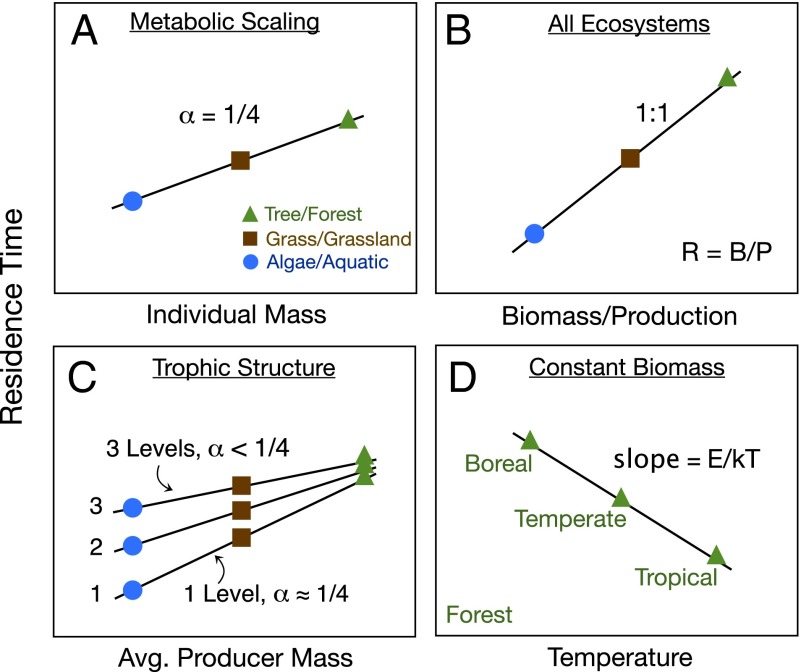
Fig. 2.

Schematic presentations of model predictions for residence time plotted on logarithmic axes with α giving the scaling exponent. (A) Residence time or half-life of carbon (${\widehat{t}}_{ind}$) within an individual organism increases with increasing body mass as a power function with α = 1/4. (B) Residence time of carbon within an ecosystem increases linearly with the ratio of total biomass to primary productivity (Eq. 1) so all ecosystems fall along a single line with slope = 1.0. Position of different ecosystem types along this line vary: residence times increase with increasing body sizes of the organisms and decrease with increasing environmental temperature. (C) If the temperature remains constant, residence times of different ecosystems generally increase with increasing body sizes of the primary producers, from pelagic marine ecosystems with tiny phytoplankton to forests with large trees. The slope of this relationship is <1/4, because animal consumers contribute proportionately more to total biomass in pelagic marine ecosystems, whereas trees dominate the biomass of forests. (D) If total biomass remains constant, residence times of different ecosystems decrease with increasing environmental temperature.

Many ecosystems are composed of organisms of different kinds, organized into networks of trophic compartments that flux carbon, other materials, and energy from photosynthetic primary producers to heterotrophic consumers (Fig. 1). Initially, for purposes of illustration, we develop the theory in terms of such autotrophy-based ecosystems. The uptake rate of any compartment is simply the sum of the uptake of all individuals. Similarly, the total biomass of any compartment is the sum of the masses of all individuals. Following Eq. 1, the average residence time of carbon within any compartment is equal to the total biomass divided by the total uptake rate. The expression for residence time in an entire ecosystem is slightly different, however, because the relevant uptake rate is of carbon entering the system, so in autotrophy-based ecosystems (Fig. 1), it is the rate of gross primary production (GPP). Ecosystem biomass is the sum of the body masses of all individual organisms in all trophic compartments. From Eq. 1 it follows that ${\widehat{t}}_{eco}=B_{eco}/P_{pro}$, where the subscript eco indicates the entire ecosystem and the subscript pro indicates that production rate is summed only for the primary producers. Therefore, in a plot of ${\widehat{t}}_{eco}$ as a function of $B_{eco}/P_{pro}$, all ecosystems fall along a single line through the origin with slope = 1.0, as in Fig. 2B. The positions of ecosystems along this line vary widely, however, depending on the body size and body temperature of the component organisms and on aspects of trophic organization, such as the number of trophic levels and amount of cycling. The exact residence time for any ecosystem can easily be calculated by applying Eq. 4 and substituting appropriate values for the uptake rate, body mass, and body temperature of the organisms (which we assume to be equal to environmental temperature for all organisms except endothermic birds and mammals) to obtain

$${\widehat{t}}_{eco}=B_{eco}/P_{pro}={{\displaystyle \sum }}^{}{M}_{ind}/{{\displaystyle \sum }}^{}{P}_{pro}={{\displaystyle \sum }}^{}{M}_{ind}/{{\displaystyle \sum }}^{}\left(P_0{M}_{pro}^{\beta }{e}^{-\left(E/kT\right)}\right).$$ [5]

The above theory makes four predictions for residence times that are shown schematically in Fig. 2:

• 1)For individual organisms, Eq. 4 predicts that residence time or half-life of carbon and other elements increases with increasing body size, with a slope of α ∼ 1/4 (Fig. 2A), and decreases with increasing temperature, with E ∼ 0.65 eV.
• 2)For ecosystems, Eqs. 1 and 5 predict that ${\widehat{t}}_{eco}=B_{eco}/P_{eco}$, so in a graph of residence times as a function of the ratio of total biomass to GPP, all ecosystems fall along a single line through the origin with slope = 1.0 (Fig. 2B).
• 3)For ecosystems, it follows from Eq. 5 that residence time is positively correlated with the body size of the primary producers, provided they account for a large fraction of total ecosystem biomass. In such cases, for example in forests dominated by trees, residence time scales with producer body mass, with α ∼ 1/4. However, when producers are small, such as pelagic systems with phytoplankton, they comprise a smaller fraction of total biomass, and the slope of this relationship is <1/4 (Fig. 2C).
• 4)For ecosystems, Eq. 5 predicts that residence time decreases exponentially with environmental temperature, and therefore with the body temperatures of all organisms except for endothermic birds and mammals, so residence times are longer in cold high-latitude than warm tropical ecosystems (Fig. 2D).

Although residence time was our primary focus, we also modeled how organismal metabolism affects two other emergent properties of ecosystems: TST and extent of recycling, as measured by the FCI (30–32). TST is the sum of all trophic flows in the system. FCI gives the percentage of molecules of organic carbon (or energy) that is recycled through the decomposer loop, in which microbes consume nonliving organic detritus and are themselves consumed by heterotrophic consumers (e.g., the second trophic level in the Forest and Pelagic 2 networks in Fig. 1). We now derive TST and FCI in terms of the flow of carbon into the system from photosynthesis (P), the metabolic induced flow of carbon at each trophic level (P_i), the number of trophic levels (n), and the efficiency of carbon transfer between trophic levels (TTE). TTE is expressed as a fraction of the carbon or energy transferred between two trophic compartments. Due to the second law of thermodynamics and the limited efficiency of metabolic biochemistry, TTE is always less than 1 and empirically often ranges between 0.01 and 0.2. We distinguish the TTE for three different fluxes of carbon: (i) the proportion of carbon leaving one trophic level and going to the next highest level is t = $\left(P_{i+1}/P_i\right)$, where $P_i$ and $P_{i+1}$ are the gross uptake rates of two successive trophic levels; (ii) the proportion leaving each trophic level and going to decomposers is d₁; and (iii) the proportion leaving decomposers and going to level 2 is d₂. Here, we assume that t, d₁, and d₂ are constant. Now the uptake of carbon by level 2 (i.e., P₂) can be divided into that coming directly from producers, Pt; that coming from producers via decomposers, Pd₁d₂; and that coming from higher levels via decomposers, P₂d₁d₂ (1 + t + t² +…+ tⁿ⁻²), which is a geometric series. Hence, P₂ = P(t + d₁d₂) + P₂d₁d₂ (1 − t^n-1)/(1 – t), i.e., P₂ = P(t + d₁d₂)(1 – t)/[1 – t – d₁d₂ (1 – tⁿ⁻¹)], and therefore

$$\mathrm{TST}=\left(P+P_2\frac{1-t^{n-1}}{1-t}\right)\left(1+d_1\right).$$ [6]

FCI is given by the sum of the flows through each compartment that have previously passed through them (TST_C) multiplied by 100 and divided by TST. In cases such as Fig. 1 where there is just one compartment at each trophic level and the flow from decomposers goes only to level 2, TST_c is given by

$$TS{T}_c=\frac{d}{1-t}\left(P{d}_1\left(1-t^{n-1}\right)+P_2\left\{d_1\frac{{\left(1-t^{n-1}\right)}^2}{1-t}+\frac{1-t^{2n-2}}{1-t^2}-\frac{t^{n-1}-t^{2n-2}}{1-t}\right\}\right).$$ [7]

See SI Appendix for proof. The above expressions for TST and FCI have not previously been derived for ecosystems. More generally our theory predicts

• 5)Because flows between successive trophic levels decrease rapidly up the trophic network (Fig. 1), TST is determined primarily by variation in GPP, which constitutes the largest fraction of TST. Therefore, TST should be strongly positively correlated with GPP, and it should secondarily increase with trophic transfer efficiency between trophic levels (t) and the strength of the decomposer recycling loop (Eq. 6).
• 6)Recycling of carbon occurs only through the decomposer loop, so FCI must be small. Where there is just one compartment at each trophic level it follows from Eqs. 6 and 7 that FCI ∼ 100d₁d₂(d₁ + t) if t, d₁, and d₂ are small (SI Appendix).

Numerical Simulations

To explore the implications of our theory, we created numerical models of idealized autotrophy-based ecosystem networks (SI Appendix, Table S1; see examples in Fig. 1). We assumed steady-state and enforced mass and energy balance on the inputs and outputs to each trophic compartment and hence throughout each network. We evaluated a wide variety of autotrophy-based networks designed to capture idealized but realistic properties of natural ecosystems: (i) terrestrial and marine; (ii) primary producers varying in size by 14 orders of magnitude from unicellular algae to grasses to trees; (iii) consumers varying in size by 14 orders of magnitude from zooplankton and insects to elephants and whales; (iv) environmental temperatures ranging from 7 °C to 27 °C; (v) containing both ectothermic consumers with body temperatures equal to environmental temperature and endothermic consumers with body temperatures equal to 37 °C; and (vi) with various amounts of recycling of detritus through the decomposer loop. Metabolic rate was assumed to vary with body mass and temperature according to Eq. 3. Four of these networks and their parameters are shown in Fig. 1, with details for all networks provided in SI Appendix, Table S1. Methods used to construct the networks and run simulations are described below.

Results of the numerical simulation models supported all of the above predictions. Residence times scaled linearly as the ratio of total biomass to GPP with a slope of 1.0, so ${\widehat{t}}_{eco}=B_{eco}/P_{eco}$ (Fig. 3A). Residence time was positively correlated with the body size of the primary producers. The slope of this relationship was <1/4 as predicted, because tiny phytoplankton comprised a lower fraction of total ecosystem biomass in pelagic marine ecosystems with than did large trees in forest ecosystems (Fig. 3B).

Fig. 3.

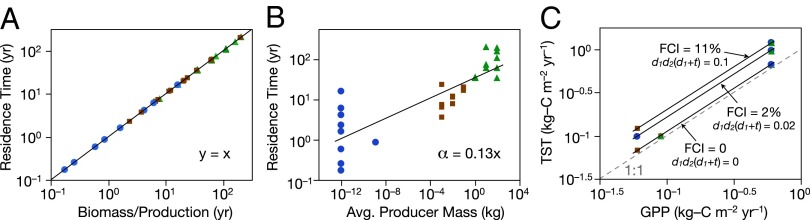
Tests of the theoretical predictions in Fig. 2 C and D with outputs of numerical simulation models of 37 idealized ecosystems. Symbol color and shape as in Fig. 2A. Solid black lines are GLM regression fit. (A) In a graph of residence times as a function of the ratio of total biomass to GPP, all ecosystems fell along a single line with slope = 1.0, so ${\widehat{t}}_{eco}=B_{eco}/P_{eco}$. (B) Residence time was positively correlated with the body size of the primary producers divided by GPP with α = 0.13, so <1/4 because of relatively long residence times in pelagic marine ecosystems. (C) TST increased primarily with increasing GPP and secondarily with the strength of the decomposer recycling loop. All 37 models are plotted here.

System properties calculated from the numerical models using Ecological Network Analysis (33) matched those calculated from Eqs. 6 and 7. The numerical models also supported the above predictions for TST and recycling (FCI). TST was positively correlated with GPP (r = 0.73), and also positively correlated with FCI (r = 0.54). TST was mainly determined by GPP, but also increased as the strength of the decomposer loop increased (Fig. 3C). An advantage of using Eq. 7 or its approximation with FCI ∼ 100d₁d₂(d₁ + t) is that this shows explicitly the individual contributions to FCI made by the trophic transfer efficiencies t, d₁, and d₂. FCI was always low; it varied from about 0% to 11% (SI Appendix, Table S1), as the percentage of carbon flowing through the decomposers varied from 0% to 10%.

The numerical models confirmed the predictions of the analytical theory that average residence times of carbon molecules in ecosystems vary (i) by orders of magnitude with the body sizes of the primary producers, from weeks in pelagic marine ecosystems with minute phytoplankton to centuries in forests with giant trees; and (ii) with trophic structure, increasing with number of trophic levels and body sizes of top predators. The numerical models also supported our theoretical predictions for total system throughflow and recycling.

Empirical Validation

The ultimate test of our theory will be its ability to predict and explain properties of real ecosystems. We performed preliminary validation by comparing theoretical predictions with available data (Fig. 4). The prediction that residence times within individual organisms scale with body mass with α ∼ 1/4 was confirmed by compiling and analyzing published data from physiological studies of half-life of carbon and nitrogen in animals (Fig. 4A). The dependence of residence time in ecosystems on the body sizes of primary producers was assessed using a large existing dataset (10). As predicted, the observed α = 0.21 was somewhat less than 1/4 (Fig. 4B). The predicted dependence of ecosystem residence time on environmental temperature was also supported; the data in Fig. 4B were already temperature-corrected using Eq. 3, which substantially reduced variation around the regression line. The prediction that ${\widehat{t}}_{eco}=B_{eco}/P_{eco}$ was evaluated using a different but overlapping dataset (12). A plot of average residence times of carbon in the ecosystems (${\widehat{t}}_{eco}$) as a function of total biomass $\left(B_{eco}\right)$ over the uptake rate (GPP, or $B_{pro}$) showed the data clustering around the predicted linear relationship with slope = 1.0 (95% CI includes slope = 1.0; Fig. 4C). Overall, the empirical data showed that residence time of carbon in both individual organisms and entire ecosystems increased with increasing system biomass. Residence time in ecosystems increased by about four orders of magnitude, from 0.05 to 100 yr, as the size of primary producers increased from tiny algae in pelagic marine ecosystems to large trees in forests.

Fig. 4.

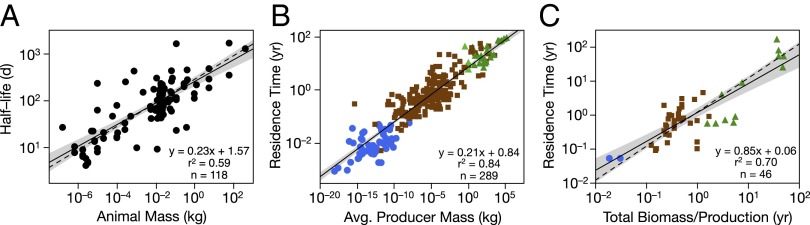
Empirical data for the residence time of carbon and nitrogen for diverse organisms and ecosystem types. Symbol color and shape as in Fig. 2A. Solid black lines are GLM regression fits (gray shading is the 95% confidence band), and black dotted lines are our predicted relationships from our theory. (A) Within individual organisms the half-life of carbon and nitrogen increases with body mass with a slope of 0. 23 ± 0.03 95% CI (this includes our predicted slope of 0.25, see prediction 1 in main text). These data have been temperature corrected to 15°C and include a large diversity of tissue types (Materials and Methods and SI Appendix, Table S2). As we also predict, in entire ecosystems, carbon residence times increase with (B) increasing body size of the primary producers (slope is 0.21 ± 0.02 95% CI; expected slope is <0.25 depending on the network, see prediction 3 in main text), data replotted from Allen et al. (10), and (C) the ratio of total biomass to primary production (slope is 0.85 ± 0.17 95% CI, see prediction 2 in main text). Production is GPP, determined by doubling NPP values in ref. 12 as per ref. 45. For terrestrial systems, biomass = plant and herbivore biomass. For freshwater pelagic systems, biomass = 3 × producer mass (46).

Discussion

The above metabolic theory of ecosystem properties provides a robust basis for estimating the flux and storage of carbon, other materials, and energy in terrestrial, marine, and freshwater ecosystems throughout the world. The theory makes two important advances over previous treatments. It shows (i) how carbon residence time and other whole-ecosystem properties depend on biological metabolism and specifically on the effects of body sizes and temperatures of the organisms in the different trophic levels; and consequently, (ii) that residence time increases linearly with the ratio of two ecosystem-level properties, total biomass, and gross primary production, so that that ${\widehat{t}}_{eco}=B_{eco}/P_{eco}$ and all ecosystems fall along the same line with slope = 1.0. Additionally, it predicts that the absolute values of residence time (i.e., the position along the line) increase by several orders of magnitude with increasing body sizes of the primary producers (from algae to large trees) and by a factor of about 40 with decreasing environmental temperature (from 40 °C to 0 °C). The predictions are relatively insensitive to the precise scaling of metabolic rate with body size and temperature (values of β and E in Eq. 3), but somewhat more sensitive to variation in the trophic transfer efficiency between levels, t, and the strength of the decomposer recycling loop d₁d₂(d₁ + t). These predictions are supported by numerical simulation models parameterized with realistic values and by empirical data for real ecosystems.

There is abundant scope to test, extend, and apply our theory. We have evaluated the theory using data from only a modest number of simulated and real autotroph-based ecosystems and analyzing the effect of only a few variables. However, because the theory incorporates theoretically and empirically well-established scaling relations, it can be generalized and applied to a wide variety of systems. For example, it can be extended to other elements in addition to carbon and used to address roles of organisms in nutrient cycling. It can be applied to subsystems within ecosystems, such as single trophic levels or individual organisms (see analysis of residence times of carbon and nitrogen molecules within individual organisms in Fig. 4A). Finally, the theory can be applied to address the roles of different kinds of organisms in heterotrophy-based ecosystems, such as the soil and deep sea, where the input of carbon is in preformed organic molecules (detritus) rather than CO₂ fixed in photosynthesis.

Additionally instead of carbon, units of energy or other elements could be used, for example, to explore metabolic effects on nutrient cycling. The theory suggests ways to parameterize and evaluate the accuracy of empirically derived trophic networks. For example, Fig. 4B shows that the predicted linear relationship between residence time and the ratio of total biomass to primary productivity, ${\widehat{t}}_{eco}=B_{eco}/P_{eco}$, is strongly supported, but there is considerable unexplained residual variation. All of our analyses support Eq. 1; the deviations from exact linear scaling in Fig. 4B are presumably due to violations of model assumptions, such as steady-state or mass balance, or to measurement errors. Because we demonstrated that Eq. 1 is robustly supported by mathematical theory, numerical simulations, and empirical evidence, deviations from exact linear scaling in Fig. 4B are presumably due to violations of model assumptions, such as steady-state or mass balance, or to measurement errors. Although there are many datasets on ecosystem properties (34), most do not contain information on the body sizes and temperatures of the organisms in each trophic compartment, making them problematic for rigorous empirical evaluation of our theory. There are also significant challenges in precisely measuring GPP, total biomass, and residence time for entire ecosystems (34). The assumption of steady state is especially critical, and it can potentially be evaluated by estimating mass and energy balance at different levels, from individual organisms to trophic compartments to the entire ecosystem. To account accurately for the carbon budget, it is important not only to include all photosynthesis, respiration, and fluxes between trophic levels but also any net export or storage of organic carbon.

Our theory extends the bottom-up individual-based framework of metabolic theory (10, 17, 35) to ecosystems to incorporate organisms and their metabolism explicitly into ecological systems theory (15, 16, 20, 21, 31). It reveals how the size and temperature of the plants, animals, and microbes in different trophic compartments affect carbon residence time, and other emergent ecosystem properties such as TST and recycling (FCI). Systems ecologists have predicted that TST and FCI increase over time as ecosystems reorganize during ecological succession or evolve over geological time (15, 16, 21). Our theory and numerical models show that, although this may be true, the magnitudes of changes are limited by powerful metabolic constraints: TST by GPP and FCI by d₁d₂(d₁ + t). TST is predicted to increase over primary and secondary succession, due primarily to an increase in GPP. Recycling is also expected to increase as ecosystems age. Over both ecological and evolutionary time the number of species and metabolic pathways should increase as different microbes colonize and evolve, consuming detrital resources more completely by adding specialized pathways to obtain energy from diverse and refractory organic compounds (such as lignin or chitin). The magnitude of recycling of carbon and energy through microbial loops is modest and strongly constrained by the Second Law of Thermodynamics as shown by Finn (32) and above in the powerful constraint on d₁d₂(d₁ + t) (Fig. 1 and Eq. 7). However, our analyses apply only to cycling of organic carbon or energy, which are dissipated in the trophic network as organic molecules are metabolized. A much greater proportion of nutrients, such as nitrogen or phosphorous, may be recycled (32).

Our theory not only generates testable predictions that are supported by data from real systems, it also provides a powerful basis for assessing natural spatial and temporal variation and impacts of human activities on the carbon cycle. With respect to natural variation, the model should provide a straightforward and robust basis for quantitatively estimating the flux rates and residence times of carbon in different ecosystems based on the body sizes of the dominant organisms (especially the primary producers) and temperature. Collection and synthesis of such data should provide a quantitative basis for assessing the contributions of different ecosystem types and geographic regions (e.g., tropical vs. high latitude, marine vs. terrestrial, forest vs. grassland) to the global carbon cycle. Our theory should also help predict human impacts on the carbon cycle on scales from local ecosystems to the biosphere. For example, overharvesting of large animals can significantly alter ecosystem biomass and GPP, impacting carbon residence times (3, 36–38). Both deforestation, which replaces forests with agricultural fields and grasslands (39–42), and a warmer climate, which increases metabolic rates, should decrease the residence time of carbon in local ecosystems and in the biosphere as a whole. More generally, our theory is a synthesis of systems and metabolic approaches that shows explicitly and quantitatively how organisms control the carbon cycle at all scales from individuals to ecosystems to the biosphere.

Materials and Methods

Numerical Model.

Fig. 1 represents four examples of how we modeled the carbon flows between the compartments of ecosystems in our numerical simulations. All individuals within a compartment were for simplicity assumed to have the same individual body mass m. The order of calculations was as follows: (i) calculate the carbon uptake $P_{ind}$ of each individual primary producer (kg C/ind⋅y) using Eq. 3 with parameter values P₀ = 2.16 × 10⁹ (25); k = 8.62 × 10⁻⁵ eV/K; E = 0.65 eV; ectotherm T = 7 °C or 20 °C or 27 °C or 37 °C; $\beta$ = 0.67 or 0.75; (ii) calculate total number of individuals in the compartment, assuming net primary production = 1/2 GPP (kg C/y⋅m²), and then n = 0.5 GPP/$P_{ind}$ (ind/m²) (43, 44); (iii) calculate total biomass in the compartment, X = N × M (kg/m²); (iv) using a trophic transfer efficiency t, calculate carbon flow to the next trophic level (t = 0.1 for all TTEs not associated with the decomposers, but some models t = 0.01 between trophic levels 1 and 2 only; SI Appendix, Table S1); and (v) repeat steps i–iv, replacing primary producers by the individuals in the next trophic level. For models with decomposers, all compartments transferred d₁ = 0.40 to decomposers, and the decomposer trophic transfer efficiencies were assumed to be either d₂ = 0.1 or 0.5 depending on model objective. Thirty-six such models were constructed. Once all carbon storages and flows (intercompartmental, input, and output) were known for the balanced model, ecological analysis software (33) was used to calculate TST, FCI, and residence time. An Excel spreadsheet was used to calculate the parameters for each trophic network (Fig. 1 and SI Appendix, Table S1 and Fig. S1).

Empirical Data.

Data to test how body size affects residence times of C and N in individual organisms (Fig. 4A) were obtained from the literature (SI Appendix, Table S2). These data were recorded as half-lifes—the amount of time required for the stable-isotopic signature of tissue to reach a midpoint between the enriched and original value—and were not converted to residence times because of differences between studies in how half-life was calculated. Data in Fig. 4A were temperature corrected to 15 °C using Eq. 3. Empirical evaluation of our predictions for residence times in ecosystems (Fig. 4 B and C) requires high-quality data on residence time (or turnover rate), total biomass, and GPP for real ecosystems composed of organisms of varying size operating at different environmental temperatures. Despite a plethora of empirical whole-ecosystem models, especially in marine habitats (30), only a few studies provide independently measured estimates of all three variables. From a large dataset compiled by Cebrian et al. (12), we obtained the relevant data for 46 ecosystems representing a variety of habitats (terrestrial and marine), environmental temperatures (temperate to tropical), and organism body sizes (phytoplankton to trees and whales). The predicted dependence of ecosystem residence time on the body sizes of primary producers was evaluated using a different but overlapping dataset (10).