Protein dynamics and the enzymatic reaction coordinate

Introduction

Fifteen years ago we suggested¹ that a possible explanation for anomalous experimental enzyme kinetics may be direct coupling of picosecond protein dynamics to reaction. The last 15 years have seen this suggestion, and in fact the general proposal that enzyme dynamics is important in enzyme chemistry debated with unusual fervor. While the importance of protein motion to such phenomena as ligand rebinding in myoglobin² has been acknowledged and seemingly accepted for almost 40 years, the suggestion we made 15 years ago is different for 2 reasons. First, ligand binding, while a chemical event, does not involve change in chemical identity. This is a difference that is psychological, but the alteration in language associated with chemistry has proven significant. Second, the experimental claims made for ligand binding relate to conformational heterogeneity, implying that transitions between conformations are slow compared to the time to rebind, and so static on the timescale of the event of interest. Theoretical models can then be built from direct averaging over rate constants that are indexed by conformation³. We have proposed that protein motions on all timescales ranging from those equivalent to barrier passage (or penetration) to slow conformational rearrangement are potentially important for the chemical event in enzymes. These differences in focus between enzymatic chemistry and ligand binding have resulted in a significantly larger level of debate, and as such; this debate has focused the science very effectively. This focus has lent significantly greater clarity to the issues in the last few years, and these investigations will be the topic of this review.

A good part of the argument that has arisen around the subject of protein dynamics and enzymatic function has been driven by semantics, and so we now wish to clearly and carefully state the subject of this investigation. We quite simply wish to understand how enzymes work. From a chemist’s perspective, this means we want to understand in atomic detail how chemical reaction occurs at an enzyme active site. It is our goal to investigate this question in a completely unbiased fashion. The only “modeling” that has been used in the investigations we have reported come from the use of widely accepted numerical tools such as the CHARMM⁴ molecular mechanics potential augmented by QM/MM technologies⁵ at the reaction center. Our stated goal is to make no assumption as to mechanism, but rather to allow mechanism to be discovered in the process of the computations we undertake. This mechanism is described by the “reaction coordinate,” in other words the set of all atomic motions necessary to allow reaction to occur. Given the complexity of chemical reaction in enzymatic systems, special techniques are needed, and they will be described in this review.

We will review studies of three separate enzyme systems (lactate dehydrogenase (LDH), purine nucleoside phosphorylase (PNP), and dihydrofolate reductase (DHFR).) Most of our results will be theoretical, but in cases in which direct collaborations have resulted in experiment we will report those as well. The end result is that in both LDH and PNP, there is direct coupling of protein motion on the timescale of barrier passage as part of the basic mechanism or reaction coordinate. Further, in LDH we have shown evidence for the fact that this motion, or promoting vibration, is created by the protein architecture itself. In other words the motion that corresponds to the promoting vibration is not simply part of the reaction coordinate, is a unique direction in the protein structure. In DHFR, this is not in fact the case. There is no organized promoting vibration. We will discuss how these results fit with other results in the literature, both for specific enzymes and in the general framework of rate theories.

Dynamics in Enzymes and the reaction coordinate – the picosecond timescale

Since our suggestion 15 years ago that protein dynamics could play a role in passage over the chemical barrier in enzymatic systems, a continuing feature of interest to us and consternation to others has been the fact that the protein motion is quite rapid when considered relative to normal enzymatic turnover rates. Most enzymes have a turnover rate of about 1 per millisecond. The motions we have discovered – promoting vibrations – have been in the 100’s of femtosecond to pico-second timescale. In fact, several other investigators over the years have now found other enzymes in which such rapid promoting vibrations are of import⁶. There is of course no contradiction in this disparity of timescale; the rate-limiting step for many enzymes is in fact product release or substrate binding. What this implies is that the enzyme spends the vast majority of the time from its initial encounter with substrate until product release “engaged in activities” other than barrier passage (to be discussed in a later section.) In the following section of this review we discuss our results describing these rapid promoting vibrations. In particular we find that 2 of 3 enzymes of very different chemistry employ such a mechanism (LDH and PNP,) and one (DHFR,) which catalyzing the same chemistry as LDH appears to not support a promoting vibration. The section starts with a brief description of the computational methodologies we employ. Should this not be of interest to the reader, the section can be skipped.

Methodologies

In order to rigorously understand the process of chemical reaction in an enzyme using theoretical methods we need to follow the atomic motions in the entire system as reaction occurs. Because chemical reaction in an enzyme is an extremely rare event, simply running trajectories using quantum mechanics to determine reactive potential energy surfaces (QM/MM techniques for example) will not yield the desired information. What is needed is a rare event simulation methodology. We choose to use the Transition Path Sampling⁷ (TPS) methodology of Chandler and co-workers. The critical idea behind this advance was to find “reactive” trajectories for complex phenomena via a Monte Carlo walk in trajectory space. (The word reactive is in quotes because it certainly can be applied to situations in which chemical reaction is not involved⁸.) Gathering a large number of these trajectories allows further calculation of an object known as the stochastic separatrix⁹. The stochastic separatrix is the statistical analogue of the transition state, or more precisely, the transition state ensemble. It is the collection of points in conformation space where initiation of trajectories with random momenta chosen from a Boltzmann distribution will result in 50% of the trajectories proceeding to products and 50% returning to reactants.

In fact, this analysis of the stochastic separatrix provides methods for testing of a reaction coordinate. Motion along the stochastic separatrix is motion that does not progress the reaction to either products or reactants. Thus, a putative reaction coordinate can be tested by restraining the reaction coordinate degrees of freedom while all other degrees of freedom are allowed to evolve dynamically. If the choice of the degrees of freedom is correct, then unrestrained trajectories will yield a distribution of probabilities to react strongly peaked about .5. Initial methods of reaction coordinate identification involved such a “guess and check” approach. We have developed a method based on the structure of the separatrix itself¹⁰. This method is highly successful and extremely efficient; yielding a good representation of the reaction coordinate “for free” when the separatrix is calculated. The method is distinct from the committor distribution fitting methods that have been developed¹¹ for the determination of reaction coordinates. The fitting methods are best applied to diffusive barrier passage, whereas our methods are best applied to direct barrier passage; the kind most often encountered in enzymatic chemical reactions. Our definition of the components of the reaction coordinate is simply those degrees of freedom that do not change on the separatrix. In this sense then, the separatrix must be narrow in these degrees of freedom. The problem is that we do not have a mathematical description of the separatrix, only points in space. The separatrix is likely “narrow” in these special degrees of freedom in some non-Cartesian coordinate system. Thus what is needed is a method that identifies the correct parameterization of the separatrix and in doing so finds the coordinates for which there is minimal change. Finding the correct coordinate system in which to describe the separatrix is a non-linear fitting problem, and we use methods from machine learning known as kernel PCA¹². A usable representation of the topology of the separatrix is obtained when a single non-linear component is shown to accurately reproduce the entire separatrix. The members of the reaction coordinate are then identified as those that make minimal contribution to this single non-linear principle component. We have shown¹⁰, that the components found closely align with those we “guessed and checked” in the past. The identification of reaction coordinates will likely continue to be one of the most challenging areas in rare event simulation. We note that it is critical that any proposed reaction coordinate be checked with the committor distribution method we have described. This method, first suggested by Onsager⁹ and later expanded upon by Chandler and co-workers⁷, demonstrates that motion does not just accompany reaction, but is in fact a causal necessity for reaction.

LDH

The first enzyme to which we applied the TPS methodology was human heart lactate dehydrogenase¹³. A large number of reactive trajectories were gathered and they were tested for decorrelation. Examination of the trajectories made it immediately clear that, human heart LDH has as part of each reactive trajectory a compressive motion that extends across the body of the protein to cause the donor and acceptor to approach closely. This motion is shown graphically in Figure 1. Testing showed that this motion is an obligate part of the reaction coordinate. The timescale of this motion is roughly 150 femtoseconds. We thus now know that there is motion in the body of the protein that brings the donor and acceptor sites in LDH closer together. This promoting vibration, however, need not be any specially selected motion in the vibrations of the protein matrix. It could simply be the case that there are all types of diffusive heat transfer in the protein, and it just so happens that this specific mode is effective in contributing to catalysis. This is exactly the way proton transfer in solution occurs. In a completely stochastic way, donor and acceptor are caged and randomly brought into close enough proximity that reaction can occur. The question then is, are all vibrational motions in the protein “created equal,” or is the promoting vibration in some way a special outgrowth of the architecture of the protein. In some sense, this is not important to understanding how the chemistry works, but it is critically important to developing an understanding of how the enzyme is constructed.

Figure 1.

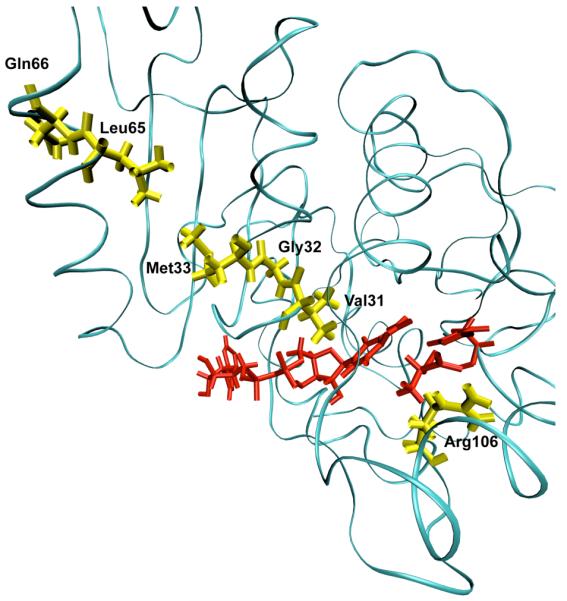
A ribbon diagram of a monomer of human heart lactate dehydrogenase demonstrating the promoting vibration. The donor and acceptor: the nicotinamide ring, and lactate are colored red. The promoting vibration residues, Val31, Gly32, Met33, Leu65, Gln66 (yellow) are compressed towards the active site bringing the NC4 of the nicotinamide ring and substrate carbon closer together while Arg106 (yellow) relaxes away locking the substrate in product formation. These residues span the entire length of the monomer to the edge of the protein. Reprinted with permission from J. Chem. Phys. B. 10.1021/jp207876k 2011

Recent work¹⁴ in our group has addressed exactly this question. In order to investigate this question we performed a numerical experiment much like that which Straub has implemented for myoglobin¹⁵. We pumped heat into the active site and monitored the temperature at residues in the promoting vibration and the rest of the protein. Figure 2 shows the result of the temperature of the solvent, the protein as a whole, and that of the promoting vibration. It is clear from these data that not only is the promoting vibration unique in terms of chemistry, it is also unique in terms of protein architecture. Thermal energy transferred from the active site is preferentially channeled through the promoting vibration. In fact in this work we were also able to show that in concentric shells in the protein, the residue(s) of the promoting vibration are statistically “hotter” than almost all other residues a similar distance from the active site. In addition, it is worth mentioning that these calculations provide a perfect experimental test for the existence of a promoting vibration. Laser spectroscopic methods are able to monitor such bration. Laser spectroscopic methods are able to monitor such temperature differences¹⁶.

Figure 2.

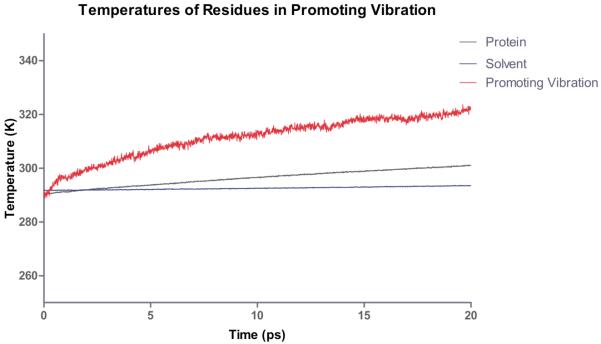
Computational heating experiment of the active site of LDH. The nicotinamide ring is heated and the temperature of the solvent, protein and residues along the promoting vibration are monitored. The promoting vibration is clearly hotter than the rest of the protein indicating a preferred direction of thermal energy transfer. Reprinted with permission from J. Chem. Phys. B. 10.1021/jp207876k 2011

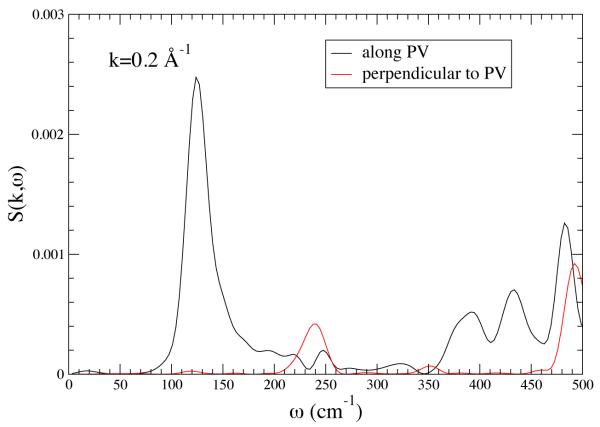
These results show that the promoting vibration in LDH is in fact a unique direction in the protein backbone, but it really does not directly inform on the mechanism for the promoting vibration transferring local heat energy from the exterior to the active site. In other words, when thermal fluctuations occur on the surface of the protein, are they preferentially channeled inward in the same way that the simulated laser radiation is channeled outward. To address this question we computed the dynamic structure factor both orthogonal to and along the direction of the promoting vibration. This quantity, which is the experimental observable in say a neutron scattering experiment, is the Fourier transform of the density-density correlation function, and along a given wavevector k , and it describes time dependent mass fluctuation. A peak at a given frequency component indicates that along that wavevector there is significant mass movement. Representative results are shown in Figure 3. It is clear that in the range of 150 wavenumbers there is a significant peak in the direction of the promoting vibration showing that density fluctuations in the appropriate time regime are located along the promoting vibration axis. This shows that the promoting vibration is in fact a “soft” direction in the protein, and vibrational energy is easily transmitted along it. There is no obvious reason for this physical property to be developed in the protein, but speculation is possible. It is certainly a possibility that the promoting vibration was in some way a selected characteristic favored by evolution. Another equally plausible (perhaps more so) explanation is this “soft” direction is a part of the protein folding pathway for the particular enzyme, and it has been co-opted for chemistry.

Figure 3.

The structure factor S(k,ω) for k = 0.2 A°⁻¹ along the PV axis (black line) and along an axis perpendicular to the promoting vibration. There is strong anisotropy. The sharpness of the peak at about 150 cm⁻¹ means that there are stable fluctuations along the PV axis for that frequency. Reprinted with permission from J. Chem. Phys. B. 10.1021/jp210347h 2011

PNP

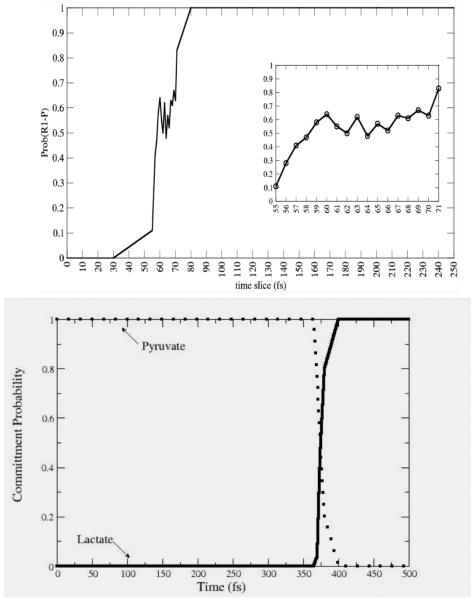
Though the dehydrogenases/reductases are central to metabolism, we must ask whether the hydrogen transfer reactions are unique in the involvement of protein dynamics in chemical barrier passage. We thus became interested in seeing if a promoting vibration was present in a very different class of enzymatic chemistry. We studied the reaction catalyzed by purine nucleoside phosphorylase: scission of the ribosidic bond in nucleosides. From a variety of experimental evidence we had reason to believe that this may well be the case. First, mutation on the surface of this protein that had absolutely no effect on the structure of the active site of the enzyme, increases the rate of on enzyme chemistry¹⁷. In addition, crystal structures of transition state inhibitors showed a unique stacking of electronegative oxygen atoms directly adjacent to the scissile ribosidic bond. Our hypothesis was that compression of this bond could sufficiently polarize the electron density as to make the base a better leaving group. A variety of computations¹⁸ confirmed this hypothesis. The reaction mechanism from an atomistic point of view was also seen to be more complex than that of the hydride transfer of LDH. Figure 4 shows the difference between a committor distribution for a complex reaction like PNP (in the top panel) and one for a direct mechanism like that for LDH (bottom panel.). It is clear that more time is spent in the transition region for PNP. It should, however be emphasized that this “long” residence time is still measured in femtoseconds! The PNP reaction is actually a 2 step process, with the first rise in committor coming from a promoting vibration compression and initial breaking of the ribosidic bond; and the second rise coming from the relative motion of the ribose ring towards the phosphate to form the ribose-1-phosphate product.

Figure 4.

Commitment probability values were calculated for both PNP (top panel) and LDH (lower panel) along sample trajectories from the reactive path ensembles for the respective enzymes. It is clear that the transition region for LDH is far shorter in time duration than for PNP, but even for PNP, the residence time is on the order of 10-20 fsecs. Reprinted with permission from J. Chem. Phys. B. 10.1021/jp207876k 2011

DHFR

There remains controversy in the field as to whether promoting vibrations on this timescale are important in what might be termed the “hydrogen atom” of hydride transfer: dihydrofolate reductase. There is a suggestion in work of Hammes-Schiffer and colleagues¹⁹ that in fact faster motions accompany reaction. What is not studied in their computations is the central issue of causality. That is, do motions of protein atoms simply happen at the same time as reaction at the active site, or are they in fact causal of reaction. In order to answer this question, we have recently begun TPS calculations on this enzyme, and have performed our non-linear kernel analysis on the separatrix generated²⁰. Analysis of the separatrix shows that there are motions that accompany reaction, but examination of the structure of the enzyme, along with the nature of the movement of the identified residues finds that the architecture of the enzyme does not permit the type of compressional vibration across the body of the enzyme through the active site to allow shortening of donor acceptor distance. The motions are subtler – those accompanying the final positioning of the substrate as it approaches the transition state. In addition, committor distribution analysis including these degrees of freedom does not show them to be causal of individual reactive events. In this case a purely statistical view of rapid motions is likely warranted. The nature of the fast timescale motion we find in DHFR is shown graphically in Figure 5. These findings speak to the fact of the lack of prior evidence for rapid motions contributing to the catalytic effect in DHFR²¹. This evidence was not found because these motions are not in fact causal and part of the reaction coordinate.

Figure 5.

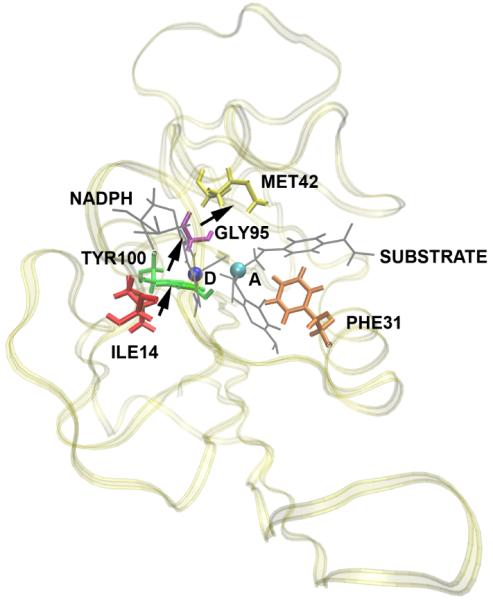
A representation of the direction of motion of residues found in DHFR to be concurrent with the reaction. D is the donor and A is the acceptor. The substrate and the NADPH molecules are shown in gray and the rest of the protein is shown as ribbons. Subsequent committor analysis showed that this motion was not in fact part of the reaction coordinate, and so not a causal part of the reaction mechanism.

Dynamics in enzymes – the extended reaction coordinate and conformational fluctuations

As was described above, the importance of conformational distributions has long been understood and accepted in enzymatic function. Hammes-Schiffer’s view of coupled motions²² fits within this realm. The idea here is simply that transitions between states is slow on the timescale of barrier passage. What we wish to understand now is first, what those transitions actually are; and second, develop an understanding of how these transitions relate to the rapid motions we have already identified in LDH and PNP. In addition, since it is obvious that actual barrier passage is quite rapid (femtoseconds to picoseconds), but the time between substrate binding and product release is many order of magnitude slower; what might actually be happening in a single instance of the enzyme during this process. Another way of describing this is we wish to extend the reaction coordinate back from the barrier closer to substrate binding, at least in a general statistical sense. The times-cales are simply far too long to just continue classical trajectories, and even if we could complete a single classical trajectory, the more important investigation is a statistical study of multiple conformations and their interconversions – not the traversal of a single reactive trajectory. We again first describe the methodologies we employ. As in the previous section, this can be skipped if one wishes to avoid the technical details.

Methodologies

The first technical difficulty presented by this endeavor is the timescales are simply too long for convention molecular dynamics. Obviously, one cannot simply take the reactive trajectories we have generated and extend them back in time long enough to view the earlier processes that occur in a catalytic event. In some fashion, then a method is needed to search the highly complex free energy surface of the protein. This then highlights the second technical difficulty, which is that this free energy surface is almost assuredly quite complex with a great many local minima. If one simply performed a Monte Carlo walk on the surface with annealing to local minima, one would find only a tiny fraction of the possible minima, and those may well not all be functionally relevant. The goal is to search the surface in such a fashion that the chemically distinct basins²³ are in at least a reasonable fashion explored.

Our method to accomplish this grew out of the recognition that in the reaction catalyzed by LDH, the distance of the donor and acceptor is central to reactivity. Thus, if one wishes to locate the functionally important conformations, they must all have the donor acceptor distance within a range that allows reaction²⁴. The specific computational tool we choose was to restrain this distance to that found in the crystal structure, and allow the rest of the protein to explore conformational space via Langevin dynamics and minimization²⁵. Once a set of candidate conformations were obtained in this fashion, they were further minimized with gradual release of the donor acceptor constraints. Cases in which the donor acceptor distance remained short were deemed catalytically competent, and those in which it grew beyond a specified cutoff were deemed to be not catalytically competent. Once these conformations were obtained, we wish to get some physical picture of how they interconvert. Again, because interconversion is a very rare event, and in fact is far too long for simple molecular dynamics, we are forced to develop a multistep process. First, a minimum free energy path between the conformations is found using a temperature dependent string method²⁶. Once this minimum free energy path is located (assumed to dominate conformation interconversion,) the actual free energy along this physical coordinate (labeled by RMSD from the starting structure²⁷,) can be found by umbrella sampling. Finally, using a simplified reaction coordinate, we can employ QM/MM sampling to obtain the chemical barrier along the conformational coordinate. These methods have been described in detail²⁵.

Conformational fluctuations in LDH

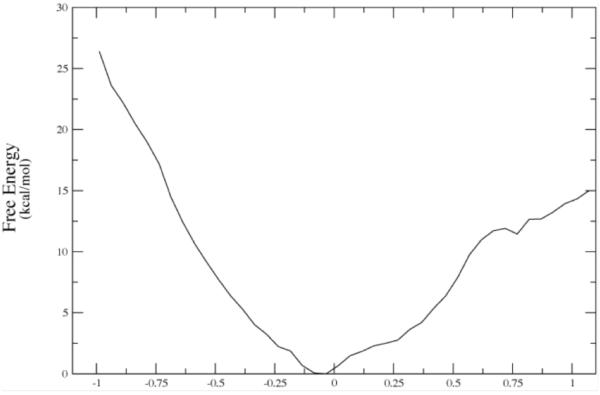
The first observation that we made was that in the vast majority of cases, release of the constraints allows the donor and acceptor to move far beyond the selected range and so to fall into conformations that are not catalytically competent. In fact, the number was far less than 10%. We have now studied this process on both sides of the chemical barrier in the reaction, and have obtained similar results. We next wanted to understand the energetics of conformational motion in the enzyme. To do this we found the minimum free energy path between all sets of basins that had low donor acceptor distance. The minimum average potential energy path and the associated free energies we discovered on a selected path are shown in Figure 6. Discovery of these abstract paths is worthwhile, but the real goal of this investigation is developing an understanding of the types of physical changes the enzyme undergoes in these longer time interconversions. These basins have relatively small but detectable differences in geometry of the active site, and this is shown graphically in Figure 7. The central difference between the various low donor acceptor distance conformations was in the positioning of the active site loop over the reactive center. It is known that reaction cannot occur in LDH if this loop is not closed, and this result shows how critical positioning of this loop is to catalysis. In fact, analysis of the paths between the short donor acceptor conformations both always involve a significant widening of the donor acceptor distance, and partial opening of the loop conformation. The effective free energy barrier to these motions from the free energy minimum (that is not reactive) was always in the 10 kcal/mol range. This is simply a statement of the rarity of these catalytically competent conformations. In addition, we have shown that at the conformational free energy maxima – the short donor acceptor distance has the lowest chemical barrier to reaction – almost zero.

Figure 6a.

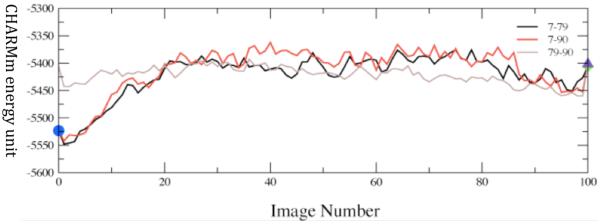
Converged average potential energies between stable, low-distance donor acceptor conformations. The energies are computed using finite temperature string methods. Numerical labels are arbitrary names given to clusters of conformations that structural analysis showed to be identical. The x-axis, which denotes conformational variation, is the string image number. Reprinted with permission from J. Chem. Phys. B. 10.1021/jp207876k 2011

Figure 7.

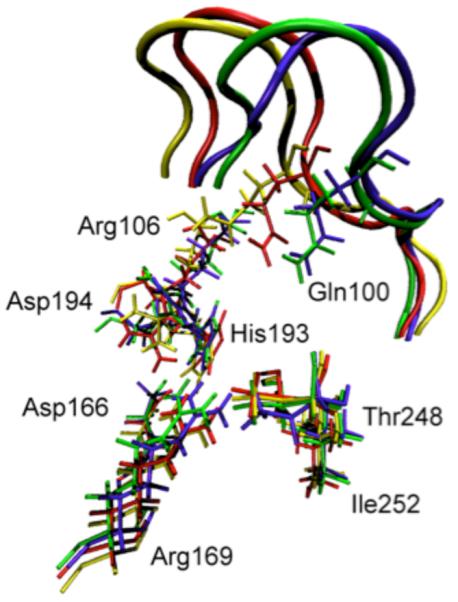
Overlay of the active site residues of 4 representative potential energy stable conformations (three of which are part of Figure 5a.) Residues belonging to the same conformation are shown with the same color. At the top of the picture, the active site loop is shown (residues 96–106, its residues 100 and 106 are shown explicitly) The 4 residues at the bottom of the figure are related to each other by a simple translation. However, the important residues His193, Arg106, Gln100 and Asp194 are being pushed by the active site loop (which has a different closed position in each of the 4 conformations), and their geometric arrangement is different in a non-trivial way among the 4 conformations. Transitions between these conformations were seen to always involve partial loop opening. Reprinted with permission from J. Chem. Phys. B. 10.1021/jp207876k 2011

Thus to summarize, we have found the nature of motions and conformations that bring the system to the catalytically competent state that have short donor-acceptor distance. These conformations are very rare and, there is a free energy barrier of entropic origin toward these competent conformations. This last finding suggests that perhaps an appropriate description of catalysis in this enzyme is a search for these rare competent conformations, followed by the reactive event that is assisted by fast sub-picosecond protein motions. More artfully put, one may describe the function of the enzyme as a conformational filter that performs a stochastic, but efficient search through conformation space that allows chemical reaction to happen in an almost barrierless fashion. The tradeoff in free energy is simply associated with the wait for the enzyme to locate a catalytically competent conformation in which there is essentially no barrier to reaction. This focuses the view of enzymatic catalysis on the probabilistic rather than energetic component. It also highlights the value of mechanistic investigations such as have been described. A great many theoretical studies of enzymatic chemistry have come to the not especially helpful conclusion that enzymes lower the free energy barrier to reaction. A completely equivalent way of stating this fact is that enzymes are catalysts and make chemical reactions go faster. The real scientific question is how do they accomplish this feat.

Rate Theories

None of the work we have described involves the computations of rates, but an important question is how our results might inform on methods of doing so. One of the most popular methods of rate calculation is transition state theory. Given the inherent complexity of a reaction in any condensed phase, especially that of an enzyme, it seems almost incredible that it can provide reasonable accuracy. In fact it often can, but involves treatments far more complex than the original theory. We now discuss both why it can provide useful rates and why modifications to the original theory are called for if it is to be applied to the types of reactions we have analyzed in this review. Finally we close this section with a description of other rigorous rate theories.

The original transition state theory or “Absolute Rate Theory” as proposed by Eyring²⁸ was based on the claim that there is an equilibrium established between the reactants and the transition state. Our TPS calculations clearly show that the transition state is far too ephemeral for such equilibrium to occur. This of course in no way invalidates the potential accuracy of TST, as it is well known that no equilibrium is needed to derive the approach^29,30 Truhlar has developed a comprehensive suite of methods that allow correction to the simplest transition state formulae³¹. There are two issues that on first glance would leave a skeptical critic thinking that TST had no chance of working. The first is simply that in a complex system the topology of the free energy surface is such that there should be many, many saddles, and so it is likely that there should be many, many transition states. In fact our calculations show convincingly that this is simply not what nature has arranged, at least as far as donor and acceptor pairs are concerned. In our calculations in LDH we have shown that though the reactive trajectories that are members of the transition path ensemble arrive at the transition state (the separatrix) in many ways, when there, they are highly similar in characteristics, and the separatrix seems to be fairly low dimensional³². The concern may be raised that the search we performed for TPS in the LDH case was simply not broad enough. We have reinitiated these calculations with a far larger perturbation in the “shooting” move. We have never found members of the stochastic separatrix for either LDH or the “more floppy” DHFR that show wide conformational divergence. It should be emphasized that this was not a required outcome. There could have been multiple highly divergent paths through the separatrix. It should also be stated that it is always possible that the Monte Carlo sampling of TPS is incomplete in the cases we have studied, but given our attempts to find other regions of trajectory space have all failed, we suppose this not to be the case.

The second question one may pose is: if there is a promoting vibration, and a multidimensional reaction coordinate, how does one identify a transition state in low dimension. There still is a bottleneck; it simply is embedded in a higher dimensional space. The crucial point here is that the promoting vibrations we have found are motions on a similar timescale to that of barrier passage. They are not so fast that they can be simply averaged over to obtain a single free energy barrier, and they are not so slow that they can be assumed fixed for the purposes of rate calculation. In the language of transition state theory, these dynamics effect both the location of the TS and the height of the free energy barrier. We have discussed these issues and the relation to Grote-Hynes theory previously³³. In the Generalized Langevin Equation (GLE) formulation we presented in Reference 32, the promoting vibration creates a GLE with a fluctuating reaction coordinate potential (i.e. the simple reaction coordinate has a free energy barrier modulated by another degree of freedom on a similar timescale to its own dynamics.) The best analogy to these models in TST would be found in the ensemble averaged variational transition state methods Truhlar and co-workers have devised³⁴. Barriers in which the promoting vibration had strongly compressed the donor acceptor would have a lower probability in the ensemble of rates but have a greater contribution to the rate. In this view of TST, one cannot locate a singe TS that accurately dominates the rate computation. It should be emphasized that this is a mathematical tool and not necessarily indicative of the actual stochastic separatrix.

One erroneous argument that has been made against the importance of dynamics in enzymatic chemistry is that since the TST recrossing statistic (κ) for enzymatic reactions has always been computed to be close to 1, there can be no dynamic effects. Dynamical effects such as promoting vibrations raise the rate of reaction. Their presence or absence could never be detected by the value of κ - as stated above, they are part of the free energy. For example we have extended our barrier crossing calculations for many nanoseconds, and have never seen a recrossing event – we are in total agreement that κ is 1.

Another question that has been raised is how much of an effect a fast motion such as the promoting vibration may have on the free energy barrier. Some years ago, a rough calculation on HLADH suggested that the promoting vibration lowers the barrier by 30% over the static case³³. Clearly this will be significantly different from system to system. There is no clear way to test this number – there is not a simple mutation that breaks the promoting vibration, but we are investigating this possibility with experimental collaborators. The results described here in no way invalidate the possible overriding importance of such well-described effects as dipolar stabilization. On the other hand, we did try to initiate reactive trajectories in LDH with the promoting vibration restrained. This resulted in no reactive trajectories. This was not published because the restrained unsuccessful trajectories do not form a recognizable ensemble distribution.

Another point of contention that has been raised is how a motion so much faster than the rate of turnover could be involved in catalysis. This is in fact not surprising given that chemistry is almost never rate limiting in enzymatically-catalyzed reactions. Active sites are optimized to catalyze chemistry at a far greater rate than turnover, and it is likely that turnover is regulated for the biological system of interest. In a similar fashion, one would not be surprised that there is almost perfect charge complementarity in many active sites even though the chemistry this charge distribution catalyzes happens at a far faster rate than release of product from the enzyme. While enzymes never seem to have rates of turnover as fast as possible, they do seem to have individual steps that are highly optimized for their function. Whether that function is chemical change or substrate binding and release at a physiologically relevant rate.

A final rate theory we would be remiss to not mention is the forward flux formulation of Chandler³⁵. This is of course an exact formulation of the rate, much like the flux correlation formulation³⁶ is a formally exact method to compute the quantum rate. In these correlation function theories, TST like results are recovered from a t→0 limit. The usefulness of the result depends on the choice of the dividing surface, as in TST. To obtain an accurate result in the enzymatic case, this dividing surface would have to be found for the full reaction coordinate, not simply particle transfer. So if there were a promoting vibration as part of the reaction coordinate, it would be included in the dividing surface search. It should be emphasized that such an approach does not guarantee accuracy – obviously the short time limit of the correlation functions involved is a drastic approximation to the rigorous full formulation.

Conclusions and future directions

It is time to see where this field stands 15 years after our suggestion that rapid motions of the protein matrix are in fact part of the reaction coordinate. From a computational perspective, the proposition seems well proven for both LDH and PNP on the basis of TPS computations followed by reaction coordinate identification. The continuing consternation in some quarters that the timescale of the promoting vibration is so much faster than the timescale of enzymatic turnover should not cause worry – in the cases we study the rate of enzymatic turnover is never limited by chemistry. In fact the rate of chemical barrier passage is very rapid, and on the same timescale as the promoting vibration. This perhaps begs the question of how the promoting vibration was “fashioned” by the evolutionary process because chemistry is not rate limiting, but the same is true for any aspect of chemistry in enzymes. Even though in the enzymes we observe today, chemistry is almost never rate limiting, active sites have been carefully tuned to facilitate catalysis.

A continuing question is how these propositions can be tested experimentally. A method often used in mechanistic enzymology is mutation. While this is certainly a fairly blunt edged instrument for this question, it is a viable means of testing. As such we are currently performing TPS calculations on a number of mutants in which the promoting vibration has been disrupted. Interpretation of such results is always difficult, because mutation inside the protein seldom changes only one aspect of the structure, but it is to be hoped that such results will eventually inform on the involvement of promoting vibrations in the function of enzymes.

The Schramm group has developed a recent, highly promising, experimental technique³⁷. Their idea was to create a “heavy” enzyme in which all non-exchangeable protein atoms are replaced by their heavy isotopic analogues. Termed a “Born-Oppenheimer” enzyme (because there is no change in potential energy, only vibrational structure,) they have found changes of 30% in the rate of chemistry in the heavy enzyme. We are currently analyzing TPS calculations on the heavy enzyme to illuminate the specific changes in fast motion that causes this change in rates.

Finally, it is worthwhile to discuss future directions for this work. One critical issue is that of quantum dynamics in the reactive events. The TPS calculations we have done are completely classical in atomic dynamics. It has been suggested for many years that tunneling is critically important to a variety of hydride transfer enzymes³⁸, and so an important goal is the development of approaches that allow inclusion of tunneling in TPS simulations. Because TPS is an inherently classical phase space method, an approximate inclusion of quantum dynamics is needed. We have suggested employing centroid molecular dynamics as such a method³⁹, and are currently developing the capability to pursue such computations. The second crucial area we would hope to see addressed is the inclusion of protein dynamics in the protein design paradigm. The ab initio creation of artificial enzymes is obviously decades away, but limited enzyme engineering has proven possible⁴⁰. Since static design pictures, such as the catalytic antibody approach⁴¹, have not been able to come close to matching natural enzyme’s catalytic proficiency, it is worthy of speculation as to whether the subject of this volume – protein dynamics – could provide some of the missing functionality in such approaches. It is obviously difficult to envision exactly how these concepts could be made part of protein engineering design principles, but this may well be the next frontier for catalysis and protein dynamics.

Figure 6b.

The converged free energy corresponding to one of the potential energy curves above (red curve labeled 7-90.) Note that the minima in average potential energy are on the edges of a rising free energy. The minima on Figure 6a given in string images correspond to −.50 and + .69 angstroms in Δ-RMSD units along the string coordinate on 6b. Reprinted with permission from J. Chem. Phys. B. 10.1021/jp207876k 2011